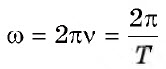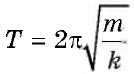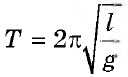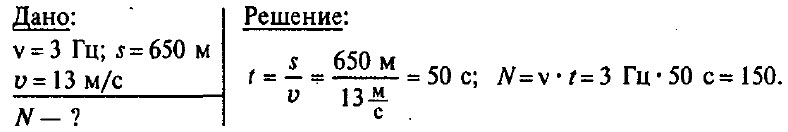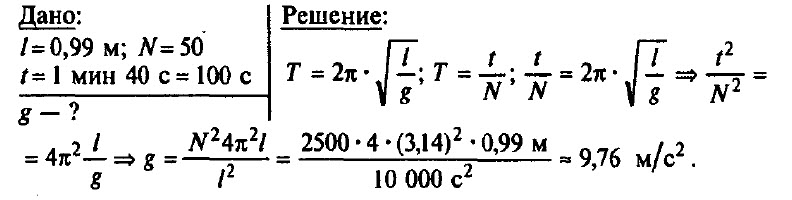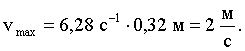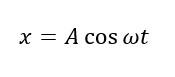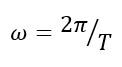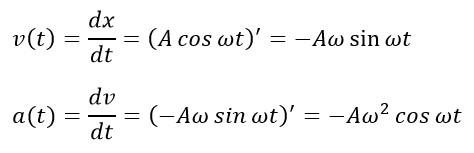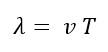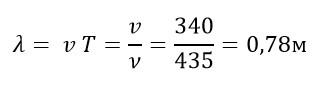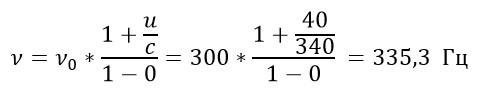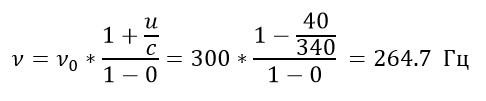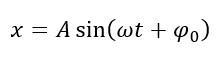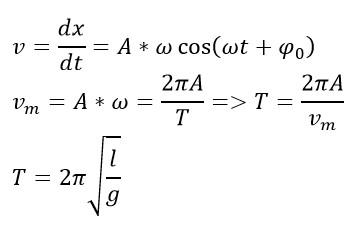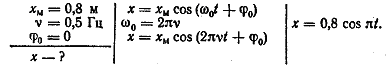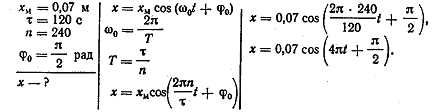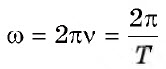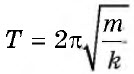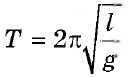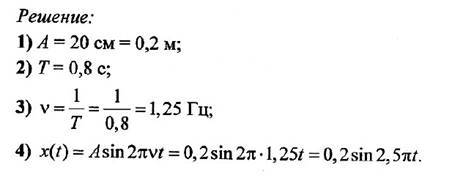Как найти амплитуду колебаний задачи

Задачи на Механические колебания с решениями

Формулы, используемые на уроках «Задачи на Механические колебания».

Название величины	Обозначение	Единица измерения	Формула
Амплитуда колебаний	A	м
Период колебаний	T	с	T = 1 / v ; T = t / N
Частота колебаний	v	Гц	v = 1 / T ; v = N / t
Число колебаний за какое-то время	N		N = t /T ; N = vt
Время	t	с	t = NT ; t = N / v
Циклическая частота колебаний	ω	Гц
Период колебаний пружинного маятника	T	c
Период колебаний математического маятника	T	c
Уравнение гармонических колебаний			x(t) = Asin(ωt+φ0)

---

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

---

Задача № 1.
 Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.

---

Задача № 2.
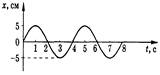
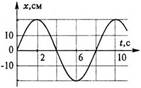
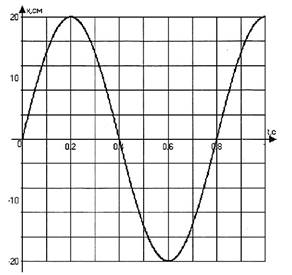
 На рисунке изображен график зависимости координаты от времени колеблющегося тела.

По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.

---

Задача № 3.
 Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?

---

Задача № 4.
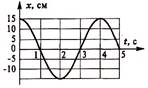
 Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.

---

Задача № 5.
 Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с².

---

Задача № 6.
 Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.

---

Задача № 7.
 Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?

---

Задача № 8.
 Гармоническое колебание описывается уравнением 
 Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?

---

Задача № 9.
 Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π² = 9,87.)

---

Задача № 10.
  ОГЭ
 Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?

---

Задача № 11.
   ЕГЭ
 Два математических маятника за одно и то же время совершают — первый N₁ = 30, а второй — N₂ = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?

---

Краткая теория для решения Задачи на Механические колебания.

---

Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия:

• Перейти к теме: ЗАДАЧИ на 
• Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

Примеры решения задач

1. Исходя из осциллограммы колебательного процесса, представленного на рисунке 10, определите амплитуду A, период T и частоту  данных колебаний.

Р е ш е н и е

Максимальное отклонение колеблющейся точки (см. рис. 10) составляет

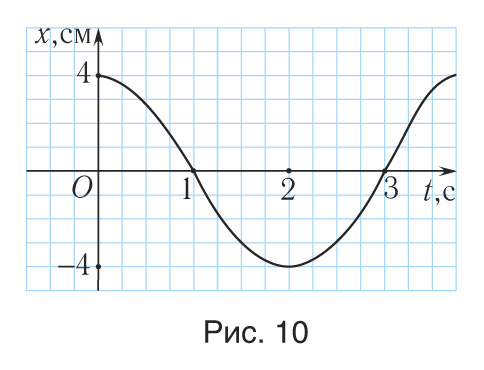
х_max  =  А  =  4,0 см.

Период колебаний — это время, за которое тело совершает одно колебание, т. е. точка опять окажется в положении с координатой  х_max  =  А  =  4,0 см. Следовательно, Т = 4,0 с.

Частота колебаний

Гц

О т в е т: А = 4,0 см, Т = 4,0 с,  = 0,25 Гц. 

2. Материальная точка совершает гармонические колебания по закону: (м) 

Определите амплитуду A, частоту , период T колебаний, координату x точки в момент времени
t₁ = 5,0 c.

Дано:
(м)
t₁ = 5,0 c

A — ? T — ?  — ?

Решение: 

Координата точки, совершающей гармонические колебания, определяется соотношением:

                                                          (м)  

Тогда из условия задачи находим, что амплитуда A = 0,40 м, частота

                                                                                                                  .

период

                                                                                                       .

Координата точки х при t₁ = 5,0 c равна

                                                                                                     .

О т в е т: A = 0,40 м, v = 4,0 Гц, T = 0,25 с, х = 0,20 м.

Примеры решения задач по колебаниям и волнам

Задача
1. Материальная
точка массой 10 г совершает гармоническое
колебание с периодом Т=1 с. Определить
амплитуду колебаний, максимальную
скорость и ускорение колеблющейся
точки, если полная энергия точки равна
0,02 Дж.

Дано:
Найти:

Решение:
Уравнение гармонического колебания
запишем в виде:

(1)

где х – смещение
материальной точки от положения
равновесия;
А – амплитуда;
ω – циклическая
(круговая) частота;
t – время;
α –
начальная фаза.

Скорость колеблющейся
точки среды определяется как первая
производная от смещения по времени:

Максимальное
значение скорости:

Ускорение точки
определяется как производная от скорости
по времени:

Максимальное
значение ускорения:

Полная энергия
складывается из кинетической и
потенциальной энергии и равна максимальной
потенциальной или максимальной
кинетической энергии:

Круговая частота
связана с периодом:
.
Тогда:

Из этого выражения
найдем амплитуду:

Проверим размерность:

Произведем
вычисления:

Ответ:  
А = 0,32 м,  V_max
= 2 м/с,  a_max
= 12,6 м/с²

Задача
2. Найти
амплитуду и начальную фазу гармонического
колебания, полученного от сложения
одинаково направленных гармонических
колебаний, данных уравнениями: x₁
= 0,02cos (5πt + π/2) м и x₂
= 0,03cos (5πt + π/4) м. Построить векторную
диаграмму сложения амплитуд.

Дано:     
  x₁
= 0,02cos (5πt + π/2)

         x₂
= 0,03cos (5πt + π/4)

Найти:  
А, α. Дать векторную диаграмму.

Решение:
Построить векторную диаграмму – это
значит представить колебание в виде
вектора, длина которого равна амплитуде
колебаний, а угол наклона к оси абсцисс
равен начальной фазе колебаний. При
вращении вектора с угловой скоростью
ω проекция его конца на ось будет
совершать гармонические колебания.

Из условия задачи
 А₁=0,02
м = 2 см,  α₁=
π/2,

      А₂=0,03
м = 3 см,  α₂
= π/4.

Векторная диаграмма
изображена на рисунке 5.

Рис.
5

Результирующую
амплитуду найдем по теореме косинусов:

Начальная фаза
результирующего колебания находится
из формулы:

Вычисления:

Ответ:  
А = 4,6 м;  α=62^о
46′.

Задача
3. Период
затухающих колебаний Т = 4 с, логарифмический
декремент затухания χ = 1,6; начальная
фаза равна нулю. Смещение точки в
начальный момент времени равно 4,5 см.
Написать уравнение колебаний и найти
смещение точки в момент времени спустя
период.

Дано:
Найти:

Решение:
Уравнение затухающих колебаний имеет
вид:

(1)

где β – коэффициент
затухания,
ω – частота затухающих
колебаний.

Найдем  ω:

Логарифмический
декремент затухания связан с коэффициентом
затухания:
.
Отсюда:

Подставим ω, β, α
в (1) и найдем смещение:

Для начального
момента времени при t = 0:

Уравнение колебаний
имеет вид:

Смещение
в момент
:

Ответ:

4. Оптика

Оптика
– это раздел физики, изучающий природу
светового излучения, его распространение
и взаимодействие с веществом. Световые
волны – это электромагнитные волны.
Длина волны световых волн заключена в
интервале [0,4·10^-6
м ÷ 0,76·10^-6
м]. Волны такого диапазона воспринимаются
человеческим глазом.Свет распространяется
вдоль линий, называемых лучами. В
приближении лучевой (или геометрической)
оптики пренебрегают конечностью длин
волн света, полагая, что λ→0. Необходимо
изучить законы геометрической оптики
(в контрольной работе это задачи 401-410).

Геометрическая
оптика во многих случаях позволяет
достаточно хорошо рассчитать оптическую
систему. Простейшей оптической системой
является линза (в контрольной работе
это задачи 411-420).

При изучении
интерференции света следует помнить,
что интерференция наблюдается только
от когерентных источников и что
интерференция связана с перераспределением
энергии в пространстве. Здесь важно
уметь правильно записывать условие
максимума и минимума интенсивности
света и обратить внимание на такие
вопросы, как цвета тонких пленок, полосы
равной толщины и равного наклона (в
контрольной работе это задачи 421-430).

При изучении
явления дифракции света необходимо
уяснить принцип Гюйгенса-Френеля, метод
зон Френеля, понимать, как описать
дифракционную картину на одной щели и
на дифракционной решетке (в контрольной
работе это задачи 431-440).

При изучении
явления поляризации света нужно понимать,
что в основе этого явления лежит
поперечность световых волн. Следует
обратить внимание на способы получения
поляризованного света и на законы
Брюстера и Малюса (в контрольной работе
это задачи 441-450).

При изучении темы
“Взаимодействие света с веществом”
необходимо рассмотреть следующие
явления.
Во-первых, при распространении
световой волны в веществе скорость
зависит от длины волны (или частоты).
Это явление называется дисперсией
света. Изучение явления дисперсии света,
т.е. зависимости показателя преломления
от длины волны, посвящены задачи 451-460 в
контрольной работе.
Во-вторых, необходимо
изучить такие явления, как поглощение
света и рассеяние света.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Трепещите и радуйтесь: сегодня занимаемся решением задач по теме «Механические колебания и волны». 

И конечно, подписывайтесь на наш телеграм-канал, чтобы получать полезную рассылку каждый день. Не важно, технарь вы, или гуманитарий – интересно будет всем.

Задачи по теме механические колебания и волны с решениями

Здесь мы постарались собрать несколько типовых и при этом разноплановых задач на механические колебания.

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Задача №1. Гармонические колебания

Условие

Точка совершает колебания по гармоническому закону. Амплитуда колебаний равна 5 см, а период – 4 секунды. Каковы максимальная скорость колеблющейся точки и её ускорение?

Решение

Запишем уравнение гармонических колебаний:

Здесь омега – циклическая частота:

 Скорость и ускорение точки вычисляются по формулам механики:

Модули ускорения и скорости максимальны тогда, когда значение тригонометрической функции в выражениях равно единице:

 Ответ: 8 см/с; 12 см/с^2.

Задача №2. Длина волны

Условие

Какова длина волны основного тона ноты «ля» частотой 435 Гц? Скорость звука в воздухе принять равно 340 м/с.

Решение

Известно, период – величина, обратная частоте. А длина волны связана с периодом колебаний и скоростью их распространения соотношением:

 Тогда можно записать:

Ответ: 0,78 м.

Задача №3. Затухающие колебания

Условие

Груз массой 0,2 кг подвешен на пружине и помещен в масло. Коэффициент сопротивления r в масле равен 0,5 кг/с. Коэффициент жесткости пружины k равен 50 Н/м. Найти частоту затухающих колебаний груза.

Решение

Циклическая частота затухающих колебаний можно определяется по формуле:

Теперь определим обычную частоту:

Ответ: 2,51 Гц.

Задача №4. Эффект Доплера

Условие

Гудок неподвижного электровоза дает сигнал с частотой 300 Гц. Какова кажущаяся частота гудка для пассажира, который в другом поезде приближается к электровозу со скоростью 40 м/с? Удаляется от него с той же скоростью?

Подробнее про эффект Доплера читайте в отдельной статье нашего блога.

Решение

Формула, связывающая испускаемую и воспринимаемую частоты при эффекте Доплера:

Здесь с – скорость волн в среде (в нашем случае скорость звука), u – скорость приемника относительно среды, v – скорость источника относительно среды. Когда поезд приближается:

При движении от источника звука:

Ответ: 335,3 Гц; 264,7 Гц.

Задача №5. Математический маятник

Условие

Математический маятник колеблется с амплитудой А и максимальной скоростью Vm. Найти длину маятника l.

Решение

Запишем уравнение гармонических колебаний математического маятника:

Взяв первую производную, получим скорость и выразим период:

В итоге получаем:

Ответ: см. решение.

Вопросы на тему «Механические колебания и волны»

Вопрос 1. Что такое волна?

Ответ. Волна – это колебания, распространяющиеся в среде с течением времени. Волны могут иметь разную физическую природу, они бывают механические, электромагнитные и т.д.

Вопрос 2. Что такое колебание?

Ответ. Колебание – процесс изменения состояний системы, в той или иной степени повторяющийся во времени.

Принципиальное отличие волн от колебаний: при колебаниях отсутствует перенос энергии.

Вопрос 3. Приведите примеры механических колебаний в повседневной жизни.

Ответ. Механические колебания:

• маятник часов;
• раскачивающиеся качели;
• вибрации гитарной струны;
• качка корабля на волнах и т.д.

Вопрос 4. Приведите примеры механических волн.

Ответ. Механические волны:

• звук;
• морские волны;
• сейсмические волны.

Вопрос 5. Какие колебания называются гармоническими?

Ответ. Гармонические колебания – это колебания, в которых изменение какой-либо физической величины происходит по закону синуса или косинуса.

Держите под рукой полезные формулы, которые пригодятся при решении задач. А перед тем как начать самостоятельно решать задачи, рекомендуем ознакомиться с универсальной памяткой.

Нужна помощь в решении задач и прочих студенческих заданий? Профессиональный студенческий сервис готов оказать ее в любое время, обращайтесь за консультациями к проверенным специалистам.

.09.Цели урока:

а)  образовательная:  проверить  усвоение  физических  формул  и  умений
   брать  первую  и

вторую  производную  от  тригонометрических
 функций,  формировать  умения  решать

расчетные и качественные задачи,
анализировать графики и физические закономерности.

б)  развивающая:  развивать  творческое
 мышление,  развивать  умение  применять  знания  в

новой  нестандартной ситуации, развивать
умение анализировать, делать выводы.

в)  воспитательная: 
воспитывать
 доброжелательное
 отношение  друг  к  другу,

взаимопонимание и взаимопомощь. 

09.11.2021г.     11 класс

Тема урока «Решение задач по теме:
Гармонические колебания».

Цели урока:

образовательная: проверить  усвоение  физических 
формул  и  умений    брать  первую  и

вторую  производную  от 
тригонометрических  функций,  формировать  умения  решать

расчетные и качественные задачи,
анализировать графики и физические закономерности.

развивающая: развивать  творческое  мышление, 
развивать  умение  применять  знания  в

новой  нестандартной ситуации,
развивать умение анализировать, делать выводы.

воспитательная: воспитывать  доброжелательное 
отношение  друг  к  другу,

взаимопонимание и взаимопомощь. 

Выполнила: Керимова Ирина С.

                                     
                    Ход урока:

       I.           
Организационный
момент урока.

    II.           
Организация внимания учащихся.

Тема
нашего урока: Решение задач «Гармонические
колебания».                                    Сегодня
мы вспомним понятия периода, частоты, амплитуды колебаний и научимся применять
эти понятия  при решении задач.

 III.           
Повторение
пройденного материала

1)     
Прежде
чем перейти к решению задач, предлагаю проверить как вы к этому готовы.

Решить
кроссворд

Вопросы	Ответы
По вертикали: 1.  Греческая буква, обозначающая частоту колебаний 2.  Отклонение точки от положения равновесия 4.  Величина, от которой зависит состояние колеблющейся точки 6. Частота колебаний. 7. Время одного полного колебания. 8. Величина пропорциональная смещению	1. Омега. 2. Смещение 4. Фаза 6.  Циклическая. 7. Период 8. Ускорение
По горизонтали: Колебания, совершаемые по закону синуса 5. Вид механической энергии 9. Вид механической энергии. 10. Величина, от которой зависит кинетическая энергия колеблющейся точки 11. Максимальное положение смещения точки от положения равновесия. 12. Единица измерения смещения 13. Единица измерения частоты	3. Гармонические. 5. Потенциальная. 9. Кинетическая. 10. Скорость 11. Амплитуда 12. Метр 13. Герц

 IV.           
Решение
задач.

1)     
Алгоритм
решения задач
(есть у каждого)

1.      Внимательно
прочитать условие задачи и увидеть мысленным взором конкретную 
ситуацию, представленную в задаче.

2.      Записать
кратко  условие задачи, перейти, если необходимо в систему СИ.

3.      (А
вот теперь!) Проанализировать условие задачи на предмет, что известно в задаче
и что надо найти.

4.      Составить
систему уравнений и решить ее относительно неизвестных.

5.      Вывести
размерность в полученных формулах, сделать расчет ответов.

6.      Проанализировать
ответы (эта часть решения задачи хоть и заключительная, но не самая легкая:
необходимо рассмотреть, для каких случаев работает полученная формула, когда
ответ не имеет физического смысла и реален ли полученный численный ответ).                                            

2)      Работа с текстом.

А.   
Рассмотрите
график и заполните пропущенные записи в тексте.    

График колебания: t – время в
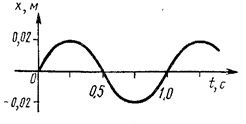
секундах;  X –смещение в
метрах.                          

По графику
колебаний  определяют амплитуду смещения и период

(Х _м =
0,02 м = 2см;     Т= 1 с).                                                  

Частоту
колебаний   рассчитывают по формуле:   (v =;   v =  = 1 Гц)  (1 колебание за 1 секунду).

Б.      По графикам
определить амплитуду смещения, период. Рассчитать по формуле частоту. Решение
оформить следующим образом, графики не рисовать:

График 1	График  2	График  3
Х м = 5см Т = 4с v = 0,25 Гц	Х м = 20см Т = 8с v = 0,125 Гц	Х м =15см Т = 4с v = 0,25Гц

3)      Задачи

1.       Напишите
уравнение гармонических колебаний, если частота равна 0,5 Гц, амплитуда 80 см.
Начальная фаза колебаний равна нулю.

Решение: 

2.      Напишите уравнение гармонических колебаний, если амплитуда
равна 7 см и за 2 мин совершается 240 колебаний. Начальная фаза колебаний равна
π /2 рад.

Решение: 

3.      Ай да Фуко (данная
презентация готовится учащимся класса)

– Как использовался математический маятник для
доказательства вращения Земли?

          
Одно из самых наглядных доказательств было найдено французским физиком Фуко. 
В  1850  году  он  подвесил  огромный маятник  в  парижском  Пантеоне-зале  с 
очень  высоким  куполом. Длина подвеса была равна 67 м. Масса шара 28 кг.
Маятник качался несколько часов подряд. Снизу шар имел острие, а на полу
насыпали кольцом  грядочку  из  песка.  Маятник раскачивали.  Острие  стало
оставлять  на  песке  бороздки.  Через  несколько  часов  он  чертил бороздки 
в  другой  части  грядочки.  Плоскость  колебаний  маятника словно
поворачивалась по часовой стрелке. На самом деле плоскость

колебаний маятника
сохранялась.  Вращалась  планета,  увлекая  за собой  Пантеон  с  его  куполом 
и  песочной  грядкой  (на  экране  фото маятника Фуко).

– Был ли в России повторен опыт Фуко?

Опыт Фуко был
повторен в Исаакиевском соборе в Петербурге.

Маятник совершал   
3 колебания за минуту.  Исходя  из  этих  данных

вы можете оценить
длину маятника, следовательно, и высоту

Исаакиевского
собора.

4.     
Первый маятник Фуко (1891, Париж) имел период колебаний 16 с. Определите
длину маятника. Примите g =9,8 м/с².

Решение:          

Т=16с            

g=9,8м/с²           

                        l=

l –?

   
V.           
Домашнее
задание

·        
Повторить
тему из математики «Производные функции»;

·        
Р№
429, 430

·        
§§18-22

 VI.           
Подведение итогов урока.

Название величины	Обозначение	Единица измерения	Формула
Амплитуда колебаний	A	м
Период колебаний	T	с	T = 1 / v ; T = t / N
Частота колебаний	v	Гц	v = 1 / T ; v = N / t
Число колебаний за какое-то время	N		N = t /T ; N = vt
Время	t	с	t = NT ; t = N / v
Циклическая частота колебаний	ω	Гц
Период колебаний пружинного маятника	T	c
Период колебаний математического маятника	T	c
Уравнение гармонических колебаний			x(t) = Asin(ωt+φ0)

 Шарик на нити совершил 60
колебаний за 2 мин. Определите период и частоту колебаний шарика.

Задача № 2.  На рисунке изображен
график зависимости координаты от времени колеблющегося тела.

По графику определите: 1) амплитуду
колебаний; 2) период колебаний; 3) частоту колебаний; 4)
запишите уравнение координаты.

Цели урока:

а)  образовательная:  проверить  усвоение  физических  формул  и  умений
   брать  первую  и

вторую  производную  от  тригонометрических
 функций,  формировать  умения  решать

расчетные и качественные задачи,
анализировать графики и физические закономерности.

б)  развивающая:  развивать  творческое
 мышление,  развивать  умение  применять  знания  в

новой  нестандартной ситуации, развивать
умение анализировать, делать выводы.

в)  воспитательная: 
воспитывать
 доброжелательное
 отношение  друг  к  другу,

взаимопонимание и взаимопомощь. 

Скачано с
www.znanio.ru