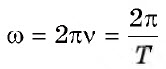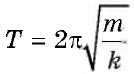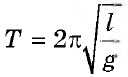Уравнение амплитуды скорости и амплитуды ускорения
• Т — период колебаний — минимальный промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание
• ω0 — циклическая (круговая) частота — число полных колебаний за 2π секунд:
Частота и период гармонических колебаний не зависят от амплитуды. Изменяя амплитуду колебаний груза на пружине, мы не изменяем частоту колебаний этой системы.
Колебания характеризуются не только смещением, но и скоростью vx, и ускорением ax. Если смещение описывается уравнением x = A cos(ω0t + φ), то, по определению, .
В этих уравнениях vm =ω0A — амплитуда скорости; am =ω0 2 A — амплитуда ускорения.
Из уравнений (2.1.5) и (2.1.6) видно, что скорость и ускорение также являются гармоническими колебаниями.
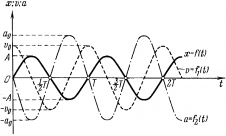
2.1.3. Графики смещения скорости и ускорения
Параметры колебаний запишем в виде системы уравнений:
Из этой системы уравнений можно сделать следующие выводы:
• скорость колебаний тела максимальна и по абсолютной величине равна амплитуде скорости в момент прохождения через положение
Гармонические колебания.
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями.
Например, в случае механических гармонических колебаний:.
В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 +π/2 полностью совпадают.
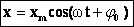
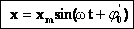
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0.
Выражение, стоящее под знаком cos или sin, наз. фазой колебания: 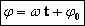 .
.
Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.
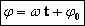
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).
Скорость и ускорение при гармонических колебаниях.
Согласно определению скорости, скорость – это производная от координаты по времени 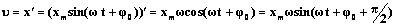
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2.
Величина 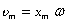 — максимальная скорость колебательного движения (амплитуда колебаний скорости).
— максимальная скорость колебательного движения (амплитуда колебаний скорости).
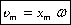
Следовательно, для скорости при гармоническом колебании имеем: 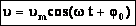 , а для случая нулевой начальной фазы
, а для случая нулевой начальной фазы  (см. график).
(см. график).
Согласно определению ускорения, ускорение – это производная от скорости по времени:
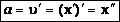 — вторая производная от координаты по времени. Тогда:
— вторая производная от координаты по времени. Тогда: 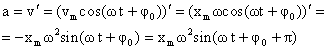 .
.
Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе).
Величина 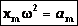
— максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: 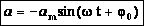 , а для случая нулевой начальной фазы:
, а для случая нулевой начальной фазы: 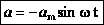 (см. график).
(см. график).
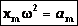
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения).
Сравним выражения для смещения и ускорения при гармонических колебаниях:
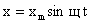 и
и 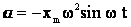 .
.
Можно записать:  —
—
т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота.

Часто бывает удобно записывать уравнения для колебаний в виде: 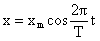 ,
,
где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: 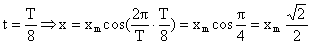 . Аналогично для скорости и ускорения.
. Аналогично для скорости и ускорения.
I. Механика
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.


Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени


График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой  .
.
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса


Если колебание описывать по закону синуса


Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле


Как получить зависимости v(t) и a(t)
Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).
При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.
источники:
http://www.eduspb.com/node/1780
http://fizmat.by/kursy/kolebanija_volny/garmonicheskoe
Зависимость
скорости точки, совершающей гармонические колебаний, от времени в единицах СИ
определяется уравнением v(t) = 1,2 cos 50t (м/с). Определите амплитуду смещения точки.
Решение.
Смещение
точки от положения равновесия при ее гармонических колебаниях вдоль оси OX описывается следующей формулой.
A – амплитуда смещения,
ω – циклическая частота колебаний, j0 – их начальная фаза. Проекция скорости точки тогда равна v(t).
В
этой формуле vmax = Aω –
амплитуда скорости точки. Отсюда A = vmax/ω.
Сравнивая
общее и заданные в условии задачи выражения для v(t), видим, что vmap
= 1,2 м/с, ω = 50 рад/с. Тогда A = 1,2/50 м = 2,4•10-2
м = 24 мм.
Ответ:
A
= 24 мм.
Источник: Подготовка к тестированию по физике. Шепелевич. В. Г.
Определить амплитуду колебаний
io
Знаток
(416),
закрыт
12 лет назад
Тело совершает гармонические колебания. Период колебаний Т=0.15 с., максимальная скорость V=8м/с. Определить амплитуду. Подскажите двоешнику пожалуйста…
Юлия Даниленко
Знаток
(411)
12 лет назад
: Амплитуда – модуль максимального отклонения тела от положения равновесия. Например:
амплитуда для механического колебания тела (вибрация) , для волн на струне или пружине — это расстояние и записывается в единицах длины;
0,15 * 8 = 1,2м
Задачи на Механические колебания с решениями
Формулы, используемые на уроках «Задачи на Механические колебания».
Название величины |
Обозначение |
Единица измерения |
Формула |
Амплитуда колебаний |
A |
м |
|
Период колебаний |
T |
с |
T = 1 / v ;T = t / N |
Частота колебаний |
v |
Гц |
v = 1 / T ;v = N / t |
Число колебаний за какое-то время |
N |
N = t /T ;N = vt |
|
Время |
t |
с |
t = NT ;t = N / v |
Циклическая частота колебаний |
ω |
Гц |
|
Период колебаний пружинного маятника |
T |
c |
|
Период колебаний математического маятника |
T |
c |
|
Уравнение гармонических колебаний |
x(t) = Asin(ωt+φ0) |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.

Задача № 2.
На рисунке изображен график зависимости координаты от времени колеблющегося тела.

По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.

Задача № 3.
Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?

Задача № 4.
Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.


Задача № 5.
Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с2.

Задача № 6.
Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.

Задача № 7.
Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?
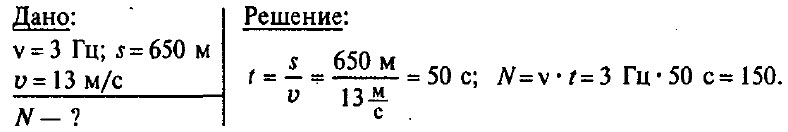
Задача № 8.
Гармоническое колебание описывается уравнением
![]() Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?
Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?

Задача № 9.
Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π2 = 9,87.)
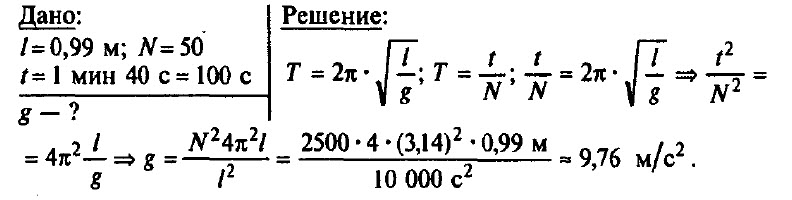
Задача № 10.
ОГЭ
Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?

Задача № 11.
ЕГЭ
Два математических маятника за одно и то же время совершают — первый N1 = 30, а второй — N2 = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?

Краткая теория для решения Задачи на Механические колебания.


Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Амплитуда скорости груза, теория и онлайн калькуляторы
Амплитуда скорости груза
Скорость груза пружинного маятника
Рассмотрим пружинный маятник, который представляет собой груз массой $m$, подвешенный на пружине, которую считают абсолютно упругой (ее коэффициент упругости равен $k$). Пусть груз движется вертикально, движения происходят под воздействием силы упругости пружины и силы тяжести, если система выведена из состояния равновесия и предоставлена самой себе. Массу пружины считаем малой в сравнении с массой груза. Начало отсчета поместим на оси X (ось направлена вниз) в точке равновесия груза.
Пружинный маятник является примером гармонического осциллятора. Колебания гармонического осциллятора служат важным примером периодического движения и являются моделью во многих задачах физики. Колебания такого груза можно считать гармоническими и описывать при помощи уравнения:
[xleft(tright)=A{cos left({omega }_0t+alpha right)left(1right), }]
где $xleft(tright)$ – смещение груза от положения равновесия в момент времени ($t$); ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$- амплитуда колебаний; ${(omega }_0t+alpha )$ – фаза колебаний; $alpha $ – начальная фаза колебаний.
Скорость колебаний груза при этом найдем как:
[frac{dx}{dt}=-A{omega }_0{sin left({omega }_0t+alpha right)left(2right). }]
Амплитудой скорости колебаний груза при этом является величина равная:
[{left(frac{dx}{dt}right)}_{max}=A{omega }_0left(3right).]
Для пружинного маятника амплитуда колебаний скорости груза равна:
[{left(frac{dx}{dt}right)}_{max}=Asqrt{frac{k}{m}}left(4right).]
Амплитуда скорости колебаний математического и физического маятников
Будем считать математический маятник шариком (грузом), подвешенным на длинной невесомой и нерастяжимой нити. Математический маятник является примером гармонического осциллятора, совершающим колебания, которые описывает уравнение:
[ddot{varphi }+{omega }^2_0varphi =0 left(5right).]
Решением уравнения (5) является выражение:
[varphi ={varphi }_0{cos left({omega }_0t+alpha right)left(6right), }]
где $varphi $ – угол отклонения нити от положения равновесия, $alpha $ – начальная фаза колебаний; ${varphi }_0$ – амплитуда колебаний; ${omega }_0=sqrt{frac{g}{l}}$ – циклическая частота колебаний.
Амплитудой скорости колебаний груза на нити в данном случае является величина равная:
[{left(frac{dvarphi }{dt}right)}_{max}={varphi }_0{omega }_0left(7right).]
Для математического маятника амплитуда скорости колебаний груза равна:
[{left(frac{dvarphi }{dt}right)}_{max}={varphi }_0sqrt{frac{g}{l}}left(8right).]
Примеры задач на амплитуду скорости груза
Пример 1
Задание. Колебательная система представляет собой груз, массы $m, $подвешенный на упругой пружине (рис.1). Смещение груза вдоль оси X изменяется по закону: $x(t)=2{cos (10 t)(м) }.$ Чему равно максимальное значение кинетической энергии груза ($E_{k max}$)?
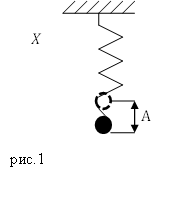
Решение. Кинетическую энергию груза можно найти и определения:
[E_{k }=frac{m{(frac{dx}{dt})}^2}{2} left(1.1right).]
Из уравнения колебаний груза найдем уравнение изменения его скорости:
[frac{dx}{dt}=frac{d}{dt}left(2{cos left(10 tright) }right)=-20{sin left(10 tright)left(frac{м}{с}right)(1.2). }]
Используя выражение (1.2) получим уравнение изменения кинетической энергии в виде:
[E_{k }=frac{m}{2}{(20{sin (10t) })}^2=frac{400m}{2}{sin}^2left(10tright)left(1.3right).]
Из выражения (1.3) следует, что максимальное значение кинетической энергии (ее амплитуда), учитывая, что ${sin}^2left(10tright)le 1$ равно:
[E_{k max}=200cdot mleft(Джright).]
Ответ. $E_{k max}=200cdot m$ Дж
Пример 2
Задание. Скорость колебаний груза на нити (математический маятник) изменяется в соответствии с гармоническим законом: $frac{dvarphi }{dt}(t)=5{sin left(2pi tright) }$. Чему равны амплитуда скорости амплитуда угла отклонения ${varphi }_0$? Запишите уравнение $varphi (t)$ для этих колебаний.textit{}
Решение. Амплитуду скорости изменения угла отклонения мы видим непосредственно в уравнении:
[frac{dvarphi }{dt}(t)=5{sin left(2pi tright)left(2.1right). }]
Она равна:
[{left(frac{dvarphi }{dt}right)}_{max}=5 .]
Амплитуду угла отклонения найдем, используя соотношение:
[{left(frac{dvarphi }{dt}right)}_{max}={varphi }_0{omega }_0left(2.2right),]
где ${omega }_0=2pi $ исходя из уравнения (2.1). Получаем:
[{varphi }_0=frac{{left(frac{dvarphi }{dt}right)}_{max}}{{omega }_0}=frac{5}{2pi } left(2.3right).]
Уравнение $varphi (t)$, учитывая (2.3) будет иметь вид:
[varphi left(tright)=-frac{5}{2pi }{cos left(2pi tright) }.]
Ответ. 1) ${left(frac{dvarphi }{dt}right)}_{max}=5. 2) {varphi }_0=frac{5}{2pi }$. 3) $varphi left(tright)=-frac{5}{2pi }{cos left(2pi tright) }$
Читать дальше: виды равновесия.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!