Как найти амплитуду магнитной индукции

Амплитуда – магнитная индукция

Cтраница 3

В каком режиме работают трансформатор тока и трансформатор напряжения, на какие примерно амплитуды магнитных индукций рассчитывают их магнитопроводы.
 [31]

На рис. 2 – 10 приведены кривые удельных потерь Рст в зависимости от амплитуды магнитной индукции Ви при разных частотах приложенного синусоидального напряжения.
 [33]

Поскольку, однако, выполнение схем сравнения абсолютных значений электрических величин требует стабилизации амплитуды магнитной индукции, что связано с определенными практическими трудностями, в настоящее время в основном применяются схемы сравнения фаз двух электрических величин. Не вызывают затруднений также схемы сравнения квадратов электрических величин.
 [35]

W ] / BmSCT, потери мощности в магни-топроводе, которые примерно пропорциональны квадрату амплитуды магнитной индукции, намного меньше, чем при номинальном напряжении, и значительно меньше потерь в обмотках трансформатора при номинальном токе и ими можно пренебречь.
 [36]

Приняв за единицу магнитной индукции ее амплитудное значение Bs, можно выразить относительную величину амплитуды переменной составляющей магнитной индукции 5 при заданном токе управления через соответствующее относительное значение выпрямленного тока нагрузки.
 [37]

В каком режиме работают трансформатор тока и трансформатор напряжения, на какие, примерно, амплитуды магнитных индукций рассчитываются их магиитопроводы.
 [38]

Следовательно, в любой момент результирующее магнитное после двухфазной обмотки имеет неизменное значение, равное амплитуде магнитной индукции одной фазы.
 [39]

На рис. 10.8 изображены положительные направления токов в фазах обмотки статора и соответствующие им положительные направления амплитуд магнитных индукций двухполюсного асинхронного двигателя, а на рис. 10.9 – графики мгновенных значений токов в фазах обмотки статора.
 [41]

У какого из трансформаторов массы проводов обмоток GM и маг-нитопровода GCT больше, если плотности тока и амплитуды магнитных индукций у трансформаторов равны.
 [42]

У какого из трансформаторов массы проводов обмоток См и магнитопровода GCT больше, если плотность тока и амплитуды магнитных индукций у трансформаторов равны.
 [43]

Располагая конкретными значениями ( 5с50) др, остается решить вопрос о выборе материала и конструкции магнитопровода, амплитуде магнитной индукции и числе витков дросселя, чтобы обеспечить, заданное значение индуктивности.
 [44]

Страницы:  

   1

   2

   3

   4

Контрольные вопросы

1. Как
   объяснить линейный рост графика
   зависимости B
   от H
   ферромагнетике при достаточно больших
   H?

2. Чем
   объяснить большое значение B
   в ферромагнетиках?

3. Нарисуйте вид
   “петли гистерезиса” для парамагнетика.

4. Как изменится
   площадь петли гистерезиса ферромагнетика
   при повышении температуры?

5. Почему при
   многократном перемагничивании
   ферромагнетик нагревается?

Литература

1. Скорохватов Н.А.
   Курс лекций по электромагнетизму. М:
   МИИГАиК, 2006.

2.
Савельев И.В., Курс общей физики, т. 2
(любое издание).

Лабораторная
работа № 255 .

Изучение магнитного поля соленоида

Приборы
и принадлежности:
лабораторная установка с соленоидом,
источник питания, милливольтметр,
амперметр.

Краткая теория

Соленоидом
называется цилиндрическая катушка,
содержащая большое, число витков провода,
по которому идет ток. Если шаг вин­товой
линии проводника, образующего катушку,
мал, то каждый ви­ток с током можно
рассматривать как отдельный круговой
ток, а соленоид – как систему последовательно
соединенных круговых токов одинакового
радиуса, имеющих общую ось.

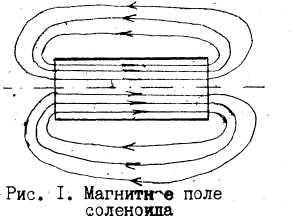
Магнитное поле
внутри соленоида можно представить как
сумму магнитных полей, создаваемых
каждым витком. Вектор индукции маг­нитного
поля внутри соленоида перпендикулярен
плоскости витков, т.е. направлен по оси
соленоида и образует с направлением
кольце­вых токов витков правовинтовую
систему. Примерная картина силовых
линий магнитного поля соленоида показана
на рис. 1. Силовые линии магнитного поля
замкнуты.

На рис, 2 показано
сечение соленоида длиной L
и с числом витков N
и радиусом поперечного сечения R. Кружки
с точками обозначают сечения витков
катушки, по которым идет ток I , на­правленный
от чертежа на нас, а кружки с крестиками
– сечения вит­ков, в которых ток
направлен за чертеж. Число витков на
единицу длины соленоида обозначим
.

Индукция магнитного
поля в точке А , расположенной на оси
соленоида, определяется путем
интегрирования магнитных полей,
со­здаваемых каждым витком, и равна

,
(1)

где
и– углы, образуемые с осью соленоида
радиус-векто­рамии,
проведенными из точки А к крайним виткам
солено­ида,-магнитная
проницаемость среды,магнитная постоянная.

Таким образом,
магнитная индукция В прямо пропорциональна
си­ле тока, магнитной проницаемости
среды, заполняющей соленоид, и числу
витков на единицу длины. Магнитная
индукция также зависит от положения
точки А относительно концов соленоида.
Рассмотрим нес­колько частных случаев:

1. Пусть точка А
   находится в центре соленоида, тогда
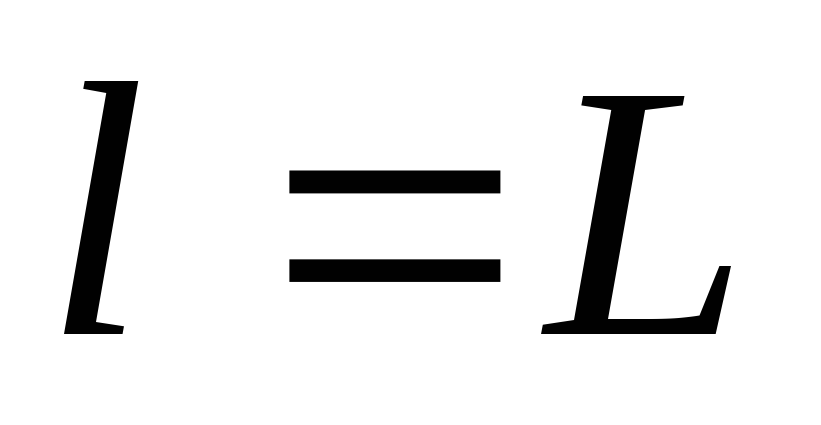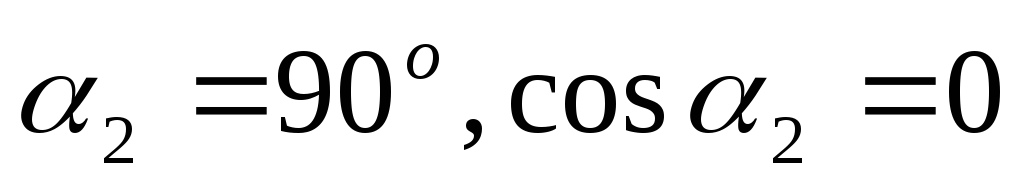   ,и.
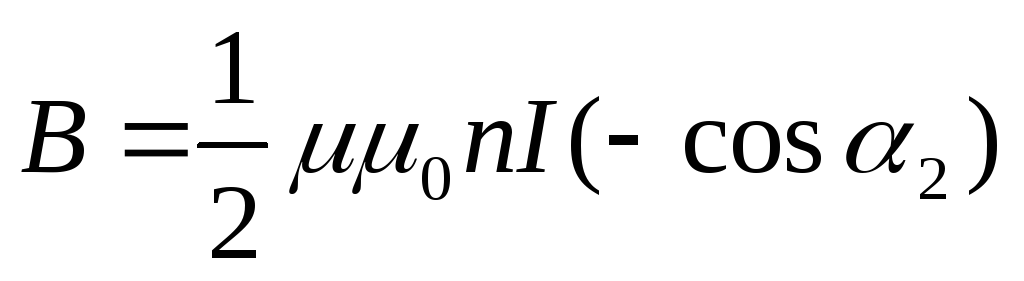   Если соленоид достаточно длинный, то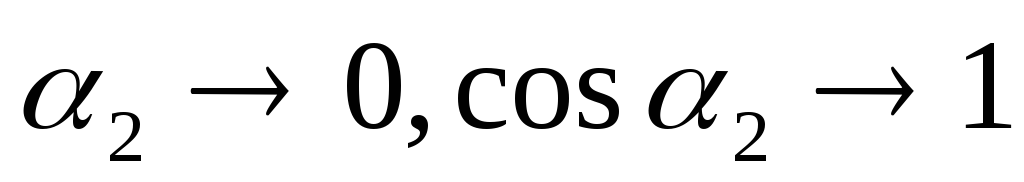и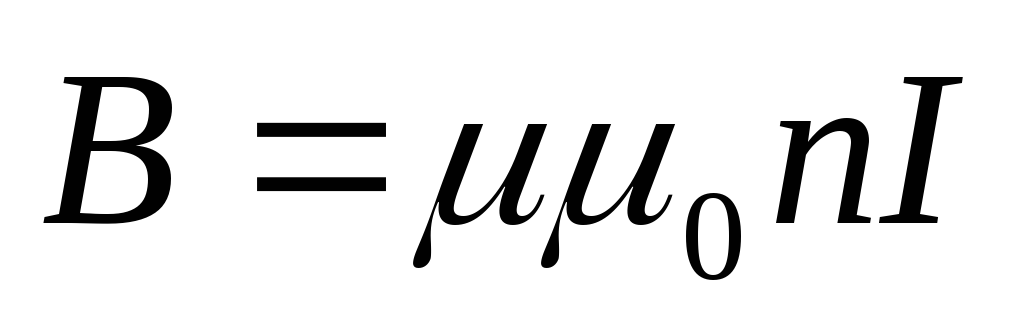(2)

2. Пусть точка A
   находится в центре крайнего витка,
   тогда
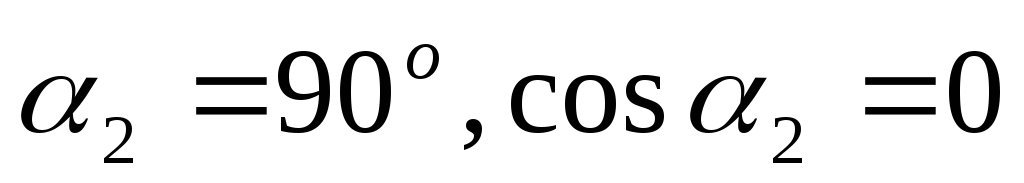   ,и.
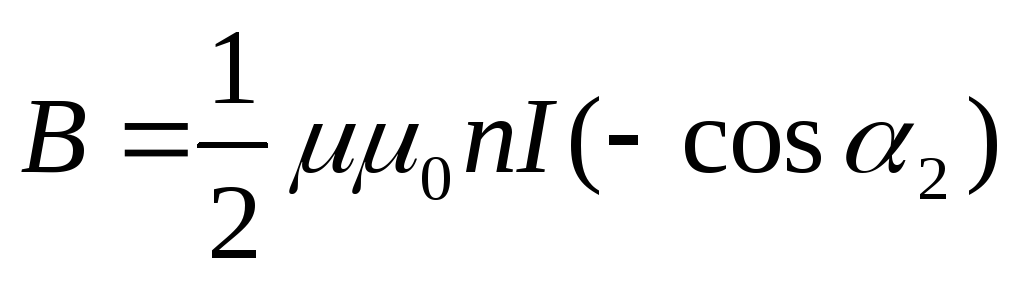   Если солено­ид достаточно длинный,
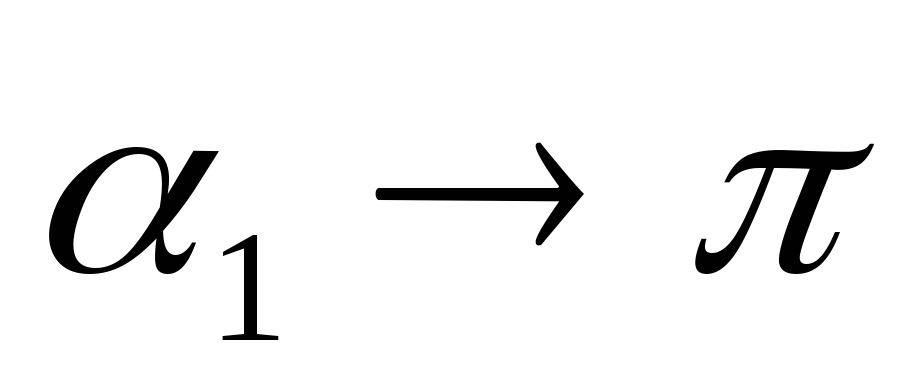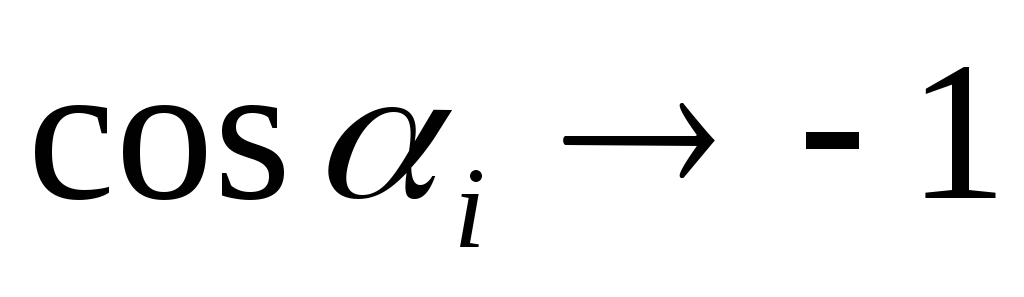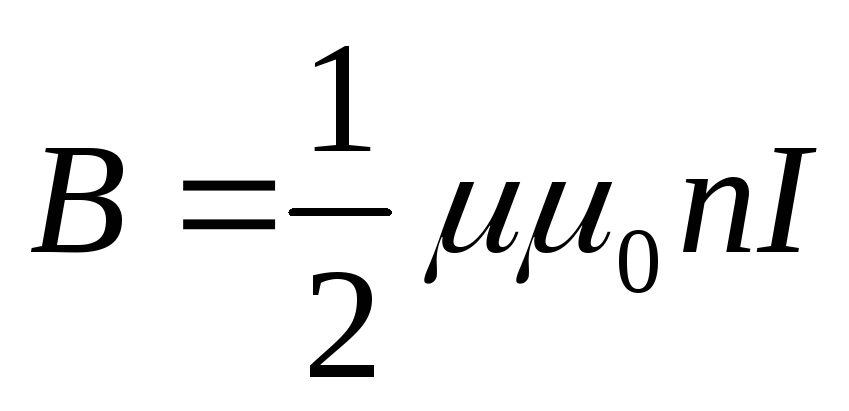   то,и(3)

Из формул (2) и (3)
видно, что магнитная индукция соленоида
на его краю вдвое меньше по сравнению
с ее величиной в центре.

1. Если длина соленоида
   во много раз больше радиуса его
   витков
   (“бесконечно” длинный
   соленоид), то для всех точек, лежащих
   внутри
   соленоида на его оси, можно
   положить
   .
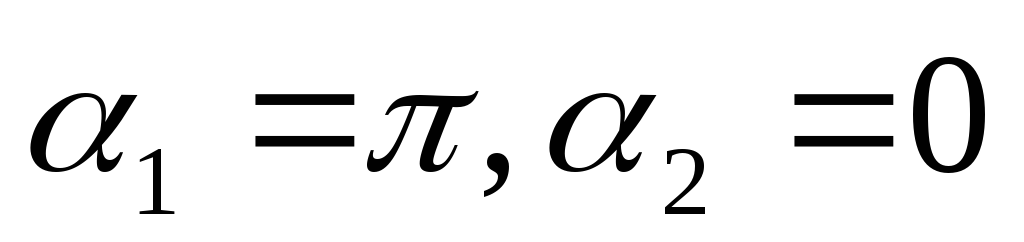   Тогда
   поле можно считать в центральной
   части соленоида однородным и рассчитывать
   его по формуле

(4)

Однородность
магнитного поля нарушается вблизи краев
соленоида. В этом случае индукцию можно
определять по формуле

,
(5)

где k
– коэффициент, учитывающий неоднородность
поля.

Экспериментальное
изучение магнитного поля соленоида в
данной работе осуществляется с помощью
специального зонда – маленькой катушки,
укрепленной внутри штока с масштабной
линейкой. Ось катуш­ки совпадает с
осью соленоида, катушка подключается
к милливольт­метру переменного тока,
входное сопротивление которого много
боль­ше сопротивления катушки-зонда.
Если через соленоид идет перемен­ный
ток

стандартной частоты (=50
Гц), то внутри соленоида и на его краях
индукция переменного магнитного поля
изменяется по закону (см. (5)):

Амплитуда магнитной
индукции
в этой формуле зависит от положения
точки внутри соленоида. Если поместить
в соленоид катуш­ку-зонд, то в
соответствии с законом электромагнитной
индукции, в ней возникает ЭДС индукции:

,
(6)

где
N₁
– число витков в катушке, S
– площадь поперечного сече­ния катушки,
Ф – магнитный поток (,
т.к. ось катушки совпадает с осью соленоида
и, следовательно, вектор магнитной
ин­дукцииперпендикулярен плоскости поперечного
сечения катушки.).

Так как величина
индукции B
изменяется по закону
,
,
то из (6) получается формула для расчета
ЭДС:

(7)

Из выражения (7)
видно, что амплитуда ЭДС
зависит от.
Таким образом, измеряя амплитуду ЭДС,
можно определить:

(8)

Коэффициент k
учитывающий неоднородность магнитного
поля соленоида на краях, можно о
определить., по формуле. (5), зная
и:

(9)

где
– амплитуда переменного тока, идущего
через соленоид.

Из формул (7) и (9)
следует, что амплитуда ЭДС индукции
прямо пропорциональна амплитуде
переменного тока
:

(10)

Включенные в цепь
переменного тока амперметр и милливольт­метр
измеряют действующие значения тока
и ЭДС,
которые связаны с амплитудамиисоотношениями:

;

Для действующих
значений тока и ЭДС формула (10) имеет
вид

(11)

Из формулы (11)
следует, что отношение
пропорциональ­но
коэффициентуK
неоднородности индукции магнитного
поля в точке соленоида, где проводятся
измерения

(12)

где А – коэффициент
пропорциональности.

В данной работе
требуется выполнить два задания: 1)
опреде­лить распределение индукции
вдоль оси соленоида при некотором
постоянном значении тока; 2) определить
значение коэффициента к.

Техника
безопасности:

1. Не подключают/
   самостоятельно источник питания и
   милливольтметр к сети 220 В.

2. Не производить
   переключения цепей, находящихся под
   напряжением.

Не прикасаться к
неизолированным частям цепей.

1. Не оставлять без
   присмотра включенную схему.

Порядок выполнения
работы

Задание № 1.
Исследование распределения индукции
магнитного поля вдоль оси соленоида.

1. Собрать
измерительную цепь по схеме, приведенной
на рис. 3. Для этого в цепь соленоида
включить источник питания и амперметр,
а к выводам катушки – зонда – милливольтметр
(для измерения
)
В данной установке катушка-зонд имеет
следующие параметры:=200 витков,S=2*10^-4м²,
частота переменного тока
= 50 Гц, Число витков на единицу длины
соленоидаn
= 2400 1/м

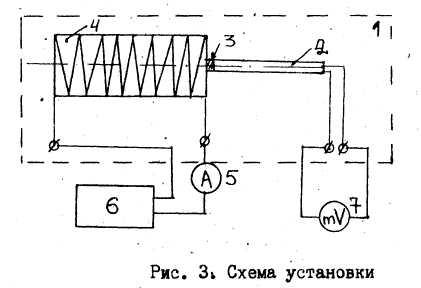
1- лабораторный
стенд Z – шток «

2- катушка-зонд

3- соленоид
5-
амперметр

6- источник питания
с регулятором выход­ного напряжения
(тока), 7- милливольтметр.

2. Установить шток
с масштабной линейкой так, чтобы
катушка-зонд оказалась примерно в
середине соленоида.

3.Включить источник
питания соленоида и установить ток
соленоида (по амперметру), равный
=25мА. Включить милливольтметр и после
прогрева (5 мин) снять показания.

4.Перемещая шток
с масштабной линейной, измерить при
помощи
милливольтметра действующее
значение ЭДС индукции через каждый
сантиметр
положения линейки. По формуле (8) вычислить
.
Результаты
измерений и расчетов занести в таблицу
1 (учтите, что).

Таблица I

№ п/п	Положение линейки-Х
1
2
3
…

Погрешность
в каждой точке, соленоида определяется
как систематическая погрешность
косвенных измерений:

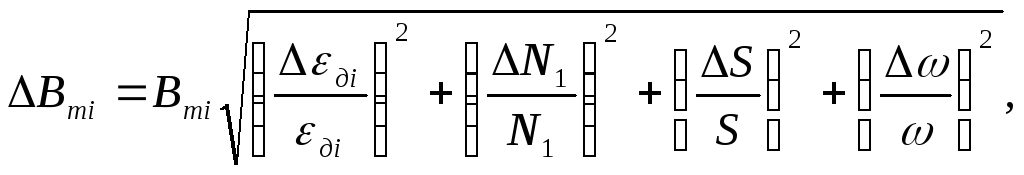
где
м²,
виток;=1
Гц;–
погреш­ность измерения;
по милливольтметру.

5.Построить график

6.Зная амплитуду
тока
и число витков на единицу
длины
соленоидаn,
определить
в центре соленоида по
формуле (4) и
сравнить с измеренным в той же точке
значением

Задание
2. Измерение
коэффициента неоднородности’ магнитного

поля соленоида.

1. Снять
   зависимость
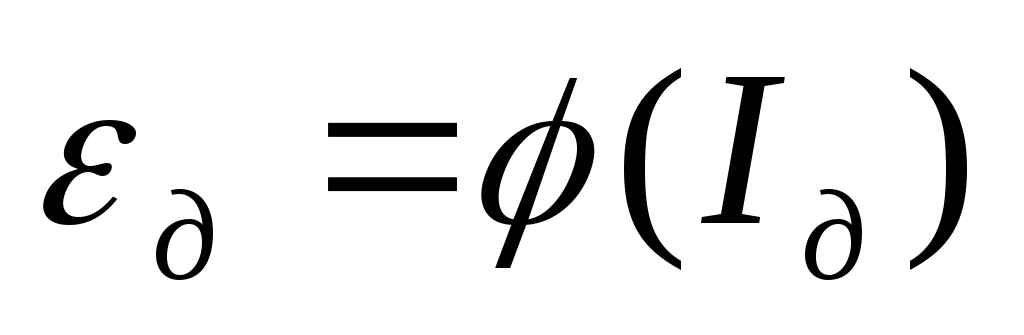   для данного соленоида. Дня этого
   установить шток в положение, когда
   катушка-зонд находится у края соленоидами,
   изменяя действующее значение тока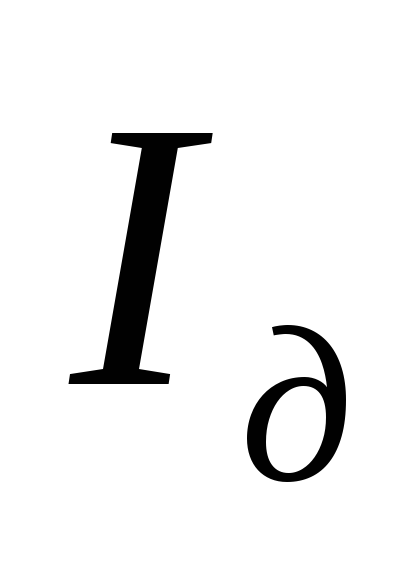соленоида с помощью источника питания,
   снять значения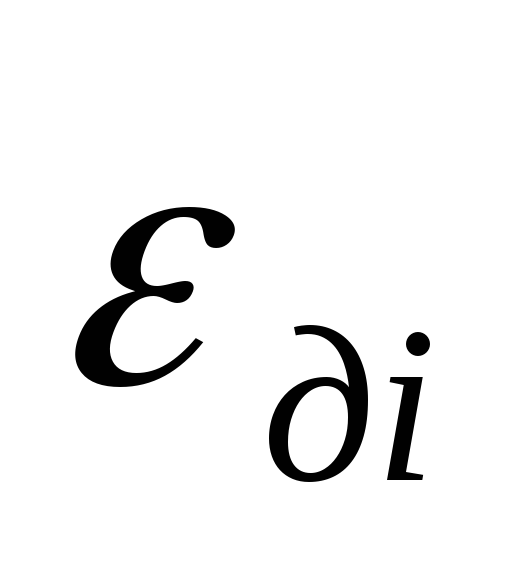и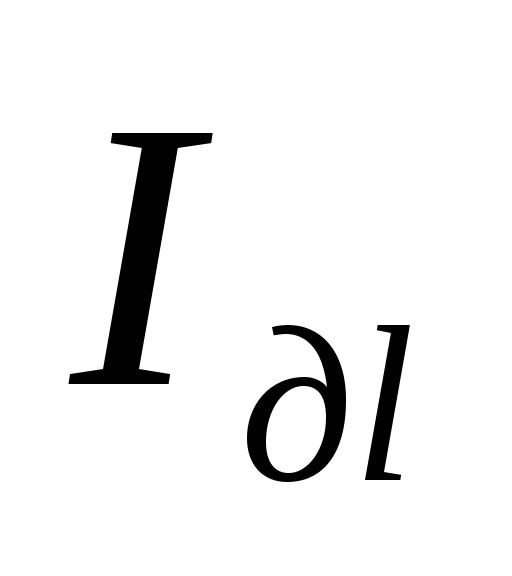и занести в таблицу 2.

Таблица 2.

Измерения
1
2
3
…

По
формуле (12) рассчитать
,
где

Контрольные
вопросы

1. Сформулируйте
   закон электромагнитной индукции.

2. Нарисуйте картину
   силовых линий соленоида.

3. Перечислите
   основные способы исследования магнитного
   поля.

4. В каких случаях
   для исследования магнитного поля можно
   исполь­зовать катушку-зонд?

5. Выведите формулу
   для вектора магнитной индукции бесконечно
   длинного соленоида.

Литература

1. Скорохватов Н.А.
   Курс лекций по электромагнетизму. М:
   МИИГАиК, 2006.

2. Савельев
   И.В., Курс общей физики, т. 2 (любое
   издание).

3. Трофимова
   Т.И., Курс физики (любое издание).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Трансформаторы

Определить намагничивающий ток трансформатора (рис. 8.9, а).

Дано: ω 1 = 250 витков; l c т =25 см; l 0 =0,01 см; S c т =18 см 2 ; U 1 = 120 В; f =50 Гц. Кривая намагничивания стали магнитопровода изображена на рис. 8.9,6. Указать правильный ответ.

1) 2,4 А. 2) 1,7 А. 3) 4,2 А. 4) 1,3 А.

Намагничивающий ток определяется с помощью закона полного тока

I ст H ст +H 0 l 0 =I μ w 1 .

Напряженность магнитного поля определяется для стали по кривой намагничивания, для воздуха—из выражения Н 0 = В 0 /μ 0 .

Магнитная индукция в магнитопроводе трансформатора определяется из выражения

U 1 =E 1 =4,44w 1 fB m S ст , откуда

В m =U 1 /(4,44 w 1 fS ст )=120/(4,44∙250∙50∙18∙10 -4 )=1,2 Тл

По кривой намагничивания рис. 8,9, а магнитной индукции В m =1,2 Тл соответствует напряженность магнитного поля Н c т =20 А/см.

Напряженность поля в воздушном зазоре равна

Н 0 =В 0 /μ 0 =1,2/1,256∙10 -6 =10 6 А/м.

Амплитуда намагничивающего тока

I μm =(H c т l ст +H 0 l 0 )/w 1 =(20∙25+10 6 ∙0,01∙10 -2 )=2,4 A.

Намагничивающий ток равен

I μ = I μm /√2=2,41/1,41=1,7.A. Ответ : 2.

Как изменится ток холостого хода и потери в магнитопроводе трансформатора, если напряжение на первичной обмотке окажется больше номинального? Указать правильный ответ.

1) I 0 не изменится. 2) I 0 уменьшится . 3) ∆P ст не изменится. 4) ∆P ст увеличится.

Из выражения U≈E 1 =4,44fw 1 B m S ст следует, что с увеличением напряжения в той же степени возрастает амплитуда магнитной индукции В m . Вследствие увеличения магнитной индукции возрастает напряженность магнитного поля, а значит и намагничивающий ток трансформатора I μ , так как по закону полного тока имеем

I ст H ст +H 0 l 0 =I μ w 1 .

Из выражения ∆Р ст =Gp 1,0 B m n (f/50) 1/3 следует, что при увеличении магнитной индукции возрастут потери в магнитопроводе и, следовательно, активная составляющая тока холостого трансформатора I а =∆Р ст /U 1 . Таким образом, ток холостого хода I 0 = (I μ 2 – I а 2 ) 1/2 увеличится. Ответ : 4.

Определить потери в стали магнитопровода трансформатора (рис. 8.24)

Дано: w 1 =795 витков, l =25 см, S =18 см 2 , U =380 В, f =50 Гц, p =3,2 Вт/кг, p =1,42 Вт/кг.

1) 10,2 Вт. 2) 14,3 Вт. 3) 5,1 Вт. 4) 7,15 Вт.

Амплитуда магнитной индукции в магнитопроводе трансформатора

B m =U 1 /4,44w 1 fS ст =380/4,44∙795∙50∙18∙10 -4 = 1,2 Тл.

G=l ст S ст γ =25∙18∙7,8=3500 г=3,5 кг.

N=5,69 lg (p 1,5 /p 1,0 ) = 5.69 lg (3,2/1,42) = 2.

Потери мощности в магнитопроводе

∆P ст = Gp 1,0 B m n (f/50) 1,3 = 3,5∙1,42∙1,2 2 (50/50) 1,3 =7,15 Вт . Ответ : 4.

Вкаком соотношении находятся токи короткого замыкания для трех значений расстояния между первичной и вторичной обмотками трансформатора l 1 >l 2 >l 3

(рис. 8.28,а)? Указать правильный ответ.

1) I k1 >I k2 >I k3 . 2) I k1 =I k2 =I k3 . 3) I k1 k2 k3 .

Решение 8-29. С увеличением расстояния между вторичной и первичной обмотками трансформатора уменьшается коэффициент связи между ними, т. е. увеличиваются потокосцепления рассеяния первичной Ψ 1 и вторичной Ψ 2 обмоток. При этом увеличиваются индуктивные сопротивления обмоток, так как они равны

X 1 = 2πfL 1 = 2πf Ψ 1 /I 1 ; X 2 = 2πfL 2 = 2πf Ψ 2 /I 2 . Таким образом, ток короткого замыкания

I k =U/[(r 1 +r 2 ‘ ) 2 +(x 1 +x 2 ‘ ) 2 ] 1/2

увеличением расстояния будет уменьшаться. Ответ : 3.

Два трансформатора одинаковой конструкции, равной номинальной мощности и одинаковых первичных и вторичных напряжений выполнены так, что у первого ( a)

U 1 /w 1 =1, у второго (б) U 1 /w 1 = 2. У какого из трансформаторов массы проводов обмоток G M и магнитопровода G ст больше, если плотности тока и амплитуды магнитных индукций у трансформаторов равны? Указать правильный ответ.

1) G м,а =G м,б . 2) G м, а G м ,б . 3) G ст,а =G ст,б . 4) G ст,а ст,б .

Решение 8-34. Из выражения U≈E 1 =4,44fw 1 B m S ст следует, что

Так как по условию задачи амплитуды магнитных индукций для трансформаторов одинаковы, можно записать:

U 1 /w 1а = 1 = kS ст,а ; (1) для второго

U 1 /w 1 б = 2 = kS ст , б . (2) Из (1) и (2) следует

Таким образом, сечение и, следовательно, масса сердечника второго трансформатора больше, чек первого. Числа витков и обмоток трансформаторов равны:

Число витков второго трансформатора меньше, чем первого. Поскольку трансформаторы имеют равные номинальные мощности и напряжения, номинальные токи трансформаторов

I 2ном =S ном /U 2ном ; I 1ном ≈ S ном /U 1ном

будут одинаковыми. При равных плотностях токов J обмоток (по условию задачи) сечения обмоток S м трансформаторов (соответственно первичных и вторичных) будут одинаковыми:

Таким образом, можно утверждать, что, поскольку число витков обмоток второго трансформатора меньше, чем первого, а сечения одинаковы, масса меди обмоток второго трансформатора будет меньше, чем первого. Однако средние длины витков обмоток трансформаторов из-за различия сечений их магнитопроводов будут неодинаковыми. Отношение масс обмоток строго не будет равно 2. Обмотки трансформаторов несколько отличаются по размерам, будут неодинаковы и длины сердечников, поэтому отношение масс сердечников не будет равно точно 2. Ответ: 4.

На рис. 8.40, 6 даны зависимости I 1 , I 2 , I 3 , Р 1 , n и U 2 от w 2 /w 1 для автотрансформатора рис. 8.40, а . (Изменение w 2 /w 1 достигается перемещением движка А.) Принять U 1 =200 В, r н =10 Ом. Током холостого хода пренебречь. Какой из графиков изображен неправильно?

1) I 1 . 2) I 2 . 3) I 3 , U 2 . 4) n. 5) P 1 .

Решение 8-40. Коэффициент трансформации равен

Напряжение на потребителе равно

U 2 ≈E 2 = U 1 w 1 /w 2 =200 w 1 /w 2 (2)

I 3 =U 2 /r н = U 1 w 2 /w 1 r н =10 w 2 /w 1

Тока I 1 и I 2 определяем из уравнения МДС. Так Как по условию задачи I c =0 , то

İ 1 (w 1 – w 2 )+ İ 2 w 2 =0. (4)

Ток I 2 , как это следует из первого закона Кирхгофа, равен

İ 2 = İ 1 + İ 3 Преобразуя (4), получаем , İ 2 w 2 + İ 2 w 2 + İ 2 w 2 + İ 2 w 2 =0 откуда

İ 1 = — İ 3 w 2 /w 1 или I 1 = I 3 w 2 /w 1 (5)

Подставив в (5) значение тока I 3 из (3), получим

Зависимость тока I 1 от w 2 /w 1 может быть установлена также на основании закона сохранения энергии: U 2 I 3 = U 2 I 3 , откуда

I 1 = U 2 I 3 /U 1 = U 1 /r н ∙ (w 2 /w 1 ) 2 =10 (w 2 /w 1 ) 2

Ток I 2 определяется из (4):

Подставив в (7) I 1 из (6), получим

I 2 =10 (w 2 /w 1 ) 2 (w 1 – w 2 )/w 2 (8)

Путем простых преобразований легко показать, что ток I 2 является арифметической разностью токов I 3 и I 1 :

I 2 =10 [w 2 2 w 1 /w 1 2 w 2 — w 2 2 w 2 /w 1 2 w 2 ]=10 w 2 /w 1 — 10 (w 2 /w 1 ) 2 =I 3 – I 1 .

Мощность, потребляемая из сети, равна

P 1 =U 1 I 1 = U 1 U 1 /r н ∙ (w 2 /w 1 ) 2 =2000(w 2 /w 1 ) 2

На рис. 8-40, б построены графики зависимости искомых величин. График мощности P 1 изображен неправильно, так как он не соответствует выражению (9). График Р 1 должен иметь такой же вид, как и график тока I 1 . Ответ: 5.

Два трансформатора с равными номинальными мощностями и напряжениями первичных и вторичных обмоток, но разными напряжениями короткого замыкания соединены параллельно. В каком соотношении находятся токи первичных обмоток трансформаторов (первого I 1а , и второго I 1б ) при нагрузке, если напряжение короткого замыкания первого трансформатора больше, чем второго? Указать правильный ответ.

1) I 1 а > I 1 б . 2) I 1 а = I 1 б . 3) I 1 а I 1 б .

Поскольку трансформаторы имеют равные номинальные мощности и напряжения первичных и вторичных обмоток, номинальные токи их первичных обмоток также будут равными. Напряжение короткого замыкания первого трансформатора равно

то же для второго трансформатора:

Так как U к,а = U к,б , а номинальные токи равны, то

Из схемы замещения параллельно включенных трансформаторов (рис. 13.8.51) следует

I 1а =│Ủ 1 — İ Z Н │/ z к,а ; I 1б =│Ủ 1 — İ Z Н │/ z к,б .

Так как числители выражений токов I 1а и I 1б одинаковы, а z к,б > z к,б то, следовательно,

Трехфазный трансформатор при нагрузке 810 А и со s φ=0,8 имел установившуюся допустимую температуру. Какую активную мощность он может отдавать потребителю, если коэффициент мощности нагрузки будет cos φ=0,6 ? Номинальное напряжение вторичной обмотки U 2ном = 400 В. Указать правильный ответ.

1) 560 кВт . 2) 336 кВт. 3) 324 кВт. 4) 448 кВт.

При длительной номинальной нагрузке трансформатор нагревается до допустимой температуры. Следовательно, в данном случае ток 810 А является номинальным током трансформатора.

Номинальная мощность трансформатора равна

S ном =√3 I 2ном U 2ном =1,73∙810∙400∙10 -3 = 560кВ∙А.

Активная мощность, которую трансформатор может отдавать длительно при cos φ=0,6, π авна

p 2 = s hom cos φ= 560∙0,6 = 336 кВт . Ответ: 2.

Для измерения мощности трехфазного потребителя использованы два ваттметра (рис. 8.71). Определить мощность потребителя, если стрелка одного ваттметра указывала 50 делений, второго 25 . Коэффициенты трансформации трансформаторов напряжения и тока равны: K U = 100, K I = 20 . Ваттметр имеет 100 делений, на его шкале написано 5 А, 100 В. Указать правильный ответ.

1) 250 кВт. 2) 750 кВт. 3) 1300 кВт.

Цена деления прибора равна

С W = I ном U ном /N =100∙5/100 = 5 Вт/дел.

Цена деления прибора в схеме с трансформаторами тока я напряжения равна

C=C W K I K U = 5∙20∙100∙10 -3 = 10 кВт/дел.

Мощность потребителя равна

P =P 1 +P 2 =CN 1 +CN 2 = 10∙50 + 10∙25 = 750 кВт. Ответ: 2.

Источник

Как определить амплитуду магнитной индукции в магнитопроводе трансформатора

Определение параметров сетевого трансформатора.

Магнитный поток, проходящий через площадь S равен:

Ф = BScosα;

где:

Ф ― величина магнитного потока [Вб],

S ― площадь контура [м2],

B ― индукция магнитного поля [Тл],

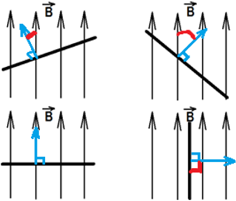
α ― угол между нормалью $overrightarrow{n}$ к площади контура и вектором индукции магнитного поля $overrightarrow{B}$.

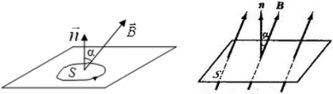
Если вектор индукции магнитного поля $overrightarrow{B}$ перпендикулярен площади контура, то магнитный поток равен:

Ф = BScos90° = BS;

Максимальное значение потока будет тогда, когда косинус будет максимальным (cosα = 1), то есть угол между вектором $overrightarrow{B}$ и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.

Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.

ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.

Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:

$varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

где:

$varepsilon_i $ ― ЭДС электромагнитной индукции [B],

$frac{Delta text{Ф}}{Delta t}$ ― скорость изменения магнитного потока [Вб/с],

∆Ф ― изменение магнитного потока [Вб],

∆t ― время, за которое происходит это изменение [c].

Кроме того, ЭДС индукции равна производной магнитного потока по времени:

$varepsilon_i = -text{Ф}_t’$

где:

• ― ЭДС электромагнитной индукции [B],
• ― производная магнитного потока по времени [Вб/с].

Задача 1

Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?

Решение:

Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.

Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.

По закону электромагнитной индукции $varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени $varepsilon_i = -text{Ф}_t’$

И это очень важный момент, без которого мы не сможем решить такого рода задачу.

Теперь посчитаем ЭДС индукции.

Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.

ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.

Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса

$text{Ф} underset{text{множитель}}{underbrace{aS}} ;; cdot ;; underset{text{сложная функция}}{underbrace{cos(bt)}}$.

Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что $varepsilon_i = -text{Ф}_t’$

Подставив сюда значение производной, получим $varepsilon_i = -text{Ф}_t’$ = abS · sin (bt).

Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.

По закону Ома $I = frac{varepsilon}{R}$ , подставив сюда значение ЭДС, получаем $I = frac{abScdot sin(bt)}{R}$.

Мы получили зависимость силы тока от времени.

Из-за синуса, который стоит в этой формуле, ток постоянно меняет свое значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.

В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.

Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, $I_{max} = frac{abS}{R}$.

Отсюда можно легко выразить площадь контура $S = frac{I_{max}R}{ab}$, подставив сюда все значения, получим $S = frac{I_{max}R}{ab} = frac{35cdot 10^{-3} Acdot 1,2text{Ом}}{6cdot 10^{-3}text{Тл} cdot 35000c^{-1}} = 0,002text{м}^2$

Ответ: 0,002

Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:

• увеличением или уменьшением модуля индукции магнитного поля (т. е. величины $frac{Delta B}{Delta t}$);
• изменением направления вектора магнитного поля (т. е. изменением угла α);
• деформацией контура, причем такой деформацией, при которой изменяется площадь контура (т. е. изменением величины $frac{Delta S}{Delta t}$ );
• изменением нескольких из этих величин одновременно.

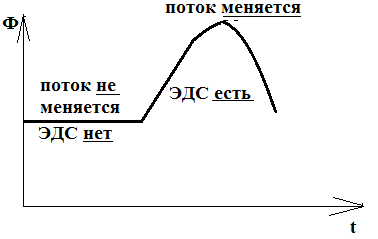
Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.

Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.

Либо так, тогда будет меняться поток и возникать ЭДС:

Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.

Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.

Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.

Задача 2

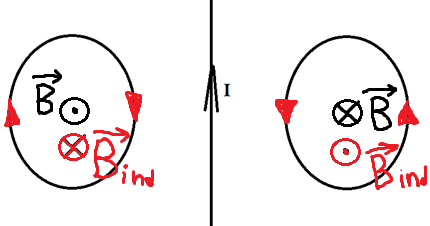
Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?

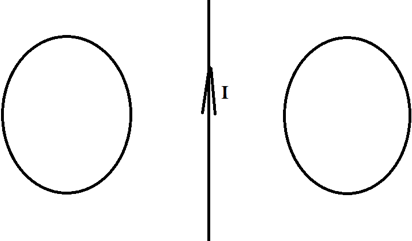
Решение:

Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?

Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.

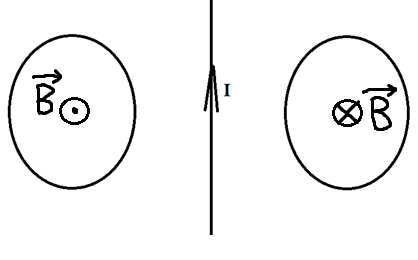
Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?

Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.

Движение проводников

Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).

Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС $|varepsilon_i| = Blvsinalpha$;

где:

$varepsilon_i$― ЭДС электромагнитной индукции [B],

B ― индукция магнитного поля [Тл],

l ― длина проводника [м],

v ― скорость движения проводника [м/с],

α ― угол между направлением вектора скорости $overrightarrow{v}$ и длиной проводника $overrightarrow{l}$ , если вектор индукции магнитного поля $overrightarrow{B}$перпендикулярен проводнику и вектору скорости его движения: $overrightarrow{B} perp overrightarrow{v}, overrightarrow{B} perp overrightarrow{l}$

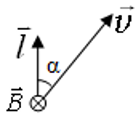
Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.

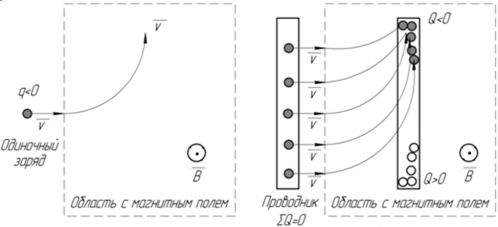
В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.

На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создаёт ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.

В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.

В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;

где:

U — разность потенциалов [В],

l — длина проводника [м],

v — скорость движения проводника $big[ frac{text{м}}{c} big]$

B — индукция магнитного поля [Тл],

α — угол между направлением скорости и длиной проводника.

В случае, если есть какой-то замкнутый контур, то ЭДС в нем возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.

В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу $varepsilon_i = – frac{Delta text{Ф}}{Delta t}$

В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу $varepsilon$ =U= lvBsinα.

Задача 3

В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?

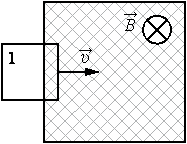
Решение:

Составим цепочку.

Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.

Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).

Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.

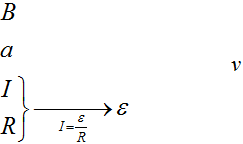
А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.

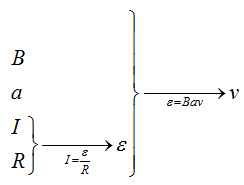
Пройдёмся вдоль этой цепочки.

Запишем закон Ома $I = frac{varepsilon}{R}$, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим $I = frac{varepsilon}{R} = frac{Bav}{R}$отсюда выразим скорость, и, подставив все величины, получим $v = frac{IR}{Ba} = frac{1cdot 10^{-3} Acdot 10text{Ом}}{0,1 text{Тл} cdot 0,1 text{м}} = 1 frac{text{м}}{c}$

Ответ: 1

Магнитная индукция

Магнитная индукция — это силовая характеристика магнитного поля в выбранной точке пространства. Она определяет силу, с которой магнитное поле воздействует на заряженную частицу, что движется внутри него. Магнитная индукция считается фундаментальной характеристикой магнитного поля (как напряжённость для электрического поля).

Магнитная индукция описывает магнитную силу (вектор) на тестовом объекте (например, на куске железа) в каждой точке пространства. Простыми словами: если естественный магнит поднести к магнитным веществам (таким, как железо, никель, кобальт и т. д.), это вызовет в них магнитные свойства, которые называются “магнитной индукцией”. Магнитная индукция используется для создания искусственных магнитов.

Магнитная индукция также называется плотностью магнитного потока.

Магнитная индукция измеряется:

• в системе СИ единицей тесла (Тл),
• в системе СГС единицей гаусс (Гс).

Соотношение между Тл и Гс: 1 Тл = 10 000 Гс.

Магнитная индукция — это векторная величина и обозначается буквой B со стрелочкой:

Индукция (от лат. inducere — вводить, наведение) — производство токов в цепи под действием магнита или другого тока.

Формулы вычисления магнитной индукции

Формула магнитной индукции:

Где:

• B — индукция магнитного поля (в Тл)
• Mmax — максимальный крутящий момент магнитных сил, приложенных к рамке (в Нм)
• l — длина проводника (в м)
• S — площадь рамки (в м²)

Другие формулы, где встречается B

Эти формулы также можно использовать для её расчёта.

Сила Ампера:

Где:

• Fa — сила Ампера (в Н — ньютон)
• I — сила тока (в А — ампер)
• B — индукция магнитного поля (в Тл)
• L — длина проводника (в м)
• α — угол между вектором В и одним из направлений (силы тока, скорости или др.; измеряется в рад. или град.)

Сила Лоренца:

Где:

• Fл — сила Лоренца (в Н — ньютон)
• q — заряд частицы (в Кл — кулон)
• v — скорость (в м/с)
• B — индукция (в Тл)
• α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))

Магнитный поток:

Где:

• Ф — магнитный поток (в Вб – вебер)
• B — индукция (в Тл)
• S — площадь рамки (в м²)
• α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))

Электромагнитная индукция и магнитная индукция: какая между ними разница?

Электромагнитная индукция — это производство электродвижущей силы, создаваемой в результате относительного движения между магнитным полем и проводником.

Магнитная индукция может производить постоянный магнит, но может и не производить.

Электромагнитная индукция создаёт ток, но таким образом, что этот созданный ток противодействует изменению магнитного поля.

В электромагнитной индукции используются магниты и электрические цепи, а в магнитной индукции используются только магниты и магнитные материалы.

Узнайте также про:

• Магнитное поле,
• Магнитное поле Земли,
• Уравнения Максвелла
• Напряженность электрического поля.