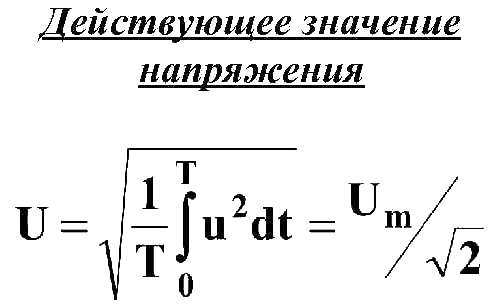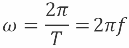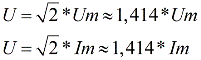Как найти амплитуду напряжения по графику

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Действующее напряжение и амплитудное напряжение — что это, и в чем отличие

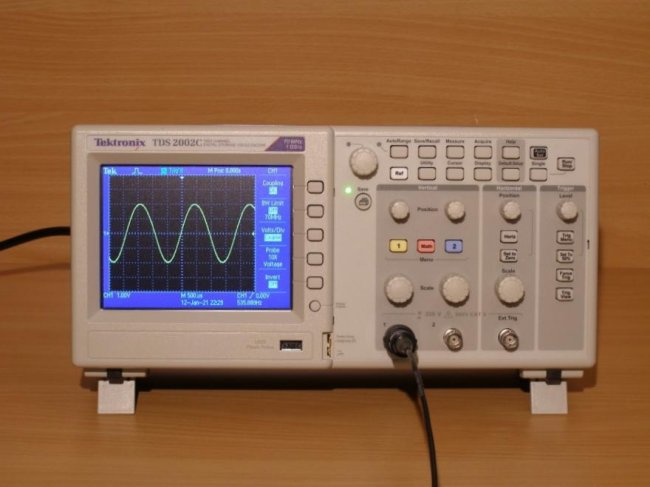
Все знают, что действующее напряжение в розетке 220 Вольт (230 по новым нормам, но для данной темы это не имеет особого значения). Это легко проверить при помощи мультиметра, который измерит разность потенциалов между фазой и рабочим нулевым проводником. То есть, при идеальных условиях, потенциал на нулевом проводе 0, а на фазном 220 Вольт. На самом деле все немного не так — переменный ток имеет синусоидальную форму с потенциалом на пиках 310 и -310 Вольт (амплитудное напряжение). Для того чтобы это увидеть, необходимо воспользоваться осциллографом.

Синусоида действующего и амплитудного напряжения

Понятно, что данный материал в большей степени ориентирован на простую аудиторию, у которой не то, что осциллографа нет, даже мультиметр наверняка не у каждого есть. Поэтому все примеры будут браться из среды программы Electronics Workbench, доступной каждому.

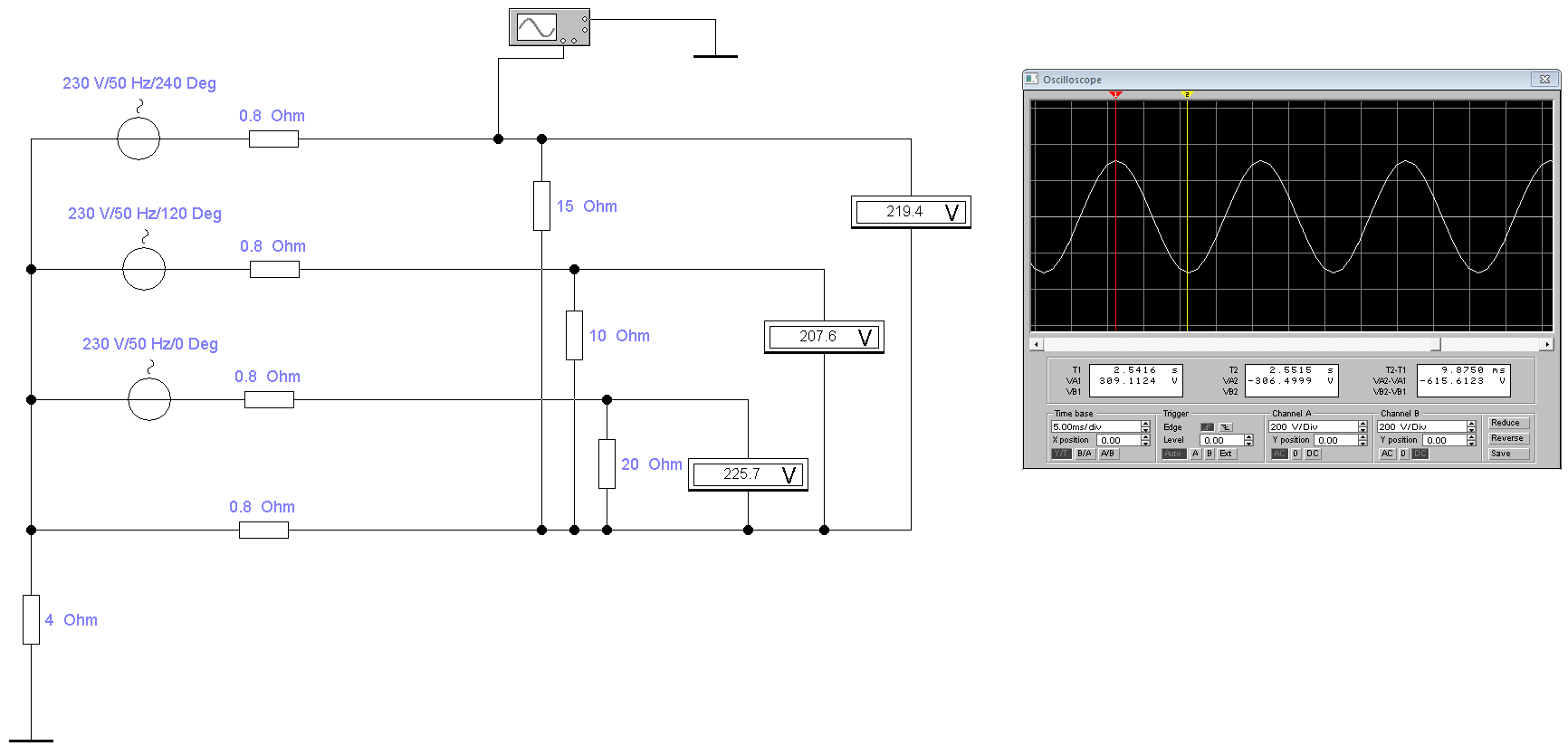
И первое, что нам нужно посмотреть — это синусоиду напряжения фазы из розетки. Для этого в программе отрисуем трехфазную сеть и подключим осциллограф к одной из фаз:

Как видно при показании вольтметра 219,4 Вольт между одной из фаз и PEN проводником, осциллограф показал синусоиду с амплитудой 309,1 Вольт. Это значение напряжения называется максимальным (амплитудным). А 219,4 Вольт, которые показывает вольтметр — это действующее напряжение. Его также называют среднеквадратичным или эффективным. И прежде чем перейти к рассмотрению данной особенности, кратко, простыми словами пройдемся по отрисованной схеме трехфазной сети и разберемся в природе синусоиды.

Начнем со схемы:

• Слева на право — три источника переменного напряжения с фазовыми углами 0, 120, 240 градусов и соединенными звездой.
• Резистор 4 Ом — это заземление нейтрали трансформатора.
• Резисторы по 0,8 Ом — условное сопротивление проводов, зависящее от сечения провода и длины линии.
• Резисторы 15, 10 и 20 Ом — нагрузка потребителей по трем фазам.
• К одной из фаз подключен осциллограф, показывающий амплитуду 309,1 Вольт.

Теперь рассмотрим синусоиду. Переменное напряжение в отличие от постоянного, график которого прямая на осциллографе, непрерывно изменяется как по величине, так и по направлению. Причем изменения эти происходят периодически, то есть точно повторяются через равные промежутки времени.

Переменное напряжение генерируется на электростанциях и посредством повышающих и понижающих распределительных трансформаторов попадает к конечному потребителю. При этом трансформация по пути никак не сказывается на синусоиде напряжения.

Видео — действующее напряжение и амплитудное

С полным и наглядным изложением рассматриваемого вопроса вы можете ознакомиться в следующем видео:

Работа генератора трехфазного переменного тока

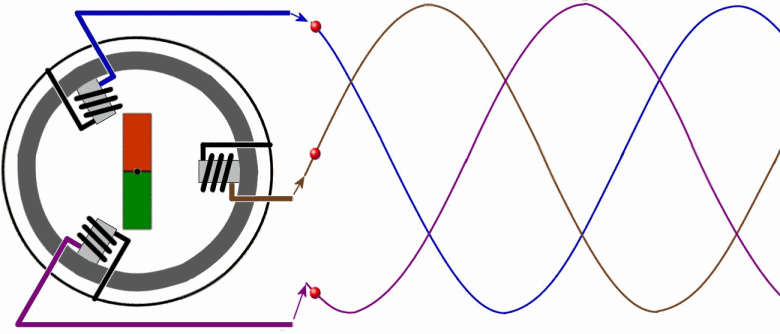
Рассмотрим упрощенно работу генератора трехфазного переменного тока. Обмотки статора (фазы А, В и С) генератора расположены под углом 120 градусов относительно друг друга. Ротор с магнитом вращаясь индуцирует в обмотках статора периодически изменяющиеся ЭДС. Выглядит это следующим образом:

Такое вращение происходит с частотой 50 оборотов в секунду, то есть с частотой 50 Герц. Это значит, что электроны движутся в течение 1 секунды 50 раз в одном направлении (положительный полупериод синусоиды), и 50 — в обратном (отрицательный полупериод), 100 раз проходя чрез нулевое значение. Получается, что к примеру обычная лама накаливания, включенная в сеть с такой частотой, будет затухать и вспыхивать примерно 100 раз за секунду, однако мы этого не замечаем в силу особенностей своего зрения.

Определение действующего напряжения

Теперь непосредственно о том, почему произошел переход от максимального, амплитудного значения напряжения 310 Вольт к действующему 220 Вольт. Ответ можно найти в самом определении.

Действующее (эффективное или среднеквадратичное) значение напряжения — это такое напряжение постоянного тока, которое на такой же резистивной нагрузке выделит такую же мощность, как измеряемое переменное напряжение. Соответственно, действующее значение силы тока — такое значение силы постоянного тока, при прохождении которого через резистивную нагрузку выделится такая же мощность, что и при прохождении измеряемого тока.

Можно сформулировать и немного иначе. Действующее значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведет такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.

Общая формула расчета действующего напряжения произвольной формы следующая:

Объяснение действующего напряжения

Определение и формула — это хорошо. Но лучше все понять на наглядном примере. Объяснить все можно через мощность. Причем есть сложный для восприятия способ и более простой, который мы и рассмотрим далее.

Нам нужно взять один период синусоиды переменного напряжения, на этом промежутке построить синусоиду переменного тока и проанализировать мощность. Начнем с периода синусоиды переменного напряжения. Здесь же построим синусоиду переменного тока с учетом условной резистивной нагрузки (например, лампочки). По закону Ома сила тока равна напряжению, деленному на сопротивление.

Точные значения в конкретный момент при данном объяснении не принципиальны, поэтому все построения приблизительные. Естественно нужно понимать, что деля напряжение на сопротивление, мы получим синусоиду переменного тока с амплитудой в R раз меньшей, чем у напряжения. R – это значение сопротивления.

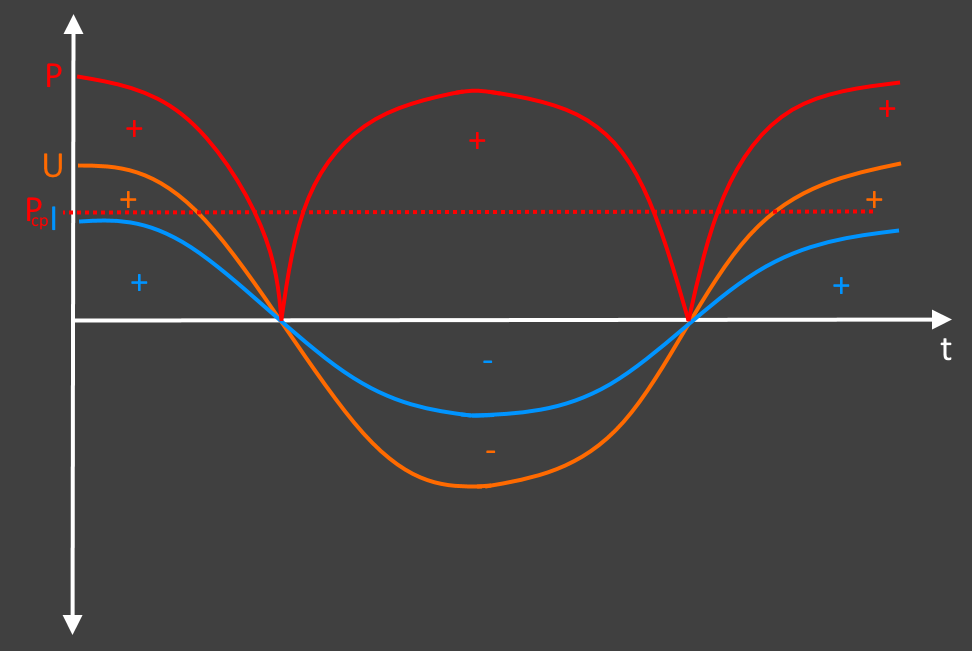
Теперь по двум синусоидам строим график мощности по формуле мощность равна силе тока умноженной на напряжение (P = I × U). Так как напряжение и ток имеют общие нулевые точки, то график мощности не будет заходить в отрицательную область. То есть сила тока со знаком «+» и напряжение со знаком «+» дадут мощность со знаком «+», так же как и сила тока со знаком «-» и напряжение со знаком «-» дадут мощность со знаком «+».

Анализируя полученный график можно отметить, что мощность пульсирующая. Она поднимается до максимального значения и падает до нуля, потом опять поднимается и снова падает. Как на эти колебания мощности реагируют электроприборы? Никак. Поскольку частота переменного тока 50 Герц, то эти колебания происходят очень быстро. Электроприборы откликаются не на максимальные и минимальные значения мощности, а на усредненные. То есть берется максимальное значение мощности и делится на два. Это значение называется действующим и находится по следующей формуле:

Pд = (Imax × Umax) / 2, где Pд — мощность действующая, Imax — сила тока максимальная, Umax — напряжение максимальное.

Двойку можно представить в виде корень из двух умножить на корень из двух. Получаем Действующее значение мощности = сила тока максимальная деленная на корень из двух умноженная на напряжение максимальное деленное на корень из двух (Pд = (Imax/√2) × (Umax/√2)).

Соответственно сила тока максимальная деленная на корень из двух — это действующее значение силы переменного тока, а напряжение максимальное деленное на корень из двух – это действующее значение переменного напряжения.

И действительно, если мы возьмем максимальное напряжение из предыдущего примера 309,1 Вольт и разделим на корень из двух, то получим действующее напряжение (то, которое показывает вольтметр) 219,4 Вольт.

Источник

Действующие значения тока и напряжения

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.

Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.

Действующее значение переменного тока — это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.

Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.

Мощность Р постоянного тока I , проходящего через сопротивление r , будет Р = Р 2 r .

Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от ( Im х sin ω t ) 2 х r за то же время.

Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √ M ,

Величина I называется действующим значением переменного тока.

Среднее значение i2 при переменном токе определим следующим образом.

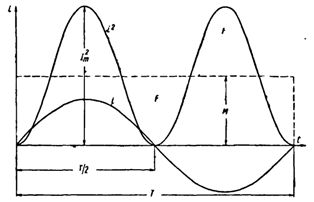
Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.

Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (- i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины.

Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно 1/2I 2 m . Следовательно, М = 1/2I 2 m

Так как действующее значение I переменного тока равно I = √ M , то окончательно I = Im / √ 2

Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:

Действующие значения переменных величин обозначаются прописными буквами без индексов ( I , U, Е).

На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.

При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √ 2 раз. От этого расположение векторов на диаграмме не изменяется.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Основные параметры переменного тока: период, частота, фаза, амплитуда, гармонические колебания

Переменный ток — электрический ток, направление и сила которого изменяются периодически. Так как обычно сила переменного тока изменяется по синусоидальному закону, то переменный ток представляет собой синусоидальные колебания напряжения и силы тока.

Поэтому к переменному току применимо все то, что относится к синусоидальным электрическим колебаниям. Синусоидальные колебания — колебания, при которых колеблющаяся величина изменяется по закону синуса. В данной статье поговорим о параметрах переменного тока.

Изменение ЭДС и изменение тока линейной нагрузки, подключенной к такому источнику, будет происходить по синусоидальному закону. При этом переменные ЭДС, переменные напряжения и токи, можно характеризовать основными четырьмя их параметрами:

Есть и вспомогательные параметры:

Далее рассмотрим все эти параметры по отдельности и во взаимосвязи.

Период — время, в течение которого система, совершающая колебания, проходит через все промежуточные состояния и нале снова возвращается к исходному.

Периодом Т переменного тока называется промежуток времени, за который ток или напряжение совершает один полный цикл изменений.

Поскольку источником переменного тока является генератор, то период связан со скоростью вращения его ротора, и чем выше скорость вращения витка или ротора генератора, тем меньшим оказывается период генерируемой переменной ЭДС, и, соответственно, переменного тока нагрузки.

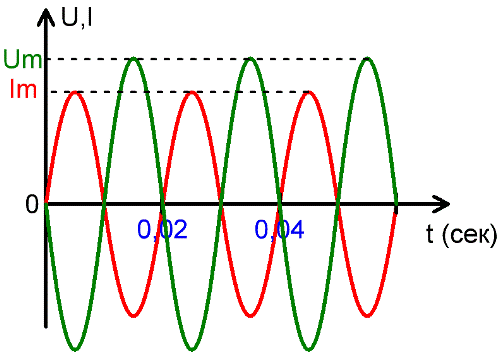
Период измеряется в секундах, миллисекундах, микросекундах, наносекундах, в зависимости от конкретной ситуации, в которой данный ток рассматривается. На вышеприведенном рисунке видно, как напряжение U с течением времени изменяется, имея при этом постоянный характерный период Т.

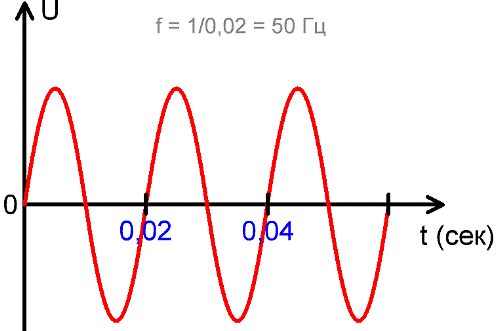
Частота f является величиной обратной периоду, и численно равна количеству периодов изменения тока или ЭДС за 1 секунду. То есть f = 1/Т. Единица измерения частоты — герц (Гц), названная в честь немецкого физика Генриха Герца, внесшего в 19 веке немалый вклад в развитие электродинамики. Чем меньше период, тем выше частота изменения ЭДС или тока.

Сегодня в России стандартной частотой переменного тока в электрических сетях является 50 Гц, то есть за 1 секунду происходит 50 колебаний сетевого напряжения.

В других областях электродинамики используются и более высокие частоты, например 20 кГц и более — в современных инверторах, и до единиц МГц в более узких сферах электродинамики. На приведенном выше рисунке видно, что за одну секунду происходит 50 полных колебаний, каждое из которых длится 0,02 секунды, и 1/0,02 = 50.

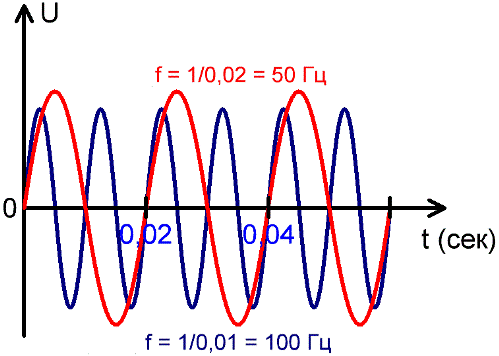
По графикам изменения синусоидального переменного тока с течением времени видно, что токи различной частоты содержат разное количество периодов на одном и том же отрезке времени.

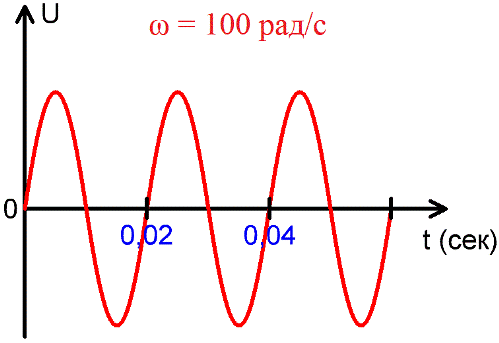
Угловая частота — число колебаний, совершаемых за 2пи сек.

За один период фаза синусоидальной ЭДС или синусоидального тока изменяется на 2пи радиан или на 360°, поэтому угловая частота переменного синусоидального тока равна:

Пользоваться числом колебаний на 2пи сек. (а не за 1 сек.) удобно потому, что в формулах, выражающих закон изменения напряжений и токов при гармонических колебаниях, выражающих индуктивное или емкостное сопротивление переменному току, и во многих других случаях частота колебаний n фигурируют вместе с множителем 2пи.

Фаза — состояние, стадия периодическою процесса. Более определенный смысл имеет понятие фаза в случае синусоидальных колебаний. На практике обычно играет роль не фаза сама по себе, а сдвиг фаз между какими-либо двумя периодическими процессами.

В данном случае под термином «фаза» понимают стадию развития процесса, и в данном случае, применительно к переменным токам и напряжениям синусоидальной формы, фазой называют состояние переменного тока в определенный момент времени.

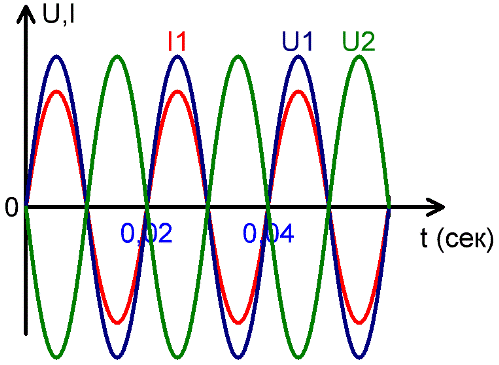
На рисунках можно видеть: совпадение напряжения U1 и тока I1 по фазе, напряжения U1 и U2 в противофазе, а также сдвиг по фазе между током I1 и напряжением U2. Сдвиг по фазе измеряется в радианах, долях периода, в градусах.

Говоря о величине синусоидального переменного тока или синусоидальной переменной ЭДС, наибольшее значение ЭДС или тока называют амплитудой или амплитудным (максимальным) значением.

Амплитуда — наибольшее значение величины, совершающей гармонические колебания (например, максимальное значение силы тока в переменном токе, отклонение колеблющегося маятника от положения равновесия), наибольшее отклонение колеблющейся величины от некоторого значения, условно принятого за начальное нулевое.

Строго говоря, термин амплитуда относится только к синусоидальным колебаниям, но его обычно (не вполне правильно) применяют в указанном выше смысле ко всяким колебаниям.

Если речь о генераторе переменного тока, то ЭДС на его выводах дважды за период достигает амплитудного значения, первое из которых +Eм, второе -Eм, соответственно во время положительного и отрицательного полупериодов. Аналогичным образом ведет себя и ток I, и обозначается соответственно Iм.

Гармонические колебания — колебания, в которых колеблющаяся величина, например напряжение в электрической цепи, меняется во времени по гармоническому синусоидальному или косинусоидальному закону. Графически представляются кривой — синусоидой.

Реальные процессы могут лишь приближенно быть гармоническими колебаниями. Однако если колебания отражают наиболее характерные черты процесса, то такой процесс считают гармоническими, что существенно облегчает решение многих физических и технических задач.

Движения, близкие к гармоническим колебаниям, совершаются в различных системах: механических (колебания маятника), акустических (колебания столба воздуха в органной трубе), электромагнитных (колебания в LC-контуре) и др. Теория колебаний рассматривает эти различные по физической природе явления с единой точки зрения и определяет их общие свойства.

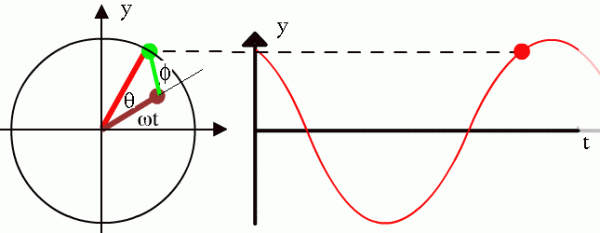
Графически гармонические колебания удобно представить с помощью вектора, вращающегося с постоянной угловой скоростью вокруг оси, перпендикулярной к этому вектору и проходящей через его начало. Угловая скорость вращения вектора соответствует круговой частоте гармонического колебания.

Векторная диаграмма одного гармонического колебания

Периодический процесс любой формы может быть разложен в бесконечный ряд простых гармонических колебаний с различными частотами, амплитудами и фазами.

Гармоника — гармоническое колебание, частота которого в целое число раз больше частоты некоторого другого колебания, называемого основным тоном. Номер гармоники указывает, во сколько именно раз частота ее больше частоты основного тона (например, третья гармоника — гармоническое колебание с частотой, втрое большей, чем частота основного тона).

Всякое периодическое, но не гармоническое (т. е. отличающееся по форме от синусоидального) колебание может быть представлено в виде суммы гармонических колебаний — основного тона и ряда гармоник. Чем больше рассматриваемое колебание отличается по форме от синусоидального, тем большее число гармоник оно содержит.

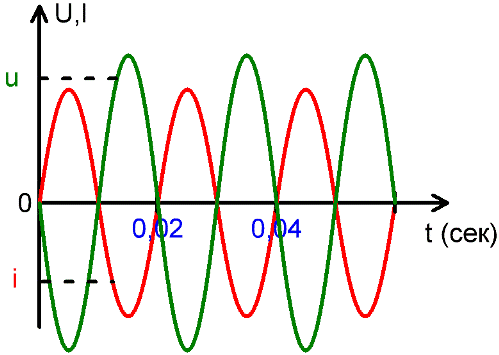
Мгновенное значение u и i

Значение ЭДС или тока в конкретный текущий момент времени называется мгновенным значением, они обозначаются маленькими буквами u и i. Но поскольку эти значения все время меняются, то судить о переменных токах и ЭДС по ним неудобно.

Действующие значения I, E и U

Способность переменного тока к совершению какой-нибудь полезной работы, например механически вращать ротор двигателя или производить тепло на нагревательном приборе, удобно оценивать по действующим значениям ЭДС и токов.

Так, действующим значением тока называется значение такого постоянного тока, который при прохождении по проводнику в течение одного периода рассматриваемого переменного тока, производит такую же механическую работу или такое же количество теплоты, что и данный переменный ток.

Действующие значения напряжений, ЭДС и токов обозначают заглавными буквами I, E и U. Для синусоидального переменного тока и для синусоидального переменного напряжения действующие значения равны:

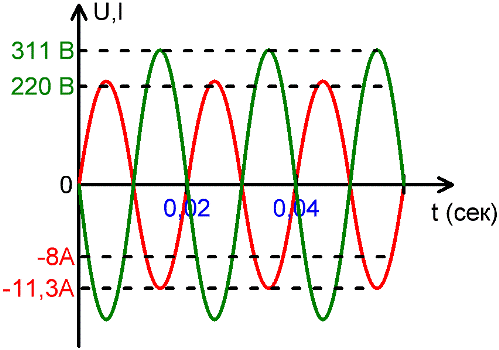
Действующее значение тока и напряжения удобно практически использовать для описания электрических сетей. Например значение в 220-240 вольт — это действующее значение напряжения в современных бытовых розетках, а амплитуда гораздо выше — от 311 до 339 вольт.

Так же и с током, например когда говорят, что по бытовому нагревательному прибору протекает ток в 8 ампер, это значит действующее значение, в то время как амплитуда составляет 11,3 ампер.

Так или иначе, механическая работа и электрическая энергия в электроустановках пропорциональны действующим значениям напряжений и токов. Значительная часть измерительных приборов показывает именно действующие значения напряжений и токов.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):

• амплитуда,
• период,
• частота,
• циклическая частота,
• фаза,
• начальная фаза.

Такие величины, как амплитуду и период, можно определить по графику колебаний.

Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.

Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.

А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.

Что такое амплитуда

Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.

Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.

В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.

Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.

К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.

Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».

С помощью графика амплитуду можно определить так (рис. 2):

Что такое период

Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.

Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.

( large T left( c right) ) – период колебаний.

Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.

Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Период – это время одного полного колебания.

На графике период найти удобнее одним из таких способов (рис. 4):

Что такое частота

Обозначают ее с помощью греческой буквы «ню» ( large nu ).

Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».

Поэтому, размерность частоты — это единицы колебаний в секунду:

( large nu left( frac{1}{c} right) ).

Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large  displaystyle frac{1}{c} = c^{-1} ).

Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.

Одно колебание в секунду соответствует частоте в 1 Герц.

[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]

Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:

[ large boxed{ nu = frac{1}{T} }]

Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Что такое циклическая частота

Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.

Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:

( large displaystyle omega left( frac{text{рад}}{c} right) )

Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).

Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».

Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:

[ large boxed{ omega = 2pi cdot nu }]

Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.

Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.

Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).

И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.

Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.

Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Что такое начальная фаза и как определить ее по графику колебаний

Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).

(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).

Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.

Определим угол (large varphi_{0} ) с помощью графика колебаний.

Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

• Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
• Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.

[large T = 5 – 1 = 4 left( text{сек} right)]

Из графика следует, что период T = 4 сек.

• Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):

[large frac{Delta t }{T} = frac{1}{4} ]

Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.

• Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.

Для этого используем формулу:

[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]

(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )

Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.

• В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

[large varphi_{0} = — frac{pi }{2} ]

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».

Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).

Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».

А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».

Примечания:

1. Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
2. На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.

Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.

Что такое фаза колебаний

Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).

Различия между фазой и начальной фазой

Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.

Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.

Как на графике колебаний отметить фазу

На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.

На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.

Как определить фазу с помощью формулы

Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.

Время колебаний t будет величиной переменной.

Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:

[large boxed{ varphi = omega cdot t + varphi_{0} }]

Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.

Что такое разность фаз

Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.

Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.

Обозначим их:

( large varphi_{01}) – для первого процесса и,

( large varphi_{02}) – для второго процесса.

Определим разность фаз между первым и вторым колебательными процессами:

[large boxed{ Delta varphi = varphi_{01} —  varphi_{02} }]

Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.

Как связаны характеристики колебаний — формулы

Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.

Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.

• Связь между периодом, количеством колебаний и общим временем колебательного процесса:

[large boxed{ T cdot N = t }]

( large T left( c right) ) – время одного полного колебания (период колебаний);

( large N left( text{шт} right) ) – количество полных колебаний;

( large t left( c right) ) – общее время для нескольких колебаний;

• Период и частота колебаний связаны так:

[large boxed{ T = frac{1}{nu} }]

(large nu left( text{Гц} right) ) – частота колебаний.

• Количество и частота колебаний связаны формулой:

[large boxed{ N = nu cdot t}]

• Связь между частотой и циклической частотой колебаний:

[large boxed{ nu cdot 2pi = omega }]

(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.

• Фаза и циклическая частота колебаний связаны так:

[large boxed{ varphi = omega cdot t + varphi_{0} }]

(large varphi_{0} left( text{рад} right) ) — начальная фаза;

(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;

• Между фазой и количеством колебаний связь описана так:

[large boxed{ varphi = N cdot 2pi }]

• Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:

[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]

(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.

Какое напряжение между фазой и нулём в отечественной электросети: 220 или 310? На самом деле и одно и другое! Всё дело в том, что в наших сетях протекает синусоидальный ток, а у синусоиды есть ряд характеристик и особенностей, которые мы попытаемся рассмотреть простым языком в этой статье.

Речь далее пойдет только о синусоидальном переменном токе или напряжении. Для тока другой формы всё сказанное далее, в принципе, справедливо, но будут отличаться формулы для вычисления и, соответственно, числовые значения.

Синусоида, её амплитуда и другие характеристики

Все мы знаем, что между фазой и нулём 220 вольт (230В по ГОСТу), но многие знают что выпрямленное и сглаженное сетевое напряжение превышает 300 вольт, да и конденсаторы в фильтры выпрямителей подбирают не ниже чем 400 вольт, откуда они берутся? Для начала рассмотрим график, на котором изображено синусоидальное напряжение в привычной всем розетке 220В.

На рисунке 1 по вертикали размечено напряжение в вольтах, а по горизонтали время. Обратите внимание, что напряжение в электросети периодично изменяется от -310 вольт, до + 310 вольт, каждый период изменений длится 20 миллисекунд, после чего повторяется.

Точно описать любую величину, изменяющуюся по синусоидальному закону можно с помощью трёх характеристик:

1. Амплитуда — это высота синусоиды от нуля до верхней или нижней точки. В нашем случае это 310В. Обозначается буквами Im или Um, для тока и напряжения соответственно.
2. Период — расстояние между двумя соседними максимумами или минимумами синусоиды. В электросетях РФ он равен 20 миллисекунд, так как стандартная частота — 50 Гц. Обозначается буквой T.
3. Начальный фазовый угол — это величина, которая отражает насколько сдвинута синусоида по горизонтали относительно начального момента времени наблюдения (нулевой секунды). Если проще, то на графике выше фаза в начале графика начинается с 0, значит она не сдвинута, если бы начиналась с другой величины — то была бы сдвинутой на определенный угол.

При рассмотрении однофазной сети начальный фазовый угол нас не интересует, он используется при исследовании трёхфазного напряжения.

Рассмотрим этот график еще раз, но отметим на нём амплитуду и период.

График описывает формула синусоидального напряжения (для тока аналогично, но U меняется на I):

Из этого следует, что величина напряжения (или тока) в каждый конкретный момент времени разная, такая величина называется мгновенной. Соответственно и мгновенная мощность, выделяемая на активной нагрузке (R) в каждый момент будет разной:

Это подходящая формула для описания мгновенного состояния электрической цепи, но совершенно неудобная и неподходящая для измерения параметров и описания электрических цепей в общем. Поэтому используют какие-то усреднённые значения электрической мощности, напряжения и тока.

В литературе принято объяснять смысл действующих и амплитудных значений на примере силы тока. К тому же по определения, формулы и их смысл аналогичны, и для напряжения, и для тока. Поэтому я немного отойду от синусоидального напряжения, и далее пойдет речь о токе.

Действующее, среднеквадратичное, эффективное?

Теперь вы знаете, что амплитуда фазного напряжения в электросети равна 310В, но что такое 220В и откуда они берутся? Дело в том, что — 220В это действующее напряжение, его же называют среднеквадратичным или эффективным.

Это значит, что если на лампочку накаливания или нагревательную спираль подать переменный ток с действующим значением (силой) в 1 ампер, то на ней выделится та же мощность (количество тепла), как если бы через неё протекал постоянный ток в 1 ампер.

Для нахождения среднего значения переменного синусоидального тока за половину периода, необходимо проинтегрировать формулу этого тока, при этом пределами интегрирования выбирается половина периода:

Как отмечалось выше, формула для среднего переменного синусоидального напряжения (как и для ЭДС) будет аналогичной:

Но это средние величины, которые на практике не используется так часто, как действующие величины. Действующее напряжение или ток, находится подобным образом, при вычислениях интегрируется та же формула, но возведенная в квадрат, после чего извлекается корень. Пределы интегрирования уже не половина, а целый период. Кстати, поэтому действующее значение называется еще и «среднеквадратичным». Формулу действующего значения переменного синусоидального тока:

Действующий ток (Iд) или напряжение (Uд), в корень из двух раз меньше, чем амплитудное. Чтобы его вычислить, нужно амплитудное значение разделить на 1.41, или умножить на 0.707.

Uд=Um/1.41=0.707*Um

И наоборот, чтобы узнать амплитудное значение при известном действующем, нужно умножить его на 1.41 или разделить на 0.707. Приведем пример, из графика на рисунке 1, мы узнали, что амплитуда напряжения в однофазной электросети 310 вольт, найдем его действующее значение:

Uд=Um/1.41=310/1.41=219,8~220В

Мы получили привычные нам 220В. Как отмечалось ранее, действующие значения напряжения и тока удобно использовать для расчетов и описания электрических цепей, поэтому и говорят «в розетке 220В», «линейное напряжение 380В» и так далее.

Повторим пройденное: непрерывное тепловое воздействие переменного синусоидального тока на какую-то активную нагрузку за определенный период времени будет численно равно тепловому воздействию постоянного тока за тот же период, при условии, что величина постоянного тока была в 1.41 раз меньше амплитуды переменного. То есть за то же время выделится столько же теплоты.

В таком случае, при активной нагрузке (резисторы, ТЭНы, нихромовые спирали, лампы накаливания), можно приравнять действующее значение переменного тока или напряжения, к такому же по величине постоянному току или напряжению.

Какое напряжение измеряет мультиметр, амперметр или вольтметр?

В подавляющем большинстве случаев если на измерительном приборе вы выбираете режим измерения переменного тока или напряжения (U~, I~), вы измерите именно действующие значения. Однако есть и специфичные приборы, измеряющие амплитудные значения параметров в электрической сети, а также на электронных осциллографах могут выводится и действующие, и амплитудные величины измеряемых сигналов. Измерение амплитудных значений может обозначаться как Im.

При этом далеко не все приборы могут измерять переменный ток по форме отличный от синусоидального — пилообразный, прямоугольный и так далее. Вы могли видеть, что на хороших мультиметрах написано загадочное «TRUE RMS», что расшифровывается как: «True Root Mean Sqare», а переводится как — истинное среднеквадратичное значение. Такие измерительные приборы показывают действующие значения напряжений и токов любых форм (не только синусоидальных).

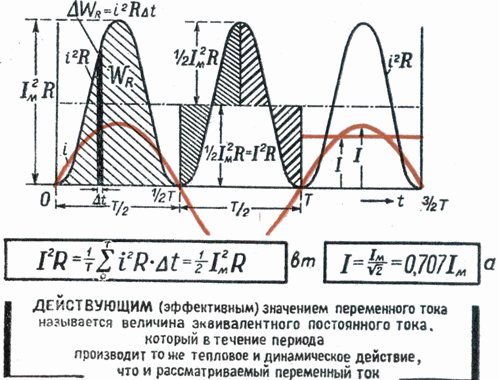
В завершение этой статьи, предлагаю вам закрепить знания и ознакомиться с прекрасным советским плакатом, на эту тему

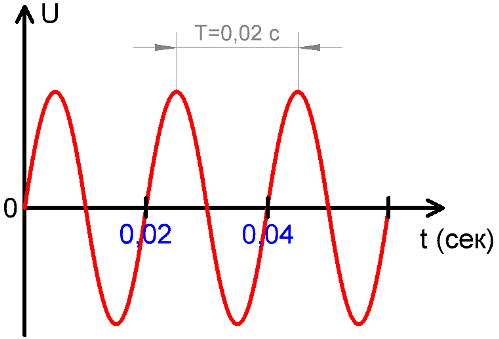
Помогите пожалуйста!!! По графику определите амплитуду напряжения и период колебания….