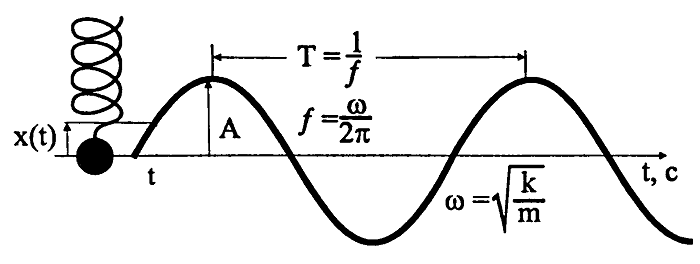
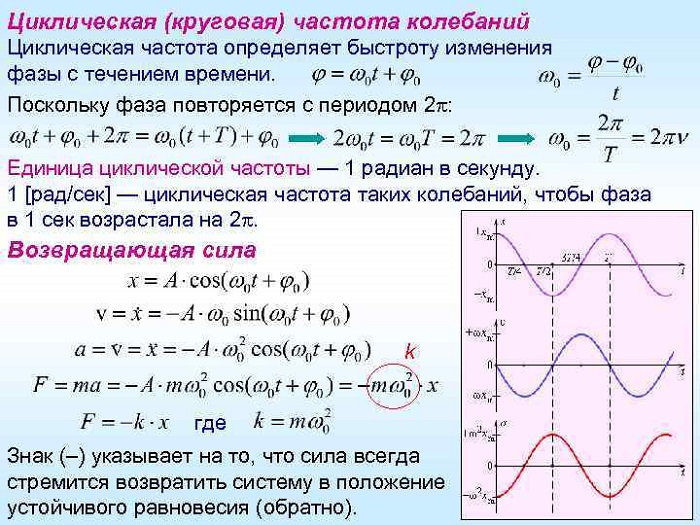
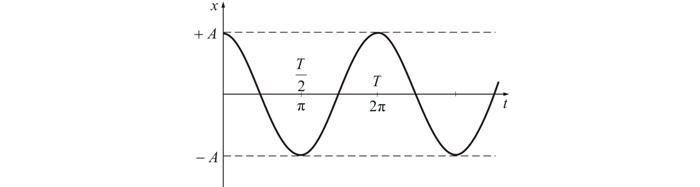
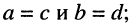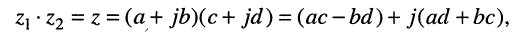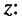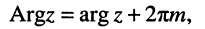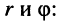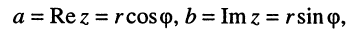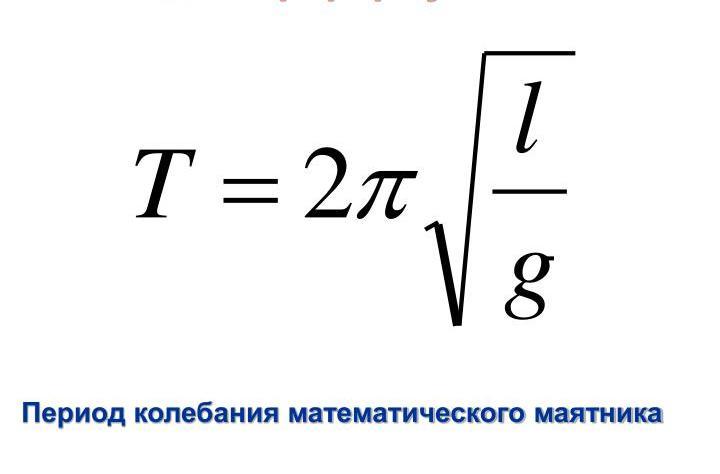Электромагнитные колебания и волны
Свободные электромагнитные колебания. Колебательный контур
Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.
Колебательный контур — это замкнутый контур, образованный последовательно соединенными конденсатором и катушкой.
Сопротивление катушки ( R ) равно нулю.
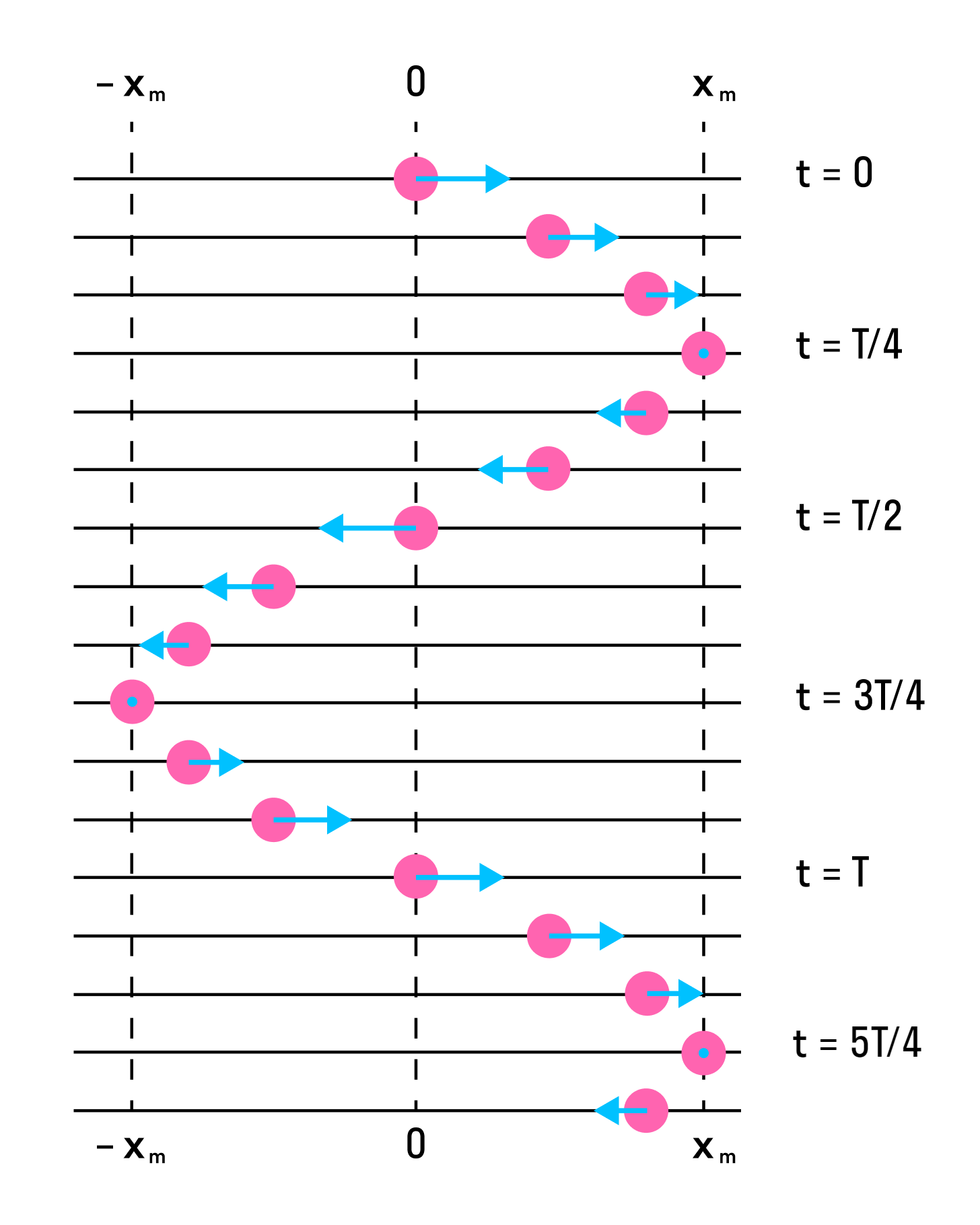
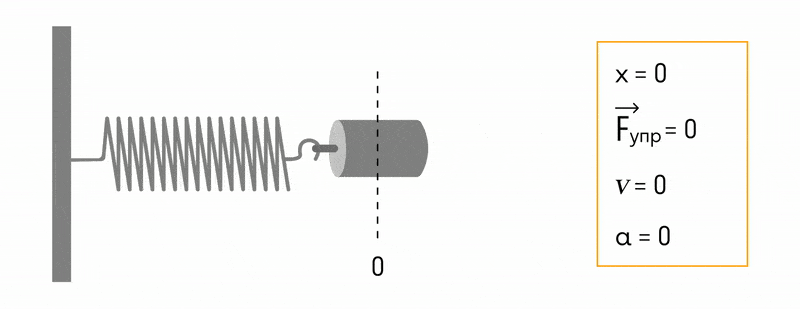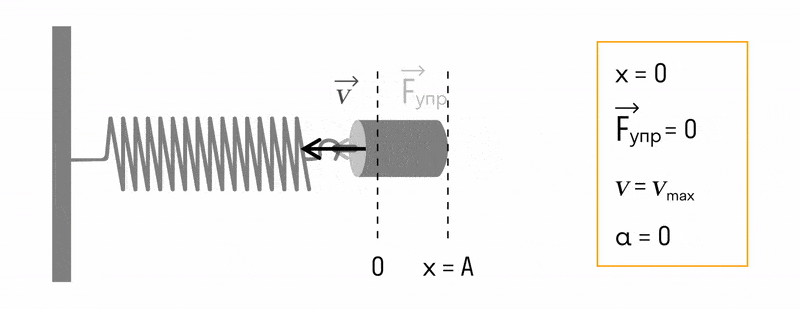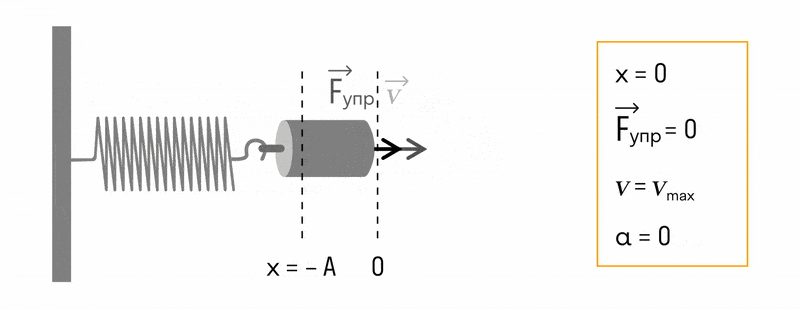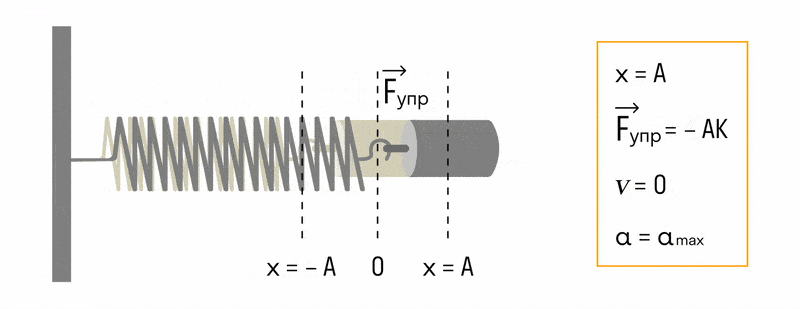
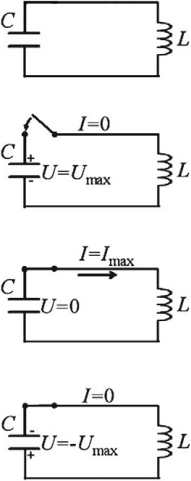
Если зарядить конденсатор до напряжения ( U_m ) , то в начальный момент времени ( t_1=0 ) , напряжение на конденсаторе будет равно ( U_m ) . Заряд конденсатора в этот момент времени будет равен ( q_m=CU_m ) . Сила тока равна нулю.
Полная энергия системы будет равна энергии электрического поля:
Конденсатор начинает разряжаться, по катушке начинает течь ток. Вследствие самоиндукции в катушке конденсатор разряжается постепенно.
Ток достигает своего максимального значения ( I_m ) в момент времени ( t_2=T/4 ) . Заряд конденсатора в этот момент равен нулю, напряжение на конденсаторе равно нулю.
Полная энергия системы в этот момент времени равна энергии магнитного поля:
В следующий момент времени ток течет в том же направлении, постепенно (вследствие явления самоиндукции) уменьшаясь до нуля. Конденсатор перезаряжается. Заряды обкладок имеют заряды, по знаку противоположные первоначальным.
В момент времени ( t_3=T/2 ) заряд конденсатора равен ( q_m ) , напряжение равно ( U_m ) , сила тока равна нулю.
Полная энергия системы равна энергии электрического поля конденсатора.
Затем конденсатор снова разряжается, но ток через катушку течет в обратном направлении.
В момент времени ( t_4=3T/4 ) сила тока в катушке достигает максимального значения, напряжение на конденсаторе и его заряд равны нулю. С этого момента ток в катушке начинает убывать, но не сразу (явление самоиндукции). Энергия магнитного поля переходит в энергию электрического поля. Конденсатор начинает заряжаться, и через некоторое время его заряд равен первоначальному, а сила тока станет равной нулю.
Через время, равное периоду ( T ) , система возвращается в начальное состояние. Совершилось одно полное колебание, дальше процесс повторяется.
Важно!
Колебания, происходящие в колебательном контуре, – свободные. Они совершаются без какого-либо внешнего воздействия — только за счет энергии, запасенной в контуре.
В контуре происходят превращения энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно. В любой произвольный момент времени полная энергия в контуре равна:
где ( i, u, q ) – мгновенные значения силы тока, напряжения, заряда в любой момент времени.
Эти колебания являются затухающими. Амплитуда колебаний постепенно уменьшается из-за электрического сопротивления проводников.
Вынужденные электромагнитные колебания. Резонанс
Вынужденными электромагнитными колебаниями называют периодические изменения заряда, силы тока и напряжения в колебательном контуре, происходящие под действием периодически изменяющейся синусоидальной (переменной) ЭДС от внешнего источника:
где ( varepsilon ) – мгновенное значение ЭДС, ( varepsilon_m ) – амплитудное значение ЭДС.
При этом к контуру подводится энергия, необходимая для компенсации потерь энергии в контуре из-за наличия сопротивления.
Резонанс в электрической цепи – явление резкого возрастания амплитуды вынужденных колебаний силы тока в колебательном контуре с малым активным сопротивлением при совпадении частоты вынужденных колебаний внешней ЭДС с частотой собственных колебаний в контуре.
Емкостное и индуктивное сопротивления по-разному изменяются в зависимости от частоты. С увеличением частоты растет индуктивное сопротивление, а емкостное уменьшается. С уменьшением частоты растет емкостное сопротивление и уменьшается индуктивное сопротивление. Кроме того, колебания напряжения на конденсаторе и катушке имеют разный сдвиг фаз по отношению к колебаниям силы тока: для катушки колебания напряжения и силы тока имеют сдвиг фаз ( varphi_L=-pi/2 ) , а на конденсаторе ( varphi_C=pi/2 ) . Это означает, что когда растет энергия магнитного поля катушки, то энергия электрического поля конденсатора убывает, и наоборот. При резонансной частоте индуктивное и емкостное сопротивления компенсируют друг друга и цепь обладает только активным сопротивлением. При резонансе выполняется условие:
Резонансная частота вычисляется по формуле:
Важно!
Резонансная частота не зависит от активного сопротивления ( R ) . Но чем меньше активное сопротивление цепи, тем ярче выражен резонанс.
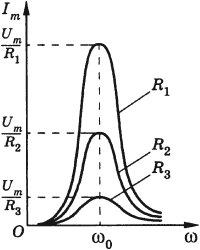
Чем меньше потери энергии в цепи, тем сильнее выражен резонанс. Если активное сопротивление очень мало ( (Rto0) ) , то резонансное значение силы тока неограниченно возрастает. С увеличением сопротивления максимальное значение силы тока уменьшается, и при больших значениях сопротивления резонанс не наблюдается.
График зависимости амплитуды силы тока от частоты называется резонансной кривой. Резонансная кривая имеет больший максимум в цепи с меньшим активным сопротивлением.
Одновременно с ростом силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке. Эти напряжения становятся одинаковыми и во много раз больше внешнего напряжения. Колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. При резонансе амплитуды этих напряжений одинаковы и они компенсируют друг друга. Падение напряжения происходит только на активном сопротивлении.
При резонансе возникают наилучшие условия для поступления энергии от источника напряжения в цепь: при резонансе колебания напряжения в цепи совпадают по фазе с колебаниями силы тока. Установление колебаний происходит постепенно. Чем меньше сопротивление, тем больше времени требуется для достижения максимального значения силы тока за счет энергии, поступающей от источника.
Явление резонанса используется в радиосвязи. Каждая передающая станция работает на определенной частоте. С приемной антенной индуктивно связан колебательный контур. При приеме сигнала в катушке возникают переменные ЭДС. С помощью конденсатора переменной емкости добиваются совпадения частоты контура с частотой принимаемых колебаний. Из колебаний всевозможных частот, возбужденных в антенне, контур выделяет колебания, равные его собственной частоте.
Резонанс может привести к перегреву проводов и аварии, если цепь не рассчитана на работу в условиях резонанса.
Гармонические электромагнитные колебания
Гармоническими электромагнитными колебаниями называются периодические изменения заряда, силы тока и напряжения, происходящие по гармоническому – синусоидальному или косинусоидальному – закону.
В электрических цепях это могут быть колебания:
- силы тока – ( i=I_mcos(omega t+varphi+frac<pi><2>); )
- напряжения – ( u=U_mcos(omega t+varphi); )
- заряда – ( q=q_mcos(omega t+varphi); )
- ЭДС – ( varepsilon=varepsilon_msinomega t. )
В этих уравнениях ( omega ) –циклическая частота, ( varphi ) – начальная фаза колебаний, амплитудные значения: силы тока – ( I_m ) , напряжения – ( U_m ) и заряда – ( q_m ) .
Важно!
Если в начальный момент времени заряд имеет максимальное значение, а сила тока равна нулю, то колебания заряда совершаются по закону косинуса с начальной фазой, равной нулю. Если в начальный момент времени заряд равен нулю, а сила тока максимальна, то колебания заряда совершаются по закону синуса.
Сила тока равна первой производной заряда от времени:
Амплитуда колебаний силы тока равна:
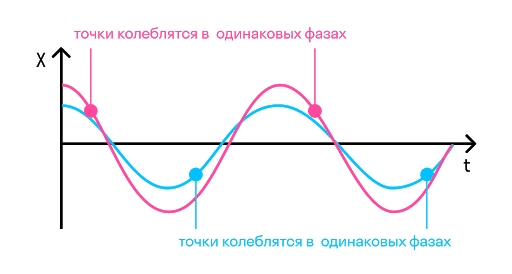
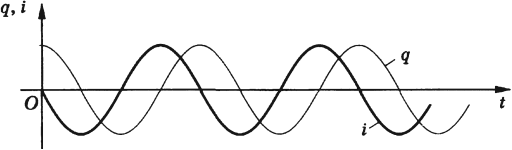
Колебания заряда и напряжения в колебательном контуре происходят в одинаковых фазах. Амплитуда напряжения равна:
Колебания силы тока смещены по фазе относительно колебаний заряда на ( pi/2 ) .
Период свободных электромагнитных колебаний
Период свободных электромагнитных колебаний находится по формуле Томсона:
где ( L ) – индуктивность катушки, ( C ) – электроемкость конденсатора.
Важно!
Период и циклическая частота не зависят от начальных условий, а определяются только индуктивностью катушки и электроемкостью конденсатора. Амплитуда колебаний заряда и силы тока определяются начальным запасом энергии в контуре.
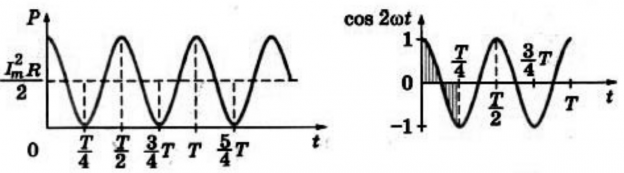
При свободных гармонических колебаниях происходит периодическое преобразование энергии. Период колебаний энергии в два раза меньше, чем период колебаний заряда, силы тока и напряжения. Частота колебаний энергии в два раза больше частоты колебаний заряда, силы тока и напряжения.
Переменный ток. Производство, передача и потребление электрической энергии
Переменным называется ток, изменяющийся по величине и направлению по гармоническому закону.
Переменный ток представляет пример вынужденных электромагнитных колебаний. Для описания переменного электрического тока используют следующие величины:
• мгновенное значение силы тока – i;
• мгновенное значение напряжения – u;
• амплитудное значение силы тока – Im;
• амплитудное значение напряжения –Um.
Цепь переменного тока представляет собой колебательный контур, к которому приложена внешняя синусоидальная ЭДС. В цепь переменного тока могут включаться различные нагрузки: резистор, катушка, конденсатор.
Активное сопротивление
Проводник, преобразующий всю энергию электрического тока во внутреннюю, называется активным сопротивлением ( R ) . (Эту величину мы раньше называли сопротивлением.) Активное сопротивление зависит от материала проводника, его длины и площади поперечного сечения и не зависит от частоты переменного тока.
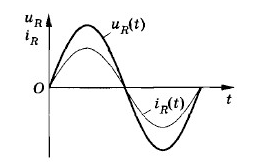
В проводнике с активным сопротивлением колебания силы тока и напряжения совпадают по фазе:
Мгновенное значение мощности: ( p=i^2R, )
среднее значение мощности за период: ( overline
=frac<2>. )
Действующим значением силы переменного тока ( I_Д ) называют значение силы постоянного тока, который в том же проводнике выделяет то же количество теплоты , что и переменный ток за то же время:
Действующим значением напряжения переменного тока ( U_Д ) называют значение напряжения постоянного тока, который в том же проводнике выделяет то же количество теплоты, что и переменный ток за то же время:
Для цепи с активным сопротивлением выполняется закон Ома для мгновенных, амплитудных и действующих значений.
Индуктивное сопротивление
Катушка в цепи переменного тока имеет большее сопротивление, чем в цепи постоянного тока. В такой цепи колебания напряжения опережают колебания силы тока по фазе на ( pi/2 ) . Колебания силы тока и напряжения происходят по закону:
Амплитуда силы тока в катушке:
где ( L ) – индуктивность катушки.
Индуктивным сопротивлением ( X_L ) называют физическую величину, равную произведению циклической частоты на индуктивность катушки:
Индуктивное сопротивление прямо пропорционально частоте. Физический смысл индуктивного сопротивления: ЭДС самоиндукции препятствует изменению в ней силы тока. Это приводит к существованию индуктивного сопротивления, уменьшающего силу тока.
Для цепи с индуктивным сопротивлением выполняется закон Ома.
Емкостное сопротивление
В цепи постоянного тока через конденсатор ток не идет. Для переменного тока конденсатор обладает конечным сопротивлением, обратно пропорциональным его емкости. В цепи переменного тока сопротивление конденсатора меньше, чем в цепи постоянного тока.
В такой цепи колебания напряжения отстают от колебаний силы тока по фазе на ( pi/2 ) . Колебания силы тока и напряжения происходят по закону:
Амплитуда силы тока в катушке: ( I_m=Comega U_m. ) .
Если ввести обозначение ( X_C=frac<1> <omega C>) , то получим соотношение между амплитудными значениями силы тока и напряжения, аналогичное закону Ома: ( I_m=frac. )
Емкостным сопротивлением ( X_C ) называют величину, обратную произведению циклической частоты на электроемкость конденсатора. Емкостное сопротивление обратно пропорционально частоте.
Физический смысл емкостного сопротивления: изменению переменного тока в любой момент времени противодействует электрическое поле между обкладками конденсатора.
В цепи переменного тока колебания силы тока и ЭДС происходят по синусоидальному закону с одинаковой циклической частотой ( omega ) и разностью фаз ( varphi ) :
Соотношения амплитудных значений силы тока ( I_m ) и ЭДС ( varepsilon_m ) в цепи переменного тока связаны между собой законом Ома для цепи переменного тока:
Он гласит: амплитуда силы переменного тока прямо пропорциональна амплитуде ЭДС и обратно пропорциональна полному сопротивлению цепи:
Величина ( Z ) называется полным сопротивлением цепи переменного тока.
Электрическая энергия имеет перед другими видами энергии следующие преимущества:
- можно передавать на большие расстояния с малыми потерями;
- удобно распределять между потребителями;
- легко превращать в другие виды энергии.
В настоящее время производится и используется энергия переменного тока. Это связано с возможностью преобразовывать его напряжение и силу тока с малыми потерями энергии, что особенно важно при передаче электроэнергии на большие расстояния.
Различают следующие типы электростанций:
Получение переменного тока
Переменный ток получают с помощью генератора переменного тока.
Генератор переменного тока (электромеханический генератор переменного тока) – это устройство, преобразующее механическую энергию в электрическую. В основе работы генератора переменного тока лежит явление электромагнитной индукции.
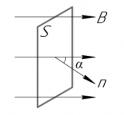
Процесс получения переменного тока можно рассмотреть на примере вращения витка провода в однородном магнитном поле. Магнитный поток через площадь витка равен:
Если период вращения витка ( T ) , то угол ( alpha=frac<2pi t>=omega t ) .
ЭДС индукции изменяется по закону ( e=-Phi’=BSomegasinomega t=varepsilon_msinomega t. )
Амплитуда ЭДС ( varepsilon_m=BSomega. )
Если рамка содержит ( N ) витков, то ( varepsilon_m=NBSomega. )
Основные части генератора переменного тока:
- обмотка статора с большим числом витков, в ней индуцируется ЭДС. Статор состоит из отдельных пластин из электротехнической стали для уменьшения нагрева от вихревых токов;
- ротор (вращающаяся часть генератора) создает магнитное поле. Для получения нужной частоты переменного тока может иметь несколько пар полюсов. На гидроэлектростанциях в генераторе число пар полюсов равно 40–50, на тепловых электростанциях – 10 -16 ;
- клеммы для снятия напряжения.
Промышленные генераторы вырабатывают напряжение порядка 10 4 В. Промышленная частота переменного тока в нашей стране 50 Гц.
Передача электроэнергии
Электроэнергия производится в основном вдалеке от основных потребителей энергии, там, где есть топливные ресурсы.
С электростанции переменный ток по проводам линии электропередач (ЛЭП) поступает к различным потребителям электрической энергии. Для уменьшения потерь при передаче переменного тока необходимо использовать высокое напряжение. Чем длиннее линия, тем выше должно быть напряжение. В высоковольтных ЛЭП оно может достигать 500 кВ. Генераторы на электростанциях вырабатывают напряжение 16–20 кВ. Потребителям не нужно высокое напряжение. Возникает необходимость преобразования напряжения. С электростанции электрический ток поступает на повышающую подстанцию, затем передается по линии электропередач на понижающую подстанцию, где напряжение понижается до 6–10 кВ, а затем до 220–380 В. Для преобразования напряжения используют трансформатор.
Трансформатор – устройство, преобразующее переменное напряжение без изменения его частоты.
На схемах трансформатор обозначается:
Основные части трансформатора:
- замкнутый сердечник из электротехнической стали;
- две катушки-обмотки.
Катушка, подключаемая к источнику переменного напряжения, называется первичной обмоткой; катушка, к которой подключается нагрузка, – вторичной обмоткой.
Сердечник набирается из отдельных пластин для уменьшения потерь на нагревание вихревыми токами.
Принцип действия основан на явлении электромагнитной индукции. При подключении первичной обмотки к полюсам источника напряжения в ней возникает переменный ток. Напряжение изменяется с течением времени по гармоническому закону. С такой же частотой будут изменяться сила тока в катушке и магнитный поток, создаваемый этим током.
При изменении магнитного потока в каждом витке провода первичной обмотки возникает переменная ЭДС самоиндукции. Этот магнитный поток будет пронизывать и вторую катушку. В каждом ее витке возникает ЭДС индукции, изменяющаяся по гармоническому закону с той же частотой. Число витков в обмотках различно. Отношение ЭДС самоиндукции ( varepsilon_1 ) в первичной обмотке к ЭДС индукции во вторичной обмотке ( varepsilon_2 ) равно отношению числа витков в первичной обмотке ( N_1 ) к числу витков во вторичной обмотке ( N_2 ) :
Режим работы
- Режим холостого хода – разомкнута цепь вторичной обмотки. Напряжение ( U_2 ) на ее концах в любой момент времени равно ЭДС индукции ( varepsilon_2 ) , взятой с противоположным знаком. Поэтому можно записать:
где ( k ) – коэффициент трансформации.
Если ( k>1 ) , то трансформатор понижающий, если ( k , то повышающий.
- Режим нагрузки. При подключении нагрузки к концам вторичной обмотки в ней возникает переменный ток. Напряжение ( U_2 ) на ее концах в любой момент времени отличается от ЭДС индукции ( varepsilon_2 ) на величину падения напряжения на внутреннем сопротивлении вторичной обмотки ( r ) : ( U_2=varepsilon_2-I_2r ) или ( U_2=I_2R ) .
Мощность тока в обмотках одинакова. Поэтому увеличение напряжения на входе повышающего трансформатора в ( k ) раз сопровождается уменьшением силы тока во вторичной катушке во столько же раз.
В трансформаторе нет потерь на трение, так как нет вращающихся частей. Потери в сердечнике состоят из потерь на нагревание и на перемагничивание.
Отношение мощности ( P_2 ) , потребляемой нагрузкой, к мощности ( P_1 ) , потребляемой первичной обмоткой трансформатора, называется коэффициентом полезного действия трансформатора:
Потребление электрической энергии: промышленность – около 70%; сельское хозяйство; транспорт; строительство; средства связи; в быту.
Электромагнитное поле
Электромагнитное поле – это особый вид материи, с помощью которого осуществляется электромагнитное взаимодействие заряженных тел или частиц.
Это понятие было введено Д. Максвеллом, развившим идеи Фарадея о том, что переменное магнитное поле порождает вихревое электрическое поле.
Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты. Вихревое электрическое поле порождает появление вихревого магнитного поля и так далее. Эти переменные электрическое и магнитное поля, существующие одновременно, и образуют единое электромагнитное поле.
Характеристиками этого поля являются вектор напряженности и вектор магнитной индукции.
Если электрический заряд покоится, то вокруг него существует только электрическое поле.
Если напряженность электрического поля равна нулю, а магнитная индукция отлична от нуля, то обнаруживается только магнитное поле.
Если электрический заряд двигается с постоянной скоростью, то вокруг него существует электромагнитное поле.
Максвелл предположил, что при ускоренном движении зарядов в пространстве будет возникать возмущение, которое будет распространяться в вакууме с конечной скоростью. Когда это возмущение достигнет второго заряда, то изменится сила, с которой электромагнитное поле действует на этот заряд.
При ускоренном движении заряда происходит излучение электромагнитной волны. Электромагнитное поле материально. Оно распространяется в пространстве в виде электромагнитной волны.
Свойства электромагнитных волн
Электромагнитная волна – это изменяющееся во времени и распространяющееся в пространстве электромагнитное поле.
Существование электромагнитных волн было теоретически предсказано английским физиком Дж. Максвеллом в 1864 году. Электромагнитные волны были открыты Г. Герцем.
Источник электромагнитной волны – ускоренно движущаяся заряженная частица – колеблющийся заряд.
Важно!
Наличие ускорения – главное условие излучения электромагнитной волны. Интенсивность излученной волны тем больше, чем больше ускорение, с которым движется заряд.
Источниками электромагнитных волн служат антенны различных конструкций, в которых возбуждаются высокочастотные колебания.
Электромагнитная волна называется монохроматической, если векторы ( vec ) и ( vec ) совершают гармонические колебания с одинаковой частотой (частотой волны).
Длина электромагнитной волны: ( lambda=cT=frac<nu>, )
где ( c ) – скорость электромагнитной волны, ( T ) – период, ( nu ) – частота электромагнитной волны.
Свойства электромагнитных волн
- В вакууме электромагнитная волна распространяется с конечной скоростью, равной скорости света 3·10 8 м/с.
- Электромагнитная волна поперечная. Колебания векторов напряженности переменного электрического поля и магнитной индукции переменного магнитного поля взаимно перпендикулярны и лежат в плоскости, перпендикулярной к вектору скорости волны.
- Электромагнитная волна переносит энергию в направлении распространения волны.
Важно!
Электромагнитная волна в отличие от механической волны может распространяться в вакууме.
Плотность потока или интенсивность – это электромагнитная энергия, переносимая через поверхность единичной площади за единицу времени.
Обозначение – ( I ) , единица измерения в СИ – ватт на квадратный метр (Вт/м 2 ).
Важно!
Плотность потока излучения электромагнитной волны от точечного источника убывает обратно пропорционально квадрату расстояния от источника и пропорциональна четвертой степени частоты.
Электромагнитная волна обладает общими для любых волн свойствами, это:
- отражение,
- преломление,
- интерференция,
- дифракция,
- поляризация.
Электромагнитная волна производит давление на вещество. Это означает, что у электромагнитной волны есть импульс.
Различные виды электромагнитных излучений и их применение
Электромагнитные излучения имеют длины волн от 10 -12 до 10 4 м или частоты от 3·10 4 до 3·10 20 .
Различают следующие виды электромагнитных излучений:
- радиоволны;
- инфракрасное излучение;
- видимое излучение (свет);
- ультрафиолетовое излучение;
- рентгеновское излучение;
- гамма-излучение.
Границы между диапазонами условны, но излучения имеют качественные различия в свойствах. При переходе от излучений с малой частотой к излучениям с большей частотой волновые свойства проявляются слабее, а корпускулярные (квантовые) – сильнее.
( lambda ) = 10 3 –10 -3 м, ( nu ) = 10 5 –10 11 Гц. Источники радиоволн – колебательный контур, вибратор.
- длинные (длина больше 1 км);
- средние (от 100 м до 1 км);
- короткие (от 10 до 100 м);
- ультракороткие (меньше 10 м).
Свойства: отражение, поглощение, интерференция, дифракция. Применение: радиосвязь, телевидение, радиолокация.
Радиосвязью называется передача информации с помощью радиоволн. Радиосвязь осуществляется с помощью модулированных радиоволн. Модуляцией радиоволны называется изменение ее параметров (амплитуды, частоты, начальной фазы) с частотой, меньшей частоты передаваемой волны.
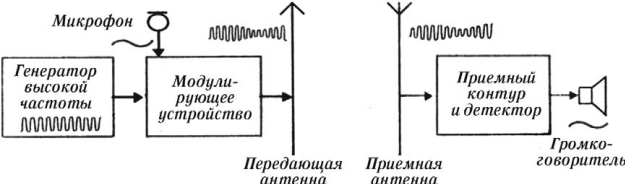
Схема радиосвязи показана на рисунке:
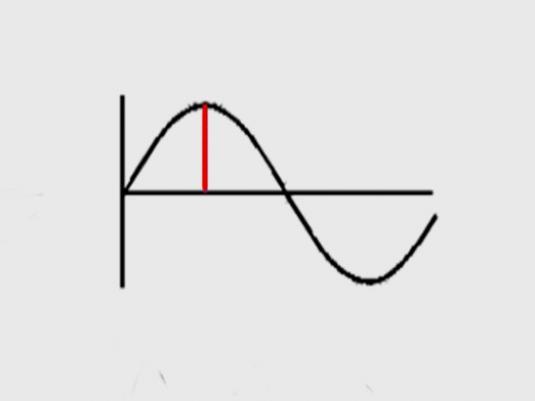
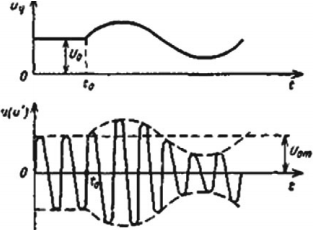
Передача радиоволн. Генератор высокой частоты вырабатывает высокочастотные колебания несущей частоты. Звуковые колебания поступают в микрофон, где преобразуются в электромагнитные колебания. В модуляторе эти колебания преобразуются в модулированные колебания. После усиления модулированные колебания поступают в передающую антенну, которая излучает электромагнитные волны. На рисунке показан звуковой сигнал низкой частоты и модулированный высокочастотный сигнал.
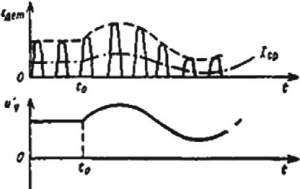
Прием радиоволн. Электромагнитные колебания поступают в приемную антенну и вызывают электромагнитные колебания в приемном контуре. Эти колебания поступают в усилитель, а затем в детектор. В качестве детектора используют устройство с односторонней проводимостью. Это может быть полупроводниковый диод. В детекторе сигнал демодулируют (детектируют). Процесс детектирования заключается в выделении из высокочастотных модулированных колебаний колебаний низкой (звуковой) частоты. После сглаживания и усиления сигнал поступает в динамик. На рисунке показаны процессы детектирования (демодуляции) и сглаживания.
Радиолокацией называют обнаружение и определение местоположения объектов с помощью радиоволн. Излучение осуществляется короткими импульсами. В интервале времени между излучением двух последовательных импульсов осуществляется прием отраженного от объекта сигнала. Для радиолокации используют ультракороткие радиоволны.
Инфракрасное (тепловое) излучение
( lambda ) = 10 -3 – 10 -7 м, ( nu ) = 10 11 – 10 14 Гц. Источники – атомы и молекулы вещества.
Это излучение испускают все тела при температуре, отличной от 0 К. Свойства: нагревает вещество при поглощении; интерференция; дифракция; проходит через дождь, снег, дымку; невидимо; преломление, отражение. Применение: в приборах ночного видения, в физиотерапии, промышленности (для сушки). Регистрируют с помощью термопары, болометра, фотографическим методом.
Видимое излучение
( lambda ) = 8·10 -7 – 4·10 -7 м, ( nu ) = 4·10 11 – 8·10 14 Гц.
Это излучение воспринимается глазом. Свойства: отражение, преломление, поглощение, интерференция, дифракция.
Ультрафиолетовое излучение
( lambda ) = 10 -8 – 4·10 -7 м, ( nu ) = 8·10 14 – 3·10 15 Гц. Источники – кварцевые лампы.
Ультрафиолетовое излучение дают светящиеся пары ртути и твердые тела, у которых температура выше 1000°С. Свойства: химическое действие; большая проникающая способность; биологическое действие; невидимо. Применение: в медицине, промышленности. Регистрируют фотографическими методами.
Рентгеновское излучение
( lambda ) = 10 -8 – 10 -11 м, ( nu ) = 3·10 16 – 3·10 19 Гц. Источник – рентгеновские трубки.
Возникает при торможении быстрых электронов. Свойства: высокая химическая активность; биологическое действие; интерференция; дифракция на кристаллической решетке; высокая проникающая способность. Применение: в медицине, промышленности, науке.
Гамма-излучение
Длина волны меньше 10 -11 м, частота от 10 20 Гц и выше. Источник – ядерные реакции.
Свойства: высокая проникающая способность, сильное биологическое действие. Применение: в медицине, промышленности (дефектоскопия), науке.
Шкала электромагнитных излучений позволяет сделать вывод: все электромагнитные излучения обладают одновременно волновыми и квантовыми свойствами, которые дополняют друг друга.
Важно!
Волновые свойства сильнее выражены при малых частотах и больших длинах волн, а квантовые – при больших частотах и малых длинах волн.
Решение задач по теме «Электромагнитные колебания и волны»
По этой теме можно выделить четыре группы задач:
- на определение параметров колебательного контура;
- на уравнения гармонических электромагнитных колебаний;
- на применение закона Ома;
- на расчет мощности и КПД трансформатора.
Решение первой группы задач на определение параметров колебательного контура основано на использовании формулы Томсона (формулы периода свободных электромагнитных колебаний) и закона сохранения и превращения энергии в колебательном контуре. Поэтому необходимо записать уравнения для мгновенных значений заряда и напряжения на конденсаторе и силы тока в катушке; записать уравнение для полной энергии колебательного контура в произвольный момент времени. В качестве дополнительных формул могут понадобиться формулы электроемкости плоского конденсатора, индуктивности катушки и длины электромагнитной волны. Помните, что скорость распространения электромагнитной волны в вакууме равна скорости света – 3·10 8 м/с. В среде с показателем преломления ( n ) скорость света можно рассчитать по формуле: ( v=frac. )
Важно!
Амплитудное значение напряжения – ( U_m=frac ) , амплитудное значение силы тока – ( I_m=q_momega ) .
При решении второй группы задач на уравнения гармонических электромагнитных колебаний рекомендуется записать заданное в задаче уравнение и уравнение гармонических колебаний в общем виде. Сравнить эти уравнения и определить основные характеристики: амплитуду, частоту, фазу.
При решении задач на закон Ома нужно помнить, что электроизмерительные приборы показывают действующие значения напряжения и силы тока. Действующие значения величин пропорциональны амплитудным значениям. Важно помнить, что резонанс возникает при равенстве индуктивного и емкостного сопротивлений.
Решение четвертой группы задач на расчет мощности и КПД трансформатора опирается на знание формул КПД и мощности в цепи.
Источник
Содержание:
Гармонические напряжения и токи:
В предыдущих лекциях рассматривались электрические цепи при условии, что они находятся под воздействием постоянных напряжений и токов. В действительности же действующие в электрических цепях токи и напряжения являются переменными, т. е. представляют собой электрические колебания. Напомним, что колебаниями называются процессы, которые характеризуются определенной повторяемостью во времени. Различают непериодические и периодические колебания.
Простейшим и в то же время наиболее важным типом периодических колебаний являются гармонические, когда колеблющаяся величина
Исключительная роль гармонических колебаний в теории и практике радиотехники объясняется следующими обстоятельствами:
- они широко используются для передачи сигналов и электрической энергии (например, промышленный ток с частотой 50 Гц);
- применяются как простейший испытательный сигнал;
- являются единственным типом колебаний, форма которых не изменяется при прохождении через любую линейную систему;
- любое периодическое негармоническое колебание может быть представлено в виде суммы (наложения) различных гармонических колебаний (такое представление называют спектром негармонического колебания).
Замечание:
Если временной интервал ограничен 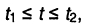
Определение гармонических напряжений и токов
Электрическое гармоническое колебание аналитически записывают в виде функции:
или
Традиционно в электротехнике используют синусную форму записи, а в теории электрических цепей (радиотехнике) — косинусную, которой, если это не оговаривается особо, и будем пользоваться в дальнейшем:
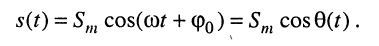
Если под колебанием 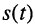
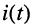
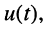
Гармоническое колебание определено полностью, если заданы все три его параметра: 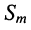
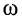
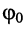
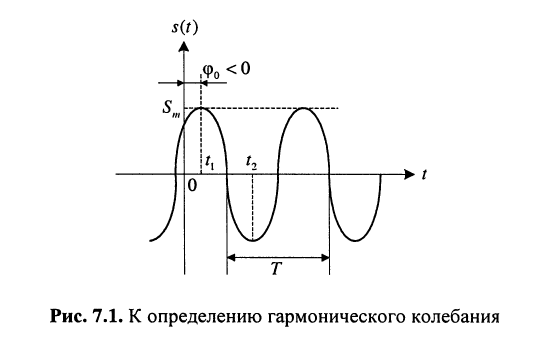
Рассмотрим смысл указанных параметров (рис. 7.1):
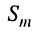
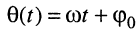
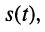
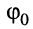
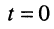
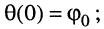
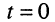
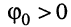
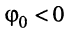
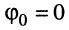
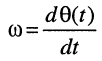
т. е. круговая частота численно равна изменению мгновенной фазы за единицу времени (секунду).
Введём ещё два характерных для периодических колебаний параметра: период и частоту.
Т — период колебания — наименьший интервал времени, через который процесс повторяется, а именно:
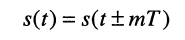
этому периоду соответствует изменение фазы на 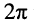
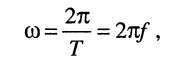
где величина
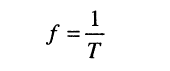
называется циклической частотой и измеряется в герцах (Гц).
В ряде практических задач требуется знать фазовые соотношения между гармоническими колебания одинаковой частоты. Фазовые соотношения характеризуют разностью фаз сравниваемых колебаний.
Пусть рассматриваются два колебания
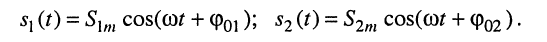
Тогда величина
называется разностью фаз или сдвигом фаз этих колебаний. Если 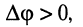
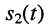
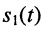
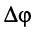
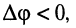
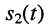
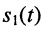
Если сдвиг фаз между двумя колебаниями равен 0, 
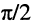
При практических расчётах часто начальную фазу выражают в градусах (°). Поскольку 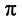
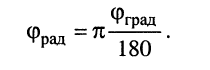
Линейные операции над гармоническими колебаниями
К линейным операциям над гармоническими колебаниями относятся: умножение на постоянное число (константу), дифференцирование, интегрирование и алгебраическое сложение гармонических колебаний одинаковой частоты. Результатом таких операций являются новые гармонические колебания той же частоты. Рассмотрим эти операции.
1. Умножение на константу
даёт новое гармоническое колебание, амплитуда которого отличается от амплитуды исходного колебания в 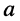
а фаза остаётся неизменной.
2. Дифференцирование
Из полученного результата следует, что при дифференцировании получается гармоническое колебание той же частоты; однако амплитуда и начальная фаза изменяются и оказываются равными
соответственно.
3. Интегрирование
даёт гармоническое колебание той же частоты, но амплитуда и начальная фаза изменяются и оказываются равными:
соответственно при условии равенства нулю постоянной интегрирования.
4. Сложение (наложение, суперпозиция) гармонических колебаний одинаковой частоты
Воспользуемся известной формулой сложения аргументов
и представим гармонические колебания в виде:
Складывая и группируя слагаемые, получаем:
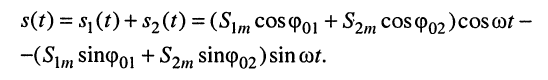
Обозначим в (7.7)
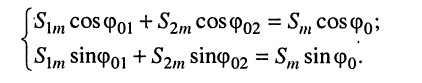
Подставляя (7.8) в (7.7)
получаем
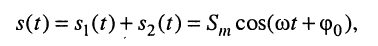
где при условии (7.8)
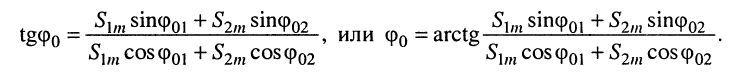
Остаётся найти амплитуду 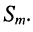
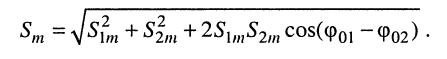
Помня, что 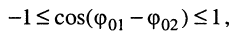
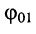
• 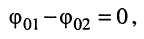
• 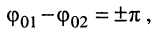
• 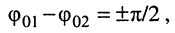
Выводы:
- линейные операции над гармонической функцией приводят лишь к изменению её амплитуды и начальной фазы;
- наложение двух гармонических колебаний равных частот образует гармоническое колебание той же частоты; амплитуда результирующего колебания зависит от соотношения начальных фаз слагаемых колебаний и лежит в пределах
- наложение любого числа гармонических колебаний одной частоты образует гармоническое колебание той же частоты
- амплитуду и начальную фазу результирующего колебания можно найти, последовательно применяя формулы сложения гармонических колебаний для каждой пары колебаний.
Энергетические характеристики гармонических колебаний
Кроме указанных в разд. 7.1.1 параметров, гармонические колебания описываются энергетическими характеристиками:
- мгновенной мощностью,
- средней мощностью,
- действующими (эффективными) значениями амплитуд напряжения и тока.
Мгновенная мощность гармонических колебаний при согласном выборе положительных направлений тока 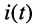
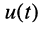
Заменив произведение косинусов на полусумму косинусов разности и суммы аргументов, получаем
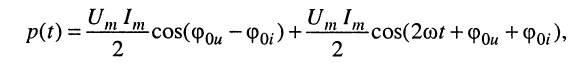
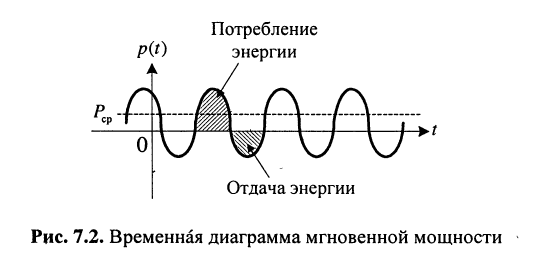
откуда следует, что потребляемая мгновенная мощность содержит постоянную составляющую (первое слагаемое, на графике Рср), относительно которой она колеблется с удвоенной частотой 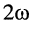
Положительным значениям мощности соответствует потребление цепью электрической энергии, а отрицательным значениям — отдача электрической энергии. В пассивных цепях это происходит за счёт энергии, запасаемой в конденсаторах (энергия электрического поля) и/или в индуктивностях (энергия магнитного поля). Для цепей, содержащих активные элементы, это означает, что цепь генерирует электрическую энергию.
Средняя (активная) мощность произвольных колебаний определяется как отношение энергии, подведённой к цепи за некоторый промежуток времени, к длительности этого промежутка 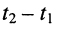
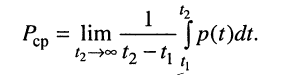
Для гармонических колебаний пределы интегрирования в (7.12) можно ограничить периодом колебания Т, полагая 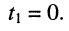
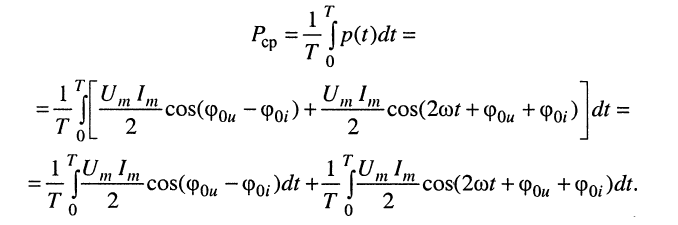
Левый интеграл в полученной сумме равен:
Обратимся к правому интегралу конечного выражения (7.13), представляющему собой интеграл от функции косинуса на периоде:
Найдём этот интеграл:
Числитель дроби равен нулю, поскольку, во-первых,
и, во-вторых, в силу периодичности функции синуса справедливы равенства:
Таким образом, правый интеграл в (7.13) равен нулю, т. е. попутно доказано, что интеграл от функции косинуса за период равен нулю (это справедливо и для функции синуса).
Следовательно, средняя мощность гармонического колебания равна:
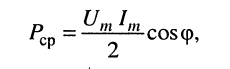
где 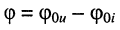
- средняя, или активная мощность пропорциональна амплитудам напряжения и тока и косинусу сдвига фазы между ними;
- чем меньше разность фаз, тем больше активная мощность;
- для пассивных цепей согласно принципу сохранения энергии
при наличии зависимых источников это неравенство может не иметь силы;
- средняя мощность, потребляемая цепью, должна быть равна арифметической сумме средних мощностей, потребляемых в каждом элементе цепи
где 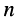
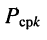
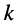
На практике необходимо также знать среднеквадратичные значения произвольных напряжений и токов, которые определяются по формулам:
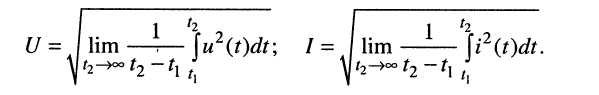
Отсюда для периодических, в том числе и гармонических, колебаний в соответствии с (7.13) имеем:
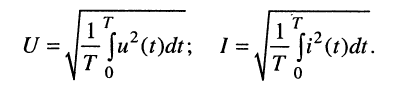
Подставляя в (7.16) выражения для мгновенных напряжений и токов
получаем:
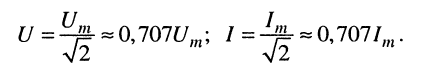
Среднеквадратические значения напряжений и токов называют действующими (эффективными). Они меньше амплитуд соответствующих колебаний в 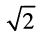
Покажем вывод формул (7.17) на примере напряжения:
После замены:
подкоренное выражение примет вид:
поскольку по доказанному ранее второй интеграл последней суммы равен нулю.
Действующие значения напряжения и тока позволяют записать среднюю мощность в форме:
Символическое изображение гармонических колебаний
Гармонические напряжения и токи в линейной цепи находятся в результате решения задач анализа, которые даже для относительно простых цепей, как это будет видно из дальнейшего, оказываются достаточно трудоёмкими. На практике используются функциональные преобразования, в результате которых операции над исходными функциями заменяются более простыми операциями над некоторыми новыми функциями. Исходные функции называются оригиналами, а соответствующие им новые функции — изображениями или символами.
Решение любой задачи методом функционального преобразования состоит из трёх следующих основных этапов:
- Прямого преобразования оригиналов к их изображениям (символам).
- Вычисления изображений искомых функций по правилам операций над изображениями.
- Обратного преобразования полученных изображений искомых функций к их оригиналам.
Рассматриваемое здесь функциональное преобразование, получившее название символического изображения гармонических колебаний, не является единственным; в лекции 16 будет рассмотрено более общее преобразование — преобразование Лапласа.
Идея символического изображения гармонических колебаний состоит в замене гармонических функций комплексными числами. Возможность такого изображения гармонических функций заложена в том, что в режиме гармонических колебаний все колебания имеют одну и ту же заранее известную частоту 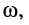
достаточно охарактеризовать только двумя вещественными числами: 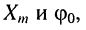
Представим гармоническое колебание в виде действительной части новой комплексной функции, опустив для простоты записи индекс 0 при
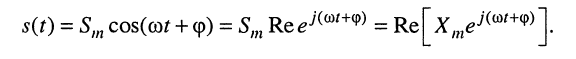
Тогда комплексная функция, стоящая в правой части равенства, может быть представлена как произведение некоторой комплексной функции на комплексную экспоненту
Определение:
Комплексная функция
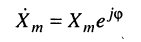
называется комплексной амплитудой или символическим изображением гармонического колебания: её модуль равен амплитуде 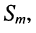
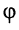
Восстановление 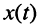
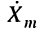
имеет комплексную амплитуду (символическое изображение) вида:
Соответствия между линейными операциями над гармоническими колебаниями и операциями над их символическими изображениями
1. Умножение на константу:
Полученная формула показывает, что умножению гармонического колебания на константу соответствует умножение на константу его комплексной амплитуды.
2. Сложение: пусть гармоническое колебание 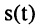
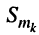
Применим к обеим частям данного равенства преобразование (7.41) с учётом того, что суммируемые колебания имеют одну и ту же частоту. Тогда получим:
Следовательно, операции сложения (суммирования) гармонических колебаний соответствует операция сложения их комплексных амплитуд.
3. Дифференцирование: дифференцируя функцию
получаем
Комплексная амплитуда, т. е. символическое изображение найденной функции, оказывается такой:
поскольку согласно формуле Эйлера (7.40)
Следовательно, операции дифференцирования гармонического колебания соответствует операция умножения его комплексной амплитуды на оператор
4. Интегрирование: интегрируя функцию
получаем
Символическое изображение этой функции имеет вид:
поскольку
Следовательно, операции интегрирования гармонического колебания соответствует операция деления символического изображения на оператор
Заметим, что комплексные амплитуды напряжения и тока имеют вид:
Например, мгновенному значению гармонического напряжения
В соответствует комплексная амплитуда напряжения
а комплексной амплитуде тока
при известной круговой частоте 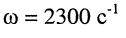
Законы Ома и Кирхгофа для комплексных амплитуд
Обозначим:
- комплексную амплитуду тока
- комплексную амплитуду напряжения
Покажем, что изученные ранее законы Ома и Кирхгофа справедливы и для комплексных амплитуд.
Закон Ома в символической форме:
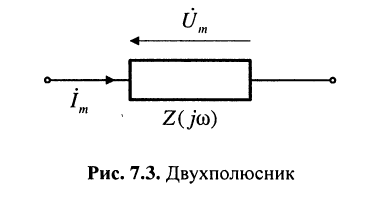
для определения закона Ома необходимо установить связи между комплексными токами и напряжениями, действующими в некотором двухполюснике (рис. 7.3).
Введём следующие определения:
Комплексным сопротивлением двухполюсника 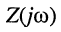
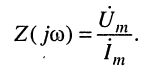
Комплексное сопротивление называют также комплексом полного сопротивления, или импедансом.
Комплексной проводимостью двухполюсника 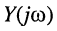
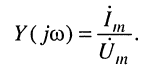
Комплексную проводимость называют также комплексом полной проводимости, или адмитансом.
Из определений следует соотношение:
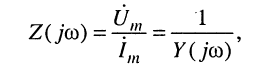
откуда вытекает, что комплексные амплитуды напряжений и токов на входе двухполюсника формально удовлетворяют закону Ома:
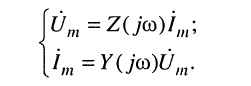
Комплексные сопротивления и проводимости двухполюсников представляют собой в общем случае комплексные величины, зависящие как от параметров цепи, так и от частоты воздействия.
Первый закон Кирхгофа в символической форме:
сумма комплексных амплитуд токов всех N ветвей, подключённых к каждому из узлов электрической цепи, равна нулю.
Действительно, для мгновенных значений токов имеем:
где 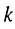
Второй закон Кирхгофа в символической форме.
сумма комплексных амплитуд напряжений на всех N ветвях, входящих в любой контур цепи, равна нулю.
Это показывается так же, как и для первого закона:
Комплексные сопротивления и проводимости
Поставим задачу установить связь между активными и реактивными составляющими комплексных сопротивлений и проводимостей, для чего подробнее рассмотрим комплексные амплитуды напряжения и тока (7.45).
Из комплексной амплитуды напряжения имеем:
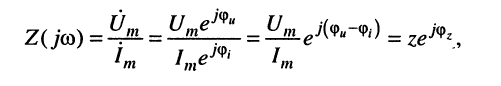
где
называется модулем комплексного сопротивления, или полным сопротивлением двухполюсника. Таким образом, полное сопротивление двухполюсника равно отношению амплитуды гармонического напряжения на зажимах двухполюсника к амплитуде гармонического тока, протекающего через эти зажимы.
Аналогично из соотношения
можно выделить модуль комплексной проводимости, или полную проводимость двухполюсника:
Замечание:
Аргументы комплексного сопротивления и комплексной проводимости у пассивных двухполюсников могут меняться только в пределах:
Для решения поставленной задачи представим комплексное сопротивление и комплексную проводимость в алгебраической форме:
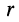
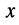
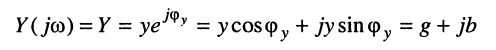
устанавливаются:
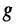
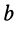
Наконец, установим связь между активными и реактивными составляющими комплексных сопротивлений и проводимостей:
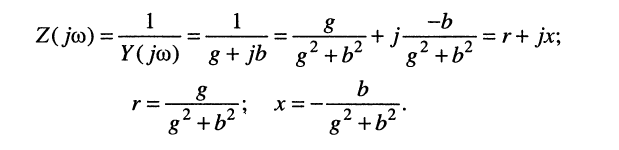
Аналогично получаем соотношения:
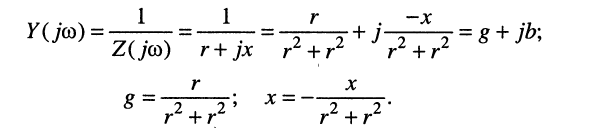
Выводы:
Комплексные числа и операции над ними
Рассмотрим всевозможные пары действительных (обычных) чисел, взятых в определённом порядке. Каждую такую упорядоченную пару 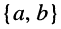
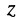
где символ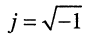
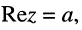
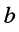
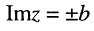
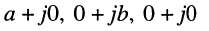
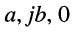
Запишем формулы для натуральных степеней числа
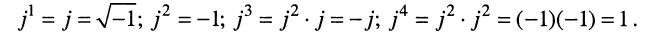
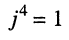
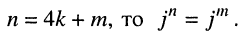
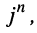
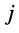
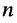
Арифметические действия над комплексными числами
- Два комплексных числа считаются равными, если равны их действительные и мнимые части.
- Сложение, вычитание и умножение комплексных чисел следует производить так, словно это многочлены относительно буквы
при этом произведение
заменяется на -1.
Пусть 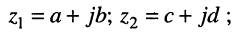
• равенство 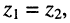
• сумму 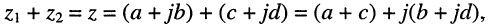
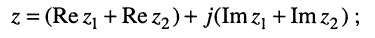
• разность:
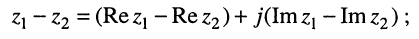
• произведение:
или в общей форме
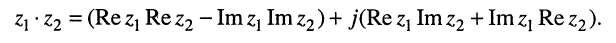
3. Деление комплексных чисел определяется как действие, обратное умножению: частным от деления комплексного числа 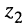
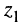
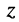
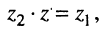
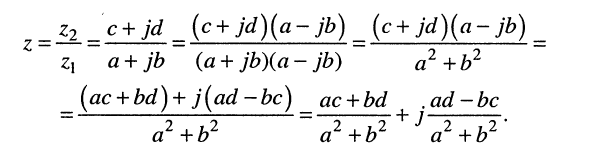
4. Полезные тождества:
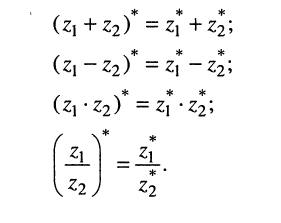
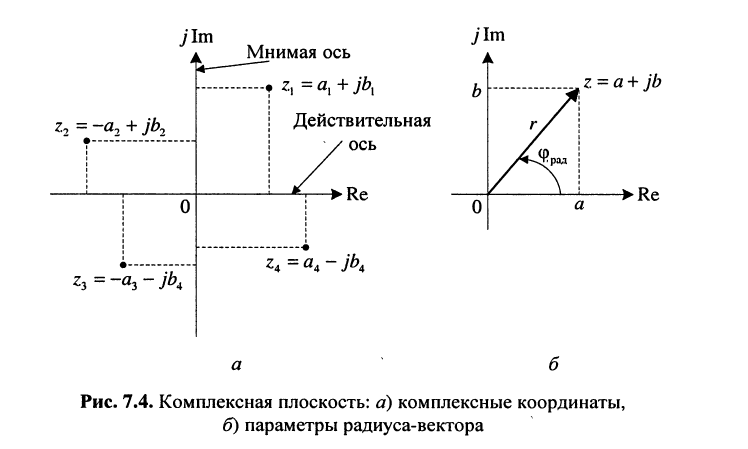
Геометрический смысл комплексных чисел
Как известно, положение точки Z на координатной плоскости задаётся двумя действительными числами, являющимися координатами этой точки, что записывается в виде 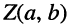
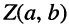
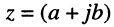
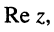
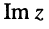
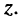
С другой стороны, на той же комплексной плоскости выберем произвольный радиус-вектор 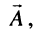
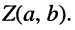
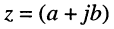
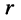
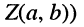
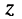
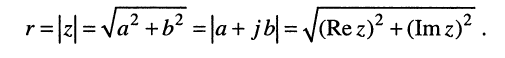
Угол 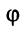
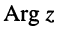
где 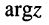
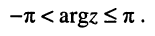
Из рис. 7.4, б следует, что
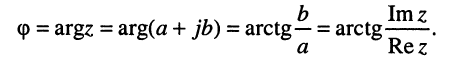
Аргумент считается положительным при отсчёте против часовой стрелки и отрицательным — при отсчёте в противоположном направлении.
Формулы Эйлера и Муавра
Вновь обратимся к рис. 7.4, б и найдём значения 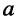
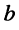
которые позволяют записать комплексное число 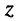
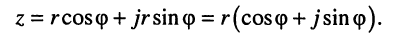
В 1743 году Эйлер предложил обозначить
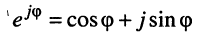
и назвать полученное соотношение мнимой экспонентой. Тогда комплексное число z можно записать в показательной (полярной) форме
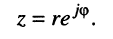
Из (7.40) следуют две формулы, выражающие через 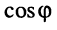
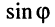
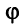
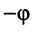
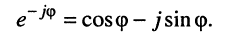
Складывая и вычитая почленно (7.40) и (7.42), получаем:
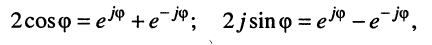
откуда следуют интересующие нас формулы:
Заметим также, что модуль комплексной экспоненты равен единице; действительно:
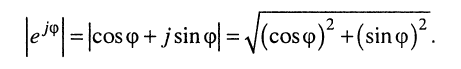
Найдём выражение, соответствующее степени 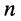
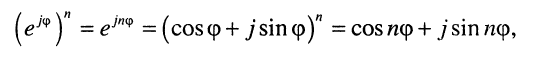
откуда следует:
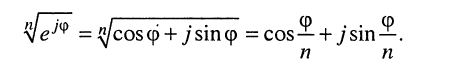
Формулы (7.45) и (7.2) называются формулами Муавра.
- Энергетические характеристики двухполюсников
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
- Электрические цепи несинусоидального тока
- Несинусоидальный ток
- Электрические цепи с распределенными параметрами
- Резистивные электрические цепи и их расчёт
Как будут выглядеть графики колебания напряжения, придуманные вами, можно увидеть здесь.
В этом уравнении:
Um = ImLω = qmLω 2 – максимальные значения
Уравнение колебаний напряжения U = 40sin(10Пиt)?
Физика | 10 – 11 классы
Уравнение колебаний напряжения U = 40sin(10Пиt).
Определите амплитудное и действующее значение напряжения, период и частоту колебаний.
Ответ : Объяснение : Дано : u = 40·sin (10π·t)____________U₀ – ?
Запишем уравнение колебаний в общем виде : u(t) = U₀·sin (ω·t) ВИмеем : Амплитудное значение : U₀ = 40 ВДействующее значение : U = U₀ / √2 = 40 / √2 ≈ 28 BЦиклическая частота : ω = 10π с⁻¹Период : T = 2π / ω = 2π / 10π = 0, 2 сЧастота : ν = 1 / Т = 1 / 0, 2 = 5 Гц.
В цепи переменного тока с активным сопротивлением амплитудное значение напряжения 100 В, частота колебаний 100 Гц, сопротивление R = 50 Ом, напишите уравнение колебаний тока в этой цепи?
В цепи переменного тока с активным сопротивлением амплитудное значение напряжения 100 В, частота колебаний 100 Гц, сопротивление R = 50 Ом, напишите уравнение колебаний тока в этой цепи.
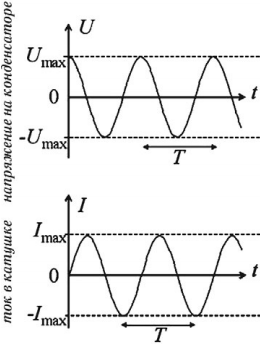
На рисунке показан график зависимости напряжения на концах катушки с током от времени?
На рисунке показан график зависимости напряжения на концах катушки с током от времени.
Определите амплитуду, период и частоту колебаний напряжения.
Электрическое напряжение на обкладках конденсатора колебательного контура меняется по закону u = 6cos100П t?
Электрическое напряжение на обкладках конденсатора колебательного контура меняется по закону u = 6cos100П t.
Определить амплитудное и действующее значение напряжения, его циклическую частоту и период колебаний, а также напряжение на конденсаторе через 0, 005с после начала колебаний.
Напряжение в цепи меняется по закону U = 40sin10Пt определите амплитудное и действующее значения напряжения период и частоту колебании?
Напряжение в цепи меняется по закону U = 40sin10Пt определите амплитудное и действующее значения напряжения период и частоту колебании.
На рисунке показан график зависимости напряжения на концах катушки с током от времени?
На рисунке показан график зависимости напряжения на концах катушки с током от времени.
Определите амплитуду, период и частоту колебаний напряжения.
По графику определить : амплитуду напряжения, период колебаний, записать ур – е мгновенного значения напряжения?
По графику определить : амплитуду напряжения, период колебаний, записать ур – е мгновенного значения напряжения.
Уровенение колебания напряжения в цепи переменного тока задано уравнением u = 200 sin 4t?
Уровенение колебания напряжения в цепи переменного тока задано уравнением u = 200 sin 4t.
Определить амплитуду колебаний, период, циклическую и ленейную частоту колебаний.
Напряжение в цепи изменяется по закону u = 120sin20πt?
Напряжение в цепи изменяется по закону u = 120sin20πt.
Определить амплитудное и действующее значение напряжения, частоту и период.
Напряжение в цепи переменного тока изменяется по закону u = 280, cos = 200пт?
Напряжение в цепи переменного тока изменяется по закону u = 280, cos = 200пт.
Чему равны амплитудное значение напряжения, циклическая частота, период и частота электромагнитный колебаний.
Чему равна фаза колебаний и напряжение в момент времени 0, 01 с.
Период колебаний напряжения в колебательном контуре равен 2 с?
Период колебаний напряжения в колебательном контуре равен 2 с.
Найдите значение частоты колебаний.
Перед вами страница с вопросом Уравнение колебаний напряжения U = 40sin(10Пиt)?, который относится к категории Физика. Уровень сложности соответствует учебной программе для учащихся 10 – 11 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.
Какое из них? Или все? Вы блин объясняйте.
L = 0, 7 м = 70 см h = 750 м = 75 000 см 900 мм² = 900 * 10⁻⁶ м² = 0, 0009 м² 70 м² ни при каком условии не может равняться м³ 65 мкм = 65 * 10⁻³ мм = 0, 065 мм 0, 85 м = 0, 85 * 10³ мм = 850 мм 88 см² = 88 * 10⁻⁴ м² = 0, 0088 м².
Vср = S / t vср = (2 / 3S + 1 / 3S) / (t1 + t2) = S / (t1 + t2) найдем время движения. Оно состоит из 2 частей t1 = s1 / v1 = (2 / 3)S / v1 t2 = s2 / v2 = (1 / 3)S / v2 vср = S / ((2 / 3)S / v1 + (1 / 3)S / v2) = (v1 * v2) / (2 / 3 * v2 + 1 / 3 * v1..
V = S / t t = в корне 2h / g = в корне 6, 4 / 10 = в корне 0, 64 = 0, 8 V = 6, 4 / 0, 8 = 8м / с ответ : 8м / с (вроде бы так).
Автомобиль, движущийся по горизонтальной дороге с выключенным двигателем ;..
Переменный электрический ток
теория по физике 🧲 колебания и волны
Свободные электромагнитные колебания в контуре быстро затухают. Поэтому они практически не используются. Наиболее важное практическое значение имеют незатухающие вынужденные колебания.
Переменный ток — вынужденные электромагнитные колебания.
Ток в осветительной сети квартиры, ток, применяемый на заводах и фабриках, представляет собой переменный ток. В нем сила тока и напряжение изменяются со временем по гармоническому закону. Колебания легко обнаружить с помощью осциллографа. Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять сбой синусоиду:
Зная скорость движения луча в горизонтальном направлении (она определяется частотой пилообразного напряжения), можно определить частоту колебаний.
Частота переменного тока — это количество колебаний за 1 с.
Стандартная частота переменного промышленного тока составляет 50 Гц. Это значит, что на протяжении 1 секунды ток 50 раз течет в одну сторону и 50 раз — в другую. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц.
Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводника будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц, и, следовательно, гармонические колебания силы тока.
При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменение поля происходит с большой скоростью, но она не бесконечно большая. Она равна скорости света (3∙10 8 м/с).
Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока (см. рисунок ниже).
Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции.
Численно магнитный поток определяется формулой:
При равномерном вращении рамки угол α увеличивается пропорционально времени:
где n — частота вращения. Поэтому поток магнитной индукции меняется гармонически:
Φ = B S cos . 2 π n t
Здесь множитель 2 π n представляет собой число колебаний магнитного потока за 2 π секунд. Это не что иное, как циклическая частота колебаний:
Φ = B S cos . ω t
Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «минус» скорости изменения потока магнитной индукции, т.е. производной потока магнитной индукции по времени:
e = − Φ ´ = − B S ( cos . ω t ) ´ = B S ω sin . ω t = ε m a x sin . ω t
ε m a x — амплитуда ЭДС индукции, равная:
Напряжение в цепи переменного тока может меняться по закону синуса или по закону косинуса:
u = U m a x sin . ω t
u = U m a x cos . ω t
где U m a x — амплитуда напряжения (максимальное по модулю значение напряжения).
Сила тока меняется с той частотой, что и напряжение — ω . Но колебания тока необязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока i в любой момент времени определяется по формуле:
i = I m a x sin . ( ω t + φ с )
где I m a x — амплитуда силы тока (максимальное по модулю значение силы тока), φ с — разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Пример №1. Найти напряжение в цепи переменного тока в момент времени t = π, если циклическая частота электромагнитных колебаний равна 300,25 Гц, а амплитуда напряжения составляет 12В. Считать, что напряжения меняется по закону косинуса.
u = U m a x cos . ω t = 12 cos . 300 , 25 π = 12 √ 2 2 . . ≈ 8 , 5 ( В ) .
Активное сопротивление в цепи переменного тока
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (см. рисунок ниже).
Внимание! Ранее под величиной R мы понимали электрическое сопротивление. Но правильно его называть сопротивлением активным. Дело в том, что в цепи переменного тока могут быть сопротивления иного характера. Сопротивление же R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
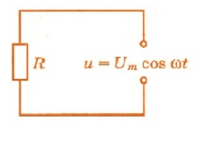
Будем считать, что напряжение на зажимах цепи меняется по закону косинуса:
u = U m a x cos . ω t
Для нахождения мгновенного значения силы тока мы можем воспользоваться законом Ома, так как эта величина прямо пропорционально мгновенному значению напряжения:
i = u R . . = U m a x cos . ω t R . . = I m a x cos . ω t
В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:
I m a x = U m a x R . .
Мощность в цепи с резистором
В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.
Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.
Мощность постоянного тока определяется формулой:
Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:
Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:
p = ( I m a x cos . ω t ) 2 R
Вспомним из курса математики:
cos 2 . α = 1 + cos . 2 α 2 . .
p = I 2 m a x 2 . . R ( 1 + cos . 2 ω t ) = I 2 m a x R 2 . . + I 2 m a x R 2 . . cos . 2 ω t
График зависимости мгновенной мощности от времени:
На протяжении первой четверти периода, когда cos . 2 ω t > 0 , мощность в любой момент времени больше величины I 2 m a x R 2 . . . На протяжении второй четверти периода, когда cos . 2 ω t 0 , мощность в любой момент времени меньше этой величины. Среднее за период значение cos . 2 ω t = 0 , следовательно, средняя за период мощность равна I 2 m a x R 2 . . .
Средняя мощность − p равна:
− p = I 2 m a x R 2 . . = − i 2 R
Пример №2. Сила переменного тока в цепи меняется по закону i = I m a x cos . ω t . Определить мгновенную мощность в момент времени t = 1 с, если циклическая частота колебаний ω = 100π Гц при сопротивлении R = 10 Ом. Амплитуда силы тока равна 1 А.
p = ( I m a x cos . ω t ) 2 R = 10 ( 1 · cos . ( 100 π · 1 ) 2 = 10 ( Д ж )
Действующие значения силы тока и напряжения
Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:
− i 2 = I 2 m a x 2 . .
Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.
I = √ − i 2 = I m a x √ 2
Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.
Аналогично определяется действующее значение напряжения U:
U = √ − u 2 = U m a x √ 2 . .
Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:
Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.
P = ( I m a x √ 2 . . ) 2 R = I 2 m a x 2 . . R = 2 2 2 . . · 5 = 10 ⎛ ⎝ Д ж ⎞ ⎠
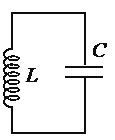
[spoiler title=”источники:”]
http://fizika.my-dict.ru/q/96138_uravnenie-kolebanij-naprazenia-u-40sin10pit/
[/spoiler]
-
Физика
Предыдущий вопрос
Следующий вопрос
belphegor1996
8 лет назад
Ответ
Проверено экспертом
Ответ дан
DedStar
Ответ:
Объяснение:
Дано:
u = 40·sin (10π·t)
____________
U₀ – ?
U – ?
T – ?
ν – ?
Запишем уравнение колебаний в общем виде:
u(t) = U₀·sin (ω·t) В
Имеем:
Амплитудное значение:
U₀ = 40 В
Действующее значение:
U = U₀ / √2 = 40/√2 ≈ 28 B
Циклическая частота:
ω = 10π с⁻¹
Период:
T = 2π / ω = 2π / 10π = 0,2 с
Частота:
ν = 1 / Т = 1/0,2 = 5 Гц
Ответы и объяснения
- belphegor1996
Не тот ответ, который тебе нужен?
Найди нужный
Как обозначается амплитуда колебаний? Как найти амплитуду?
Начиная с седьмого класса в школах начинают преподавать такую тему, как «Механические колебания». Начиная с ОГЭ и заканчивая ЕГЭ, эта тема прослеживается во многих экзаменах и вступительных испытаниях. Важной частью ее является изучение понятия амплитуды колебаний. Поэтому для начала ознакомимся с тем, что такое амплитуда колебаний и как обозначается амплитуда колебаний в физике, ведь со временем многое забывается, а именно данной переменной почему-то во многих школах уделяют меньше всего внимания.
Что такое амплитуда колебаний?
Амплитуда колебаний — это максимально возможное отклонение или смещение величины в большую или меньшую сторону от положения равновесия или от среднего значения. К примеру, для пружинного маятника положение равновесия — это покоящийся на пружине груз, а когда он начинает двигаться, то обретает определенную амплитуду, которая определяется растяжением или сжатием пружины.
Для математического же маятника немного проще — максимальное отклонения груза от положения покоя — это и есть амплитуда колебаний.
В то время как амплитуда колебаний радиоволн считается именно по отклонению от среднего значения.
Теперь перейдем к тому, какой буквой обозначается амплитуда колебаний.
Обозначение
В седьмом классе детей приучают обозначать амплитуду колебаний простой буквой «А». Например: А=4 см, то есть амплитуда равна четырем сантиметрам.
Но уже в восьмом классе ученики изучают такое понятие, как механическая работа, и именно она в физике обозначается буквой «А». Ученики начинают путаться в этих значениях, и к 10-11-у классу не имеют четкого представления о том, как обозначается амплитуда колебаний в физике.
В случае с пружинными и математическими маятниками лучше всего записывать амплитуду через максимальные значения. То есть Хмакс. означает максимальное отклонения от положения равновесия. Например Хмакс.=10 см, то есть пружина, как вариант, растянется максимум на 10 см. Это и будет амплитудой колебаний.
В 11-м классе выпускники изучают электромагнитные колебания. И там встречаются колебания заряда, напряжения и силы тока. Для того чтобы записать амплитуду напряжения, принято обозначать ее как максимальное значение. Для заряда и прочих величин соответственно.
Как найти амплитуду колебаний?
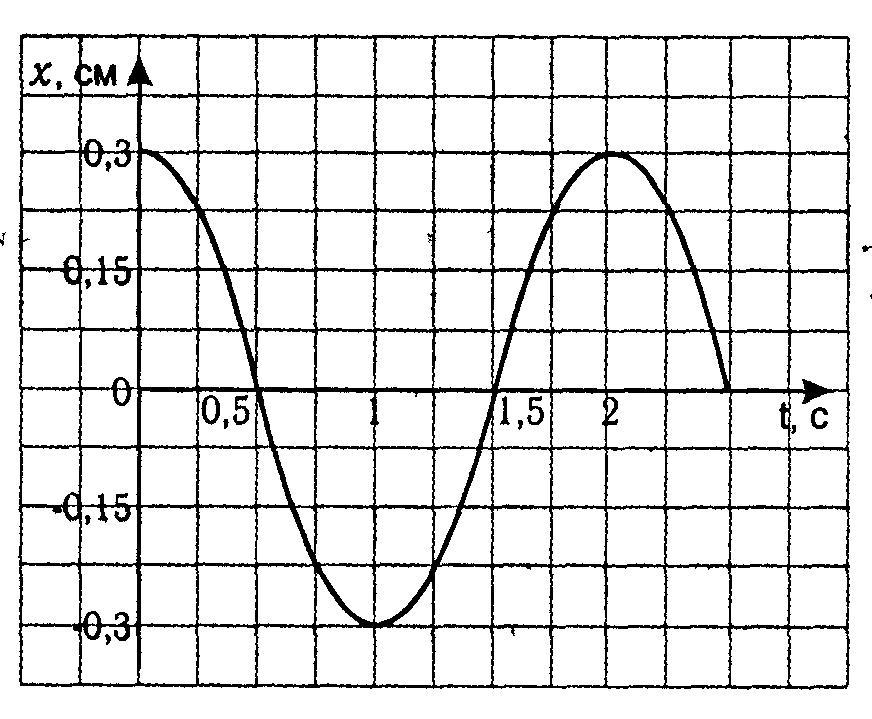
Обычно в задачах на нахождение амплитуды представлен график, подобный тому, что нарисован на картинке выше. В таком случае амплитудой будет являться максимальное значение по вертикальной оси Y. Амплитуда показано красной чертой.
Например, на данном рисунке изображен график колебаний математического маятника.
Зная, что амплитуда колебаний математического маятника — это максимальное удаление от положение равновесия, можем определить, что максимальное значение Х=0,3 см.
Найти амплитуду с помощью вычислений можно следующими способами:
1. Если груз совершает гармонические колебания и в задаче известны путь, который проходит тело, и количество колебаний, то амплитуда находится как отношение пути к количеству колебаний, умноженному на 4.
2. Если в задаче дан математический маятник, то при известных максимальной скорости и длине нити можно найти амплитуду, которая будет равна произведению максимальной скорости на квадратный корень из отношения длины к ускорению свободного падения. Эта формула похожа на формулу периода математического маятника.
Только вместо 2п используется максимальная скорость.
В уравнениях же амплитудой является все то, что записано до косинуса, синуса или переменной омеги.
Заключение
В этой статье было сказано о том, как обозначается амплитуда колебаний и как она находится. Данная тема является лишь малой долей большого раздела колебательных процессов, но это не снижает ее важности. Ведь не понимая, что такое амплитуда, невозможно работать с графиками правильно и решать уравнения.
Гармонические колебания
О чем эта статья:
9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Механические колебания
Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.
Колебания делятся на два вида: свободные и вынужденные.
Свободные колебания
Это колебания, которые происходят под действием внутренних сил в колебательной системе.
Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.
Вынужденные колебания
А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.
Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.
Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.
Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.
Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.
Автоколебания
Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.
У автоколебательной системы есть три важных составляющих:
- сама колебательная система
- источник энергии
- устройство обратной связи, обеспечивающей связь между источником и системой
Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.
Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.
Характеристики колебаний
Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.
Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.
Формула периода колебаний
T = t/N
N — количество колебаний [—]
Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.
Формула частоты
ν = N/t = 1/T
N — количество колебаний [—]
Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .
Она используется в уравнении гармонических колебаний:
Гармонические колебания
Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:
Уравнение гармонических колебаний
x — координата в момент времени t [м]
t — момент времени [с]
(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ
Фаза колебаний
t — момент времени [с]
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:
Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.
Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.
На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.
В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.
Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.
Математический маятник
Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.
Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.
Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:
Формула периода колебания математического маятника
l — длина нити [м]
g — ускорение свободного падения [м/с 2 ]
На планете Земля g = 9,8 м/с 2
Пружинный маятник
Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.
Формула периода колебания пружинного маятника
m — масса маятника [кг]
k — жесткость пружины [Н/м]
Закон сохранения энергии для гармонических колебаний
Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.
Рассмотрим его на примере математического маятника.
- Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
- Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Амплитуда колебаний — определение, характеристика и формулы
Амплитуда колебаний – это максимальное значение отклонения от нулевой точки. В физике данный процесс анализируется в разных разделах.
Он изучается при механических, звуковых и электромагнитных колебаниях. В перечисленных случаях амплитуда измеряется по-разному и по своим законам.
Амплитуда колебаний
Амплитудой колебания называют максимальную отдаленную точку нахождения тела от положения равновесия. В физике она обозначается буквой А и измеряется в метрах.
За амплитудой можно наблюдать на простом примере пружинного маятника.
В идеальном случае, когда игнорируется сопротивление воздушного пространства и трение пружинного устройства, устройство будет колебаться бесконечно. Описание движения выполняется с помощью функций cos и sin:
x(t) = A * cos(ωt + φ0) или x(t) = A * sin(ωt + φ0),
величина А – это амплитуда свободных движений груза на пружине;
(ωt + φ0) – это фаза свободных колебаний, где ω — это циклическая частота, а φ0 – это начальная фаза, когда t = 0.
В физике указанную формулу называют уравнением гармонических колебаний. Данное уравнение полностью раскрывает процесс, где маятник движется с определенной амплитудой, периодом и частотой.
Период колебаний
Результаты лабораторных опытов показывают, что циклический период движения груза на пружине напрямую зависит от массы маятника и жесткости пружины, но не зависит от амплитуды движения.
В физике период обозначают буквой Т и описывают формулами:
Исходя из формул, период колебаний – это механические движения, повторяющиеся через определенный промежуток времени. Простыми словами периодом называют одно полное движение груза.
Частота колебаний
Под частотой колебаний следует понимать количество повторений движения маятника или прохождения волны. В разных разделах физики частота обозначается буквами ν, f или F.
Данная величина описывается выражением:
v = n/t – количество колебаний за промежуток времени,
n – это единица колебаний;
t – отрезок времени.
В Международной системе измерений частоту измеряют в Гц (Герцах). Она относится к точным измеряемым составляющим колебательного процесса.
Например, наукой установлена частота вращения Солнца вокруг центра Вселенной. Она равна -10 35 Гц при одинаковой скорости.
Циклическая частота
В физике циклическая и круговая частота имеют одинаковое значение. Данная величина еще называется угловой частотой.
Обозначают ее буквой омега. Она равна числу собственных колебательных движений тела за 2π секунд времени:
Данная величина нашла свое применение в радиотехнике и, исходя из математического расчета, имеет скалярную характеристику. Ее измерения проводят в радианах на секунду. С ее помощью значительно упрощаются расчеты процессов в радиотехнике.
Например, резонансное значение угловой частоты колебательного контура рассчитывают по формуле:
Тогда как обычная циклическая резонансная частота выражается:
В электрике под угловой частотой следует понимать число полных трансформаций ЭДС или число оборотов радиуса – вектора. Здесь ее обозначают буквой f.
Как определить амплитуду, период и частоту колебаний по графику
Для определения на графике составляющих колебательного механического процесса или, например, колебания температуры, нужно разобраться в терминах этого процесса.
расстояние испытываемого объекта от исходной точки – называют смещением и обозначают х;
наибольшее отклонение – амплитуда смещения А;
фаза колебания – определяет состояние колебательной системы в любой момент времени;
начальная фаза колебательного процесса – когда t = 0, то φ = φ0.
Из графика видно, что значение синуса и косинуса может меняться от -1 до +1. Значит, смещение х может быть равно –А и +А. Движение от –А до +А называют полным колебанием.
Построенный график четко показывает период и частоту колебаний. Стоить отметить, что фаза не воздействует на форму кривой, а только влияет на ее положение в заданный промежуток времени.
источники:
http://skysmart.ru/articles/physics/garmonicheskie-kolebaniya
http://nauka.club/fizika/amplituda-kolebaniy.html

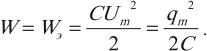
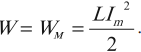
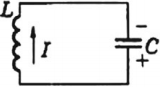
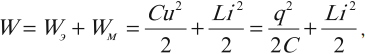
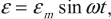
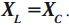
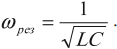
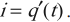
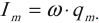
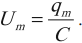
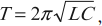
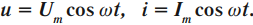
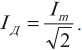
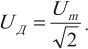
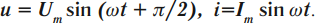
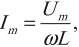
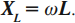
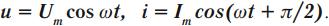
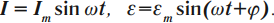
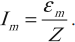
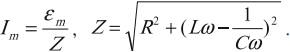
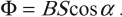
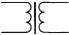
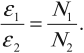
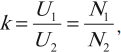
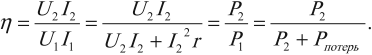
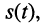
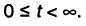
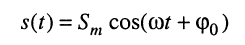
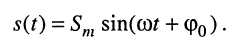
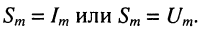
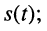
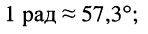
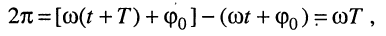
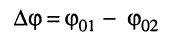
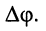
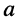
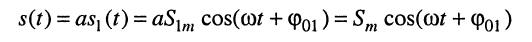
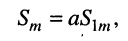
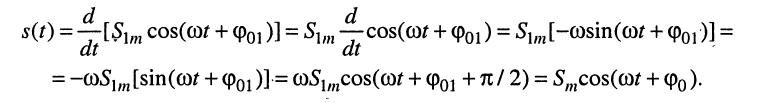
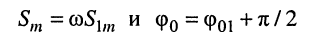
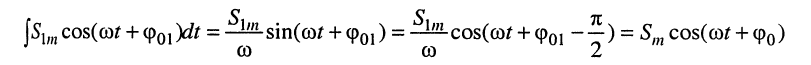
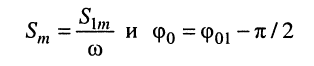
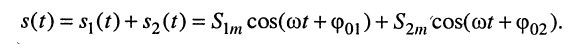
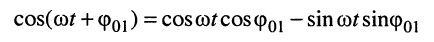
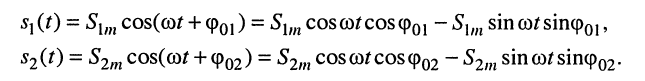
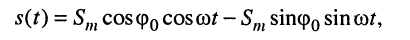
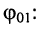
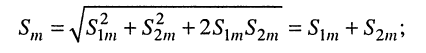
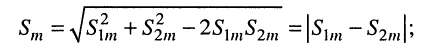
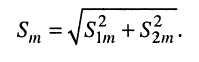
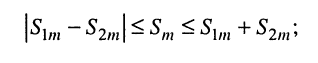
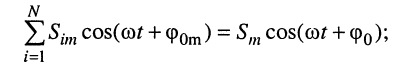
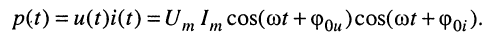
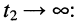
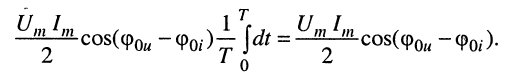
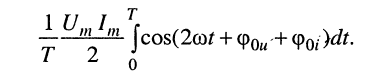
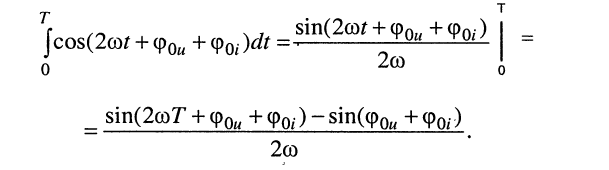
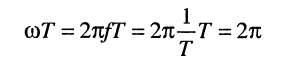
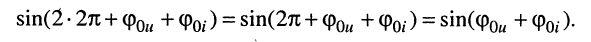
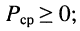 при наличии зависимых источников это неравенство может не иметь силы;
при наличии зависимых источников это неравенство может не иметь силы;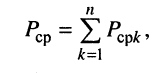
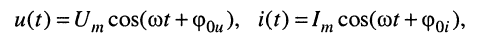
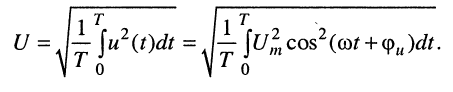
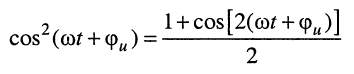
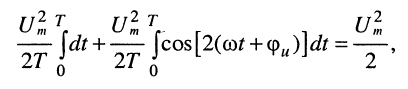
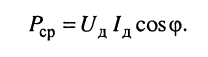
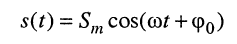
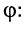
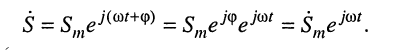
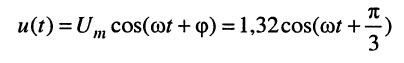
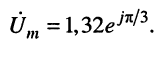
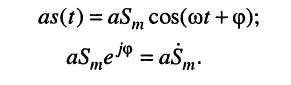
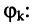
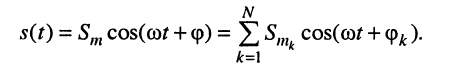
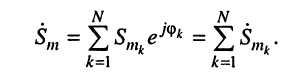
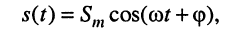
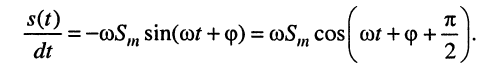
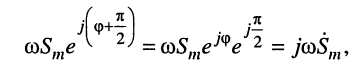
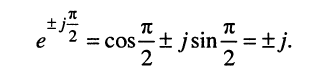
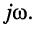
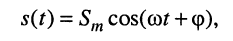
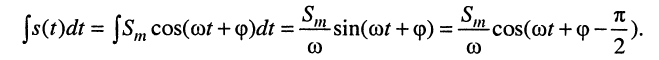
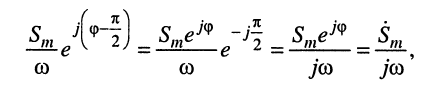
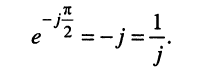
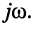
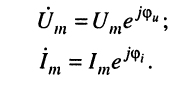
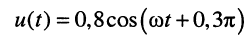
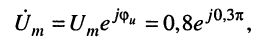
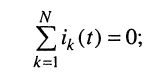
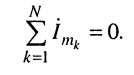
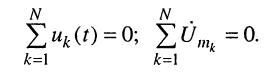
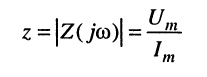
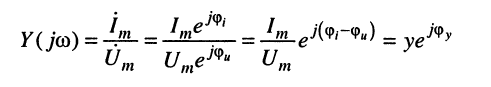
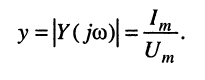
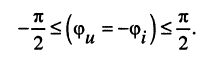
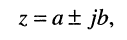
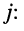
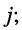 при этом произведение
при этом произведение 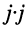 заменяется на -1.
заменяется на -1.