Пример 1. Плоская электромагнитная волна распространяется в однородной и изотропной среде с e = 2 и m = 1. Амплитуда напряженности электрического поля волны Е0 = 12 В/м. Определить: 1) фазовую скорость волны; 2) амплитуду напряженности магнитного поля волны.
Дано: e = 2; m = 1; Е0 = 12 В/м.
Определить: 1) v; 2) Н0.
Решение. Фазовая скорость электромагнитных волн равна:
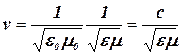 ,
,
где с = 3×108 м/с – скорость распространения света в вакууме.
В бегущей электромагнитной волне мгновенные значения Е и Н в любой точке связаны соотношением:
![]() .
.
Тогда для амплитуд напряженностей электрического и магнитного полей волны
![]() ,
,
откуда искомая амплитуда напряженности магнитного поля волны равна:
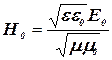 .
.
Вычисляя, получим: 1) v = 2,12×108 м/с; 2) Н0 = 45 мА/м.
Пример 2. В вакууме вдоль оси x распространяется плоская электромагнитная волна. Интенсивность волны, т.е. средняя энергия, проходящая через единицу поверхности за единицу времени, составляет 21,2 мкВт/м2. Определить амплитуду напряженности электрического поля волны.
Дано: e = 1; m = 1; I = 21,2 мкВт/м2 = 2,12×10-5 Вт/м2.
Определить Е0.
Решение. Так как интенсивность электромагнитной волны определена как средняя энергия, проходящая через единицу поверхности за единицу времени, то
![]() , (1)
, (1)
где j – модуль вектора плотности потока электромагнитной энергии – модуль вектора Умова-Пойнтинга.
Согласно определению,
![]() ,
,
где Е и Н – соответственно мгновенные значения напряженностей электрического и магнитного полей волны, описываемые уравнениями:
![]() ;
;
![]() .
.
Здесь Е0 и Н0 – соответственно амплитуды напряженностей электрического и магнитного полей волны; w – круговая частота; ![]() – волновое число (j – начальная фаза колебаний, принятая равной нулю).
– волновое число (j – начальная фаза колебаний, принятая равной нулю).
Мгновенное значение модуля вектора Умова-Пойнтинга равно:
![]() ,
,
а его среднее значение
![]() (2)
(2)
(учли, что ![]() ). Записав
). Записав
![]() ,
,
получим:
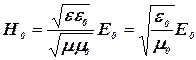 (3)
(3)
(учли, что электромагнитная волна распространяется в вакууме).
Подставив (3) в (2) и учитывая (1), найдем искомую амплитуду напряженности электрического поля волны:
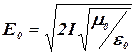 .
.
Вычисляя, получим: Е0 = 126 мВ/м.
Рассмотрим безграничное
трехмерное пространство, в котором
распространяется электромагнитная
волна. При этом будем полагать, что
среда, заполняющая это пространство,
является однородной,
изотропной и
линейной. Это значит,
что свойства его не зависят от координат,
направления распространения и амплитуды
волны. Для такого пространства мы
получили математическое описание
зависимости векторов напряженности
электрического и магнитного поля от
координаты z
и времени t.
Это формула (3.6) и (3.7).
Пусть вектор напряженности электрического
поля направлен по оси х. Тогда его можно
описать следующим образом:
|
|
(4.1) |
|
|
(4.2) |
Эти формулы по-разному
описывают один и тот же вектор: он
комплексный, направлен по оси х и имеет
амплитуду Е0.
Они полностью эквивалентны. В дальнейшем
мы чаще всего будем пользоваться второй
формой (4.2).
Функция времени и расстояния
в круглых скобках – текущая
фаза волны. Она
является текущей, то есть переменной,
потому, что зависит от времени t
и расстояния z.
Какой бы из этих параметров не изменился,
фаза также изменится, «утечет». Кроме
того, фаза зависит и от свойств среды,
в которой распространяется электромагнитная
волна. Свойства среды учитываются
волновым числом, в формулах (4.1) и (4.2) –
комплексным.
Это полное описание вектора
напряженности электрического поля с
использованием комплексных чисел.
Однако часто, особенно в средах без
потерь, удобно пользоваться мгновенными
значениями
напряженности поля волны. Для того чтобы
перейти к мгновенному значению, надо
взять действительную
часть формулы (4.2).
Кроме того положим, что потерь в среде
нет. Получим:
|
|
(4.3) |
Переход к соотношению (4.3) выполнен с
помощью формулы Эйлера, которая позволяет
преобразовать экспоненциальную форму
представления комплексного числа в
тригонометрическую:
|
|
(4.4) |
Действительная часть формулы (4.4) –
косинус. Кроме того, в формуле (4.3) учтено,
что в среде без потерь волновое число
γ – действительное и равно коэффициенту
фазы β.
Формула (4.3) описывает мгновенное
значениеплоской монохроматической
волны, распространяющейся вдоль
оси z:
-
значение мгновенное потому, что описывает
величину напряженности электрического
поля в фиксированный момент времени в
фиксированной точке пространства. -
волна распространяется вдоль оси zпотому, что только от этой координаты
зависит ее фаза; -
волна плоская потому, что фаза постоянна
на плоскости, описываемой уравнением
ωt- βz=const; -
волна монохроматическая потому, что
зависимость фазы от времени и координаты
описывается гармонической функцией
cos, которая монохроматическая
по определению.
Для проведения расчетов с использованием
метода комплексных амплитуд необходимо
из формулы (4.2) выделить комплексную
амплитуду напряженности электрического
поля. Получим:
|
|
(4.5) |
Для того чтобы полностью описать
электромагнитную волну надо найти
комплексную амплитуду напряженности
магнитного поля. Это можно сделать двумя
способами. Можно воспользоваться
решением однородного волнового уравнения
для вектора напряженности магнитного
поля, полученным в главе 3. Математически
это правильно, а физически не слишком.
Дело в том, что полученные таким образом
описания электрической и магнитной
составляющих электромагнитного поля
волны не будут связаны между собой. Они
не будут учитывать тот факт, что переменное
электрическое поле порождает переменное
магнитное поле и наоборот. Значит, эти
решения надо будет объединять
дополнительно.
Поэтому для нахождения комплексной
амплитуды вектора напряженности
магнитного поля правильнее воспользоваться
вторым уравнением Максвелла:
|
|
(4.6) |
Из него необходимо выразить вектор
напряженности магнитного поля:
|
|
(4.7) |
Теперь подставим сюда комплексную
амплитуду вектора напряженности
электрического поля (4.5) и раскроем
оператор rot. После простейших преобразований
получим:
|
|
(4.8) |
Таким образом, мы задали
характеристики вектора напряженности
электрического поля и по ним нашли
вектор напряженности магнитного поля.
Вектор напряженности электрического
поля мы направили по оси х, а вектор
напряженности магнитного поля получился
направленным по оси у. Следовательно,
векторы напряженности
электрического и магнитного полей
ортогональны.
Векторы напряженности электрического
и магнитного полей взаимно перпендикулярны
Формулируя задачу, мы условились о том,
что волна распространяется вдоль оси
z, а векторы напряженности
поля получились направленными по осям
х и у, то есть перпендикулярно направлению
распространения. Следовательно, мы
получилипоперечную волны.
Плоские электромагнитные волны в
свободном пространстве являются
поперечным
Формула (4.8) учитывает
параметры среды, которые определяют
волновое число и абсолютную магнитную
проницаемость. Из нее следует, что
между векторами напряженности
электрического и магнитного поля
существует очевидная пропорциональность:
|
|
(4.9) |
Определим размерность этого отношения.
Это проще всего сделать по левой части
формулы. Размерность напряженности
электрического поля в числителе В/м, а
размерность напряженности магнитного
поля в знаменателе – А/м. Следовательно,
размерность результата деления будет
В/А, то есть Ом. Поэтому отношение
комплексных амплитуд векторов
напряженности электрического и магнитного
полей назвали волновым сопротивлением:
|
|
(4.10) |
Волновым сопротивлением среды
называется отношение комплексных
амплитуд векторов напряженности
электрического и магнитного полей
В общем случае векторы напряженности
электрического и магнитного поля имеют
проекции на обе оси координат. У вектора
напряженности электрического поля
может появится проекция на ось у, а у
вектора напряженности магнитного поля
– проекция на ось х. Если волновое
сопротивление сформировать из отношения
второй пары проекций, модуль его не
изменится, но появится знак минус:
|
|
(4.11) |
Таким образом, волновое сопротивление
в общем случае описывается следующей
формулой:
|
|
(4.12) |
Из этой формулы следует весьма важный
вывод.
Волновое сопротивление полностью
определяется параметрами среды
Знание волнового сопротивления среды
позволяет находить электрическое поле
по известному магнитному полю и наоборот.
Рассмотрим правую часть формулы (4.12).
Она записана для среды с потерями. В
такой среде абсолютная диэлектрическая
проницаемость и абсолютная магнитная
проницаемость – комплексные величины.
Это означает, что отношение напряженностей
поля имеет не только модуль, но и аргумент,
и векторы напряженности электрического
и магнитного полей сдвинуты по фазе.
В среде с потерями векторы напряженности
электрического и магнитного полей
сдвинуты по фазе
В среде без потерь сдвига фаз между
электрическим и магнитным полем не
будет, то есть они буду синфазны.
В среде без потерь векторы напряженности
электрического и магнитного полей
синфазны
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Решение.
Фазовая скорость — скорость перемещения точки, обладающей постоянной фазой колебательного движения в пространстве, вдоль заданного направления.
Фазовую скорость определим по формуле:
[ begin{align}
& upsilon =frac{1}{sqrt{{{varepsilon }_{0}}cdot {{mu }_{0}}}}cdot frac{1}{sqrt{varepsilon cdot mu }}(1),c=frac{1}{sqrt{{{varepsilon }_{0}}cdot {{mu }_{0}}}}(2),upsilon =frac{c}{sqrt{varepsilon cdot mu }}(3). \
& upsilon =frac{3cdot {{10}^{8}}}{sqrt{3cdot 1}}=1,73cdot {{10}^{8}}. \
end{align} ]
с – скорость света в вакууме, с = 3∙108 м/с, ε0 = 8,854∙10-12 Ф/м – электрическая постоянная, μ0 = 4∙π∙10-7 Гн/м – магнитная постоянная.
Учитываем, что в электромагнитной волне в любой момент времени плотности энергии электрического и магнитного полей равны, определим амплитуду напряжённости магнитного поля волны.
[ begin{align}
& w=frac{varepsilon cdot {{varepsilon }_{0}}cdot {{E}^{2}}}{2}(4),w=frac{mu cdot {{mu }_{0}}cdot {{H}^{2}}}{2}(5),frac{varepsilon cdot {{varepsilon }_{0}}cdot {{E}^{2}}}{2}=frac{mu cdot {{mu }_{0}}cdot {{H}^{2}}}{2}, \
& H=sqrt{frac{varepsilon cdot {{varepsilon }_{0}}cdot {{E}^{2}}}{mu cdot {{mu }_{0}}}}(6). \
& H=sqrt{frac{3cdot 8,85cdot {{10}^{-12}}cdot {{10}^{2}}}{1cdot 4cdot 3,14cdot {{10}^{-7}}}}=4,6cdot {{10}^{-2}}. \
end{align} ]
Ответ: 1,73∙108 м/с, 4,6∙10-2 А/м.
Амплитуда электромагнитной волны
#44184
2021-11-21 07:09 GMT
цитата:” Электромагнитные волны распространяются в пространстве”. .._________ Если волна распространяется в пространстве, то у этой волны должна быть амплитуда. Как вычислить/найти амплитуду поперечной электромагнитной волны?
![]()
отредактировал(а) Пушкарь: 2021-11-21 07:14 GMT
#44187
2021-11-21 08:51 GMT
#44184
Пушкарь :цитата:” Электромагнитные волны распространяются в пространстве”. .._________ Если волна распространяется в пространстве, то у этой волны должна быть амплитуда. Как вычислить/найти амплитуду поперечной электромагнитной волны?

Замечательный пример того, как безграмотное высказывание приводит к неверным выводам.
Повтарю написанный идиотизм — ” Электромагнитные волны распространяются в пространстве”.
После таких слов в голову неграмотных людей всплывает вид волн в море.
Что-то типа этого —
Такие волны могут быть ТОЛЬКО на границе жидкой и газообразной сред
Но проблема в том, что волны могут быть двух видов –
продолные и поперечные —
Продолные волны бывают ТОЛЬКО ВНУТРИ среды.
На эту темы много литературы, нужно только не лениться.
Писать о поперечной электромагнитной волне, все равно, что писать о кривом молоке.
«Целкни кобылу в нос — она взмахнет хвостом.»
«Зри в корень» К.Прутков С
Я умею читать мысли других, но только тогда, когда они у них есть
#44188
2021-11-21 09:15 GMT
#44187
Anderis :
…..
Писать о поперечной электромагнитной волне, все равно, что писать о кривом молоке.
Согласен. «Кривое молоко», это оксюморон. Следовательно, электромагнитная волна, это тоже ≈ художественный образ в физике ( мягко говоря). Логично?
#44192
2021-11-21 11:08 GMT
#44188
Пушкарь :#44187
Anderis :
…..
Писать о поперечной электромагнитной волне, все равно, что писать о кривом молоке.
Согласен. «Кривое молоко», это оксюморон. Следовательно, электромагнитная волна, это тоже ≈ художественный образ в физике ( мягко говоря). Логично?
НЕТ ТАКОГО В ПРИРОДЕ — электромагнитная волна
И это НЕ логично.
Ты учился по надписям на стенах сортиров, а не по учебникам.
«Целкни кобылу в нос — она взмахнет хвостом.»
«Зри в корень» К.Прутков С
Я умею читать мысли других, но только тогда, когда они у них есть
#44194
2021-11-21 11:17 GMT
….
![]()
…..
#44229
2021-11-22 13:18 GMT
#44192
Anderis :
Молодец, затролили человека.
#44184
Пушкарь :цитата:” Электромагнитные волны распространяются в пространстве”. .._________ Если волна распространяется в пространстве, то у этой волны должна быть амплитуда. Как вычислить/найти амплитуду поперечной электромагнитной волны?

Вот у вас есть полувибратор. Это 2 метлических стержня соединенные между собой сопротивлением. Обычно в 50 или 75 Ом.
В одну часть накачивают электроны потом они перебигают в вторую часть. Затем электроны откачивают из первойй части и излишние электроны возвращаются из второй части в первую.

На приемнике под действием напряжения, согласно силы кулона электроны так же перебигают с одного вибратора на другой.
Решаем уравнения Максвела получаем ток. Идущий в вибраторе.
Если на передатчике у нас 0,250 Вт. А сопротивление 50 то ток равен I=0,005 Ампер.
При передачи мощьность падает на более чем 32 дБ т.е Подение со спутника типовое это 45-55 дБ
10Log(x)=32 дб -> x=1584 раза
10Log(x)=50 дб -> x=100 000 раза
Ток на приемнике
I=0,00000005=5 *10 ^-8
Ампитуда волны это плотность электронов их колличество в вибраторе.
I=Q/t
t=2/f
f- частота. t — полу периуд волны
Возьмем для примера f= 1 ГГц = 10^9 Гц.
t=2*10^-9
(N=frac{Q}{e}=frac{I*t}{e}=frac{5 cdot10 ^{-8}*2cdot 10^{-9}}{1.6 cdot 10^{-19}} =6.25 cdot10^{19-16}=625)
шт электронов
отредактировал(а) Очепятка: 2021-11-22 14:26 GMT
#44231
2021-11-22 13:47 GMT
#44229
Очепятка :#44184
Пушкарь :цитата:” Электромагнитные волны распространяются в пространстве”. .._________ Если волна распространяется в пространстве, то у этой волны должна быть амплитуда. Как вычислить/найти амплитуду поперечной электромагнитной волны?

… Ампитуда волны это плотность электронов их колличество в вибраторе.
I=Q/t
t=2/f
f- частота. t — полу периуд волны
Возьмем для примера f= 1 ГГц = 10^9 Гц.
t=2*10^-9
(N=frac{Q}{e}=frac{I*t}{e}=frac{5 cdot10 ^{-8}*2cdot 10^{-9}}{1.6 cdot 10^{-19}} =6.25 cdot10^{19-16}=625)
Плотность электронов в вашем сообщении, это скалярная величина ( на бумаге). …….._________. А я говорю об электромагнитной волне в пространстве. Длина электромагнитной волны может быть 1000 метров и более, а какова амплитуда такой волны в метрах.
#44237
2021-11-22 15:20 GMT
Плотность электронов в вашем сообщении, это скалярная величина ( на бумаге). …….._________. А я говорю об электромагнитной волне в пространстве. Длина электромагнитной волны может быть 1000 метров и более, а какова амплитуда такой волны в метрах.
Выше была показана ссылка с полу вибратором


P=U*I=U^2/R
U=0.250*50=12.5 Вольт.
Вот остается найти d.
Ах да длину полувибратора берету как 1/4 от длины волны. Так что d в начальной точке довольно большое.
Впрочем сращу возьмем готовую формулу.
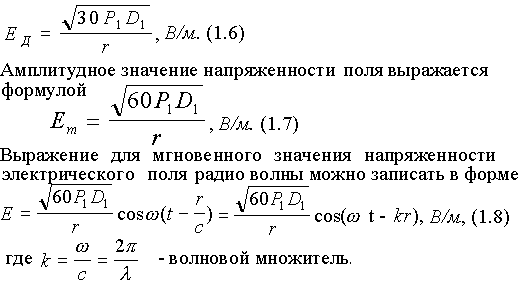
Пусть растояние между передатчиком и приемниом r=100 км E_m=3.8*10^{-5} В/м амплитуда напряженности.
(E_m=kfrac{q}{h^2})
(h=sqrt{kq/E_m})
(=sqrt{9*10^9*625*1.6*10^{-19}/3.8*10^{-5}})
=0.12 метра амплитуда против длины в 0,3 м длины волны
С удалением амплитуда возрастает. При приближении падает. И мощьность передатчиков бывает разная где-то несколько десятков мкВт, а где-то как в радарах дальнего обноружения МВт.
Вообщем как-то так это считается. Подробнее ищите в книгах по радио технике.
#44239
2021-11-22 15:25 GMT
#44237
Очепятка :Выше была показана ссылка с полу вибратором
Ты можешь пользоватьвсем, чем хочешь, но зачем же об этом писать?
«Целкни кобылу в нос — она взмахнет хвостом.»
«Зри в корень» К.Прутков С
Я умею читать мысли других, но только тогда, когда они у них есть
#44252
2021-11-22 18:19 GMT
#44237
Очепятка :Плотность электронов в вашем сообщении, это скалярная величина ( на бумаге). …….._________. А я говорю об электромагнитной волне в пространстве. Длина электромагнитной волны может быть 1000 метров и более, а какова амплитуда такой волн
(E_m=kfrac{q}{h^2})
(h=sqrt{kq/E_m})
(=sqrt{9*10^9*625*1.6*10^{-19}/3.8*10^{-5}})Вообщем как-то так это считается. Подробнее ищите в книгах по радио технике.
Искал. Нашёл задачник. В задачнике есть примеры решения задач по расчёту амплитуды напряжённости поля. Ответ: E= 0,94 в/м. Судя по единице измерения «в/м», это что-то другое, поскольку амплитуда волны, это высота «горы», поэтому она измеряется просто в метрах ( система СИ) .___________ В общем, мои смутные сомнения подтвердились. У электромагнитной волны нет амплитуды. Из этого следует вывод, что электромагнитные волны, волнами не являются. _________________________Термин «электромагнитная волна», — это лирическая аллегория, взятая физиками у лириков и не имеющая физического смысла.
![]()
отредактировал(а) Пушкарь: 2021-11-22 18:49 GMT
#44260
2021-11-23 00:07 GMT
цитата:” Электромагнитные волны распространяются в пространстве”. … Если волна распространяется в пространстве, то у этой волны должна быть амплитуда. Как вычислить/найти амплитуду поперечной электромагнитной волны?
——————————-
Вы должны сформулировать задачу.Что дано, что известно. Поперечные электромагнитные волны например бывают в изотропном диэлектрике или магнетике. Поперечные колебания совершают векторы электрического и магнитного полей.
В какой среде ваша поперечная волна? Если вы этого не понимаете и не знаете параметры среды, то ничего подсчитать нельзя. Это все равно что спрашивать, какая орбита у небесного тела, который вращается?
Вас сразу спросят. Вращается вокруг чего? Вокруг своей оси или Солнца, Земли, Луны. О каком теле вы говорите?
Видно, что тот кто задал вопрос, его не сформулировал. Это изучают в университете.
—
,, Термин «электромагнитная волна», — это лирическая аллегория, взятая физиками у лириков и не имеющая физического смысла”.
Нет, это означает, что вы невежественный человек, который не знаком с основными процессами в природе.
#44270
2021-11-23 08:05 GMT
#44260
marsdmitri :….
—
,, Термин «электромагнитная волна», — это лирическая аллегория, взятая физиками у лириков и не имеющая физического смысла”.
Нет, это означает, что вы невежественный человек, который не знаком с основными процессами в природе.
Вы вырвали мою фразу из контекста. И я вас понимаю, поскольку весьма сложно аргументированно опровергнуть это моё утверждение.
#44271
2021-11-23 08:10 GMT
#44260
marsdmitri :Вы должны сформулировать задачу.Что дано, что известно. Поперечные электромагнитные волны например бывают в изотропном диэлектрике или магнетике. Поперечные колебания совершают векторы электрического и магнитного полей.
В какой среде ваша поперечная волна? ….
Моя поперечная электромагнитная волна распространяется в космическом пространстве. В космическом вакууме. …… Но если по вашему мнению этого не достаточно для вычислений, то добавьте всё, что считаете необходимым. Я всецело полагаюсь на ваш вкус.
![]()
__________________________________________________PS … Не сердитесь. It’s not Personal. Только научнодискуссионный интерес.
отредактировал(а) Пушкарь: 2021-11-24 10:20 GMT
#44273
2021-11-23 08:52 GMT
#44271
Пушкарь :
Моя электромагнитная волна распространяется в пространстве. В космическом вакууме. ……
Нет электромагнитных волн и нет пространства и нет космического вакуума — это всё он безграмотности.
«Целкни кобылу в нос — она взмахнет хвостом.»
«Зри в корень» К.Прутков С
Я умею читать мысли других, но только тогда, когда они у них есть
Методы измерения основных параметров, характеризующих высокочастотное электромагнитное поле
Страницы работы
Содержание работы
Введение
Методы измерения основных параметров, характеризующих
высокочастотное электромагнитное поле
Общие сведения
Электромагнитное
поле характеризуется рядом параметров, но в условиях учебной лаборатории
обычно измеряют напряженность электрического поля или величину, пропорциональную
квадрату напряженности (мощность), а также плотность потока мощности, т.е.
мощность, приходящуюся на единицу площади некоторой поверхности. Везде мы
рассматриваем только процессы, изменяющиеся во времени по гармоническому
закону. Поэтому все величины, в том числе и напряженность электрического
поля, изменяются во времени по закону ![]() .
.
Напряженность
электрического поля ![]() – это в общем случае векторная
– это в общем случае векторная
комплексная величина, которая характеризуется амплитудой, фазой и
поляризацией, т.е. ориентацией вектора ![]() в
в
пространстве. В соответствии с этим можно записать ![]() ,
,
где E – амплитуда напряженности электрического поля (в
системе единиц СИ она измеряется в вольтах на метр);
j –
фаза напряженности электрического поля;
![]() – поляризация, т.е. ориентация вектора
– поляризация, т.е. ориентация вектора ![]() электрического поля.
электрического поля.
Измерение амплитуды напряженности поля
Рассмотрим измерение амплитуды напряженности
электрического поля. Во многих случаях нам не обязательно знать абсолютное
значение амплитуды напряженности (в вольтах на метр), а достаточно знать,
как изменяется амплитуда напряженности поля при перемещении из одной точки
пространства в другую. Такие измерения называются относительными.
 |
При измерениях напряженности электрического
поля используется устройство, называемое зондом. Имеется ряд вариантов
конструкции зонда (они рассмотрены ниже), но все они обязательно содержат
элемент, называемый детектором. Детектор предназначен для преобразования
высокочастотных модулированных колебаний в низкочастотные (колебания с частотой
модуляции) или для преобразования высокочастотных немодулированных
колебаний в постоянное напряжение (ток). На СВЧ в качестве детекторов, как правило,
используются полупроводниковые диоды, конструкция которых изображена на
рисунке 1. Там же показано изображение детектора на принципиальной схеме, которое
будет использоваться в дальнейшем.
При
измерениях чаще всего используются следующие варианты конструкции зондов:
 |
1). Зонд в виде электрического диполя Герца
или симметричного электрического вибратора. Диполь Герца и плечи вибратора
должны быть ориентированы параллельно линиям вектора ![]() измеряемого поля. В качестве плеч диполя
измеряемого поля. В качестве плеч диполя
Герца или симметричного вибратора на СВЧ можно использовать выводы полупроводникового
диода (рисунок 2-а).
2).
Зонд в виде специальной детекторной секции волноводного типа (рисунок 2-б). В
этом случае детектор устанавливается в прямоугольном волноводе, который играет
роль приемной антенны. Вектор ![]() измеряемого поля должен
измеряемого поля должен
быть перпендикулярен широкой стенке волновода.
3).
Зонд, состоящий из приемной антенны малых размеров (обычно – пирамидального
рупора), присоединенный к детекторной секции (рисунок 2-в). Ориентация вектора
![]() такая же, как и в предыдущем случае.
такая же, как и в предыдущем случае.
4).
Зонд, состоящий из приемной антенны в виде несимметричного вибратора (обычно
– это штырь, помещенный в волновод или объемный резонатор), присоединенного
к детекторной секции коаксиального типа (рисунок 2-г). Вектор ![]() измеряемого поля при этом должен быть
измеряемого поля при этом должен быть
параллелен штырю.
Первые
3 варианта зонда используются для измерения амплитуды напряженности поля
или мощности в различных точках пространства (в том числе – и в раскрыве излучающего
волновода или рупора). Четвертый вариант обычно используется для измерения
распределения амплитуды напряженности поля вдоль волновода или объемного резонатора.
Зонд в виде штыря при этом перемещается вдоль щели, прорезанной в стенке волновода
или резонатора.
Любой
зонд, помещенный в некоторую точку, в которой мы хотим измерить напряженность
электрического поля, искажает поле в этой точке. Для того, чтобы это искажение
было малым, необходимо, чтобы размер зонда был мал по сравнению с длиной
волны.
Аппаратура для измерения
абсолютной и относительной амплитуды напряженности поля
При измерении абсолютной амплитуды напряженности поля
измерительный зонд (приемная антенна) присоединяется к специальной
измерительной аппаратуре. Чаще всего используются два вида аппаратуры:
1). Высокочувствительный приемник, снабженный
индикатором выхода. Для калибровки усиления такого приемника используется
метод сравнения (компарирования), поэтому такие приемники называют
компараторами.
2). Высокочастотный микровольтметр. Он также содержит
высокочувствительный приемник с индикатором выхода и устройство для
калибровки усиления. Детектор при этом конструктивно входит в состав
компаратора или микровольтметра.
При измерении относительной амплитуды напряженности
поля используют один из выше перечисленных вариантов конструкции зонда с
детектором. Сигнал, принятый зондом, после детектора подается на индикатор,
который фиксирует измеряемую величину. Используемые индикаторы могут быть
2-х типов:
1). Приборы постоянного тока (микроамперметры,
миллиамперметры) или усилители постоянного тока, снабженные индикатором
выхода.
2). Усилители переменного низкочастотного напряжения,
снабженные индикатором выхода.
Похожие материалы
- Исследование дифракции электромагнитных волн на цилиндре (Отчет по лабораторной работе № 4)
- Исследование поверхностных волн (Отчет по лабораторной работе № 2)
- Ферритовые устройства на прямоугольных волноводах (Отчет по лабораторной работе № 6)
Информация о работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
