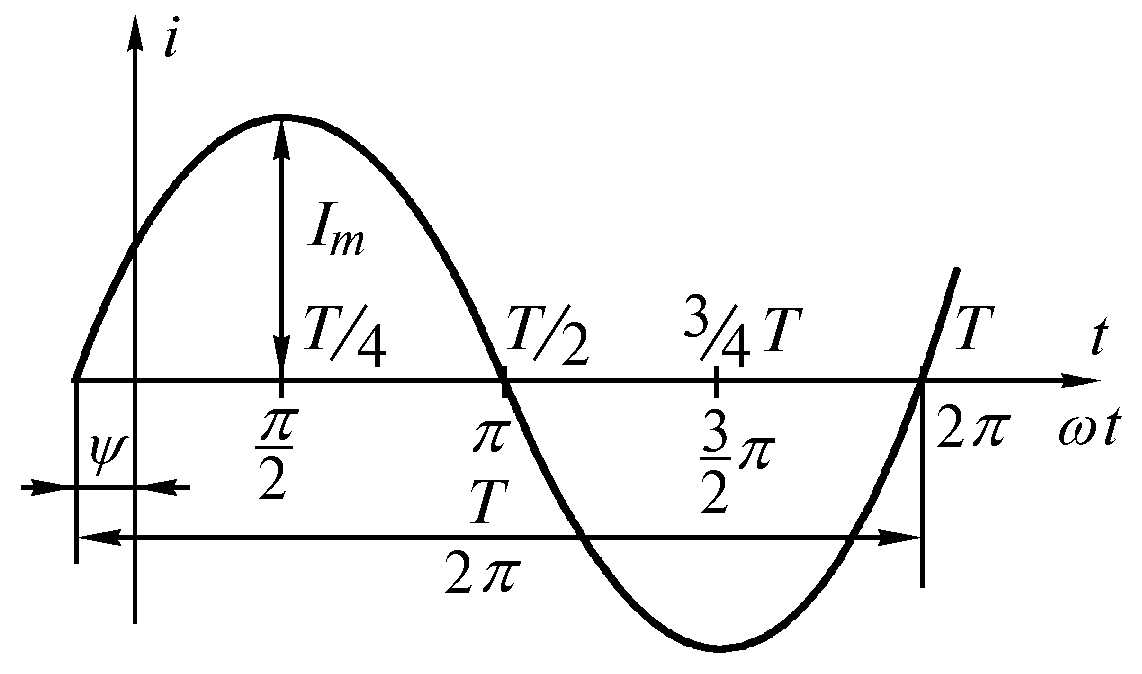Как найти амплитуду синусоидального тока

2.1. Общие сведения

В электроэнергетике используют в
основном переменный ток. В настоящее
время почти вся электрическая энергия
вырабатывается в виде энергии переменного
тока. Основное преимущество переменного
тока по сравнению с постоянным током
заключается в возможности просто и с
минимальными потерями пре­образовывать
напряжение при передаче энергии.
Генераторы и двигатели перемен­ного
тока имеют более простое устройство,
надежней в работе и проще в эксплуата­ции
по сравнению с машинами постоянного
тока.

2.1.1. Амплитуда, частота и фаза синусоидального тока и напряжения

В современной технике широко используются
переменные токи: синусоидаль­ные,
прямоугольные, треугольные и др. (рис.
2.1). Значение тока в любой момент времени
называется мгновеннымзначением.
Мгновенные значе­ния тока, напряжения,
ЭДС обозначаются буквами.

Токи, мгновенные значения которых
повторяются через равные промежутки
времени, называютпе­риодическими,
а наименьший про­межуток времени,
через который эти повторения наблюдаются,
назы­ваютпериодомТ(рис.
2.1).

Если кривая изменения пе–

Рис. 2.1
рио­дического тока описывается
синусоидой, ток называется синусоидальным.
Если кривая отличается от синусоиды –
ток несинусоидальный. В электрических
це­пях переменного тока наиболее
часто используют синусоидальную форму,
харак­теризующуюся тем, что все
напряжения и токи являются синусоидальными
функ­циями времени. В генераторах
переменного тока стремятся получить
ЭДС, изме­няющуюся во времени по закону
синуса. Тем самым обеспечивается наиболее
вы­годный эксплуатационный режим
работы электрических установок.

Все синусоидальные функции времени
(например, ток) записывают в одина­ковой
форме:

(2.1)

где
–
мгновенное значение тока;–максимальное (амплитудное)значение
тока (рис. 2.2);– угловая частота;– начальная фаза.

Аргумент синуса
называетсяфазой.
Угол
равен фазе в начальный момент времени=
0 и по­этому называетсяначальной
фазой. Фаза
с течением времени непрерывно растет
(рис 2.2). После ее увеличения на
весь цикл изменения тока повто­ряется.
В течение периодафаза увеличивается на.
Поэтому отношениеопределяет скорость изменения фазы и
называетсяугловой
часто­той

Рис. 2.2

(2.2)

где
– частота, равная числу периодов в
секунду,Гц. При
стандартной частоте
=
50 Гцугловая частотаЗа
аргумент си­нусоидальной функции
принимают времяили угол.

Таким образом, для
определения мгновенных значений
инеобходимо опре­делить их параметры:
амплитуду, угловую частоту и начальную
фазу.

Постоянный ток
можно рассматривать как частный случай
переменного тока, частота которого
равна нулю. В современной технике
используется широ­кий диапазон частот
переменных токов от сотых долей до
миллиардов Герц. В электроэнергетике
нашей страны и Европы стандартная
частота 50 Гц,
США – 60 Гц.

Рис. 2.3

Синусоидальные ЭДС в современной
технике получают различными мето­дами
в электромашинных или электрон­ных
генераторах и других устройствах.
Наглядным примером является наведе­ние
ЭДС за счет электромагнитной ин­дукции
в рамке, вращающейся в одно­родном
магнитном поле (рис. 2.3).

Допустим, что рамка площадью
содержитвитков и вращается с посто­янной
угловой скоростьюв магнит­ном поле с индукцией.
Тогда потокосцепление рамки

.

По закону электромагнитной индукции
в рамке наводится ЭДС

.

Следовательно, ЭДС изменяется по
синусоидальному закону.

Рассмотренный способ получения ЭДС
является лишь наглядной иллюстра­цией
и в технике не используется ввиду
экономической нецелесообразности
соз­давать достаточно сильное
равномерное магнитное поле в таком
большом воз­душном промежутке.

В промышленности для получения
синусоидальных ЭДС применяют электри­ческие
машины – синхронные генераторы,
приводимые во вращение теп­ловыми,
газовыми, гидравлическими и др.
двигателями.

Соседние файлы в папке Лекции

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Период, частота, амплитуда и фаза переменного тока

Период и частота переменного тока

Время, в течение которого совершается одно полное изме­нение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания пере­менного тока (рисунок 1).

Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.

Период выражают в секундах и обозначают буквой Т.

Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.

1 мкс=0,001 мс = 0,000001сек =10 -6 сек.

Число полных изменений ЭДС или число оборотов ради­уса-вектора, то есть иначе говоря, число полных циклов колеба­ний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.

Частота обо­значается буквой f и выражается в периодах в секунду или в герцах.

Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.

1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;

1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;

Чем быстрее происходит изменение ЭДС, то есть чем бы­стрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.

Математическая связь между периодом и частотой переменного тока и напряжения выра­жается формулами

Например, если частота тока равна 50 Гц, то период будет равен:

И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:

Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.

Частоты от 20 до 20 000 Гц называются звуковыми часто­тами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие вы­сокие частоты называются радиочастотами или колебаниями высокой частоты.

Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.

Амплитуда переменного тока

Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно бук­вами Im, Em и Um (рисунок 1).

Угловая (циклическая) частота переменного тока.

Скорость вращения радиуса-вектора, т. е. изменение ве­личины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (оме­га). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.

Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.

Рисунок 2. Радиан.

1рад = 360°/2

Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в тече­ние одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его ко­нец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ? .

? = 6,28*f = 2f

Фаза переменного тока.

Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза пока­зывает, убывает ли ЭДС или возрастает.

Рисунок 3. Фаза переменного тока.

Полный оборот радиуса-вектора равен 360°. С началом но­вого оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следова­тельно, все фазы ЭДС будут повторяться в прежнем поряд­ке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обо­их этих случаях радиус-вектор занимает одинаковое положе­ние, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Источник

Часть III. Цепи синусоидального тока

Тема 3. Цепи синусоидального тока

1. Общие сведения и определения
2. Комплексная амплитуда
3. Действующие значения синусоидальной функции
4. Изображение синусоидальных функций векторами. Векторная диаграмма
5. Изображение синусоидальной функции комплексными числами
6. Закон Ома в комплексной форме
7. Уравнения элементов в комплексной форме

• § 3.1. Общие сведения и определения:

Переменный ток имеет большее распространение, чем постоянный.

• конструкция электродвигателей и генераторов переменного тока гораздо проще;
• генераторы переменного тока могут быть выполнены для более высокого напряжения;
• переменный ток легко преобразовывается с помощью трансформатора, что необходимо при распределении электроэнергии и т.д.

Переменный ток – ток, периодически меняющий свое значение и направление. Наибольшее значение переменного тока – его амплитуда.

Переменный ток характеризуется:

Амплитуда – наибольшие (положительные или отрицательные) величины.

Период – время, в течение которого происходит полное колебание тока в проводнике.

Фаза – характеризует состояние переменного тока в любой момент времени.

Основным видом переменного тока является синусоидальный (гармонический) ток. Закон изменения такого тока описывается синусоидальной функцией.

В линейных электрических цепях, в которых действуют синусоидальные источники, все электрические параметры изменяются по синусоидальному закону.

ЭДС: .

Напряжение: .

Ток: ;

e(t), u(t), i(t) – мгновенные значения;

ω = 2π – угловая частота, [рад/с];

ƒ = 1 Т – циклическая частота, [Гц];

Любую синусоидальную функцию можно изобразить в виде графика, который называется графиком временных значений или временной диаграммой.

Расчет цепей синусоидального тока с использованием мгновенных значений требует громоздкой вычислительной работы и применим для простейших электрических цепей.

Для расчета цепей синусоидального тока синусоидальную функцию заменяют эквивалентной величиной.

где j = √ — 1 – мнимая единица.

– комплексная амплитуда.

– сопряженная комплексная амплитуда.

– поворотный множитель.

Последняя запись означает, что синусоидальное напряжение можно представить на комплексной плоскости в виде двух векторов, длина которых равна U_m и которые равномерно вращаются со скоростями, равными ω в противоположные стороны.

• § 3.3. Действующие значения синусоидальной функции:

Действующее значение синусоидальной функции – ее количественная оценка.

Действующие значения – среднеквадратичные за период значения синусоидальной функции, то есть, если:

Аналогично и для тока I и ЭДС ε .

Часто используются выражения, связывающие между собой амплитуду и действующее значение:

Действующее значение – это постоянная величина, которую обычно обозначают той же буквой, что и амплитуду, только без индекса m.

Действующее значение тока оказывает такое же тепловое действие на проводник с сопротивлением R , что и переменный ток, в течение времени, равном периоду. Поэтому большинство электроизмерительных приборов фиксируют и реагируют на действующие значения.

• § 3.4. Изображение синусоидальных функций векторами. Векторная диаграмма:

где a – проекция вектора на ось y в момент времени t.

рис. а рис. б

Любому равномерно вращающемуся радиус-вектору соответствует некоторая синусоидальная функция, и наоборот.

Посмотрим, как условный графический образ синусоидальной функции – радиус-вектор – может быть применим при расчетах цепей переменного тока. Определим ток:

если: и .

Как известно, сумма двух синусоид одинаковой частоты ω представляет собой также синусоиду частотой ω , то есть i = I_msin (ωt + ψ ) и, следовательно, задача сводится к нахождению амплитуды I_m и начальной фазы Ψ суммарного тока i. Искомые параметры I_m и Ψ можно найти, воспользовавшись известными тригонометрическими преобразованиями.

Проведем решение задачи с помощью радиус-векторов I_1m и I_2m , вращающихся с частотой ω, положение которых для момента времени t = 0 показаны на рисунке ниже и осуществим геометрическое суммирование этих радиус-векторов по правилу параллелограмма. Результирующий радиус-вектор I_m будет вращаться с частотой ω и является изображением некоторой синусоидальной функцией времени.

Следовательно, i = i₁ + i₂ – геометрическое изображение искомого тока.

Измерив дугу суммарного радиус-вектора и, зная выбранный масштаб, можно определить амплитуду I_m тока. Непосредственно по чертежу определяется и начальная фаза Ψ.

Рассмотренная совокупность радиус-векторов, изображающих синусоидальные функции времени, называется векторной диаграммой.

• § 3.5. Изображение синусоидальной функции комплексными числами:

Для введения комплексного изображения перенесем радиус-вектор, изображающий синусоидальную функцию времени в декартовой плоскости на плоскость комплексных чисел. Для чего совместим ось x с осью действительных чисел Re, а ось y – с Im.

Любому вектору A, расположенному на комплексной плоскости, однозначно соответствует комплексное число, которое может быть записано в трех формах:

Все три формы записи в соответствии с формулой Эйлера равнозначны:

Переход от одной формы записи к другой:

где a₁ – действительная часть;

Запишем в трех формах выражение для единичных действительных и мнимых комплексных чисел ( A = 1 ):

Отношение комплексной амплитуды напряжения к комплексной амплитуде тока называется комплексным сопротивлением:

Модуль комплексного сопротивления, называемый полным сопротивлением, равен отношению амплитуды напряжения к амплитуде тока, а аргумент Ψ комплексного сопротивления – разности начальных фаз напряжения и тока:

Закон Ома в комплексной форме соответственно для амплитудных и действительных значений:

.

Добавить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Источник

Переменный электрический ток

Переменный ток (AC – Alternating Current) – электрический ток, меняющий свою величину и направление с течением времени.

Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC.
Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.

DC – Direct Current – постоянный ток, не меняющий своей величины и направления.

В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.

При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.

Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.

Величина тока будет равна квадратному корню из суммы квадратов двух величин – значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.

Термины AC и DC применимы как для тока, так и для напряжения.

Параметры переменного тока и напряжения

Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:

Период T – время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.

Частота  f – величина, обратная периоду, равная количеству периодов за одну секунду.

Один период в секунду это один герц (1 Hz). Частота f = 1/T

Циклическая частота  ω – угловая частота, равная количеству периодов за 2π секунд.

ω = 2πf = 2π/T

Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°

Начальная фаза  ψ – величина угла от нуля (ωt = 0) до начала периода.
Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.

Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.

Мгновенное значение – величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.

i = i(t);   u = u(t)

Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:

i = I_ampsin(ωt);   u = U_ampsin(ωt)

С учётом начальной фазы:

i = I_ampsin(ωt + ψ);   u = U_ampsin(ωt + ψ)

Здесь I_amp и U_amp – амплитудные значения тока и напряжения.

Амплитудное значение – максимальное по модулю мгновенное значение за период.

I_amp = max|i(t)|;   U_amp = max|u(t)|

Может быть положительным и отрицательным в зависимости от положения относительно нуля.

Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) – максимальное отклонение от нулевого значения.

Среднее значение (avg) – определяется как среднеарифметическое всех мгновенных значений за период T.

Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.

Средневыпрямленное значение – среднеарифметическое модулей всех мгновенных значений за период.

Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.

Среднеквадратичное значение (rms) – определяется как квадратный корень из среднеарифметического квадратов всех
мгновенных значений за период.

Для синусоидального тока и напряжения амплитудой I_amp (U_amp)
среднеквадратичное значение определится из расчёта:

---

Коэффициент амплитуды и коэффициент формы

---

Характеристики электрической цепи синусоидального тока

Электротехнические устройства синусоидального тока широко используются в различных областях промышленности, сельском хозяйстве и т.п., в процессах генерирования, передачи, распределения, преобразования, трансформации электрической энергии. Основное преимущество использования цепей синусоидального тока заключается в том, что при передаче и распределении электроэнергии ее потери самые маленькие по сравнению с другими видами энергии. Еще одно преимущество синусоидального тока – -возможность создания источников электрической энергии большой мощности. Например, современные турбинные генераторы обладают мощностью от 100 до 1500 мегаватт. Асинхронные и синхронные двигатели синусоидального тока являются самыми дешевыми и простыми преобразователями электрической энергии. Стандартная частота электротехнических установок в большинстве стран, в том числе и Российской Федерации составляет 50 герц.

Пример функции синусоидальной электрической цепи изображен на рисунке ниже.

Как видно из функции выше, синусоидальный ток изменяется с течением времени. К его основным характеристика относятся:

1. Частота.
2. Амплитуда.
3. Начальная фаза.

Частота представляет собой характеристику, которая показывает сколько колебаний совершается за одну единицу времени, измеряемая в герцах. Величина, являющаяся обратной частоте – период (полное время колебания) и рассчитывается следующим образом:

$Т = 1 / f$

где, f – частота.

«Электрические цепи синусоидального тока» 👇

Начальная фаза представляет собой время, на которое синусоида опережает или отстает от начального момента времени. Математически синусоидальный ток можно описать следующей формулой:

$i = Imsinwt$

где, Im – амплитуда синусоидального тока; wt – фаза синусоидального тока.

Параметр w, который входит в состав выражения фазы синусоидального тока называется угловой частотой и рассчитывается следующим образом:

$w = 2пf = 2п / Т$

Где: f – частота синусоидального тока; Т – период синусоидального тока; 2п – центральный угол окружности.

Способы представления электрических цепей синусоидального тока

На практике используются три основных способа представления синусоидального тока:

1. Аналитический способ.
2. Временная диаграмма.
3. Графоаналитический способ.

При использовании аналитического способа представления, выражения для основных параметров цепи выглядят следующим образом:

Электрический ток:

$I(t) = Imsin(wt+ji)$

Для напряжения:

$U(t) = Umsin(wt+ju)$

Для электродвижущей силы:

$e(t) = Emsin(wt+je)$

где, Im – амплитуда электрического тока; Um – амплитуда напряжения; Em – амплитуда электродвижущей силы; ji, ju, je – начальные фазы тока, напряжения и электродвижущей силы; w – угловая частота синусоидального тока.

Временная диаграмма представляет собой графическое изображение какой-либо синусоидальной величины в установленном масштабе, в зависимости от времени:

$i(t) = Imsin(wt+ji)$

При применении графоаналитического способа представления величины изображаются в виде вращающегося вектора, как показано на рисунке ниже.

Предполагается, что вращение осуществляется против часовой стрелки с частотой w, величина вектора – амплитудное значение, а проекция на вертикальную ось – мгновенное значение величины. Совокупность векторов, которые изображают ток, напряжение и электродвижущую силу, называется векторной диаграммой. Сами векторные величины сверху отмечаются точкой. Применение векторных диаграмм значительно упрощается анализ электрических цепей синусоидального тока и делает его более наглядным.

Действующее и среднее значения синусоидально изменяющейся величины

Средним значением синусоидальной величины является ее среднее значение на половину периода. Для тока формула для расчета среднего значения будет выглядеть следующим образом.

Таким образом среднее значение электрического тока составляет 0,63 от амплитудного.

При анализе электрических цепей синусоидального тока также широко используется действующее значение синусоидальных величин, которое можно рассчитать по формуле:

То есть действующее значение тока составляет 0,707 от амплитудного. Аналогично можно рассчитать действующие значения напряжения и электродвижущей силы:

Численно действующее значение электрического тока равняется значению постоянного тока, выделяющему за промежуток времени, который равен периоду синусоидального тока, такое же количество теплоты. Подавляющее большинство измерительных приборов показывают действующее значение.

Рассмотрим подробнее кривую, изображающую зависимость мгновенного значения технического переменного тока (или напряжения) от времени (рис. 293). Прежде всего обращает на себя внимание тот факт, что этот ток (или напряжение) изменяется периодически, т. е. каждое мгновенное значение этих величин, например значение, соответствующее точке

 (или точке

), повторяется через один и тот же промежуток времени. Другими словами, сила тока (или напряжение) пробегает за этот промежуток времени все возможные значения, возвращаясь к исходному, т. е. совершает полное колебание. Промежуток времени, в течение которого сила тока (или напряжение) совершает полное колебание и принимает прежнее по модулю и знаку мгновенное значение, называется периодом переменного тока. Его принято обозначать буквой

. Для сетей СССР и большинства других стран

 с, а так как изменение направления тока происходит два раза в течение каждого периода, то технический ток меняет свое направление 100 раз в секунду.

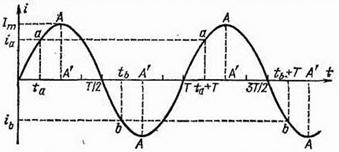
Рис. 293. Зависимость силы переменного тока от времени

Максимальное значение, которое может иметь переменный ток (или напряжение) в том или другом направлении, называется амплитудой этой величины. На рис. 293 амплитуда изображается отрезками

. Амплитуду токов и напряжений обозначают

 или

, а их мгновенные значения –

 и

.

Число полных колебаний (циклов) синусоидального тока или напряжения за единицу времени называют частотой соответствующей величины и обозначают буквой

. Очевидно,

,

. (153.1)

За единицу частоты принимают частоту, равную одному колебанию в секунду. Эту единицу называют герцем (Гц) по имени немецкого физика Генриха Герца (1857-1394). Таким образом, технический переменный ток имеет частоту 50 Гц.

Вместо частоты

 вводят также величину

, которую называют циклической или круговой частотой тока (напряжения). Она представляет собой число полных колебаний (циклов) данной величины за

 секунд.

Пока мы имеем дело только с одним синусоидальным переменным током или переменным напряжением, частота и амплитуда являются полными и исчерпывающими характеристиками этих величии, потому что начальный момент отсчета времени мы можем выбрать произвольно. Но когда нам приходится сопоставлять друг с другом две или несколько величин такого рода, мы должны учитывать и тот факт, что они могут достигать максимального значения не в один и тот же момент времени.

Две кривые на рис. 294, а изображают форму двух синусоидальных переменных токов с одной и той же частотой и амплитудой, но кривые эти смещены по оси абсцисс (оси времени) на отрезок, равный четверти, периода. Начальная точка отсчета времени выбрана так, что для первой кривой нулевые значения достигаются в моменты

 а амплитудные – в моменты

. Вторая же кривая проходит через нулевые значения в моменты

 а через амплитудные – в моменты

.

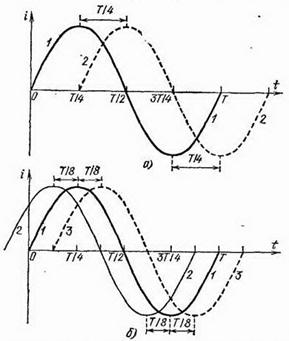
Рис. 294. Графическое изображение переменных токов одинаковой частоты и амплитуды, смещенных по фазе: а) два синусоидальных тока, смещенные по фазе на четверть периода; б) токи, изображаемые кривыми 2 и 3, смещены по фазе относительно кривой 1 на одну восьмую часть периода

В подобных случаях говорят, что эти два тока (или две другие синусоидальные величины) сдвинуты друг относительно друга по фазе, или, иначе, что между ними существует некоторый сдвиг фаз (или разность фаз), равный в данном примере четверти периода. Так как кривая 1 проходит через амплитудное значение, так же как и через любое другое соответствующее значение, раньше, чем кривая 2, то говорят, что она опережает кривую 2 по фазе или, иначе, что кривая 2 отстает по фазе от кривой 1.

153.1.
На рис. 294, б кривые 2 и 3 сдвинуты относительно кривой 1 по фазе на одну восьмую периода. Определите, какая из этих кривых отстает по фазе от кривой 1 и какая опережает ее. Какова разность фаз между кривыми 2 и 3?

Во всех случаях, когда приходится сопоставлять синусоидальные величины или рассматривать их совместное действие (складывать или перемножать их), вопрос о соотношении фаз между этими величинами имеет очень важное значение. Таким образом, в общем случае, когда имеется несколько синусоидальных токов или напряжений, нужно характеризовать каждый из них тремя величинами: частотой, амплитудой и фазой или, точнее, сдвигом фаз между данным током (или напряжением) и каким-нибудь другим, относительно которого мы рассматриваем сдвиг фаз всех остальных.

Соотношения между фазами различных синусоидальных переменных токов очень удобно изучать при помощи петлевого осциллографа, имеющего в отличие от прибора, описанного в §152, не одну, а две отдельные рамки (петли), помещенные в общее магнитное поле (рис. 295). Развертка формы обоих токов, проходящих по этим петлям, по оси времени осуществляется одним и тем же вращающимся барабаном, так что точки двух получающихся на экране кривых, расположенные друг над другом, изображают мгновенные значения сравниваемых токов, соответствующие одному и тому же моменту времени.

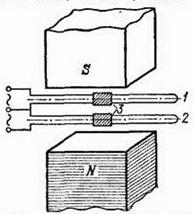
Рис. 295. Двухпетлевой осциллограф для одновременной записи двух переменных токов, проходящих через петли 1 и 2

Точное математическое определение фазы синусоидальной переменной величины (тока или напряжения) таково. Мгновенное значение этой величины в какой-нибудь момент времени

 определяется значением величины

, стоящей под знаком функции

 в формуле (151.2). Если начальный момент отсчета времени выбран уже так, чтобы мгновенное значение тока проходило через нуль в моменты

 то, вообще говоря, другой ток будет проходить через нуль в моменты

, и закон его изменения со временем будет иметь вид

, (153.2)

где буквой

 обозначено произведение

. Фазой тока (или напряжения) в общем случае называют значение величины, стоящей под знаком функции

 в формуле (153.2), а величина

 определяет разность фаз сравниваемых токов (или напряжений). Если эта величина положительна, то первый ток опережает по фазе второй ток, а если она отрицательна, то первый ток отстает по фазе от второго. Фаза измеряется в радианах.