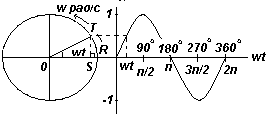Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида. Вариант для печати.
- Графики тригонометрических функций.
- Углы произвольной величины
- Построение синусоиды и косинусоиды
- Синусоидальные и косинусоидальные графики
- Периодические функции и период
- Углы запаздывания и опережения
- Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.
Графики тригонометрических функций.
Все углы А по умолчанию приведены в градусах. Все таблицы значений и формулы синусов, косинусов, тангенсов, котангенсов (здесь). Во всех формулах пределов и разложений в ряд – углы в радианах.
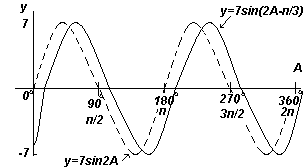
Графики функций y=sinA, y=cosA, y=tgA,построенные для диапазона от 0o до 360o, показаны на рисунках ниже.
Из графиков видно что:
- Графики синуса и косинуса колеблются в пределах между -1 и 1
- Кривая косинуса имеет ту же форму, что и кривая синуса, но сдвинута относительно нее на 90o
- Кривые синуса и косинуса непрерывны и повторяются с периодом 360o , кривая тангенса имеет разрывы и повторяется с периодом 180o .
Углы произвольной величины
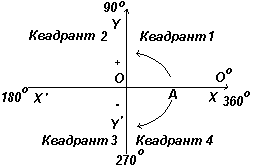
График. Положительное или отрицательное направление при движении по окружности.
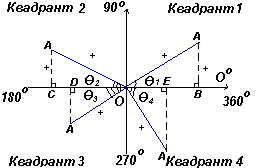
Пусть ОА вращается дальше таким образом, что Θ2 – любой угол во втором квадранте, и построим АС так, чтобы образовался прямоугольный треугольник ОАС. Тогда sin Θ2=+/+ = +; cos Θ2=+/- = -; tg Θ2=+/- = -. Пусть ОА вращается дальше таким образом, что Θ3 – любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ3= -/+ = -; cos Θ3= -/+ = -; tg Θ3 = -/- =+ .
График. Поcтроение углов в различных квадрантах.
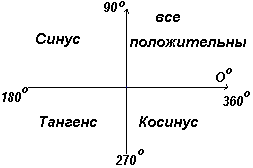
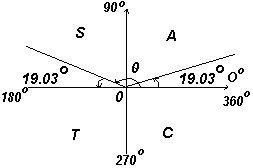
В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем – только тангенс, в четвертом только косинус, что и показано на рис. слева.
График. Положительные и отрицательные значения синусов, косинусов и тангенсов.
Знание углов произвольной величины необходимо при нахождении, например, всех углов между 0o и 360o , синус которых равен, скажем, 0,3261. Если ввести в калькулятор 0,3261 и нажать кнопку sin-1, получим ответ 19,03o . Однако существует второй угол между 0o и 360o , который калькулятор не покажет. Синус также положителен во втором квадранте. Другой угол показан на рис. ниже как угол Θ, где Θ=180o – 19,03o = 160,97o . Таким образом, 19,03o и 160,97o – это углы в диапазоне от 0o до 360o , синус которых равен 0,3261.
Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины.
График. Нахождение всех углов по заданному значению синуса (пример)
Пример 1
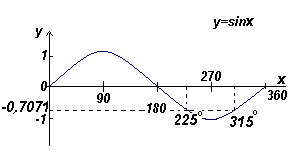
Найти все углы в диапазоне от 0o до 360o , синус которых равен -0,7071
Решение:
Углы, синус которых равен -0,7071o находятся в третьем и четвертом квадранте, поскольку синус отрицателен в этих квадрантах (смотри рис. слева).
График. Нахождение всех углов по заданному значению синуса (пример)
Из следующего рисунка Θ = arcsin 0,7071 = 45o. Два угла в диапазоне от 0o до 360o, синус которых равен -0,7071, это 180o +45o =225o и 360o – 45 o = 315o .
Примечание. Калькулятор дает только один ответ.
График. Нахождение всех углов по заданному значению синуса (пример)
Пример 2
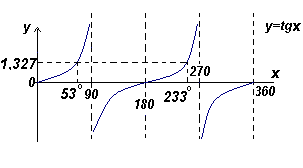
Найти все углы между 0o и 360o , тангенс которых равен 1, 327.
Решение:
Тангенс положителен в первом и третьем квадрантах – рис. слева.
График. Нахождение всех углов по заданному значению тангенса (пример)
Из рис ниже Θ = arctg1,327= 53o .
Два угла в диапазоне от 0o до 360o , тангенс которых равен 1,327, это 53o и 180o + 53 o, т.е. 233o .
График. Нахождение всех углов по заданному значению тангенса (пример)
Построение синусоиды и косинусоиды
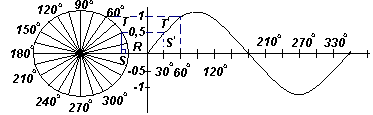
График. Построение синусоиды.
Из определения тригонометрических функций
sin30o=TS/TO=TS/1, т.е. TS= sin30o и cos30o=OS/TO=OS/1, т.e. OS=cos30o
Вертикальную составляющую TS можно перенести на график в виде T’S’, что равно значению, соответствующему углу 30o на графике зависимости y от угла х. Если все вертикальные составляющие, подобно TS, перенести на график, то получится синусоида, показанная на рис. выше.
Если все горизонтальные составляющие, подобные OS, спроецировать на график зависимости у от угла х, получится косинусоида. Эти проекции легко визуализировать, перерисовывая круг с радиусом OR и началом отсчета углов от вертикали, как показано на рисунке слева.
Из рис. слева видно, что синусоида имеет ту же форму, что и косинусоида, но смещенная на 90o.
График. Построение косинусоиды.
Синусоидальные и косинусоидальные графики
Периодические функции и период
Каждый из графиков функций, показанных на четырех рис. выше, повторяется при увеличении угла А, поэтому их называют периодическими функциями.
Функции y=sinA и y=cosA повторяются через каждые 360o (или 2π радиан), поэтому 360o называется периодом этих функций. Функции y=sin2A и y=cos2A повторяются через каждые 180o (или π радиан),поэтому 180o – это период для данных функций.
В общем случае если y=sinpA и y=cospA (где р – константа), то период функции равен 360o/p (или 2π/p радиан ). Следовательно, если y=sin3A, то период этой функции равен 360o/3= 120o, если y=cos4A, то период этой функции равен 360o/4= 90o.
Амплитуда
Амплитудой называется максимальное значение синусоиды. Каждый из графиков 1-4 имеет амплитуду +1 (т.е. они колеблются между +1 и -1). Однако, если y=4sinA, каждая из величин sinA умножается на 4, таким образом, максимальная величина амплитуды – 4. Аналогично для y=5cos2A амплитуда равна 5, а период – 360o/2= 180o.
Пример 3.
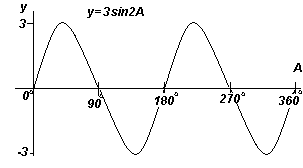
Построить y=3sin2A в диапазоне от А= 0o до А=360o.
Решение:
Амплитуда =3, период = 360o/2 =180o.
График. Построение y=3sin2A (синусоида).
Пример 4.
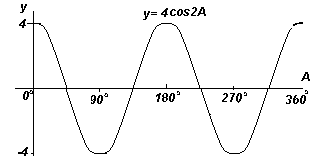
Построить график y=4cos2x в диапазоне от х=0o до х=360o
Решение:
Амплитуда = 4. период = 360o/2 =180o.
График. Построение y=4cos2x (косинусоида).
Углы запаздывания и опережения
Кривые синуса и косинуса не всегда начинаются в 0o . Чтобы учесть это обстоятельство, периодическая функция представляется в виде y=sin(A± α), где α – сдвиг фазы относительно y=sinA и y=cosA.
.gif)
График. y=sin(A-60o) (синусоида).
.gif)
Если кривая y=cosA начинается в 0o, то кривая y=cos(A+45o) начинается на 45o левее (т.е. ее нулевая величина находится на 45o раньше ).
Таким образом, говорят, что график y=cos(A+45o) опережает график y=cosA на 45o.
График. y=cos(A+45o) (косинусоида).
В общем виде, график y=sin(A-α) запаздывает относительно y=sinAна угол α.
Косинусоида имеет ту же форму, что и синусоида, но начинается на 90o левее, т.е. опережает ее на 90o. Следовательно, cosA=sin(A+90o).
Пример 5.
Построить график y=5sin(A+30o) в диапазоне от А=0o до А=360o
Решение:
Амплитуда = 5, период = 360o/1 = 360o.
5sin(A+30o) опережает 5sinA на 30o т.е. начинается на 30o раньше.
График y=5sin(A+30o) (синусоида).
Пример 6.
Построить график y=7sin(2A-π/3) в диапазоне от А=0o до А=360o.
Решение:
Амплитуда = 7, период =2π/2= π радиан
В общем случае y=sin(pt-α) запаздывает относительно y=sinpt на α/p, следовательно 7sin(2A-π/3) запаздывает относительно 7sin2A на ( π/3)/2, т.е. на π/6 радиан или на 30o
График. y=7sin2A и y=7sin(2A-п/3) (синусоиды).
Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.
Пусть OR на рис. слева представляет собой вектор, свободно вращающийся против часовой стрелки вокруг О со скоростью ω радиан/с. Вращающийся вектор называется фазовым вектором. Через время t секунд OR повернется на угол ωt радиан (на рис. слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.
Если все подобные вертикальные составляющие спроецировать на график зависимости у от ωt, получится синусоида с амплитудой OR.
График. Фазовый угол. Сдвиг по фазе.
Если фазовый вектор OR делает один оборот (т.е. 2π радиан) за Т секунд, то угловая скорость ω=2π/Т рад/с, откуда
Т=2π/ ω (с), где
Т – это период
Число полных периодов, проходящих за 1 секунду, называется частотой f.
Частота = (количество периодов)/(секунда) = 1/ T = ω/2π Гц, т.е. f= ω/2π Гц
Следовательно, угловая скорость
ω=2πf рад/с.
Если в общем виде синусоидальная функция выглядит, как y=sin(ωt± α), то
А – амплитуда
ω – угловая скорость
2π/ ω – период Т, с
ω/2π – частота f, Гц
α – угол опережения или запаздывания (относительно y=Аsinωt ) в радианах, он называется также фазовым углом.
Пример 7.
Переменный ток задается как i=20sin(90πt+0,26) ампер. Определить амплитуду, период, частоту и фазовый угол (в градусах)
Решение:
i=20sin(90πt+0,26)А, следовательно,
амплитуда равна 20 А
угловая скорость ω=90π, следовательно,
период Т = 2π/ ω = 2π/ 90π = 0,022 с = 22мс
частота f = 1/Т = 1/0,022 = 45,46 Гц
фазовый угол α = 0,26 рад. = (0,26*180/π)o = 14,9o.
Пример 8.
Колебательный механизм имеет максимальное смещение 3 м и частоту 55 Гц. Во время t=0 смещение составляет 100см. Выразить смещение в общем виде Аsin(ωt± α).
Решение
Амплитуда = максимальное смещение = 3м
Угловая скорость ω=2πf = 2π(55) = 110 πрад./с
Следовательно, смещение 3sin(110πt + α) м.
При t=0 смещение = 100см=1м.
Следовательно, 1= 3sin(0 + α), т.е. sinα=1/3=0,33
Следовательно α=arcsin0,33=19o
Итак, смещение равно 3sin(110 πt + 0,33).
Пример 9.
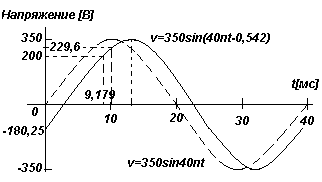
Значение мгновенного напржения в схеме переменного тока в любые t секунд задается в виде v=350sin(40πt-0,542)В. Найти:
а) Амплитуду, период, частоту и фазовый угол (в градусах)
б) значение напряжения при t =0
в) значение напряжения при t =10 мс
г) время, за которое напряжение впервые достигнет значения 200 В.
Решение:
а) Амплитуда равна 350 В, угловая скорость равна ω=40π
Следовательно,
период Т=2π/ ω=2π/40π=0,05 с =50мс
частота f=1/Т=1/0,05=20 Гц
фазовый угол = 0,542 рад (0,542*180/π) = 31oс запаздыванием относительно v=350sin(40πt)
б) Если t =0, то v=350sin(0-0,542)=350sin(-31o)=-180,25 В
в) Если t =10 мс, то v=350sin(40π10/103-0,542)=350sin(0,714)=350sin41o =229,6 В
г) Если v=200 И, то 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)
График. Колебательный механизм (пример, синусоида).
v=350sin(40πt-0,542) Следовательно, (40πt-0,542)=arcsin200/350=35o или 0,611 рад.
40πt= 0,611+0,542=1,153.
Следовательно, если v=200В, то время t=1,153/40π=9,179 мс
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.
Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.
Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.
Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.
Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Вычисляю амплитуду полезной синусоиды из записанных аппаратно данных (в записи присутствуют шумы, нелинейные эффекты, ошибки дискретизации и т.д всего понемногу). После оконной функции и БПФ нормирую данные и нахожу максимум в спектре. Для вычисления амплитуды синусоиды необходимо посчитать сумму гармоник вокруг основной.
Так вот вопрос: сколько гармоник суммировать или каким образом вычислять ширину “области суммирования”? Пробовал фиксированное количество гармоник, “пока гармоника не ниже порога”, суммировать между локальными минимумами и еще несколько вариантов. Во всех случаях проблема выражается в том, что для целого и нецелого кол-ва волн в записанном семпле результат получается разный (погрешность десятки процентов), видимо спектр “растекается” по-разному. Как сделать правильно? Какую оконную функцию лучше всего применить?
Спасибо.
-
Вопрос заданболее трёх лет назад
-
1397 просмотров
Период, частота, амплитуда и фаза переменного тока
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мкс=0,001 мс = 0,000001сек =10 -6 сек.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2
Рисунок 2. Радиан.
1рад = 360°/2
Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2
? = 6,28*f = 2f
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Источник
Часть III. Цепи синусоидального тока
Тема 3. Цепи синусоидального тока
- Общие сведения и определения
- Комплексная амплитуда
- Действующие значения синусоидальной функции
- Изображение синусоидальных функций векторами. Векторная диаграмма
- Изображение синусоидальной функции комплексными числами
- Закон Ома в комплексной форме
- Уравнения элементов в комплексной форме
- § 3.1. Общие сведения и определения:
Переменный ток имеет большее распространение, чем постоянный.
- конструкция электродвигателей и генераторов переменного тока гораздо проще;
- генераторы переменного тока могут быть выполнены для более высокого напряжения;
- переменный ток легко преобразовывается с помощью трансформатора, что необходимо при распределении электроэнергии и т.д.
Переменный ток – ток, периодически меняющий свое значение и направление. Наибольшее значение переменного тока – его амплитуда.
Переменный ток характеризуется:
Амплитуда – наибольшие (положительные или отрицательные) величины.
Период – время, в течение которого происходит полное колебание тока в проводнике.
Фаза – характеризует состояние переменного тока в любой момент времени.
Основным видом переменного тока является синусоидальный (гармонический) ток. Закон изменения такого тока описывается синусоидальной функцией.
В линейных электрических цепях, в которых действуют синусоидальные источники, все электрические параметры изменяются по синусоидальному закону.
ЭДС: 
Напряжение: 
Ток: 
e(t), u(t), i(t) – мгновенные значения;
ω = 2π – угловая частота, [рад/с];
ƒ = 1 Т – циклическая частота, [Гц];
Любую синусоидальную функцию можно изобразить в виде графика, который называется графиком временных значений или временной диаграммой.
Расчет цепей синусоидального тока с использованием мгновенных значений требует громоздкой вычислительной работы и применим для простейших электрических цепей.
Для расчета цепей синусоидального тока синусоидальную функцию заменяют эквивалентной величиной.
где j = √ — 1 – мнимая единица.



Последняя запись означает, что синусоидальное напряжение можно представить на комплексной плоскости в виде двух векторов, длина которых равна Um и которые равномерно вращаются со скоростями, равными ω в противоположные стороны.
- § 3.3. Действующие значения синусоидальной функции:
Действующее значение синусоидальной функции – ее количественная оценка.
Действующие значения – среднеквадратичные за период значения синусоидальной функции, то есть, если:
Аналогично и для тока I и ЭДС ε .
Часто используются выражения, связывающие между собой амплитуду и действующее значение:
Действующее значение – это постоянная величина, которую обычно обозначают той же буквой, что и амплитуду, только без индекса m.
Действующее значение тока оказывает такое же тепловое действие на проводник с сопротивлением R , что и переменный ток, в течение времени, равном периоду. Поэтому большинство электроизмерительных приборов фиксируют и реагируют на действующие значения.
- § 3.4. Изображение синусоидальных функций векторами. Векторная диаграмма:
где a – проекция вектора на ось y в момент времени t.

Любому равномерно вращающемуся радиус-вектору соответствует некоторая синусоидальная функция, и наоборот.
Посмотрим, как условный графический образ синусоидальной функции – радиус-вектор – может быть применим при расчетах цепей переменного тока. Определим ток:
если: 

Как известно, сумма двух синусоид одинаковой частоты ω представляет собой также синусоиду частотой ω , то есть i = Imsin (ωt + ψ ) и, следовательно, задача сводится к нахождению амплитуды Im и начальной фазы Ψ суммарного тока i. Искомые параметры Im и Ψ можно найти, воспользовавшись известными тригонометрическими преобразованиями.
Проведем решение задачи с помощью радиус-векторов I1m и I2m , вращающихся с частотой ω, положение которых для момента времени t = 0 показаны на рисунке ниже и осуществим геометрическое суммирование этих радиус-векторов по правилу параллелограмма. Результирующий радиус-вектор Im будет вращаться с частотой ω и является изображением некоторой синусоидальной функцией времени.
Следовательно, i = i1 + i2 – геометрическое изображение искомого тока.
Измерив дугу суммарного радиус-вектора и, зная выбранный масштаб, можно определить амплитуду Im тока. Непосредственно по чертежу определяется и начальная фаза Ψ.
Рассмотренная совокупность радиус-векторов, изображающих синусоидальные функции времени, называется векторной диаграммой.
- § 3.5. Изображение синусоидальной функции комплексными числами:

Любому вектору A, расположенному на комплексной плоскости, однозначно соответствует комплексное число, которое может быть записано в трех формах:
Все три формы записи в соответствии с формулой Эйлера равнозначны:
Переход от одной формы записи к другой:
где a1 – действительная часть;
Запишем в трех формах выражение для единичных действительных и мнимых комплексных чисел ( A = 1 ):
Отношение комплексной амплитуды напряжения к комплексной амплитуде тока называется комплексным сопротивлением:
Модуль комплексного сопротивления, называемый полным сопротивлением, равен отношению амплитуды напряжения к амплитуде тока, а аргумент Ψ комплексного сопротивления – разности начальных фаз напряжения и тока:
Закон Ома в комплексной форме соответственно для амплитудных и действительных значений:

Добавить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Источник
Синусоида – плоская
кривая выражающая закон изменения
синуса угла в зависимости от изменения
величины угла.
Величина
называется амплитудой синусоиды; в
задании это – длиной волны или периодом
синусоиды. Длина волны синусоиды равна
2Р.
Для
построения синусоиды проводят
горизонтальную ось и на ней откладывают
заданную длину волны АА12
(рис. 5.8). Отрезок АА12
делят на несколько равных частей,
например на 12. Слева вычерчивают
окружность радиуса, который равен
величине амплитуды, и делят ее на 12
равных частей, точки деления нумеруют
и через них проводят горизонтально
прямые. Из точек деления отрезка АА12
восстанавливают перпендикуляры к оси
синусоиды и на них пересечении с
горизонтальными прямыми точки синусоиды.
Полученные точки синусоиды А1,
А2,
А3,…,
А12
соединяют по лекалу кривой.
Чертить
синусоиды в технике приходится довольно
часто, например, при точном изображении
проекций винтовых поверхностей (червяков,
лопастей валов винтовых конвейеров,
гребных винтов и т.д.), при вычерчивании
графиков так называемых гармонических
колебательных процессов, кулачков с
синусоидальным профилем и пр. (рисунок
5.9)
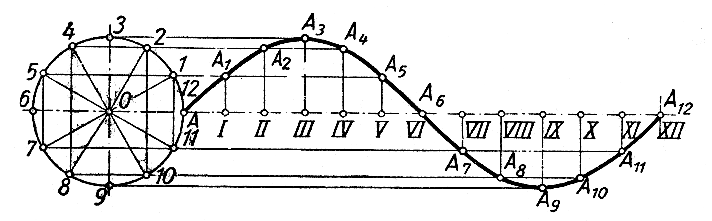
Рисунок
5.8
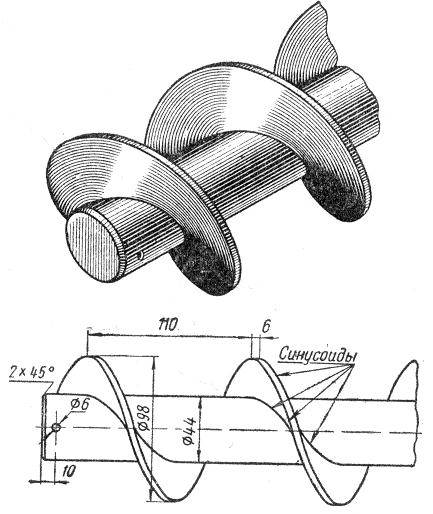
Рисунок
5.9
5.5 Эвольвента
Эвольвентой
окружности называется траектория,
описываемая каждой точкой прямой линии,
перекатываемой по окружности без
скольжения.
В машиностроении
профили зубьев колес и зуборезный
инструмент -пальцевую фрезу – выполняют
по эвольвенте (рисунок 5.10).
Для
построения эвольвенты рисунок 5.11,
заданную окружность диаметра делят на
12 равных частей, которые нумеруются 1,
2, 3, …, 12. Из конечной точки 8 проводят
касательную к окружности и на ней
откладывают длину окружности, равную
D.
Из точек деления окружности 1, 2, 3, …, 12
проводят касательные, направленные в
одну сторону, и на них откладывают
отрезки прямых. На первой касательной
один отрезок равный ??, на второй – два,
на третьей – три и т.д., получают ряд
точек, которые соединяют по лекалу.
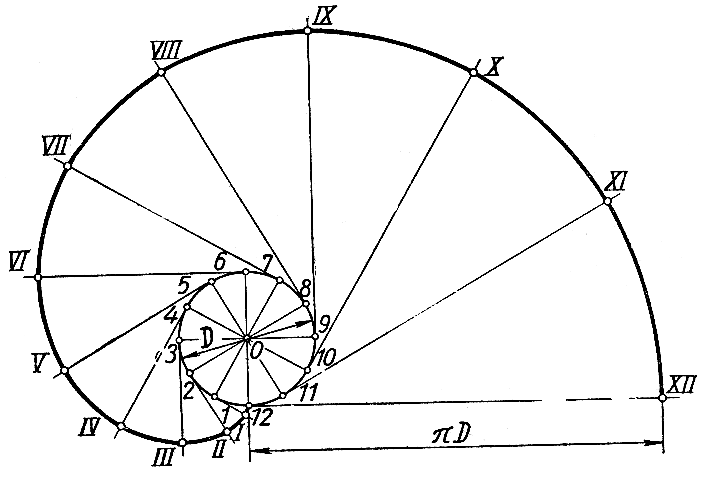
Рисунок
5.11
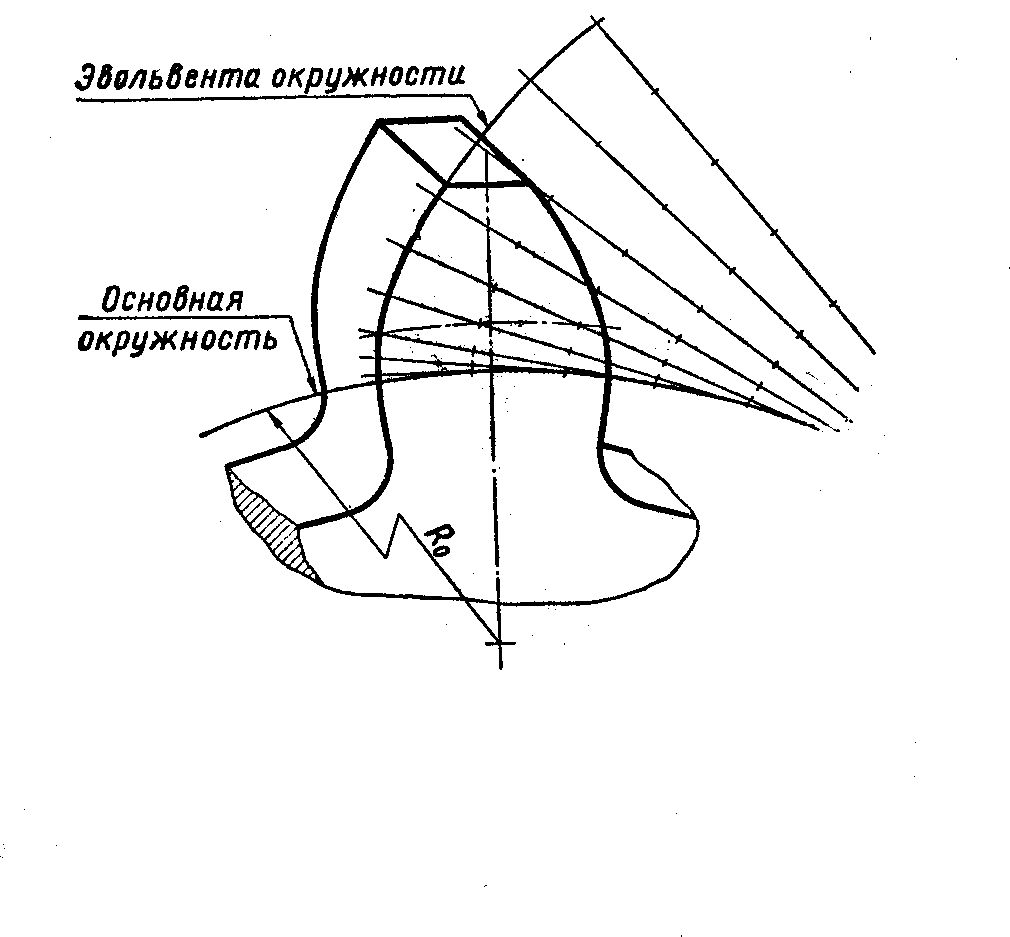
Рисунок
5.10
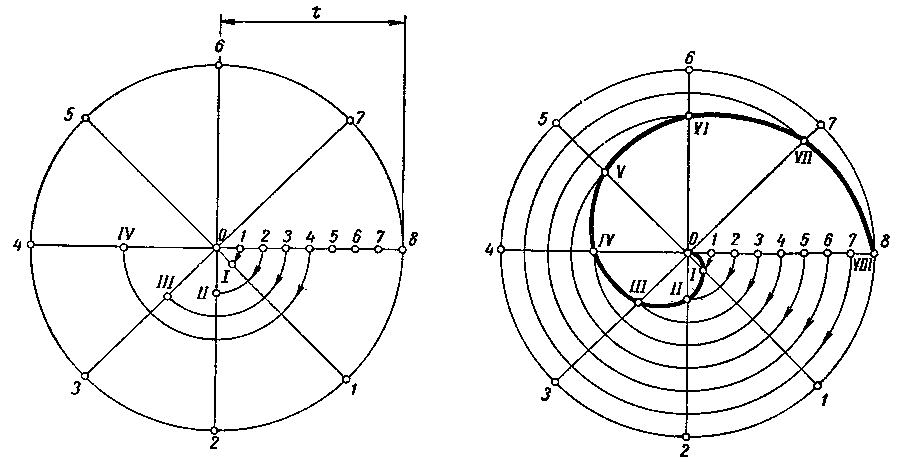
5.6 Спираль Архимеда
Спираль
Архимеда – плоская кривая, которую
описывает точка, движущаяся
равномерно-поступательно от центра О
по равномерно вращающемуся радиусу
(рисунок 5.11).
Для
построения спирали Архимеда задается
шаг спирали – а, и центр О. Из центра О
описывают окружность радиусом Р = а.
Делят окружность на несколько равных
частей, например, на восемь (точки 11
21,
…, 81).
На столько же частей делят отрезок О81
( точки 1, 2, …, 8 ). Из центра О радиусами
О1, О2, и т.д. проводят дуги окружности,
точки А1,
А2,
… пересечения которых с соответствующими
радиусами-векторами принадлежат спирали,
так , например дуга, проведенная через
точку 3, пересекается с радиусом-вектором,
проходящим через точку 31,
в точке А3,
принадлежащей спирали.
В
машиностроении спираль Архимеда
применяется, например, для сообщения
движения по радиусу кулачкам зажимного
патрона токарного станка.
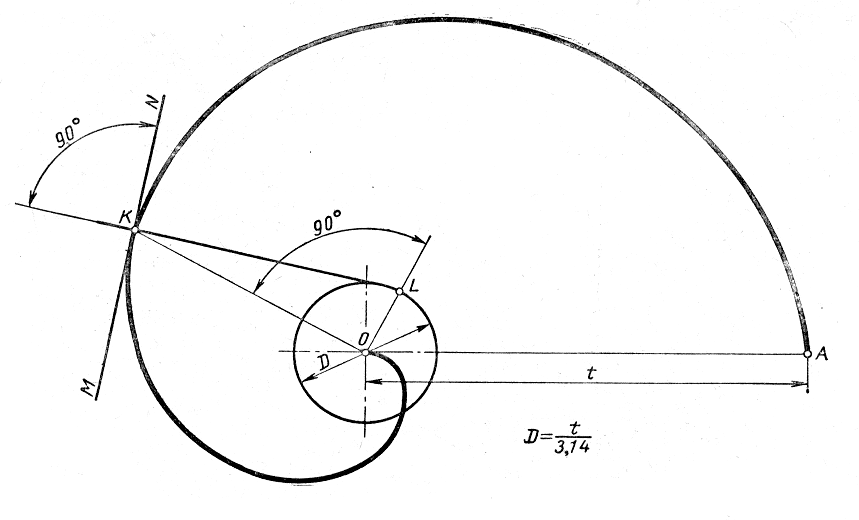
Рисунок
5.11
6 Уклон и конусность
Уклоном называется,
величина, характеризующая наклон одной
прямой линии к другой прямой. Уклон
выражается простой дробью или в процентах.
Уклон
отрезок ВС относительно отрезка ВА
определяют отношением катетов
прямоугольного треугольника АВС (рисунок
6.1), т.е.
.
Рисунок
6.1
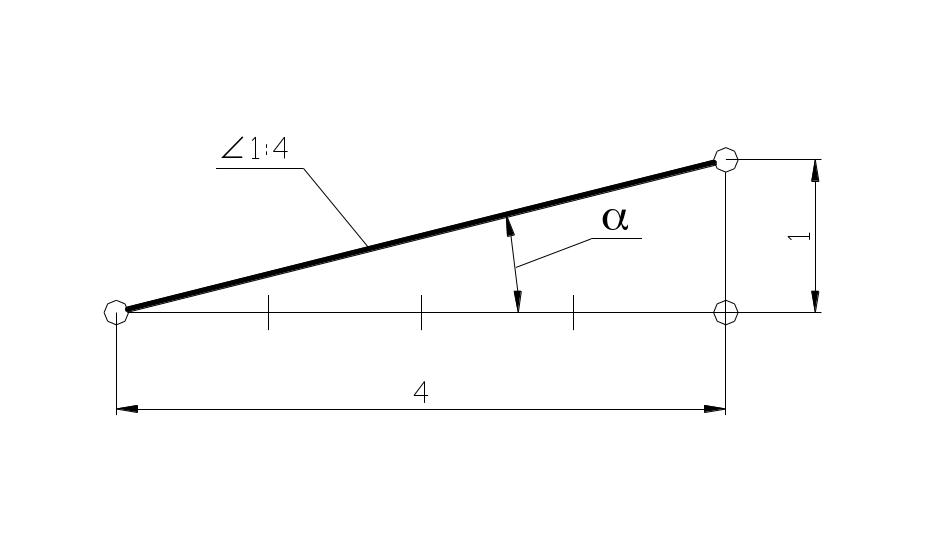
Для
построения прямой ВС, с заданной величиной
уклона к горизонтальной прямой, например
1: 4, необходимо от точки А влево отложить
отрезок АВ, равный четырем единицам
длины, а вверх отрезок АС, равный одной
единицы длины. Точки С и В соединяют
прямой СВ, которая дает направление
искомого уклона.
По ГОСТ 2.307-68 перед
размерным числом, определяющим уклон,
наносят условный знак, острый угол
которого должен быть направлен в сторону
уклона, (рисунок 6.2).
Уклоны
применяются при вычерчивании многих
деталей, например, при выполнении
чертежей профилей стальных балок и
рельсов, изготовляемых на прокатных
станах, и изготовленных литьем.
Конусностью
называется отношение диаметра основания
конуса к его высоте (рисунок 6.3);
обозначается конусность буквой С.
Конусность определяется в виде отношения
по формуле:
С
=
,
где
С – конусность, Д – большой диаметр
конуса, d
– малый диаметр конуса, L-высота
конуса.
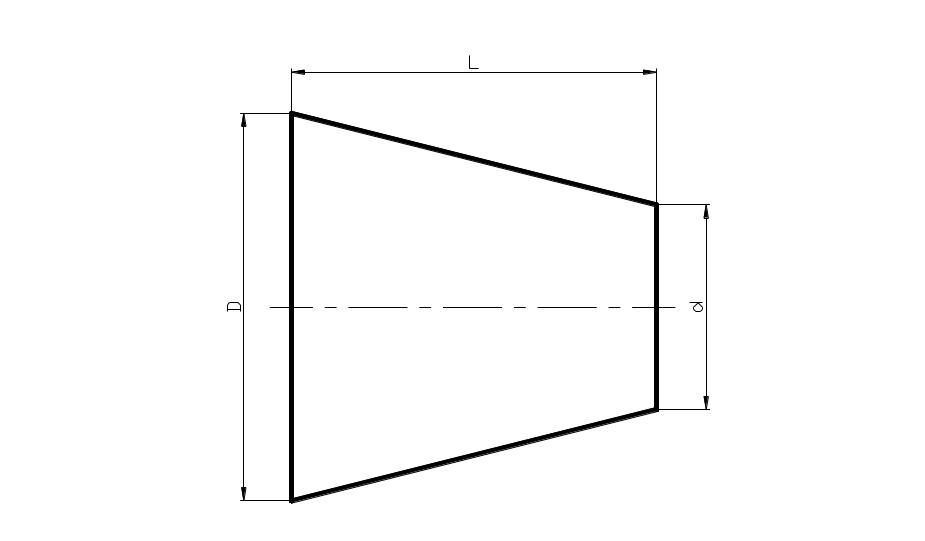
Рисунок 6.2
По
ГОСТ 2.307-68 перед размерным числом,
характеризующим конусность необходимо
наносить условный знак конусности,
который имеет вид равнобедренного
треугольника с вершиной, направленной
в сторону вершины конуса (см. рис. 6.3).
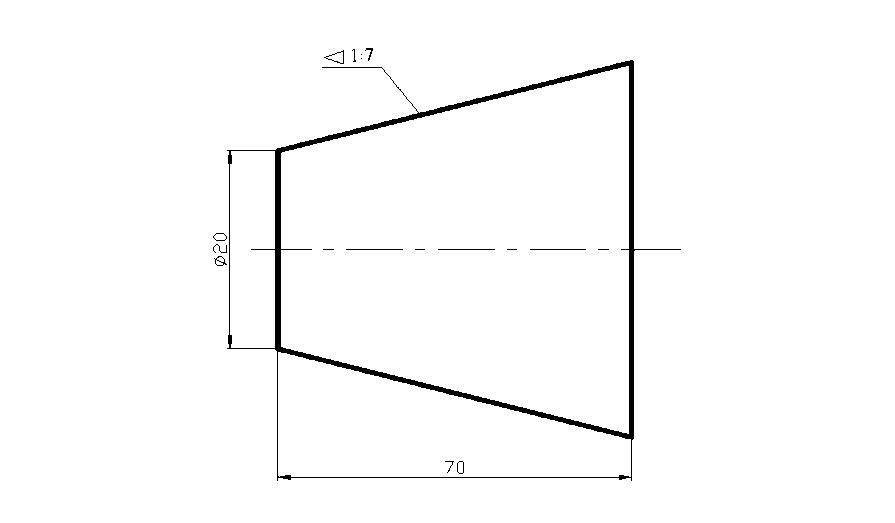
Рисунок
6.3
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
.gif)
.gif)
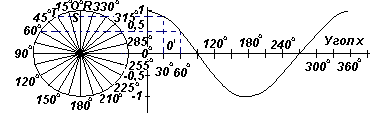
.gif)