МИНИСТЕРСТВО
ОБРАЗОВАНИЯ НАУКИ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
ФЕДЕРАЛЬНО
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
МОСКОВСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРИБОРОСТРОЕНИЯ
И ИНФОРМАТИКИ
В.
В. Филинов
Электроника
и схемотехника.
Расчёт
спектров электрических сигналов.
Учебно-методическое
пособие
Москва
– 2014
УДК
621.38
ББК
32.85
Рекомендовано
к изданию в качестве учебно-методического
пособия редакционно-издательским
советом МГУПИ
Рецензент:
д.т.н.
профессор Шкатов П. Н. (МГУПИ)
Филинов
В.В.
Электроника
и схемотехника. Расчет спектров
электрических сигналов.
Учебно-методическое пособие. М.: МГУПИ,
2014
Учебно-методическое
пособие предназначено для студентов
(бакалавров и специалистов) специальностей
по радиоэлектронике и информационной
безопасности, изучающих курс лекций
“Электроника и схемотехника”,
предназначено при подготовке к выполнению
практических и расчетно-графических
работ (РГР) по теме “Расчет спектров
электрических сигналов”. Приведены
примеры расчета спектров периодических
и непериодических сигналов, а также
задания для выполнения РГР. Полезно для
магистров и аспирантов технических
направлений МГУПИ.
Утверждено
и рекомендовано решением УМС факультета
«Приборостроения и радиоэлектроники»
МГУПИ в качестве учебно-методического
пособия.
©
Московский Государственный Университет
Приборостроения и Информатики, 2014
©
Филинов В.В., 2014
Оглавление
Стр.
Введение.
Необходимые формулы
………………………………………4
-
Спектры
амплитуд и фаз периодических сигналов
..…………6
Пример
1 ……………………………………………………………………6
Пример
2 …………………………………………………………………..10
Пример
3 …………………………………………………………………..11
Пример
4 …………………………………………………………………..12
Пример
5 …………………………………………………………………..13
Пример
6 …………………………………………………………………..14
Пример
7 …………………………………………………………………..16
Пример
8 …………………………………………………………………..17
Пример
9 …………………………………………………………………..18
Пример
10 …………………………………………………………………23
Пример
11 …………………………………………………………………24
-
Спектральная
плотность амплитуд и фаз периодических
сигналов
……..….…………..………………………..…….………………27
Пример
12 …………………………..……………………….……………27
Пример
13 …………………………..……………………….……………29
Пример
14 …………………………..……………………….……………31
Пример
15 …………………………..……………………….……………31
Пример
16 …………………………..……………………….……………33
Пример
17 …………………………..……………………….……………34
Пример
18 …………………………..……………………….……………36
Пример
19 …………………………..……………………….……………37
-
Литература
……………………………………………………………….39 -
Задания
для расчетно-географических
работ…………..………39
Необходимые
формулы.
Применительно
к периодическому гармоническому
напряжению
можно использовать разложение в ряд
Фурье:
(1)
Простейшим
периодическим сигналом является
гармоническое колебание вида
Разложение
последовательности прямоугольных
импульсов рис. 1.1 имеет вид:
(2)
Разложение
последовательности пилообразных
импульсов рис. 1.2 имеет вид:
(3)
Две
равнозначные записи ряда Фурье:
Ряд Фурье в
комплексной форме:
Выражение
для комплексного спектра сигнала:
Ряд
Фурье периодической последовательности
прямоугольных импульсов амплитудой U
(рис. 1.5а)
имеет вид:
Напряжение
на участках цепи находят, используя
принцип суперпозиции, например напряжение
на резисторах:
Расчет
цепи от отдельных постоянной и
гармонических составляющих напряжения
проводится в символической форме. При
этом нужно иметь в виду, что на k-й
гармонике сопротивление индуктивности

а сопротивление емкости
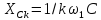
Интеграл
Фурье:
Уравнения
(10) и (11) являются основными в теории
спектров непериодических сигналов,
причем (10) называется прямым,
а (11) –
обратным
преобразованием Фурье (интегралом
Фурье).
Комплексная
придаточная функция по напряжению:
Из
выражений:
следует,
что спектральная плотность амплитуд
реакции цепи равна произведению
спектральной плотности амплитуд
воздействия АЧХ
цепи, а спектральная плотность фаз
реакции цепи равна сумме спектральной
плотности фаз
воздействия и ФЧХ
цепи.
-
Спектры амплитуд и фаз периодических сигналов.
Пример
1.
Определим параметры синусоид, формирующих
последовательности прямоугольных (рис.
1.1, а) и пилообразных (рис. 1.2, а) импульсов,
имеющих амплитуду U = 10 В
и период Т = 20 мс.
а)
Для формирования периодической
последовательности прямоугольных
импульсов амплитуда основной синусоиды
должна быть
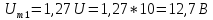
Частота
колебаний этой синусоиды обратно
пропорциональна периоду:
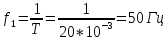
Круговая
частота

Таким образом, основная синусоида
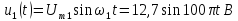
Все
последующие синусоиды в соответствии
с (2) должны иметь амплитуды в нечетное
количество раз меньшие, а частоты – в
это же нечетное количество раз большие,
чем у основной синусоиды:

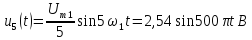
и
т.д.
Последовательность
прямоугольных импульсов, изображенных
на рис. 1.1, а,
–
это сумма синусоид:
.
Сигнал
изображен
на рис. 1.1, д.
6)
Для формирования последовательности
пилообразных импульсов необходимо,
чтобы амплитуда основной синусоиды
была, как мы уже знаем [1, 3], равна
Частота
основной синусоиды

Таким
образом,
Рис.
1.1. Последовательность прямоугольных
импульсов и образующие ее синусоиды
Рис.
1.2. Последовательность пилообразных
импульсов и образующие ее синусоиды
Таблица
1.1. Ряды Фурье наиболее часто встречающихся
сигналов
|
Сигнал |
Ряд |
|
|
|
|
|
|
|
|
|
|
|
k-четные; |
|
|
k-четные; |
|
|
|
Последующие
синусоиды в соответствии с (3) будут
иметь вид
и
т.д.
Последовательность
пилообразных импульсов – это сумма
синусоид:
.
Чем
больше синусоид используется при
формировании сигнала, тем ближе его
форма к пилообразной (рис. 1.е).
Пример
2.
Определим гармонический состав
последовательности треугольных
импульсов, изображенных на рис. 1.3,
имеющих амплитуду, U
= 10 B
и период Т = 10 мс.
Периодический
сигнал на рис. 1.3 отличается от сигнала
во второй строке табл. 1.1 на величину
постоянной составляющей
Частота
основной составляющей сигнала
или
Амплитуда
основной составляющей сигнала
рассчитывается по формуле, приведенной
в табл. 1.1, или по одной из формул (1):
Четная
функция (рис. 1.3) содержит только
косинусоиды, амплитуды и частоты
которых определяются по формулам,
приведенным во второй строке табл. 1.1.
Амплитуда
и частота третьей гармоники:
Рис.
1.3. Последовательность треугольных
импульсов
Амплитуда
и частота пятой гармоники:
Амплитуда
и частота седьмой гармоники:
и
т.д.
Гармонический
состав последовательности треугольных
импульсов (рис.1.3) имеет вид:
Пример
3.
Представим переменное напряжение,
выпрямленное двухполупериодным
выпрямителем (пятая строка табл. 1.1),
рядом Фурье в тригонометрической форме
(5).
Из
табл. 1.1 следует, что переменное напряжение
u(t) представлено рядом Фурье:
k
– четные.
Постоянная
составляющая напряжения u(
t)
рассчитывается по формуле

0,635U.
Нечетные
гармоники отсутствуют в ряде Фурье,
поскольку функция u(
t)–
четная.
Для
расчета амплитуд четных гармоник
нео6ходимо определить

1,27U.
Тогда амплитуда второй гармоники
Начальная
фаза второй гармоники равна нулю:
Амплитуда
четвертной гармоники
Фаза
четвертой гармоники
, так как в ряде Фурье перед слагаемым
стоит знак «минус».
Амплитуда
шестой гармоники
а
ее фаза, а также фазы десятой, четырнадцатой
и т.д. гармоник равны нулю.
Амплитуда
восьмой гармоники
а
ее начальная фаза, так же как и фазы
гармоник с номерами 12, 16, 20 и т.д., равна
180˚.
Тригонометрическая
форма ряда Фурье рассматриваемого
напряжения имеет вид:
.
Пример
4.
Представим ряд Фурье, полученный в
примере 3, в комплексной форме, ограничив
его восьмой гармоникой.
В
соответствии с (6) значения постоянной
составляющей и амплитуд гармоник
уменьшаются в 2 раза по сравнению со
значениями, которые 6ыли рассчитаны в
примере 3. Поэтому ряд Фурье в комплексной
форме имеет вид
Пример
5.
Построим спектр амплитуд и фаз
выпрямленного напряжения
(строка
5 табл, 1.1), имеющего амплитуду U
= 10 В и период Т = 10 мс.
При
решении примера 3 была получена
тригонометрическая форма ряда Фурье,
соответствующая выпрямленному напряжению:
.
Частота
основной составляющей сигнала
определяется
периодом колебаний:
В
спектре сигнала отсутствуют нечетные
гармоники, так как само колебание
является четной функцией. Частоты высших
гармоник с четными номерами кратны этим
номерам: частота второй гармоники равна
2
= 200 Гц, четвертой, шестой, восьмой гармоник
– 400, 600, 800 Гц соответственно и т.д.
Постоянная
составляющая
Амплитуды
четных гармоник спектра в соответствии
с выражениями, полученными для ряда
Фурье, имеют следующие значения:
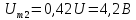

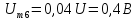
и
т.д.
Фазы
гармоник поочередно принимают значения
0 и 180˚.
Рис.
1.4. Спектры амплитуд и фаз выпрямленного
напряжения
Пример
6.
Рассмотрим периодическую последовательность
прямоугольных импульсов, показанную
на рис. 1.5, а:
Рис.
1.5. Последовательности прямоугольных
импульсов
Она
имеет постоянную составляющую, равную
в соответствии с (1)
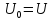
Коэффициенты
вычисляются
по формуле (1):
Здесь
6ыло учтено, что

1/Т.
Коэффициенты
вычисляются по формуле (1):
Выражение
удовлетворяет соотношению
Поэтому
Форма
ряда Фурье будет содержать только
синусоиды с нечетными гармоническими
частотами:
что,
естественно, с точностью до постоянной
составляющей U
совпадает с полученным ранее выражением
(2).
Переход
к форме ряда Фурье (5) дает
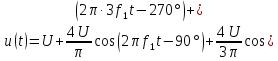
Спектр
такого сигнала без постоянной составляющей
показан на рис. 1.6:
Рис.
1.6. Спектры амплитуд и фаз сигнала рис.
1.5а
Пример
7.
Представим спектр сигнала
из примера 6 в комплексной форме.
Комплексный
спектр периодической последовательности
прямоугольных импульсов рассчитывается
по формуле (7):
Функция
имеет значения
Это
значит, что комплексный спектр
существует только для нечетных гармоник:
Заметим,
что в спектре
нет постоянной составляющей

которая рассчитывается по формуле (1) и
равна U.
Полученный
комплексный спектр
соответствует спектрам амплитуд и фаз,
изображенным на рис. 1.6.
Пример
8.
Найдем спектр последовательности
прямоугольных импульсов, изображенных
на рис. 1.7.
Сигнал,
изображенный на рис. 1.7, имеет следующие
параметры: амплитуда U
= 10 В, длительность импульса τ= 10 мс,
период повторения импульсов Т
= 40 мс, скважность q
= Т/τ = 4. Спектр этого сигнала в форме
(Табл. 1.1, строка 6) имеет вид
Постоянная
составляющая
Частота
первой гармоники
Частоты
высших гармоник кратны 100 Гц. Амплитуды
первых шести гармоник, рассчитываемые
по формуле (3.28)
имеют
следующие значения:
Фазы
первой, второй, третьей гармоник равны
0˚, фазы пятой и шестой гармоник равны
180˚, так как при расчете
и
получены отрицательные значения.
Амплитуды и фазы последующих гармоник
рассчитывают аналогичным образом.
Причем, амплитуды гармоник, кратных
скважности q, т.е. четвертой, восьмой,
двенадцатой, шестнадцатой гармоник и
т.д., равны нулю. Спектры амплитуд и фаз
сигнала, изображенного на рис. 1.7,
приведены на рис. 1.8.
Рис.
1.7. Последовательность прямоугольных
импульсов со скважностью q = 4
Рис.
1.8. Спектр последовательности прямоугольных
импульсов со скважностью q = 4
Пример
9.
Определим напряжение на резисторе
в
последовательном колебательном контуре,
на который подается последовательность
прямоугольных импульсов (рис. 1.10).
Параметры элементов контура и сигнала
заданы: R = 2 Ом; L = 0,704 мГн; С = 4 мкФ; U = 5
В; Т = 1 мс; τ = 0,5 мс.
Найдем
параметры постоянной и гармонических
составляющих сигнала (рис. 1.10),
представленного рядом Фурье (8). Частота
первой гармоники
или
Частоты
третьей, пятой и т.д. гармоник равны
соответственно: 3
= 18,84 рад/с; 3
= 3 кГц; 5
= 31,4 рад/с; 5
= 5 кГц; … .
Амплитуды
четных гармоник равны нулю. Амплитуды
нечетных гармоник рассчитываются по
формуле (1):
.
Ряд
Фурье сигнала имеет вид:
Рис.
1.9. Последовательный колебательный
контур с источником периодического
сигнала
Рис.
1. 10. Последовательность прямоугольных
импульсов
Определим
резонансную частоту
и
контура
(рис. 1.9):
Резонанс
в контуре наступает на частоте третьей
гармоники входного напряжения.
Добротность
контура
Определим
гармонические составляющие тока в цепи
и напряжения на резисторе в каждой из
составляющих ряда Фурье схем, изображенных
на рис. 1.9.
Схема
последовательного колебательного
контура с источником постоянного
напряжения

= 2,5 В приведена на рис. 1.11. В этой цепи
сопротивление индуктивности равно
нулю, а сопротивление конденсатора
равно бесконечности, поэтому
= 0;
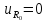
В
цепи, изображенной на рис. 1.12, в контур
включен источник напряжения, соответствующий
напряжению первой гармоники. Синусоидальное
напряжение
заменено
на комплексное

На частоте
= 1 кГц (
)
сопротивление индуктивности
а
сопротивление емкости
Рис.
1.11. Контур с источником постоянного
напряжения
Рис.
1.12. Контур с источником напряжения
первой гармоники
Комплексное
сопротивление цепи
Определим
комплексные значения тока
и напряжение
:
Это
соответствует составляющей синусоидального
напряжения (9) в исходной цепи:
На
третьей гармонике синусоидальный
источник заменяется источником
комплексного напряжения
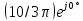
В результате имеем цепь, изображенную
на рис. 1.13.
На
частоте
= 3 кГц (
)
в цепи наступает резонанс напряжений.
Сопротивления индуктивности и емкости
равны по величине и противоположны по
знаку:
Комплексное
сопротивление цепи
= R = 2 Ом. Ток
Рис.
1.13. Контур с источником третьей гармоники
Рис.
1.14. Контур с источником напряжения
пятой гармоники
Напряжение
на резисторе
равно входному напряжению:

пятой гармонике синусоидальный источник
заменяется
источником комплексного напряжения
(рис. 1.14). На частоте
= 5 кГц (
)
сопротивления индуктивности и емкости
равны соответственно
и
Комплексное
сопротивление цепи
рассчитаем
по формуле:
Напряжение
на резисторе
Таким
образом, ряд Фурье напряжения на резисторе
имеет вид,
Рис.
1.15. Спектры амплитуд и фаз входного
напряжения и напряжения на резисторе
в колебательном контуре
Спектры
амплитуд и фаз этого напряжения изображены
на рис. 1.15
( 6, в).
Анализ спектра
показывает, что колебательный контур
выделил третью гармонику из входной
последовательности и подавил остальные
гармоники, т.е. явление резонанса можно
использовать для, выделения отдельных
гармоник из периодического несинусоидального
сигнала.
Пример
10.
Сравним спектры амплитуд (рис. 1.15) входной
последовательности прямоугольных
импульсов
и напряжения
на резисторе колебательного контура
из примера 9, чтобы определить коэффициенты
передачи по напряжению цепи на частотах
гармоник.
В
соответствии с формулой и рис. 1.15 (а),
постоянная составляющая
в спектре напряжения
равна 2,5 В. Амплитуды первой, третьей и
пятой гармоник имеют значения:
Постоянная
составляющая в спектре напряжения
на резисторе (рис. 3.15, б)
равна нулю, а амплитуды нечетных гармоник
равны соответственно
Коэффициенты
передачи по напряжению
на частотах гармоник рассчитаем по
формуле
На
частоте f
= 0 кГц получаем
= 0/2,5 = 0. На частоте f
= 1 кГц (частота основной составляющей)
= 0,18/3,2 = 0,056.
Рис.
1.16. Коэффициенты передачи по напряжению
на резисторе R на частотах гармоник
На
частоте
f=3
кГц (третья гармоника)
= 1,06/1,06 = 1.
На
частоте f=
5 кГц (пятая гармоника)
= 0,089/0,64= 0,14.
На
рис. 1.16 приведен график зависимости
коэффициента передачи контура от частоты
гармоник. На частоте резонанса коэффициент
передачи максимален и равен 1. На частотах
первой и пятой гармоник коэффициент
передачи резко уменьшается.
Пример
11.
Определим спектр амплитуд напряжения
на резисторе в цепи, изображенной на
рис. 1.17, а,
на вход которой поступает периодическая
последовательность прямоугольных
импульсов (рис. 1.17, б),
если заданы R
= 50 Ом, L
= 10 мГн, U
= 10 В, τ = 1 мс, Т = 4 мс.
Рис.
1.17. RL-цепь
и сигнал на ее входе
Найдем
комплексный спектр входного сигнала
u(t),
воспользовавшись (7):
Применив
формулу Эйлера, получим
Вычислим
амплитуды спектральных составляющих
Амплитуда
постоянной составляющей
Частота
основной составляющей
а
ее амплитуда
Аналогичным
образом определяются частоты и амплитуды
высших гармоник:
|
При |
k=2 |
2 |
|
|
k=3 |
3 |
|
|
|
k=4 |
4 |
|
|
|
k=5 |
5 |
|
|
|
k=6 |
6 |
|
|
|
k=7 |
7 |
|
|
|
k=8 |
8 |
|
|
|
k=9 |
9 |
|
|
|
k=10 |
10 |
|
Спектр
амплитуд
входного сигнала изображен на рис.
1.18, а.
Огибающая спектра амплитуд прямоугольных
импульсов изменяется по закону

нули спектра расположены на частотах,
кратных
=1 кГц (четвертая, восьмая, двенадцатая
и т.д. гармоники). Комплексная передаточная
функция цепи (рис. 1.17, а) определяется
по формуле
|
При |
k=0 |
|
|
k=1 |
|
|
|
k=2 |
|
|
|
k=3 |
|
|
|
k=4 |
|
|
|
k=5 |
|
|
|
k=6 |
|
|
|
k=7 |
|
|
|
k=8 |
|
|
|
k=9 |
|
|
|
k=10 |
|
Рис.
1.18. Спектры амплитуд последовательности
прямоугольных импульсов и напряжения
на резисторе в RL-цепи
и коэффициенты передачи цепи
График
зависимости коэффициента передачи
RL-цепи
от частоты изображен на рис. 3.18 (б).
Спектр
амплитуд
напряжения на резисторе, рассчитываем
в виде:
принимает
значения:
и
приведен на рис. 1.18 (в).
Простыми словами о преобразовании Фурье
Уровень сложности
Средний
Время на прочтение
14 мин
Количество просмотров 988K
Я полагаю что все в общих чертах знают о существовании такого замечательного математического инструмента как преобразование Фурье. Однако в ВУЗах его почему-то преподают настолько плохо, что понимают как это преобразование работает и как им правильно следует пользоваться сравнительно немного людей. Между тем математика данного преобразования на удивление красива, проста и изящна. Я предлагаю всем желающим узнать немного больше о преобразовании Фурье и близкой ему теме того как аналоговые сигналы удается эффективно превращать для вычислительной обработки в цифровые.

Без использования сложных формул и матлаба я постараюсь ответить на следующие вопросы:
- FT, DTF, DTFT — в чем отличия и как совершенно разные казалось бы формулы дают столь концептуально похожие результаты?
- Как правильно интерпретировать результаты быстрого преобразования Фурье (FFT)
- Что делать если дан сигнал из 179 сэмплов а БПФ требует на вход последовательность по длине равную степени двойки
- Почему при попытке получить с помощью Фурье спектр синусоиды вместо ожидаемой одиночной “палки” на графике вылезает странная загогулина и что с этим можно сделать
- Зачем перед АЦП и после ЦАП ставят аналоговые фильтры
- Можно ли оцифровать АЦП сигнал с частотой выше половины частоты дискретизации (школьный ответ неверен, правильный ответ — можно)
- Как по цифровой последовательности восстанавливают исходный сигнал
Я буду исходить из предположения что читатель понимает что такое интеграл, комплексное число (а так же его модуль и аргумент), свертка функций, плюс хотя бы “на пальцах” представляет себе что такое дельта-функция Дирака. Не знаете — не беда, прочитайте вышеприведенные ссылки. Под “произведением функций” в данном тексте я везде буду понимать “поточечное умножение”
Начать надо, наверное, с того что обычное преобразование Фурье — это некая такая штука которая, как можно догадаться из названия, преобразует одни функции в другие, то есть ставит в соответствие каждой функции действительного переменного x(t) её спектр или фурье-образ y(w):
Если приводить аналогии, то примером аналогичного по смыслу преобразования может послужить например дифференцирование, превращающее функцию в её производную. То есть преобразование Фурье — такая же, по сути, операция как и взятие производной, и её часто обозначают схожим образом, рисуя треугольную “шапочку” над функцией. Только в отличие от дифференцирования которое можно определить и для действительных чисел, преобразование Фурье всегда “работает” с более общими комплексными числами. Из-за этого постоянно возникают проблемы с отображением результатов этого преобразования, поскольку комплексные числа определяются не одной, а двумя координатами на оперирующем действительными числами графике. Удобнее всего, как правило, оказывается представить комплексные числа в виде модуля и аргумента и нарисовать их по раздельности как два отдельных графика:
График аргумента комплексного значения часто называют в данном случае “фазовым спектром”, а график модуля — “амплитудным спектром”. Амплитудный спектр как правило представляет намного больший интерес, а потому “фазовую” часть спектра нередко пропускают. В этой статье мы тоже сосредоточимся на “амплитудных” вещах, но забывать про существование пропущенной фазовой части графика не следует. Кроме того, вместо обычного модуля комплексного значения часто рисуют его десятичный логарифм умноженный на 10. В результате получается логарифмический график, значения на котором отображаются в децибелах (дБ).
Обратите внимание что не очень сильно отрицательным числам логарифмического графика (-20 дБ и менее) при этом соответствуют практически нулевые числа на графике “обычном”. Поэтому длинные и широкие “хвосты” разнообразных спектров на таких графиках при отображении в “обычные” координаты как правило практически исчезают. Удобство подобного странного на первый взгляд представления возникает из того что фурье-образы различных функций часто необходимо перемножать между собой. При подобном поточечном умножении комплекснозначных фурье-образов их фазовые спектры складываются, а амплитудные — перемножаются. Первое выполняется легко, а второе — сравнительно сложно. Однако логарифмы амплитуды при перемножении амплитуд складываются, поэтому логарифмические графики амплитуды можно, как и графики фаз, просто поточечно складывать. Кроме того, в практических задачах часто удобнее оперировать не «амплитудой» сигнала, а его «мощностью» (квадратом амплитуды). На логарифмической шкале оба графика (и амплитуды и мощности) выглядят идентично и отличаются только коэффициентом — все значения на графике мощности ровно вдвое больше чем на шкале амплитуд. Соответственно для построения графика распределения мощности по частоте (в децибелах) можно не возводить ничего в квадрат, а посчитать десятичный логарифм и умножить его на 20.
Заскучали? Погодите, еще немного, с занудной частью статьи, объясняющей как интерпретировать графики, мы скоро покончим :). Но перед этим следует понять одну крайне важную вещь: хотя все вышеприведенные графики спектров были нарисованы для некоторых ограниченных диапазонов значений (в частности, положительных чисел), все эти графики на самом деле продолжаются в плюс и минус бесконечность. На графиках просто изображается некоторая “наиболее содержательная” часть графика, которая обычно зеркально отражается для отрицательных значений параметра и зачастую периодически повторяется с некоторым шагом, если рассматривать её в более крупном масштабе.
Определившись с тем, что же рисуется на графиках, давайте вернемся собственно к преобразованию Фурье и его свойствам. Существует несколько разных способов как определить это преобразование, отличающихся небольшими деталями (разными нормировками). Например в наших ВУЗах почему-то часто используют нормировку преобразования Фурье определяющую спектр в терминах угловой частоты (радианов в секунду). Я буду использовать более удобную западную формулировку, определяющую спектр в терминах обычной частоты (герцах). Прямое и обратное преобразование Фурье в этом случае определяются формулами слева, а некоторые свойства этого преобразования которые нам понадобятся — списком из семи пунктов справа:
Первое из этих свойств — линейность. Если мы берем какую-то линейную комбинацию функций, то преобразование Фурье этой комбинации будет такой же линейной комбинацией образов Фурье этих функций. Это свойство позволяет сводить сложные функции и их фурье-образы к более простым. Например, фурье-образ синусоидальной функции с частотой f и амплитудой a является комбинацией из двух дельта-функций расположенных в точках f и -f и с коэффициентом a/2:
Если взять функцию, состоящую из суммы множества синусоид с разными частотами, то согласно свойству линейности, фурье-образ этой функции будет состоять из соответствующего набора дельта-функций. Это позволяет дать наивную, но наглядную интерпретацию спектра по принципу “если в спектре функции частоте f соответствует амплитуда a, то исходную функцию можно представить как сумму синусоид, одной из которых будет синусоида с частотой f и амплитудой 2a”. Строго говоря, эта интерпретация неверна, поскольку дельта-функция и точка на графике — это совершенно разные вещи, но как мы увидим дальше, для дискретных преобразований Фурье она будет не так уж и далека от истины.
Второе свойство преобразования Фурье — это независимость амплитудного спектра от сдвига сигнала по времени. Если мы подвинем функцию влево или вправо по оси x, то поменяется лишь её фазовый спектр.
Третье свойство — растяжение (сжатие) исходной функции по оси времени (x) пропорционально сжимает (растягивает) её фурье-образ по шкале частот (w). В частности, спектр сигнала конечной длительности всегда бесконечно широк и наоборот, спектр конечной ширины всегда соответствует сигналу неограниченной длительности.
Четвертое и пятое свойства самые, пожалуй, полезные из всех. Они позволяют свести свертку функций к поточечному перемножению их фурье-образов и наоборот — поточечное перемножение функций к свертке их фурье-образов. Чуть дальше я покажу насколько это удобно.
Шестое свойство говорит о симметрии фурье-образов. В частности, из этого свойства следует что в фурье-образе действительнозначной функции (т.е. любого “реального” сигнала) амплитудный спектр всегда является четной функцией, а фазовый спектр (если его привести к диапазону -pi…pi) — нечетной. Именно по этой причине на графиках спектров практически никогда не рисуют отрицательную часть спектра — для действительнозначных сигналов она не дает никакой новой информации (но, повторюсь, и нулевой при этом не является).
Наконец последнее, седьмое свойство, говорит о том, что преобразование Фурье сохраняет “энергию” сигнала. Оно осмысленно только для сигналов конечной продолжительности, энергия которых конечна, и говорит о том, что спектр подобных сигналов на бесконечности быстро приближается к нулю. Именно в силу этого свойства на графиках спектров как правило изображают только “основную” часть сигнала, несущую в себе львиную долю энергии — остальная часть графика просто стремится к нулю (но, опять же, нулем не является).
Вооружившись этими 7 свойствами, давайте посмотрим на математику “оцифровки” сигнала, позволяющую перевести непрерывный сигнал в последовательность цифр. Для этого нам понадобится взять функцию, известную как “гребенка Дирака”:
Гребенка Дирака — это просто периодическая последовательность дельта-функций с единичным коэффициентом, начинающаяся в нуле и идущая с шагом T. Для оцифровки сигналов, T выбирают по возможности малым числом, T<<1. Фурье-образ этой функции — тоже гребенка Дирака, только с гораздо большим шагом 1/T и несколько меньшим коэффициентом (1/T). С математической точки зрения, дискретизация сигнала по времени — это просто поточечное умножение исходного сигнала на гребенку Дирака. Значение 1/T при этом называют частотой дискретизации:
Вместо непрерывной функции после подобного перемножения получается последовательность дельта-импульсов определенной высоты. При этом согласно свойству 5 преобразования Фурье, спектр получившегося дискретного сигнала есть свертка исходного спектра с соответствующей гребенкой Дирака. Несложно понять, что исходя из свойств свертки, спектр исходного сигнала при этом как бы “копируется” бесконечное число раз вдоль оси частот с шагом 1/T, а затем суммируется.
Заметим, что если исходный спектр имел конечную ширину и мы использовали достаточно большую частоту дискретизации, то копии исходного спектра не будут перекрываться, а следовательно и суммироваться друг с другом. Несложно понять что по подобному “свернутому” спектру будет легко восстановить исходный — достаточно будет просто взять компоненту спектра в районе нуля, “обрезав” лишние копии уходящие на бесконечность. Простейший способ это сделать — это домножить спектр на прямоугольную функцию, равную T в диапазоне -1/2T…1/2T и нулю — вне этого диапазона. Подобный Фурье-образ соответствует функции sinc(Tx) и согласно свойству 4, подобное умножение равнозначно свертке исходной последовательности дельта-функций с функцией sinc(Tx)
То есть с помощью преобразования Фурье мы получили способ легко восстановить исходный сигнал из дискретизированного по времени, работающий при условии что мы используем частоту дискретизации, по крайней мере вдвое (из-за наличия в спектре отрицательных частот) превышающую максимальную частоту присутствующую в исходном сигнале. Этот результат широко известен и называется “теорема Котельникова / Шеннона-Найквиста”. Однако, как несложно теперь (понимая доказательство) заметить, этот результат вопреки широко распространенному заблуждению определяет достаточное, но не необходимое условие для восстановления исходного сигнала. Все что нам требуется — это добиться того, чтобы интересующая нас часть спектра после дискретизации сигнала не накладывалась друг на друга и если сигнал достаточно узкополосный (имеет малую “ширину” ненулевой части спектра), то этого результата часто можно добиться и при частоте дискретизации намного ниже чем удвоенная максимальная частота сигнале. Подобная техника называется “undersampling” (субдискретизация, полосовая дискретизация) и довольно широко используется при обработке всевозможных радиосигналов. Например, если мы берем FM-радио действующее в полосе частот от 88 до 108 МГц, то для его оцифровки можно использовать АЦП с частотой всего 43.5 МГц вместо предполагающихся по теореме Котельникова 216 МГц. При этом, правда, понадобится качественный АЦП и хороший фильтр.
Замечу, что “дублирование” высоких частот частотами меньших порядков (алиасинг) — непосредственное свойство дискретизации сигнала, необратимо “портящее” результат. Поэтому если в сигнале в принципе могут присутствовать частоты высокого порядка (то есть практически всегда) перед АЦП ставят аналоговый фильтр, “отсекающий” все лишнее непосредственно в исходном сигнале (так как после дискретизации делать это уже будет поздно). Характеристики этих фильтров, как аналоговых устройств, неидеальны, поэтому некоторая “порча” сигнала при этом все равно происходит, и на практике из этого следует что наибольшие частоты в спектре, как правило, недостоверны. Чтобы уменьшить эту проблему, сигнал нередко сэмплируют с завышенной частотой дискретизации, ставя при этом входной аналоговый фильтр на меньшую полосу пропускания и используя только нижнюю часть теоретически доступного частотного диапазона АЦП.
Еще одно распространенное заблуждение, кстати, — это когда сигнал на выходе ЦАП рисуют “ступеньками”. “Ступеньки” соответствуют свертке дискретизированной последовательности сигналов с прямоугольной функцией ширины T и высоты 1:
Спектр сигнала при таком преобразовании умножается на фурье-образ этой прямоугольной функции, а у подобной прямоугольной функции это снова sinc(w), “растянутый” тем сильнее, чем меньше ширина соответствующего прямоугольника. Спектр дискретизированного сигнала при подобном “ЦАП” поточечно умножается на этот спектр. При этом ненужные высокие частоты с “лишними копиями” спектра обрезаются не полностью, а верхняя часть “полезной” части спектра, напротив, ослабляется.
На практике так, естественно, никто не делает. Существует много разных подходов к построению ЦАП, но даже в наиболее близких по смыслу ЦАП взвешивающего типа прямоугольные импульсы в ЦАП напротив выбираются по возможности короткими (приближающимися к настоящей последовательности дельта-функций) чтобы избежать излишнего подавления полезной части спектра. “Лишние” частоты в получившемся широкополосном сигнале практически всегда гасят, пропуская сигнал через аналоговый фильтр низких частот, так что «цифровых ступенек» нет ни «внутри» преобразователя, ни, тем более, на его выходе.
Однако вернемся обратно к преобразованию Фурье. Описанное выше преобразование Фурье, примененное к заранее дискретизированной последовательности сигналов называется преобразованием Фурье дискретного времени (DTFT). Спектр получаемый подобным преобразованием всегда 1/T-периодичен, поэтому спектр DTFT полностью определяется её значениями на отрезке [0…1/T), поэтому часто этим отрезком спектр DTFT и ограничивают. При этом результат DTFT несмотря на то что это спектр дискретизированного сигнала — по-прежнему “аналоговая” функция. Кроме того, для “обычных” действительнозначных сигналов вторая половина этого спектра в силу свойства 6 зеркально повторяет левую половину, отраженную относительно частоты Найквиста 1/2T.
До сих пор мы предполагали что на вход наших преобразований поступает сигнал определенный от минус до плюс бесконечности. Однако реальные доступные нам сигналы всегда имеют конечную длину — что делать? Для решения этой проблемы в FT и DTFT конечный сигнал просто дополняют слева и справа на бесконечность нулями. Если исходный сигнал изначально был конечным (скажем, это отдельный импульс) и в преобразование Фурье он попал полностью, то этот подход напрямую дает желаемый результат. Однако часто «конечный» сигнал используемый для преобразования Фурье на самом деле является частью более длинного, возможно бесконечного сигнала, такого как, например, синусоида. В этом случае дополнение конечного отрезка нулями интерпретируют следующим образом: считают что исходный сигнал имеет бесконечно большую длину, но затем умножается на некоторую взвешивающую функцию — “окно”, обращающуюся в ноль вне доступного нам для измерения отрезка. В простейшем случае роль “окна” играет просто прямоугольная функция, соответствующая тому что мы просто дополняем конечный сигнал слева и справа бесконечным числом нулей. В более сложных — исходную последовательность умножают на весовые коэффициенты определяемые функцией “окна” и затем, опять же, дополняют нулями.
Пользуясь уже хорошо нам знакомым свойством 5, несложно сообразить, что при подобном умножении исходный сигнал прсто сворачивается со спектром функции окна. Например если мы пытаемся измерить спектр синусоиды (дельта-функцию), но ограничиваем интервал измерений прямоугольным окном, то в получившимся спектре на месте дельта-функции мы увидим спектр окна — т.е. Tsinc(T(x-f)):
В данном случае T — это длина интервала которым мы ограничили наш сигнал, так что чем длиннее будет входной сигнал — тем “уже” и ближе к истинной дельта-функции будет наблюдаемый нами спектр. Конечная “ширина” главного лепестка приводит к невозможности уверенно различать наличие в исходном сигнале синусоид близких друг к другу по частоте, а наличие “боковых лепестков” вносит небольшие искажения и в далеко расположенные частоты, мешая точному измерению амплитуды отдельных частот, особенно если нужно измерять спектр в областях небольшой амплитуды при наличии в спектре на порядок более мощных компонент. Этот эффект называют “спектральной утечкой” и полностью победить его для конечных сигналов невозможно, но чем длиннее интервал на котором измеряется сигнал — тем меньше влияние этой утечки. Выбором функции окна можно контролировать “ширину” этой утечки, либо концентрируя её вокруг главной частоты (сильно “размывая” спектр, но зато не мешая соседним частотам), либо размазывая её повсюду (размытие пиков уменьшается но сильно растет “шум” и как следствие — погрешность измерения амплитуды отдельных частот). Заметьте, что выбранная частота дискретизации в спектральной утечке почти не играет роли — короткий отрезок сигнала можно сэмплировать хоть на 10 ГГц, но это увеличит только количество поддающихся измерению частот, тогда как точность определения каждой отдельной частоты все равно останется низкой.
Интересным частным случаем является ситуация, в которой сигнал с набором дискретных частот nF дискретизируется на частоте mF, где m,n — целые числа. В этом случае нули “окна” и расположение дельта-функций в спектре в точности совпадают и хотя частоты все равно “размазываются”, но их амплитуда в точках mF совпадает с истинной — “шум” равен нулю. Это свойство позволяет доказать аналог теоремы Котельникова для дискретного преобразования Фурье, но на практике такие сигналы, к сожалению, фактически не встречаются.
Итак, со “входом” мы разобрались — из непрерывной функции бесконечной длины мы получили конечное число дискретных отсчетов, с которыми можем работать а взамен получили ограничения по ширине спектра и утечку частот. Однако “выход” DTFT по-прежнему является непрерывной функцией, работать с которой компьютеру проблематично. На практике эту проблему решают очень просто — полный отрезок [0,1/T) делят на k равных частей и считают DTFT в точках fi=i/kT, где i = 0,1,… k-1. Получившуюся конструкцию называют “дискретным преобразованием Фурье” (DFT).
Последнее преобразование удобно нормализовать, убрав из него T и вопросы связанные с выбором “окна”. Эту нормализованную запись часто используют в качестве определения DFT как преобразования последовательности из N комплексных чисел:
Прелесть преобразования Фурье записанного в такой форме — в том что сохраняя все достоинства DTFT, подобное DTF для “гладких” k (например, степеней двойки) можно вычислять чрезвычайно быстро, за время порядка k log(k). Соответствующие алгоритмы называют “быстрым преобразованием Фурье” (БПФ, FFT) и их, вообще говоря, существует несколько. С практической точки зрения, впрочем, их все можно рассматривать как “черные ящики”, получающие последовательность комплексных чисел на входе и выдающих последовательность комплексных чисел на выходе. Таким образом, работа с дискретизированным сигналом конечной длины сводится к тому, что этот сигнал вначале умножается на подходящую взвешивающую функцию, затем дополняется нужным числом нулей справа и передается в алгоритм БПФ.
Как интерпретировать получившийся результат? С учетом всего вышеизложенного,
- Получившиеся значения есть равномерная сетка отсчетов по спектру DTFT. Чем больше отсчетов — тем мельче сетка, тем подробнее виден спектр. Дописывая к известной последовательности нужное число нулей можно посчитать сколь угодно близкое приближение к непрерывному спектру
- Спектр DTFT задан на отрезке частот от 0 до 1/T (где 1/T — частота дискретизации) и периодически повторяется на бесконечность вне этого отрезка
- Этот спектр задан комплексными числами (парами действительных). Амплитуда определяется как модуль комплексного числа, фаза — как аргумент.
- Для действительнозначного входного сигнала, спектр в диапазоне 1/2T…1/T просто зеркально повторяет спектр 0…1/2T и не несет соответственно полезной нагрузки (для визуализации спектра его можно просто обрезать)
- Если исходный сигнал содержал частоты выше половины частоты дискретизации, то они будут отображены в более низкие частоты (возможно накладываясь поверх уже существующего сигнала этой частоты) — алиасинг
- В спектре всегда присутствует “спектральная утечка” определяющаяся выбранной взвешивающей “оконной функцией”. Чем длиннее исходный сигнал (до дополнения нулями!) — тем эта утечка меньше.
- Спектральная утечка ограничивает осмысленность расчета БПФ с большим дополнением нулями. Однако дополнение все же часто бывает полезным, поскольку, например, позволяет точнее определить максимум узкополосного синусоидального сигнала, если он не попадает точно в одну из частот вида k/T.
- Синусоиде амплитуды A в амплитудном спектре (при выбранной мной нормировке преобразования Фурье) соответствует значение A*N/2, за исключением нулевой частоты, которая не раскладывается на “плюс” и “минус” частоту и потому имеет амплитуду A*N, а также частоты Найквиста 1/2T в которой касаются в предельном случае друг друга отдельные копии спектра (там тоже будет A*N, но, в отличие от нуля в выход БПФ это значение не попадает да и достоверным в реальных схемах все равно никогда не является). Здесь N = T1/T0, где T1 — это длина исходного сигнала (она определяет коэффициент перед спектром «окна»), а T0 — длина одного периода дискретизации (она определяет коэффициент у гребенки Дирака) и по смыслу это, как несложно видеть, попросту число отсчетов в исходном сигнале (до его дополнения нулями)
Ну вот, в общем, и всё. Надеюсь преобразование Фурье и алгоритмы БПФ будут теперь для Вас простыми, понятными и приятными в обращении инструментами.
A Fourier series ([1]) is an expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series, but not all trigonometric series are Fourier series.[2] By expressing a function as a sum of sines and cosines, many problems involving the function become easier to analyze because trigonometric functions are well understood. For example, Fourier series were first used by Joseph Fourier to find solutions to the heat equation. This application is possible because the derivatives of trigonometric functions fall into simple patterns. Fourier series cannot be used to approximate arbitrary functions, because most functions have infinitely many terms in their Fourier series, and the series do not always converge. Well-behaved functions, for example smooth functions, have Fourier series that converge to the original function. The coefficients of the Fourier series are determined by integrals of the function multiplied by trigonometric functions, described in Common forms of the Fourier series below.
The study of the convergence of Fourier series focus on the behaviors of the partial sums, which means studying the behavior of the sum as more and more terms from the series are summed. The figures below illustrate some partial Fourier series results for the components of a square wave.
-
A square wave (represented as the blue dot) is approximated by its sixth partial sum (represented as the purple dot), formed by summing the first six terms (represented as arrows) of the square wave’s Fourier series. Each arrow starts at the vertical sum of all the arrows to its left (i.e. the previous partial sum).
-
The first four partial sums of the Fourier series for a square wave. As more harmonics are added, the partial sums converge to (become more and more like) the square wave.
-
Function
(in red) is a Fourier series sum of 6 harmonically related sine waves (in blue). Its Fourier transform
is a frequency-domain representation that reveals the amplitudes of the summed sine waves.
Fourier series are closely related to the Fourier transform, which can be used to find the frequency information for functions that are not periodic. Periodic functions can be identified with functions on a circle, for this reason Fourier series are the subject of Fourier analysis on a circle, usually denoted as 


Since Fourier’s time, many different approaches to defining and understanding the concept of Fourier series have been discovered, all of which are consistent with one another, but each of which emphasizes different aspects of the topic. Some of the more powerful and elegant approaches are based on mathematical ideas and tools that were not available in Fourier’s time. Fourier originally defined the Fourier series for real-valued functions of real arguments, and used the sine and cosine functions in the decomposition. Many other Fourier-related transforms have since been defined, extending his initial idea to many applications and birthing an area of mathematics called Fourier analysis.
Common forms of the Fourier series[edit]
The Fourier series can be represented in different forms. The sine-cosine form, exponential form, and amplitude-phase form are expressed here for a periodic function 
Fig 1. The top graph shows a non-periodic function s(x) in blue defined only over the red interval from 0 to P. The Fourier series can be thought of as analyzing the periodic extension (bottom graph) of the original function. The Fourier series is always a periodic function, even if original function s(x) wasn’t.
Sine-cosine form[edit]
The Fourier series coefficients[3] are defined by the integrals:
Fourier series coefficients
|
|
(Eq. 1) |
It is notable that, 

With these coefficients defined the Fourier series is:
Fourier series
|
|
(Eq. 2) |
Many others use the 




The integer index 





Example[edit]
Plot of the sawtooth wave, a periodic continuation of the linear function 
Animated plot of the first five successive partial Fourier series
Consider a sawtooth function:
In this case, the Fourier coefficients are given by
It can be shown that the Fourier series converges to 


-
(Eq.8)
When 


This example leads to a solution of the Basel problem.
Exponential form[edit]
It is possible to simplify the integrals for the Fourier series coefficients by using Euler’s formula.
With the definitions
Complex Fourier series coefficients
|
|
(Eq. 3) |
By substituting equation Eq. 1 into Eq. 3 it can be shown that:[4]
Complex Fourier series coefficients

Given the Complex Fourier series coefficients, it is possible to recover 

Complex Fourier series coefficients

With these definitions the Fourier series is written as:
Fourier series, exponential form
|
|
(Eq. 4) |
This is the customary form for generalizing to Complex-valued functions. Negative values of 
Amplitude-phase form[edit]
The Fourier series in amplitude-phase form is:
Fourier series, amplitude-phase form
|
|
(Eq. 5) |
Clearly Eq. 5 can represent functions that are just a sum of one or more of the harmonic frequencies. The remarkable thing, for those not yet familiar with this concept, is that it can also represent the intermediate frequencies and/or non-sinusoidal functions because of the potentially infinite number of terms (
Fig 2. The blue curve is the cross-correlation of a square wave and a cosine function, as the phase lag of the cosine varies over one cycle. The amplitude and phase lag at the maximum value are the polar coordinates of one harmonic in the Fourier series expansion of the square wave. The corresponding rectangular coordinates can be determined by evaluating the cross-correlation at just two phase lags separated by 90º.
The coefficients 




![{displaystyle [x_{0},x_{0}+P],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74358f52e616039efc9b1fcc9568f99f6ae93463)
|
|
(Eq. 6) |
is essentially a matched filter, with template 







The maximum of 








Combining this with Eq. 6 gives:
which introduces the definitions of 



The derivative of 
And the correlation peak value is:
Therefore 



Extensions to non-periodic functions[edit]
Fourier series can also be applied to functions that are not necessarily periodic. The simplest extension occurs when the function 
![{displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)




For functions which have compact support, meaning that values of 
![{displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)
![{displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)
For both the cases above, it is sometimes desirable to take an even or odd reflection of the function, or extend it by zero in the case the function is only defined on a finite interval. This allows one to prescribe desired properties for the Fourier coefficients. For example, by making the function even you ensure 
In the case where the function doesn’t have compact support and is defined on entire real line, one can use the Fourier transform. Fourier series can be taken for a truncated version of the function or to the periodic summation.
Partial Sum Operator[edit]
Frequently when describing how Fourier series behave, authors introduce the partial sum operator 

|
|
(Eq. 8) |
Where 

Convergence[edit]
A proof that a Fourier series is a valid representation of any periodic function (that satisfies the Dirichlet conditions) is overviewed in § Fourier theorem proving convergence of Fourier series.
In engineering applications, the Fourier series is generally assumed to converge except at jump discontinuities since the functions encountered in engineering are better-behaved than functions encountered in other disciplines. In particular, if 



![{displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)
-
Four partial sums (Fourier series) of lengths 1, 2, 3, and 4 terms, showing how the approximation to a square wave improves as the number of terms increases (animation)
-
Four partial sums (Fourier series) of lengths 1, 2, 3, and 4 terms, showing how the approximation to a sawtooth wave improves as the number of terms increases (animation)
-
Example of convergence to a somewhat arbitrary function. Note the development of the “ringing” (Gibbs phenomenon) at the transitions to/from the vertical sections.
Other common notations[edit]
The notation 

![{displaystyle {hat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4759449679108f08a78be5a080c3db89dc27ffea)
![{displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)
In engineering, particularly when the variable 
Another commonly used frequency domain representation uses the Fourier series coefficients to modulate a Dirac comb:
where 




The constructed function 
History[edit]
The Fourier series is named in honor of Jean-Baptiste Joseph Fourier (1768–1830), who made important contributions to the study of trigonometric series, after preliminary investigations by Leonhard Euler, Jean le Rond d’Alembert, and Daniel Bernoulli.[D] Fourier introduced the series for the purpose of solving the heat equation in a metal plate, publishing his initial results in his 1807 Mémoire sur la propagation de la chaleur dans les corps solides (Treatise on the propagation of heat in solid bodies), and publishing his Théorie analytique de la chaleur (Analytical theory of heat) in 1822. The Mémoire introduced Fourier analysis, specifically Fourier series. Through Fourier’s research the fact was established that an arbitrary (at first, continuous[8] and later generalized to any piecewise-smooth[9]) function can be represented by a trigonometric series. The first announcement of this great discovery was made by Fourier in 1807, before the French Academy.[10] Early ideas of decomposing a periodic function into the sum of simple oscillating functions date back to the 3rd century BC, when ancient astronomers proposed an empiric model of planetary motions, based on deferents and epicycles.
The heat equation is a partial differential equation. Prior to Fourier’s work, no solution to the heat equation was known in the general case, although particular solutions were known if the heat source behaved in a simple way, in particular, if the heat source was a sine or cosine wave. These simple solutions are now sometimes called eigensolutions. Fourier’s idea was to model a complicated heat source as a superposition (or linear combination) of simple sine and cosine waves, and to write the solution as a superposition of the corresponding eigensolutions. This superposition or linear combination is called the Fourier series.
From a modern point of view, Fourier’s results are somewhat informal, due to the lack of a precise notion of function and integral in the early nineteenth century. Later, Peter Gustav Lejeune Dirichlet[11] and Bernhard Riemann[12][13][14] expressed Fourier’s results with greater precision and formality.
Although the original motivation was to solve the heat equation, it later became obvious that the same techniques could be applied to a wide array of mathematical and physical problems, and especially those involving linear differential equations with constant coefficients, for which the eigensolutions are sinusoids. The Fourier series has many such applications in electrical engineering, vibration analysis, acoustics, optics, signal processing, image processing, quantum mechanics, econometrics,[15] shell theory,[16] etc.
Beginnings[edit]
Joseph Fourier wrote:[dubious – discuss]

Multiplying both sides by
, and then integrating from
to
yields:

This immediately gives any coefficient ak of the trigonometrical series for φ(y) for any function which has such an expansion. It works because if φ has such an expansion, then (under suitable convergence assumptions) the integral
can be carried out term-by-term. But all terms involving 

In these few lines, which are close to the modern formalism used in Fourier series, Fourier revolutionized both mathematics and physics. Although similar trigonometric series were previously used by Euler, d’Alembert, Daniel Bernoulli and Gauss, Fourier believed that such trigonometric series could represent any arbitrary function. In what sense that is actually true is a somewhat subtle issue and the attempts over many years to clarify this idea have led to important discoveries in the theories of convergence, function spaces, and harmonic analysis.
When Fourier submitted a later competition essay in 1811, the committee (which included Lagrange, Laplace, Malus and Legendre, among others) concluded: …the manner in which the author arrives at these equations is not exempt of difficulties and…his analysis to integrate them still leaves something to be desired on the score of generality and even rigour.[citation needed]
Fourier’s motivation[edit]
Heat distribution in a metal plate, using Fourier’s method
The Fourier series expansion of the sawtooth function (above) looks more complicated than the simple formula 

![{displaystyle (x,y)in [0,pi ]times [0,pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18734f151b17b5d3e325f79c7000826ab832610)




Here, sinh is the hyperbolic sine function. This solution of the heat equation is obtained by multiplying each term of Eq.6 by 



Complex Fourier series animation[edit]
Complex Fourier series tracing the letter ‘e’. (The Julia source code that generates the frames of this animation is here[18] in Appendix B.)
An example of the ability of the complex Fourier series to trace any two dimensional closed figure is shown in the adjacent animation of the complex Fourier series tracing the letter ‘e’ (for exponential). Note that the animation uses the variable ‘t’ to parameterize the letter ‘e’ in the complex plane, which is equivalent to using the parameter ‘x’ in this article’s subsection on complex valued functions.
In the animation’s back plane, the rotating vectors are aggregated in an order that alternates between a vector rotating in the positive (counter clockwise) direction and a vector rotating at the same frequency but in the negative (clockwise) direction, resulting in a single tracing arm with lots of zigzags. This perspective shows how the addition of each pair of rotating vectors (one rotating in the positive direction and one rotating in the negative direction) nudges the previous trace (shown as a light gray dotted line) closer to the shape of the letter ‘e’.
In the animation’s front plane, the rotating vectors are aggregated into two sets, the set of all the positive rotating vectors and the set of all the negative rotating vectors (the non-rotating component is evenly split between the two), resulting in two tracing arms rotating in opposite directions. The animation’s small circle denotes the midpoint between the two arms and also the midpoint between the origin and the current tracing point denoted by ‘+’. This perspective shows how the complex Fourier series is an extension (the addition of an arm) of the complex geometric series which has just one arm. It also shows how the two arms coordinate with each other. For example, as the tracing point is rotating in the positive direction, the negative direction arm stays parked. Similarly, when the tracing point is rotating in the negative direction, the positive direction arm stays parked.
In between the animation’s back and front planes are rotating trapezoids whose areas represent the values of the complex Fourier series terms. This perspective shows the amplitude, frequency, and phase of the individual terms of the complex Fourier series in relation to the series sum spatially converging to the letter ‘e’ in the back and front planes. The audio track’s left and right channels correspond respectively to the real and imaginary components of the current tracing point ‘+’ but increased in frequency by a factor of 3536 so that the animation’s fundamental frequency (n=1) is a 220 Hz tone (A220).
Other applications[edit]
Another application is to solve the Basel problem by using Parseval’s theorem. The example generalizes and one may compute ζ(2n), for any positive integer n.
Table of common Fourier series[edit]
Some common pairs of periodic functions and their Fourier series coefficients are shown in the table below.
Time domain 
|
Plot | Frequency domain (sine-cosine form) 
|
Remarks | Reference |
|---|---|---|---|---|

|
|

|
Full-wave rectified sine | [19]: p. 193 |

|
|

|
Half-wave rectified sine | [19]: p. 193 |

|
|

|

|
|

|
|

|
[19]: p. 192 | |

|
|

|
[19]: p. 192 | |

|
|

|
[19]: p. 193 |
Table of basic properties[edit]
This table shows some mathematical operations in the time domain and the corresponding effect in the Fourier series coefficients. Notation:
| Property | Time domain | Frequency domain (exponential form) | Remarks | Reference |
|---|---|---|---|---|
| Linearity | 
|
![{displaystyle acdot S[n]+bcdot R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23622be4a50d54928d05c273e803240a2cb1e413)
|

|
|
| Time reversal / Frequency reversal | 
|
![{displaystyle S[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab628b28c49c04cab81d0bd30d19ee0797b0587c)
|
[20]: p. 610 | |
| Time conjugation | 
|
![{displaystyle S^{*}[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f6ea8a947b86f8a31046070359f6b8111a0bae)
|
[20]: p. 610 | |
| Time reversal & conjugation | 
|
![{displaystyle S^{*}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3776c67c40997d8044720ef84de7575679cf9638)
|
||
| Real part in time | 
|
![{displaystyle {frac {1}{2}}(S[n]+S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2eb44dffaae6c85870914249c054e33236b02cc8)
|
||
| Imaginary part in time | 
|
![{displaystyle {frac {1}{2i}}(S[n]-S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc039a9c12ae20a4b47337ae55bf8a7bc26d2e11)
|
||
| Real part in frequency | 
|
![{displaystyle operatorname {Re} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/140ebff319eb8eb7965d0ca86dcaadb21685177a)
|
||
| Imaginary part in frequency | 
|
![{displaystyle operatorname {Im} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c726948120015ce0d482f5f7f4af81713342b5c)
|
||
| Shift in time / Modulation in frequency | 
|
![{displaystyle S[n]cdot e^{-i{frac {2pi x_{0}}{P}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fb7150e991a2642dc0c62cdee40602d99227420)
|

|
[20]: p. 610 |
| Shift in frequency / Modulation in time | 
|
![{displaystyle S[n-n_{0}]!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07385c0e5fd45d4e07a279a91668cf8894963e0c)
|

|
[20]: p. 610 |
Symmetry properties[edit]
When the real and imaginary parts of a complex function are decomposed into their even and odd parts, there are four components, denoted below by the subscripts RE, RO, IE, and IO. And there is a one-to-one mapping between the four components of a complex time function and the four components of its complex frequency transform:[21]
From this, various relationships are apparent, for example:
- The transform of a real-valued function (sRE + sRO) is the even symmetric function SRE + i SIO. Conversely, an even-symmetric transform implies a real-valued time-domain.
- The transform of an imaginary-valued function (i sIE + i sIO) is the odd symmetric function SRO + i SIE, and the converse is true.
- The transform of an even-symmetric function (sRE + i sIO) is the real-valued function SRE + SRO, and the converse is true.
- The transform of an odd-symmetric function (sRO + i sIE) is the imaginary-valued function i SIE + i SIO, and the converse is true.
Other properties[edit]
Riemann–Lebesgue lemma[edit]
If 
![{textstyle lim _{|n|to infty }S[n]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc04d857f6462ae29422edcada981c8a798d4b5)


Parseval’s theorem[edit]
If 


![{textstyle {frac {1}{P}}int _{P}|s(x)|^{2},dx=sum _{n=-infty }^{infty }{Bigl |}S[n]{Bigr |}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/263e69a5a58598591a5c06ca7e17ef8cfe92bdad)
If 


![{displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)

for ![{displaystyle S[n]in mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5ef3e51d1a6c9fe833f0a436ad2906cfaa4d5a3)
![{displaystyle {frac {1}{P}}int _{P}|s(x)|^{4},dx=sum _{k=0}^{M-1}S[k]sum _{l=0}^{M-1}S^{*}[l]{Bigg [}{underset {kgeq l}{sum _{m=k-l}^{M-1}}}S^{*}[m]S[m-(k-l)]+{underset {k<l}{sum _{m=l-k}^{M-1}}}S^{*}[m-(l-k)]S[m]{Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39c359b6c8df5068b8df3c592e303ee7be010e33)
and for ![{displaystyle S[n]in mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b094e88b3fbb3d7754e0a9ea0138c296f4b0d137)
![{displaystyle {frac {1}{P}}int _{P}|s(x)|^{4},dx=sum _{k=0}^{M-1}S[k]sum _{l=0}^{M-1}S[l]sum _{m=|k-l|}^{M-1}S[m]S[m-|k-l|]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9aa31cd2ec580a3b95affae1462abed113a86f12)
Plancherel’s theorem[edit]
If 


![{displaystyle S[n]=c_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4375307afdf29e78a31ef64b699dcb3e2fde140)

Convolution theorems[edit]
Given 


![{displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)
![{displaystyle R[n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d8bbe147f3eb3fb318d09437a3540e054b0289)

Derivative property[edit]
We say that 





Compact groups[edit]
One of the interesting properties of the Fourier transform which we have mentioned, is that it carries convolutions to pointwise products. If that is the property which we seek to preserve, one can produce Fourier series on any compact group. Typical examples include those classical groups that are compact. This generalizes the Fourier transform to all spaces of the form L2(G), where G is a compact group, in such a way that the Fourier transform carries convolutions to pointwise products. The Fourier series exists and converges in similar ways to the [−π,π] case.
An alternative extension to compact groups is the Peter–Weyl theorem, which proves results about representations of compact groups analogous to those about finite groups.
Riemannian manifolds[edit]
If the domain is not a group, then there is no intrinsically defined convolution. However, if 




![[-pi ,pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)

Locally compact Abelian groups[edit]
The generalization to compact groups discussed above does not generalize to noncompact, nonabelian groups. However, there is a straightforward generalization to Locally Compact Abelian (LCA) groups.
This generalizes the Fourier transform to 



![[-pi ,pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)


Extensions[edit]
Fourier series on a square[edit]
We can also define the Fourier series for functions of two variables 

![{displaystyle [-pi ,pi ]times [-pi ,pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb)
Aside from being useful for solving partial differential equations such as the heat equation, one notable application of Fourier series on the square is in image compression. In particular, the JPEG image compression standard uses the two-dimensional discrete cosine transform, a discrete form of the Fourier cosine transform, which uses only cosine as the basis function.
For two-dimensional arrays with a staggered appearance, half of the Fourier series coefficients disappear, due to additional symmetry.[24]
Fourier series of Bravais-lattice-periodic-function[edit]
A three-dimensional Bravais lattice is defined as the set of vectors of the form:
where 





where 




Thus we can define a new function,
This new function, 



This enables us to build up a set of Fourier coefficients, each being indexed by three independent integers 

![{displaystyle left[0,a_{1}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187cf2c27876a96c668f73266f673002808773ac)

And then we can write:
Further defining:
We can write 
Finally applying the same for the third coordinate, we define:
We write 
Re-arranging:
Now, every reciprocal lattice vector can be written (but does not mean that it is the only way of writing) as 









So it is clear that in our expansion of 
where
Assuming
we can solve this system of three linear equations for 











which after some calculation and applying some non-trivial cross-product identities can be shown to be equal to:
(it may be advantageous for the sake of simplifying calculations, to work in such a rectangular coordinate system, in which it just so happens that 





We can write now 



writing 



Hilbert space interpretation[edit]
In the language of Hilbert spaces, the set of functions 
![{displaystyle L^{2}([-pi ,pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)
![[-pi ,pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)


where
is the complex conjugate of
The basic Fourier series result for Hilbert spaces can be written as
This corresponds exactly to the complex exponential formulation given above. The version with sines and cosines is also justified with the Hilbert space interpretation. Indeed, the sines and cosines form an orthogonal set:
(where δmn is the Kronecker delta), and
furthermore, the sines and cosines are orthogonal to the constant function 
![{displaystyle L^{2}([-pi ,pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)



Fourier theorem proving convergence of Fourier series[edit]
These theorems, and informal variations of them that don’t specify the convergence conditions, are sometimes referred to generically as Fourier’s theorem or the Fourier theorem.[25][26][27][28]
The earlier Eq.7
is a trigonometric polynomial of degree 
Least squares property[edit]
Parseval’s theorem implies that:
Theorem — The trigonometric polynomial 




where the Hilbert space norm is defined as:
Convergence theorems[edit]
Because of the least squares property, and because of the completeness of the Fourier basis, we obtain an elementary convergence result.
Theorem — If 







We have already mentioned that if 
![{displaystyle (icdot n)S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a89ae55b94c8d25d1f3927c5ba4eb65ac7c4762)





Theorem — If 


This result can be proven easily if 

![{displaystyle n^{2}S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/340e0b24995005f3669a865a57edb4035b77ca2d)




proves uniform convergence.
Many other results concerning the convergence of Fourier series are known, ranging from the moderately simple result that the series converges at 



Divergence[edit]
Since Fourier series have such good convergence properties, many are often surprised by some of the negative results. For example, the Fourier series of a continuous T-periodic function need not converge pointwise.[citation needed] The uniform boundedness principle yields a simple non-constructive proof of this fact.
In 1922, Andrey Kolmogorov published an article titled Une série de Fourier-Lebesgue divergente presque partout in which he gave an example of a Lebesgue-integrable function whose Fourier series diverges almost everywhere. He later constructed an example of an integrable function whose Fourier series diverges everywhere (Katznelson 1976).
See also[edit]
- ATS theorem
- Dirichlet kernel
- Discrete Fourier transform
- Fast Fourier transform
- Fejér’s theorem
- Fourier analysis
- Fourier sine and cosine series
- Fourier transform
- Gibbs phenomenon
- Half range Fourier series
- Laurent series – the substitution q = eix transforms a Fourier series into a Laurent series, or conversely. This is used in the q-series expansion of the j-invariant.
- Least-squares spectral analysis
- Multidimensional transform
- Spectral theory
- Sturm–Liouville theory
- Residue theorem integrals of f(z), singularities, poles
Notes[edit]
- ^ Some authors define
differently so that the same integral can be used to define
and
. This changes Eq. 2 so that the first term needs to be divided by 2, and is no longer the average value.
- ^ The scale factor
which could be inserted later, results in a series that converges to
instead of
- ^ Since the integral defining the Fourier transform of a periodic function is not convergent, it is necessary to view the periodic function and its transform as distributions. In this sense
is a Dirac delta function, which is an example of a distribution.
- ^ These three did some important early work on the wave equation, especially D’Alembert. Euler’s work in this area was mostly comtemporaneous/ in collaboration with Bernoulli, although the latter made some independent contributions to the theory of waves and vibrations. (See Fetter & Walecka 2003, pp. 209–210).
- ^ These words are not strictly Fourier’s. Whilst the cited article does list the author as Fourier, a footnote indicates that the article was actually written by Poisson (that it was not written by Fourier is also clear from the consistent use of the third person to refer to him) and that it is, “for reasons of historical interest”, presented as though it were Fourier’s original memoire.
References[edit]
- ^ “Fourier”. Dictionary.com Unabridged (Online). n.d.
- ^ Zygmund, A. (2002). Trigonometric Series (3nd ed.). Cambridge, UK: Cambridge University Press. ISBN 0-521-89053-5.
- ^ Haberman, Richard (1987). Elementary Applied Partial Differential Equations (2nd ed.). Englewood Cliffs, New Jersey: Prentice Hall. p. 77. ISBN 0-13-252875-4.
- ^ Pinkus, Allan; Zafrany, Samy (1997). Fourier Series and Integral Transforms (1st ed.). Cambridge, UK: Cambridge University Press. pp. 42–44. ISBN 0-521-59771-4.
- ^ Dorf, Richard C.; Tallarida, Ronald J. (1993). Pocket Book of Electrical Engineering Formulas (1st ed.). Boca Raton,FL: CRC Press. pp. 171–174. ISBN 0849344735.
- ^ Katznelson, Yitzhak (1976). An introduction to Harmonic Analysis (2nd corrected ed.). New York, NY: Dover Publications, Inc. p. 46. ISBN 0-486-63331-4.
- ^ Tolstov, Georgi P. (1976). Fourier Series. Courier-Dover. ISBN 0-486-63317-9.
- ^ Stillwell, John (2013). “Logic and the philosophy of mathematics in the nineteenth century”. In Ten, C. L. (ed.). Routledge History of Philosophy. Vol. VII: The Nineteenth Century. Routledge. p. 204. ISBN 978-1-134-92880-4.
- ^ Fasshauer, Greg (2015). “Fourier Series and Boundary Value Problems” (PDF). Math 461 Course Notes, Ch 3. Department of Applied Mathematics, Illinois Institute of Technology. Retrieved 6 November 2020.
- ^ Cajori, Florian (1893). A History of Mathematics. Macmillan. p. 283.
- ^ Lejeune-Dirichlet, Peter Gustav (1829). “Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données” [On the convergence of trigonometric series which serve to represent an arbitrary function between two given limits]. Journal für die reine und angewandte Mathematik (in French). 4: 157–169. arXiv:0806.1294.
- ^ “Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe” [About the representability of a function by a trigonometric series]. Habilitationsschrift, Göttingen; 1854. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, vol. 13, 1867. Published posthumously for Riemann by Richard Dedekind (in German). Archived from the original on 20 May 2008. Retrieved 19 May 2008.
- ^ Mascre, D.; Riemann, Bernhard (1867), “Posthumous Thesis on the Representation of Functions by Trigonometric Series”, in Grattan-Guinness, Ivor (ed.), Landmark Writings in Western Mathematics 1640–1940, Elsevier (published 2005), p. 49, ISBN 9780080457444
- ^ Remmert, Reinhold (1991). Theory of Complex Functions: Readings in Mathematics. Springer. p. 29. ISBN 9780387971957.
- ^ Nerlove, Marc; Grether, David M.; Carvalho, Jose L. (1995). Analysis of Economic Time Series. Economic Theory, Econometrics, and Mathematical Economics. Elsevier. ISBN 0-12-515751-7.
- ^ Wilhelm Flügge, Stresses in Shells (1973) 2nd edition. ISBN 978-3-642-88291-3. Originally published in German as Statik und Dynamik der Schalen (1937).
- ^ Fourier, Jean-Baptiste-Joseph (1888). Gaston Darboux (ed.). Oeuvres de Fourier [The Works of Fourier] (in French). Paris: Gauthier-Villars et Fils. pp. 218–219 – via Gallica.
- ^ Sepesi, G (13 February 2022). “Zeno’s Enduring Example”. Towards Data Science. pp. Appendix B.
- ^ a b c d e Papula, Lothar (2009). Mathematische Formelsammlung: für Ingenieure und Naturwissenschaftler [Mathematical Functions for Engineers and Physicists] (in German). Vieweg+Teubner Verlag. ISBN 978-3834807571.
- ^ a b c d Shmaliy, Y.S. (2007). Continuous-Time Signals. Springer. ISBN 978-1402062711.
- ^ Proakis, John G.; Manolakis, Dimitris G. (1996). Digital Signal Processing: Principles, Algorithms, and Applications (3rd ed.). Prentice Hall. p. 291. ISBN 978-0-13-373762-2.
- ^ Sharkas, Hesham (2022). “Solution of Integral of The Fourth Power of a Finite-Length Exponential Fourier Series”. ResearchGate. doi:10.13140/RG.2.2.31527.83368/2.
- ^ “Characterizations of a linear subspace associated with Fourier series”. MathOverflow. 2010-11-19. Retrieved 2014-08-08.
- ^ Vanishing of Half the Fourier Coefficients in Staggered Arrays
- ^ Siebert, William McC. (1985). Circuits, signals, and systems. MIT Press. p. 402. ISBN 978-0-262-19229-3.
- ^ Marton, L.; Marton, Claire (1990). Advances in Electronics and Electron Physics. Academic Press. p. 369. ISBN 978-0-12-014650-5.
- ^ Kuzmany, Hans (1998). Solid-state spectroscopy. Springer. p. 14. ISBN 978-3-540-63913-8.
- ^ Pribram, Karl H.; Yasue, Kunio; Jibu, Mari (1991). Brain and perception. Lawrence Erlbaum Associates. p. 26. ISBN 978-0-89859-995-4.
Further reading[edit]
- William E. Boyce; Richard C. DiPrima (2005). Elementary Differential Equations and Boundary Value Problems (8th ed.). New Jersey: John Wiley & Sons, Inc. ISBN 0-471-43338-1.
- Joseph Fourier, translated by Alexander Freeman (2003). The Analytical Theory of Heat. Dover Publications. ISBN 0-486-49531-0. 2003 unabridged republication of the 1878 English translation by Alexander Freeman of Fourier’s work Théorie Analytique de la Chaleur, originally published in 1822.
- Enrique A. Gonzalez-Velasco (1992). “Connections in Mathematical Analysis: The Case of Fourier Series”. American Mathematical Monthly. 99 (5): 427–441. doi:10.2307/2325087. JSTOR 2325087.
- Fetter, Alexander L.; Walecka, John Dirk (2003). Theoretical Mechanics of Particles and Continua. Courier. ISBN 978-0-486-43261-8.
- Felix Klein, Development of mathematics in the 19th century. Mathsci Press Brookline, Mass, 1979. Translated by M. Ackerman from Vorlesungen über die Entwicklung der Mathematik im 19 Jahrhundert, Springer, Berlin, 1928.
- Walter Rudin (1976). Principles of mathematical analysis (3rd ed.). New York: McGraw-Hill, Inc. ISBN 0-07-054235-X.
- A. Zygmund (2002). Trigonometric Series (third ed.). Cambridge: Cambridge University Press. ISBN 0-521-89053-5. The first edition was published in 1935.
External links[edit]
- “Fourier series”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Hobson, Ernest (1911). “Fourier’s Series” . Encyclopædia Britannica. Vol. 10 (11th ed.). pp. 753–758.
- Weisstein, Eric W. “Fourier Series”. MathWorld.
- Joseph Fourier – A site on Fourier’s life which was used for the historical section of this article at the Wayback Machine (archived December 5, 2001)
This article incorporates material from example of Fourier series on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
Преобразование Фурье непериодических сигналов
Содержание
Обнаружили ошибку?
Выделите ее мышью
и нажмите

Предельный переход от ряда Фурье к преобразованию Фурье
Использование периодических функций для представления периодических сигналов выглядит вполне логичным и позволяет перевести анализ в частотную область. Таким образом, мы можем заменить сигнал 

(1)
где 


Однако, периодические функции могут быть использованы и для частотного представления непериодических сигналов.
В данном разделе мы произведем переход от ряда Фурье (1) к интегральному преобразованию Фурье для непериодических сигналов 
Для начала рассмотрим, что будет происходить, если мы будем увеличивать период повторения 






Рисунок 1. Амплитудный спектр 
при увеличении периода повторения 
Из рисунка 1 видно, что при увеличении периода 



При увеличении периода повторения 


Подставим в уравнение (1) для сигнала 

(2)
Непериодический сигнал 

(3)
Учитывая, что 

(4)
Значения частот дискретных гармоник:
(5)
и (3) с учетом (4) и (5):
(6)
Сумма бесконечно-малых площадей, где 


(7)
Окончательно, из выражения (7) можно выделить пару интегральных преобразований Фурье для непериодического сигнала:
(8)
(9)
Уравнение (8) определяет прямое преобразование Фурье непериодического сигнала. Прямое преобразование Фурье обозначается оператором ![mathcal{F}[bullet]](https://ru.dsplib.org/content/fourier_transform/img/eqlin-15.png)



Выражение (9) представляет собой обратное преобразование Фурье, которое обозначается оператором ![mathcal{F}^{-1}[bullet]](https://ru.dsplib.org/content/fourier_transform/img/eqlin-17.png)


В терминах частоты 

(10)
(11)
Пояснения понятия спектральной плотности сигнала
Часто спектральную плотность непериодического сигала 

Для пояснения отличия понятия спектра периодического сигнала от спектральной плотности непериодического сигнала рассмотрим следующую аналогию.
Пусть имеется стержень длины 



Рисунок 2. Стрежень состоящий из 
сплава меди и алюминия в различных пропорциях
Каждый сегмент имеет постоянную плотность 


(12)
где 
Также как стержень в приведенном примере состоит из отдельных сегментов конечных масс, так и периодический сигнал состоит из суммы дискретных гармоник конечной амплитуды, в соответствии с рядом Фурье.
Предположим теперь, что такой же стержень представляет собой непрерывно-меняющийся по длине сплав меди и алюминия, как это показано на рисунке 3.

Рисунок 3. Стрежень состоящий из непрерывного по длине
сплава меди и алюминия
Плотность такого стержня непрерывно уменьшается по длине. Тогда массу мы не можем представить как сумму конечных дискретных масс, а только как интеграл плотности 
(13)
Другими словами, конечная масса 



Аналогично, спектральная плотность 





Единица измерения плотности 



Таким образом, размерность спектральной плотности непериодического сигнала отличается от размерности спектра периодического сигнала и эти два термина отождествлять не следует.
Связь спектральной плотности непериодического сигнала и огибающей коэффициентов ряда Фурье
В предыдущем параграфе мы привели пояснения понятия спектральной плотности непериодического сигнала физической аналогией с плотностью непрерывного сплава двух металлов. Мы говорили, что спектральная плотность 




И хотя физический смысл спектральной плотности отличается от физического смысла спектра периодического сигнала, равно как масса стержня отличается от плотности, но оба этих представления находятся в тесной связи друг с другом. Эту взаимосвязь спектра периодического сигнала и спектральной плотности мы проследим на примере одиночного импульса 

Пример одиночного импульса 



Рисунок 4. Периодическое повторение одиночного импульса
Периодический сигнал 


Преобразование Фурье 

(14)
Периодический сигнал 



(15)
Сравнивая (14) и (15) на фиксированной секте частот 
(16)
Таким образом, если периодический сигнал представляет собой повторенный импульс 






Непрерывная по частоте спектральная плотность, деленная на период повторения 


Рисунок 5. Cпектральная плотность 

Забегая немного вперед, можем заметить, что периодическое повторение одиночного импульса привело к дискретизации непрерывной по частоте огибающей 

Условия существования преобразования Фурье
Мы осуществили передельный переход от периодического сигнала 

При увеличении периода 

Таким образом мы можем утверждать, что преобразование Фурье (8) и (9) существует для всех ограниченных во времени сигналов 
выполняется условие Дирихле
[1, стр. 165].
Представим теперь, что сигнал 
(17)
Говорят, что 

Рисунок 6. График функции 
В качестве примера абсолютно интегрируемой функции можно привести 






Таким образом, функция 

Можно заметить, что всякий ограниченный во времени сигнал, удовлетворяющий условиям Дирихле также является абсолютно интегрируемым.
Приведенные рассуждения не являются строгим математическим доказательством условий существования преобразования Фурье, а скорее дают интуитивно-понятное разъяснение (17). Строгое доказательство условий существования преобразования Фурье можно найти [1, стр. 199] или в [2, стр. 511].
Выводы
В данном разделе мы рассмотрели предельных переход от периодического сигнала
к непериодическому и получили выражения для прямого и обратного интегрального преобразования Фурье.
Мы отметили, что в отличии от спектра периодических сигналов, преобразование Фурье непериодического сигнала возвращает спектральную плотность сигнала, выраженную в единицах измерения сигнала, деленного на частоту. Были даны необходимые пояснения к понятию спектральной плотности.
Также были рассмотрены условия существования преобразования Фурье.
В следующих разделе мы рассмотрим
свойства преобразования Фурье,
a также
спектральные плотности некоторых сигналов.
Смотри также
Представление периодических сигналов рядом Фурье
Некоторые свойства разложения периодических сигналов в ряд Фурье
Свойства преобразования Фурье
Спектральные плотности некоторых сигналов
Список литературы
[1]
Теория рядов.
Москва, Наука, Главная редакция физико-математической литературы, 1979, 408 с.
[2]
Будак, Б.М., Фомин, С.В.
Кратные интегралы и ряды.
Москва, Наука, 1965, 608 c.
[3]
Баскаков, С.И.
Радиотехнические цепи и сигналы.
Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4
[4]
Гоноровский И.С.
Радиотехнические цепи и сигналы
Москва, Советское радио, 1977, 608 c.
[5]
Дёч, Г.
Руководство по практическому применению преобразования Лапласа.
Москва, Наука, 1965, 288 c.
[6]
Bracewell R.
The Fourier Transform and Its Applications
McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6
Последнее изменение страницы: 12.05.2022 (19:42:44)
Страница создана Latex to HTML translator ver. 5.20.11.14
Ряд Фурье́ — представление функции 

Этот ряд может быть также записан в виде
где
— амплитуда
-го гармонического колебания,
— круговая частота гармонического колебания,
— начальная фаза
-го колебания,
—
-я комплексная амплитуда
В более общем виде, рядом Фурье элемента некоторого пространства функций называется разложение этого элемента по полной системе ортонормированных функций или другими словами по базису, состоящему из ортогональных функций. В зависимости от используемого вида интегрирования говорят о рядах Фурье — Римана, Фурье — Лебега и т. п.[1]
Существует множество систем ортогональных многочленов и других ортогональных функций (например, функции Хаара, Уолша и Котельникова), по которым может быть произведено разложение функции в ряд Фурье.
Разложение функции в ряд Фурье является мощным инструментом при решении самых разных задач благодаря тому, что ряд Фурье прозрачным образом ведёт себя при дифференцировании, интегрировании, сдвиге функции по аргументу и свёртке функций.
Существуют многочисленные обобщения рядов Фурье в различных разделах математики. Например, любую функцию на конечной группе можно разложить в ряд, аналогичный ряду Фурье, по матричным элементам неприводимых представлений этой группы (теорема полноты).
История[править | править код]
Ряд Фурье назван в честь французского математика Жана-Батиста Жозефа Фурье (1768—1830), внесшего важный вклад в изучение тригонометрических рядов после предварительных исследований Леонарда Эйлера, Жана Лерона д’Аламбера и Даниила Бернулли[2]. Фурье представил ряд с целью решения уравнения теплопроводности в металлической пластине, написав свои первоначальные результаты в своем «Воспоминании о распространении тепла в твердых телах» («Трактат о распространении тепла в твердых телах») и опубликовав в Аналитической теории тепла (Théorie analytique de la chaleur) в 1822 году. В Воспоминании приведен анализ Фурье, в частности ряд Фурье. Благодаря исследованиям Фурье был установлен факт того, что произвольная (непрерывная)[3] функция может быть представлена тригонометрическим рядом. Первое объявление об этом великом открытии было сделано Фурье в 1807 году перед Французской академией[4]. Ранние идеи разложения периодической функции на сумму простых осциллирующих функций относятся к 3 веку до нашей эры, когда древние астрономы предложили эмпирическую модель движения планет, основанную на семействах и эпициклах.
Уравнение теплопроводности является уравнением в частных производных. До работы Фурье в общем случае не было известно решение уравнения теплопроводности, хотя были известны конкретные решения, если бы источник тепла вел себя простым образом, в частности, если источником тепла была волна синуса или косинуса. Эти простые решения теперь иногда называют собственными решениями. Идея Фурье состояла в том, чтобы смоделировать сложный источник тепла как суперпозицию (или линейную комбинацию) простых синусоидальных и косинусных волн и записать решение как суперпозицию соответствующих собственных решений. Эта суперпозиция или линейная комбинация называется рядом Фурье.
С современной точки зрения, результаты Фурье несколько неформальны из-за отсутствия точного понятия функции и интеграла в начале девятнадцатого века. Позднее Петер Густав Лежён Дирихле[5] и Бернхард Риман[6][7][8] выразили результаты Фурье с большей точностью и формальностью.
Хотя первоначальной мотивацией было решение уравнения теплопроводности, позже стало очевидно, что те же методы можно применять к широкому кругу математических и физических задач, особенно тех, которые включают линейные дифференциальные уравнения с постоянными коэффициентами, для которых собственные решения являются синусоидами. Ряд Фурье имеет много применений в области электротехники, вибрации анализа, акустики, оптики, обработки сигналов, обработки изображений, квантовой механики, эконометрики[9], теории перекрытия-оболочки[10] и т. д.
Тригонометрический ряд Фурье[править | править код]
Тригонометрическим рядом Фурье функции ![{displaystyle fin {mathcal {L}}([-pi ,pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92aa58d626b8727d9d8907f6d7187afba35d3ac7)
![{displaystyle ([-pi ,pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29ff6ff22577090b4ccc15d2d0644494c12a43a2)
(1)
где
Числа 




![{displaystyle fin {mathcal {L}}([-pi ,pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92aa58d626b8727d9d8907f6d7187afba35d3ac7)




![[-pi,pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)


Ряд (1) для функции 
![{displaystyle {mathcal {L}}_{2}([-pi ,pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dccc9dba55628dc13689087f3a616e08cff40331)

,
то их среднеквадратичное отклонение от функции 
.
Несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно.
Часто при работе с рядами Фурье бывает удобнее в качестве базиса использовать вместо синусов и косинусов экспоненты мнимого аргумента. Мы рассматриваем пространство ![{displaystyle {mathcal {L}}^{2}([-pi ,pi ],mathbb {C} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acab138aad0d81ddb7f1b8fb5ab32358305f1fb2)
.
Мы также рассматриваем систему функций
-
.
Как и прежде, эти функции являются попарно ортогональными и образуют полную систему, и, таким образом, любая функция ![{displaystyle fin {mathcal {L}}^{2}([-pi ,pi ],mathbb {C} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9dd9f8be496e976aa4264b3208bbbd1ad98fe36)
,
где ряд в правой части сходится к 
![L^2([-pi,pi],mathbb{C})](https://wikimedia.org/api/rest_v1/media/math/render/svg/31dbda1e2403eda880c8a98c040056904747f933)
.
Коэффициенты 
Для вещественнозначной функции коэффициенты 

Обобщения[править | править код]
Ряды Фурье в гильбертовом пространстве[править | править код]
Описанную выше конструкцию можно обобщить со случая пространства ![L^2[-pi,pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/20068d1913d7c592e020af9f2b46f4654ae2fc27)

и 



Домножим это выражение на 


Числа
называются координатами, или коэффициентами Фурье элемента 

называется рядом Фурье элемента 

Ряд Фурье любого элемента 



-
.
Если эти условия не выполняются, то сумма ряда Фурье элемента 

Двойственность Понтрягина[править | править код]
При обобщении теории рядов Фурье на случай гильбертовых пространств теряются свойства, выражающие связь рядов Фурье со свёрткой — то, что коэффициенты Фурье свертки функций являются почленными произведениями их коэффициентов Фурье, и наоборот, коэффициенты Фурье произведения представляются сверткой коэффициентов Фурье сомножителей. Эти свойства являются ключевыми для приложений теории Фурье к решению дифференциальных, интегральных и других функциональных уравнений. Поэтому большой интерес представляют такие обобщения теории рядов Фурье, при которых эти свойства сохраняются. Таким обобщением является теория двойственности Понтрягина. Она рассматривает функции, заданные на локально-компактных абелевых группах. Аналогом ряда Фурье такой функции будет функция, заданная на двойственной группе.
Сходимость ряда Фурье[править | править код]
Обзор результатов о сходимости ряда Фурье[править | править код]
Обозначим через 

.
Далее обсуждается сходимость последовательности функций 



![[-pi,pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)
- Если
, то последовательность
сходится к функции
в смысле
. Кроме того,
являются наилучшим (в смысле расстояния в
) приближением функции
тригонометрическим многочленом степени не выше
.
- Сходимость ряда Фурье в заданной точке
— локальное свойство, то есть, если функции
и
совпадают в некоторой окрестности
, то последовательности
и
либо одновременно расходятся, либо одновременно сходятся, и в этом случае их пределы совпадают. (Принцип локализации).
- Если функция
дифференцируема в точке
, то её ряд Фурье в этой точке сходится к
. Более точные достаточные условия в терминах гладкости функции
задаются признаком Дини.
- Функция, непрерывная в точке
, может иметь расходящийся в ней ряд Фурье. Однако, если он сходится, то непременно к
. Это следует из того, что для непрерывной в
функции
последовательность
сходится по Чезаро к
.
- Если функция
разрывна в точке
, но имеет пределы в этой точке справа и слева
то при некоторых дополнительных условиях
сходятся к
. Подробнее см. модифицированный признак Дини.
- Теорема Карлесона: если
, то её ряд Фурье сходится к ней почти всюду. Это верно и если
. Однако, существуют функции из
, ряд Фурье которых расходится во всех точках (пример такой функции построен Колмогоровым[11]).
- Зафиксируем точку
. Тогда множество всех непрерывных функций, ряд Фурье которых сходится в этой точке, является множеством первой категории в пространстве
. В некотором смысле это означает, что «типичная» непрерывная функция имеет расходящийся ряд Фурье.
Убывание коэффициентов Фурье и аналитичность функции[править | править код]
Существует фундаментальная связь между аналитичностью функции и скоростью убывания её коэффициентов Фурье. Чем «лучше» функция, тем быстрее её коэффициенты стремятся к нулю, и наоборот. Степенное убывание коэффициентов Фурье присуще функциям класса 
См. также[править | править код]
- Преобразование Фурье
- Быстрое преобразование Фурье
- Тригонометрический ряд
- Признак Жордана
- Признак Дини
- Числовой ряд
- АТС-теорема
- Натуральный звукоряд
- Явление Гиббса[en]
Примечания[править | править код]
- ↑ Математический энциклопедический словарь. — М.: «Сов. энциклопедия », 1988. — С. 619.
- ↑ Fetter, Alexander L. Theoretical Mechanics of Particles and Continua / Alexander L. Fetter, John Dirk Walecka. — Courier, 2003. — P. 209—210. — ISBN 978-0-486-43261-8. Архивная копия от 18 апреля 2021 на Wayback Machine
- ↑ Stillwell, John (англ.) (рус.. Logic and the philosophy of mathematics in the nineteenth century // Routledge History of Philosophy / Ten, C. L.. — Routledge, 2013. — Т. Volume VII: The Nineteenth Century. — С. 204. — ISBN 978-1-134-92880-4. Архивная копия от 16 мая 2020 на Wayback Machine
- ↑ Florian Cajori. A History of Mathematics. — Macmillan, 1893. — С. 283.
- ↑ Lejeune-Dirichlet, Peter Gustav (англ.) (рус.. Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données (фр.) // Journal für die reine und angewandte Mathematik. — 1829. — Vol. 4. — P. 157—169. — arXiv:0806.1294.
- ↑ Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe (неопр.). Habilitationsschrift, Göttingen; 1854. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, vol. 13, 1867. Published posthumously for Riemann by Richard Dedekind. Архивировано 20 мая 2008 года.
- ↑ Mascre, D. & Riemann, Bernhard (1867), Posthumous Thesis on the Representation of Functions by Trigonometric Series, in Grattan-Guinness, Ivor, Landmark Writings in Western Mathematics 1640–1940, Elsevier, 2005, <https://books.google.com/books?id=UdGBy8iLpocC>
- ↑ Remmert, Reinhold. Theory of Complex Functions: Readings in Mathematics (англ.). — Springer, 1991. — P. 29. Архивная копия от 16 мая 2020 на Wayback Machine
- ↑ Nerlove, Marc; Grether, David M.; Carvalho, Jose L. Analysis of Economic Time Series. Economic Theory, Econometrics, and Mathematical Economics (англ.). — Elsevier, 1995. — ISBN 0-12-515751-7.
- ↑ Flugge, Wilhelm. Statik und Dynamik der Schalen (нем.). — Berlin: Springer-Verlag, 1957. Архивная копия от 14 мая 2020 на Wayback Machine
- ↑ В. М. Тихомиров, В. В. Успенский. Пеpвые филдсовские лауpеаты и советская математика 30-х годов. I. — Матем. просв., сер. 3, 2, МЦНМО, М., 1998, 21-40.
Литература[править | править код]
- Жук В. В., Натансон Г. И. Тригонометрические ряды Фурье и элементы теории аппроксимации. — Л.: Изд-во Ленингр. ун-та, 1983. — 188 с.
- Рудин У. Основы математического анализа. — 1976.
- Пискунов Н. С. Дифференциальное и интегральное исчисления для ВТУЗов. — М.: «Наука», 1964. — Т. 2.
- Зигмунд А. Тригонометрические ряды. — М.: «Мир», 1965. — Т. 1.
- Харди Г. Х., Рогозинский В. В.ruen. Ряды Фурье. — М.: Физматгиз, 1959.
Ссылки[править | править код]
- Представление периодических сигналов. Ряд Фурье.
- Некоторые свойства разложения периодических сигналов в ряд Фурье.

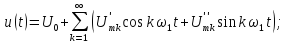
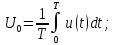
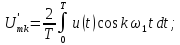

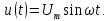
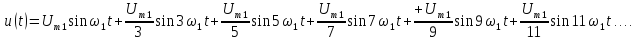
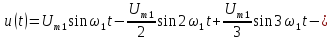
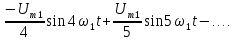


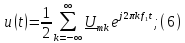

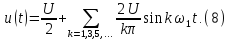

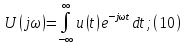
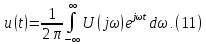
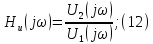
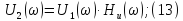
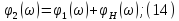


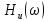
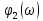

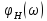

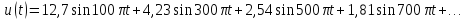

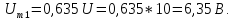

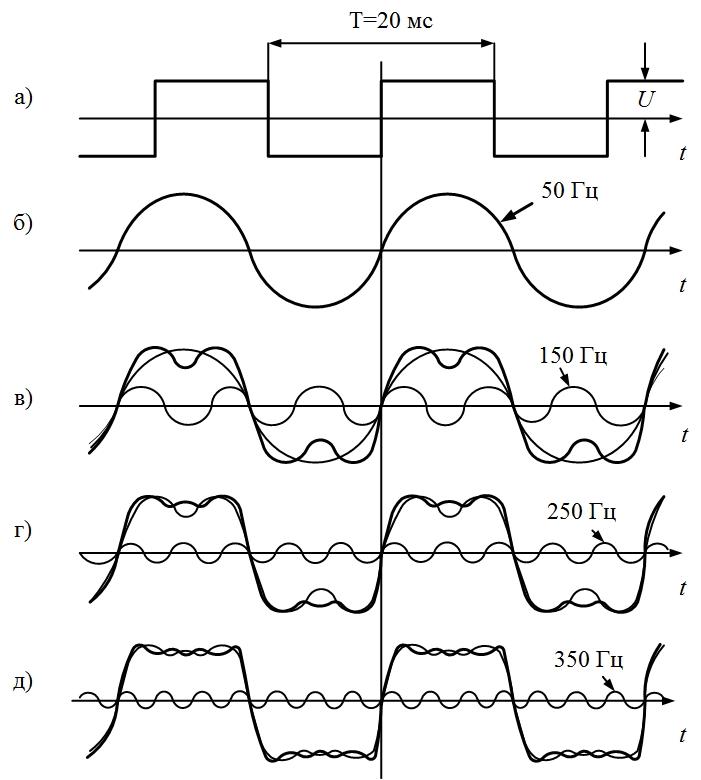
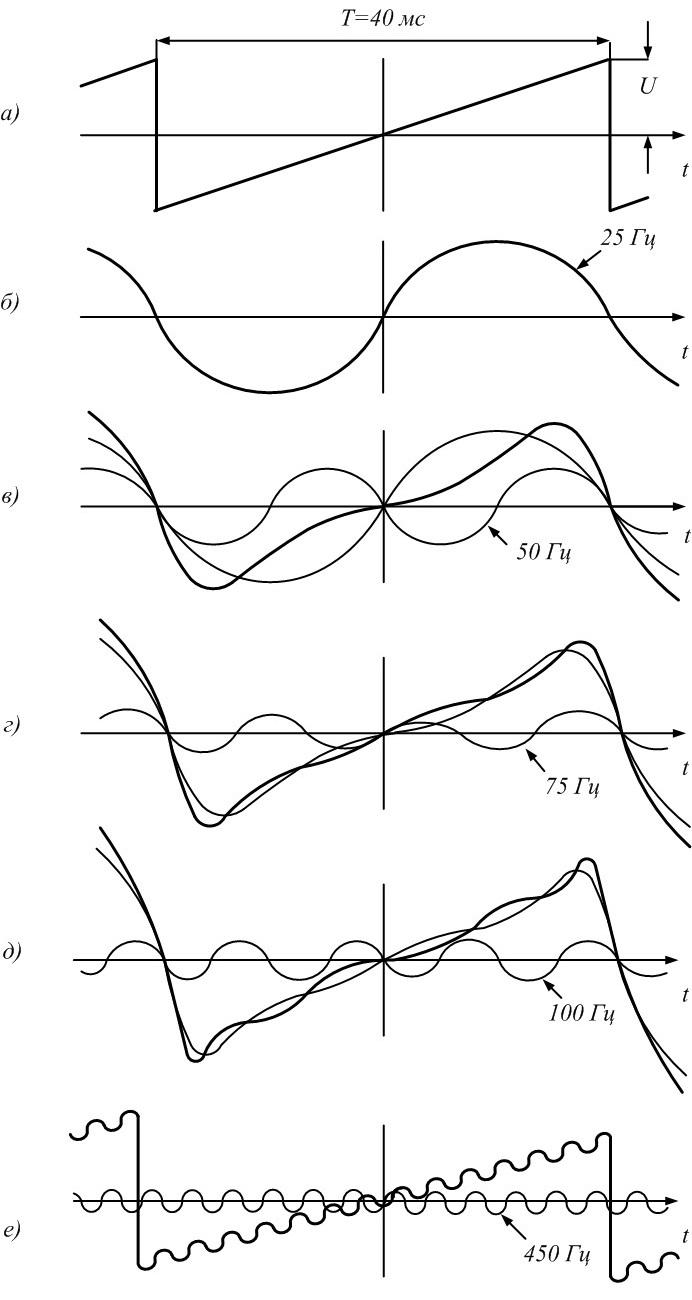


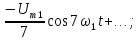
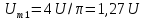
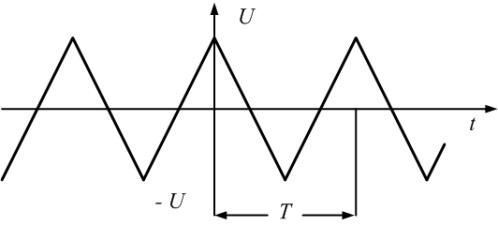
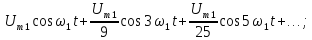


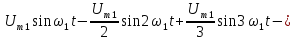

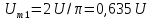
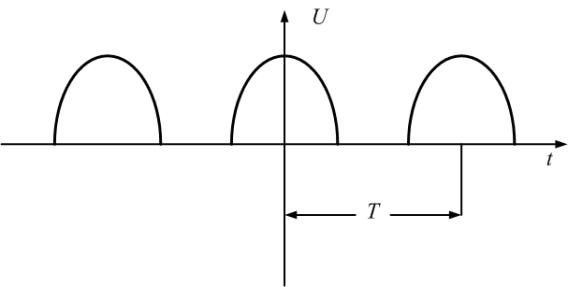
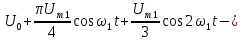
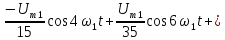


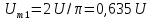
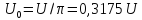
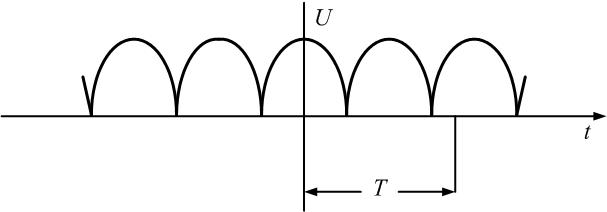
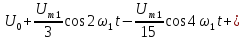

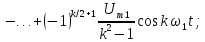
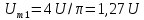

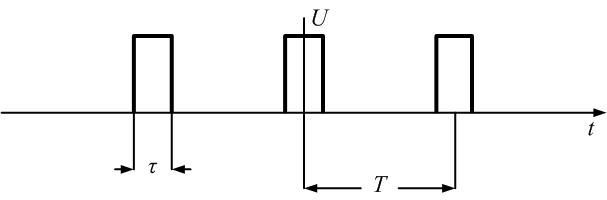
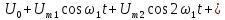
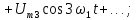
 ;
; ;
;
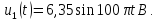

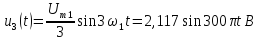
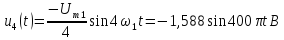

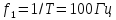
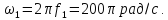
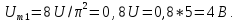


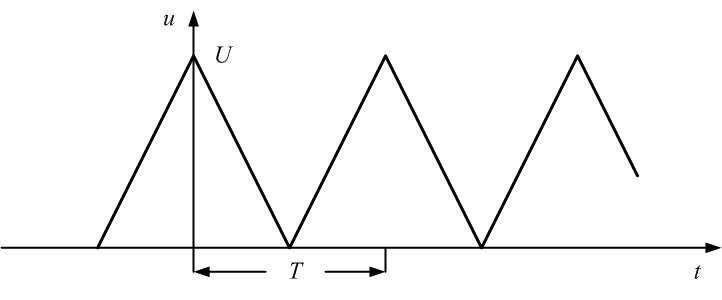

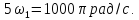
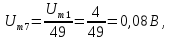


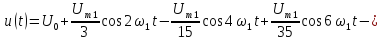
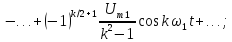
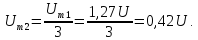

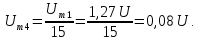
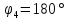
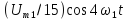


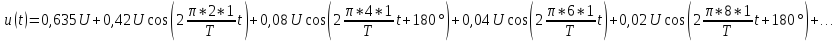
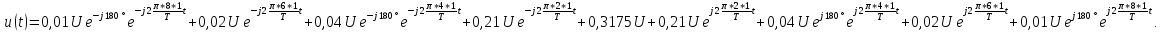
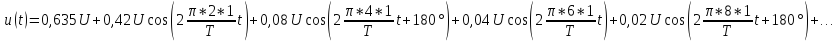
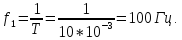
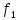
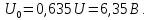


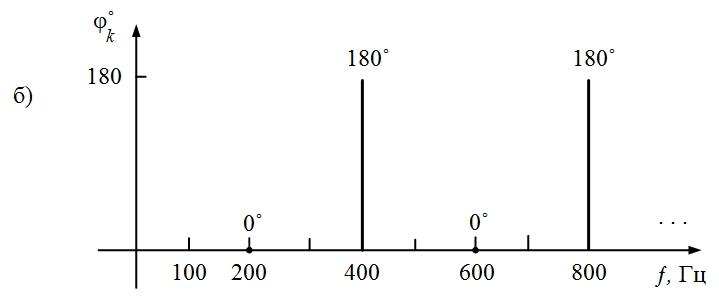
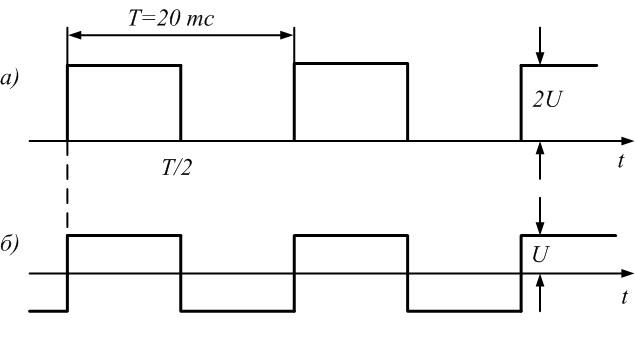
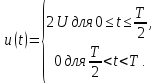
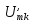



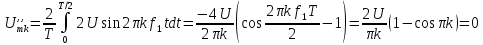
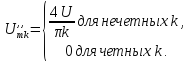
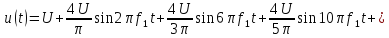



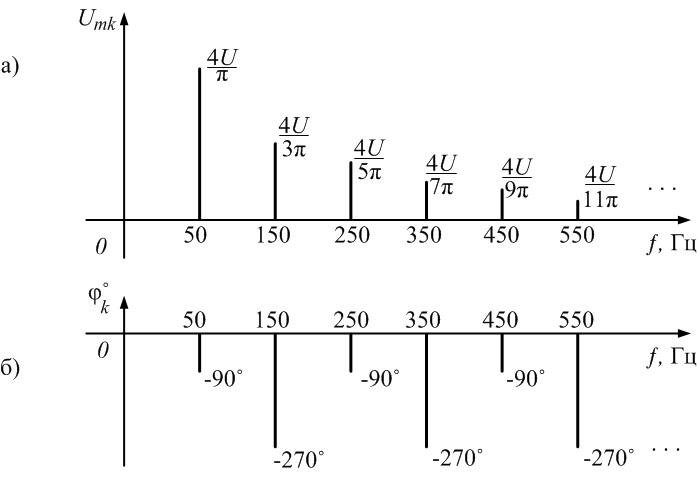





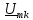
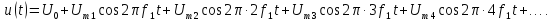
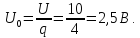

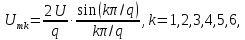

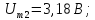

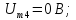
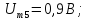
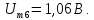
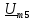


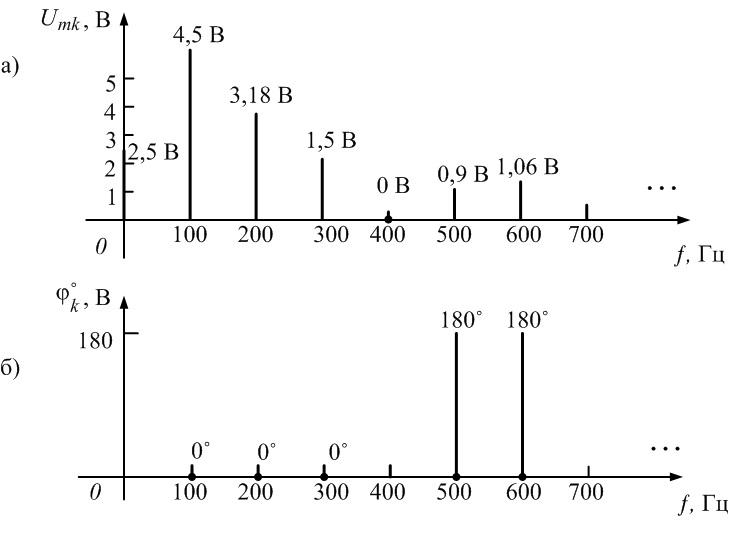
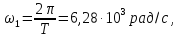
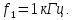

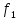



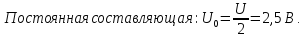
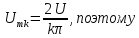
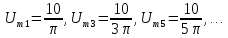

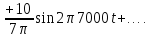

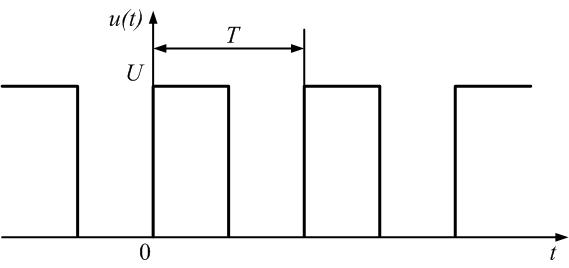
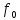
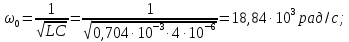



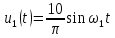
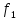
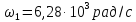
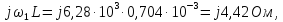
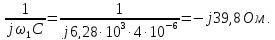


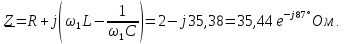






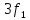
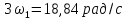



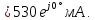




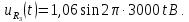
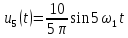





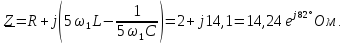
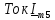
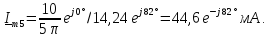
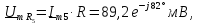
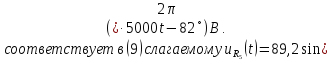

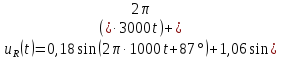

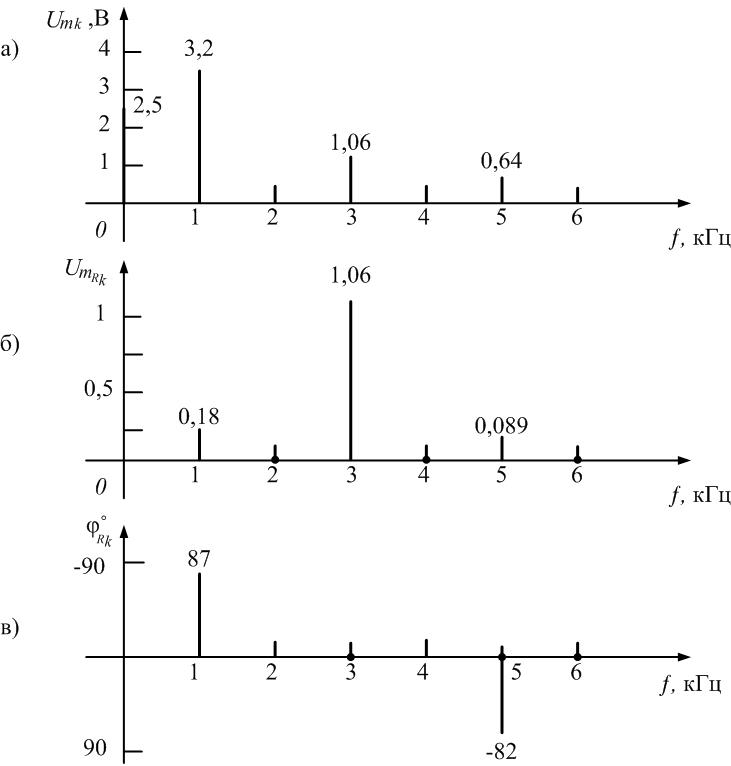

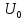

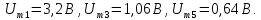
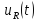
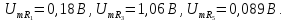

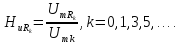

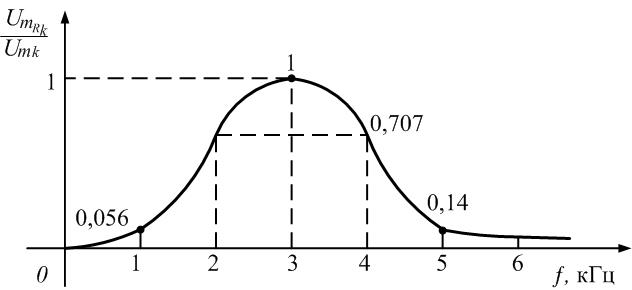
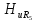
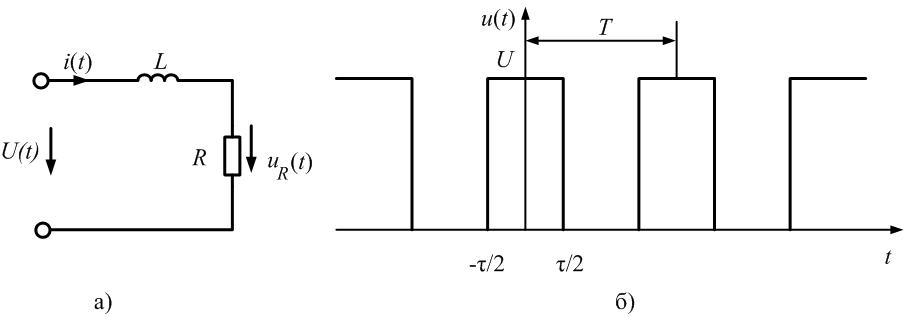

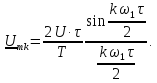
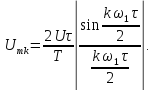
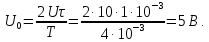

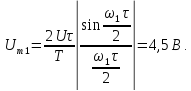
 =0,5
=0,5 =3,28
=3,28 =0,75
=0,75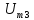 =1,5
=1,5 =1
=1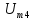 =0
=0 =1,25
=1,25 =0,9
=0,9 =1,5
=1,5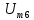 =1,06
=1,06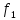 =1,75
=1,75 =0,64
=0,64 =2,0
=2,0 =0
=0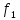 =2,25
=2,25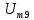 =0,5
=0,5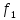 =2,5
=2,5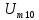 =0,64
=0,64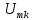

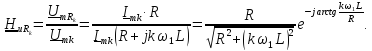
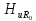 =1;
=1; =0,95;
=0,95;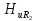 =0,85;
=0,85;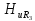 =0,73;
=0,73; =0,62;
=0,62; =0,54;
=0,54;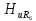 =0,47;
=0,47;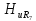 =0,41;
=0,41;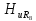 =0,37;
=0,37;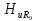 =0,33;
=0,33; =0,3.
=0,3.
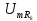




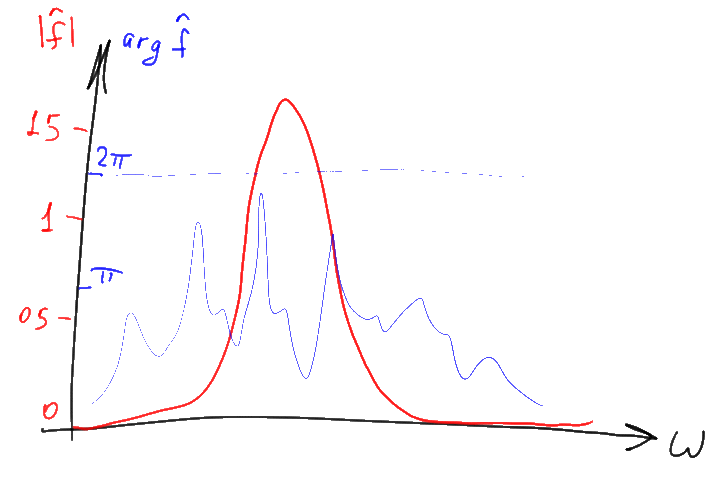
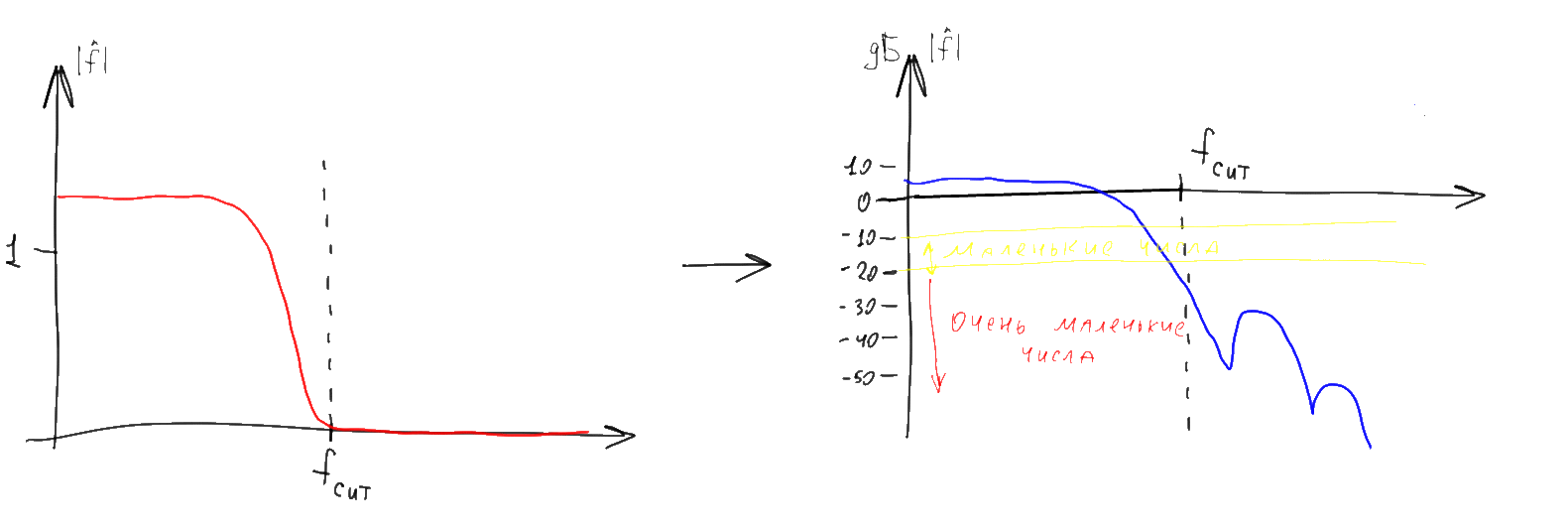
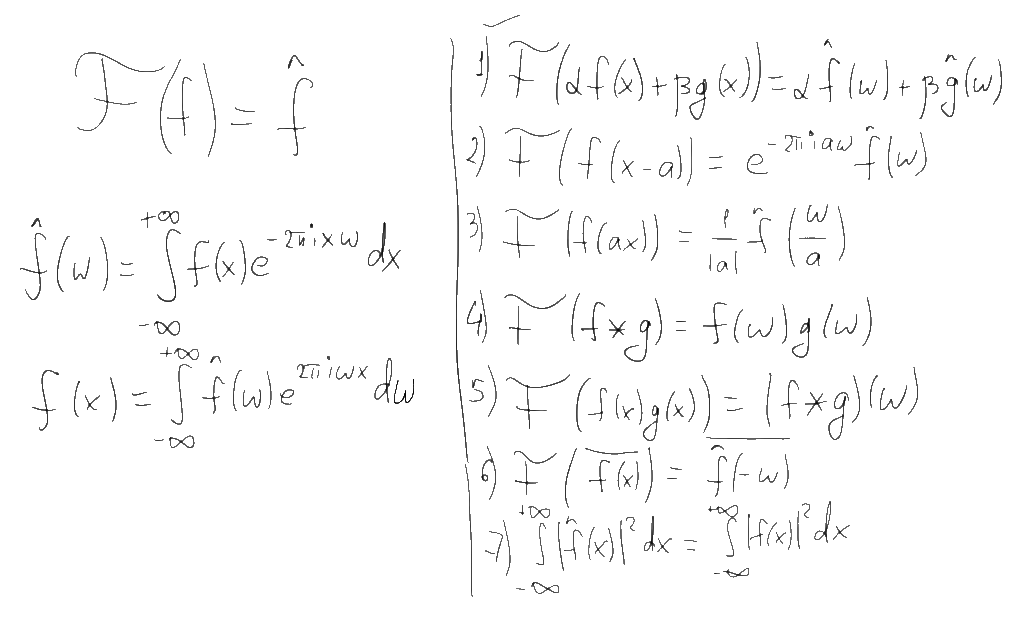

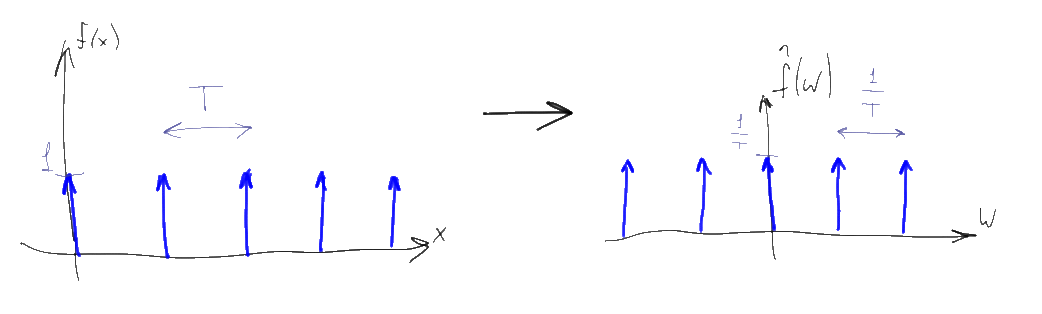

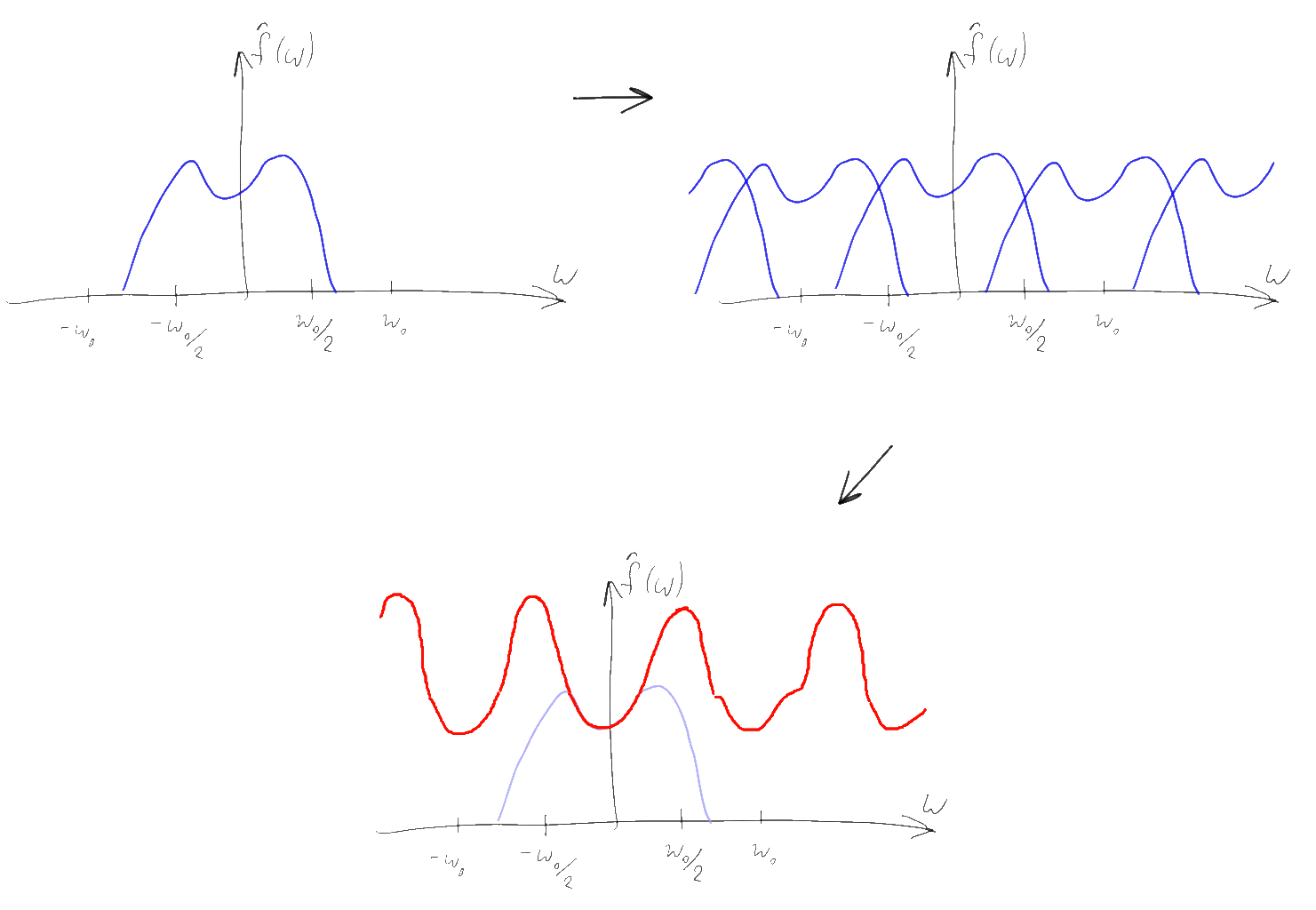
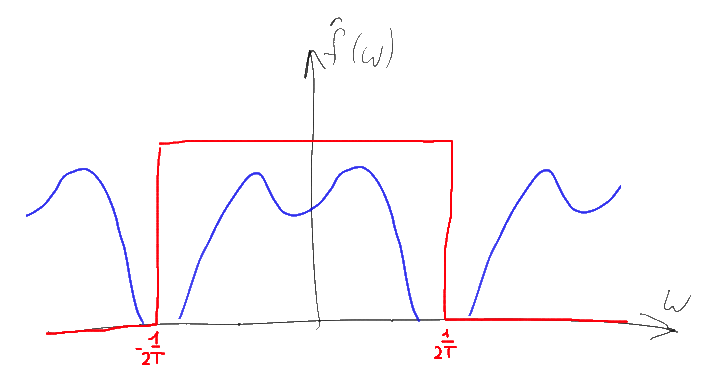

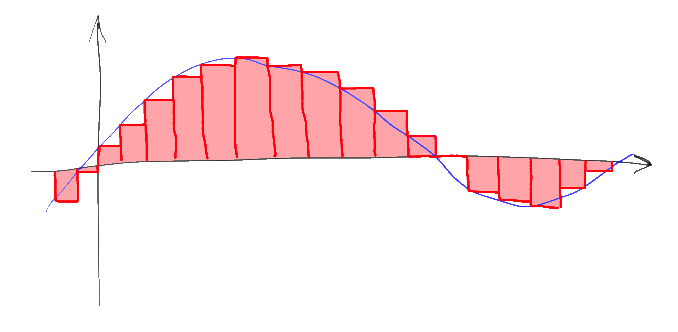
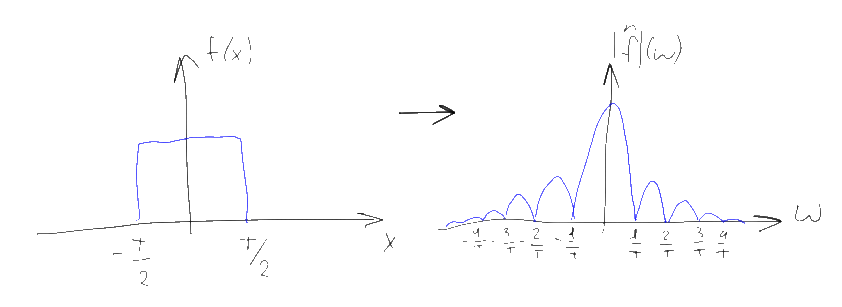
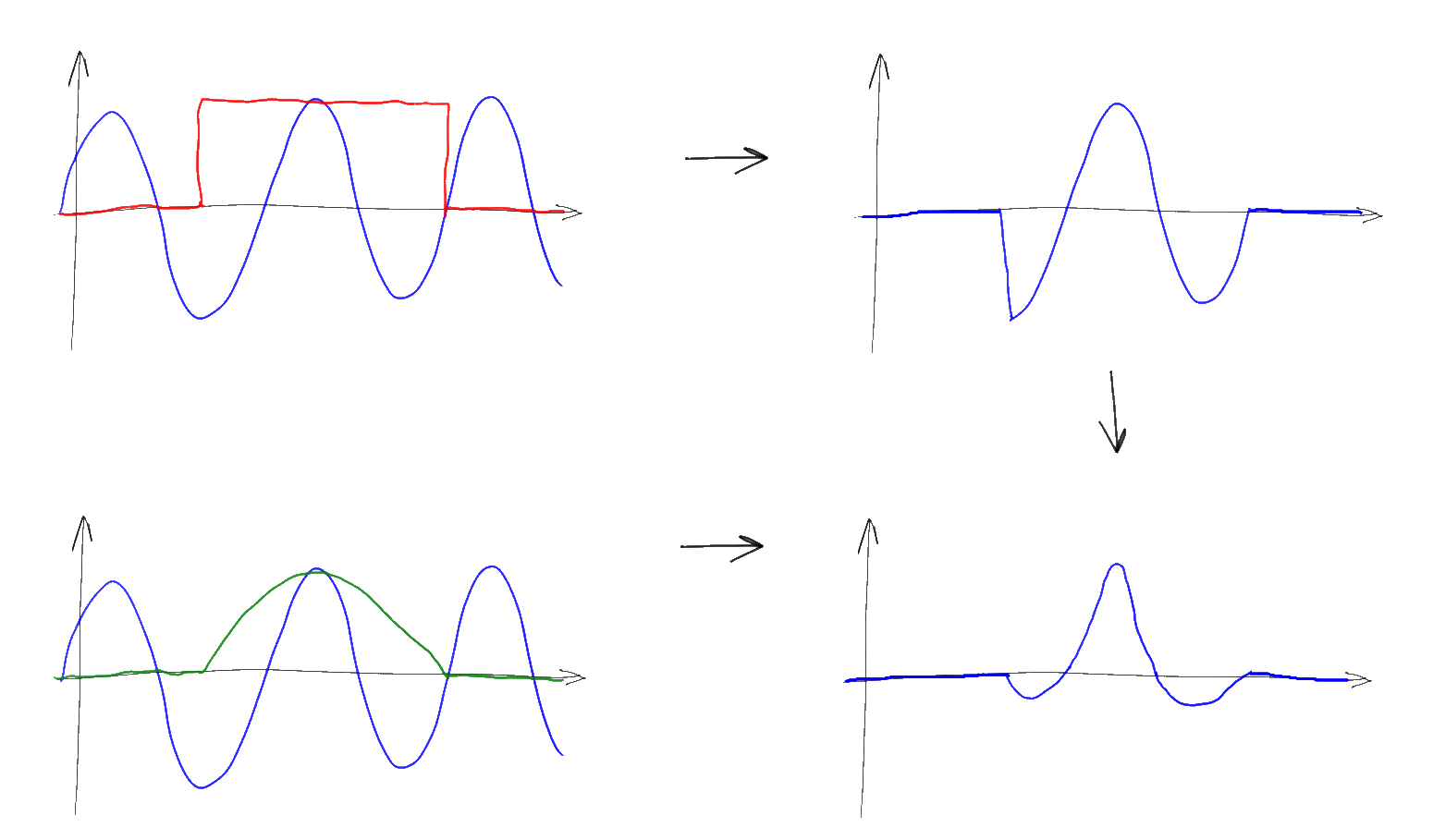











![(-pi ,pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)



![{displaystyle {begin{aligned}A_{n}&={frac {1}{pi }}int _{-pi }^{pi }s(x)cos(nx),dx=0,quad ngeq 0.\[4pt]B_{n}&={frac {1}{pi }}int _{-pi }^{pi }s(x)sin(nx),dx\[4pt]&=-{frac {2}{pi n}}cos(npi )+{frac {2}{pi ^{2}n^{2}}}sin(npi )\[4pt]&={frac {2,(-1)^{n+1}}{pi n}},quad ngeq 1.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60820ad01df637675beb2c56a9db388cd0539490)
![{displaystyle {begin{aligned}s(x)&=A_{0}+sum _{n=1}^{infty }A_{n}cos left(nxright)+B_{n}sin left(nxright)\[4pt]&={frac {2}{pi }}sum _{n=1}^{infty }{frac {(-1)^{n+1}}{n}}sin(nx),quad mathrm {for} quad x-pi notin 2pi mathbb {Z} .end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cb0668def0fb376e8a1d8541263b10508260a77)




![{displaystyle mathrm {X} _{f}(tau )={tfrac {2}{P}}int _{P}s(x)cdot cos left(2pi f(x-tau )right),dx;quad tau in left[0,{tfrac {2pi }{f}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2868da53c5e3ed8528137f2aaf139400251e74e)
![{displaystyle {begin{aligned}mathrm {X} _{n}(varphi )&={tfrac {2}{P}}int _{P}s(x)cdot cos left(2pi {tfrac {n}{P}}x-varphi right),dx;quad varphi in [0,2pi ]\&=cos(varphi )cdot underbrace {{tfrac {2}{P}}int _{P}s(x)cdot cos left(2pi {tfrac {n}{P}}xright),dx} _{A_{n}}+sin(varphi )cdot underbrace {{tfrac {2}{P}}int _{P}s(x)cdot sin left(2pi {tfrac {n}{P}}xright),dx} _{B_{n}}\&=cos(varphi )cdot A_{n}+sin(varphi )cdot B_{n}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b72e0b83fd20619ddc5f938cf5280cfd3443820)




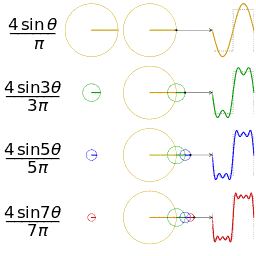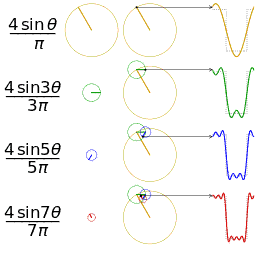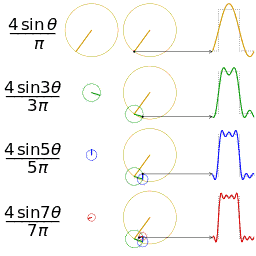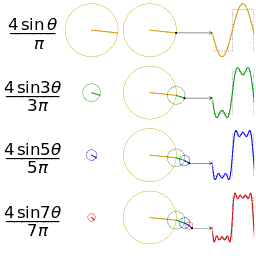


![{displaystyle {begin{aligned}s(x)&=sum _{n=-infty }^{infty }{hat {s}}(n)cdot e^{2pi inx/P}&&{text{common mathematics notation}}\&=sum _{n=-infty }^{infty }S[n]cdot e^{i,2pi nx/P}&&{text{common engineering notation}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e8427f6c9d293e4fd06f52432445973be52c41e)
![{displaystyle S(f) triangleq sum _{n=-infty }^{infty }S[n]cdot delta left(f-{frac {n}{P}}right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)
![{displaystyle {begin{aligned}{mathcal {F}}^{-1}{S(f)}&=int _{-infty }^{infty }left(sum _{n=-infty }^{infty }S[n]cdot delta left(f-{frac {n}{P}}right)right)e^{i2pi fx},df,\[6pt]&=sum _{n=-infty }^{infty }S[n]cdot int _{-infty }^{infty }delta left(f-{frac {n}{P}}right)e^{i2pi fx},df,\[6pt]&=sum _{n=-infty }^{infty }S[n]cdot e^{i,2pi nx/P} triangleq s_{infty }(x).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/446316db0d563e8ceac0da5d5d078b67f0c0f4e5)









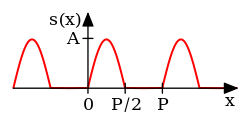

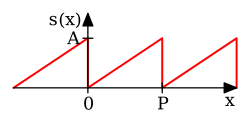




![{displaystyle {begin{aligned}f(x,y)&=sum _{j,kin mathbb {Z} }c_{j,k}e^{ijx}e^{iky},\[5pt]c_{j,k}&={frac {1}{4pi ^{2}}}int _{-pi }^{pi }int _{-pi }^{pi }f(x,y)e^{-ijx}e^{-iky},dx,dy.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aec3723d7051701ab4530dce39f1480cef835981)






![{displaystyle {begin{aligned}h^{mathrm {two} }(m_{1},m_{2},x_{3})&triangleq {frac {1}{a_{2}}}int _{0}^{a_{2}}h^{mathrm {one} }(m_{1},x_{2},x_{3})cdot e^{-i2pi {frac {m_{2}}{a_{2}}}x_{2}},dx_{2}\[12pt]&={frac {1}{a_{2}}}int _{0}^{a_{2}}dx_{2}{frac {1}{a_{1}}}int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})cdot e^{-i2pi left({frac {m_{1}}{a_{1}}}x_{1}+{frac {m_{2}}{a_{2}}}x_{2}right)}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/342f2441863562e2188c632ea98d105ddb4ce5f1)

![{displaystyle {begin{aligned}h^{mathrm {three} }(m_{1},m_{2},m_{3})&triangleq {frac {1}{a_{3}}}int _{0}^{a_{3}}h^{mathrm {two} }(m_{1},m_{2},x_{3})cdot e^{-i2pi {frac {m_{3}}{a_{3}}}x_{3}},dx_{3}\[12pt]&={frac {1}{a_{3}}}int _{0}^{a_{3}}dx_{3}{frac {1}{a_{2}}}int _{0}^{a_{2}}dx_{2}{frac {1}{a_{1}}}int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})cdot e^{-i2pi left({frac {m_{1}}{a_{1}}}x_{1}+{frac {m_{2}}{a_{2}}}x_{2}+{frac {m_{3}}{a_{3}}}x_{3}right)}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a8c3fac5e04d1272c87fd58d3217a691214d09b)






![{displaystyle {begin{vmatrix}{dfrac {partial x_{1}}{partial x}}&{dfrac {partial x_{1}}{partial y}}&{dfrac {partial x_{1}}{partial z}}\[12pt]{dfrac {partial x_{2}}{partial x}}&{dfrac {partial x_{2}}{partial y}}&{dfrac {partial x_{2}}{partial z}}\[12pt]{dfrac {partial x_{3}}{partial x}}&{dfrac {partial x_{3}}{partial y}}&{dfrac {partial x_{3}}{partial z}}end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5df9134486606d6a55c8ec4a96ee3ca353e924)











![{displaystyle s_{_{N}}(x)=sum _{n=-N}^{N}S[n] e^{i{tfrac {2pi }{P}}nx},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b030eaf773387de3787b4a003ef7599624be959)
![{displaystyle p_{_{N}}(x)=sum _{n=-N}^{N}p[n] e^{i{tfrac {2pi }{P}}nx}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a29c02020f3c186b790b680deabe8e985ebcd700)


![{displaystyle sup _{x}|s(x)-s_{_{N}}(x)|leq sum _{|n|>N}|S[n]|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8225d322a5b676b2b1709c2a636dcd092ff11ec)



















































![fin L_2([-pi,pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/a98b9866136e1b2964922c7dcfc2cbe624f051be)






![fin L_p([-pi,pi]), p>1](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dac0ede6f46583238f3753a37400b84d3b708b3)
![L_1([-pi,pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/b93096ec2dab6eecb12e20fc91df465356e074f0)

![C([-pi,pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7f1487c87ed13f3571e53d5f9b5a98f6cb5a270)
