Как найти аналитический сигнал

Лекция № 2

Метрологические
основы методов экологических исследований

После
отбора и подготовки пробы наступает
стадия химического анализа, на которой
и проводят обнаружение компонента или
определение его количества. С этой целью
измеряют аналитический
сигнал. В
отдельных случаях возможно непосредственное
определение содержания. Так, например,
в гравиметрическом методе иногда прямо
измеряют массу определяемого компонента,
например элементарной серы или углерода.
В большинстве же методов аналитическим
сигналом служит среднее из измерений
физической величины на заключительной
стадии анализа,
функционально
связанной с со­держанием определяемого
компонента.
Это может быть сила тока, ЭДС системы,
оптическая плотность, интенсивность
излучения и т. д.

В
случае необходимости обнаружения
какого-либо компонента обычно фиксируют
появление
аналитического сигнала — появление
осадка, окраски, линии в спектре и т. д.
Появление аналитического сигнала должно
быть надежно зафиксировано. При
определении количества компонента
измеряется величина
аналитического
сигнала: масса осадка, сила тока,
интенсивность линии спектра и т. д. Затем
рассчитывают содержание компонента с
использованием функциональной зависимости
аналитический сигнал — содержание:
y=f(c),
которая устанавливается расчетным или
опытным путем и может быть представлена
в виде формулы, таблицы или графика.
Содержание при этом может быть выражено
абсолютным количеством определяемого
компонента в молях, в единицах массы
или через соответствующие концентрации.

При
измерении аналитического сигнала
учитывают наличие полезного аналитического
сигнала, являющегося функцией содержания
определяемого компонента, и аналитического
сигнала
фона,
обусловленного примесями определяемого
компонента и мешающими компонентами в
растворах, растворителях и матрице
образца, а также «шумами», возникающими
в измерительных приборах, усилителях
и другой аппаратуре. Эти шумы не имеют
отношения к определяемому компоненту,
но накладываются на его собственный
аналитический сигнал. Задача аналитика
состоит в том, чтобы максимально снизить
величину аналитического сигнала фона
и, главное, сделать минимальными его
колебания. Обычно аналитический сигнал
фона учитывают при проведении контрольного
(холостого) опыта,
когда через все стадии химического
анализа проводится проба, не содержащая
определяемого компонента. Полезным
сигналом при этом будет аналитический
сигнал, равный разности измеренного
аналитического сигнала и аналитического
сигнала фона

.

Метод градуировочного
графика ,

метод добавок…Метод
стандартов.

На
основании существующей зависимости
между аналитическим сигналом и содержанием
находят концентрацию определяемого
компонента. Обычно при этом используют
методы градуировочного графика,
стандартов или добавок. Описанные в
литературе другие способы определения
содержа­ния компонента, как правило,
являются модификацией этих трех основных
методов.

Наиболее
распространен метод
градуировочного графика.
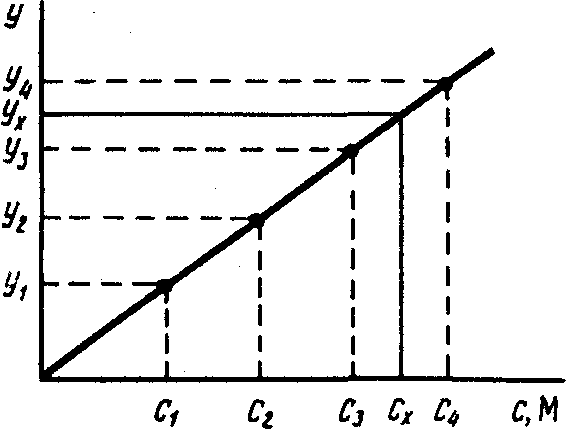
При этом в координатах аналитический
сигнал — содержание компонента строят
график с использованием образцов
сравнения с различным и точно известным
со­держанием определяемого компонента.
Затем, измерив величину аналитиче­ского
сигнала в анализируемой пробе, находят
содержание определяемого компонента
по градуировочному графику (рис. 2.2).

В
методе
стандартов
измеряют аналитический сигнал в образце
сравнения (эталонном образце) с известным
содержанием компонента и в анализируемой
пробе: у_эт
= Sc_эт
и у_х
= Sc_х,
где S
— коэффициент пропорциональности. Если
определенное в идентичных условиях
значение S заранее известно, то ‘можно
провести расчет по формуле c_х
= y_х/S.
Обычно же применяют соотношение у_эт/у_х
= с_эт/с_х,
откуда

Сх=Y_xC_эт/Y_эт

Иногда
используют два эталонных образца, в
которых содержание компонента отличается
от предполагаемого в анализируемой
пробе в одном случае в меньшую, в другом
— в большую сторону. Этот вариант метода
стандартов называют иногда методом
ограничивающих растворов.
Содержание определяемого компонента
рассчитывают по формуле:

C_x=С_эт,1+(С_эт,₂
– С_эт,1)(Y_x
– Y_эт,1)
/ Y_эт,2
– Y_эт,1

В
тех случаях, когда при определении малых
количеств компонента нужно учесть
влияние матрицы образца на величину
аналитического сигнала, часто используют
метод добавок
— расчетный и графический.

Рис.
2.2. Метод градуировочного
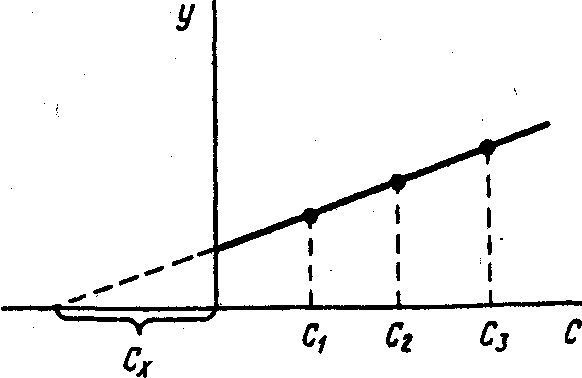
Рис. 2.3. Метод добавок
графика

При
определении содержания расчетным
методом берут две аликвоты раствора
анализируемой пробы. В одну из них вводят
добавку определяемого компонента
известного содержания. В обеих пробах
измеряют аналитический сигнал — Ух ^и
Ух+цоб- Неизвестную концентрацию
определяемого компонента рассчитывают
по формуле

C_x=Y_xV_добС_доб
/
Y_x+добV_доб
+ (Y_x+доб
– Y_x)V

При
определении содержания компонента
графическим методом берут аликвоты
анализируемой пробы: 1, 2, 3, …, п. В аликвоты
2, 3, …, п вводят известные, возрастающие
количества определяемого компонента.
Во всех аликвотах измеряют аналитический
сигнал и строят график в координатах
аналитический сигнал — содержание
определяемого компонента, приняв за
условный нуль содержание определяемого
компонента в аликвоте без добавки
(аликвота 1). Экстраполяция полученной
прямой до пересечения с осью абсцисс
дает отрезок, расположенный влево от
условного нуля координат, величина
которого в выбранном масштабе и единицах
измерения соответст­вует искомому,
содержанию (с^) определяемого компонента
(рис. 2.3).

Метод
стандартов и метод добавок применимы
для линейной градуиро-вочной функции.
Метод градуировочного графика допускает
использование как линейной, так и
нелинейной функций аналитический сигнал
— содержание. В последнем случае
требуется большее число экспериментальных
данных и результат определения содержания
компонента бывает, как правило, менее
точным.

Для
построения градуировочного графика,
наилучшим образом удовлетворяющего
экспериментальным данным, обычно
используют метод наименьших квадратов
(МНК). Основное положение МНК утверждает,
что если для каждой из т экспериментальных
точек провести на оптимальную кривую
прямые, параллельные оси ординат, то
для Оптимальной (теоретической) кривой
сумма квадратов отклонений точек от
кривой ( д,) должна быть минимальной, т.
е.

В
химическом анализе чаще всего используют
прямолинейные градуировочные графики,
построенные для определенного диапазона
определяемых содержаний, т. е. в области
значений, предусмотренных данной
методикой. Уравнение прямой можно
записать в виде у = а + Ъх. Если имеется
т экспериментальных точек (xi>>),
x-iYi,
…, х^Уу,), то, используя постулат МНК
,можем найти параметры а и Ъ прямой,
наилучшим образом удовлетворяющей
экспериментальным данным

Заметим,
что параметры а и Ъ тем точнее и,
следовательно, построенный градуировочный
график тем ближе к теоретическому, чем
в более широком диапазоне определяемых
содержаний строится график и чем большее
число образцов сравнения (эталонов) т
было взято для его построения.

Во
всех методах определения неизвестного
содержания компонента используют
функциональную зависимость у = Sx.
Коэффициент чувствительности S
(иногда его называют просто чувствительность)
характеризует отклик аналитического
сигнала на содержание компонента.
Коэффициент чувствительности — это
значение первой производной градуировочной
функции при данном определенном
содержании. Для прямолинейный
градуировочных графиков – это тангенс
угла наклона прямой (см. рис.2,2)

Чем
больше коэффициент чувствительности
S,
тем меньшие количества компонента можно
обнаруживать и определять, получая один
и тот же аналитический сигнал. Чем выше
S,
тем точнее можно определить одно и то
же количество вещества. Вот почему при
разработке нового метода или методики
химического анализа исследователь,
стремясь увеличить коэффициент
чувствительности, использует различные
приемы: концентрирование, усовершенствование
аппаратуры, создание новых реагентов
и т. п.

Во
всех рассмотренных способах используют
образцы сравнения (эталоны), т. е. образцы,
пробы, растворы с точно установленным
содержанием компонента. Методы анализа,
использующие образцы сравнения — это
так называемые относительные методы
химического анализа. Абсолютных
(безэталонных) методов в аналитической
химии немного — например, методы
гравиметрии, прямой кулонометрии,
некоторые варианты радиохимических
методов.

Образцы
сравнения для относительных методов
анализа могут быть приготовлены из
химически чистых, устойчивых веществ
известного состава (стандартные
вещества). В этом случае содержание
определяемого компонента вычисляют по
химической формуле стандартного
вещества. Возможно приготовление
образцов сравнения в отдельной
лаборатории, учреждении, отрасли, когда
содержание компонента устанавливают
разными методами, на разных приборах
многие аналитики. Наиболее надежные
результаты получают, когда в качестве
образцов сравнения используют стандартные
образцы (СО) — специально приготовленные
материалы, состав и свойства которых
достоверно установлены и официально
аттестованы специальными го­сударственными
метрологическими учреждениями.

В
химических методах анализа
для
качественного и количественного
определения вещества используют его
химические свойства, а также процессы
растворения-осаждения.
Аналитическая реакция представляет
собой химическую реакцию аналитически
активной формы определяемого компонента
с другим веществом – аналитическим
реагентом, в результате чего происходят
видимые или доступные для регистрации
изменения в анализируемой системе. Для
химических методов анализа характерно
использование специальных реагентов,
способных к практически полному
необратимому
взаимодействию с определяемым компонентом.
Само измерение
носит косвенный характер,
поскольку непосредственно определяется
не число определенных частиц, а их
совокупная масса
(в гравиметрии),
расход
реагента (в титриметрии)
или другие параметры, пропорциональные
массе.

Чувствительность
реакции
в аналитической химии может определяться
предельной концентрацией или открываемым
минимумом.

Предельная
концентрация
–
наименьшеая концентрация вещества в
растворе, ниже которой данная аналитическая
реакция не дает положительного результата.
При концентрации определяемого компонента
равной предельной
отмечается
очень слабый, но заметный результат
(появление помутнения, бледной окраски
и т.п.). Чем чувствительнее реакция, тем
меньше предельная концентрация.

Предельная
концентрация может быть выражена в
единицах молярной концентрации
определяемого вещества или как отношение
1 массы определяемого вещества к массе
растворителя. Например, для реакции
определения ионов железа по реакции с
роданид-ионом:

Предельная
концентрация равна 610^-6
моль/л или 1: 310⁶.
Это значит, что можно обнаружить ионы
железа по реакции образования окрашенного
роданида железа при концентрации железа
610^-6
моль/л или при содержании 1 г ионов
железа

в 310⁶
г растворителя (наблюдается едва заметная
розовая окраска) . При меньшей концентрации
железа окрашивания раствора при
добавлении роданида не обнаруживается,
при большей концентрации железа
добавление роданида вызывает появление
хорошо заметной красной окраски раствора.

Открываемый
минимум
–
минимальное количество вещества, которое
может быть обнаружено в данных условиях.
Величина открываемого минимума зависит
от предельной концентрации и объема
раствора. По существу, открываемый
минимум – это масса вещества, которая
содержится в данном объеме раствора
при концентрации раствора равной
предельной концентрации.

Например,
для реакции ионов железа с роданид-ионом
предельная концентрация равна 610^-6
моль/л. Тогда открываемый минимум m
может быть определен, используя
определение молярной концентрации:

;

;

, г

Так,
если для анализа взяты разные объемы
исследуемых растворов, то значения
открываемого минимума также будут
разными:

• Объем исследуемого
  раствора 1 мл

• Объем исследуемого
  раствора 10 мл

.

Чувствительность
реакции зависит от многих факторов:
объема раствора, концентрации, порядка
добавления реактивов, рН и температуры
раствора, условий наблюдения за
результатами реакции и др. Данные
о чувствительности какой-либо реакции,
приведенные без указания условий ее
выполнения, являются величинами весьма
неопределенными и невоспроизводимыми.
Чем чувствительнее реакция, тем больше
возникает трудностей и препятствий при
анализе малых концентраций веществ,
тем больше следует обращать внимания
на самые разные факторы. Так, при
определении чувствительности реакции
или метода приходится считаться с тем
обстоятельством, что в контрольном
опыте с одними только реактивами и
чистой водой также может наблюдаться
слабый результат реакции – бледное
окрашивание в случае цветных реакций,
слабое помутнение в реакциях осаждения
и др. Поэтому при анализе используют
так называемую «холостую
пробу».

Физические
методы анализа – это методы, в которых
аналитический сигнал представляет
собой регистрируемую величину какого-либо
физического свойства вещества либо
результат взаимодействия излучения с
веществом. В
физических методах анализа для получения
аналитического сигнала используется
не аналитическая реакция, но аналитический
процесс.
Например, в ИК-спектроскопии под
аналитическим процессом следует понимать
процесс взаимодействия анализируемого
вещества с внешним по отношению к нему
источником электромагнитного излучения,
сопровождающийся поглощением
характеристических порций энергии –
квантов энергии. Обычно в физических
методах анализа для определения наличия
и величины аналитического сигнала
необходимо определенное устройство –
детектор, входящий в состав соответствующего
аналитического прибора. Физические
методы анализа являются инструментальными
методами.
Измерительное устройство должно
обеспечивать проведение аналитического
процесса, детектирование аналитического
сигнала и его регистрацию (цифровую
при помощи различного вида шкал или
компьютерную с применением специальных
программ обработки экспериментальных
данных).

Физико-химические
методы анализа включают элементы как
физических, так и химических методов
анализа.
Как правило, химические реакции здесь
проводят для получения аналитически
активной формы анализируемого компонента.
Причем, аналитически активная форма
компонента может быть получена как на
стадии подготовки пробы к анализу, так
и на стадии измерений. Аналитический
сигнал является результатом реализации
некоторого аналитического процесса.
Детектирование
аналитического сигнала и его регистрацию
проводят инструментальными методами,
использующими зависимость физических
и физико-химических свойств вещества
от содержания его в объекте анализа.

Х
– аналитический
сигнал.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

1

Аналитический сигнал (аналитическое представление сигнала) — используемое в теории обработки сигналов математическое представление аналогового сигнала в виде комплекснозначной аналитической функции времени. Обычный, действительный сигнал x является при этом действительной частью аналитического представления x_a.

Идея преобразования — оставить лишь неотрицательные частоты в спектре сигнала, достаточные для его восстановления в силу эрмитовой симметрии: .

Аналитический сигнал является обобщением понятия комплексной амплитуды на случай сигналов, отличных от гармонического.

Определение[править | править код]

Пусть x(t) — представляющая сигнал действительнозначная функция, преобразование Фурье (т.е. спектр) которой обозначим X(f),^[1], а u(f) — функция Хевисайда.

Тогда:

содержит лишь неотрицательную часть спектра X(f).

Подвергая полученный спектр обратному преобразованию Фурье, мы и получаем аналитический сигнал:

где * — свёртка,  — преобразование Гильберта функции а означает мнимую единицу.

Примеры[править | править код]

Пусть   для некоторой частоты

Тогда:

Это комплексная функция с возрастающим по времени аргументом.

Практические применения[править | править код]

Устранение «отрицательных частот» используется в аналоговой передаче звука (АМ-радиовещание, аналоговая телефонная связь) для экономии полосы частот.

Примечания[править | править код]

См. также[править | править код]

• Комплексное сопротивление

Внешние ссылки[править | править код]

• Преобразование Гильберта. Аналитический сигнал.
• Преобразование Гильберта. Аналитический сигнал.

В математике и обработке сигналов, аналитический сигнал – это комплексная функция, не имеющая компонентов отрицательной частоты. Реальная и мнимая части аналитического сигнала – это функции с действительными значениями, связанные друг с другом с помощью преобразования Гильберта.

Аналитическое представление функции вещественных значений имеет следующий вид: аналитический сигнал, содержащий исходную функцию и ее преобразование Гильберта. Это представление облегчает многие математические манипуляции. Основная идея заключается в том, что отрицательные частотные компоненты преобразования Фурье (или спектра ) действительной функции являются излишними из-за эрмитовой симметрии функции такой спектр. Эти отрицательные частотные составляющие можно отбросить без потери информации, при условии, что вместо этого вы захотите иметь дело с комплексной функцией. Это делает определенные атрибуты функции более доступными и облегчает получение методов модуляции и демодуляции, таких как односторонняя полоса.

Пока управляемая функция не имеет отрицательных частотных составляющих (то есть она все еще аналитическая), преобразование из комплексного обратно в реальное – это просто вопрос отбрасывания мнимой части. Аналитическое представление является обобщением концепции фазора : в то время как вектор ограничен неизменными во времени амплитудой, фазой и частотой, аналитический сигнал допускает параметры, изменяющиеся во времени.

Содержание

• 1 Определение
  • 1.1 Отрицательные частотные составляющие
• 2 Примеры
  • 2.1 Пример 1
  • 2.2 Пример 2
  • 2.3 Пример 3
• 3 Свойства
  • 3.1 Мгновенная амплитуда и фаза
  • 3.2 Комплексная огибающая / основная полоса
• 4 Расширения аналитического сигнала до сигналов нескольких переменных
  • 4.1 Многомерный аналитический сигнал на основе специального направления
  • 4.2 Моногенный сигнал
• 5 См. Также
  • 5.1 Приложения
• 6 Примечания
• 7 Ссылки
• 8 Дополнительная литература
• 9 Внешние ссылки

Определение

Передаточная функция для создания аналитического сигнала

Если s (t) { displaystyle s (t)}– функция с действительным знаком с преобразованием Фурье S (f) { displaystyle S (f)}, тогда преобразование имеет эрмитову симметрию относительно оси f = 0 { displaystyle f = 0}:

S (- f) = S (f) ∗, { Displaystyle S (-f) = S (f) ^ {*},}

где S (f) ∗ { displaystyle S (f) ^ {*}}– это комплексно сопряженное из S (f) { di splaystyle S (f)}. Функция:

S a (f) ≜ {2 S (f), для f>0, S (f), для f = 0, 0, для f < 0 = 2 u ⁡ ( f) ⏟ 1 + sgn ⁡ ( f) S ( f) = S ( f) + sgn ⁡ ( f) S ( f), {displaystyle {begin{aligned}S_{mathrm {a} }(f)triangleq {begin{cases}2S(f),{text{for}} f>0, \ S (f), { text {for}} f = 0, \ 0, { text {for}} f <0end{cases}}\=underbrace {2operatorname {u} (f)} _{1+operatorname {sgn}(f)}S(f)=S(f)+operatorname {sgn}(f)S(f),end{aligned}}}

, где

содержит только неотрицательные частотные компоненты S (е) { Displaystyle S (f)}. И операция обратима из-за эрмитовой симметрии S (f) { displaystyle S (f)}:

S (f) = {1 2 S a (f), для f>0, S a (f), для f = 0, 1 2 S a (- f) ∗, для f < 0 (Hermitian symmetry) = 1 2 [ S a ( f) + S a ( − f) ∗ ]. {displaystyle {begin{aligned}S(f)={begin{cases}{frac {1}{2}}S_{mathrm {a} }(f),{text{for}} f>0, \ S _ { mathrm {a}} (f), { text {for}} f = 0, \ { frac {1} {2}} S _ { mathrm {a}} (- f) ^ {*}, { text {for}} f <0 {text{(Hermitian symmetry)}}end{cases}}\={frac {1}{2}}[S_{mathrm {a} }(f)+S_{mathrm {a} }(-f)^{*}].end{aligned}}}

. Аналитический сигнал из s (t) { displaystyle s (t)}– это обратное преобразование Фурье для S a (f) { displaystyle S _ { mathrm {a}} (f)}:

sa (t) ≜ F – 1 [S a (f)] = F – 1 [S (f) + sign ⁡ (f) ⋅ S (f)] = F – 1 {S (f)} ⏟ s (t) + F – 1 {sign ⁡ (f)} ⏟ j 1 π t ∗ F – 1 {S (f)} ⏟ s (t) ⏞ свертка = s (t) + j [1 π t ∗ s (t)] ⏟ H ⁡ [s (t)] = s (t) + js ^ (t), { displaystyle { begin {align} s _ { mathrm {a}} (t) треугольникq { mathcal {F}} ^ {- 1} [S _ { mathrm {a}} (f)] \ = { mathcal {F}} ^ {- 1} [S (f) + operatorname {sgn} (f) cdot S ( f)] \ = underbrace {{ mathcal {F}} ^ {- 1} {S (f) }} _ {s (t)} + overbrace { underbrace {{ mathcal {F }} ^ {- 1} { operatorname {sgn} (f) }} _ {j { frac {1} { pi t}}} * underbrace {{ mathcal {F}} ^ {- 1} {S (f) }} _ {s (t)}} ^ { text {convolution}} \ = s (t) + j underbrace { left [{1 over pi t } * s (t) right]} _ { operatorname { mathcal {H}} [s (t)]} \ = s (t) + j { hat {s}} (t), конец {выровнен}}}

где

. Отметим, что s (t) = s (t) ∗ δ (t), { displaystyle s (t) = s (t) * delta (t),}это также можно выразить как операцию фильтрации, которая непосредственно удаляет отрицательные частотные составляющие :

sa (t) = s (t) ∗ [δ (t) + j 1 π t] ⏟ F – 1 {2 u (f)}. { Displaystyle s _ { mathrm {a}} (t) = s (t) * underbrace { left [ delta (t) + j {1 over pi t} right]} _ {{ mathcal {F}} ^ {- 1} {2u (f) }}.}

Отрицательные частотные компоненты

Так как s (t) = Re ⁡ [sa (t)] { displaystyle s (t) = operatorname {Re} [s _ { mathrm {a}} (t)]}, восстановление отрицательных частотных составляющих – это простой вопрос отбрасывания Im ⁡ [ sa (t)] { displaystyle operatorname {Im} [s _ { mathrm {a}} (t)]}, что может показаться нелогичным. Мы также можем отметить, что комплексное сопряжение s a ∗ (t) { displaystyle s _ { mathrm {a}} ^ {*} (t)}содержит только отрицательные частотные компоненты. И поэтому s (t) = Re ⁡ [sa ∗ (t)] { displaystyle s (t) = operatorname {Re} [s _ { mathrm {a}} ^ {*} (t)]}восстанавливает подавленные положительные частотные составляющие. Другая точка зрения состоит в том, что мнимая составляющая в любом случае – это член, который вычитает частотные составляющие из s (t). Оператор Re { displaystyle operatorname {Re}}удаляет вычитание, создавая впечатление добавления новых компонентов.

Примеры

Пример 1

s (t) = cos ⁡ (ω t), { displaystyle s (t) = cos ( omega t),}где ω>0. { displaystyle omega>0.}

Тогда:

s ^ (t) = cos ⁡ (ω t – π 2) = sin ⁡ (ω t), { displaystyle { hat {s}} ( t) = cos left ( omega t – { frac { pi} {2}} right) = sin ( omega t),}

sa (t) = s (t) + js ^ (T) знак равно соз ⁡ (ω T) + J грех ⁡ (ω T) = Ej ω T. { Displaystyle s _ { mathrm {a}} (t) = s (t) + j { hat {s }} (t) = cos ( omega t) + j sin ( omega t) = e ^ {j omega t}.}Третье равенство – это формула Эйлера.

A следствие из формулы Эйлера : cos ⁡ (ω t) = 1 2 (ej ω t + ej (- ω) t). { displaystyle cos ( omega t) = { tfrac {1} {2}} left (e ^ {j omega t} + e ^ {j (- omega) t} right).}В общем, аналитический представление простой синусоиды получается выражением ее в терминах комплексных экспонент, отбрасывая отрицательную частотную составляющую и удваивая положительную частотную составляющую энт. А аналитическое представление суммы синусоид – это сумма аналитических представлений отдельных синусоид.

Пример 2

Здесь мы используем формулу Эйлера, чтобы идентифицировать и отбросить отрицательную частоту.

s (t) знак равно соз ⁡ (ω t + θ) = 1 2 (ej (ω t + θ) + e – j (ω t + θ)) { displaystyle s (t) = cos ( омега t ​​+ theta) = { frac {1} {2}} left (e ^ {j ( omega t + theta)} + e ^ {- j ( omega t + theta)} right)}

Тогда:

sa (t) = {ej (ω t + θ) = ej | ω | t ⋅ e j θ, если ω>0, e – j (ω t + θ) = e j | ω | t ⋅ e – j θ, если ω < 0. {displaystyle s_{mathrm {a} }(t)={begin{cases}e^{j(omega t+theta)} = e^{j|omega |t}cdot e^{jtheta },{text{if}} omega>0, \ e ^ {- j ( omega t + theta)} = e ^ {j | omega | t} cdot e ^ {- j theta }, { text {if}} omega <0.end{cases}}}

Пример 3

Это еще один пример использования метода преобразования Гильберта для удаления отрицательных частотных составляющих. Заметим, что ничто не мешает нам вычислить sa (t) { displaystyle s _ { mathrm {a}} (t)}для комплексного значения s (t) { displaystyle s (t)}. Но это может быть не обратимое представление, потому что исходный спектр в целом несимметричен. Таким образом, за исключением этого примера, в общем обсуждении предполагается, что вещественное значение s (t) { displaystyle s (t)}.

s (t) = e – j ω t { displaystyle s (t) = e ^ {- j omega t}}, где ω>0 { displaystyle omega>0}.

Затем:

s ^ (t) = je – j ω t, { displaystyle { hat {s}} (t) = je ^ {- j omega t},}

sa (t) = e – j ω t + j 2 e – j ω t = e – j ω T – E – J ω T = 0. { Displaystyle s _ { mathrm {a}} (t) = e ^ {- j omega t} + j ^ {2} e ^ {- j omega t} = e ^ {- j omega t} -e ^ {- j omega t} = 0.}

Свойства

Мгновенные амплитуда и фаза

Функция, выделенная синим цветом, и величина ее аналитическое представление красным цветом, показывающее эффект огибающей.

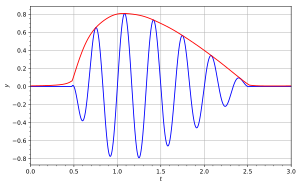
Аналитический сигнал также может быть выражен в полярных координатах :

sa (t) = sm (t) ej ϕ (t), { displaystyle s _ { mathrm {a}} (t) = s _ { mathrm {m}} (t) e ^ {j phi (t)},}

где вводятся следующие изменяющиеся во времени величины:

На прилагаемой диаграмме синяя кривая изображает s (t) { displaystyle s (t)}и красная кривая изображает соответствующую см (t) { displaystyle s _ { mathrm {m}} (t)}.

Производная по времени от развернутой мгновенной фазы имеет единицы радиан / секунду, и называется мгновенной угловой частотой:

ω (t) ≜ d ϕ dt (t). { displaystyle omega (t) треугольникq { frac {d phi} {dt}} (t).}

мгновенная частота (в герцах ) следовательно:

f (t) ≜ 1 2 π ω (t). { displaystyle f (t) Triangleq { frac {1} {2 pi}} omega (t).}

Мгновенная амплитуда, мгновенная фаза и частота используются в некоторых приложениях для измерения и обнаружения локальные особенности сигнала. Другое применение аналитического представления сигнала относится к демодуляции модулированных сигналов. Полярные координаты удобно разделяют эффекты амплитудной модуляции и фазовой (или частотной) модуляции и эффективно демодулируют определенные виды сигналов.

Комплексная огибающая / основная полоса

Аналитические сигналы часто смещены по частоте (преобразованы с понижением частоты) в сторону 0 Гц, что может создавать [несимметричные] отрицательные частотные компоненты:

sa ↓ (t) ≜ sa (t) е – j ω 0 T знак равно sm (t) ej (ϕ (t) – ω 0 t), { displaystyle {s _ { mathrm {a}}} _ { downarrow} (t) треугольник q s _ { mathrm {a}} (t) e ^ {- j omega _ {0} t} = s _ { mathrm {m}} (t) e ^ {j ( phi (t) – omega _ {0} t)},}

где ω 0 { displaystyle omega _ {0}}– произвольная опорная угловая частота.

Эта функция имеет различные названия, такие как сложный конверт и сложный baseband. Сложный конверт не уникален; он определяется выбором ω 0 { displaystyle omega _ {0}}. Эта концепция часто используется при работе с сигналами полосы пропускания. Если s (t) { displaystyle s (t)}является модулированным сигналом, ω 0 { displaystyle omega _ {0}}может быть приравнивается к его несущей частоте.

. В других случаях ω 0 { displaystyle omega _ {0}}выбирается где-то посередине желаемой полосы пропускания. Тогда простой фильтр нижних частот с действительными коэффициентами может вырезать интересующую часть. Другой мотив – снизить максимальную частоту, что снижает минимальную скорость выборки без псевдонимов. Сдвиг частоты не подрывает математическую управляемость представления комплексного сигнала. Таким образом, в этом смысле сигнал, преобразованный с понижением частоты, остается аналитическим. Однако восстановление представления с действительным знаком – это уже не просто извлечение реального компонента. Может потребоваться преобразование с повышением частоты, и если сигнал был дискретизирован (дискретное время), также может потребоваться интерполяция (повышающая дискретизация ), чтобы избежать алиасинг.

Если ω 0 { displaystyle omega _ {0}}выбрано больше максимальной частоты sa (t), { displaystyle s _ { mathrm {a}} (t),}, затем sa ↓ (t) { displaystyle {s _ { mathrm {a}}} _ { downarrow} (t)}не имеет положительных частот. В этом случае извлечение реального компонента восстанавливает их, но в обратном порядке; низкочастотные компоненты теперь высокие, и наоборот. Это может использоваться для демодуляции типа сигнала одной боковой полосы, называемого нижней боковой полосой или инвертированной боковой полосой.

Другие варианты задания частоты

Иногда ω 0 { displaystyle омега _ {0}}выбрано, чтобы минимизировать

∫ 0 + ∞ (ω – ω 0) 2 | S a (ω) | 2 d ω. { displaystyle int _ {0} ^ {+ infty} ( omega – omega _ {0}) ^ {2} | S _ { mathrm {a}} ( omega) | ^ {2} , d omega.}

В качестве альтернативы можно выбрать ω 0 { displaystyle omega _ {0}}, чтобы минимизировать среднеквадратичную ошибку при линейной аппроксимации развернутой мгновенной фазы ϕ (t) { displaystyle phi (t)}:

∫ – ∞ + ∞ [ω (t) – ω 0] 2 | s a (t) | 2 dt { displaystyle int _ {- infty} ^ {+ infty} [ omega (t) – omega _ {0}] ^ {2} | s _ { mathrm {a}} (t) | ^ {2} , dt}

или другая альтернатива (для некоторого оптимального θ { displaystyle theta}):

∫ – ∞ + ∞ [ϕ (t) – (ω 0 t + θ)] 2 dt. { displaystyle int _ {- infty} ^ {+ infty} [ phi (t) – ( omega _ {0} t + theta)] ^ {2} , dt.}

В В области частотно-временной обработки сигналов было показано, что аналитический сигнал был необходим для определения распределения Вигнера – Вилля, чтобы метод мог иметь желаемые свойства, необходимые для практических приложений.

Иногда фраза «комплексная огибающая» имеет более простой смысл комплексной амплитуды вектора (постоянной частоты); в других случаях комплексная огибающая s m (t) { displaystyle s_ {m} (t)}, как определено выше, интерпретируется как зависящее от времени обобщение комплексной амплитуды. Их соотношение мало чем отличается от реального случая: изменяющаяся огибающая обобщающая константа амплитуда.

Расширение аналитического сигнала на сигналы нескольких переменных

Концепция аналитического signal четко определен для сигналов одной переменной, которая обычно является временем. Для сигналов двух или более переменных аналитический сигнал может быть определен по-разному, и ниже представлены два подхода.

Многомерный аналитический сигнал на основе специального направления

Прямое обобщение аналитического сигнала может быть выполнено для многомерного сигнала после того, как установлено, что подразумевается под отрицательными частотами для Это дело. Это можно сделать, введя единичный вектор u ^ { displaystyle { boldsymbol { hat {u}}}}в область Фурье и пометив любой частотный вектор ξ { displaystyle { boldsymbol { xi}}}как отрицательное, если ξ ⋅ u ^ < 0 {displaystyle {boldsymbol {xi }}cdot {boldsymbol {hat {u}}}<0}. Затем получают аналитический сигнал путем удаления всех отрицательных частот и умножения результата на 2 в соответствии с процедурой, описанной для случая сигналов с одной переменной. Однако нет конкретного направления для u ^ { displaystyle { boldsymbol { hat {u}}}}, которое следует выбрать, если нет дополнительных ограничений. Следовательно, выбор u ^ { displaystyle { boldsymbol { hat {u}}}}является специальным или зависит от приложения.

Моногенный сигнал

Реальная и мнимая части аналитического сигнала соответствуют двум элементам векторно-значного сигнала, как это определено для сигналов с одной переменной. Однако моногенный сигнал может быть расширен до произвольного числа переменных прямым способом, создавая (n + 1) -мерную векторнозначную функцию для случая сигналов с n переменными.

См. Также

Приложения

Примечания

Ссылки

Дополнительная литература

• Леон Коэн, Частотно-временной анализ, Prentice Hall, Upper Saddle River, 1995.
• Frederick W. King, Hilbert Transforms, vol. II, Cambridge University Press, Кембридж, 2009.
• B. Боашаш, Частотно-временной анализ и обработка сигналов: исчерпывающий справочник, Elsevier Science, Oxford, 2003.

Внешние ссылки

From Wikipedia, the free encyclopedia

In mathematics and signal processing, an analytic signal is a complex-valued function that has no negative frequency components.^[1]  The real and imaginary parts of an analytic signal are real-valued functions related to each other by the Hilbert transform.

The analytic representation of a real-valued function is an analytic signal, comprising the original function and its Hilbert transform. This representation facilitates many mathematical manipulations. The basic idea is that the negative frequency components of the Fourier transform (or spectrum) of a real-valued function are superfluous, due to the Hermitian symmetry of such a spectrum. These negative frequency components can be discarded with no loss of information, provided one is willing to deal with a complex-valued function instead. That makes certain attributes of the function more accessible and facilitates the derivation of modulation and demodulation techniques, such as single-sideband.

As long as the manipulated function has no negative frequency components (that is, it is still analytic), the conversion from complex back to real is just a matter of discarding the imaginary part. The analytic representation is a generalization of the phasor concept:^[2] while the phasor is restricted to time-invariant amplitude, phase, and frequency, the analytic signal allows for time-variable parameters.

Definition[edit]

If is a real-valued function with Fourier transform , then the transform has Hermitian symmetry about the axis:

where is the complex conjugate of .
The function:

where

contains only the non-negative frequency components of . And the operation is reversible, due to the Hermitian symmetry of :

The analytic signal of is the inverse Fourier transform of :

where

Noting that this can also be expressed as a filtering operation that directly removes negative frequency components:

Negative frequency components[edit]

Since , restoring the negative frequency components is a simple matter of discarding which may seem counter-intuitive. We can also note that the complex conjugate comprises only the negative frequency components. And therefore restores the suppressed positive frequency components. Another viewpoint is that the imaginary component in either case is a term that subtracts frequency components from The operator removes the subtraction, giving the appearance of adding new components.

Examples[edit]

Example 1[edit]

  where  

Then:

The last equality is Euler’s formula, of which a corollary is In general, the analytic representation of a simple sinusoid is obtained by expressing it in terms of complex-exponentials, discarding the negative frequency component, and doubling the positive frequency component. And the analytic representation of a sum of sinusoids is the sum of the analytic representations of the individual sinusoids.

Example 2[edit]

Here we use Euler’s formula to identify and discard the negative frequency.

Then:

Example 3[edit]

This is another example of using the Hilbert transform method to remove negative frequency components. We note that nothing prevents us from computing for a complex-valued . But it might not be a reversible representation, because the original spectrum is not symmetrical in general. So except for this example, the general discussion assumes real-valued .

, where .

Then:

Properties[edit]

Instantaneous amplitude and phase[edit]

An analytic signal can also be expressed in polar coordinates:

where the following time-variant quantities are introduced:

In the accompanying diagram, the blue curve depicts and the red curve depicts the corresponding .

The time derivative of the unwrapped instantaneous phase has units of radians/second, and is called the instantaneous angular frequency:

The instantaneous frequency (in hertz) is therefore:

 ^[3]

The instantaneous amplitude, and the instantaneous phase and frequency are in some applications used to measure and detect local features of the signal. Another application of the analytic representation of a signal relates to demodulation of modulated signals. The polar coordinates conveniently separate the effects of amplitude modulation and phase (or frequency) modulation, and effectively demodulates certain kinds of signals.

Complex envelope/baseband[edit]

Analytic signals are often shifted in frequency (down-converted) toward 0 Hz, possibly creating [non-symmetrical] negative frequency components:

where is an arbitrary reference angular frequency.^[2]

This function goes by various names, such as complex envelope and complex baseband. The complex envelope is not unique; it is determined by the choice of . This concept is often used when dealing with passband signals. If is a modulated signal, might be equated to its carrier frequency.

In other cases, is selected to be somewhere in the middle of the desired passband. Then a simple low-pass filter with real coefficients can excise the portion of interest. Another motive is to reduce the highest frequency, which reduces the minimum rate for alias-free sampling. A frequency shift does not undermine the mathematical tractability of the complex signal representation. So in that sense, the down-converted signal is still analytic. However, restoring the real-valued representation is no longer a simple matter of just extracting the real component. Up-conversion may be required, and if the signal has been sampled (discrete-time), interpolation (upsampling) might also be necessary to avoid aliasing.

If is chosen larger than the highest frequency of then has no positive frequencies. In that case, extracting the real component restores them, but in reverse order; the low-frequency components are now high ones and vice versa. This can be used to demodulate a type of single-sideband signal called lower sideband or inverted sideband.

Other choices of reference frequency are sometimes considered:

In the field of time-frequency signal processing, it was shown that the analytic signal was needed in the definition of the Wigner–Ville distribution so that the method can have the desirable properties needed for practical applications.^[5]

Sometimes the phrase “complex envelope” is given the simpler meaning of the complex amplitude of a (constant-frequency) phasor;^[a][b]
other times the complex envelope as defined above is interpreted as a time-dependent generalization of the complex amplitude.^[c] Their relationship is not unlike that in the real-valued case: varying envelope generalizing constant amplitude.

Extensions of the analytic signal to signals of multiple variables[edit]

The concept of analytic signal is well-defined for signals of a single variable which typically is time. For signals of two or more variables, an analytic signal can be defined in different ways, and two approaches are presented below.

Multi-dimensional analytic signal based on an ad hoc direction[edit]

A straightforward generalization of the analytic signal can be done for a multi-dimensional signal once it is established what is meant by negative frequencies for this case. This can be done by introducing a unit vector in the Fourier domain and label any frequency vector as negative if . The analytic signal is then produced by removing all negative frequencies and multiply the result by 2, in accordance to the procedure described for the case of one-variable signals. However, there is no particular direction for which must be chosen unless there are some additional constraints. Therefore, the choice of is ad hoc, or application specific.

The monogenic signal[edit]

The real and imaginary parts of the analytic signal correspond to the two elements of the vector-valued monogenic signal, as it is defined for one-variable signals. However, the monogenic signal can be extended to arbitrary number of variables in a straightforward manner, producing an (n + 1)-dimensional vector-valued function for the case of n-variable signals.

See also[edit]

• Practical considerations for computing Hilbert transforms
• Negative frequency

Applications[edit]

• Single-sideband modulation
• Quadrature filter
• Causal filter

Notes[edit]

References[edit]

Further reading[edit]

• Leon Cohen, Time-frequency analysis, Prentice Hall, Upper Saddle River, 1995.
• Frederick W. King, Hilbert Transforms, vol. II, Cambridge University Press, Cambridge, 2009.
• B. Boashash, Time-Frequency Signal Analysis and Processing: A Comprehensive Reference, Elsevier Science, Oxford, 2003.

External links[edit]

• Analytic Signals and Hilbert Transform Filters