Как найти аномалии в данных

Поиск аномалий во временных рядах

Вокруг нас появляется все больше различных устройств, систем, комплексов, платформ – технологических, информационных, киберфизических. Мы не задумываемся о том, как кофеварка варит кофе, робот-пылесос выбирает маршрут при уборке квартиры, система биометрической идентификации определяет человека на видеокадре, а портал государственных услуг обрабатывает наше заявление на получение справки об отсутствии судимости. Мы привыкаем к этим системам как к «черным ящикам», которые дают предсказуемый результат на выходе, не заботясь о том, как эти системы себя «чувствуют». Такой потребительский подход простителен пользователям, но совсем по-другому относятся к этому компании-разработчики и те, кто занимается эксплуатацией технологических систем. Для них и описан далее один из оригинальных методов поиска аномалий во временных рядах, т.е. состояний, по которым можно понять, что системе становится «плохо» (либо станет в ближайшем будущем). 

Для эффективной эксплуатации сложных технологических систем нужны мониторинг и различные методы аналитики, позволяющие контролировать, управлять, упреждающе менять параметры. Мониторинг, как правило, обеспечивается типовыми инструментами (в большинстве случаев достаточно надежной системы сбора и визуализации данных). А вот для создания эффективных аналитических инструментов необходимы дополнительные исследования, эксперименты и хорошее знание предметной области. Как правило выделяют четыре основных вида аналитики данных [1]:

• Описательная аналитика визуализирует накопленные данные, в том числе преобразованные для наглядности и интерпретируемости. Описательная аналитика – самый простой вид анализа, но и самый важный для применения других методов анализа.

• С помощью диагностической аналитики исследуют причину возникновения событий в прошлом, при этом выявляются тренды, аномалии, наиболее характерные черты описываемого процесса, ищут причины и корреляции (взаимосвязи).

• Прогнозная аналитика предсказывает вероятные результаты на основе выявленных тенденций и статистических моделей, полученных с помощью исторических данных.

• Предписывающая аналитика позволяет получить оптимальное решение производственной задачи на основе прогнозной аналитики. Например, это может быть оптимизация параметров работы оборудования или бизнес-процессов, перечень мер по предотвращению аварийной ситуации.

Для прогнозной и предписывающей аналитики как правило используются методы моделирования, в том числе машинное обучение. Эффективность этих моделей зависит от качественной организации сбора, обработки и предварительного анализа данных. Перечисленные виды аналитики различаются как по сложности используемых моделей, так и по степени участия человека.

Сфер применения инструментов аналитики очень много – информационная безопасность, банковский сектор, государственное управление, медицина и многие другие предметные области. Часто один и тот же метод эффективно работает для разных предметных областей, поэтому разработчики систем аналитики создают универсальные модули, содержащие различные алгоритмы.

Для многих технологических систем результаты мониторинга можно представить в виде временных рядов [2]. Свойствами временного ряда являются:

• привязка каждого измерения (сэмпла, дискрета) ко времени его возникновения,

• равное расстояние по времени между измерениями,

• возможность из данных предыдущего периода восстановить поведение процесса в текущем и последующих периодах.

Временные ряды могут описывать не только численно измеримые процессы. Применение различных методов и архитектур моделей, включая глубокие нейронные сети, позволяет работать с данными из задач обработки естественного языка (NLP), компьютерного зрения (CV) и т.п. Например, сообщения в чате можно преобразовать в числовые векторы (эмбеддинги), которые последовательно появляются в определенное время, а видео представляет из себя ни что иное как матрицу чисел, изменяющуюся во времени.

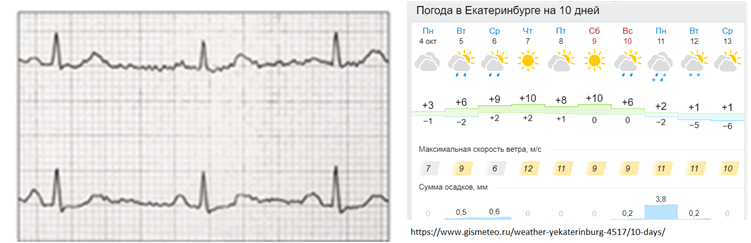
Итак, временные ряды очень полезны для описания работы сложных устройств и часто используются для типовых задач: моделирование, прогнозирование, выделение признаков, классификация, кластеризация, поиск паттернов, поиск аномалий. Примеры такого использования: электрокардиограмма, изменение стоимости акций или валюты, значения прогноза погоды, изменение в объеме сетевого трафика, параметры работы двигателя и многое другое.

У временных рядов есть типовые характеристики, которые достаточно точно описывают характер временного ряда:

• период – временной отрезок постоянной для всего ряда длины, на концах которого ряд принимает близкие значения,

• сезонность – свойство периодичности (сезон=период),

• цикл – характерные изменения ряда, связанные с глобальными причинами (например, циклы в экономике), нет постоянного периода,

• тренд – тенденция к долгосрочному увеличению или уменьшению значений ряда.

Временные ряды могут содержать аномалии. Аномалия — это отклонение в стандартном поведении какого-то процесса. Алгоритмы машинного поиска аномалий используют данные о работе процесса (датасеты). В зависимости от предметной области в датасете могут быть аномалии разного вида. Принято различать несколько видов аномалий:

• точечные аномалии, когда наблюдается отклонение в поведении в отдельных точках;

• групповые аномалии, в которых аномально ведут себя группа точек, каждая из которых отдельно аномальной не является;

• аномалии контекста, когда аномалия связана с внешними данными, не касающимися значений ряда (например, отрицательная температура на улице летом).

Точечные аномалии распознаются проще всего – это отдельные точки, в которых поведение процесса резко отличается от других точек. Например, можно наблюдать резкое отклонение значений параметра в отдельной точке.

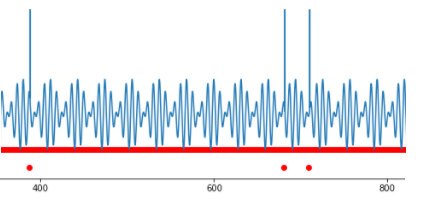
Такие значения называются «выбросы», они сильно влияют на статистические показатели процесса и их легко обнаружить, установив пороговые значения для наблюдаемой величины.

Сложнее обнаружить аномалию в ситуации, когда в каждой точке процесс ведет себя «нормально», но в совокупности значения в нескольких точках ведут себя «странно». К такому аномальному поведению можно отнести, например, изменение формы сигнала, изменение статистических показателей (среднее значение, мода, медиана, дисперсия), появление взаимной корреляции между двумя параметрами, небольшие или краткосрочные аномальные изменения амплитуды и так далее. И в этом случае задача заключается в распознавании аномального поведения параметров, которое нельзя выявить обычными статистическими методами.

Поиск аномалий очень важен. В одной ситуации надо данные очищать от аномалий, чтобы получать более реальную картину, в другой же ситуации аномалии должны внимательно исследоваться, так как могут свидетельствовать о возможном скором переходе устройства в аварийный режим.

Поиск аномалий во временных рядах непрост (нечеткое определение аномалии, отсутствие разметки, неочевидная корреляция). До сих пор SOTA алгоритмы по поиску аномалий во временных рядах имеют высокий уровень False Positive.

Вручную можно обнаружить только небольшое количество аномалий, в основном точечных, при наличии хорошей визуализации данных. Групповые аномалии сложнее обнаружить вручную, особенно если речь идет о большом количестве данных и анализе информации о нескольких устройствах. Также сложным для выявления является случай «аномалии во времени», когда нормальный по параметрам сигнал появляется в «неправильное» время. Поэтому при поиске аномалий во временных рядах целесообразно применять методы автоматизации.

Большой проблемой в поиске аномалий на реальных данных является то, что данные как правило не размечены, поэтому изначально строго не определено, что такое аномалия, нет правил для поиска. В таких ситуациях необходимо применять методы обучения без учителя (unsupervised learning), при этом модели самостоятельно определяют взаимосвязи и характерные законы в данных.

Используемые для поиска аномалий во временных рядах методы принято разделять на группы [3]:

• proximity-based: выявление аномалии на основе информации о близости параметров или последовательности параметров фиксированной длины, подходит для выявления точечных аномалий и выбросов, но не позволит выявить изменения в форме сигнала,

• prediction-based: построение прогнозной модели и сравнение прогноза и фактической величины, лучше всего применимо ко временным рядам с выраженными периодами, циклами или сезонностью,

• reconstruction-based: методы, основанные на реконструкции фрагментов данных, используют восстановление (реконструкцию) фрагмента данных, поэтому может выявлять как точечные аномалии, так и групповые аномалии, в том числе изменения в форме сигнала.

Proximity-based методы ориентированы на поиск значений, существенно отклоняющихся от поведения всех остальных точек. Самый простой и наглядный пример реализации такого метода – контроль превышения заданного порога значений.

В prediction-based методах основная задача – построить качественную модель процесса, чтобы смоделировать сигнал и сравнить полученные смоделированные значения с исходными (истинными). Если предсказанный и истинный сигнал близки, то поведение считается «нормальным», а если значения в модели сильно отличаются от истинных, то поведение системы на этом участке объявляется аномальным.

Наиболее распространенные методы для моделирования временных рядов – SARIMA [4] и рекуррентные нейронные сети [5].

Оригинальный подход используется в reconstruction-based моделях – сначала модель обучают кодировать и декодировать сигналы из имеющейся выборки, при этом закодированный сигнал имеет гораздо меньшую размерность, чем исходный, поэтому модели приходится учиться «сжимать» информацию. Вот пример такого сжатия для картинок 32 на 32 пикселя в матрицу из 32 чисел.

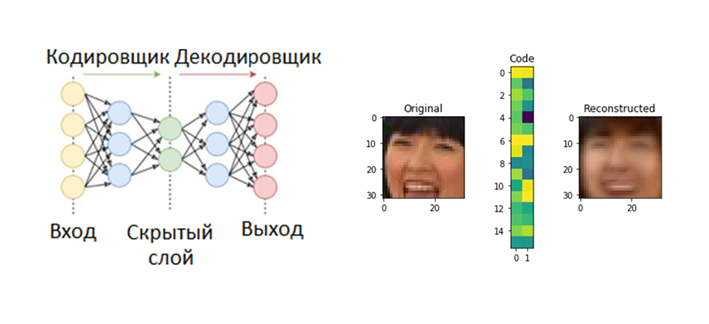
После обучения модели дают на вход сигналы, являющиеся отрезками исследуемого временного ряда, и если кодирование-декодирование проходит успешно, то поведение процесса считается «нормальным», в противном случае поведение объявляется аномальным.

Одним из недавно разработанных reconstruction-based методов, показывающих хорошие результаты в обнаружении аномалий, является TadGAN [3], разработанный исследователями из MIT в конце 2020 года. Архитектура метода TadGAN содержит в себе элементы автокодировщика и генеративных состязательных сетей.

Ɛ действует как кодировщик, переводящий отрезки временных рядов x в векторы скрытого пространства z, а G – декодер, восстанавливающий из скрытого представления z отрезки временных рядов. Cx – критик, оценивающий качество восстановления G(Ɛ(х)), а Cz – критик, оценивающий похожесть скрытого представления z = Ɛ(х) на белый шум. Кроме того, действует контроль «похожести» исходного и восстановленного сэмплов с использованием L2 – меры по идеологии «Cycle consistency loss» (обеспечивает общую похожесть сгенерированных образцов на исходные сэмплы в GAN) [6]. Итоговая целевая функция – объединение всех метрик для оценки качества работы критиков Cx, Cz и меры похожести исходного и восстановленного сигнала.

Для создания и обучения нейронной сети могут быть использованы различные стандартные пакеты (например, TensorFlow или PyTorch), имеющие высокоуровневое API. Пример реализации архитектуры, аналогичной TadGAN, с использованием пакета TensorFlow для обучения весов можно посмотреть в репозитории [7]. При обучении этой модели оптимизировались пять метрик:

• aeLoss – среднеквадратичное отклонение между исходным и восстановленным временным рядом, т.е. разница между x и G(Ɛ(х)),

• cxLoss – бинарная кросс-энтропия критика Cx, определяющего разницу между истинным отрезком временного ряда и искусственно сгенерированным,

• cx_g_Loss – бинарная кросс-энтропия, ошибка генератора G(Ɛ(х)), характеризующая его неспособность «обманывать» критика Cx,

• czLoss – бинарная кросс-энтропия критика Cz, определяющего разницу между скрытым вектором, который сгенерировал кодировщик Ɛ и белым шумом, обеспечивает похожесть скрытого вектора Ɛ(х) на случайный вектор, не давая модели «заучивать» отдельные паттерны в исходных данных,

• cz_g_Loss – бинарная кросс-энтропия, ошибка генератора Ɛ(х), характеризующая его неспособность создавать скрытые векторы, похожие на случайные, и тем самым «обманывать» критика Cz.

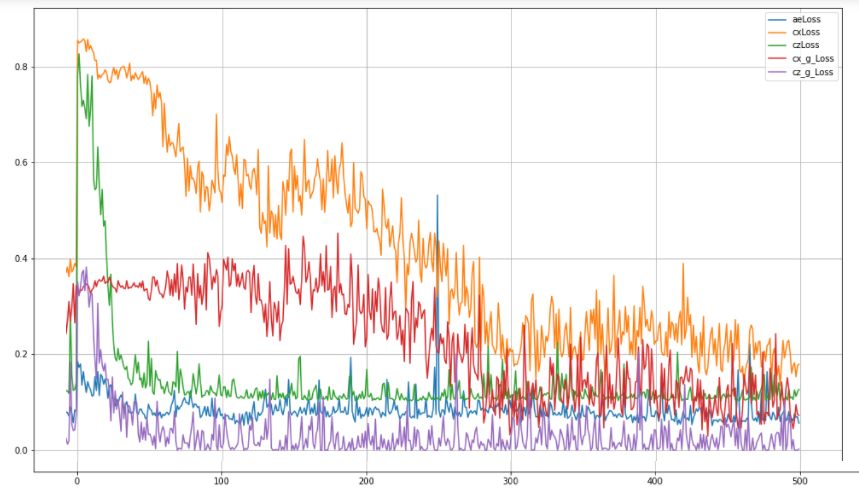
После обучения модели проводится реконструкция отдельных отрезков исследуемого временного ряда и сравнение исходного и реконструированного ряда, которое может осуществляться одним из методов:

• поточечное сравнение;

• сравнение площадей кривых в заданной области вокруг каждого сэмпла (длина области – гиперпараметр);

• Dynamic Time Warping [9].

Качество оценивается по F1-метрике для задачи бинарной классификации, «positive» (нулевая гипотеза) – есть аномалия, «negative» (альтернативная гипотеза) – нет аномалии.

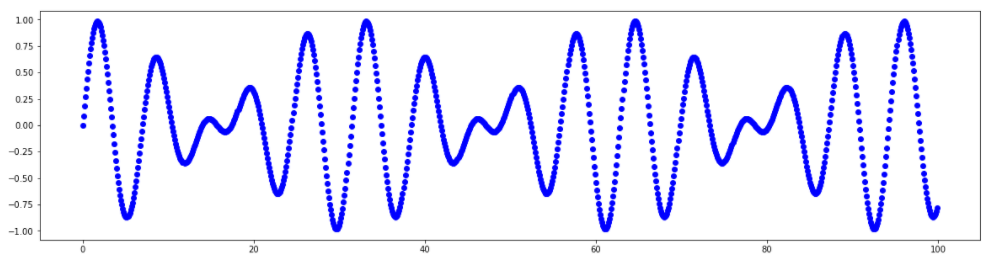
Для демонстрации работы метода используем синтетический (искусственно сгенерированный) ряд без аномалий, являющийся суммой двух синусоид, значения которого меняются в диапазоне от -1 до 1

 График этого ряда:

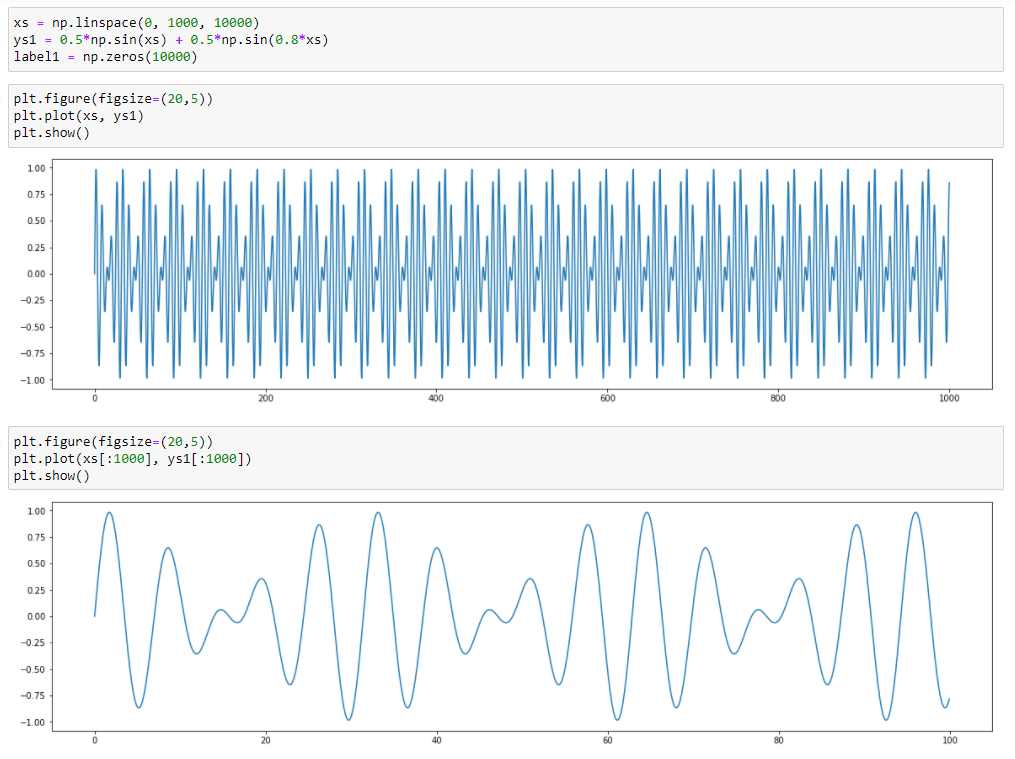
Восстановленный ряд с использованием TadGAN для разного количества эпох (4 и 80) выглядит так:

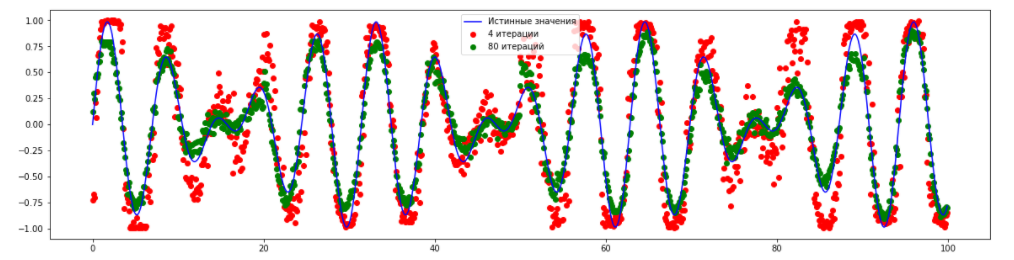
Видно, что модель достаточно точно научилась предсказывать основные закономерности в данных. Попробуем добавить различные аномалии в данных и затем обнаружить их с помощью модели TadGAN. Сначала добавим несколько точечных аномалий.

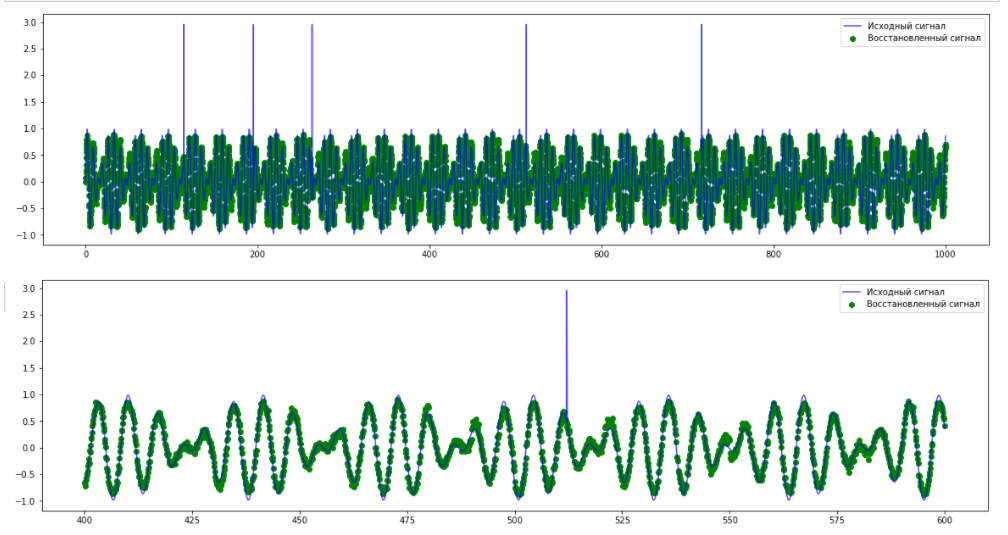
Из графика исходного и предсказанного сигналов видно, что модель не может восстановить «пики» аномальных значений, что с высокой точностью может использоваться для определения точечных аномалий. Однако в такой ситуации польза сложной модели TadGAN неочевидна – подобные аномалии можно обнаружить и с помощью оценки превышения пороговых значений.

Теперь рассмотрим сигнал с другим типом аномалии – периодический сигнал с аномальным изменением частоты. В этом случае нет превышения порога – с точки зрения амплитуды все элементы ряда являются «нормальными» значениями, и аномалия выявляется только в групповом поведении нескольких точек. В этом случае TadGAN также не может восстановить сигнал (как это видно на рисунке) и это может быть использовано в качестве признака наличия групповой аномалии.

На этих двух примерах проиллюстрирована работа метода. Читатель и сам может попробовать создать свои датасеты и проверить возможности модели в различных ситуациях.

Более сложные примеры датасетов можно найти в статье авторов метода TadGAN [3]. Там же приведена ссылка на библиотеку Orion, являющуюся разработкой специалистов MIT, которая с использованием машинного обучения распознает редкие аномалии во временных рядах, используя подход обучения без учителя (unsupervised learning).

В заключении отметим, что методов, использующих реконструирование сигнала (reconstruction-based) для обнаружения аномалии сейчас очень много, например в ресурсе arxiv.org десятки статей, описывающих различные модификации подхода с использованием автокодировщиков и генеративных состязательных сетей. Для каждой конкретной задачи целесообразно подбирать свою модель, с учетом требований задачи и знаний о предметной области.

Ссылки

1. «Что такое аналитика данных?», https://www.intel.ru/content/www/ru/ru/analytics/what-is-data-analytics.html

2. В.В. Домбровский. Эконометрика. http://sun.tsu.ru/mminfo/2016/Dombrovski/start.htm

3. “TadGAN: Time Series Anomaly Detection Using Generative Adversarial Networks”, https://arxiv.org/abs/2009.07769

4. “An Introductory Study on Time Series Modeling and Forecasting”, описание SARIMA https://arxiv.org/ftp/arxiv/papers/1302/1302.6613.pdf

5. Fundamentals of RNN, https://arxiv.org/abs/1808.03314

6. Cycle Consistency Loss, https://paperswithcode.com/method/cycle-consistency-loss

7. https://github.com/CyberLympha/Examples/tree/main/Разбор статей/TadGAN

8. Библиотека для распознавания аномалий в сигналах, https://github.com/signals-dev/Orion

9. Алгоритм Dynamic Time Warping, https://towardsdatascience.com/dynamic-time-warping-3933f25fcdd

10. https://medium.com/mit-data-to-ai-lab/time-series-anomaly-detection-in-the-era-of-deep-learning-dccb2fb58fd

11. https://medium.com/mit-data-to-ai-lab/time-series-anomaly-detection-in-the-era-of-deep-learning-f0237902224a

В этом посте поговорим об одной важной проблеме обучения без учителя (Unsupervised Learning) – задаче поиска аномалий (Anomaly Detection). Интересно, что в русскоязычных учебных курсах об этой задаче часто забывают. Даже в русской версии страницы обучение без учителя нет упоминания об этой задаче, в английской, конечно же, есть.

Строго говоря, в анализе данных есть два направления, которые занимаются поиском аномалий: детектирование выбросов (Outlier Detection) и «новизны» (Novelty Detection). Как и выброс «новый объект» — это объект, который отличается по своим свойствам от объектов (обучающей) выборки.  Но  в отличие от выброса, его в самой выборке пока нет (он появится через некоторое время, и задача как раз и заключается в том, чтобы обнаружить его при появлении). Например, если вы анализируете замеры температуры и отбрасываете аномально большие или маленькие, то Вы боретесь с выбросами. А если Вы создаёте алгоритм, который для каждого нового замера оценивает, насколько он похож на прошлые, и выбрасывает аномальные — Вы «боретесь с новизной».

Выбросы являются следствием:

• ошибок в данных (неточности измерения, округления, неверной записи и т.п.)
• наличия шумовых объектов (неверно классифицированных объектов)
• присутствия объектов «других» выборок (например, показаниями сломавшегося датчика).

На рис. 1 видно, что шум (noise) — это выброс «в слабом смысле» (он может немного размывать границы класса/кластера). Нас же интересуют, прежде всего, выбросы «в сильном смысле», которые искажают эти границы.

Новизна, как правило, появляется в результате принципиально нового поведения объекта. Скажем, если наши объекты – описания работы системы, то после проникновения в неё вируса объекты становятся «новизной». Ещё пример – описания работы двигателя после поломки. Здесь важно понимать, что «новизна» называется новизной по той причине, что такие описания для нас абсолютно новые, а новые они потому, что мы не можем в обучающей выборке иметь информацию о всевозможных заражениях вирусами или всевозможных поломках. Формирование такой обучающей выборки трудозатратно и часто не имеет смысла. Зато можно набрать достаточно большую выборку примеров нормальной (штатной) работы системы или механизма.

Приложений здесь море:

• Обнаружение подозрительных банковских операций (Credit-card Fraud)
• Обнаружение вторжений (Intrusion Detection)
• Обнаружение нестандартных игроков на бирже (инсайдеров)
• Обнаружение неполадок в механизмах по показаниям датчиков
• Медицинская диагностика (Medical Diagnosis)
• Сейсмология

Стоит отметить, что возможных постановок задач здесь тоже много. Например, задача Positive-Unlabeled Classification (PU learning) – это когда часть выбросов обозначена (класс 1), но в остальных объектах  обучения (класс 0) также могут содержаться выбросы. Например, нам эксперт сказал, что оборудование давало сбой в такие-то моменты времени, но он мог заметить не все сбои.

Даже когда задачи обнаружения аномалий похожи на обычные задачи классификации, есть особенности, скажем дисбаланс классов (например, поломки оборудования относительно редки).

Аномалии бывают не только в табличных данных, они могут быть в графах, временных рядах и т.д.

Функционалы качества в задачах детектирования аномалий используют примерно такие же, как и в задачах классификации: PR AUC, AUROC, здесь всё определяется контекстом задачи (заказчиком).

Методы обнаружения выбросов

1. Статистические тесты

Как правило, применяют для отдельных признаков и отлавливают экстремальные значения (Extreme-Value Analysis). Для этого используют, например, Z-value или Kurtosis measure.

Любой практик имеет какой-нибудь свой проверенный способ нахождения экстремальных значений для определённых типов данных. Многие методы визуализации, например ящик с усами, имеют встроенные средства для детектирования и показа таких экстремальных значений.

Важно понимать, что экстремальное значение и аномалия это разные понятия. Например, в небольшой выборке

[1, 39, 2, 1, 101, 2, 1, 100, 1, 3, 101, 1, 3, 100, 101, 100, 100]

значение 39 можно считать аномалией, хотя оно не является максимальным или минимальным. Также стоит отметить, что аномалия характеризуется, как правило, не только экстремальными значениями отдельных признаков (см. рис. 5)

2. Модельные тесты

Идея очень простая – мы строим модель, которая описывает данные. Точки которые сильно отклоняются от модели (на которых модель сильно ошибается) и есть аномалии (см. рис. 2). При выборе модели мы можем учесть природу задачи, функционал качества и т.п.

Такие методы хороши для определения новизны, но хуже работают при поиске выбросов. Действительно, при настройке модели мы используем данные, в которых есть выбросы (и она под них «затачивается»).

На рис. 6 показано применение модельного подхода. У нас есть матрица и требуется найти в ней выбросы. Мы используем неполное сингулярное разложение (SVD), чтобы найти матрицу небольшого ранга максимально похожую на нашу (для наглядности все числа округлены). Элементы, которые сильно отличаются от соответствующих элементов матрицы небольшого ранга, будем считать выбросами.

3. Итерационные методы

Методы, которые состоят из итераций, на каждой из которых удаляется группа «особо подозрительных объектов». Например, в n-мерном признаковом пространстве можно удалять выпуклую оболочку наших точек-объектов, считая её представителей выбросами. Как правило, методы этой группы достаточно трудоёмки.

4. Метрические методы

Судя по числу публикаций, это самые популярные методы среди исследователей. В них постулируется существование некоторой метрики в пространстве объектов, которая и помогает найти аномалии. Интуитивно понятно, что у выброса мало соседей, а у типичной точки много. Поэтому хорошей мерой аномальности может служить, например «расстояние до k-го соседа» (см. метод Local Outlier Factor). Здесь используются специфические метрики, например расстояние Махаланобиса.

5. Методы подмены задачи

Когда возникает новая задача, есть большой соблазн решить её старыми методами (ориентированными на уже известные задачи). Например, можно сделать кластеризацию, тогда маленькие кластеры, скорее всего, состоят из аномалий. Если у нас есть частичная информация об аномалиях (как в задаче PUC), то можно решить её как задачу классификации с классами 1 (размеченные аномалии) и 0 (все остальные объекты). Если бы класс 0 состоял только из нормальных объектов, то такое решение было бы совсем законным, иначе остаётся надеяться, что недетектированных аномалий в нём немного.

6. Методы машинного обучения

А что если воспринять задачу нахождения аномалий как новую задачу машинного обучения (отличную от классификации и кластеризации)?!

Самые популярные алгоритмы (есть реализация даже в scikit-learn) здесь:

• Метод опорных векторов для одного класса (OneClassSVM)
• Изолирующий лес (IsolationForest)
• Эллипсоидальная аппроксимация данных (EllipticEnvelope)

Первый метод — это обычный SVM, который отделяет выборку от начала координат. Идея немного сомнительна, но оказалась довольно работоспособной (см. рис. 10). Здесь правда не так много разнообразия в выборе параметров, как при решении задач классификации, поскольку в качестве ядра подойдёт лишь rbf (радиальные базисные функции), все остальные ядра показывают феноменально отвратительный результат. Интересно , что многие годы задачи детектирования поломок сложных механизмов решались именно с помощью OneClassSVM, почему-то без рассмотрения альтернатив (на нашей кафедре также защищались дипломы на эту тему). Полезно помнить, что OneClassSVM это скорее алгоритм поиска новизны, а не выбросов, т.к. «затачивается» под обучающую выборку.

Важные параметры реализации sklearn.svm.OneClassSVM:

• kernel – ядро (линейное: linear, полиномиальное: poly, радиальные базисные функции: rbf, сигмоидальное: sigmoid, своё заданное)
• nu – верхняя граница на %ошибок и нижняя на % опорных векторов (0.5 по умолчанию)
• degree – степень для полиномиального ядра
• gamma – коэффициент для функции ядра (1/n_features по умолчанию)
• coef0 – параметр в функции полиномиального или сигмоидального ядра

Изолирующий лес  (Isolation Forest) – это одна из вариаций идеи случайного леса. Как всегда: простая и надёжная.

• Состоит из деревьев
• Каждое дерево строится до исчерпании выборки
• Для построения ветвления в дереве: выбирается случайный признак и случайное расщепление
• Для каждого объекта мера его нормальности – среднее арифметическое глубин листьев, в которые он попал (изолировался)

Логика алгоритма простая: при описанном «случайном» способе построения деревьев выбросы будут попадать в листья на ранних этапах (на небольшой глубине дерева), т.е. выбросы проще «изолировать» (напомним, что дерево строится до тех пор, пока каждый объект не окажется в отдельном листе). Алгоритм хорошо отлавливает именно выбросы (см. рис. 12).

Важные параметры реализации sklearn.ensemble.IsolationForest

• n_estimators – число деревьев
• max_samples – объём выборки для построения одного дерева (если вещественное число, то процент всей выборки)
• contamination – доля выбросов в выборке (для выбора порога)
• max_features – число (или %) признаков, которые используются при построении одного дерева (пока работает только со значением 1.0)
• bootstrap – включение режима бутстрепа при формировании подвыборки

Эллипсоидальная аппроксимация данных — из названия понятно, что облако точек моделируется как внутренность эллипсоида. Метод хорошо работает только на одномодальных данных, а совсем хорошо – на нормально распределённых. Степень новизны здесь фактически определяется по расстоянию Махаланобиса.

7. Ансамбли алгоритмов

В методы решения задач обнаружения аномалий также проникла идея «один алгоритм хорошо, а сто лучше», поэтому часто строят много разных алгоритмов. Каждый из них даёт оценку аномальности и эти оценки потом «усредняют».

Поскольку ключевым моментов в реальных задачах обнаружения аномалий является выбор признаков, которые характеризуют те или иные отклонения от нормы, алгоритмы из ансамбля строят пытаясь угадать хорошие пространства. Здесь популярны:

• Feature Bagging (не очень удачное название) – для каждого алгоритма берут случайное признаковое подпространство,
• Rotated Bagging – в выбранном случайном признаковом подпространстве совершают случайный поворот.

Кстати, здесь «усреднение» не обязательно означает среднее арифметическое всех оценок, интуитивно понятно, что часто может сработать максимум (если какой-то алгоритм уверен в аномальности объекта, то скорее всего так оно и есть).

История из практики

В задачах поиска аномалий важно понимать, как работают алгоритмы поиска, и объяснить это заказчику. Например, когда автор последний раз участвовал в решении подобной задачи, заказчик хотел средство для детектирования поломок, но из-за природы модели получился алгоритм детектирования «неправильного функционирования оборудования», т.е. он давал сигнал не только в случае поломок, но и в случае некорректной эксплуатации прибора, а также при работе в очень редких режимах. Некоторые поломки (очень частые) он всё-таки пропускал, т.к. «они уже стали для прибора нормой». Понятно, что при наличии большой размеченной выборки таких проблем не возникало бы, но на практике оборудование работает не так долго, поломок тоже мало (и не все возможные случаются), а некоторые поломки могли не заметить или заметить с запозданием. Кроме того, некоторые поломки никак не отражаются на показаниях датчиков. Изначально качество очень расстроило заказчика, но когда ему объяснили, как работает алгоритм, заказчик сверился с данными испытаний и убедился, что алгоритм очень полезный, даже если не находит какие-то поломки: его можно использовать как верификатор «работает ли прибор в штатном режиме», а это самое главное.

П.С. Код для получения рис.10 можно взять здесь.

  Перевод

  Ссылка на автора

Что такое аномалия / выброс?

В статистике, выбросы – это точки данных, которые не принадлежат определенной популяции. Это ненормальное наблюдение, которое находится далеко от других ценностей. Выделение – это наблюдение, которое отличается от хорошо структурированных данных.

Например, вы можете ясно увидеть выбросы в этом списке: [20,24,22,19,29,18,4300, 30,18]

Это легко идентифицировать, когда наблюдения представляют собой просто набор чисел, и он одномерный, но когда у вас есть тысячи наблюдений или многомерных измерений, вам понадобятся более умные способы обнаружения этих значений. Это то, что эта статья будет освещать.

Почему мы заботимся об аномалиях?

Обнаружение выбросов или аномалий является одной из основных проблем интеллектуального анализа данных. Появляющееся расширение и продолжающийся рост данных и распространение устройств IoT заставляют нас переосмыслить подход к аномалиям и варианты использования, которые могут быть построены с учетом этих аномалий.

Теперь у нас есть умные часы и браслеты, которые могут определять сердцебиение каждые несколько минут. Обнаружение аномалий в данных сердцебиения может помочь в прогнозировании сердечных заболеваний. Аномалии в схемах движения могут помочь в прогнозировании аварий. Его также можно использовать для выявления узких мест в сетевой инфраструктуре и трафика между серверами. Следовательно, варианты использования и решения, основанные на обнаружении аномалий, безграничны.

Еще одна причина, по которой нам необходимо обнаруживать аномалии, заключается в том, что при подготовке наборов данных для моделей машинного обучения действительно важно обнаружить все выбросы и либо избавиться от них, либо проанализировать их, чтобы понять, почему они были у вас в первую очередь.

Теперь давайте рассмотрим 5 распространенных способов обнаружения аномалий, начиная с самого простого.

Метод 1 – Стандартное отклонение:

В статистике, если распределение данных приблизительно нормальное, то около 68% значений данных находятся в пределах одного стандартного отклонения от среднего, а около 95% находятся в пределах двух стандартных отклонений, иоколо 99,7%лежат в пределах трех стандартных отклонений

Поэтому, если у вас есть какая-либо точка данных, которая более чем в 3 раза превышает стандартное отклонение, то эти точки, скорее всего, будут аномальными или выбросами.

Давайте посмотрим код.

Выход этого кода представляет собой список значений выше 80 и ниже -40. Обратите внимание, что набор данных, который я передаю, является одномерным набором данных. Теперь давайте рассмотрим более продвинутые методы для многомерных наборов данных.

Метод 2 – Боксплоты

Графики представляют собой графическое изображение числовых данных через их квантили. Это очень простой, но эффективный способ визуализации выбросов. Думайте о нижнем и верхнем усиках как о границах распределения данных. Любые точки данных, которые показывают выше или ниже усов, могут считаться выбросами или аномальными. Вот код для построения прямоугольного графика:

Приведенный выше код отображает график ниже. Как вы можете видеть, он считает все, что выше 75 или ниже ~ -35, как выброс. Результаты очень близки к методу 1 выше.

Boxplot Анатомия:

Концепция ЯСеверный квартал(IQR) используется для построения графиков бокса. IQR – это понятие в статистике, которое используется для измерения статистической дисперсии и изменчивости данных путем разделения набора данных на квартили.

Проще говоря, любой набор данных или любой набор наблюдений делится на четыре определенных интервала на основе значений данных и того, как они сравниваются со всем набором данных. Квартиль – это то, что делит данные на три точки и четыре интервала.

Межквартильный диапазон (IQR) важен, потому что он используется для определения выбросов. Это разница между третьим квартилем и первым квартилем (IQR = Q3 -Q1). Выбросы в этом случае определяются как наблюдения, которые ниже (Q1 – 1,5x IQR) илинижний усыили выше (Q3 + 1,5x IQR) иливерхний усы,

Метод 3 – Кластеризация DBScan:

DBScan – это алгоритм кластеризации, который использует кластерные данные в группы. Он также используется в качестве метода обнаружения аномалий на основе плотности как с одиночными, так и с многомерными данными. Другие алгоритмы кластеризации, такие как k-средних и иерархическая кластеризация, также могут быть использованы для обнаружения выбросов. В этом случае я покажу вам пример использования DBScan, но прежде чем мы начнем, давайте рассмотрим некоторые важные концепции. DBScan имеет три важных понятия:

• Основные пункты:Чтобы понять концепцию ключевых точек, нам нужно посетить некоторые гиперпараметры, используемые для определения задания DBScan. Первый гиперпараметр (HP)min_samples.Это просто минимальное количество базовых точек, необходимых для формирования кластера.,Второй важный HPEPS. прибыль на акциюмаксимальное расстояние между двумя выборками для них, которые должны рассматриваться как в одном кластере
• Пограничные пунктынаходятся в том же кластере, что и основные точки, но гораздо дальше от центра кластера.

• Все остальное называетсяШумовые очки,это точки данных, которые не принадлежат ни одному кластеру. Они могут быть аномальными или не аномальными и требуют дальнейшего изучения. Теперь давайте посмотрим код.

Вывод вышеуказанного кода94.Это общее количество шумных точек. SKLearn помечает шумные точки как (-1). Недостатком этого метода является то, что чем выше размер, тем менее точным он становится. Вы также должны сделать несколько предположений, таких как оценка правильного значения дляEPS Wкоторый может быть сложным.

Метод 4 – Изоляция леса:

Isolation Forest – это алгоритм обучения без присмотра, который принадлежит к семейству деревьев решений ансамбля. Этот подход отличается от всех предыдущих методов. Все предыдущие пытались найти нормальную область данных, а затем идентифицировали что-либо за пределами этой определенной области как отклонение или аномальность.

Этот метод работает по-другому. Он явно выделяет аномалии вместо того, чтобы профилировать и строить нормальные точки и области, назначая оценку каждой точке данных. Он использует тот факт, что аномалии являются точками данных меньшинства и что они имеют значения атрибутов, которые сильно отличаются от значений в обычных случаях. Этот алгоритм отлично работает с наборами данных очень большого размера, и он оказался очень эффективным способом обнаружения аномалий. Поскольку в этой статье основное внимание уделяется реализации, а не ноу-хау, я не буду подробно останавливаться на том, как работает алгоритм. Тем не менее, полная информация о том, как это работает, рассматривается в этом бумага,

Теперь давайте рассмотрим код:

Этот код выведет прогнозы для каждой точки данных в массиве. Если результат равен -1, это означает, что эта конкретная точка данных является выбросом. Если результат равен 1, то это означает, что точка данных не является выбросом

Метод 5 – Устойчивый лес случайных рубок:

Алгоритм Random Cut Forest (RCF) – это неконтролируемый алгоритм Amazon для обнаружения аномалий. Это работает, связывая оценку аномалии также. Низкие значения указывают на то, что точка данных считается «нормальной». Высокие значения указывают на наличие аномалии в данных. Определения «низкий» и «высокий» зависят от приложения, но общепринятая практика предполагает, что оценки, превышающие три стандартных отклонения от среднего значения, считаются аномальными. Детали алгоритма можно найти в этом бумага,

Самое замечательное в этом алгоритме то, что он работает с данными очень большого размера. Он также может работать с потоковыми данными в режиме реального времени (встроенными в AWS Kinesis Analytics), а также с автономными данными.

Я объясняю концепцию более подробно в видео ниже:

В документе приведены некоторые показатели производительности по сравнению с Isolation Forest. Вот результаты из статьи, которая показывает, что RCF намного точнее и быстрее, чем Isolation Forests.

Полный пример кода можно найти здесь:

Вывод:

Мы живем в мире, где данные увеличиваются с каждой секундой. Значение данных может уменьшаться со временем, если не используется должным образом. Поиск аномалий в режиме онлайн в потоке или в автономном режиме в наборе данных имеет решающее значение для выявления проблем в бизнесе или создания упреждающего решения для потенциального обнаружения проблемы до ее возникновения или даже на этапе анализа предварительных данных (EDA) для подготовки набора данных для ML , Я надеюсь, что вы найдете эту статью полезной, дайте мне знать, что вы думаете в разделе комментариев ниже.

Выявление аномалий (обнаружение выбросов^[1]) — опознавание во время интеллектуального анализа данных редких данных, событий или наблюдений, которые вызывают подозрения ввиду существенного отличия от большей части данных^[1]. Обычно аномальные данные характеризуют некоторый вид проблемы, такой как мошенничество в банке^[en], структурный дефект, медицинские проблемы или ошибки в тексте. Аномалии также упоминаются как выбросы, необычности, шум, отклонения или исключения^[2].

Общее обсуждение[править | править код]

Выявление аномалий в контексте обнаружения злоумышленного использования и вторжения в сеть, интересующие нас объекты часто не являются редкими, но проявляют неожиданную вспышку активности. Это не соответствует обычному статистическому определению выбросов как редких объектов и многие методы обнаружения выбросов (в частности, методы без учителя) терпят неудачу на таких данных, пока данные не будут сгруппированы подходящим образом. Зато алгоритмы кластерного анализа способны заметить микрокластеры, образованные таким поведением^[3].

Существует широкий набор категорий техник выявления аномалий^[4].
Техника выявления аномалий без учителя обнаруживает аномалии в непомеченных наборах тестовых данных при предположении, что большая часть набора данных нормальна, путём поиска представителей, которые меньше подходят к остальному набору данных. Техника выявления аномалий с учителем требует предоставления данных, помеченных как «нормальные» и «ненормальные», и использует обучение классификатора (ключевое отличие от многих других задач классификации заключается в неотъемлемой несбалансированной природе выявления выбросов). Техника выявления аномалий с частичным учителем строит модель, представляющую нормальное поведение из заданного набора нормального тренировочного набора, а затем проверяет правдоподобие полученной модели.

Приложения[править | править код]

Выявление аномалий применимо к широкому кругу областей, таких как система обнаружения вторжений, обнаружение мошенничества, обнаружение неисправностей, мониторинга здоровья, обнаружение событий в сетях датчиков и обнаружение нарушений в экологической сфере. Часто выявление аномалий используется для предварительной обработки данных с целью удаления аномалий. При обучении с учителем удаление аномальных данных из набора часто приводит к существенному статистическому увеличению точности^[5][6].

Популярные техники[править | править код]

В литературе было предложено несколько техник выявления аномалий^[7]. Вот некоторые популярные техники:

• Техники, основанные на плотности (k-ближайшие соседи^[8][9][10], локальный уровень выброса^[11], изолирующие леса^[12] и многие другие варианты этой концепции^[13]).
• Обнаружение выбросов на основе подпространств^[14] и на основе корреляции^[15] для данных высокой размерности^[16].
• Метод опорных векторов для одного класса^[17].
• Репликатор нейронных сетей^[18].
• Байесовские сети^[18].
• Скрытые марковские модели (СММ) ^[18].
• Выявление выбросов на основе кластерного анализа^[19][20].
• Отклонения от ассоциативных правил и часто встречающихся наборов.
• Выявление выбросов на основе нечёткой логики.
• Техника создания ансамблей, использующая бэггинг признаков^[en][21][22], усреднение оценки^[23][24] и различение источников несхожести^[25][26].

Эффективность различных методов зависит от данных и параметров и имеют слабые систематические преимущества один перед другим, если сравнивать по многим наборам данных и параметров^[27][28].

Приложение к защите данных[править | править код]

Выявление аномалий предложила для систем обнаружения вторжений Дороти Деннинг в 1986 году^[29]. Выявление аномалий для систем обнаружения вторжений обычно выполняется с заданием порога и статистики, но может быть сделано с помощью мягких вычислений и индуктивного обучения^[30]. Типы статистики, предлагавшиеся в 1999 году, включали профили пользователей, рабочих станций, сетей, удалённых узлов, групп пользователей и программ, основанных на частотах, средних и дисперсиях^[31]. Эквивалентом выявления аномалий в обнаружении вторжений является обнаружение злонамеренного использования^[en].

Программное обеспечение[править | править код]

• ELKI^[en] является комплектом инструментов с открытым кодом на языке Java для анализа данных, который содержит некоторые алгоритмы выявления аномалий, а также ускорители на основе индексов для них.

Примечания[править | править код]

Литература[править | править код]

• Arthur Zimek, Erich Schubert. Outlier Detection // Encyclopedia of Database Systems. — Springer New York, 2017. — ISBN 9781489979933. — doi:10.1007/978-1-4899-7993-3_80719-1.
• Hodge V. J., Austin J. A Survey of Outlier Detection Methodologies // Artificial Intelligence Review. — 2004. — Т. 22, вып. 2. — doi:10.1007/s10462-004-4304-y.
• Paul Dokas, Levent Ertoz, Vipin Kumar, Aleksandar Lazarevic, Jaideep Srivastava, Pang-Ning Tan. Data mining for network intrusion detection // Proceedings NSF Workshop on Next Generation Data Mining. — 2002.
• Chandola V., Banerjee A., Kumar V. Anomaly detection: A survey // ACM Computing Surveys. — 2009. — Т. 41, вып. 3. — doi:10.1145/1541880.1541882.
• Ivan Tomek. An Experiment with the Edited Nearest-Neighbor Rule // IEEE Transactions on Systems, Man, and Cybernetics. — 1976. — Т. 6, вып. 6. — doi:10.1109/TSMC.1976.4309523.
• Smith M. R., Martinez T. Improving classification accuracy by identifying and removing instances that should be misclassified // The 2011 International Joint Conference on Neural Networks. — 2011. — ISBN 978-1-4244-9635-8. — doi:10.1109/IJCNN.2011.6033571.
• Arthur Zimek, Peter Filzmoser. There and back again: Outlier detection between statistical reasoning and data mining algorithms // Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery. — 2018. — Т. 8, вып. 6. — ISSN 19424787. — doi:10.1002/widm.1280.
• Knorr E. M., Ng R. T., Tucakov V. Distance-based outliers: Algorithms and applications // The VLDB Journal the International Journal on Very Large Data Bases. — 2000. — Т. 8, вып. 3–4. — doi:10.1007/s007780050006.
• Ramaswamy S., Rastogi R., Shim K. Efficient algorithms for mining outliers from large data sets // Proceedings of the 2000 ACM SIGMOD international conference on Management of data – SIGMOD ’00. — 2000. — ISBN 1-58113-217-4. — doi:10.1145/342009.335437.
• Angiulli F., Pizzuti C. Fast Outlier Detection in High Dimensional Spaces // Principles of Data Mining and Knowledge Discovery. — 2002. — Т. 2431. — (Lecture Notes in Computer Science). — ISBN 978-3-540-44037-6. — doi:10.1007/3-540-45681-3_2.
• Breunig M. M., Kriegel H.-P., Ng R. T., Sander J. LOF: Identifying Density-based Local Outliers // Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. — 2000. — (SIGMOD). — ISBN 1-58113-217-4. — doi:10.1145/335191.335388.
• Fei Tony Liu, Kai Ming Ting, Zhi-Hua Zhou. Isolation Forest // 2008 Eighth IEEE International Conference on Data Mining. — 2008. — ISBN 9780769535029. — doi:10.1109/ICDM.2008.17.
• Schubert E., Zimek A., Kriegel H. -P. Local outlier detection reconsidered: A generalized view on locality with applications to spatial, video, and network outlier detection // Data Mining and Knowledge Discovery. — 2012. — Т. 28. — doi:10.1007/s10618-012-0300-z.
• Kriegel H. P., Kröger P., Schubert E., Zimek A. Outlier Detection in Axis-Parallel Subspaces of High Dimensional Data // Advances in Knowledge Discovery and Data Mining. — 2009. — Т. 5476. — (Lecture Notes in Computer Science). — ISBN 978-3-642-01306-5. — doi:10.1007/978-3-642-01307-2_86.
• Kriegel H. P., Kroger P., Schubert E., Zimek A. Outlier Detection in Arbitrarily Oriented Subspaces // 2012 IEEE 12th International Conference on Data Mining. — 2012. — ISBN 978-1-4673-4649-8. — doi:10.1109/ICDM.2012.21.
• Zimek A., Schubert E., Kriegel H.-P. A survey on unsupervised outlier detection in high-dimensional numerical data // Statistical Analysis and Data Mining. — 2012. — Т. 5, вып. 5. — doi:10.1002/sam.11161.
• Schölkopf B., Platt J. C., Shawe-Taylor J., Smola A. J., Williamson R. C. Estimating the Support of a High-Dimensional Distribution // Neural Computation. — 2001. — Т. 13, вып. 7. — doi:10.1162/089976601750264965. — PMID 11440593.
• Simon Hawkins, Hongxing He, Graham Williams, Rohan Baxter. Outlier Detection Using Replicator Neural Networks // Data Warehousing and Knowledge Discovery. — 2002. — Т. 2454. — (Lecture Notes in Computer Science). — ISBN 978-3-540-44123-6. — doi:10.1007/3-540-46145-0_17.
• He Z., Xu X., Deng S. Discovering cluster-based local outliers // Pattern Recognition Letters. — 2003. — Т. 24, вып. 9–10. — doi:10.1016/S0167-8655(03)00003-5.
• Campello R. J. G. B., Moulavi D., Zimek A., Sander J. Hierarchical Density Estimates for Data Clustering, Visualization, and Outlier Detection // ACM Transactions on Knowledge Discovery from Data. — 2015. — Т. 10, вып. 1. — doi:10.1145/2733381.
• Lazarevic A., Kumar V. Feature bagging for outlier detection // Proc. 11th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining. — 2005. — ISBN 978-1-59593-135-1. — doi:10.1145/1081870.1081891.
• Nguyen H. V., Ang H. H., Gopalkrishnan V. Mining Outliers with Ensemble of Heterogeneous Detectors on Random Subspaces // Database Systems for Advanced Applications. — 2010. — Т. 5981. — (Lecture Notes in Computer Science). — ISBN 978-3-642-12025-1. — doi:10.1007/978-3-642-12026-8_29.
• Kriegel H. P., Kröger P., Schubert E., Zimek A. Interpreting and Unifying Outlier Scores // Proceedings of the 2011 SIAM International Conference on Data Mining. — 2011. — ISBN 978-0-89871-992-5. — doi:10.1137/1.9781611972818.2.
• Schubert E., Wojdanowski R., Zimek A., Kriegel H. P. On Evaluation of Outlier Rankings and Outlier Scores // Proceedings of the 2012 SIAM International Conference on Data Mining. — 2012. — ISBN 978-1-61197-232-0. — doi:10.1137/1.9781611972825.90.
• Zimek A., Campello R. J. G. B., Sander J. R. Ensembles for unsupervised outlier detection // ACM SIGKDD Explorations Newsletter. — 2014. — Т. 15. — doi:10.1145/2594473.2594476.
• Zimek A., Campello R. J. G. B., Sander J. R. Data perturbation for outlier detection ensembles // Proceedings of the 26th International Conference on Scientific and Statistical Database Management – SSDBM ’14. — 2014. — ISBN 978-1-4503-2722-0. — doi:10.1145/2618243.2618257.
• Guilherme O. Campos, Arthur Zimek, Jörg Sander, Ricardo J. G. B. Campello, Barbora Micenková, Erich Schubert, Ira Assent, Michael E. Houle. On the evaluation of unsupervised outlier detection: measures, datasets, and an empirical study // Data Mining and Knowledge Discovery. — 2016. — Т. 30, вып. 4. — ISSN 1384-5810. — doi:10.1007/s10618-015-0444-8.
• Denning D. E. An Intrusion-Detection Model // IEEE Transactions on Software Engineering. — 1987. — Т. SE-13, вып. 2. — doi:10.1109/TSE.1987.232894.
• Teng H. S., Chen K., Lu S. C. Adaptive real-time anomaly detection using inductively generated sequential patterns // Proceedings of the IEEE Computer Society Symposium on Research in Security and Privacy. — 1990. — ISBN 978-0-8186-2060-7. — doi:10.1109/RISP.1990.63857.
• Anita K. Jones, Robert S. Sielken. Computer System Intrusion Detection: A Survey // Technical Report, Department of Computer Science,. — University of Virginia, Charlottesville, VA, 1999.

Ссылки[править | править код]

• Архив данных для сравнения алгоритмов выявления аномалий Мюнхенского университета; Зеркало в Университете Сан-Паулу.
• ODDS — ODDS: Большая коллекция публично доступных наборов данных для выявления выбросов с реальными ситуациями в различных областях.