Инфоурок
›
Геометрия
›Презентации›Презентация по геометрии на тему “Цилиндр. Площадь его поверхности.” (11 класс)
Скачать материал

Скачать материал


- Сейчас обучается 1152 человека из 83 регионов




- Сейчас обучается 27 человек из 14 регионов


Описание презентации по отдельным слайдам:
-

1 слайд
Цилиндр.
Площадь его поверхности. -

2 слайд
Вопрос №1:
Какая фигура является основанием цилиндра?
а) Овал
б) Круг
в) Квадрат -

3 слайд
Вопрос №2:
Чему равна площадь основания цилиндра с радиусом 2см?
а) 4π
б) 8π
в) 4 -

4 слайд
Вопрос №3:
Как называется отрезок отмеченный красным цветом?
а) диагональ цилиндра
б) апофема цилиндра
в)образующая
цилиндра -

5 слайд
Вопрос №4:
По какой формуле можно вычислить боковую поверхность цилиндра?
а) 2πRh
б) 2πR(h+R)
в) πR2h -

6 слайд
Вопрос №5:
По какой формуле можно вычислить полную поверхность цилиндра?
а) πR2h
б) 2πRh
в) 2πR(h+R) -

7 слайд
Вопрос №6:
Вычислите боковую поверхность
данного цилиндра.
а) 15π см2
б) 30π см2
в) 48π см2
3см
5см
3см -

8 слайд
Вопрос №7:
Вычислите полную поверхность
данного цилиндра.
а) 32π см2
б) 24π см2
в) 16π см2
2см
6см -

9 слайд
Вопрос №8:
Чему равна площадь осевого сечения цилиндра радиуса 1см и образующей 3см?
а) 6 см2
б) 3 см2
в) 6π см2 -

10 слайд
Правильные ответы:
На оценку «5»-8 правильных ответов.
На оценку «4»- 6-7 правильных ответов.
На оценку «3»- 5 правильных ответов.
На оценку «2»- 4 и менее правильных ответов.
Краткое описание документа:
Презентация по геометрии на тему “Цилиндр. Площадь его поверхности.” предназначена для проверки знаний учащихся 11 класса.
Цель работы: проверить теоретические и практические знания по данной теме.
В работе содержатся задачи на вычисление площади боковой и полной поверхности цилиндра.
Данная презентация демонстрируется в начале урока и направлена на проверку знаний учащихся.
В ходе выполнения работы учащиеся пользуются формулами площади круга, длины окружности, площади боковой и полной поверхности цилиндра.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 258 192 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 10.12.2014
- 3224
- 13
- 10.12.2014
- 538
- 0
- 10.12.2014
- 528
- 0
- 10.12.2014
- 2779
- 5
- 10.12.2014
- 1866
- 1
- 10.12.2014
- 10744
- 17
Рейтинг:
4 из 5
- 10.12.2014
- 9251
- 800
-
Скачать материал
-
10.12.2014
7245
-
PPTX
525 кбайт -
64
скачивания -
Рейтинг:
5 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Алексеенко Ольга Александровна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-

- На сайте: 8 лет и 5 месяцев
- Подписчики: 0
- Всего просмотров: 310169
-
Всего материалов:
59
Как найти апофему
Апофемой в пирамиде называют отрезок, проведенный из ее вершины к основанию одной из боковых граней, если отрезок перпендикулярен этому основанию. Боковая грань такой объемной фигуры всегда имеет треугольную форму. Поэтому при необходимости вычисления длины апофемы допустимо использование свойств как многогранника (пирамиды), так и многоугольника (треугольника).

Вам понадобится
- – геометрические параметры пирамиды.
Инструкция
В треугольнике боковой грани апофема (f) является высотой, поэтому при известной длине бокового ребра (b) и угле (γ) между ним и ребром, на которое опущена апофема, можно использовать известную формулу вычисления высоты треугольника. Умножьте заданную длину ребра на синус известного угла: f = b*sin(γ). Эта формула применима к пирамидам любой (правильной или неправильной) формы.
Для вычисления каждой из трех апофем (f) правильной треугольной пирамиды достаточно знать всего один параметр – длину ребра (a). Это объясняется тем, что грани такой пирамиды имеют форму равносторонних треугольников одинаковых размеров. Для нахождения высот каждого из них вычислите половину произведения длины ребра на квадратный корень из трех: f = a*√3/2.
Если известна площадь (s) боковой грани пирамиды, в дополнение к ней достаточно знать длину (a) общего ребра этой грани с основанием объемной фигуры. В этом случае длину апофемы (f) находите удвоением соотношения между площадью и длиной ребра: f = 2*s/a.
Зная общую площадь поверхности пирамиды (S) и периметр ее основания (p) тоже можно вычислить апофему (f), но только для многогранника правильной формы. Удвойте площадь поверхности и разделите результат на периметр: f = 2*S/p. Форма основания в этом случае не имеет значения.
Количество вершин или сторон основания (n) нужно знать в том случае, если в условиях даны длина ребра (b) боковой грани и величина угла (α), который образуют два смежных боковых ребра правильной пирамиды. При таких исходных условиях вычисляйте апофему (f) умножением числа сторон основания на синус известного угла и возведенную в квадрат длину бокового ребра с последующим делением полученной величины пополам: f = n*sin(α)*b²/2.
В правильной пирамиде с четырехугольным основанием для нахождения длины апофемы (f) можно использовать высоту многогранника (H) и длину ребра основания (a). Извлеките квадратный корень из суммы возведенной в квадрат высоты и четверти от возведенной в квадрат длины ребра: f = √(H²+a²/4).
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Тела и поверхности вращения. Цилиндр
План урока
- Тела и поверхности вращения;
- Вычисление площади боковой поверхности и объема цилиндра.
Цели урока
- Знать, что такое тела и поверхности вращения;
- Знать, что такое цилиндр и его составные элементы;
- Знать, что такое осевое сечение цилиндра;
- Знать формулу объема цилиндра;
- Знать, что такое развертка боковой поверхности цилиндра и чему равна ее площадь;
- Уметь находить полную площадь боковой поверхности прямого цилиндра, объем цилиндра.
Разминка
- Какой многогранник называется пирамидой?
- Что такое призма?
- Какие составные элементы пирамиды вы знаете?
- Какая пирамида называется правильной?
- Что такое апофема правильной пирамиды?
- Чему равна площадь боковой поверхности правильной пирамиды?
- Как найти площадь полной поверхности пирамиды?
- Чему равна площадь круга? Длина окружности?
Тела и поверхности вращения. Цилиндр
Тело, образуемое вращением какой-нибудь плоской фигуры около неподвижной прямой линии, называется
телом вращения
. Неподвижная прямая называется
осью вращения
.
Вырежем из картона прямоугольник и насадим его на ось и будем очень быстро вращать вокруг этой оси. Наш глаз примерно в течении 116 секунды удерживает зрительное впечатление. Поэтому, если прямоугольник будет делать 15-20 оборотов в секунду, мы перестанем различать отдельные его положения, а увидим сплошное круглое тело.
Цилиндр
– фигура, полученная вращением прямоугольника вокруг одной из его сторон.
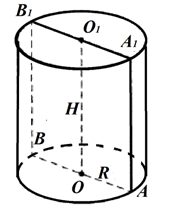
Рис. 1. Цилиндр
На рисунке 1 цилиндр, полученный вращением прямоугольника AA1O1O вокруг одной из его сторон OO1 или прямоугольника AA1B1B вокруг прямой OO1, которая проходит через серединные точки противолежащих сторон.
Прямая OO1 называется осью цилиндра, отрезки AA1 и BB1 –
образующие цилиндра
. В качестве
высоты цилиндра
можно выбрать любой из отрезков AA1=BB1=OO1. Два круга, лежащих в параллельных плоскостях, которые образовались при вращении, называют
основаниями цилиндра
.
Радиус цилиндра
– это радиус его основания R=OA=OB.
При вращении стороны AA1, образуется поверхность, состоящая из множества отрезков (образующих цилиндра), параллельных оси цилиндра. Ее называют
цилиндрической
или
боковой поверхностью
.
Таким образом, цилиндр – это тело, ограниченное двумя равными кругами и цилиндрической поверхностью.
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевым сечением цилиндра является прямоугольник AA1B1B (рис. 1).
Тела, имеющие форму цилиндра, встречаются довольно часто. Оси колес, стержни, валы, колонны, столбы, обтесанные бревна и многие другие предметы имеют форму цилиндра. Например, трубы, банки, стаканы, ведра имеют форму цилиндра, пустого внутри.
Объем цилиндра равен произведению площади основания на высоту
V=S·h,
где V – объем цилиндра, S – площадь основания, h – высота цилиндра.
Так как основанием цилиндра является круг, а его площадь равна πR2, то объем цилиндра также можно вычислить по формуле:
V=πR2h.
Пример 1
Найдите объем цилиндра, если диаметр его основания равен 12 см, а высота равна 5 см (π=3,14).
Решение
Сначала найдем радиус основания, как половину диаметра:
R=12÷2=6 см.
Найдем объем цилиндра по формуле V=πR2h:
V=3,14·62·5=565,2 см3.
Ответ: 565,2 см3.
На рисунке 2 изображен цилиндр. Представьте себе,что его боковую часть разрезали по образующей AA1 и развернули таким образом, что получился прямоугольник. Этот прямоугольник называется
разверткой
боковой
поверхности
цилиндра
. Длина данного прямоугольника равна длине окружности основания, а ширина AA1 равна высоте цилиндра. Таким образом, легко получить формулу для вычисления площади боковой поверхности цилиндра.
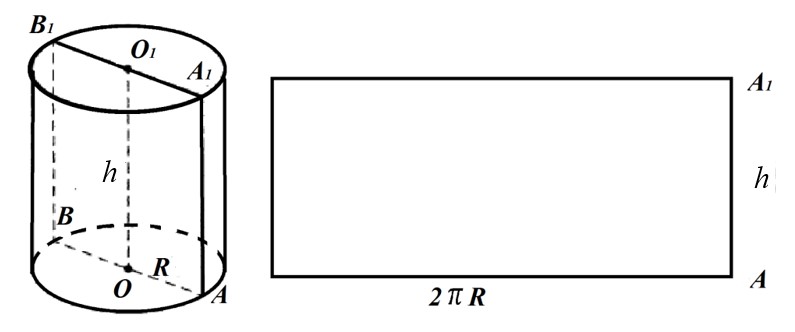
Рис. 2. Развёртка боковой поверхности цилиндра
Площадь Sбок боковой поверхности цилиндра равна площади ее развертки и находится по формуле:
Sбок=2πRh.
Площадь полной поверхности прямого цилиндра состоит из двух равных площадей оснований и площади боковой поверхности. Таким образом:
S=Sбок+2Sосн=2πRh+2πR2.
Пример 2
Точки O и O1 – центры оснований цилиндра, OA – радиус основания, AA1 – образующая цилиндра. Найдите площадь боковой поверхности и объем цилиндра, если O1A1=3 см, OO1=6 см (π=3,14).
Решение
Радиус R основания цилиндра R=OA=O1A1=3 см, OO1 будет являться высотой, т.е. h=OO1=6 см.
Найдем площадь боковой поверхности по формуле:
Sбок=2πRh
Sбок=2·3,14·3·6=113,04 см2
2. Найдем объем по формуле:
V=πR2h
V=3,14·32·6=169,56 см3
Ответ: 113,04 см2, 169,56 см3.
Упражнение 1
1. Найдите объем цилиндра, если диаметр его основания равен 20 см, а высота равна 12 см (π=3,14).
2. Точки O и O1 – центры оснований цилиндра, OA – радиус основания. Найдите площадь боковой поверхности и объем цилиндра, если OA=4 см, OO1=9 см (π=3,14).
Контрольные вопросы
1. Объясните, какое тело называется цилиндром?
2. Объясните, что такое цилиндрическая поверхность?
3. По какой формуле можно найти объем цилиндра?
4. Как вычислить площадь боковой поверхности цилиндра?
Ответы
Упражнение 1
1. 3768 см3;
2. 226,08 см2, 452,16 см3.
- Альфашкола
- Уроки по математике
- Стереометрия
- Цилиндр.
Цилиндр. – онлайн урок
В уроке по теме “Стереометрия это“, 10 класс, геометрия. Рассматриваются основные аксиомы стереометрии, следствия и задачи, формулы. Основные понятия стереометрии: пространство, плоскость, взаимное расположение фигур в пространстве, перпендикулярность и параллельность, касательные, углы между прямыми и плоскостями в пространстве, двугранный и линейный угол, расстояние, теорема о трех перпендикулярах. Подробно изучаются все многогранники и их элементы в пространстве: призма, параллелепипед, пирамида, тетраэдр, цилиндр, сфера, шар, конус, усеченные фигуры, октаэдр, икосаэдр, додэкаэдр и грани, площадь боковой поверхности, объем, апофема – элементы. Строим различные комбинации геометрических фигур в пространстве, вписанные и описанные фигуры.
Отзывы:
Мне понравилось занятие полностью! Вопросов нет.
Огромное спасибо Алле Алексеевне за занятия! Очень внимательный и требовательный преподаватель. Отвечает на любые вопросы и идет на встречу. Ребенок включается в урок, заинтересован всегда. Надеемся и дальше на плодотворные занятия! Спасибо большое!
На ваших уроках ребенок получает знания и при этом доволен, именно за это спасибо огромное!
Похожие уроки

Апофема правильного шестиугольника




Апофе́ма (греч. αποτιθημι — откладываю в сторону) — геометрический термин. В зависимости от контекста может означать следующее:
- В планиметрии — длина перпендикуляра, опущенного из центра правильного многоугольника на любую из его сторон. Апофема правильного
-угольника равна радиусу
вписанной окружности. Она связана с его стороной
и площадью
следующими соотношениями:
.
- В стереометрии — высота боковой грани правильной пирамиды (возможно, усечённой).
Литература[править | править код]
- Апофема // Казахстан. Национальная энциклопедия. — Алматы: Қазақ энциклопедиясы, 2004. — Т. I. — ISBN 9965-9389-9-7. (CC BY-SA 3.0)
- Апофема // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- Апофема // Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
При написании этой статьи использовался материал из издания «Казахстан. Национальная энциклопедия» (1998—2007), предоставленного редакцией «Қазақ энциклопедиясы» по лицензии Creative Commons BY-SA 3.0 Unported.
