Автор:
Eugene Taylor
Дата создания:
13 Август 2021
Дата обновления:
16 Май 2023

Содержание
- меры
- подсказки
Шестиугольник – это шестигранный многоугольник. Когда шестиугольник правильный, это означает, что у него шесть сторон равной длины и апофема. Это понятие относится к отрезку линии, идущему от центра многоугольника к центральной точке одной из его сторон. Обычно вам нужно знать значение апофемы при расчете площади шестиугольника. Зная размер одной стороны, можно будет оговорить длину апофемы.
меры
Метод 1 из 2: Использование теоремы Пифагора (известная длина или радиус)
-

Разделите шестиугольник на шесть равносторонних равносторонних треугольников. Для этого нарисуйте линию, соединяющую каждую вершину или точку с противоположной вершиной.
-

Выберите треугольник и обратите внимание на длину его основания. Это значение эквивалентно стороне шестиугольника.
- Например, на вашей стороне может быть шестиугольник. Следовательно, основание каждого равностороннего треугольника будет одинаковой длины.
-

Создайте два прямоугольных треугольника. Для этого из верхней вершины равностороннего треугольника проведите линию перпендикулярно его основанию. Эта линия разрежет основание треугольника пополам (представляя вершину шестиугольника). Обозначьте длину основания одного из прямоугольных треугольников.
- Например, если основание равностороннего треугольника равно, и вы разделите его пополам, каждый из оставшихся прямоугольных треугольников будет иметь основание, равное.
-

Подготовьте формулу теоремы Пифагора. В уравнении он представляет собой длину гипотенузы (сторона, противоположная прямому углу), а e представляет длины других сторон.
- Например, если у прямоугольного треугольника есть гипотенуза, одна сторона и другая сторона (), теорема Пифагора будет утверждать, что – это верно, когда вычисления будут завершены:.
- Вставьте значение длины основания прямоугольного треугольника в уравнение. Поместите его на место.
- Например, если длина основания равна, уравнение будет выглядеть так:
-

Вставьте значение длины гипотенузы в уравнение. Вы знаете это число, потому что уже знаете длину стороны шестиугольника. В правильном шестиугольнике он равен тому же измерению радиуса. Луч, в свою очередь, представляет собой линию, соединяющую центральную точку многоугольника с одной из его вершин. Вы заметите, что гипотенуза прямоугольного треугольника также равна радиусу шестиугольника, так же как сторона шестиугольника равна длине гипотенузы.
- Например, если длина в поперечном направлении равна, длина гипотенузы треугольника также будет равна. Уравнение запишется следующим образом:
-

Возведите известные значения в квадрат. Помните, что для этого просто умножьте число на себя.
- Например, возведение известных значений в квадрат приведет к следующему:
- Выделите известную переменную. Для этого вычтите большое значение с обеих сторон уравнения.
- Например:
-

Найдите значение. Для этого вычислите квадратный корень из каждой стороны уравнения. Это приведет к тому, что длина недостающей стороны будет равна длине апофемы.
- Например, вы можете определить это с помощью калькулятора. Следовательно, недостающая длина в прямоугольном треугольнике (и длина апофемы шестиугольника) равна.
Метод 2 из 2: Использование тригонометрии (известная длина или радиус)
-

Напишите формулу для определения апофемы правильного многоугольника. Это будет, где он представляет собой поперечную длину многоугольника и представляет количество сторон, которые у него есть.
-

Вставьте значение длины стороны в уравнение. Не забудьте поставить его вместо переменной.
- Например, в случае шестиугольника на его стороне это будет выглядеть так:
- Напишите количество сторон уравнения. У шестиугольника шесть сторон. Не забудьте указать это значение вместо переменной.
- Например: .
-

Завершите вычисления в скобках. Вы ищете значение в градусах, которое будет использоваться для вычисления тангенса.
- Например, чтобы уравнение выглядело так:
-

Рассчитайте касательную. Для этого воспользуйтесь калькулятором или тригонометрической таблицей.
- Например, тангенс равен, и будет помещен в формулу следующим образом :.
-

Умножьте касательную на и разделите длину стороны на результат. Далее вы узнаете длину апофемы шестиугольника.
- Например:
Таким образом, апофема правильного шестиугольника со сторонами будет иметь приблизительную длину.
- Например:
подсказки
- Термин «апотема» может относиться как к отрезку линии, так и к его длине.
- Помните, что этот прием работает только с правильными шестиугольниками. Неправильные многоугольники не имеют апофемы.
Автор:
Robert Simon
Дата создания:
23 Июнь 2021
Дата обновления:
18 Май 2023

Содержание
- Шагать
- подсказки
Шестиугольник – это многоугольник с шестью углами и сторонами. Когда шестиугольник правильный, у него шесть равных сторон и апофема. Апофема – это отрезок прямой от центра многоугольника до центра каждой стороны. Обычно для вычисления площади шестиугольника необходимо указать длину апофемы. Если вам известна длина стороны шестиугольника, вы можете рассчитать длину апофемы.
Шагать
Метод 1 из 2: Использование теоремы Пифагора (указана длина радиуса)
-

Разделите шестиугольник на шесть равносторонних равносторонних треугольников. Для этого нарисуйте линию от каждой вершины или укажите точку на противоположную вершину.
-

Выберите треугольник и обратите внимание на длину основания. Это равно длине стороны шестиугольника.
- Например, у вас есть шестиугольник с длиной стороны 8 см. Следовательно, основание каждого равностороннего треугольника составляет 8 см.
-

Составьте два прямоугольных треугольника. Вы делаете это, проводя линию от верхней вершины равностороннего треугольника перпендикулярно основанию. Эта линия разделит основание треугольника пополам (сделав его апофемой шестиугольника). Обозначьте длину основания одного из прямоугольных треугольников.
- Например, если основание равностороннего треугольника составляет 8 см, то основание каждого прямоугольного треугольника – когда вы делите треугольник на два прямоугольных треугольника – теперь равно 4 см.
-

Воспользуйтесь теоремой Пифагора. Формула:, где равно длине гипотенузы (сторона, противоположная прямому углу), а и равны длинам двух других сторон треугольника.
- Например, если у прямоугольного треугольника гипотенуза (гипотенуза) одной стороны и другой стороны приблизительно (), теорема Пифагора утверждает, что это верно, когда вы уточняете это:.
-

Подставьте в формулу длину основания прямоугольного треугольника. Замена для.
- Например, если длина основания равна 4, ваша формула будет выглядеть так:
-

Подставьте в формулу длину гипотенузы. Вы знаете длину гипотенузы, потому что знаете длину шестиугольника. Длина стороны правильного шестиугольника равна радиусу шестиугольника. Радиус – это линия, соединяющая центр многоугольника с одной из его вершин. Вы заметите, что гипотенуза прямоугольного треугольника также является радиусом шестиугольника, поэтому длина стороны шестиугольника равна длине гипотенузы.
- Например, если длина стороны шестиугольника 8 см, то длина гипотенузы прямоугольного треугольника также будет 8 см. Итак, ваша формула теперь будет выглядеть так:
-

Возведите известные значения формулы в квадрат. Помните, возведение числа в квадрат – это то же самое, что умножение этого числа на само себя.
- Например, после возведения известных значений в квадрат ваша формула будет выглядеть так:
-

Изолировать неизвестную переменную. Вы делаете это путем вычитания квадрата значения из обеих частей уравнения.
- Например:
-

Решить для. Вы делаете это, определяя квадратный корень из каждой стороны уравнения. Это даст вам длину недостающей стороны треугольника, которая равна длине апофемы шестиугольника.
- Например, с помощью калькулятора вы рассчитываете. Таким образом, недостающая длина прямоугольного треугольника и, следовательно, длина апофемы шестиугольника составляет 6,93 см.
Метод 2 из 2: Использование тригонометрии (и заданного радиуса)
-

Создайте формулу для поиска апофемы правильного многоугольника. Формула:, где равно длине стороны многоугольника и равно количеству сторон многоугольника.
-

Подставьте длину стороны в формулу. Не забудьте заменить переменную.
- Например, для шестиугольника с длиной стороны 8 см формула будет выглядеть так:.
-

Введите количество сторон в формулу. У шестиугольника 6 сторон. Не забудьте заменить переменную.
- Например: .
-

Завершите расчет в скобках. Это дает вам количество градусов, необходимое для вычисления тангенса.
- Например, как сейчас выглядит формула:
-

Определите касательную. Используйте для этого калькулятор или тригонометрическую таблицу.
- Например, тангенс 30 составляет приблизительно 0,577, поэтому формула будет выглядеть так:
-

Умножьте касательную на 2, а затем разделите длину одной стороны на это число. Таким образом, вы рассчитали длину апофемы вашего шестиугольника.
- Например:
Таким образом, апофема правильного шестиугольника со стороной 8 см составляет около 6,93 см.
- Например:
подсказки
- Термин «апофема» может относиться к фактическому отрезку линии или длине этого отрезка линии.
- Помните, что этот метод работает только с правильными шестиугольниками. Неправильные шестиугольники не имеют апофемы.
Популярные статьи
Публикации
Одевайся как европеец
Европейцы известны своим прекрасным чувством моды, и не без оснований! Они часто одеваются в лучшую, стильную одежду, которая делает моду в большинстве других стран скучной и унылой. Если вы путешеств…
Создайте тег в Instagram
Если вы хотите максимально использовать возможности In tagram, важно знать, как и когда отмечать фотографии. Следуйте приведенным ниже инструкциям, и вы быстро создадите теги как профессионал. Метод 1…
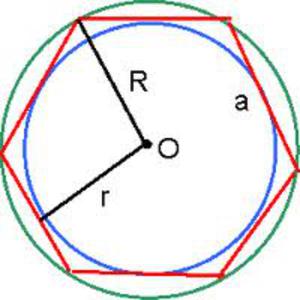
Правильный шестиугольник
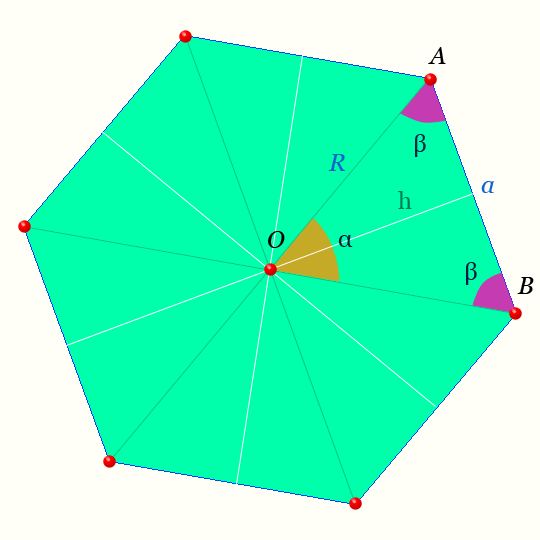
Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.
Правильный шестиугольник
Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA, OB — радиусы правильного шестиугольника.
Обозначения на рисунке для правильного шестиугольника
| n=6 | число сторон и вершин правильного шестиугольника, | шт |
|---|---|---|
| α | центральный угол правильного шестиугольника, | радианы, ° |
| β | половина внутреннего угла правильного шестиугольника, | радианы, ° |
| γ | внутренний угол правильного шестиугольника, | радианы, ° |
| a | сторона правильного шестиугольника, | м |
| R | радиусы правильного шестиугольника, | м |
| p | полупериметр правильного шестиугольника, | м |
| L | периметр правильного шестиугольника, | м |
| h | апофемы правильного шестиугольника, | м |
Основные формулы для правильного шестиугольника
Периметр правильного шестиугольника
[ L = 6a ]
Полупериметр правильного шестиугольника
[ p = 3a ]
Центральный угол правильного шестиугольника в радианах
[ α = frac{π}{3} ]
Центральный угол правильного шестиугольника в градусах
[ α = frac{180°}{3} = 60° ]
Половина внутреннего угла правильного шестиугольника в радианах
[ β = frac{π}{3} ]
Половина внутреннего угла правильного шестиугольника в градусах
[ β = frac{180°}{3} = 60° ]
Внутренний угол правильного шестиугольника в радианах
[ γ = 2β = frac{2}{3}π ]
Внутренний угол правильного шестиугольника в градусах
[ γ = frac{2}{3}180° = 120° ]
Площадь правильного шестиугольника
[ S = ph = 3ha ]
Или учитывая формулу Площади правильного шестиугольника получим
[ S = frac{3sqrt{3}}{2}a^2 ]
Отсюда получим апофему правильного шестиугольника
[ h = frac{sqrt{3}}{2}a ]
Правильный шестиугольник |
стр. 270 |
|---|
Правильный шестиугольник и его свойства
 Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.
Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
 чертится прямая линия и на ней ставится точка;
чертится прямая линия и на ней ставится точка;- из этой точки строится окружность (она является ее центром);
- из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
- после этого отрезками последовательно соединяются все точки на первой окружности.
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
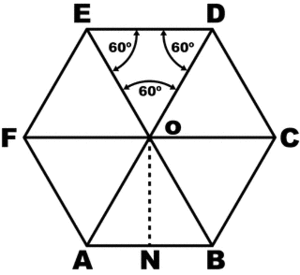
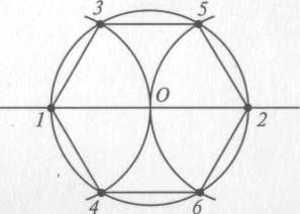 Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
R=а.
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
S=πR²
Вписанная окружность
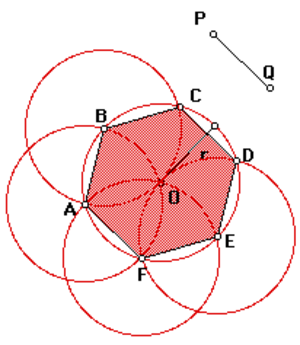 Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2.
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
 Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.- Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
- Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
- Углы новообразованного шестиугольника равняются 360-120-60-60=120°.
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
Площадь нового шестиугольника можно посчитать так:
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к практике
 Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Гексагон
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник – это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник – это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник – это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 – 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в ( sqrt <3>) раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
- инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
- nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .
Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ) :
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac<<sqrt 3 >><2>normalsize)
Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
(S = pr = largefrac<<3sqrt 3 >><2>normalsize),
где (p) − полупериметр шестиугольника.
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Правильный шестиугольник и его свойства
Определение
Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.
Замечание
Т.к. сумма всех углов (n) –угольника равна (180^circ(n-2)) , то каждый угол правильного (n) –угольника равен [alpha_n=dfracn cdot 180^circ]
Пример
Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac <4-2>4cdot 180^circ=90^circ) ;
каждый угол правильного шестиугольника равен (dfrac<6-2>6cdot 180^circ=120^circ) .
Теоремы
1. Около любого правильного многоугольника можно описать окружность, и притом только одну.
2. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Следствия
1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.
2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.
Теорема
Если (a) – сторона правильного (n) –угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin S&=dfrac n2ar\ a&=2Rcdot sindfrac<180^circ>n\ r&=Rcdot cosdfrac<180^circ>n end]
Свойства правильного шестиугольника
1. Сторона равна радиусу описанной окружности: (a=R) .
2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.
3. Все углы правильного шестиугольника равны (120^circ) .
4. Площадь правильного шестиугольника со стороной (a) равна (dfrac<3sqrt<3>><2>a^2) .
5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.
6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).
Замечание
В общем случае правильный (n) -угольник инвариантен относительно поворота на угол (dfrac<360^circ>) .
[spoiler title=”источники:”]
http://calcsbox.com/post/geksagon.html
http://shkolkovo.net/theory/77
[/spoiler]
Правильный шестиугольник — это многоугольник, состоящий из шести равных сторон и шести равных углов.
Если шесть равносторонних треугольников расположены бок о бок, то образуется правильный шестиугольник. Поэтому площадь правильного шестиугольника равна шести равносторонним треугольникам.
- Правильный шестиугольник имеет (6) сторон, (6) углов и 6 вершин.
- Сумма внутренних углов шестиугольника (-(6 − 2) · 180° = 720°).
- Внутренний угол правильного шестиугольника равен (720º / 6 = 120º).
- Центральный угол правильного шестиугольника меры: (360 : 6 = 60º).
- Количество диагоналей (- 6 · (6 − 3) : 2 = 9).
- Апофема правильного шестиугольника:
(a=sqrt{l^2-frac{l}{2}})
Свойства правильного шестиугольника
Вот некоторые свойства правильного шестиугольника:
-
Равные стороны: Все стороны правильного шестиугольника имеют одинаковую длину. Это означает, что каждая сторона равна другим сторонам в шестиугольнике.
-
Равные углы: Углы в правильном шестиугольнике равны между собой. Каждый угол равен 120 градусам.
-
Сумма углов: Сумма всех углов в правильном шестиугольнике равна 720 градусам. Это можно получить, умножив число углов (6) на величину каждого угла (120 градусов).
-
Центральная симметрия: У правильного шестиугольника есть центр симметрии, что означает, что при вращении шестиугольника вокруг этого центра на угол 60 градусов он будет выглядеть так же, как и до вращения.
-
Радиус окружности: В правильном шестиугольнике можно описать окружность, в которую все вершины шестиугольника попадают на окружность. Радиус этой окружности может быть найден с использованием формулы: радиус = сторона / (√3), где сторона – длина стороны шестиугольника.
-
Площадь: Площадь правильного шестиугольника может быть вычислена с помощью формулы: площадь = (3√3/2) * сторона^2, где сторона – длина стороны шестиугольника.
Эти свойства помогают определить и описать основные характеристики и свойства правильного шестиугольника.
Часто задаваемые вопросы:
✅ Можно ли вписать правильный шестиугольник в окружность?
↪ Да, правильный шестиугольник можно вписать в окружность таким образом, чтобы все его вершины лежали на окружности.
✅ Какие свойства имеют стороны в правильном шестиугольнике?
↪ В правильном шестиугольнике все стороны равны между собой.
✅ Какова сумма углов в правильном шестиугольнике?
↪ Сумма всех углов в правильном шестиугольнике равна 720 градусов.
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
