Апофема правильной треугольной пирамиды: формула и пример задачи
При изучении характеристик пространственных фигур в курсе стереометрии большое внимание уделяется таким свойствам, как площадь и объем. В то же время знать линейные параметры фигур важно, чтобы иметь возможность рассчитать указанные свойства. В данной статье ответим на вопрос, как найти апофему пирамиды правильной треугольной.
Какая фигура будет рассмотрена?
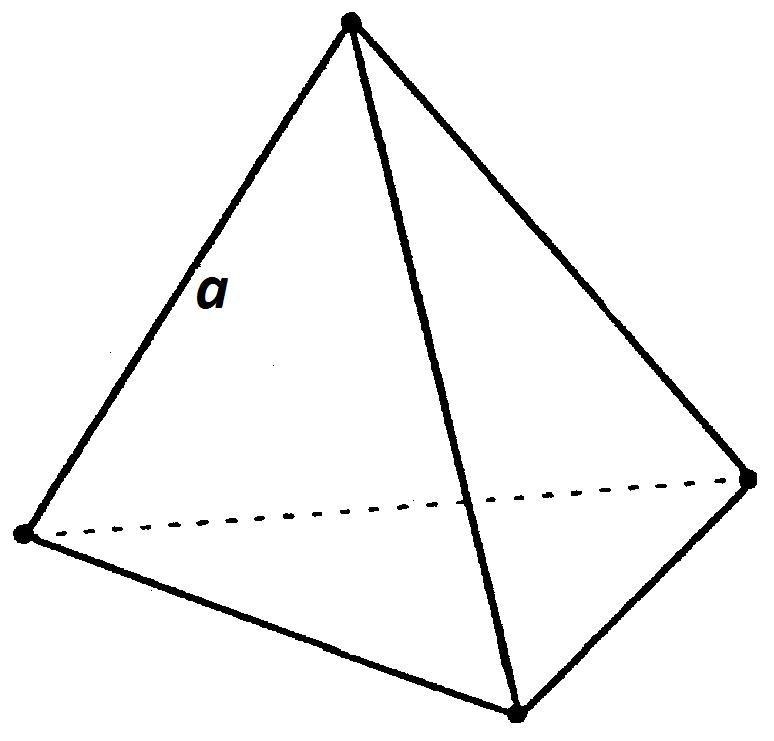
Треугольная пирамида с правильным основанием представляет собой фигуру в пространстве, которая ограничена одним равносторонним треугольником (основание) и тремя равнобедренными треугольниками (боковые стороны). Чтобы иметь возможность более четко представить эту пирамиду, покажем ее на рисунке.
 Вам будет интересно:Зазноба – это … Значение слова
Вам будет интересно:Зазноба – это … Значение слова

Важной точкой любой пирамиды является ее вершина, которая не принадлежит основанию. Если опустить перпендикуляр из нее на основание, то его длина будет высотой фигуры. В дальнейшем будем обозначать высоту буквой h. Высота правильной пирамиды падает точно в геометрический центр треугольника (точка пересечения его медиан, а также биссектрис и высот). Вторым линейным параметром, который следует знать, является длина стороны основания треугольной пирамиды, то есть длина стороны равностороннего треугольника. Обозначим ее буквой a.
Треугольная пирамида имеет собственное название – тетраэдр. Тетраэдр не является чисто теоретической геометрической фигурой. Она также встречается в некоторых природных структурах. Так, в алмазе атом углерода соединен с четырьмя такими же атомами, которые образуют тетраэдр. Другой пример – это молекула метана, в которой углерод, соединенный с четырьмя атомами водорода, образует правильную треугольную пирамиду.
Формула апофемы пирамиды правильной треугольной
Перейдем непосредственно к вопросу статьи. Для треугольной пирамиды правильной апофемой называется любая из высот боковых треугольников, опущенная из вершины фигуры. Обозначим ее hb. Поскольку рассматриваемая фигура состоит из трех боковых треугольников, которые равны друг другу, то она имеет три одинаковых апофемы hb.
Определение длины апофемы не составляет большого труда. Предположим, что высота h и длина стороны a известны. Проводим высоту фигуры и рассматриваем треугольник прямоугольный, который находится внутри пирамиды и образован следующими сторонами:
- апофемой hb (гипотенуза);
- высотой h (один катет);
- 1/3 медианы m равностороннего треугольника (второй катет).
Длина медианы m треугольника в основании равна:
m = √3/2*a
Пользуясь теоремой Пифагора, получаем формулу для длины апофемы hb:
hb = √((1/3*m)2 + h2) =>
hb = √(a2/12 + h2)
Эта формула показывает, что длина апофемы hb для любых параметров треугольной пирамиды всегда больше ее высоты h.
Решение задачи на определение значения hb

Решим интересную задачу. Рассчитаем длину апофемы для тетраэдра, у которого все ребра равны друг другу.
Обозначим длину ребра буквой a. Она же является стороной треугольника в основании. Чтобы определить hb, необходимо найти h. Сделать это не сложно, если рассмотреть прямоугольный треугольник, образованный высотой h, ребром a и двумя третями медианы m. Получаем:
h = √(a2 – 4/9*m2) = √(a2 – 4/9*3/4*a2) = a*√(2/3)
Теперь применяем формулу для апофемы, получаем:
hb = √(a2/12 + h2) = √(a2/12 + 2/3*a2) = √3/2*a
Мы получили очевидный результат. Апофема правильной пирамиды треугольной равна длине медианы любого из равносторонних треугольников.
Автор:

15-12-2018 00:52
Жду ваши вопросы и мнения в комментариях
Апофема правильной треугольной пирамиды: формула и пример задачи
При изучении характеристик пространственных фигур в курсе стереометрии большое внимание уделяется таким свойствам, как площадь и объем. В то же время знать линейные параметры фигур важно, чтобы иметь возможность рассчитать указанные свойства. В данной статье ответим на вопрос, как найти апофему пирамиды правильной треугольной.
Какая фигура будет рассмотрена?
Треугольная пирамида с правильным основанием представляет собой фигуру в пространстве, которая ограничена одним равносторонним треугольником (основание) и тремя равнобедренными треугольниками (боковые стороны). Чтобы иметь возможность более четко представить эту пирамиду, покажем ее на рисунке.
 Вам будет интересно: Зазноба – это . Значение слова
Вам будет интересно: Зазноба – это . Значение слова

Важной точкой любой пирамиды является ее вершина, которая не принадлежит основанию. Если опустить перпендикуляр из нее на основание, то его длина будет высотой фигуры. В дальнейшем будем обозначать высоту буквой h. Высота правильной пирамиды падает точно в геометрический центр треугольника (точка пересечения его медиан, а также биссектрис и высот). Вторым линейным параметром, который следует знать, является длина стороны основания треугольной пирамиды, то есть длина стороны равностороннего треугольника. Обозначим ее буквой a.
Треугольная пирамида имеет собственное название – тетраэдр. Тетраэдр не является чисто теоретической геометрической фигурой. Она также встречается в некоторых природных структурах. Так, в алмазе атом углерода соединен с четырьмя такими же атомами, которые образуют тетраэдр. Другой пример – это молекула метана, в которой углерод, соединенный с четырьмя атомами водорода, образует правильную треугольную пирамиду.

Формула апофемы пирамиды правильной треугольной
Перейдем непосредственно к вопросу статьи. Для треугольной пирамиды правильной апофемой называется любая из высот боковых треугольников, опущенная из вершины фигуры. Обозначим ее hb. Поскольку рассматриваемая фигура состоит из трех боковых треугольников, которые равны друг другу, то она имеет три одинаковых апофемы hb.
Определение длины апофемы не составляет большого труда. Предположим, что высота h и длина стороны a известны. Проводим высоту фигуры и рассматриваем треугольник прямоугольный, который находится внутри пирамиды и образован следующими сторонами:
- апофемой hb (гипотенуза);
- высотой h (один катет);
- 1/3 медианы m равностороннего треугольника (второй катет).
Длина медианы m треугольника в основании равна:
Пользуясь теоремой Пифагора, получаем формулу для длины апофемы hb:
Эта формула показывает, что длина апофемы hb для любых параметров треугольной пирамиды всегда больше ее высоты h.
Решение задачи на определение значения hb

Решим интересную задачу. Рассчитаем длину апофемы для тетраэдра, у которого все ребра равны друг другу.
Обозначим длину ребра буквой a. Она же является стороной треугольника в основании. Чтобы определить hb, необходимо найти h. Сделать это не сложно, если рассмотреть прямоугольный треугольник, образованный высотой h, ребром a и двумя третями медианы m. Получаем:
h = √(a2 – 4/9*m2) = √(a2 – 4/9*3/4*a2) = a*√(2/3)
Теперь применяем формулу для апофемы, получаем:
hb = √(a2/12 + h2) = √(a2/12 + 2/3*a2) = √3/2*a
Мы получили очевидный результат. Апофема правильной пирамиды треугольной равна длине медианы любого из равносторонних треугольников.
Апофема пирамиды. Формулы для апофемы правильной треугольной пирамиды
Пирамида – это пространственный полиэдр, или многогранник, который встречается в геометрических задачах. Основными свойствами этой фигуры являются ее объем и площадь поверхности, которые вычисляются из знания любых двух ее линейных характеристик. Одной из таких характеристик является апофема пирамиды. О ней пойдет речь в статье.
Фигура пирамида
Прежде чем приводить определение апофемы пирамиды, познакомимся с самой фигурой. Пирамида представляет собой многогранник, который образован одним n-угольным основанием и n треугольниками, составляющими боковую поверхность фигуры.
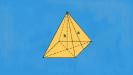
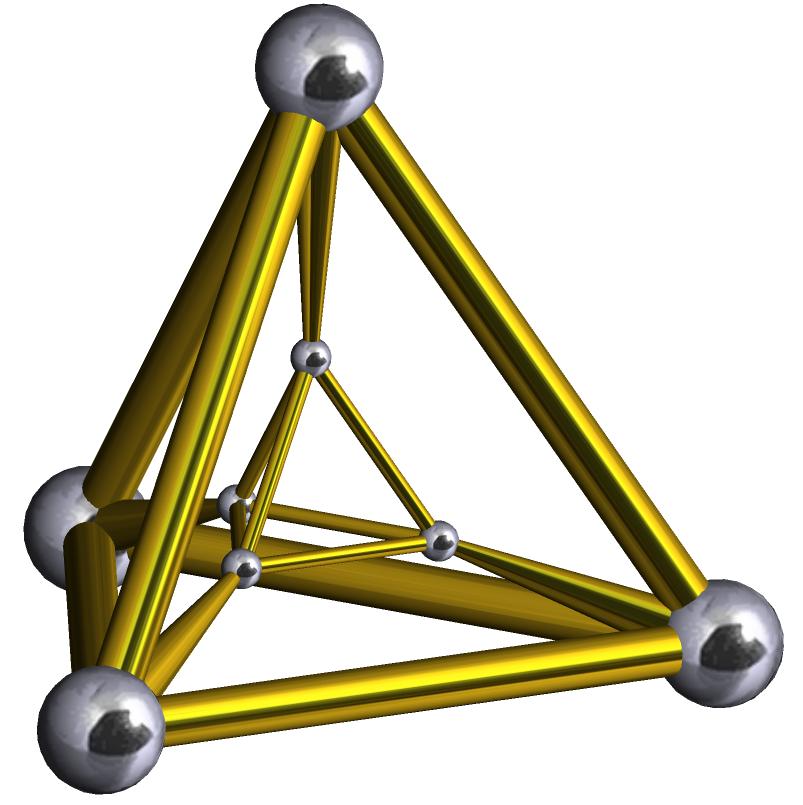
Всякая пирамида имеет вершину – точку соединения всех треугольников. Перпендикуляр, проведенный из этой вершины к основанию, называется высотой. Если высота пересекает в геометрическом центре основание, то фигура называется прямой. Пирамида прямая, имеющая равностороннее основание, называется правильной. На рисунке показана пирамида с шестиугольным основанием, на которую смотрят со стороны грани и ребра.

Апофема правильной пирамиды
Ее также называют апотемой. Под ней понимают перпендикуляр, проведенный из вершины пирамиды к стороне основания фигуры. По своему определению этот перпендикуляр соответствует высоте треугольника, который образует боковую грань пирамиды.
Поскольку мы рассматриваем пирамиду правильную с n-угольным основанием, то все n апофем для нее будут одинаковыми, поскольку таковыми являются равнобедренные треугольники боковой поверхности фигуры. Заметим, что одинаковые апофемы являются свойством правильной пирамиды. Для фигуры общего типа (наклонной с неправильным n-угольником) все n апофем будут разными.
Еще одним свойством апофемы пирамиды правильной является то, что она одновременно является высотой, медианой и биссектрисой соответствующего треугольника. Это означает, что она делит его на два одинаковых прямоугольных треугольника.
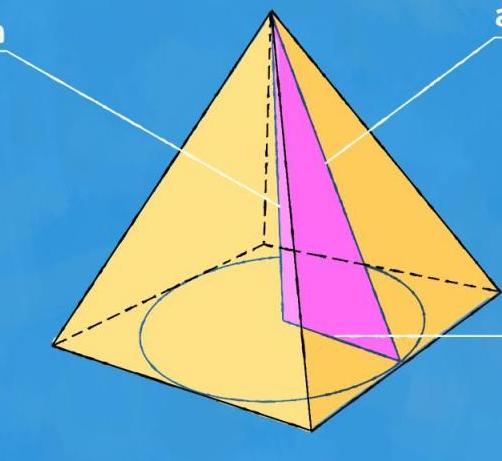
Треугольная пирамида и формулы для определения ее апофемы
В любой правильной пирамиде важными линейными характеристиками являются длина стороны ее основания, ребро боковое b, высота h и апофема hb. Эти величины друг с другом связаны соответствующими формулами, которые можно получить, если начертить пирамиду и рассмотреть необходимые прямоугольные треугольники.
Правильная треугольная пирамида состоит из 4 треугольных граней, причем одна из них (основание) должна быть обязательно равносторонней. Остальные являются равнобедренными в общем случае. Апофему треугольной пирамиды можно определить через другие величины по следующим формулам:
Первое из этих выражений справедливо для пирамиды с любым правильным основанием. Второе выражение характерно исключительно для треугольной пирамиды. Оно показывает, что апофема всегда больше высоты фигуры.
Не следует путать апофему пирамиды с таковой для многогранника. В последнем случае апофемой называется перпендикулярный отрезок, проведенный к стороне многогранника из его центра. Например, апофема равностороннего треугольника равна √3/6*a.
Задача на вычисление апофемы
Пусть дана правильная пирамида с треугольником в основании. Необходимо вычислить ее апофему, если известно, что площадь этого треугольника равна 34 см 2 , а сама пирамида состоит из 4 одинаковых граней.
В соответствии с условием задачи мы имеем дело с тетраэдром, состоящим из равносторонних треугольников. Формула для площади одной грани имеет вид:
Откуда получаем длину стороны a:
Для определения апофемы hb воспользуемся формулой, содержащей боковое ребро b. В рассматриваемом случае его длина равна длине основания, имеем:
Подставляя значение a через S, получим конечную формулу:
Мы получили простую формулу, в которой апофема пирамиды зависит только от площади ее основания. Если подставить значение S из условия задачи, то получим ответ: hb ≈ 7,674 см.
Апофема делит сторону основания пополам. Все ли вы знаете о правильной пирамиде?
Для решения задач на обширную тему “Стереометрия” нужно выучить и разобрать очень много элементов и тонкостей, полностью изучить все свойства фигур, а также не забывать свойства всех фигур, которые включены в курс “Планиметрии”.
Среди задач по объемным фигурам очень часто встречается правильная пирамида, чтобы легко решать их, нужно хорошо с ней познакомиться. Пирамида называется правильной, если в ее основании лежит правильный многоугольник, а ее вершина спроецирована в центр основания. Как раз при изучении этого многоугольника вы услышите об апофеме.

Как вы уже поняли, в геометрии понятие апофемы – это широко распространенное явление. Невозможно узнать некоторые измерения пирамиды без знания этого. Само слово “апофема” – это пришедшее к нам из греческого языка явление, и переводится оно как “откладываю”.
Определение
В планиметрии апофема – перпендикуляр (как сам, так и его длина), который проведен к стороне правильного многоугольника из центра. В стереометрии апофема пирамиды – это высота в боковой грани, которая проведена к основанию. Используется только для правильных пирамид. Соответственно, апофема правильной треугольной пирамиды – это высота ее грани, которая представлена равнобедренным треугольником.
Какова роль апофемы
Апофема – это очень важный элемент пирамиды, потому что с ее помощью можно решить огромное количество задач. В частности, боковая поверхность правильной пирамиды равна полупроизведению периметра основания и апофемы грани.
Sбп = (Pосн*h)/2; h – апофема, это ее ключевая роль.

Не путайте с H (высота объемной фигуры в стереометрии).
Также, благодаря знанию апофемы, можно найти площадь грани как равнобедренного треугольника.
Свойства апофемы
Их мало, но все же их нужно помнить. В целом это следствия, вытекающие из определения. Итак, апофема в правильной пирамиде:
- Опущена на сторону основания под углом 90 градусов.
- Делит сторону, на которую опущена, пополам, так как является высотой в равнобедренном/равностороннем треугольнике и по совместительству – медианой.
В правильной пирамиде все апофемы равны, так как все ее боковые грани также одинаковые. При нахождении длины апофемы вам придется воспользоваться как свойствами многоугольника, так и свойствами многогранника. Как же найти числовое значение апофемы в правильной пирамиде?
Как найти апофему пирамиды
Ее можно найти, применяя все ранее полученные знания, вот всего лишь несколько примеров:
- Если известны боковое ребро и сторона основания. Так как апофема делит сторону основания пополам и образует с ней угол в 90 градусов, то найти ее из прямоугольного треугольника по теореме Пифагора вам не составит труда. Также можно найти апофему, используя знания соотношений в прямоугольном треугольнике.
- Если известен радиус вписанной окружности в основание правильной пирамиды и высота всей фигуры. Радиус, проведенный к точке касания, перпендикулярен касательной, и апофема перпендикулярна этой стороне основания (которая является касательной к вписанной окружности). Высота фигуры перпендикулярна основанию и попадает в центр окружности, вписанной в основание пирамиды. Следовательно, радиус и высота фигуры являются катетами и образуют прямой угол, а вместе с апофемой – прямоугольный треугольник. И опять же по теореме Пифагора или через соотношения в прямоугольном треугольнике вы легко найдете апофему.

- Также если дана площадь грани и известно основание.
В любом случае при нахождении апофемы вам придется вспоминать все основные законы и правила планиметрии. Если неизвестны какие-то элементы из этого списка, то вы можете оперировать данными параметрами, и, постепенно находя вышеописанные данные, найти апофему вам не составит труда. Надеемся, что наша статья помогла вам в освоении такой интересной темы.
[spoiler title=”источники:”]
http://fb.ru/article/442808/apofema-piramidyi-formulyi-dlya-apofemyi-pravilnoy-treugolnoy-piramidyi
http://autogear.ru/article/409/235/vse-li-vyi-znaete-o-pravilnoy-piramide-apofema—eto/
[/spoiler]
На сегодняшний день существует несколько способов нахождения апофемы. Каждый из них стоит выбирать в
зависимости от имеющихся в задаче данных.
- Апофема правильной треугольной пирамиды через высоту и
ребро основания - Апофема правильной треугольной пирамиды через площадь
боковых поверхностей и ребро нижнего основания - Апофема правильной треугольной пирамиды через площадь
боковых поверхностей и периметр нижнего основания
Через высоту и ребро основания
Первый способ включает в себя нахождение неизвестной через высоту пирамиды H и ребро основания a. Это
возможно по следующей формуле:
L = √(H² + (a / 2 tan60º)²)
где h — высота, a — ребро основания.
Цифр после
запятой:
Результат в:
Кроме того стоит знать тригонометрические функции и их значения при различных углах. В данном случае
тангенс 60º, который равен √3.
Пример. В задаче дана пирамида, у которой имеются два известных значения: высота
равна 3, а сторона основания – 8. Требуется найти апофему правильной треугольной пирамиды. Тогда
результат: b = √(3² + (8 / 2 tan60º)²)= √(9 + (4 / √3)²) = √(9 + (16 / 3)) = √(43/3) = 3.8
Через площадь боковых поверхностей и ребро нижнего основания
Второй вариант для нахождения вышеупомянутой неизвестной основан на площадях боковых поверхностей,
которые являются треугольниками, и ребре основания a. Сначала стоит разобраться с площадью боковых
поверхностей. Она состоит из суммы трех отдельных площадей боковых граней. Площадь прямоугольного
треугольника: S = 0,5 * a * b, где а и b – это катеты прямоугольного
треугольника. Площадь равностороннего треугольника: S = (a * a√3) / 4, где
а – это ребро треугольника. Площадь произвольного треугольника: S = ah / 2, S = (a * b * sinα) / 2.
Формула для нахождения апофемы правильной пирамиды через площадь боковых граней и ребро основания:
L = Sбок / 3/2a
где Sбок — площадь боковых поверхностей, a — ребро основания.
Цифр после
запятой:
Результат в:
Пример. Необходимо найти апофему правильной треугольной пирамиды, когда площадь
боковых поверхностей равна 120, а ребро основания — 4. Решение: L = 120 / 3/2 * 4 = 20.
Через площадь боковых поверхностей и периметр нижнего основания
Есть еще и третий способ, который основан на площади боковых поверхностей и периметре основания.
Периметр основания — это сумма длин всех сторон, который принадлежат основанию. В правильном
треугольнике длину одного ребра умножают на три. Формула:
L = Sбок / 1/2P
где Sбок — площадь боковых поверхностей, P — периметр основания.
Цифр после
запятой:
Результат в:
Пример. Необходимо найти апофему правильной треугольной пирамиды, когда площадь
боковых поверхностей равна 120, а периметр — 12. Решение: апофема равна L = 120 / 1/2 * 12 = 120 * 6 = 20.
Пирамида представляет собой объемную геометрическую фигуру, многогранник, в основании которого лежит
n-угольник, а остальные n граней- треугольники с общей вершиной, называющейся вершиной пирамиды.
Правильная пирамида – это пирамида, в основании которой лежит правильный многоугольник, а боковые
ребра равны. У треугольной пирамиды за основание принимают треугольник.
Апофемой принято называть высоту боковой грани. Это перпендикуляр, который был опущен из вершины
грани на противолежащую сторону. Часто ее обозначают латинской буквой L или же h, но обязательно
маленькой, потому что большая – это высота не грани, а самой пирамиды. Все апофемы правильной
треугольной пирамиды будут равны между собой. Апофема правильной треугольной пирамиды равна
отношению площади боковых поверхностей на половину периметра нижнего основания.
Как найти апофему в пирамиде
Апофема -высота боковой грани, проведенная в правильной пирамиде из её вершины. Ее можно найти как в обычной правильной пирамиде, так и усеченной. Рассмотрим оба случая
Правильная пирамида
В ней все боковые ребра равны, боковые грани – равнобедренные равные треугольники, а основание – правильный многоугольник. Т.к. все апофемы правильной пирамиды равны, то достаточно найти одну в любом треугольнике. Треугольники являются равнобедренными, а апофема – это высота. Высота, проведенная в равнобедренном треугольнике из вершины к основанию, является медианой и биссектрисой. Медиана делит сторону пополам, а биссектриса угол на два равных угла. Высота – перпендикуляр, проведенный из вершины к основанию.
Допустим, известны все стороны равнобедренного треугольника и проведена медиана, которая делит основание на два равных отрезка. Т.к. медиана – это высота, то она является перпендикуляром, т.е. угол между медианой и основанием равен 90 градусов. Значит, получается прямоугольный треугольник. Боковая сторона является гипотенузой, половина основания и высота(медиана) – это катеты. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Таким способом можно найти высоту.
Пусть известен угол, лежащий напротив основания. И какая-нибудь одна из сторон (либо боковая, либо основание). Биссектриса, проведенная из вершины к основанию, является высотой. Поэтому опять получается прямоугольный треугольник. Известен угол и одна из сторон. С помощью синуса, косинуса и тангенса можно найти высоту. Синус – отношение противолежащего катета к гипотенузе, катет- отношение прилежащего катета к гипотенузе, тангенс – отношение синуса к косинусу или противолежащего катета к прилежащему. Подставив известные стороны, вычислите высоту.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Правильная усеченная пирамида
Боковые грани – правильные трапеции. Боковые ребра равны. Апофема – высота, проведенная в трапеции. Пусть известны два основания и боковое ребро. Из вершины проводятся высоты так, чтобы на большем основании они отсекли прямоугольник. Тогда, если мысленно убрать прямоугольник, останется равнобедренный треугольник, высоту которого можно найти по первому способу. Если известны тупые углы трапеции, то при проведении высоты, необходимо вычесть угол, равный 90 градусов(т.к. высота – это перпендикуляр)из тупого. Тогда станет известен острый угол в треугольнике. Высоту или апофему опять же можно найти по 1 способу.
![]()
2
Как найти апофему в правильной треугольной пирамиде?
2 ответа:
![]()
1
0
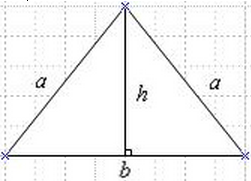
Боковыми гранями правильной треугольной пирамиды являются равнобедренные треугольники.
Апофема правильной треугольной пирамиды равна высоте треугольника составляющего одну из его сторон, поэтому рассчитывается по формуле, по которой рассчитывается высота равнобедренного треугольника.
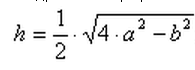
![]()
1
0
Для того, чтобы найти апофему в правильной треугольной пирамиде, потребуется использовать данную формулу: квадратный корень из h^2 + (a/2*tg 45 градусов)^2, где символ “а” является стороной условной пирамиды и символ “h” является высотой правильной пирамиды. Также, в сети существуют специальные сервисы которые вычислят в два шага апофему той или иной пирамиды, потребуется лишь ввести данные.
Читайте также
![]()
Длины параллелей в северном полушарии уменьшаются к северу и увеличиваются к югу,
пути между линиями долготы, будут короче севернее, а расстояния точек P и C от параллели одинаковые,поэтому путь, через точку P, расположенную севернее точки С ,будет короче.
Ответ:путь АРВ короче пути АСВ
![]()
Геометрию я учил, в середине прошлого века, по учебнику Киселёва. По этому же учебнику учились старшие сёстры, а книга передавалась по наследству. Учебник хранится в семье, как реликвия. Когда у дочерей, при изучении курса, возникали какие-либо вопросы, на помощь приходил учебник Киселёва. Старшая дочь, в этих случаях, говорила: ” Ну почему у Киселёва всё понятно, а в этих учебниках ничего не разобрать.” Так что по заключению двух поколений лучший учебник Киселёва.
![]()
В геометрии существует всего пять правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр. Многогранник считается правильным, только если все его грани являются правильными, все многоугольники одинаковые и равные, и все двугранные углы равны. Кроме того такие свойства у правильных многогранников: все ребра одинаковой длины, все плоские углы тоже равны, все многогранные углы имеют одно и тоже число граней и в каждой вершине сходятся одинаковое число ребер.
Это тетраэдр, гексаэдр (то есть куб), октаэдр, додекаэдр и икосаэдр.
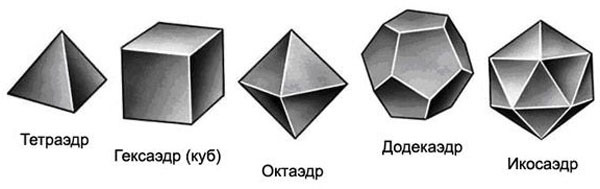
Сюда не входят, например, параллелепипед, пирамида, призма.
![]()
По теореме Пифагора
Стало быть, гипотенуза равна квадратному корню из суммы квадратов катетов. В нашем примере пусть катеты будут обозначены a и b, а гипотенуза – с. тогда с = √(a^2+b^2) = √(7^2 + 24^2) = √(49+576) = √625 = 25 (см).
Площадь треугольника равна половине произведения основания на высоту. В прямоугольных треугольниках один катет является основанием, а другой – высотой (равно как и наоборот), т.к. между ними прямой угол по определению.
S = 0.5*a*b = 0.5*7*24 = 84 (кв. см).
Кстати, гипотенузу тоже можно считать основанием, но тогда высота, проведенная к ней, будет исходить из прямого угла, что затрудняет вычисление площади, т.к. эту высоту еще надо найти. Поскольку катеты уже даны и их можно использовать при расчетах, то оптимальный вариант – использовать эти данные.
![]()
Эта задача известна как проблема Пифагоровых троек, т.е. трех таких чисел a,b,c,
для которых выполняется соотношение a^2+b^2=c^2, где все три переменные – это
натуральные числа. Не стоит здесь приводить полное решение этой проблемы – это
вряд ли кому-нужно, отметим только, что такие решения есть при следующих
соотношениях:
a=l*(m^2-n^2), b=2lmn, c=l(m^2+n^2),
где l,m,n – произвольные натуральные числа, m>n,
Например, всем известная тройка 3,4,5 образуется при l=1, m=2, n=1,
при таких значениях получаются a=3, b=4, c=5
Теперь попробуем взять значения l=3, m=3, n=2. При них получаем
a=15, b=36, c=39, проверяем:
15^2+36^2=39^2 или
225+1296=1521.
Вот Вам и еще одна пифагорова тройка, а их можно найти очень много.

