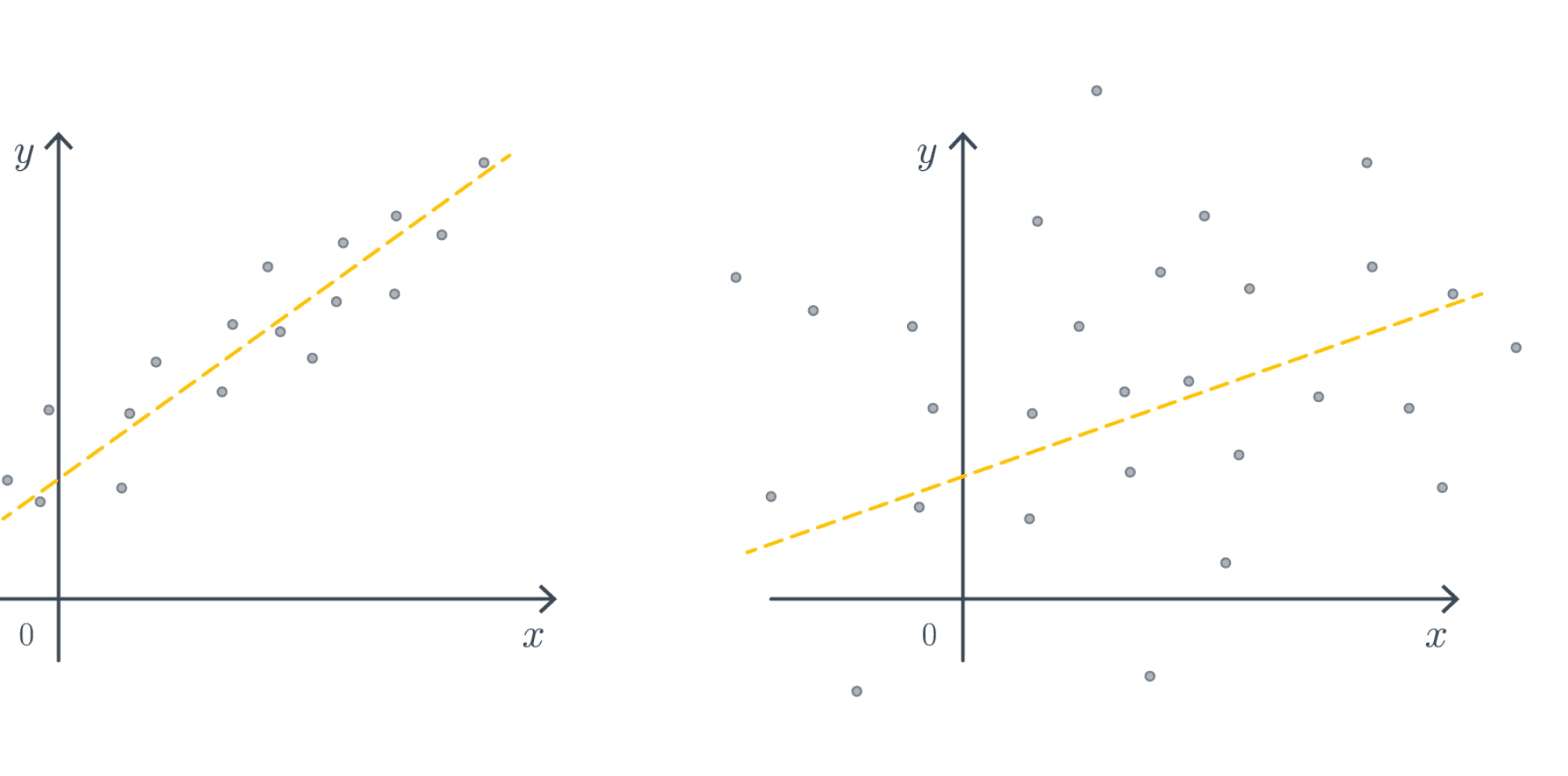Начнём с простого вопроса: как нам внести в модель априорные знания.
А зачем, собственно?
Представьте, что мы обучаем модель линейной регрессии $ysim langle x, wrangle + varepsilon$, $varepsilonsimmathcal{N}(0,sigma^2)$. С помощью MLE мы получили некоторую оценку $widehat{w}$ на веса $w$ – всякие ли их значения мы встретим с покорностью и смирением? Наверное, мы удивимся, если какие-то компоненты вектора $widehat{w}$ будут очень большими по сравнению с элементами $X$: пожалуй, наша физическая интуиция будет бунтовать против этого, мы задумаемся о том, что из-за потенциальных ошибок сокращения вычисление предсказаний $(x_i, widehat{w})$ окажутся неточным – в общем, хотелось бы по возможности избежать этого. Но как?
Будь мы приверженцами чисто инженерного подхода, мы бы сделали просто: прибавили бы к функции потерь слагаемое $+alpha|w|^2$, или $+alpha vert w vert^2$, или ещё что-то такое – тогда процедура обучения стала бы компромиссом между минимизацией исходного лосса и этой добавки, что попортило бы слегка близость $ysim langle x, w rangle$, но зато позволило бы лучше контролировать масштаб $widehat{w}$. Надо думать, вы узнали в этой конструкции старую добрую регуляризацию.
Но наша цель – зашить наше априорное знание о том, что компоненты $w$ не слишком велики по модулю, в вероятностную модель. Введение в модель априорного знания соответствует введению априорного распределения на $w$. Какое распределение выбрать? Ну, наверное, компоненты $w$ будут независимыми (ещё нам не хватало задавать взаимосвязи между ними!), а каждая из них будет иметь какое-то непрерывное распределение, в котором небольшие по модулю значения более правдоподобны, а совсем большие очень неправдоподобны. Мы знаем такие распределения? Да, и сразу несколько. Например, нормальное. Логично было бы определить
$$p(w) = prod_{i=1}^Dmathcal{N}(w_i vert 0,tau^2)$$
где $tau^2$ – какая-то дисперсия, которую мы возьмём с потолка или подберём по валидационной выборке. Отметим, что выбор нормального распределение следует и из принципа максимальной энтропии: ведь у него наибольшая энтропия среди распределений на всей числовой оси с нулевым матожиданием и дисперсией $tau^2$.
Контроль масштаба весов – это, вообще говоря, не единственное, что мы можем потребовать. Например, мы можем из каких-то физических соображений знать, что тот или иной вес в линейной модели непременно должен быть неотрицательным. Тогда в качестве априорного на этот вес мы можем взять, например, показательное распределение (которое, напомним, обладает максимальной энтропией среди распределений на положительных числах с данным матожиданием).
Оцениваем не значение параметра, а его распределение
Раз уж мы начали говорить о распределении на веса $w$, то почему бы не пойти дальше. Решая задачу классификации, мы уже столкнулись с тем, что может быть важна не только предсказанная метка класса, но и вероятности. Аналогичное верно и для задачи регрессии. Давайте рассмотрим две следующих ситуации, в каждой из коорых мы пытаемся построить регрессию $ysim ax + b$:
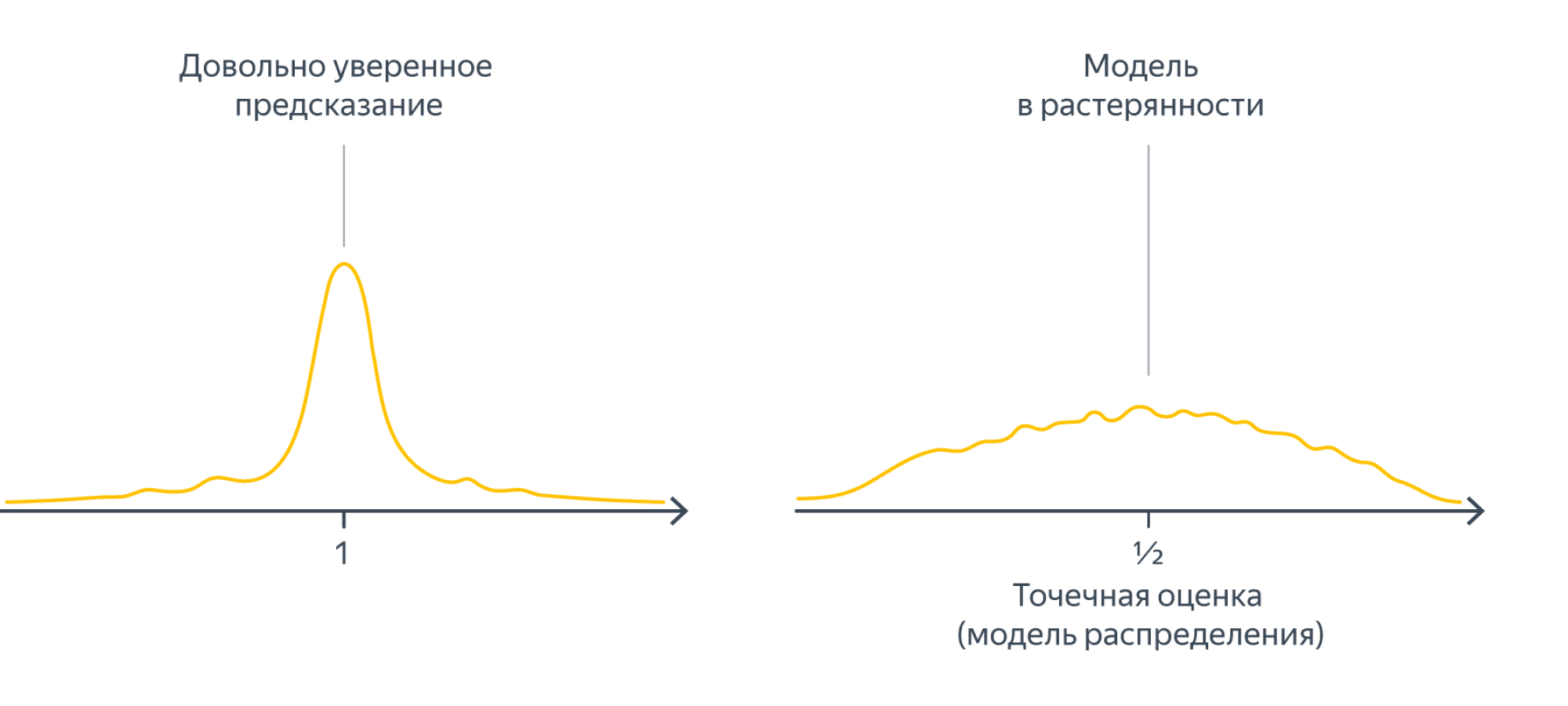
Несмотря на то, что в каждом из случаев ”точная формула” или градиентный спуск выдадут нам что-то, степень нашей уверенности в ответе совершенно различная. Один из способов выразить (не)уверенность – оценить распределение параметров. Так, для примеров выше распределения на параметр $a$ могли бы иметь какой-то такой вид:
Дальше мы постараемся формализовать процесс получения таких оценок.
Построение апостериорного распределения
Давайте ненадолго забудем про линейную регрессию и представим, что мы подобрали с полу монету, которая выпадает орлом с некоторой неизвестной пока вероятностью $theta$. До тех пор, пока мы не начали её подкидывать, мы совершенно ничего не знаем о $theta$, эта вероятность может быть совершенно любой – то есть априорное распределение на $theta$ является равномерным (на отрезке $[0,1]$):
$$p(theta) = mathbb{I}_{[0;1]}(theta)$$
Теперь представим, что мы подкинули её $n$ раз, получив результаты $Y = (y_1,ldots,y_n)$ ($0$ – решка, $1$ – орёл), среди которых $n_0 = n – sum_{i=1}^ny_i$ решек и $n_1=sum_{i=1}^ny_i$ орлов. Определённо наши познания о числе $p$ стали точнее: так, если $n_1$ мало, то можно заподозрить, что и $p$ невелико (уже чувствуете, запахло распределением!). Распределение мы посчитаем с помощью формулы Байеса:
$$color{#348FEA}{p(theta vert Y) = frac{p(theta , Y)}{p(Y)} = frac{p(Y vert theta)p(theta)}{
int p(Y vert psi)p(psi)dpsi
}}$$
в нашем случае:
$$p(theta vert Y) = frac{prod_{i=1}^ntheta^{x_i}(1 – theta)^{1 – x_i}mathbb{I}_{[0,1]}(theta)}{
int_0^1prod_{i=1}^npsi^{x_i}(1 – psi)^{1 – x_i}dpsi} =
$$
$$=frac{theta^{n_1}(1 – theta)^{n_0}mathbb{I}_{[0,1]}(theta)}{
int_0^1psi^{n_1}(1 – psi)^{n_0}dpsi}
$$
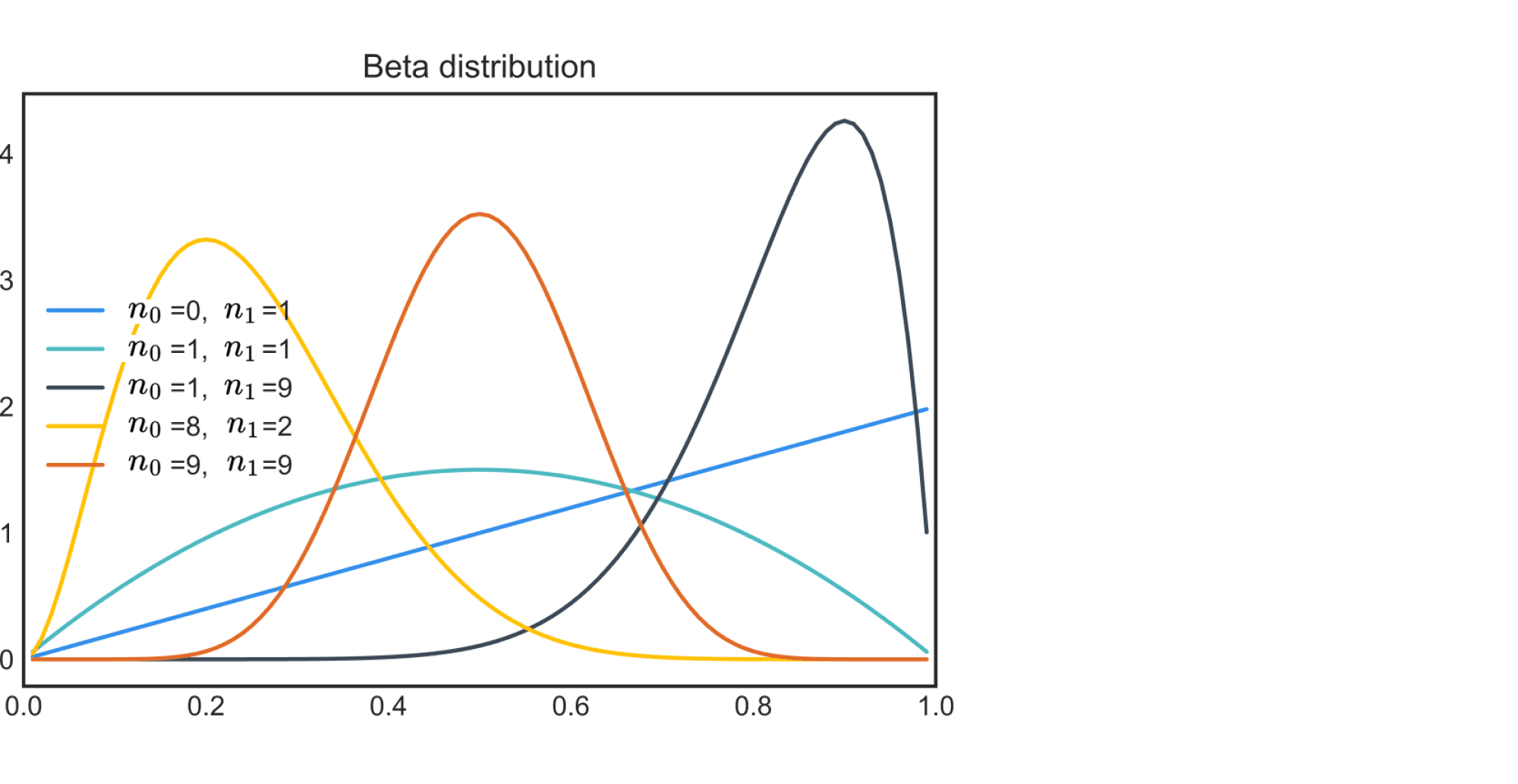
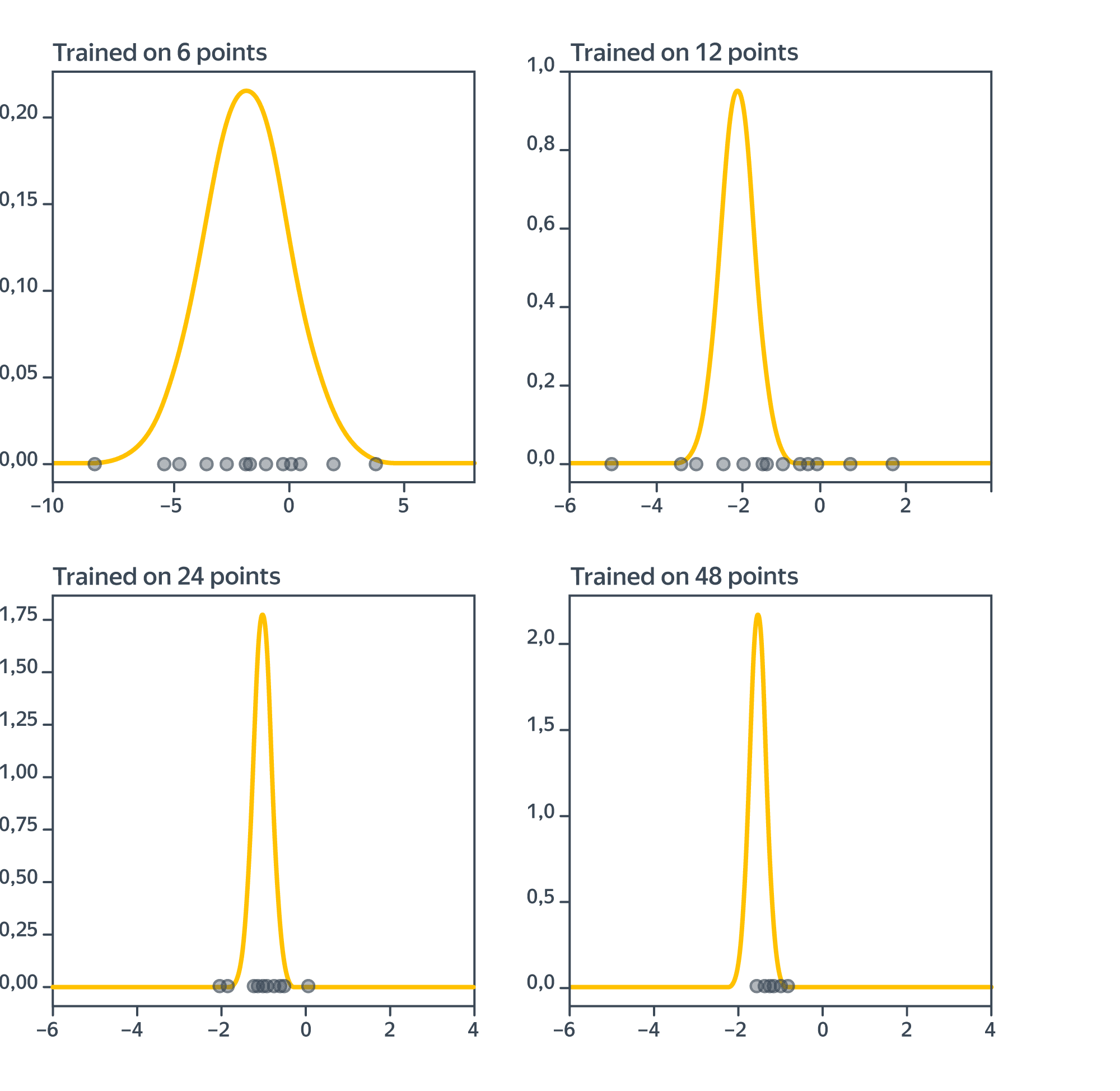
В этом выражении нетрудно узнать бета-распределение: $text{Beta}(n_1 + 1, n_0 + 1)$. Давайте нарисует графики его плотности для нескольких конкретных значений $n_0$ и $n_1$:
Как можно заметить, с ростом $n$ мы всё лучше понимаем, каким может быть $theta$, при этом если орёл выпадал редко, то пик оказывается ближе к нулю, и наоборот. Ширина пика в каком-то смысле отражает нашу уверенность в том, какими могут быть значения параметра, и не случайно чем больше у нас данных – тем уже будет пик, то есть тем больше уверенности.
Распределение $p(thetavert Y)$ параметра, полученное с учётом данных, называется апостериорным. Переход от априорного распределения к апостериорному отражает обновление нашего представления о параметрах распределения с учётом полученной информации, и этот процесс является сердцем байесовского подхода. Отметим, что если нам придут новые данные $Y’ = (y_1′,ldots,y_m’)$, в которых $m_0$ решек и $m_1$ орлов, мы сможем ещё раз обновить распределение по той же формуле Байеса:
$$p(theta vert Ycup Y’) = p([thetavert Y]vert Y’) = frac{p(Y’verttheta)p(thetavert Y)}{p(Y’)}=
$$
$$=frac{theta^{m_1}(1 – theta)^{m_0}frac{theta^{n_1}(1 – theta)^{n_0}}{B(n_1 + 1, n_0 + 1)}mathbb{I}_{[0,1]}(theta)}{
text{злой интеграл}} =
$$
$$=frac{theta^{n_1 + m_1}(1 – theta)^{n_0 + m_0}}{text{константа}}simtext{Beta}(n_1 + m_1 + 1, n_0 + m_0 + 1)$$
Вопрос на подумать. Пусть $p(yvertmu) = mathcal{N}(yvertmu,sigma^2)$ – нормальное распределение с фиксированной дисперсией $sigma^2$, а для параметра $mu$ в качестве априорного выбрано также нормальное распределение $mathcal{N}(yvert lambda,theta^2)$. Каким будет апостериорное распределение при условии данных $Y = (y_1,ldots,y_n)$?
Попробуйте посчитать сами, прежде чем смотреть решение.
$$p(theta vert Y) = frac{left[prod_{i=1}^nfrac1{sqrt{2pisigma^2}}e^{-frac{(y_i – mu)^2}{2sigma^2}}right]cdotfrac1{sqrt{2pitheta^2}}e^{-frac{(mu – lambda)^2}{2theta^2}}}{
text{злой интеграл}} =
$$
$$=frac{frac1{(2pisigma^2)^{frac{n}2}}cdotfrac1{sqrt{2pitheta^2}}e^{-frac1{2sigma^2}sum_{i=1}^n(y_i – mu)^2-frac{1}{2theta^2}(mu – lambda)^2}}{
text{злой интеграл}}$$
С точностью до множителей, не зависящих от $mu$, это экспонента квадратичной формы, то есть распределение будет нормальным. Давайте найдём его параметры. Для этого нам нужно выделить в показателе полный квадрат:
$$=frac{e^{-frac12left(frac{n}{sigma^2} + frac{1}{theta^2}right)mu^2 + left(frac1{sigma^2}sum_{i=1}^ny_i + frac1{theta^2}lambdaright)mu + text{свободный член}}}{
text{что-то, где нет }mu} = $$
Обозначим $rho^2 = left(frac{n}{sigma^2} + frac{1}{theta^2}right)^{-1}$
$$=frac{e^{-frac1{2rho^2}left[mu^2 – rho^2left(frac1{sigma^2}sum_{i=1}^ny_i + frac1{theta^2}lambdaright)right]^2 + text{остальное}}}{
text{что-то, где нет }mu}$$
Теперь уже хорошо видно, что получилось нормальное распределение с параметрами
$$lambda_{new} = left(frac{n}{sigma^2} + frac{1}{theta^2}right)^{-1}left(frac1{sigma^2}sum_{i=1}^ny_i + frac1{theta^2}lambdaright)$$
$$theta_{new}^2 = left(frac{n}{sigma^2} + frac{1}{theta^2}right)^{-1}$$
Формулы жутковатые, но проинтерпретировать их можно. Например, мы видим, что появление больших $y_i$ будет сдвигать среднее, а дисперсия уменьшается с ростом $n$.
Сопряжённые распределения
В двух предыдущих примерах нам очень сильно повезло, что апостериорные распределения оказались нашими добрыми знакомыми. Если же взять случайную пару распределений $p(yverttheta)$ и $p(theta)$, результат может оказаться совсем не таким приятным. В самом деле, нет никакой проблемы в том, чтобы посчитать числитель формулы Байеса, но вот интеграл в знаменателе может и не найтись. Поэтому выбирать распределения нужно с умом. Более того, поскольку апостериорное распределение само станет априорным, когда придут новые данные, хочется, чтобы априорное и апостериорное распределения были из одного семейства; пары (семейств) распределений $p(yverttheta)$ и $p(theta)$, для которых это выполняется, называются сопряжёнными ($ptheta)$ называется сопряжённым к $p(yverttheta)$). Полезно помнить несколько наиболее распространённых пар сопряжённых распределений:
- $p(yverttheta)$ – распределение Бернулли с вероятностью успеха $theta$, $p(theta)$ – бета распределение;
- $p(yvertmu)$ – нормальное с матожиданием $mu$ и фиксированной дисперсией $sigma^2$, $p(theta)$ также нормальное;
- $p(yvertlambda)$ – показательное с параметром $lambda$, $p(lambda)$ – гамма распределение;
- $p(yvertlambda)$ – пуассоновское с параметром $lambda$, $p(lambda)$ – гамма распределение;
- $p(yverttheta)$ – равномерное на отрезке $[0,theta]$, $p(theta)$ – Парето;
Возможно, вы заметили, что почти все указанные выше семейства распределений (кроме равномерного и Парето) относятся к экспоненциальному классу. И это не случайность! Экспоненциальный класс и тут лучше всех: оказывается, что для $p(yverttheta)$ из экспоненциального класса можно легко подобрать сопряжённое $p(theta)$. Давайте же это сделаем.
Пусть $p(yverttheta)$ имеет вид
$$p(yverttheta) = frac1{h(theta)}g(y)exp(theta^Tu(y))$$
Положим
$$p(theta) = frac1{h^{nu}(theta)}exp(eta^Ttheta)cdot f(eta, nu)$$
где $f(eta, nu)$ – множитель, обеспечивающий равенство единице интеграла от этой функции. Найдём апостериорное распределение:
$$p(thetavert Y) = frac{left[prod_{i=1}^nfrac1{h(theta)}g(y_i)exp(theta^Tu(y_i))right]frac1{h^{nu}(theta)}exp(eta^Ttheta)cdot f(eta, nu)}{text{злой интеграл}} = $$
$$= frac{frac1{h^{nu + n}(theta)}expleft(theta^Tleft[eta + sum_{i=1}^nu(y_i)right]right)}{text{что-то, где нет }theta}$$
Это распределение действительно из того же семейства, что и $p(theta)$, только с новыми параметрами:
$$eta_{new} = eta + sum_{i=1}^nu(y_i),quadnu_{new} = nu + n$$
Пример. Пусть $p(yvert q) = q^y(1 – q)^{1 – y}$ подчиняется распределению Бернулли. Напомним, что оно следующим образом представляется в привычном для экспоненциального класса виде:
$$p(yvert q) = underbrace{(1 – q)}_{=frac1{h(q)}}expleft(underbrace{y}_{=u_1(y)}underbrace{log{frac{q}{1 – q}}}_{=theta}right)$$
Предлагается брать априорное распределение вида
$$p(q) = frac{(1 – q)^{nu}expleft(etalog{frac{q}{1-q}}right)}{text{что-то, где нет}q}$$
Тогда апостериорное распределение будет иметь вид (проверьте, посчитав по формуле Байеса!)
$$p(qvert Y) = frac{(1 – q)^{nu + n}expleft(left[eta + sum_{i=1}^ny_iright]log{frac{q}{1-q}}right)}{text{что-то, где нет}q}$$
Превратив логарифм частного в сумму, а экспоненту суммы в произведение, легко убедиться, что получается то самое бета распределение, которое мы уже получали выше.
Оценка апостериорного максимума (MAP)
Апостериорное распределение – это очень тонкий инструмент анализа данных, но иногда надо просто сказать число (или же интеграл в знаменателе не берётся и мы не можем толком посчитать распределение). В качестве точечной оценки логично выдать самое вероятное значение $thetavert Y$ (интеграл в знаменателе от $theta$ не зависит, поэтому на максимизацию не влияет):
$$color{blue}{widehat{theta}_{MAP} = underset{theta}{operatorname{argmax}}{p(theta vert Y)} = underset{theta}{operatorname{argmax}}{p(Y vert theta)p(theta)}}$$
Это число называется оценкой апостериорного максимума (MAP).
Если же в формуле выше перейти к логарифмам, то мы получим кое-что, до боли напоминающее старую добрую регуляризацию (и не просто так, как мы вскоре убедимся!):
$$underset{theta}{operatorname{argmax}}{p(Y vert theta)p(theta)} = underset{theta}{operatorname{argmax}}log(p(Y vert theta)p(theta)) = $$
$$=underset{theta}{operatorname{argmax}}left(vphantom{frac12}log{p(Y vert theta)} + log{p(theta)}right)$$
Пример. Рассмотрим снова распределение Бернулли $p(yvert q)$ и априорное распределение $p(q)simtext{Beta}(qvert a, b)$. Тогда MAP-оценка будет равна
$$underset{q}{operatorname{argmax}}{p(Y vert q)p(q)} = underset{q}{operatorname{argmax}}{q^{sum_{i=1}^ny_i}(1 – q)^{n – sum_{i=1}^ny_i}cdot q^{a – 1}(1 – q)^{b – 1}} = $$
$$underset{q}{operatorname{argmax}}left((a – 1 + sum_{i=1}^ny_i)log{q} + (b – 1 + n – sum_{i=1}^ny_i)log(1 – q)right)$$
Дифференцируя по $q$ и приравнивая производную к нулю, мы получаем
$$q = frac{a + sum_{i=1}^ny_i – 1}{a + b + n – 2}$$
В отличие от оценки максимального правдоподобия $frac{sum_{i=1}^ny_i}{n}$ мы здесь используем априорное знание: параметры $(a – 1)$ и $(b – 1)$ работают как «память о воображаемых испытаниях», как будто бы до того, как получить данные $y_i$, мы уже имели $(a – 1)$ успехов и $(b – 1)$ неудач.
Связь MAP- и MLE-оценок
Оценка максимального правдоподобия является частным случаем апостериорной оценки. В самом деле, если априорное распределение является равномерным, то есть $p(theta)$ не зависит $theta$ (если веса $theta$ вещественные, могут потребоваться дополнительные усилия, чтобы понять, как такое вообще получается), и тогда
$$widehat{theta}_{MAP} = underset{theta}{operatorname{argmax}}log{p(Y vert theta)p(theta)} = underset{theta}{operatorname{argmax}}left(log{p(Y vert theta)} + underbrace{log{p(theta)}}_{=const}right) =$$
$$= underset{theta}{operatorname{argmax}}log{p(y vert theta)} = widehat{theta}_{MLE}$$
Байесовские оценки для условных распределений
В предыдущих разделах мы разобрали, как байесовский подход работает для обычных, не условных распределений. Теперь вернёмся к чему-то более близкому к машинному обучению, а именно к распределениям вида $yvert x,w$, и убедимся, что для них байесовских подход работает точно так же, как и для обычных распределений.
Имея некоторое распределение $p(yvert x, w)$, мы подбираем для него априорное распределение на веса $p(w)$ (и да, оно не зависит от $x$: ведь априорное распределение существует ещё до появления данных) и вычисляем апостериорное распределение на веса:
$$p(w vert X, y)$$
Вычислять его мы будем по уже привычной формуле Байеса:
$$color{blue}{p(w vert X, y) = frac{p(y, w vert X)}{p(y)} = frac{p(y vert X, w)p(w)}{p(y)}}$$
Повторим ещё разок, в чём суть байесовского подхода: у нас было некоторое априорное представление $color{blue}{p(w)}$ о распределении весов $color{blue}{w}$, а теперь, посмотрев на данные $(x_i, y_i)_{i=1}^n$, мы уточняем своё понимание, формулируя апостериорное представление $p(w vert X, y)$.
Если же нам нужна только точечная оценка, мы можем ограничиться оценкой апостериорного максимума (MAP): $$color{blue}{widehat{w}_{MAP} = underset{w}{operatorname{argmax}}{p(w vert X,y)} = underset{w}{operatorname{argmax}}{p(y vert X, w)p(w)}} = $$
$$=underset{w}{operatorname{argmax}}left(vphantom{frac12}log{p(y vert X, w)} + log{p(w)}right)$$
что уже до неприличия напоминает регуляризованную модель
Пример: линейная регрессия с $L^2$-регуляризацией как модель с гауссовским априорным распределением на веса
В модели линейной регрессии $y = langle x, wrangle + varepsilon$, $varepsilonsimmathcal{N}(0, sigma^2)$ введём априорное распределение на веса вида
$$color{blue}{p(w) = mathcal{N}(w vert 0, tau^2I) = prod_{j=1}^D mathcal{N}(w_j vert 0, tau^2) = prod_{j=1}^D p(w_j)}$$
Тогда $widehat{w}_{MAP}$ является точкой минимума следующего выражения:
$$-log{p(y vert X, w)} – log{p(w)} =-sum_{i=1}^Np(y_i vert x_i, w) – sum_{j=1}^Dp(w_j) =$$
$$=-sum_{i=1}^Nleft(-frac12log(2pisigma^2) – frac{(y_i – (w, x_i))^2}{2sigma^2}right)
-sum_{j=1}^Dleft(-frac12log(2pitau^2) – frac{w_j^2}{2tau^2}right)=$$
$$= frac1{2sigma^2}sum_{i=1}^N(y_i – (w, x_i))^2 + frac1{2tau^2}sum_{j=1}^D w_j^2+mbox{ не зависящие от $w$ члены}$$
Получается, что
$$color{blue}{widehat{w}_{MAP} = underset{w}{operatorname{argmin}}left(vphantom{frac12}sum_{i=1}^N(y_i – (w, x_i))^2 + frac{sigma^2}{tau^2}|w|^2right)}$$
а это же функция потерь для линейной регрессии с $L^2$-регуляризацией! Напомним на всякий случай, что у этой задачи есть ”точное” решение
$$color{blue}{widehat{w}_{MAP} = left(X^TX + frac{sigma^2}{tau^2}Iright)^{-1}X^Ty}$$
Для этого примера мы можем вычислить и апостериорное распределение $p(w vert X, y)$. В самом деле, из написанного выше мы можем заключить, что
$$log{p(w vert X, y)} = log(p(y vert X, w)p(w)) – log{p(y)} = $$
$$ =frac1{2sigma^2}(y – Xw)^T(y – Xw) + frac1{2tau^2}w^Tw+mbox{ не зависящие от $w$ члены}$$
Таким образом, $log{p(w vert X, y)}$ – это квадратичная функция от $w$, откуда следует, что апостериорное распределение является нормальным. Чтобы найти его параметры, нужно немного преобразовать полученное выражение:
$$ ldots=frac1{2sigma^2}(y^Ty – w^TX^Ty – y^TWx + w^TX^TXw) + frac1{2tau^2}w^Tw+mathrm{const}(w) =$$
$$=w^Tleft(frac1{2sigma^2}X^TX + frac1{2tau^2}Iright)w – frac{1}{2sigma^2}w^TX^Ty – frac1{2sigma^2}y^TWx + mathrm{const}(w) =$$
$$=frac12left(w – widehat{w}_{MAP}right)^Tleft(frac1{sigma^2}X^TX + frac1{tau^2}Iright)left(w – widehat{w}_{MAP}right) + mathrm{const}(w)=$$
Таким образом,
$$color{blue}{p(w vert X,y) = mathcal{N}left(widehat{w}_{MAP}, left(frac1{sigma^2}X^TX + frac1{tau^2}Iright)^{-1} right)}$$
Как видим, от априорного распределения оно отличается корректировкой как матожидания $0mapstowidehat{w}_{MAP}$, так и ковариационной матрицы $left(frac1{tau^2}Iright)^{-1}mapstoleft(frac1{sigma^2}X^TX + frac1{tau^2}Iright)^{-1}$. Отметим, что $X^TX$ – это, с точностью до численного множителя, оценка ковариационной матрицы признаков нашего датасета (элементы матрицы $X^TX$ – это скалярные произведения столбцов $X$, то есть столбцов значений признаков).
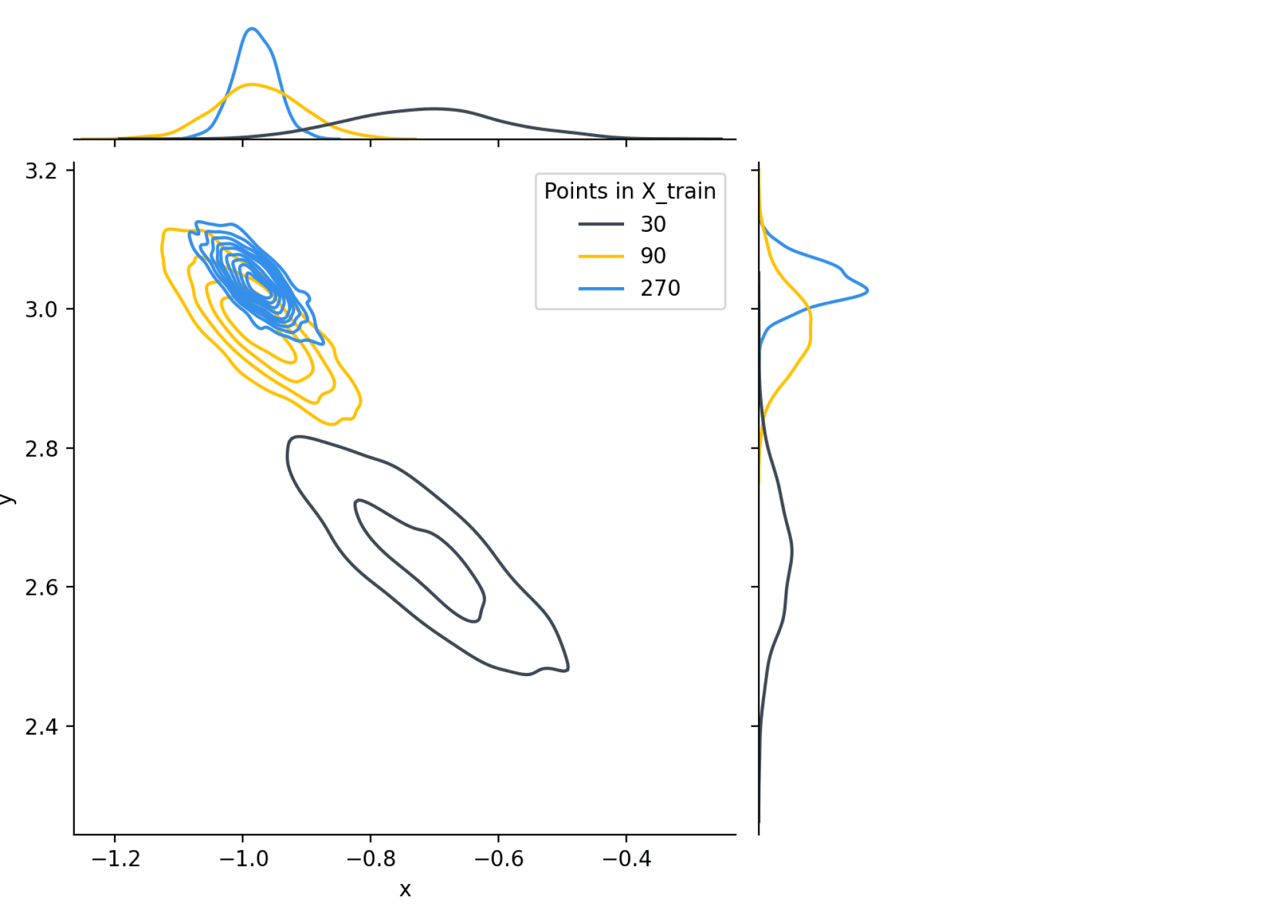
Иллюстрация. Давайте на простом примере (датасет с двумя признаками) посмотрим, как меняется апостериорное распределение $w$ с ростом размера обучающей выборки:
Как видим, не только мода распределения, то есть $widehat{w}_{MAP}$ приближается к своему истинному значению, но и дисперсия распределения постепенно уменьшается.
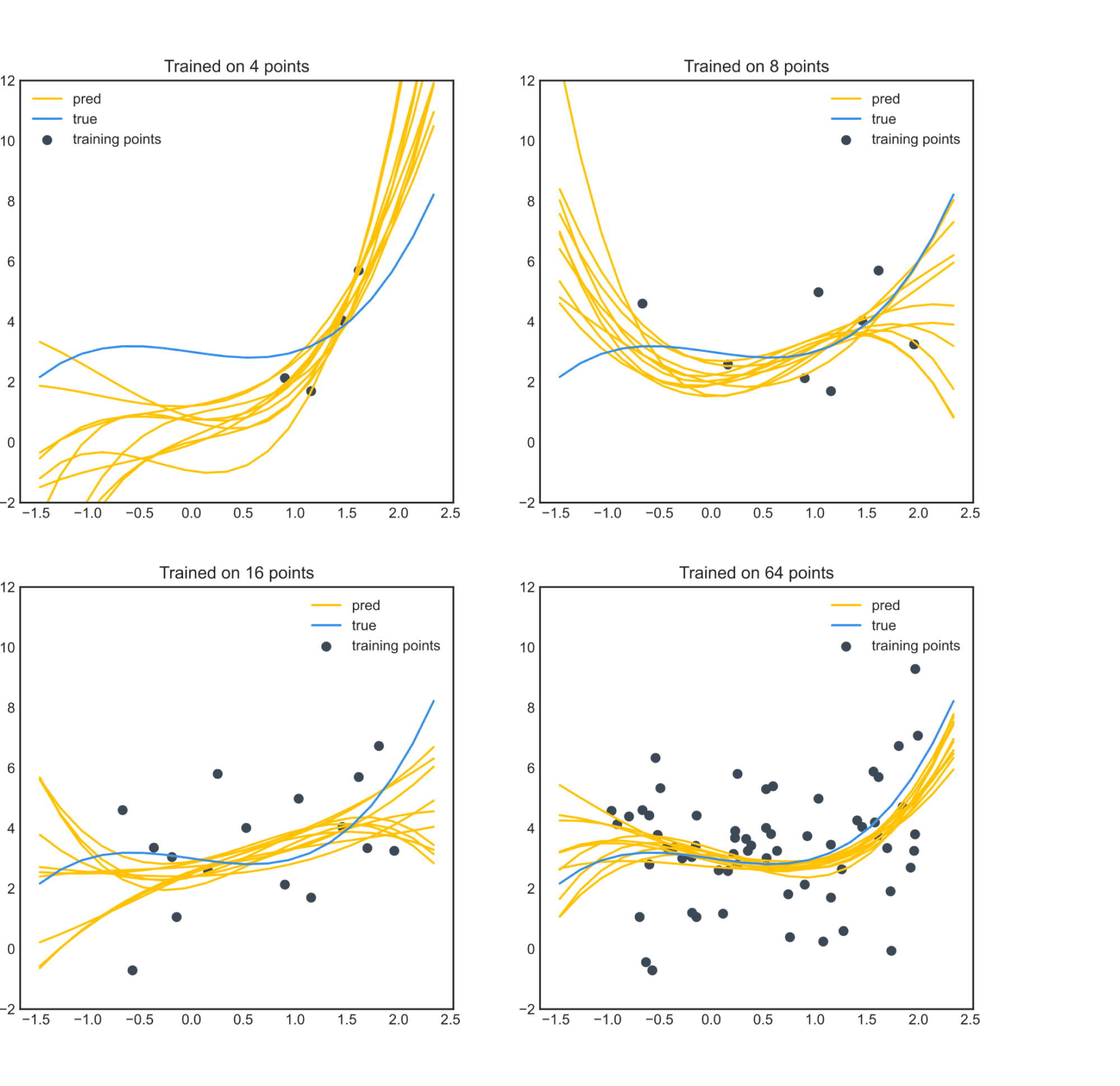
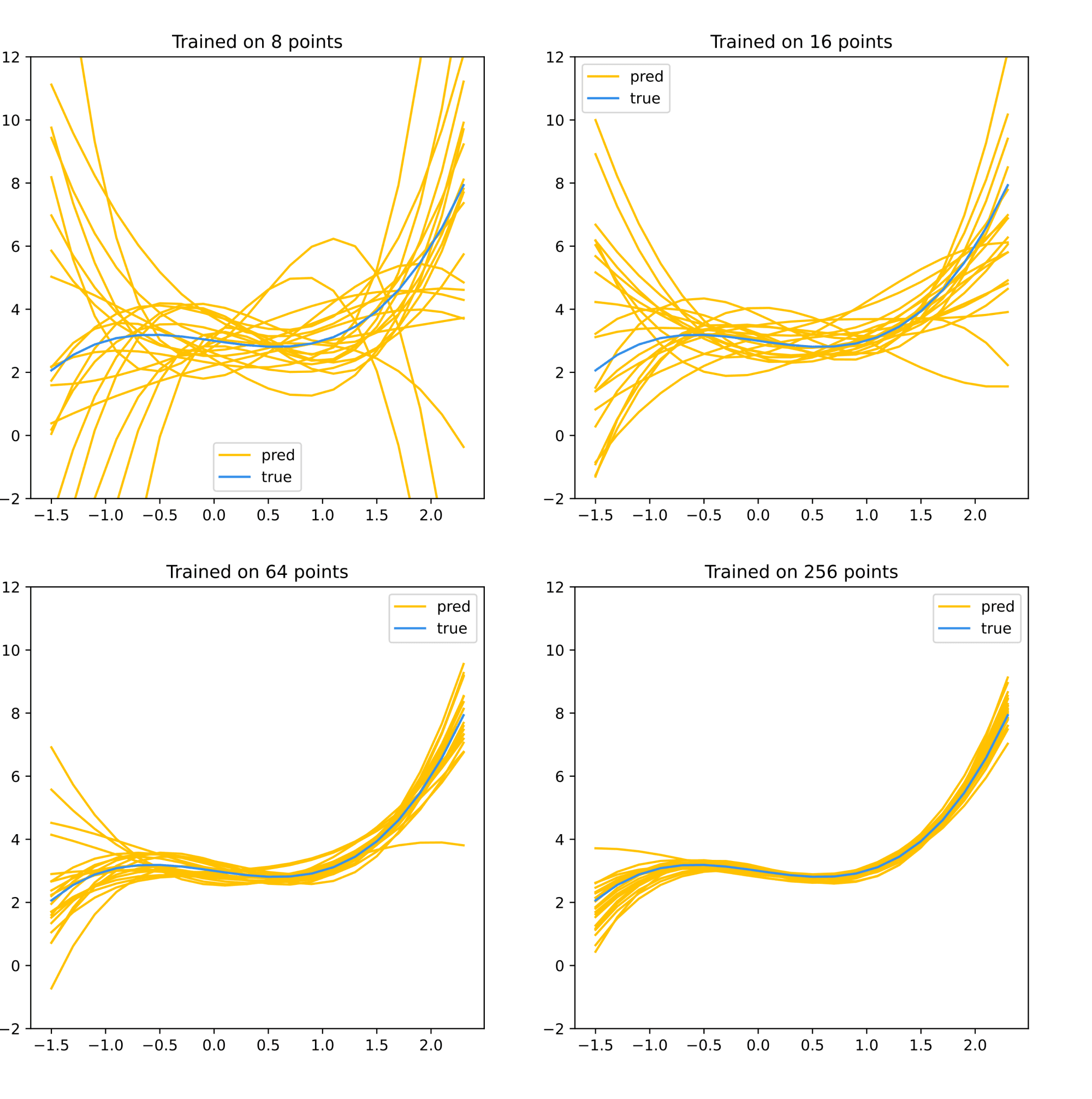
Ещё иллюстрация. Теперь рассмотрим задачу аппроксимации неизвестной функции одной переменной (чьи значения в обучающей выборке искажены нормальным шумом) многочленом третьей степени. Её, разумеется, тоже можно решать, как задачу линейной регрессии на коэффициенты многочлена. Давайте нарисуем, как будут выглядеть функции, сгенерированные из распределения ${p(w vert X,y)}$ для разного объёма обучающей выборки:
Тут тоже видим, что функции не только становятся ближе к истинной, но и разброс их уменьшается.
Пример: линейная регрессия с $L^1$-регуляризацией как модель с лапласовским априорным распределением на веса
Другим распределением, которое тоже может кодировать наше желание, чтобы небольшие по модулю значения $w_j$ были правдоподобными, а большие не очень, является распределение Лапласа. Посмотрим, что будет, если его взять в качестве априорного распределения на веса.
$$color{blue}{p(w) = prod_{j=1}^D p(w_j) = prod_{j=1}^Dfrac{lambda}{2}exp(-lambda|w_m|)}$$
Проводя такое же вычисление, получаем, что
$$color{blue}{widehat{w}_{MAP} = underset{w}{operatorname{argmin}}left(vphantom{frac12}sum_{i=1}^N(y_i – (w, x_i))^2 + lambdasum_{j=1}^D|w_j|right)}$$
а это же функция потерь для линейной регрессии с $L^1$-регуляризацией!
Если мы нашли распределение $w$, как делать предсказания?
Все изложенные выше рассуждения проводились в ситуации, когда $X = X_{train}$ – обучающая выборка. Для неё мы можем посчитать
$$p(w vert X_{train}, y_{train}) = frac{(y vert X,w)p(w)}{p(y)}$$
и точечную апостериорную оценку $widehat{w}_{MAP} = underset{w}{operatorname{argmax}}{p(y vert X,w)p(y)}$. А теперь пусть нам дан новый объект $x_0inmathbb{X}$. Какой таргет $y_0$ мы для него предскажем?
Было бы естественным, раз уж мы предсказываем распределение для $w$, и для $y_0$ тоже предсказывать распределение. Делается это следующим образом:
$$p(y_0 vert x_0, X_{train}, y_{train}) = int{p(y_0 vert x_0,w)p(w vert X_{train}, y_{train})}dw$$
Надо признать, что вычисление этого интеграла не всегда является посильной задачей, поэтому зачастую приходится ”просто подставлять $widehat{w}_{MAP}$”. В вероятностных терминах это можно описать так: вместо сложного апостериорного распределения $p(w vert X_{train}, y_{train})$ мы берём самое грубое на свете приближение
$$p(w vert X_{train}, y_{train})approxdelta(w – widehat{w}_{MAP}),$$
где $delta(t)$ – дельта-функция, которая не является честной функцией (а является тем, что математики называют обобщёнными функциями), которая определяется тем свойством, что $int f(t)delta(t)dt = f(0)$ для достаточно разумных функций $f$. Если не мудрствовать лукаво, то это всё значит, что
$$p(y_0 vert x_0,X_{train}, y_{train})approx p(y_0 vert x_0,widehat{w}_{MAP})$$
Пример. Пусть $ysim Xw + varepsilon$, $varepsilonsimmathcal{N}(0,sigma)^2$ – модель линейной регрессии с априорным распределением $p(w) = mathcal{N}(0,tau^2)$ на параметры. Тогда, как мы уже видели раньше,
$$p(w vert X,y) = mathcal{N}left(w vert widehat{w}_{MAP}, left(frac1{sigma^2}X^TX + frac1{tau^2}Iright)^{-1} right)$$
Попробуем для новой точки $x_0$ посчитать распределение на $y_0$. Рекомендуем читателю попробовать самостоятельно посчитать интеграл или же обратиться к пункту 7.6.2 книжки ”Machine Learning A Probabilistic Perspective” автора Kevin P. Murphy, убедившись, что
$$p(y_0 vert x_0, X_{train}, y_{train}) = mathcal{N}left(y_0 vert x_0widehat{w}_{MAP},
sigma^2 + sigma^2x_0^Tleft(X^TX + frac{sigma^2}{tau^2}Iright)^{-1}x_0right)$$
что, очевидно, более содержательно, чем оценка, полученная с помощью приближения $p(w vert X_{train}, y_{train})approxdelta(w – widehat{w}_{MAP})$:
$$p(y_0 vert x_0, widehat{w}_{MAP}) = mathcal{N}left(y_0left vert x_0widehat{w}_{MAP},
sigma^2right.right)$$
Собственно, видно, что в этом случае
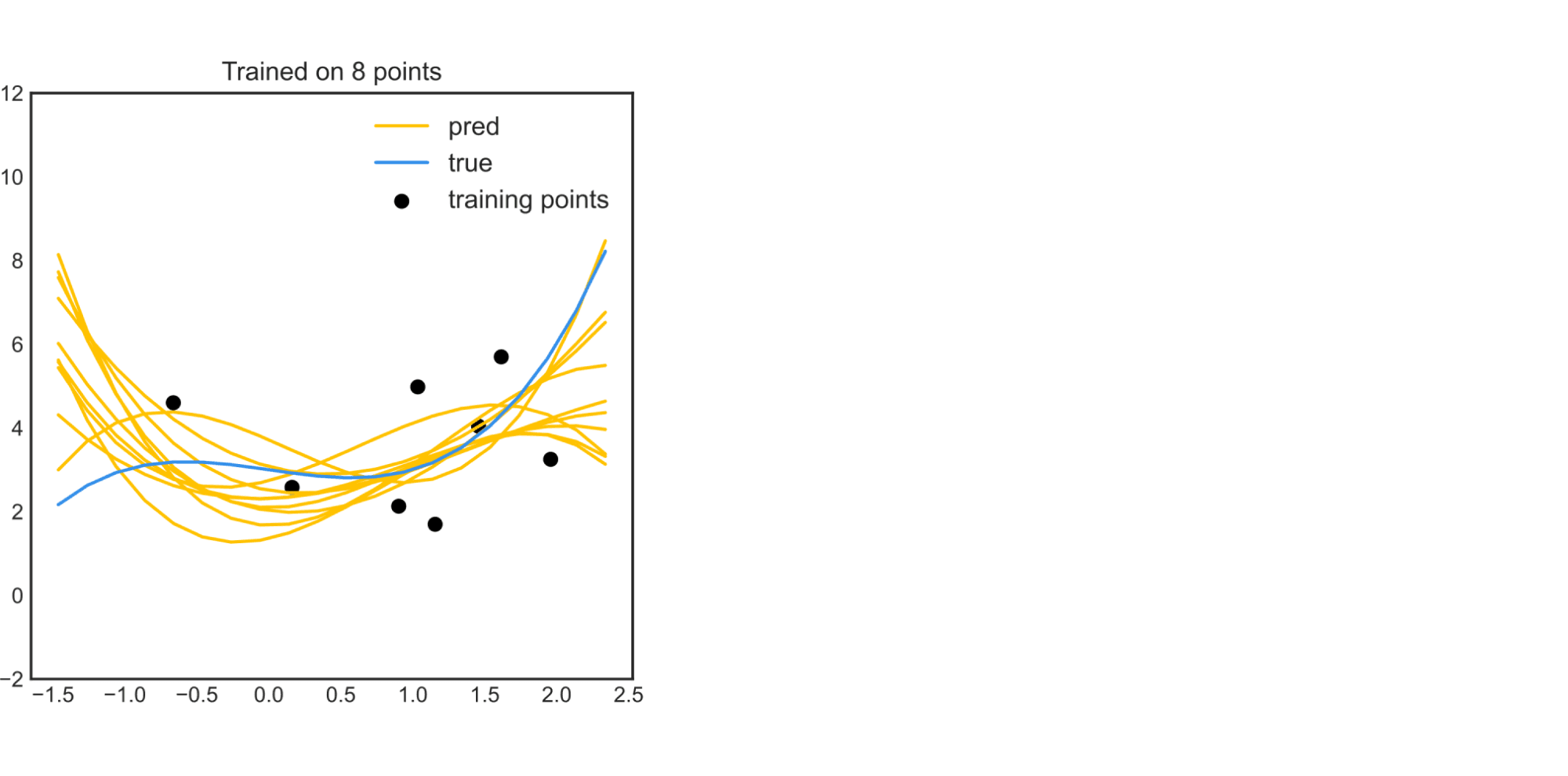
Пример в примере. Рассмотрим полюбившуюся уже нам задачу приближения функции многочленом степени не выше $3$ (в которой мы строим модели с $sigma^2 = tau^2 = 1$). Для $N = 8$ мы получали такую картинку:
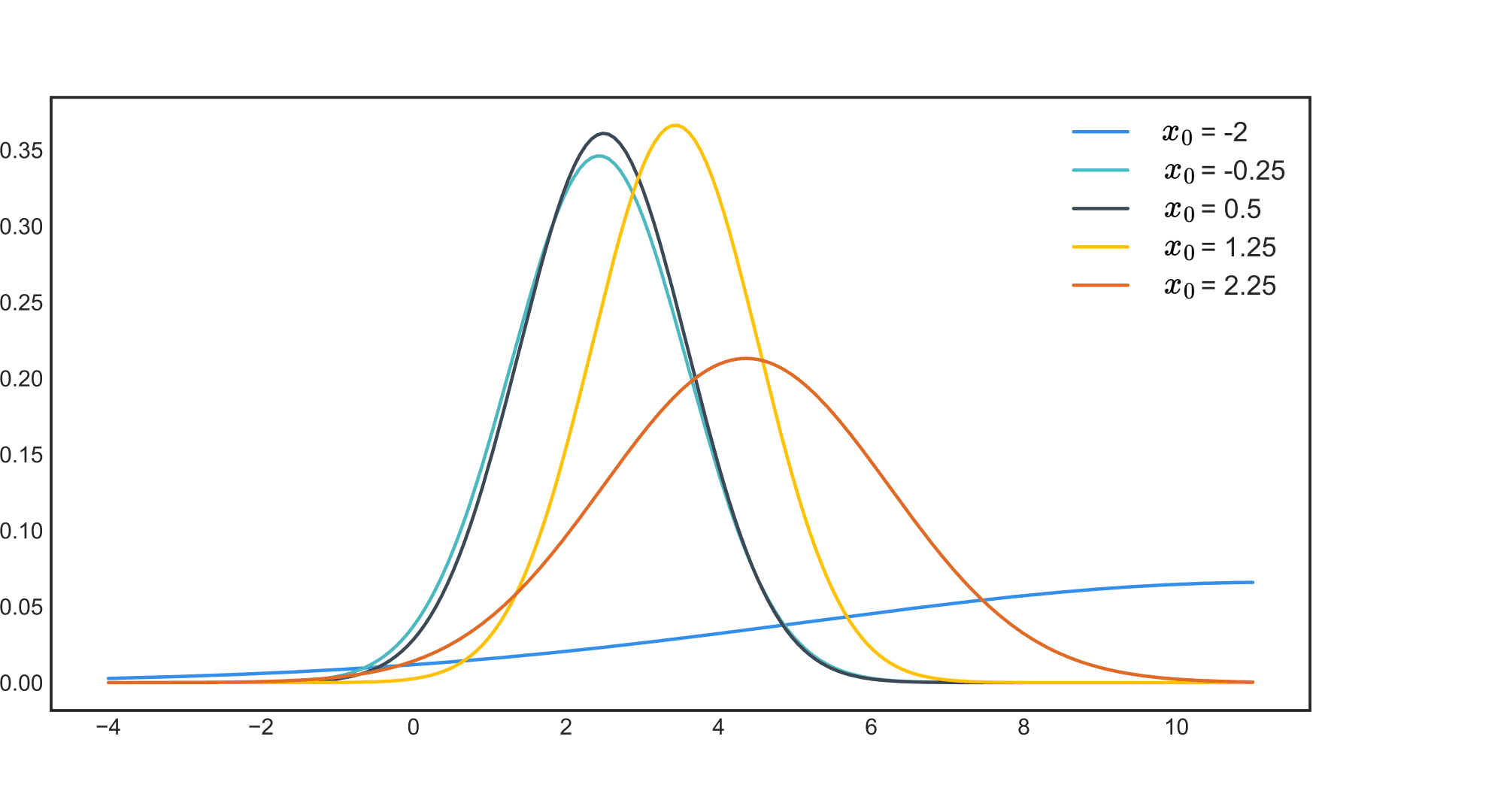
Если оценить по приведённым выше формулам $p(y_0 vert x_0, X_{train}, y_{train})$ для разных $x_0$, то можно убедиться, что модель в большей степени уверена в предсказаниях для точек из областей, где было больше точек из обучающей выборки:
Байесовский подход и дообучение моделей
До сих пор мы в основном рассуждали о моделях машинного обучения как о чём-то, что один раз обучается и дальше навсегда застывает в таком виде, но в жизни такое скорее редкость. Мы пока не будем обсуждать изменчивость истинных зависимостей во времени, но даже если истина неизменна, к нам могут поступать новые данные, которые очень хотелось бы использовать для дообучения модели.
Обычные, не байесовские вероятностные модели не предоставляют таких инструментов. Оценку максимального правдоподобия придётся пересчитывать заново (хотя, конечно, можно схитрить, использовав старое значение в качестве начального приближения при итеративной оптимизации). Байесовский же подход позволяет оформить дообучения в виде простой и элегантной формулы: при добавлении новых данных $(x_{N+1}, y_{N+1}),ldots,(x_M, y_M)$ имеем
$$pleft(wvert (x_i, y_i)_{i=1}^Mright) = frac{pleft((y_i)_{i=N+1}^Mvert (x_i)_{i=N+1}^Mright) pleft(wvert (x_i, y_i)_{i=1}^Nright)}{pleft( (y_i)_{i=N+1}^M right)}$$
Байесовский подход к выбору модели: мотивация
Нам часто приходится выбирать: дерево или случайный лес, линейная модель или метод ближайших соседей; да, собственно, и внутри наших вероятностных моделей есть параметры (скажем, дисперсия шума $sigma^2$ и $tau^2$), которые надо бы подбирать. Но как?
В обычной ситуации мы выбираем модель, обученную на выборке $(X_{train}, y_{train})$ в зависимости от того, как она себя ведёт на валидационной выборке $(X_{val}, y_{val})$ (сравниваем правдоподобие или более сложные метрики) – или же делаем кросс-валидацию. Но как сравнивать модели, выдающие распределение?
Ответим вопросом на вопрос: а как вообще сравнивать модели? Назначение любой модели – объяснять мир вокруг нас, и её качество определяется именно тем, насколько хорошо она справляется с этой задачей. Тестовая выборка – это хороший способ оценки, потому что она показывает, насколько вписываются в модель новые данные. Но могут быть и другие соображения, помогающие оценить качество модели.
Пример
Аналитик Василий опоздал на работу. Своему руководителю он может предложить самые разные объяснения – и это будет выработанная на одном обучающем примере модель, описывающая причины опоздания (и потенциально позволяющая руководителю принять решение о том, карать ли Василия). Конечно, руководитель мог бы принять изложенную Василием модель к сведению, подождать, пока появятся другие опоздавшие, и оценить её, так скажем, на тестовой выборке, но стоит ли? Давайте рассмотрим несколько конкретных примеров:
-
Модель ”Василий опоздал, потому что так получилось”, то есть факт опоздания – это просто ни от чего не зависящая случайная величина. Такая модель плоха тем, что (а) не предлагает, на самом деле, никакого объяснения тому факту, что Василий опоздал, а его коллега Надежда не опоздала и (б) совершенно не помогает решить, наказывать ли за опоздание. Наверное, такое не удовлетворит руководителя.
-
Модель ”Василий опоздал, потому что рядом с его домом открылся портал в другой мир, где шла великая битва орков с эльфами, и он почувствовал, что посто обязан принять в ней участие на стороне орков, которых привёл к победе, завоевав руку и сердце орочьей принцессы, после чего был перенсён обратно в наш скучный мир завистливым шаманом”. Чем же она плоха? Битва с эльфами – это, безусловно, важное и нужное дело, и на месте руководителя мы бы дружно согласились, что причина уважительная. Но заметим, что в рамках этой модели можно объяснить множество потенциальных исходов, среди которых довольно маловероятным представляется наблюдаемый: тот, в котором Василий не погиб в бою, не остался со своей принцессой и не был порабощён каким-нибудь завистливым шаманом. Отметим и другой недостаток этой модели: её невозможно провалидировать. Если в совершенно случайной модели можно оценить вероятность опоздания и впоследствии, когда накопятся ещё примеры, проверить, правильно ли мы её посчитали, то в мире, где открываются порталы и любой аналитик может завоевать сердце орочьей принцессы, возможно всё, и даже если больше никто не попадёт в такую ситуацию, Василий всё равно сможет бить себя в грудь кулаком и говорить, что он избранный. Так что, наверное, это тоже не очень хорошая модель.
-
Модель ”Василий опоздал, потому что проспал” достаточно проста, чтобы в неё поверить, и в то же время даёт руководителю возможность принять решение, что делать с Василием.
Пример
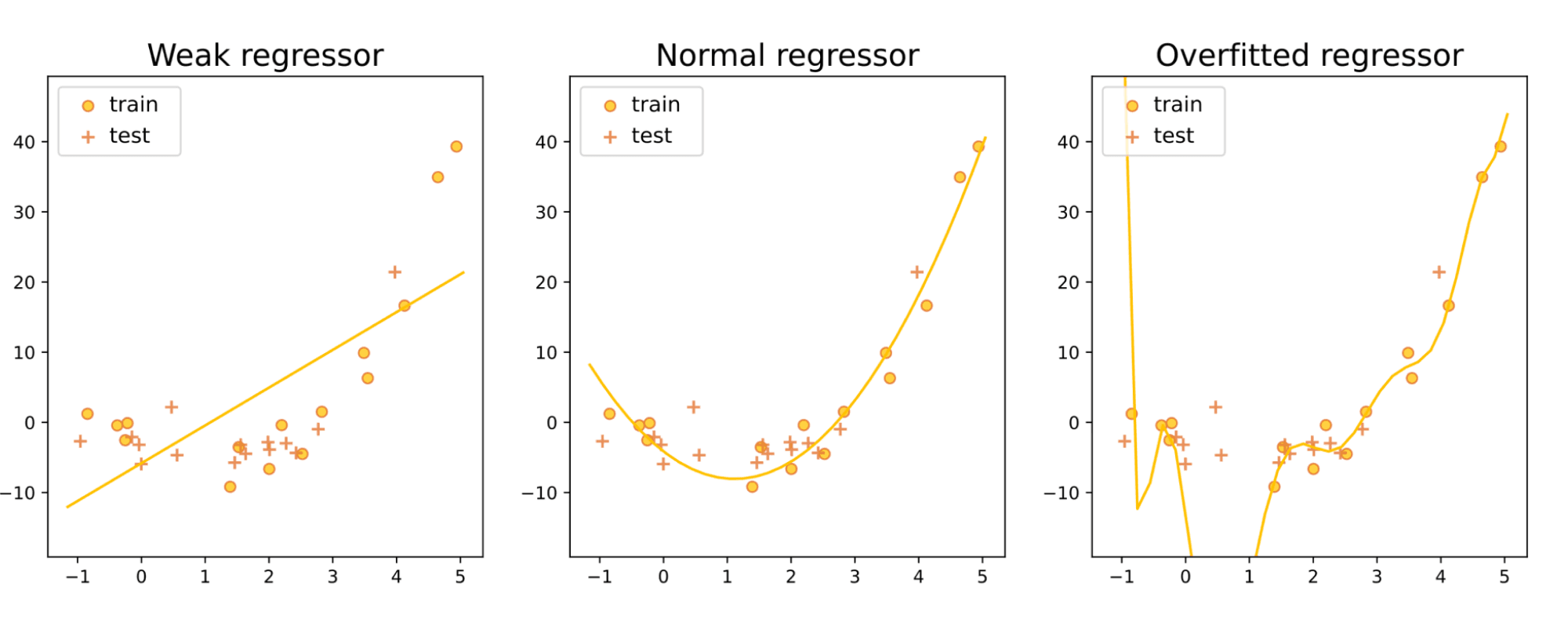
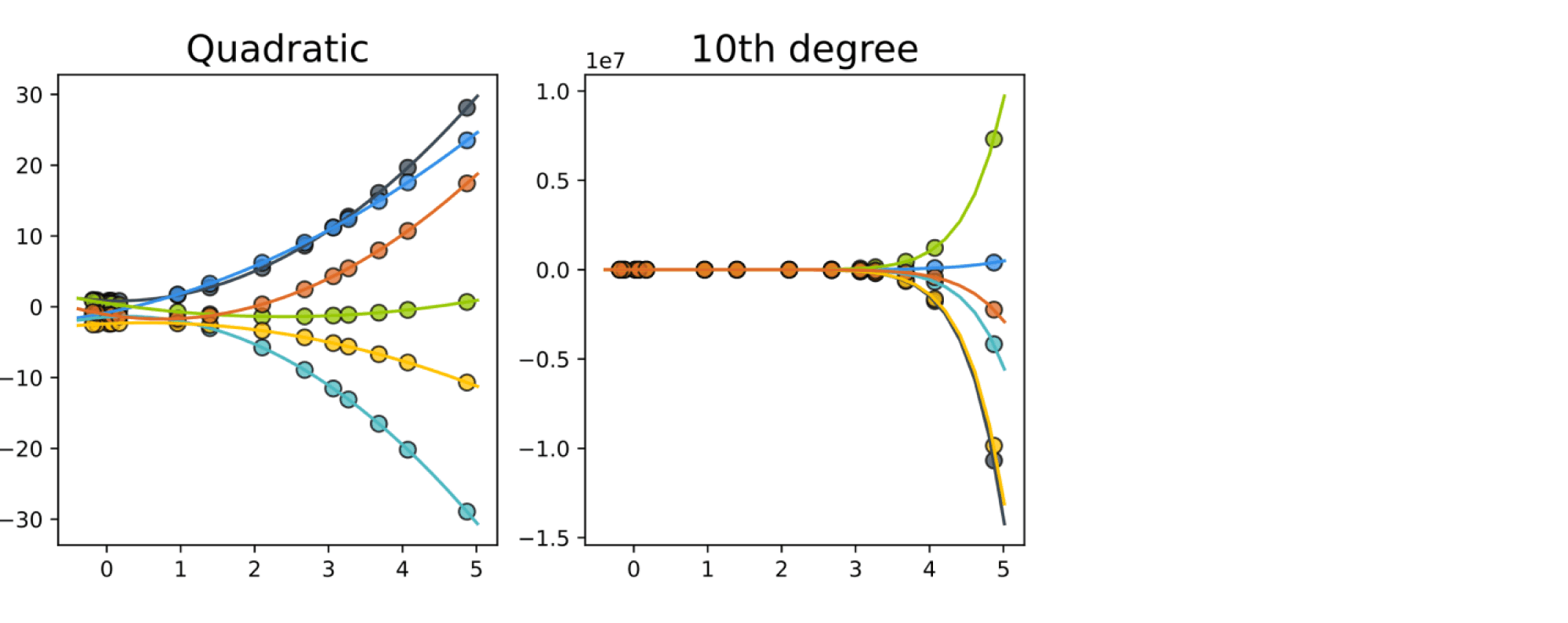
Обратимся к примеру из машинного обучения. Сравним три модели линейной регрессии:
Даже и не заправшивая тестовую выборку, мы можем сделать определённые выводы о качестве этих моделей. Средняя (квадратичная) явно лучше левой (линейной), потому что она лучше объясняет то, что мы видим: тот факт, что облако точек обучающей выборки выглядит вогнутым вниз.
А что с правым, почему мы можем утверждать, что он хуже? Есть много причин критиковать его. Остановимся вот на какой. На средней картинке у нас приближение квадратичной функцией, а на правой – многочленом довольно большой степени (на самом деле, десятой). А ради интереса: как выглядит график квадратичной функции и как – многочлена десятой степени со случайно сгенерированными коэффициентами? Давайте сгенерируем несколько и отметим их значения в точках обучающей выборки:
Обратите внимание на масштаб на графиках справа. И какова вероятность, что нам достался именно тот многочлен десятой степени, у которого значения в обучающих точках по модулю в пределах сотни? Очевидно, она очень мала. Поэтому мы можем сказать, что выбор в качестве модели многочлена десятой степени не очень обоснован.
Попробуем резюмировать
Слишком простая модель плохо объясняет наблюдаемые нами данные, тогда как слишком сложная делает это хорошо, но при этом описывает слишком многообразный мир, в котором имеющиеся у нас данные оказываются уже слишком частным случаем. В каком-то смысле наш способ выбора модели оказывается переформулировкой бритвы Оккама: из моделей, пристойно описывающих наблюдаемые явления, следует выбирать наиболее минималистичную.
Байесовский подход к выбору модели: формализация
Пусть у нас есть некоторое семейство моделей $mathcal{J}$ и для каждого $jinmathcal{J}$ задана какая-то своя вероятностная модель. В духе байесовского подхода было бы оценить условное распределение моделей
$$p(j vert y, X) = frac{p(y vert X,j)p(j)}{sumlimits_{jinmathcal{J}}p(j, y vert X)}$$
и в качестве наилучшей модели взять её моду. Если же считать все модели равновероятными, то мы сводим всё к максимизации только лишь $p(y vert X,j) = p_j(y vert X)$:
$$color{blue}{widehat{jmath} = underset{j}{operatorname{argmax}}int{p_j(y vert X,w)p_j(w)}dw =underset{j}{operatorname{argmax}}p_j(y vert X)}$$
Величина $p_j(y vert X)$ называется обоснованностью (evidence, marginal likelihood) модели.
Отметим, что такое определение вполне согласуется с мотивацией из предыдущего подраздела. Слишком простая модель плохо описывает наблюдаемые данные, и потому будет отвергнута. В свою очередь, слишком сложная модель способна описывать гораздо большее многообразие явлений, чем нам было бы достаточно. Таким образом, компромисс между качеством описания и сложностью и даёт нам оптимальную модель.
Пример
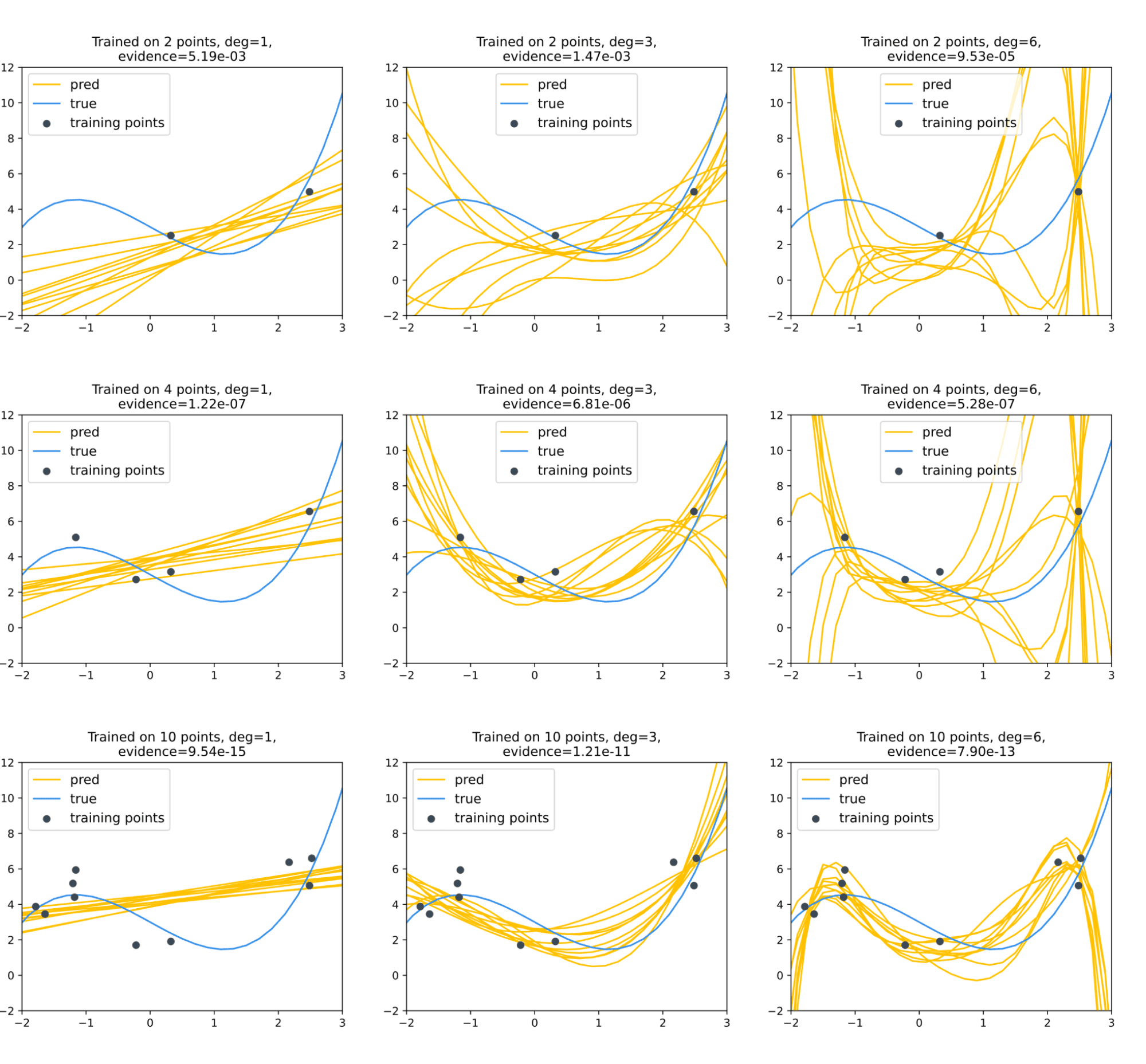
Вернёмся к нашей любимой задаче аппроксимации функции одной переменной многочленом небольшой степени по нескольким точкам, значение в которых было искажено нормальным шумом. Построим несколько моделей, приближающих многочленом степени не выше некоторого $mathrm{deg}$ (будет принимать значения 1, 3 и 6), положив в вероятностной модели $sigma^2 = tau^2 = 1$.
Мы не будем приводить полный вывод обоснованности для задачи регрессии $p(y vert X,w) = mathcal{N}(y vert Xw,sigma^2I)p(w vert tau^2I)$, а сразу выпишем ответ:
$$p(y vert X) = mathcal{N}left(0, sigma^2I + tau^2XX^Tright)$$
Посмотрим, какой будет обоснованность для разного числа обучающих точек:
Можно убедиться, что для регрессии по двум точкам наиболее обоснованной является линейная модель (и неудивительно), тогда как с ростом числа точек более обоснованной становится модель с многочленом третьей степени; слишком сложная же модель шестой степени всегда плетётся в хвосте.
Аппроксимация обоснованности и байесовский информационный критерий
Точно вычислить обоснованность может быть трудной задачей (попробуйте проделать это сами хотя бы для линейной регрессии!). Есть разные способы посчитать её приближённо; мы рассмотрим самый простой. Напомним, что
$$p(y vert X) = int{p(y vert X,w)p(w)}dw $$
Воспользуемся приближением Лапласа, то есть разложим $p(y vert X,w)$ (как функцию от $w$) вблизи своего максимума, то есть вблизи $widehat{w} := widehat{w}_{MLE}$ в ряд Тейлора:
$$log{p(y vert X,w)} approx log{p(y vert X,widehat{w})} – frac12(w – widehat{w})^TI_N(widehat{w})(w – widehat{w}),$$
где линейный член отсутствует, поскольку разложение делается в точке локального экстремума, а $I(widehat{w})$ – знакомая нам матрица Фишера $I_N(widehat{w}) = -mathbb{E}nabla^2_wlog{p(y vert X,w)}vert_{widehat{w}} = NI_1(widehat{w})$.
Далее, $p(w)$ мы можем с точностью до второго порядка приблизить $p(widehat{w}_{MAP})$. Получается, что
$$p(y vert X)approxint e^{log{p(y vert X,widehat{w})} – frac{N}2(w – widehat{w})^TI_1(widehat{w})(w – widehat{w})}p(widehat{w}_{MAP})dw =$$
$$= e^{log{p(y vert X,widehat{w})}}p(widehat{w}_{MAP})int e^{ – frac{N}{2}(w – widehat{w})^TI_1(widehat{w})(w – widehat{w})}dw = $$
$$= e^{log{p(y vert X,widehat{w})}}p(widehat{w}_{MAP})cdot (2pi)^{D/2}frac{|I_1(widehat{w})|^{-frac12}}{N^{D/2}} =$$
$$=expleft(log{p(y vert X,widehat{w})} – frac{D}2log{N} + mbox{всякие штуки}right)$$
Несмотря на то, что $p(widehat{w}_{MAP})$ и $vert I_1(widehat{w})vert^{-frac12}$, сгруппированные нами во ”всякие штуки”, существенным образом зависят от модели, при больших $N$ они вносят в показатель гораздо меньше вклада, чем первые два слагаемых. Таким образом, мы можем себе позволить вместо трудновычисляемых $p(y vert X)$ использовать для сравнения модели $ color{blue} { mbox{байесовский информационный критерий (BIC)}:} $
$$color{blue}{BIC = Dlog{N} – 2log{p(y vert X,widehat{w})}}$$
Фреквентисты против байесиан: кто кого?
Мы с вами познакомились с двумя парадигмами оценивания:
- фреквентистской (frequentist, от слова “frequency”, частота) – в которой считается, что данные являются случайным (настоящая случайность!) семплом из некоторого фиксированного распределения, которое мы стараемся оценить по этому семплу, и
- байесовской – в которой данные считаются данностью и в которой мы используем данные для обновления наших априорных представлений о распределении параметров (здесь случайности нет, а есть лишь нехватка знания).
У обеих есть свои достоинства и недостатки, поборники и гонители. К недостаткам байесовской относится, безусловно, её вычислительная сложность: возможно, вы помните, в пучину вычислений сколь мрачных нас низвергла банальная задача линейной регрессии, и дальше становиться только ещё трудней. Если мы захотим байесовский подход применять к более сложным моделям, например, нейросетям, нам придётся прибегать к упрощениям, огрублениям, приближениям, что, разумеется, ухудшает наши оценки. Но, если простить ему эту вынужденную неточность, он логичнее и честней, и мы продемонстрируем это на следующем примере.
Одним известным свойством оценки максимального правдоподобия является асимптотическая нормальность. Если оценивать наши веса $w$ по различным наборам из $N$ обучающих примеров, причём считать, что наборы выбираются случайно (не будем уточнять, как именно), то оценка $widehat{w}_{MLE}$ тоже превращается в случайную величину, которая как-то распределена. Теория утверждает, что при $Nrightarrowinfty$
$$ quad widehat{w}_{MLE}simmathcal{N}left(w^{ast}, I_N({w}^{ast})^{-1}right)$$
где $w^{ast}$ – истинное значение весов, а $I_N({w}^{ast})$ – матрица информации Фишера, которая определяется как
$$I_N({w}^{ast}) = mathbb{E}left[left(left.frac{partial}{partial w_i}log{p(y vert X,w)}right|_{w^{ast}}right)left(left.frac{partial}{partial w_j}log{p(y vert X,w)}right|_{w^{ast}}right)right]$$
что при некоторых не слишком обременительных ограничениях равно
$$I_N({w}^{ast}) = -mathbb{E}left[left.frac{partial^2}{partial w_ipartial w_j}log{p(y vert X,w)}right|_{w^{ast}}right]$$
При этом поскольку $log{p(y vert X,w)} = sum_{i=1}^Nlog{p(y vert X,w)}$, матрица тоже распадается в сумму, и получается, что $I_N({w}^{ast}) = NI_1(w^{ast})$, то есть с ростом $N$ ковариация $(NI_1(w^{ast}))^{-1}$ оценки максимального правдоподобия стремится к нулю.
На интуитивном уровне можно сказать, что матрица информации Фишера показывает, сколько информации о весах $w$ содержится в $X$.
Поговорим о проблемах. В реальной ситуации мы не знаем $w^{ast}$ и тем более не можем посчитать матрицу Фишера, то есть мы с самого начала вынуждены лукавить. Ясно, что вместо $w^{ast}$ можно взять просто $widehat{w}$, а вместо $I_N(w^{ast})$ – матрицу $I_N(widehat{w})$, которую можно даже при желании определить как
$$-left(left.frac{partial^2}{partial w_ipartial w_j}log(p(y vert X, w))right|_{w^{ast}}right)$$
безо всякого математического ожидания. Итак, хотя мы можем теперь построить доверительный интервал для оцениваемых параметров, по ходу нами было сделано много упрощений: мы предположили, что асимптотическая оценка распределения уже достигнута, от $w^{ast}$ перешли к $widehat{w}$, а для полноты чувств ещё и избавились от математического ожидания. В байесовском подходе мы такого себе не позволяем.
Если вам интересно, посмотрите, как это будет выглядеть для линейной регрессии.
Рассмотрим модель линейной регрессии $ysim Xw + varepsilon$, $varepsilonsimmathcal{N}(0, sigma^2)$. Для неё
$$log{p(y vert X,w)} = -frac{N}{2log(2pisigma^2)} – frac{1}{2sigma^2}(y – Xw)^T(y – Xw)$$
Нетрудно убедиться, что
$$nabla_wlog{p(y vert X,w)} = frac{1}{sigma^2}X^T(y – Xw)$$
$$nabla^2_wlog{p(y vert X,w)} = -frac{1}{sigma^2}X^TX$$
Соответственно,
$$I_N(widehat{w}) = frac{1}{sigma^2}X^TX$$
где $widehat{w}$ – это полученная по датасету $X$ оценка весов. Заметим, что $W^TX$ – это с точностью до коэффициента $frac{1}{N}$ оценка ковариационной матрицы признаков нашего датасета (элементы $X^TX$ – это скалярные произведения столбцов $X$, то есть столбцов признаков). Можно легко убедиться, что
$$frac{1}{sigma^2}X^TX = frac{1}{sigma^2}sum_{i=1}^Nx_i^Tx_i$$
По-хорошему, нам надо было бы ещё взять математическое ожидание. Найти его мы не можем, но можем очень наивно оценить как $C = frac1Nsum_{i=1}^Nx_i^Tx_i$. Тогда получаем, что $I_N(widehat{w}) = frac{N}{sigma^2}C$. Таким образом, имея один датасет $X$ и одну посчитанную по нему оценку $widehat{w}$, мы можем довольно грубо оценить распределение оценок максимального правдоподобия для заданного $N$ как
$$mathcal{N}left(widehat{w}, frac{N}{sigma^2}Cright)$$
Пример в примере. Давайте рассмотрим задачу аппроксимации функции одной переменной (чьи значения в обучающей выборке искажены нормальным шумом) многочленом степени не выше $3$. Положим в вероятностной модели $sigma^2 = 1$. Тогда различный выбор обучающих датасетов будет приводить к различным результатам:
Но разброс результатов падает с ростом $N$.
Ещё пример в примере. Рассмотрим ещё одну задачу регрессии с двумя признаками (в которой всё так же будем полагать $sigma^2 = 1$), для которой оценим распределение $w_0$ через первую компоненту $mathcal{N}(widehat{w}, I_N(widehat{w})^{-1})$ для одного конкретного $widehat{w}$ и нарисуем несколько различных $widehat{w}$, полученных из других датасетов той же мощности:
Видим, что средние оцененного распределения сходятся к истинному значению $-1$; при этом дисперсия падает. Красные крестики не вполне подчиняются синему распределению, но мы от них ждём лишь приближённой согласованности, которая имеет место.
From Wikipedia, the free encyclopedia
The posterior probability is a type of conditional probability that results from updating the prior probability with information summarized by the likelihood via an application of Bayes’ rule.[1] From an epistemological perspective, the posterior probability contains everything there is to know about an uncertain proposition (such as a scientific hypothesis, or parameter values), given prior knowledge and a mathematical model describing the observations available at a particular time.[2] After the arrival of new information, the current posterior probability may serve as the prior in another round of Bayesian updating.[3]
In the context of Bayesian statistics, the posterior probability distribution usually describes the epistemic uncertainty about statistical parameters conditional on a collection of observed data. From a given posterior distribution, various point and interval estimates can be derived, such as the maximum a posteriori (MAP) or the highest posterior density interval (HPDI).[4] But while conceptually simple, the posterior distribution is generally not tractable and therefore needs to be either analytically or numerically approximated.[5]
Definition in the distributional case[edit]
In variational Bayesian methods, the posterior probability is the probability of the parameters 


It contrasts with the likelihood function, which is the probability of the evidence given the parameters: 
The two are related as follows:
Given a prior belief that a probability distribution function is 


[6]
where 
for continuous 
or by summing
over all possible values of 

The posterior probability is therefore proportional to the product Likelihood · Prior probability.[8]
Example[edit]
Suppose there is a school with 60% boys and 40% girls as students. The girls wear trousers or skirts in equal numbers; all boys wear trousers. An observer sees a (random) student from a distance; all the observer can see is that this student is wearing trousers. What is the probability this student is a girl? The correct answer can be computed using Bayes’ theorem.
The event 


, or the probability that the student is a girl regardless of any other information. Since the observer sees a random student, meaning that all students have the same probability of being observed, and the percentage of girls among the students is 40%, this probability equals 0.4.
, or the probability that the student is not a girl (i.e. a boy) regardless of any other information (
is the complementary event to
). This is 60%, or 0.6.
, or the probability of the student wearing trousers given that the student is a girl. As they are as likely to wear skirts as trousers, this is 0.5.
, or the probability of the student wearing trousers given that the student is a boy. This is given as 1.
, or the probability of a (randomly selected) student wearing trousers regardless of any other information. Since
(via the law of total probability), this is
.
Given all this information, the posterior probability of the observer having spotted a girl given that the observed student is wearing trousers can be computed by substituting these values in the formula:
An intuitive way to solve this is to assume the school has N students. Number of boys = 0.6N and number of girls = 0.4N. If N is sufficiently large, total number of trouser wearers = 0.6N+ 50% of 0.4N. And number of girl trouser wearers = 50% of 0.4N. Therefore, in the population of trousers, girls are (50% of 0.4N)/(0.6N+ 50% of 0.4N) = 25%. In other words, if you separated out the group of trouser wearers, a quarter of that group will be girls. Therefore, if you see trousers, the most you can deduce is that you are looking at a single sample from a subset of students where 25% are girls. And by definition, chance of this random student being a girl is 25%. Every Bayes theorem problem can be solved in this way.[9]
Calculation[edit]
The posterior probability distribution of one random variable given the value of another can be calculated with Bayes’ theorem by multiplying the prior probability distribution by the likelihood function, and then dividing by the normalizing constant, as follows:
gives the posterior probability density function for a random variable 

Credible interval[edit]
Posterior probability is a conditional probability conditioned on randomly observed data. Hence it is a random variable. For a random variable, it is important to summarize its amount of uncertainty. One way to achieve this goal is to provide a credible interval of the posterior probability.[11]
Classification[edit]
In classification, posterior probabilities reflect the uncertainty of assessing an observation to particular class, see also Class membership probabilities.
While statistical classification methods by definition generate posterior probabilities, Machine Learners usually supply membership values which do not induce any probabilistic confidence. It is desirable to transform or re-scale membership values to class membership probabilities, since they are comparable and additionally more easily applicable for post-processing.[12]
See also[edit]
- Prediction interval
- Bernstein–von Mises theorem
- Probability of success
- Bayesian epistemology
References[edit]
- ^ Lambert, Ben (2018). “The posterior – the goal of Bayesian inference”. A Student’s Guide to Bayesian Statistics. Sage. pp. 121–140. ISBN 978-1-4739-1636-4.
- ^ Grossman, Jason (2005). Inferences from observations to simple statistical hypotheses (PhD thesis). University of Sydney. hdl:2123/9107.
- ^ Etz, Alex (2015-07-25). “Understanding Bayes: Updating priors via the likelihood”. The Etz-Files. Retrieved 2022-08-18.
- ^ Gill, Jeff (2014). “Summarizing Posterior Distributions with Intervals”. Bayesian Methods: A Social and Behavioral Sciences Approach (Third ed.). Chapman & Hall. pp. 42–48. ISBN 978-1-4398-6248-3.
- ^ Press, S. James (1989). “Approximations, Numerical Methods, and Computer Programs”. Bayesian Statistics : Principles, Models, and Applications. New York: John Wiley & Sons. pp. 69–102. ISBN 0-471-63729-7.
- ^ Christopher M. Bishop (2006). Pattern Recognition and Machine Learning. Springer. pp. 21–24. ISBN 978-0-387-31073-2.
- ^ Andrew Gelman, John B. Carlin, Hal S. Stern, David B. Dunson, Aki Vehtari and Donald B. Rubin (2014). Bayesian Data Analysis. CRC Press. p. 7. ISBN 978-1-4398-4095-5.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Ross, Kevin. Chapter 8 Introduction to Continuous Prior and Posterior Distributions | An Introduction to Bayesian Reasoning and Methods.
- ^ “Bayes’ theorem – C o r T e x T”. sites.google.com. Retrieved 2022-08-18.
- ^ “Posterior probability – formulasearchengine”. formulasearchengine.com. Retrieved 2022-08-19.
- ^ Clyde, Merlise; Çetinkaya-Rundel, Mine; Rundel, Colin; Banks, David; Chai, Christine; Huang, Lizzy. Chapter 1 The Basics of Bayesian Statistics | An Introduction to Bayesian Thinking.
- ^ Boedeker, Peter; Kearns, Nathan T. (2019-07-09). “Linear Discriminant Analysis for Prediction of Group Membership: A User-Friendly Primer”. Advances in Methods and Practices in Psychological Science. 2 (3): 250–263. doi:10.1177/2515245919849378. ISSN 2515-2459. S2CID 199007973.
Further reading[edit]
- Lancaster, Tony (2004). An Introduction to Modern Bayesian Econometrics. Oxford: Blackwell. ISBN 1-4051-1720-6.
- Lee, Peter M. (2004). Bayesian Statistics : An Introduction (3rd ed.). Wiley. ISBN 0-340-81405-5.
Про вероятности
Время на прочтение
11 мин
Количество просмотров 39K
(source)
Иногда мне приходится рассказывать другим людям как работает машинное обучение и, в частности, нейронные сети. Обычно я начинаю с градиентного спуска и линейной регрессии, постепенно переходя к многослойным перцептронам, автокодировщикам и свёрточным сетям. Все понимающе кивают головой, но в какой-то момент кто-нибудь прозорливый обязательно спрашивает:
А почему так важно, чтобы переменные в линейной регрессии были независимы?
или
А почему для изображений используются именно свёрточные сети, а не обычные полносвязные?
“О, это просто”, — хочу ответить я. — “потому что если бы переменные были зависимыми, то нам пришлось бы моделировать условное распределение вероятностей между ними” или “потому что в небольшой локальной области гораздо проще выучить совместное распределение пикселей”. Но вот проблема: мои слушатели ещё ничего не знают про распределения вероятностей и случайные переменные, поэтому приходится выкручиваться другими способами, объясняя сложнее, но с меньшим количеством понятий и терминов. А что делать, если попросят рассказать про батч нормализацию или генеративные модели, так вообще ума не приложу.
Так давайте не будем мучить себя и других и просто вспомним основные понятия теории вероятностей.
Случайные переменные
Представим, что у нас есть анкеты людей, где указаны их возраст, рост, пол и количество детей:
| age | height | gender | children |
|---|---|---|---|
| 32 | 175 | 1 | 2 |
| 28 | 180 | 1 | 1 |
| 17 | 164 | 0 | 0 |
| … | … | …. | …. |
Каждая строчка в такой таблице — это объект. Каждая ячейка — значение переменной, характеризующей этот объект. Например, возраст первого человека — 32 года, а рост второго — 180см. А что, если мы хотим описать некоторую переменную сразу для всех наших объектов, т.е. взять целую колонку? В этом случае у нас будет не одно конкретное значение, а сразу несколько, каждое со своей частотой встречаемости. Список возможных значений + соответсвующая вероятность и называется случайной переменной (random variable, r.v.).
Дискретные и непрерывные случайные переменные
Чтобы это отложилось в голове, я повторю ещё раз: случайная переменная полностью задаётся распределением вероятностей своих значений. Есть 2 основных типа случайных переменных: дискретные (discrete) и непрерывные (continuous).
Дискретные переменные могут принимать набор чётко разделимых значений. Обычно я изображаю их как-нибудь так (probability mass function, pmf):
Код на Julia
Pkg.add("Plots")
using Plots
plotly()
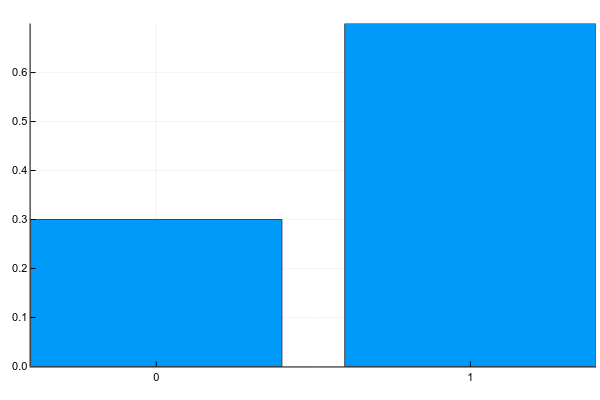
plot(["0","1"], [0.3, 0.7], linetype=:bar, legend=false)А текстом это обычно записывается так (g — gender):
Т.е. вероятность того, что случайно взятый человек из нашей выборки окажется женщиной () равна 0.3, а мужчиной (
) — 0.7, что эквивалентно тому, что в выборке было 30% женщин и 70% мужчин.
К дискретным же переменным относятся количество детей у человека, частота встречаемости слов в тексте, количество просмотров фильма и т.д. Результат классификации на конечное число классов, кстати, — это тоже дискретная случайная переменная.
Непрерывные переменные могут принимать любое значение в определённом интервале. Например, даже если мы записываем, что рост человека — 175см, т.е. округляем до 1 сантиметра, на самом деле он может быть 175.8231см. Изображают непрерывные переменные обычно с помощью кривой плотности вероятности (probability density function, pdf):
Код
Pkg.add("Distributions")
using Distributions
xs = 140:0.1:200
ys = [pdf(Normal(172, 10), x) for x in xs]
plot(xs, ys; xlabel="h", ylabel="p(h)", legend=false, show=true)График плотности вероятности — штука хитрая: в отличие от графика массы вероятности для дискретных переменных, где высота каждой колонки показывает непосредственно вероятность получить такое значение, плотность вероятности показывает относительное количество вероятности вокруг некоторой точки. Саму же вероятность в этом случае можно посчитать только для интервала. Например, в этом примере вероятность, что случайно взятый человек из нашей выборки будет иметь рост от 160 до 170см равна примерно 0.3.
Код
d = Normal(172, 10)
prob = cdf(d, 170) - cdf(d, 160)Вопрос: может ли плотность вероятности в какой-то точке быть больше единицы? Ответ — да, конечно, главное, чтобы общая площадь под графиком (или, говоря математически, интеграл плотности вероятности) был равен единице.
Ещё одна трудность с непрерывными переменными состоит в том, что их плотность вероятности не всегда возможно красиво описать. Для дискретных переменных у нас просто была таблица значение -> вероятность. Для непрерывных это уже не прокатит, поскольку значений у них, вообще говоря, бесконечное множество. Поэтому обычно стараются аппроксимировать набор данных каким-нибудь хорошо изученным параметрическим распределением. Например, график выше — это пример т.н. нормального распределения. Плотность вероятности для него задаётся формулой:
где (мат. ожидание, mean) и
(дисперсия, variance) — параметры распределения. Т.е. имея всего 2 числа мы можем полностью описать распределение, посчитать его плотность вероятности в любой точке или суммарную веростность между двумя значениями. К сожалению, далеко не для любого набора данных найдётся распределение, которое сможет его красиво описать. Есть много способов бороться с этим (взять хотя бы смесь нормальных распределений), но это уже совсем другая тема.
Другие примеры непрерывного распределения: возраст человека, интенсивность пикселя на изображении, время ответа от сервера и т.д.
Совместное, маргинальное и условное распределения
Обычно мы рассматриваем свойства объекта не по одному, а в комбинации с другими, и здесь появляется понятие совместного распределения (joint probability) нескольких переменных. Для двух дискретных переменных мы можем изобразить его в виде таблицы (g — gender, c — # of children):
| c=0 | c=1 | c=2 | |
|---|---|---|---|
| g=0 | 0.1 | 0.1 | 0.1 |
| g=1 | 0.2 | 0.4 | 0.1 |
Согласно этому распределению, вероятность встретить в нашем наборе данных женщину с 2-мя детьми равна , а бездетного мужчину —
.
Для двух непрерывных переменных, например, роста и возраста, нам снова придётся задать аналитическую функцию распределения , аппроксимировав его,
например, многомерным нормальным. Таблицей это не запишешь, зато можно нарисовать:
Код
d = MvNormal([172.0, 30.0], [10 0; 0 5])
xs = 160:0.1:180
ys = 22:1:38
zs = [pdf(d, [x, y]) for x in xs, y in ys]
surface(zs)Имея совместное распределение, мы можем найти распределение каждой переменной по отдельности, просто суммировав (в случае дискретных) или интегрировав (в случае непрерывных) остальные переменные:
Это можно представить в виде суммирования по каждой строке или столбцу таблицы и вынесением результат на поля таблицы:
| c=0 | c=1 | c=2 | ||
|---|---|---|---|---|
| g=0 | 0.1 | 0.1 | 0.1 | 0.3 |
| g=1 | 0.2 | 0.4 | 0.1 | 0.7 |
Так мы снова получаем и
. Процесс вынесения на поля (margin) даёт название и самому получившемуся распределению — маргинальное (marginal probability).
А что, если мы уже знаем значение одной из переменных? Например, мы видим, что перед нами мужчина и хотим получить распределение вероятностей количества его детей? Таблица совместной вероятности и тут нам поможет: поскольку мы уже точно знаем, что перед нами мужчина, т.е. , мы можем выбросить из рассмотрения все остальные варианты и рассматривать только одну строчку:
| c=0 | c=1 | c=2 | |
|---|---|---|---|
| g=1 | 0.2 | 0.4 | 0.1 |
Поскольку вероятности так или иначе должны суммироваться в единицу, получившиеся значения нужно нормализовать, после чего получится:
Распределение одной переменной при известном значении другой называется условным (conditional probability).
Правило цепи
А соединяются все эти вероятности одной просто формулой, которая называется правилом цепи (chain rule, не путать с правилом цепи в дифференцировании):
Формула эта симметричная, поэтому так тоже можно:
Интерпретация правила очень простая: если — вероятность того, что я пойду на красный свет, а
— вероятность того, что человек, переходящий на красный свет, будет сбит, то совместная вероятность пойти на красный свет и быть сбитым как раз и равна произведению вероятностей этих двух событий. Но вообще лучше ходите на зелёный.
Зависимые и независимые переменные
Как уже говорилось, если у нас есть таблица совместного распределения, то мы знаем про систему всё: можно вычислить маргинальную веростность любой переменной, можно условное распределение одной переменной при известной другой и т.д. К сожалению, на практике составить такую таблицу (или просчитать параметры непрерывного распределения) в большинстве случаев невозможно. Например, если мы захотим посчитать совместное распределение встречаемости 1000 слов, то нам понадобится таблица из
107150860718626732094842504906000181056140481170553360744375038837035105112493612
249319837881569585812759467291755314682518714528569231404359845775746985748039345
677748242309854210746050623711418779541821530464749835819412673987675591655439460
77062914571196477686542167660429831652624386837205668069376
(чуть больше 1e301) ячеек. Для сравнения, количество атомов в наблюдаемой вселенной равно примерно 1e81. Пожалуй, покупкой дополнительной планки памяти тут не обойдёшься.
Но есть одна приятная деталь: не все переменные зависят друг от друга. Вероятность того, пойдёт ли завтра дождь, вряд ли зависит от того, перехожу ли я дорогу на красный свет. Для независимых переменных условное распределение одной от другой равно просто маргинальному распределению:
По-честному, совместная вероятность 1000 слов записывается так:
А вот если мы “наивно” предположим, что слова не зависят друг от друга, то формула превратится в:
А чтобы сохранить вероятности для 1000 слов нужна таблица всего с 1000 ячеек, что вполне приемлемо.
Почему тогда не считать все переменные независимыми? Увы, так мы потеряем массу информации. Представим, что мы хотим посчитать вероятность того, что пациент болен гриппом в зависимости от двух переменных: боли в горле и повышенной температуры. Отдельно боль в горле может говорить как о болезни, так и том, что пациент только что громко пел. Отдельно повышенная температура может говорить как о болезни, так и о том, что человек только что вернулся с пробежки. А вот если мы одновременно наблюдаем и температуру, и боль в горле, то это уже серьёзная причина выписать пациенту больничный.
Логарифм
Очень часто в литературе можно увидеть, что используется не просто вероятность, а её логарифм. Зачем? Всё довольно прозаично:
- Логарифм — монотонно возрастающая функция, т.е. для любых
и
если
, то и
.
- Логарифм произведения равен сумме логарифмов:
.
В примере со словами вероятность встретить любое слово , как правило, сильно меньше единицы. Если мы попробуем перемножить много маленьких вероятностей на компьютере с ограниченной точностью вычислений, догадываетесь что будет? Ага, очень быстро наши вероятности округляться к нулю. А вот если мы сложим много отдельных логарифмов, то выйти за пределы точности вычислений будет практически невозможно.
Условная вероятность как функция
Если после всех этих примеров у вас сложилось впечатление, что условная вероятность всегда вычисляется подсчётом количества раз, которое встретилось некоторое значение, то спешу развеять это заблуждение: в общем случае условная вероятность — это некоторая функция одной случайной переменной от другой:
где — это некоторый шум. Виды шума — это тоже отдельная тема, в которую мы сейчас влезать не будем, а вот на функции
остановимся поподробней. В примерах с дискретными переменными выше в качестве функции мы использовали простой подсчёт встречаемости. Это само по себе хорошо работает во многих случаях, например, в наивном байесовском классификаторе для текста или поведения пользователей. Чуть более сложная модель — линейная регрессия:
Здесь тоже делается предположение о том, что переменные независимы друг от друга, но распределение
уже моделируется с помощью линейной функции, параметры которой
нужно найти.
Многослойный перцептрон — это тоже функция, но благодаря промежуточным слоям, на которые влияют все входные переменные сразу, MLP позволяет моделировать зависимость выходной переменной от комбинации входных, а не только от каждой из них по отдельности (вспомните пример с болью в горле и температурой).
Свёрточная сеть работает с распределением пикселей в локальной области, покрываемой размером фильтра. Рекуррентные сети моделируют условное распределение следующего состояния от предыдущего и входных данных, а также выходной переменной от текущего состояния. Ну, в общем, вы поняли идею.
Теорема Байеса и умножение непрерывных переменных
Помните правило сети?
Если убрать левую часть, то получим простое и очевидное равенство:
А если теперь перенесём направо, то получим знаменитую формулу Байеса:
Про произношение
Итересный факт: русское произношение “байес” в английском звучит как слово “bias”, т.е. “смещение”. А вот фамилия учёного “Bayes” читается как “бэйс” или “бэйес” (лучше послушать в Yandex Translate).
Формула настолько избитая, что каждая её часть имеет своё название:
называется априорным распределением (prior). Это то, что мы знаем ещё до того, как увидели конкретный объект, например, общее количество людей, вовремя выплативших кредит.
носит название правдоподобия (likelihood). Это вероятность увидеть такой объект (описанный переменной
) при таком значении выходной переменной
. Например, вероятность того, что у человека, отдавшего кредит, двое детей.
— маргинальное правдоподобие, вероятность вообще увидеть такой объект. Оно одинаково для всех
, так что его чаще всего не считают, а просто максимизируют числитель формулы Байеса.
— апостериорное распределение (posterior). Это распределение вероятностей переменной
после того, как мы увидели объект. Например, вероятность того, что человек с двумя детьми отдаст кредит вовремя.
Байесовская статистика — штука жутко интересная, но влезать в неё сейчас мы не будем. Единственный вопрос, который хотелось бы затронуть, — это перемножение двух распределений непрерывных переменных, которое у нас встречается, например, в числителе формулы Байеса, да и вообще в каждой второй формуле над непрерывными переменными.
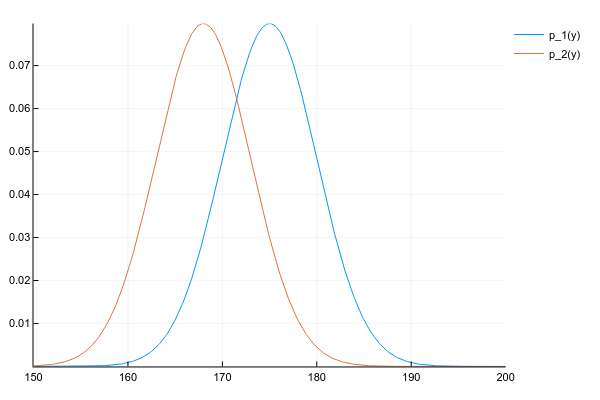
Допустим, что у нас есть два распределения и
:
Код
d1 = Normal(175, 5)
d2 = Normal(168, 5)
space = 150:0.1:200
y1 = [pdf(d1, y) for y in space]
y2 = [pdf(d2, y) for y in space]
plot(space, y1, label="p_1(y)")
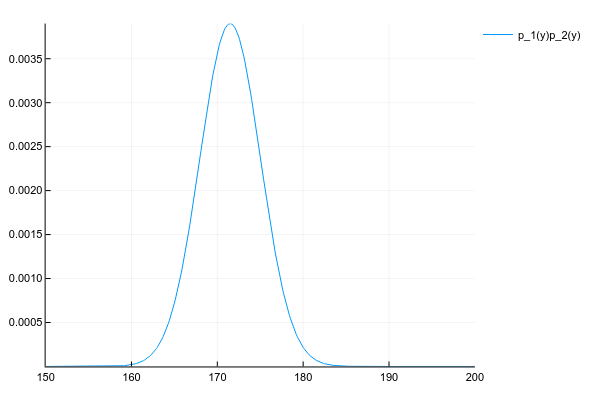
plot!(space, y2, label="p_2(y)")И мы хотим получить их произведение:
Мы знаем плотность вероятности обоих распределений в каждой точке, поэтому, по-честному и в общем случае, нам нужно перемножить плотности в каждой точке. Но, если мы вели себя хорошо, то и
у нас заданы параметрами, например, для нормального распределения 2-мя числами — матожиданием и дисперсией, а для их произведения придётся считать вероятность в каждой точке?
К счастью, произведение многих известных распределений даёт другое известное распределение с легко вычислимыми параметрами. Ключевое слово здесь — conjugate prior.
Как бы мы не вычисляли, произведение двух нормальных распределений даёт ещё одно нормальное распределение (правда, ненормализованное):
Код
# честно перемножаем плотности вероятности в каждой точке
# неэффективно, но работает для любых распределений
plot(space, y1 .* y2, label="p_1(y)p_2(y)")Ну и просто для сравнения распределение смеси 3х нормальных распределений:
Код
plot(space, [pdf(Normal(130, 5), x) for x in space] .+
[pdf(Normal(150, 20), x) for x in space] .+
[pdf(Normal(190, 3), x) for x in space])Вопросы
Раз уж это туториал и кто-нибудь наверняка захочет запомнить то, что здесь было написано, вот несколько вопросов для закрепления материала.
Пусть рост человека — нормально распределённая случайная переменная с параметрами
и
. Какова вероятность встретить человека ростом ровно 178см?
Ответ
Правильными ответами можно считать “0”, “бесконечно мала” или “не определена”. А всё потому что вероятность непрерывной переменной считается на некотором интервале. Для точки интервал — это её ширина, в зависимости от того, где вы учили математику, длину точки можно считать нулём, бесконечно малой или вообще не определённой.
Пусть
— количество детей у заёмщика кредита (3 возможными значения),
— признак того, отдал ли человек кредит (2 возможных значения). Мы используем формулу Байеса для предсказания, отдаст ли конкретный клиент с 1 ребёнком кредит. Сколько возможных значений может принимать априорное и апостериорное распределения, а также правдоподобие и маргинальное правдоподобие?
Ответ
Таблица совместного распредления двух переменных в данном случае небольшая и имеет вид:
| c=0 | c=1 | c=2 | |
|---|---|---|---|
| s=0 | p(s=0,c=0) | p(s=0,c=1) | p(s=0,c=2) |
| s=1 | p(s=1,c=0) | p(s=1,c=1) | p(s=1,c=2) |
где — признак успешно отданного кредита.
Формула Байеса в данном случае имеет вид:
Если все значения известны, то:
— это маргинальная вероятность увидеть человека с одним ребёнком, считается как сумма по колонке
и является просто числом.
— априорная/маргинальная вероятность того, что случайно взятый человек, про которого мы ничего не знаем, отдаст кредит. Может иметь 2 значения, соответствующих сумме по первой и по второй строке таблицы.
— правдоподобие, условное распределение количества детей в зависимости от успешности кредита. Может показаться, что раз уж это распределение количества детей, то возможных значений должно быть 3, но это не так: мы уже точно знаем, что к нам пришёл человек с одним ребёнком, поэтому рассматриваем только одну колонку таблицы. А вот успешность кредита пока под вопросом, поэтому возможны 2 варианта — 2 строки таблицы.
— апостериорное распределение, где мы знаем
, но рассматриваем 2 возможных варианта
.
Нейронные сети, оптимизирующие расстояние между двумя расспределениями
и
, зачастую используют в качестве оптимизационной цели кросс-энтропию (cross entropy) или расстояние Кульбака-Лейблера (Kullback-Leibler divergence). Последнее определяется как:
— это мат. ожидание по
, а почему в основной части —
— используется деление, а не просто разница между плотностями двух функций
?
Ответ
Другими словами, это и есть разница между плотностями, но в логарифмическом пространстве, которе является вычислительно более стабильным.
| Байесовская статистика |
|---|
|
|
| Теория |
|
| Техники |
|
| Портал:Статистика |
Байесовская линейная регрессия — это подход в линейной регрессии, в котором статистический анализ проводится в контексте байесовского вывода: когда регрессионная модель имеет ошибки[en], имеющие нормальное распределение, и, если принимается определённая форма априорного распределения, доступны явные результаты для апостериорных распределений вероятностей параметров модели.
Конфигурация модели[править | править код]
Рассмотрим стандартную задачу линейной регрессии, в которой для 



где 


Это соответствует следующей функции правдоподобия:
Решение обычного метода наименьших квадратов является оценкой вектора коэффициентов с помощью псевдоинверсной матрицы Мура — Пенроуза:
где 



![{displaystyle [y_{1};cdots ;y_{n}]^{rm {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f20cfbb54554244dad54e7868719f5dada5c310)
Это является частотным[en] подходом, и предполагается, что существует достаточно измерений для того, чтобы сказать что-то осмысленное о 


Регрессия с сопряжёнными распределениями[править | править код]
Сопряжённое априорное распределение[править | править код]
Для любого априорного распределения, может не существовать аналитического решения для апостериорного распределения. В этом разделе мы рассмотрим так называемое сопряжённое априорное распределение, для которого апостериорное распределение можно вывести аналитически.
Априорное распределение 




Правдоподобие теперь переписывается как
где
и
,
где 
Это указывает на вид априорного распределения:
где 
В обозначениях, введённых в статье Обратное гамма-распределение[en], это плотность распределения 







Далее, условная априорная плотность 
В обозначениях нормального распределения условное априорное распределение равно 
Апостериорное распределение[править | править код]
При указанном априорным распределении апостериорное распределение можно выразить как
После некоторых преобразований[1] апостериорная вероятность может быть переписана так, что апостериорное среднее 




Для подтверждения, что 

Теперь апостериорное распределение можно выразить как нормальное распределение, умноженное на обратное гамма-распределение[en]:
Поэтому апостериорное распределение можно параметризовать следующим образом.
где два множителя соответствуют плотностям распределений 

Это можно интерпретировать как байесовское обучение, в котором параметры обновляются согласно следующим равенствам
Обоснованность модели[править | править код]
Обоснованность модели 






Этот интеграл можно вычислить аналитически и решение задаётся следующим равенством[3]
Здесь 


Заметим, что это равенство является ни чем иным, как переформулировкой теоремы Байеса. Подстановка формулы для априорной вероятности, правдоподобия и апостериорной вероятности и упрощения получающегося выражения приводит к аналитическому выражению, приведённому выше.
Другие случаи[править | править код]
В общем случае может оказаться невозможным или нецелесообразным получать апостериорное распределение аналитически. Однако можно аппроксимировать апостериорную вероятность методом приближенного байесовского вывода[en], таким как выборка по методу Монте-Карло[4] или вариационные байесовские методы[en].
Частный случай 
Аналогичный анализ можно провести для общего случая множественной регрессии и частично для байесовской оценки ковариационной матрицы[en] — см. Байесовская мультивариантная линейная регрессия[en].
См. также[править | править код]
- Байесовская линейная статистика[en]
- Регуляризованная линейной регрессия[en]
- Метод регуляризации Тихонова
- Выбор спайковой переменной[en]
- Байесовская интерпретация ядерной регуляризации[en]
Примечания[править | править код]
- ↑ Промежуточные выкладки можно найти в книге O’Hagan (1994) в начале главы по линейным моделям.
- ↑ Промежуточные выкладки можно найти в книге Fahrmeir и др. (2009 на стр. 188.
- ↑ Промежуточные выкладки можно найти в книге O’Hagan (1994) на странице 257.
- ↑ Карлин и Луи (Carlin, Louis, 2008) и Гельман с соавторами (Gelman, et al., 2003) объяснили как использовать методы выборочных наблюдений для байесовской линейной регрессии.
Литература[править | править код]
- George E. P. Box, Tiao G. C. Bayesian Inference in Statistical Analysis. — Wiley, 1973. — ISBN 0-471-57428-7.
- Bradley P. Carlin, Thomas A. Louis. Bayesian Methods for Data Analysis, Third Edition. — Boca Raton, FL: Chapman and Hall/CRC, 2008. — ISBN 1-58488-697-8.
- Fahrmeir L., Kneib T., Lang S. Regression. Modelle, Methoden und Anwendungen. — 2nd. — Heidelberg: Springer, 2009. — ISBN 978-3-642-01836-7. — doi:10.1007/978-3-642-01837-4.
- Fornalski K.W., Parzych G., Pylak M., Satuła D., Dobrzyński L. Application of Bayesian reasoning and the Maximum Entropy Method to some reconstruction problems // Acta Physica Polonica A. — 2010. — Т. 117, вып. 6. — С. 892—899. — doi:10.12693/APhysPolA.117.892.
- Krzysztof W. Fornalski. Applications of the robust Bayesian regression analysis // International Journal of Society Systems Science. — 2015. — Т. 7, вып. 4. — С. 314–333. — doi:10.1504/IJSSS.2015.073223.
- Andrew Gelman, John B. Carlin, Hal S. Stern, Donald B. Rubin. Bayesian Data Analysis, Second Edition. — Boca Raton, FL: Chapman and Hall/CRC, 2003. — ISBN 1-58488-388-X.
- Michael Goldstein, David Wooff. Bayes Linear Statistics, Theory & Methods. — Wiley, 2007. — ISBN 978-0-470-01562-9.
- Minka, Thomas P. (2001) Bayesian Linear Regression Архивная копия от 26 октября 2008 на Wayback Machine, Microsoft research web page
- Peter E. Rossi, Greg M. Allenby, Robert McCulloch. Bayesian Statistics and Marketing. — John Wiley & Sons, 2006. — ISBN 0470863676.
- Anthony O’Hagan. Bayesian Inference. — First. — Halsted, 1994. — Т. 2B. — (Kendall’s Advanced Theory of Statistics). — ISBN 0-340-52922-9.
- Sivia, D.S., Skilling, J. Data Analysis – A Bayesian Tutorial. — Second. — Oxford University Press, 2006.
- Gero Walter, Thomas Augustin. Bayesian Linear Regression—Different Conjugate Models and Their (In)Sensitivity to Prior-Data Conflict // Technical Report Number 069, Department of Statistics, University of Munich. — 2009.
Программное обеспечение[править | править код]
- Python
- Bayesian Type-II Linear Regression code, tutorial Архивная копия от 18 декабря 2020 на Wayback Machine
- ARD Linear Regression code Архивная копия от 1 марта 2017 на Wayback Machine
- ARD Linear Regression with kernelized features code Архивная копия от 1 марта 2017 на Wayback Machine, tutorial Архивная копия от 18 декабря 2020 на Wayback Machine
В этом посте расскажем о формуле Байеса и её применении в машинном обучении. С этого года я буду читать много всяких новых курсов, в том числе, потоковый курс по «Машинному обучению и анализу данных» на факультете ВМК МГУ. Поэтому сейчас пребываю в поисках правильных формы/объёма/манеры подачи материала (чтобы не сильно лезть в теорию, но дать представление, зачем теория нужна). Постарался сделать максимально доступно, но предварительные знания по терверу нужны…
Формула Байеса хорошо известна из курса теории вероятностей и математической статистики и позволяет пересчитывать условную вероятность (или плотность) P(A|B) через P(B|A), см. рис. 1.
Прежде чем читать дальше полезно посмотреть этот небольшой пост, содержащий решение задачи «Тест на болезнь «зеленуху» имеет вероятность ошибки 0.1 (как позитивной, так и негативной), зеленухой болеет 10% населения. Какая вероятность того, что человек болен зеленухой, если у него позитивный результат теста (т.е. тест говорит «болен»)?» (а лучше попробовать самостоятельно решить эту задачу и потом проверить себя).
Кстати, задача решается очень просто графически, на рис. 2 показано множество всех людей в виде квадрата: левая часть (90%) — здоровые, правая часть (10%) — больные. Верхняя часть (90%) — те, у кого тест показывает верный результат, нижняя часть (10%) — те, у кого тест обманывает.
Розовым цветом выделено множество людей, у которых тест показывает «болен»: это больные с правильными показаниями и здоровые с ошибочными. Теперь видно, что эти две розовые группы «одного объёма». Поэтому, если тест показывает «болен», то с вероятностью 0.5 человек болен и тест верен, а с вероятностью 0.5 он здоров и тест ошибается.
Как видите, очень простое графическое решение — без всяких формул. На самом деле, почти все задачи в теории вероятностей можно решать вот так — на картинках, поскольку теория вероятностей — это часть теории меры, т.е. о том, как измерять «объём» множества, и если это множество умело изобразить, то и ответ будет понятен.
Оптимальное решение задач классификации
Предположим, что в задаче классификации на K классов мы знаем такие вероятности
— вероятности принадлежности к классам (conditional class probabilities), т.е. вероятности того, что объект принадлежит классу k при условии, что его признаковое описание x. Тогда очевидно, что для решения задачи классификации надо просто выбрать максимальную вероятность! Именно это и делает байесовский классификатор. Кстати, P может быть и плотностью (для них всё аналогично и даже формула Байеса верна, и дальше мы будем их часто «путать»).
Но как же вычислить указанные вероятности? Давайте воспользуемся формулой Байеса…
искомая вероятность выражается через априорную вероятность (prior probability) класса P(y=k) (смысл очевиден — если дан случайный объект, то с какой вероятностью он принадлежит классу k) и вероятность / плотность (density) распределения объектов класса P(x|y=k).
Смысл P(x|y=k) тоже понятен: если мы будем рассматривать только объекты класса k, то они как-то распределены… дискретное распределение описывается вероятностями, а непрерывное — плотностями. Здесь как раз стоит одна из таких функций, в которую мы подставили x (признаковое описание).
В знаменателе формулы стоит P(x) — это уже вероятность / плотность распределения всех объектов, но, по сути, она нам не очень нужна: выбор максимальной вероятности принадлежности к классам не зависит от этого значения.
Посмотрим на рис. 3 — розовая и синяя линии изображают плотности распределения двух классов в однопризнаковой задаче. Они могут быть заданы изначально, а могут быть восстановлены по данным (возможно, с некоторыми априорными предположениями, например, что данные распределены нормально). Если бы классы были равновероятны, то точки пересечения линий определяли бы «разделяющие поверхности классов» (да, у нас одномерное пространство, поэтому точки тут это «поверхности»).
Но если классы не равновероятны, то эти самые вероятности классов по формуле Байеса «масштабируют» наши плотности и смещают разделяющие поверхности, см. рис. 4:
Можно подробно рассмотреть случай однопризнаковой задачи бинарной классификации с нормальными распределениями классов:
Здесь знак «<>» означает сравнение с целью определения максимального значения и классификации. В итоге (после логарифмирования) всё свелось к неравенству порядка не выше 2 (старшая степень при x). Если дисперсии распределений обоих классов равны, то для классификации мы будем значение признака просто сравнивать с порогом, что согласуется с рис. 5.
Если дисперсии различны, то обязательно получится неравенство 2го порядка и здесь разделяющая поверхность состоит из 2х точек (см. рис. 4) или ни одной… если неравенство не имеет решения или решение — вся числовая прямая (это соответствует ситуации, когда какой-то класс очень редкий — вероятность принадлежности к нему близка к нулю).
Кстати, если классы равновероятны и нормально распределены с одинаковой дисперсией, то разделяющая поверхность — точка, которая является средним арифметическим матожиданий классов.
Аналогично можно рассмотреть двухпризнаковую задачу бинарной классификации. Там разделяющие поверхности не сложнее поверхностей 2-го порядка, т.е. в этом случае байесовский классификатор также разделяет классы достаточно простыми поверхностями.
В различных библиотеках алгоритмов машинного обучения Вы встретите, скорее всего, реализацию наивного байесовского классификатора (naive Bayes). Связано это со сложностью оценки плотностей. Вероятность класса можно оценить пропорцией, в которой представители этого класса есть в обучающей выборке. А вот плотность распределения в классе в многомерном пространстве сложно оценить надёжно из-за проклятия размерности. Поэтому делают сильное предположение, что все признаки независимы, тогда плотность представляется в виде произведения плотностей по отдельным признакам:
Не смотря на то, что предположение сильное и на практике почти никогда не выполняется (если Вы сами не преобразуете признаки), метод часто работает неплохо… почему? Потому что поиск решения в классе простых решений — хороший способ борьбы с переобучением;)
Метод максимального правдоподобия (MLE)
Прежде чем описывать байесовский подход, вспомним самый популярный метод оценивания параметров в математической статистике — метод максимального правдоподобия. Если есть плотность (вероятность) распределения p(y|θ), известная с точностью до параметра θ, то для его оценки надо максимизировать функцию правдоподобия — произведение значений вероятностей в элементах нашей выборки (предполагаем, что они независимые и распределены по p(y|*), * — неизвестное нам истинное значение параметра θ):
Точка, в которой правдоподобие достигает максимального значения называется оценкой максимального правдоподобия (MLE = Maximum Likelihood Estimation). Кстати, будем держать в уме, что параметр θ может быть вектором (т.е. это параметры).
Приведём в качестве примера проблему нечестной монетки (coin-toss problem). Пусть кто-то бросает монету и мы наблюдаем исходы: 1 — выпал орёл, 0 — выпала решка. Наша задача оценить вероятность выпадения орла. Предполагая, что наблюдаемая случайная величина подчиняется распределению Бернулли, получаем:
Здесь вместо максимизации правдоподобия применили стандартный приём — максимизацию его логарифма. Максимум ищется просто приравниванием к нулю производной (функция вогнута). Я опускаю некоторые довольно простые выкладки. Получили достаточно очевидный ответ: оценка параметра распределения Бернулли (который и является вероятностью выпадения орла) — среднее арифметическое наблюдаемых случайных величин, т.е. доля выпадения орла.
Отметим недостатки полученной оценки:
- ненадёжность при малом числе экспериментов и явная склонность к переобучению (например, если после двух бросков выпали два орла, то мы утверждаем, что вероятность равна 1).
- отсутствие возможности внести некоторую дополнительную информацию (например, до бросков мы знаем, что у этой монеты орёл выпадает чаще)
А теперь подход, который одним махом исправит все эти недостатки;)
Байесовский подход
Перепишем формулу Байеса в терминах задачи моделирования данных и приведём нужные термины:
Наша задача найти некоторый параметр θ (параметр(ы) нашей модели), у нас есть априорная плотность распределения (prior) этого параметра p(θ) , мы наблюдаем данные D, p(D) — вероятность данных (evidence), как видно выполняет роль нормировки, чтобы слева получалась плотность. p(D|θ) — правдоподобие (likehood), p(θ|D) — апостериорная плотность распределения (posterior). Для дискретных распределений плотности заменяются вероятностями, а интеграл суммой.
Апостериорная плотность именно то, что нам и нужно после наблюдения данных D. С помощью формулы Байеса мы видим, как наша априорная плотность (до наблюдения данных) превращается в апостериорную. Важно сразу понять, что формулу можно применять итерационно после поступления каждой новой порции данных. Текущее распределение параметра считается априорным, поступили данные — получили апостериорное распределение, потом, при необходимости, оно становится априорным для нового применения формулы.
Посмотрим, что даст применение байесовского подхода в задаче с монеткой… Допустим, у нас нет никаких априорных знаний о монетке, тогда считаем, что априорное распределение параметра равномерное p(θ)=1 на отрезке [0, 1]. Напомним, что это параметр распределения Бернулли и одновременно вероятность выпадения орла. Если был произведён ровно один бросок и выпал орёл, то правдоподобие p(y|θ) = θ. На рис. 8 показаны априорное распределение, правдоподобие и их произведение, нормированное так, чтобы получилась плотность (площадь под кривой равнялась единице): 1·θ / 0.5.
Теперь пусть наше априорное распределение это полученное апостериорное p(θ) = 2θ, т.е. мы верим, что скорее монета выпадает орлом, а не решкой. Пусть опять сделан ровно один бросок и выпала решка, тогда функция правдоподобия p(y|θ) = 1-θ, после применения формулы Байеса (перемножения и нормировки) получили апостериорную плотность p(θ|y) =6θ(1-θ)
Уже видно фундаментальное отличие от MLE, которое является характерным для байесовского подхода. В MLE мы получаем конкретное значение параметра, а здесь — работаем с распределениями и в итоге получаем апостериорное распределение на значение нашего параметра.
Как ответить, какая вероятность выпадения орла? Мы получили целое распределение на возможных значениях этой вероятности. Можно найти моду (точку, в которой она максимальна) — это метод максимизации апостериорной плотности (MAP = Maximum a Posteriori). На рис. 9 это 0.5, что вполне логично после двух бросков и одного выпавшего орла. Давайте прологарифмируем формулу Байеса и запишем задачу максимизации:
(максимизация производится по θ, мы удалили слагаемое, которое от него не зависит).
Видно, что метод MAP максимизирует логарифм правдоподобия (как и MLE) плюс логарифм априорного распределения. Второе слагаемое играет роль своеобразного регуляризатора, которое позволяет не переобучаться (ниже покажем почему).
Задача с монеткой и MAP
Предположим, что априорное распределение на значения оцениваемого параметра распределения Бернулли — бета-распределение:
Если вдруг Вам показалось такое предположение странным и/или Вы вообще до этого не работали с бета-распределением, боитесь гамма-функций (но они тут только для вычислений нормировочных констант), то подождите немного, дальше будет понятно, почему выбрано именно оно. Пока скажем, что это довольно большой класс распределений, на рис. 10 показаны некоторые его представители
Запишем выражение для максимизации методом MAP, возьмём производную и приравняем к нулю:
Интересно, что при α=β=1 оценки MLE и MAP совпадают. Если же α+β>2 и эти параметры целые, то по-сути они играют роль фиктивных экспериментов в количестве α+β-2 штук, в которых выпал α—1 орёл. Теперь оценка параметра будет адекватнее вести себя при малом числе экспериментов! Кстати, такая оценка часто называется сглаживанием Лапласа.
Почему же мы взяли бета-распределение? Всё дело в том, что если функцию правдоподобия для распределения Бернулли умножить на плотность бета-распределения, то мы снова получим бета-распределение:
Таким образом, мы не просто переходим от априорного распределения к апостериорному, а ещё и остаёмся в одном классе распределений! Да и вообще, все формулы красиво аналитически считаются… Распределения, которые не выводят из класса априорного распределения (как здесь Бернулли и бета), называются сопряжёнными.
С помощью бета-распределений удобно формализовать свою веру в то, что вероятность имеет определённое значение. Как мы видели, это вера будет просто эквивалентна серии фиктивных бросков. На рис. 11 показано несколько функций, которые формализуют априорную информацию о том, что θ=2/3.
Обоснование регуляризации
Вспомним статистическую теорию линейной регрессии. Пусть нам известно, что целевая переменная зависит от других линейно с точностью до нормального шума:
Тогда можно искать коэффициенты с помощью MLE:
Задача максимизации логарифма правдоподобия обучающей выборке свелась к минимизации квадратичной ошибки, что, собственно, обосновывает использование этой функции ошибки в задачах регрессии.
Теперь давайте применим байесовский подход. До наблюдения обучающей выборки мы ничего не знаем о нашей модели, но мы можем сформулировать наши пожелания. Например, пусть неизвестные (а, следовательно, случайные) коэффициенты линейной регрессии будут нормально распределены:
Тогда
В задаче минимизации мы оставили только слагаемые, которые зависят от w. Здесь легко узнаётся формула, которая используется в ридж-регрессии. Первое слагаемое — квадратичная ошибка, второе — член L2-регуляризации. Как мы и обещали, логарифм априорного распределения играет роль регуляризатора. Таким образом, мы доказали корректность регуляризации (фактически вывели её) в рамках рассматриваемых ограничений.
На рис. 12 показано, как априорная плотность «оттягивает» решение задачи MAP к нулю. MLE получает нерегуляризованное решение. С точки зрения байесовского подхода, регуляризация — априорное распределение параметров.
Отметим, что если бы коэффициенты линейной регрессии были распределены по Лапласу, то мы бы получили L1-регуляризацию. Обычно в ридж-регрессии при регуляризационном члене стоит параметр — коэффициент регуляризации. Здесь он тоже есть, более того, он теперь имеет теоретический смысл: это отношение дисперсий шума и априорного распределения параметров.

Итак, байесовский подход теоретически обосновывает регуляризацию (мы привели один пример, но примеров много), придаёт используемым параметрам теоретический смысл.
Байесовский подход к машинному обучению
До сих пор мы говорили о нахождении параметров модели, т.е. фактически о машинном обучении (как известно, сама процедура обучения и есть не что иное, как настройка параметров). Вместо одного значения параметра мы научились находить целое распределение на множестве значений. Что с ним делать дальше, когда потребуется сделать классификацию (или регрессию) новых объектов? Итак, по формуле Байеса, в случае, когда у нас есть обучающая выборка (X, Y), мы получили распределение параметров
Если со штрихами обозначить тестовый объект, то
Здесь интегрирование проводится по распределению параметра модели w. Получается своеобразный ансамбль: мы используем модель сразу при всех значениях параметра! Правда, такое интегрирование не всегда удаётся выполнить, поэтому вместо него используют модель с параметром, который получается с помощью MAP-оценки:
Предположим, что параметр w сам, в свою очередь, зависит от некоторого параметра α. Тогда надо определить значение α. Воспользуемся опять формулой Байеса:
Правдоподобие параметра α
называется обоснованностью (evidence) — интегрированием мы просто исключаем переменную w. Принцип максимальной обоснованности состоит в том, чтобы найти значение параметра
и потом при классификации / регрессии использовать его. Именно так выводится метод Relevance Vector Machine (RVM). Метод похож на SVM, но вместо опорных векторов, которые находятся на границе классов, здесь решение зависит от «релевантных векторов», которые находятся «внутри класса». Часто это преподносится как большой плюс: при моделировании мы смотрим не на пограничные случаи, а на типичные. Желающие могут почитать классическую работу Типпинга (у которой уже почти 1000 цитирований).
Итак, байесовский подход позволяет получать новые методы машинного обучения!
Что такое случайность
В теории вероятностей есть два классических подхода к пониманию того, что такое случайность. Наиболее широко распространённый — частотный подход, который предполагает, что случайность – объективная неопределённость. Поэтому, чтобы установить истину, надо делать эксперименты… в пределе она и устанавливается, подобно тому, как частота выпадения орлов сходится к вероятности. Понятно, что MLE — классический метод частотников.
Второй подход, более распространённый среди специалистов по машинному обучению, — байесовский (Bayesian). Здесь случайность – мера нашего незнания, соответственно, эксперименты просто уменьшают незнание переходом от априорной информации к апостериорной. MAP — пример метода байесианцев. Заметьте, что даже параметры в распределениях здесь случайные (они же неизвестны!).
Второй подход кажется более общим и красивым (мы уже привели значительное число плюсов). Есть правда несколько «но»
- Сама техника и многие результаты байесианцев плохо интерпретируемы для простых смертных. Можно поверить, что объекты как-то распределены (например, клиенты интернет-магазина), но вот поверить, что параметры распределений как-то распределены нормальному человеку сложнее…
- Мы не зря сказали про сопряжённые распределения, если они не сопряжённые, то нет такой красоты и эффектности.
- Утверждается, что байесовский подход работает даже при отсутствии выборки (экспериментов). Но это рекламный слоган, который описывает наличие априорного распределения, но откуда его взять? Часто его выбор просто эвристика, но тогда зачем навешивать эвристику на распределение? Можно сразу на оценку! Скажем, до сглаживания Лапласа догадываются даже те, кто понятия не имеют о байесовском подходе.
- Удобно вносить свои знания с помощью распределения, но мы можем внести и заблуждения…
- Методы вычислительно ресурсоёмкие (но об этом нужно писать подробнее).
- Методы, полученные с помощью байесовского подхода, не так хороши на практике, как многие эвристические (например, я не встречал, чтобы кто-нибудь использовал RVM в проде или на кэгле).
На самом деле, я описал лишь 2/3 того, что хотел… но пост уже получился большим. Дочитал ли кто-нибудь до конца? Все пожелания и замечания оставляйте в комментариях.
Что почитать
- Универсальный совет: читайте Бишопа и будете умными;)
- По вопросам, связанным с байесовским подходом, в России проводится целая научная школа. Доступны материалы прошлого года. Возможно, будут и этого.
- Есть курс, который так и называется «Байесовские методы машинного обучения», разработанный Д. Ветровым и Д. Кропотовым на факультете ВМК МГУ.
- Неплохая лекция Буре В.М., Грауэр Л.В.
П.С. В заключение несколько малоизвестных фактов.
1. Вы, наверное, видели изображение Томаса Байеса, см. рис.12
Так вот, точно не известно, кто изображён на этом рисунке. По одной из гипотез — Байес. На самом деле, о его жизни мы знаем очень мало… например, точно не известен год (1701 или 1702) и место рождения (скорее всего, Hertfordshire).
2. Правильно фамилия учёного произносится [бейз], т.е. надо бы говорить «формула Бейза».
3. На википедии написано, что Байес опубликовал две работы. Одна из них «Divine Benevolence, or an Attempt to Prove That the Principal End of the Divine Providence and Government is the Happiness of His Creatures«. На самом деле, автор этой работы Джон Нун. По одной из гипотез — «Нун» это псевдоним Томаса Байеса.
Немного об основной идее этой работы. Это не математическая, а философская статья, в которой рассматривается проблема существования зла: как в мире, который создал Бог (а Бог есть добро), может существовать зло. Если кратко, то ответ прост — дело в нас (людях).
4. В том виде, в котором мы знаем формулу Байеса, её вывел не Байес, а Пьер-Симон Лаплас. Они с Байесом очень не похожи друг на друга. Например, Лаплас был атеистом, а Байес — священником.
5. Термин «байесовский» (Bayesian) впервые применил Рональд Фишер. Но в его лексиконе этот термин был ругательным. Он считал, что теория Байеса «должна быть полностью отвергнута».