Как найти апостериорную вероятность гипотезы - Сайт, где вы сможете решить свои вопросы

Теорема Байеса (или формула Байеса) — одна из основных теорем элементарной теории вероятностей, которая позволяет определить вероятность события при условии, что произошло другое статистически взаимозависимое с ним событие. Другими словами, по формуле Байеса можно уточнить вероятность какого-либо события, взяв в расчёт как ранее известную информацию, так и данные новых наблюдений. Формула Байеса может быть выведена из основных аксиом теории вероятностей, в частности из условной вероятности. Особенность теоремы Байеса заключается в том, что для её практического применения требуется большое количество расчётов, вычислений, поэтому байесовские оценки стали активно использовать только после революции в компьютерных и сетевых технологиях. На сегодняшний день активно применяется в машинном обучении и технологиях искусственного интеллекта.

При возникновении теоремы Байеса вероятности, используемые в теореме, подвергались целому ряду вероятностных интерпретаций. В одной из таких интерпретаций говорилось, что вывод формулы напрямую связан с применением особого подхода к статистическому анализу. Если использовать байесовскую интерпретацию вероятности, то теорема показывает, как личный уровень доверия может кардинально измениться вследствие количества наступивших событий. В этом заключаются выводы Байеса, которые стали основополагающими для байесовской статистики. Однако теорема не только используется в байесовском анализе, но и активно применяется для большого ряда других расчётов.

Психологические эксперименты^[1] показали, что люди часто неверно оценивают реальную (математически верную) вероятность события, основываясь на некоем личном полученном опыте (апостериорная вероятность), поскольку игнорируют саму вероятность предположения (априорная вероятность). Поэтому правильный результат по формуле Байеса может сильно отличаться от интуитивно ожидаемого.

Теорема Байеса названа в честь её автора Томаса Байеса (1702—1761) — английского математика и священника, который первым предложил использование теоремы для корректировки убеждений, основываясь на обновлённых данных. Его работа «An Essay towards solving a Problem in the Doctrine of Chances» впервые опубликована в 1763 году^[2], через 2 года после смерти автора. До того, как посмертная работа Байеса была принята и прочитана в Королевском обществе, она была значительно отредактирована и обновлена Ричардом Прайсом. Однако эти идеи не предавались публичной огласке до тех пор, пока не были вновь открыты и развиты Пьером-Симоном Лапласом, впервые опубликовавшим современную формулировку теоремы в своей книге 1812 года «Аналитическая теория вероятностей».

Сэр Гарольд Джеффрис писал, что теорема Байеса «для теории вероятности то же, что теорема Пифагора для геометрии»^[3].

Формулировка[править | править код]

Формула Байеса:

${displaystyle P(Amid B)={frac {P(Bmid A),P(A)}{P(B)}}}$ ,

где

— априорная вероятность гипотезы A (смысл такой терминологии см. ниже);

— вероятность гипотезы A при наступлении события B (апостериорная вероятность);

— вероятность наступления события B при истинности гипотезы A;

— полная вероятность наступления события B.

Доказательство[править | править код]

Формула Байеса вытекает из определения условной вероятности. Вероятность совместного события двояко выражается через условные вероятности

{displaystyle P(AB)=P(Amid B)P(B)=P(Bmid A)P(A)}

Следовательно ${displaystyle P(Amid B)={frac {P(AB)}{P(B)}}={frac {P(Bmid A),P(A)}{P(B)}}}$

Вычисление P(B)[править | править код]

В задачах и статистических приложениях P(B) обычно вычисляется по формуле полной вероятности события, зависящего от нескольких несовместных гипотез, имеющих суммарную вероятность 1.

${displaystyle P(B)=sum _{i=1}^{N}P(Bmid A_{i})P(A_{i})}$

где вероятности под знаком суммы известны или допускают экспериментальную оценку.

В этом случае формула Байеса записывается так:

${displaystyle P(A_{j}mid B)={frac {P(Bmid A_{j})P(A_{j})}{sum _{i=1}^{N}P(Bmid A_{i})P(A_{i})}}}$

«Физический смысл» и терминология[править | править код]

Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной. При этом необходимо понимать, для применения теоремы причинно-следственная связь между и не является обязательной.

События, отражающие действие «причин», в данном случае называют гипотезами, так как они — предполагаемые события, повлёкшие данное. Безусловную вероятность справедливости гипотезы называют априорной (насколько вероятна причина вообще), а условную — с учётом факта произошедшего события — апостериорной (насколько вероятна причина оказалась с учётом данных о событии).

Примеры[править | править код]

Пример 1[править | править код]

Пусть событие — машина не заводится, а гипотеза — в баке нет топлива.
Очевидно, что вероятность того, что машина не заведётся, если в баке нет топлива, равняется единице.
Как следствие, апостериорная вероятность, что в баке нет топлива, если машина не заводится, то есть , равна ${displaystyle {frac {P(A)}{P(B)}}}$ , то есть отношению априорной вероятности, что в баке нет топлива, к вероятности, что машина не заводится. Например, если априорная вероятность, что в баке нет топлива, равна 0,01, а вероятность, что машина не заводится, равна 0,02, и случайно выбранная машина не завелась, то вероятность, что в её баке нет топлива, равна 0,5.

Пример 2[править | править код]

Пусть вероятность брака у первого рабочего $p_{1}=0{,}9$ , у второго рабочего — $p_{2}=0{,}5$ , а у третьего — $p_{3}=0{,}2$ . Первый изготовил $n_{1}=800$ деталей, второй — $n_{2}=600$ деталей, а третий — $n_{3}=900$ деталей. Начальник цеха берёт случайную деталь, и она оказывается бракованной. Спрашивается, с какой вероятностью эту деталь изготовил третий рабочий?

Событие — брак детали, событие $A_{i}$ — деталь произвёл рабочий . Тогда $P(A_{i})=n_{i}/N$ , где $N=n_{1}+n_{2}+n_{3}$ , а ${displaystyle P(Bmid A_{i})=p_{i}}$ .

По формуле полной вероятности

${displaystyle P(B)=sum _{i=1}^{3}P(Bmid A_{i})P(A_{i}).}$

По формуле Байеса получим:

${displaystyle P(A_{3}mid B)={frac {P(Bmid A_{3})P(A_{3})}{P(B)}}={frac {P(Bmid A_{3})P(A_{3})}{P(Bmid A_{1})P(A_{1})+P(Bmid A_{2})P(A_{2})+P(Bmid A_{3})P(A_{3})}}=}$

$={frac {p_{3}n_{3}/N}{p_{1}n_{1}/N+p_{2}n_{2}/N+p_{3}n_{3}/N}}={frac {0{,}2cdot 900/2300}{0{,}9cdot 800/2300+0{,}5cdot 600/2300+0{,}2cdot 900/2300}}=0{,}15.$

Пример 3[править | править код]

Древовидная диаграмма демонстрирует частотный пример. R, C, P и P c чёрточкой — это события, обозначающие, что жук является редким, обычным, с узором и без узора. Проценты в скобках вычисляются. Отметим, что значения трёх независимых событий даны, поэтому возможно вычислить обратное дерево (смотрите на график выше).

Энтомолог предполагает, что жук может относиться к редкому подвиду жуков, так как у него на корпусе есть узор. В редком подвиде 98 % жуков имеют узор, или P(узор | редкий) = 0,98. Среди обычных жуков только 5 % имеют узор: P(узор | обычный) = 0,05. Редкого вида жуков насчитывается лишь 0,1 % среди всей популяции: P(редкий) = 0,001. Какова вероятность того, что жук, имеющий узор, относится к редкому подвиду, то есть, чему равно P(редкий | узор)?

Из расширенной теоремы Байеса получаем (любой жук может относиться либо к редким, либо к обычным):
${displaystyle {begin{aligned}P({text{редкий}}mid {text{узор}})&={frac {P({text{узор}}mid {text{редкий}})times P({text{редкий}})}{P({text{узор}}mid {text{редкий}})times P({text{редкий}}),+,P({text{узор}}mid {text{обычный}})times P({text{обычный}})}}\[8pt]&={frac {0{,}98times 0{,}001}{0{,}98times 0{,}001+0{,}05times 0{,}999}}\[8pt]&approx 0{,}019.end{aligned}}}$

Пример 4 — парадокс теоремы Байеса[править | править код]

Пусть существует заболевание с частотой распространения среди населения 0,001 и метод диагностического обследования, который с вероятностью 0,9 выявляет больного, но при этом имеет вероятность 0,01 ложноположительного результата — ошибочного выявления заболевания у здорового человека (подробнее…). Найти вероятность того, что человек здоров, если он был признан больным при обследовании.

Обозначим событие что обследование показало, человек болен как «болен» с кавычками, болен — событие, что человек действительно больной, здоров — событие, что человек действительно здоров. Тогда заданные условия переписываются следующим образом:

, при этом , значит:

Вероятность того, что человек здоров, если он был признан больным равна условной вероятности:

Чтобы её найти, вычислим сначала полную вероятность признания больным:

${displaystyle {begin{aligned}P({text{«болен»}})&=P({text{«болен»}}mid {text{здоров}})cdot P({text{здоров}})+P({text{«болен»}}mid {text{болен}})cdot P({text{болен}})\&=0{,}01times 0{,}999+0{,}9times 0{,}001=0{,}01089end{aligned}}}$

Вероятность, что человек здоров при результате «болен»:

${displaystyle {begin{aligned}P({text{здоров}}mid {text{«болен»}})&={frac {P({text{«болен»}}mid {text{здоров}})cdot P({text{здоров}})}{P({text{«болен»}})}}\&={frac {0{,}01times 0{,}999}{0{,}01089}}approx 0{,}917end{aligned}}}$

Таким образом, 91,7 % людей, у которых обследование показало результат «болен», на самом деле здоровые люди. Причина этого в том, что по условию задачи вероятность ложноположительного результата хоть и мала, но на порядок больше доли больных в обследуемой группе людей.

Если ошибочные результаты обследования можно считать случайными, то повторное обследование того же человека будет давать независимый от первого результат. В этом случае для уменьшения доли ложноположительных результатов имеет смысл провести повторное обследование людей, получивших результат «болен». Вероятность того, что человек здоров после получения повторного результата «болен», также можно вычислить по формуле Байеса:

${displaystyle {begin{aligned}P{bigl (}({text{здоров}}mid {text{«болен»}}{bigr )}mid {text{«болен»}})&={frac {P({text{«болен»}}mid {text{здоров}})cdot {bigl (}P({text{«болен»}}mid {text{здоров}})cdot P({text{здоров}}){bigr )}}{P({text{«болен»}}mid {text{здоров}})cdot {bigl (}P({text{«болен»}}mid {text{здоров}})cdot P({text{здоров}}){bigr )}+P({text{«болен»}}mid {text{болен}})cdot {bigl (}P({text{«болен»}}mid {text{болен}})cdot P({text{болен}}){bigr )}}}\&={frac {0{,}01times 0{,}01times 0{,}999}{0{,}01times 0{,}01times 0{,}999+0{,}9times 0{,}9times 0{,}001}}approx 0{,}1098end{aligned}}}$

Варианты интерпретации вероятностей в теореме Байеса[править | править код]

Математически теорема Байеса показывает взаимоотношения между вероятностью события A и вероятностью события B, P(A) и P(B), условной вероятности наступления события А при существующем B и наступлении события B при существующем A, P(A | B) и P(B | A).

В общей форме формула Байеса выглядит следующим образом:

Значение выражения зависит от того, как интерпретируются вероятности в данной формуле.

Интерпретация Байеса[править | править код]

В интерпретации Байеса вероятность измеряет уровень доверия. Теорема Байеса связывает воедино доверие предположению до и после принятия во внимание очевидных доказательств. Например, кто-то предположил, что при подкидывании монетки она будет приземляться в 2 раза чаще решкой вверх, а орлом вниз. Первоначально степень доверия, что такое событие случится, монета упадёт именно так — 50 %. Уровень доверия может увеличиться до 70 %, если предположение будет подтверждено доказательством.^[]

Для предположения (гипотезы) A и доказательства B

P(A) — априорная вероятность гипотезы A, первоначальный уровень доверия предположению A;
P(A | B) — апостериорная вероятность гипотезы A при наступлении события B;
отношение P(B | A)/P(B) показывает, как событие B помогает изменить уровень доверия предположению A.

Частотная интерпретация[править | править код]

Иллюстрация частотной интерпретации

В частотной интерпретации теорема Байеса исчисляет доли определённых результатов события. Предположим, что некий эксперимент проводился много раз и в некоторых случаях приводил к результатам А и/или B. Тогда:

P(A) — доля случаев, когда эксперимент привёл к результату A.
P(B) — доля случаев, когда эксперимент привёл к результату B.
P(B | A) — доля случаев с результатом B среди случаев с результатом А.
P(A | B) — доля случаев с результатом A среди случаев с результатом B.

Роль теоремы Байеса лучше всего можно понять из древовидных диаграмм, представленных справа. Диаграммы демонстрируют различный порядок распределения событий по наличию или отсутствию результатов A и B. Теорема Байеса выступает как связующее звено этих распределений.

Формы[править | править код]

События[править | править код]

Простая форма[править | править код]

Для событий A и B, при условии, что P(B) ≠ 0,

${displaystyle P(Amid B)={frac {P(Bmid A),P(A)}{P(B)}}cdot }$

Во многих дополнениях к теореме Байеса указывается, что событие B известно и нужно понять, как знание о событии B влияет на уверенность в том, что произойдёт событие A. В таком случае знаменатель последнего выражения — вероятность наступления события B — известен; мы хотим изменить A. Теорема Байеса показывает, что апостериорные вероятности пропорциональны числителю:

{displaystyle P(Amid B)propto P(A)cdot P(Bmid A) }

(пропорциональность A для данного B).

Если говорить кратко: апостериорная вероятность пропорциональна априорной вероятности (смотри Lee, 2012, Глава 1).

Если события A₁, A₂, …, взаимоисключающие и исчерпывающие, то есть возможно только одно из событий, одновременно два события не могут случиться вместе, мы можем определить коэффициент пропорциональности, ориентируясь на то, что их вероятности в сумме должны составлять единицу. Например, для данного события A — само событие A и его противоположность ¬A взаимоисключающие и исчерпывающие. Обозначая коэффициент пропорциональности как C мы имеем:

{displaystyle P(Amid B)=ccdot P(A)cdot P(Bmid A) }

{displaystyle P(neg Amid B)=ccdot P(neg A)cdot P(Bmid neg A)}

Объединив эти две формулы, мы получим, что:

${displaystyle c={frac {1}{P(A)cdot P(Bmid A)+P(neg A)cdot P(Bmid neg A)}}.}$

Расширенная форма[править | править код]

Часто пространство событий (таких как {A_j}) определённо в терминах P(A_j) и P(B | A_j). Именно в этом случае полезно определить P(B), применив формулу полной вероятности:

${displaystyle P(B)={sum _{j}P(Bmid A_{j})P(A_{j})},}$

${displaystyle implies P(A_{i}mid B)={frac {P(Bmid A_{i}),P(A_{i})}{sum limits _{j}P(Bmid A_{j}),P(A_{j})}}cdot }$

В частности

${displaystyle P(Amid B)={frac {P(Bmid A),P(A)}{P(Bmid A)P(A)+P(Bmid neg A)P(neg A)}}}$

Непрерывные случайные величины[править | править код]

Диаграмма отображает смысл теоремы Байеса и применима к пространству событий, образованного непрерывными случайными величинами X и Y. Заметим, что по теореме Байеса для каждой точки в области существуют требования. На практике, эти требования могут быть представлены в параметрическом виде, с помощью обозначения плотности распределения как функция от x и y.

Рассмотрим пространство элементарных событий Ω, образованного двумя величинами X и Y. В принципе, теорема Байеса применяется к событиям A = {X = x} и B = {Y = y}. Однако выражения становятся равны 0 в точках, в которых переменная имеет конечную плотность вероятности. Для того, чтобы с пользой продолжать использовать теорему Байеса, можно её сформулировать в терминах подходящих плотностей (смотрите Вывод формул).

Простая форма[править | править код]

Если X непрерывна и Y дискретна, то

${displaystyle f_{X}(xmid Y=y)={frac {P(Y=ymid X=x),f_{X}(x)}{P(Y=y)}}.}$

Если X дискретна и Y непрерывна,

${displaystyle P(X=xmid Y=y)={frac {f_{Y}(ymid X=x),P(X=x)}{f_{Y}(y)}}.}$

Если как X, так и Y непрерывны,

${displaystyle f_{X}(xmid Y=y)={frac {f_{Y}(ymid X=x),f_{X}(x)}{f_{Y}(y)}}.}$

Расширенная форма[править | править код]

Диаграмма, показывающая, как пространство событий, образованное непрерывными случайными величинами X и Y, часто определяется.

Непрерывное пространство событий часто определяется как числитель условий A. Непрерывное пространство событий часто представляют как числитель. В дальнейшем полезно избавиться от знаменателя, используя формулу общей вероятности. Для ‘f_Y(y), это становится интегралом:

${displaystyle f_{Y}(y)=int _{-infty }^{infty }f_{Y}(ymid X=xi ),f_{X}(xi ),dxi .}$

Правило Байеса[править | править код]

Правило Байеса — это преобразованная теорема Байеса:

${displaystyle O(A_{1}:A_{2}mid B)=O(A_{1}:A_{2})cdot Lambda (A_{1}:A_{2}mid B)}$

где

${displaystyle Lambda (A_{1}:A_{2}|B)={frac {P(Bmid A_{1})}{P(Bmid A_{2})}}}$

Это называется правилом Байеса или отношением правдоподобия. Разница в вероятности наступления двух событий — это просто отношение вероятностей этих двух событий. Таким образом,

$O(A_{1}:A_{2})={frac {P(A_{1})}{P(A_{2})}}$

${displaystyle O(A_{1}:A_{2}mid B)={frac {P(A_{1}mid B)}{P(A_{2}mid B)}}}$

Вывод формул[править | править код]

Для событий[править | править код]

Теорема Байеса может быть получена из определения вероятности:

${displaystyle P(Amid B)={frac {P(Acap B)}{P(B)}},{text{ if }}P(B)neq 0,}$

${displaystyle P(Bmid A)={frac {P(Acap B)}{P(A)}},{text{ if }}P(A)neq 0,}$

{displaystyle implies P(Acap B)=P(Amid B),P(B)=P(Bmid A),P(A),}

${displaystyle implies P(Amid B)={frac {P(Bmid A),P(A)}{P(B)}},{text{ if }}P(B)neq 0.}$

Для случайных переменных[править | править код]

Для двух непрерывных случайных величин X и Y теорема Байеса может быть аналогично выведена из определения условного распределения:

${displaystyle f_{X}(xmid Y=y)={frac {f_{X,Y}(x,y)}{f_{Y}(y)}}}$

${displaystyle f_{Y}(ymid X=x)={frac {f_{X,Y}(x,y)}{f_{X}(x)}}}$

${displaystyle implies f_{X}(xmid Y=y)={frac {f_{Y}(y|X=x),f_{X}(x)}{f_{Y}(y)}}.}$

См. также[править | править код]

Байесовская фильтрация спама
Байесовское программирование
Байесовская сеть доверия
Байесовская вероятность
Некорректное априорное распределение
Парадокс Монти Холла

Примечания[править | править код]

↑ Kahneman, et al, 2005, pp. 153—160.
↑ Bayes, Thomas, and Price, Richard (1763). «An Essay towards solving a Problem in the Doctrine of Chance. By the late Rev. Mr. Bayes, communicated by Mr. Price, in a letter to John Canton, M. A. and F. R. S.». Philosophical Transactions of the Royal Society of London 53: 370—418. Дата обращения: 21 апреля 2010. Архивировано из оригинала 10 апреля 2011 года.
↑ Jeffreys, Harold (1973), Scientific Inference (3rd ed.), Cambridge University Press, p. 31, ISBN 978-0-521-18078-8

Литература[править | править код]

Гмурман В. Е. Теория вероятностей и математическая статистика, — М.: Высшее образование. 2005
Judgment under Uncertainty: Heuristics and Biases / Daniel Kahneman, et al. — 21st. — Cambridge University Press, 2005. — 555 p. — ISBN 978-0-521-28414-1.
Элиезер Юдковски. Наглядное объяснение теоремы Байеса

Для дальнейшего изучения[править | править код]

McGrayne, Sharon Bertsch. The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines & Emerged Triumphant from Two Centuries of Controversy (англ.). — Yale University Press, 2011. — ISBN 978-0-300-18822-6.
Andrew Gelman, John B. Carlin, Hal S. Stern, and Donald B. Rubin (2003), «Bayesian Data Analysis», Second Edition, CRC Press.
Charles M. Grinstead and J. Laurie Snell (1997), «Introduction to Probability (2nd edition)», American Mathematical Society (free pdf available [1].
Pierre-Simon Laplace. (1774/1986), «Memoir on the Probability of the Causes of Events», Statistical Science 1(3):364-378.
Peter M. Lee (2012), «Bayesian Statistics: An Introduction», Wiley.
Rosenthal, Jeffrey S. (2005): «Struck by Lightning: the Curious World of Probabilities». Harper Collings.
Stephen M. Stigler (1986), «Laplace’s 1774 Memoir on Inverse Probability», Statistical Science 1(3):359-363.
Stone, JV (2013). Chapter 1 of book «Bayes’ Rule: A Tutorial Introduction», University of Sheffield, England.

Ссылки[править | править код]

The Theory That Would Not Die by Sharon Bertsch McGrayne New York Times Book Review by John Allen Paulos on 5 August 2011
Weisstein, Eric W. Bayes’ Theorem (англ.) на сайте Wolfram MathWorld.
Bayes’ theorem (англ.) на сайте PlanetMath.
Bayes Theorem and the Folly of Prediction
A tutorial on probability and Bayes’ theorem devised for Oxford University psychology students
An Intuitive Explanation of Bayes’ Theorem by Eliezer S. Yudkowsky

Источник

Понятие теоремы Байеса и её применение

Содержание:

Теорема Байеса — что это простыми словами для чайников
Формула Байеса или формула гипотез
- Ловушки мотивированных рассуждений
- Как применять теорему Байеса для решения реальных задач

Теорема Байеса — что это простыми словами для чайников

Теоремой Байеса пользовались все, даже если никогда не слышали о ее существовании. Например, оценивали вероятность получить новую работу по тому, как прошло собеседование: опоздали вы или пришли вовремя, смогли ответить на все вопросы или нет. Вы добавляли новые данные – вероятность менялась. Так работает байесовский метод.

Теорема Байеса – одна из главных теорем элементарной теории вероятности. Она позволяет определить вероятность будущего события по прошлому событию, которое с ним взаимосвязано. Иными словами, выяснить причины и следствия какого-то действия.

Для получения результата необходимо произвести множество расчетов. Именно теорему Байеса стали активно использовать только после цифровой революции в двадцатом веке. С тех пор она имеет несколько вариантов интерпретаций и используется во многих сферах деятельности.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Формула Байеса или формула гипотез

Формулировка теоремы имеет математический вид:

( P (A|B) = P (B|A) * P (A) / P (B),)

где

(А )– гипотеза;

(B )– событие;

(P (A)) – априорная вероятность гипотезы (А);

(P (A|B)) – вероятность гипотезы (A) при наступлении события (B ) (апостериорная вероятность);

(P (B|A)) – вероятность наступления события (B ) при истинности гипотезы (A);

(P (B) )– полная вероятность наступления события (B).

В данном случае гипотеза – это предполагаемая причина события. Априорная вероятность – это вероятность правильности гипотезы до события B. Здесь отвечают на вопрос, возможна ли данная причина в принципе. Апостериорная вероятность – вероятность правильности гипотезы после наступления события B. То есть может ли данная гипотеза быть причиной данного события.

Ловушки мотивированных рассуждений

Исследования показывают, что люди склонны оценивать математически верную вероятность события, опираясь на свой опыт. Поэтому правильный результат может сильно отличаться от ожидаемого.

Простой пример – если вам очень нравится шоколад, вы будете игнорировать заявления стоматологов о том, что он вызывает кариес. Если вам доставили неприятность, вы будете подозревать в ее совершении человека, который вас раздражает.

Такие рассуждения называют мотивированными. Они возникают, потому что чаще всего наши эмоции воздействуют быстрее и сильнее, чем разумные доводы. Безусловная уверенность в собственной правоте и излишняя поспешность могут привести к катастрофическим последствиям.

Чтобы мыслить разумно, необходимо развивать критическое мышление. Следует всегда учитывать вероятность ошибки и воспринимать ее спокойно. Помните: если вы ошибаетесь – вы учитесь.

Как применять теорему Байеса для решения реальных задач

Теорема Байеса находит применение во многих областях жизни. К примеру, в финансах она используется для оценок риска кредитования, в медицине – для определения точности результатов медицинских анализов и тестов.

Рассмотрим решение задач с применением данной теоремы.

Задача 1

Проводится некий эксперимент. На основании условий можно сделать четыре гипотезы: (B1), (B2), (B3), (B4).

Их вероятность:

(P (B1) = 0,2);

(P (B2) = 0,1);

(P (B3) = 0,5);

(P (B4) = 0,2).

В результате эксперимента произошло событие (А). Оно невозможно при гипотезах (B1) и (B2). Оно достоверно при гипотезах (B3) и (B4). Найти апостериорные вероятности гипотез.

Решение:

Условные вероятности гипотез равны:

(P (A|B1) = 0);

(P (A|B2) = 0);

(P (A|B3) = 1);

(P (A|B4) = 1).

По формуле Байеса:

(P (B1|A) = 0);

(P (B2|A) = 0);

(P (B3|A) = 0,5 / (0,5 + 0,2) = 5/7);

(P (B4|A) = 2/7).

Ответ: с большей вероятностью причиной события ( А) стала гипотеза (В3).

Задача 2

Произошла авиакатастрофа. Исходя из условий, можно вывести четыре гипотезы: (B1), (B2), (B3), (B4).

Их вероятность:

(P (B1) = 0,2);

(P (B2) = 0,4);

(P (B3) = 0,3);

(P (B4) = 0,1).

После осмотра места крушения стало ясно, что произошло воспламенение горючего – событие (А).

По статистике, условные вероятности равны:

( P (A|B1) = 0,9);

( P (A|B2) = 0);

(P (A|B3) = 0,2);

(P (A|B4) = 0,3).

Найти апостериорные вероятности гипотез.

(P (B1|A) = 2/3);

(P (B2|A) = 0);

(P (B3|A) = 2/9);

(P (B4|A) = 1/9).

Ответ: с большей вероятностью причиной события (А ) стала гипотеза (В1).

Теорема подвергалась целому ряду различных интерпретаций. Если использовать байесовскую, то она показывает изменения личного уровня доверия вследствие произошедших событий. Эти выводы стали основополагающими для байесовского анализа и ряда других расчетов.

Источник

Понимаем теорему Байеса

Время на прочтение
8 мин

Количество просмотров 35K

Перевод статьи подготовлен специально для студентов базового и продвинутого курсов «Математика для Data Science».

Теорема Байеса – одна из самых известных теорем в статистике и теории вероятности. Даже если вы не работаете с расчетами количественных показателей, вероятно, вам в какой-то момент пришлось познакомиться с этой теоремой во время подготовки к экзамену.

P(A|B) = P(B|A) * P(A)/P(B)

Вот так она выглядит, но что это значит и как работает? Сегодня мы это узнаем и углубимся в теорему Байеса.

Основания для подтверждения наших суждений

В чем вообще заключается смысл теории вероятности и статистики? Одно из наиболее важных применений относится к принятию решений в условиях неопределенности. Когда вы принимаете решение совершить какое-либо действие (если, конечно, вы человек разумный), вы делаете ставку на то, что после завершения этого действия оно повлечет за собой результат лучший, чем если бы этого действия не произошло… Но ставки – это вещь ненадежная, как же вы в конечном итоге принимаете решение делать ли тот или иной шаг или нет?

Так или иначе вы оцениваете вероятность успешного исхода, и, если эта вероятность выше определенного порогового значения, вы предпринимаете шаг.

Таким образом, возможность точно оценить вероятность успеха имеет решающее значение для принятия правильных решений. Несмотря на то, что случайность всегда будет играть определенную роль в конечном исходе, вам следует учиться правильно использовать эти случайности и оборачивать их в свою пользу с течением времени.

Именно здесь вступает в силу теорема Байеса – она дает нам количественную основу для сохранения нашей веры в исход действия по мере изменений окружающих факторов, что, в свою очередь, позволяет нам со временем совершенствовать процесс принятия решений.

Разберем формулу

Давайте еще раз посмотрим на формулу:

P(A|B) = P(B|A) * P(A)/P(B)

Здесь:

P(A|B) – вероятность наступления события А, при условии, что событие В уже случилось;
P(B|A) – вероятность наступления события В, при условии, что событие А уже случилось. Сейчас это выглядит как какой-то замкнутый круг, но мы скоро поймем, почему формула работает;
P(A) – априорная (безусловная) вероятность наступления события А;
P(B) – априорная (безусловная) вероятность наступления события В.

P(A|B) – это пример апостериорной (условной) вероятности, то есть такой, которая измеряет вероятность какого-то определенного состояния окружающего мира (а именно состояния, при котором произошло событие В). Тогда как P(A) – это пример априорная вероятности, которая может быть измерена при любом состоянии окружающего мира.

Давайте посмотрим на теорему Байеса в действии на примере. Предположим, что недавно вы закончили курс по анализу данных от bootcamp. Вы еще не получили ответа от некоторых компаний, в которых вы проходили собеседование, и начинаете волноваться. Итак, вы хотите рассчитать вероятность того, что конкретная компания сделает вам предложение об устройстве на работу, при условии, что уже прошло три дня, а они вам так и не перезвонили.

Перепишем формулу в терминах нашего примера. В данном случае, исход А (Offer) – это получения предложения о работе, а исход В (NoCall) – «отсутствие телефонного звонка в течение трех дней». Исходя из этого, нашу формулу можно переписать так:

P(Offer|NoCall) = P(NoCall|Offer) * P(Offer) / P(NoCall)

Значение P(Offer|NoCall) — это вероятность получения предложения при условии, что звонка нет в течение трех дней. Эту вероятность оценить крайне сложно.

Однако обратной вероятности, P(NoCall|Offer), то есть отсутствию телефонного звонка в течение трех дней, при учете, что в итоге вы получили предложение о работе от компании, вполне можно привязать какое-то значение. Из разговоров с друзьями, рекрутерами и консультантами вы узнаете, что эта вероятность небольшая, но иногда компания все же может сохранять тишину в течение трех дней, если она все еще планирует пригласить вас на работу. Итак, вы оцениваете:

P(NoCall|Offer) = 40%

40% — это неплохо и кажется, еще есть надежда! Но мы еще не закончили. Теперь нам нужно оценить P(Offer), вероятность выхода на работу. Все знают, что поиск работы – это долгий и трудный процесс, и возможно вам придется проходить собеседование несколько раз, прежде чем вы получите это предложение, поэтому вы оцениваете:

P(Offer) = 20%

Теперь нам осталось оценить P(NoCall), вероятность, что вы не получите звонок от компании в течение трех дней. Существует множество причин, по которым вам могут не перезвонить в течение трех дней – они могут отклонить вашу кандидатуру или до сих пор проводить собеседования с другими кандидатами, или рекрутер просто заболел и поэтому не звонит. Что ж, есть множество причин, по которым вам могли не позвонить, так что эту вероятность вы оцениваете как:

P(NoCall) = 90%

А теперь собрав это все вместе, мы можем рассчитать P(Offer|NoCall):

P(Offer|NoCall) = 40% * 20%/90% = 8.9%

Это довольно мало, так что, к сожалению, рациональнее оставить надежду на эту компанию (и продолжать отправлять резюме в другие). Если это все еще кажется немного абстрактным, не переживайте. Я чувствовал то же самое, когда впервые узнал про теорему Байеса. Теперь давайте разберемся, как мы пришли к этим 8,9% (имейте в виду, что ваша изначальная оценка в 20% уже была низкой).

Интуиция, стоящая за формулой

Помните, мы говорили о том, что теорема Байеса дает основания для подтверждения наших суждений? Так откуда же они берутся? Они берутся из априорной вероятности P(A), которая в нашем примере зовется P(Offer), по сути, это и есть наше изначальное суждение том, насколько вероятно, что человек получит предложение о работе. В нашем примере вы можете считать, что априорная вероятность – это вероятность того, что вы получите предложение о работе в тот же момент, когда покинете собеседование.

Появляется новая информация – прошло 3 дня, а компания вам так и не перезвонила. Таким образом мы используем другие части уравнения, чтобы скорректировать нашу априорную вероятность нового события.

Давайте рассмотрим вероятность P(B|A), которая в нашем примере называется P(NoCall|Offer). Когда вы впервые видите теорему Байеса, вы задаетесь вопросом: Как понять откуда взять вероятность P(B|A)? Если я не знаю, чему равна вероятность P(A|B), то каким магическом образом я должен узнать, чему равна вероятность P(B|A)? Я вспоминаю фразу, которую однажды сказал Чарльз Мангер:

«Переворачивайте, всегда переворачивайте!»
— Чарльз Мангер

Он имел в виду, что, когда вы пытаетесь решить сложную задачу, ее нужно перевернуть с ног на голову и посмотреть на нее под других углом. Именно это и делает теорема Байеса. Давайте переформулируем теорему Байеса в терминах статистики, чтобы сделать ее более понятной (об это я узнал отсюда):

Для меня, например, такая запись выглядит понятнее. У нас есть априорная гипотеза (Hypothesis) — о том, что мы получили работу, и наблюдаемые факты — доказательства (Evidence) – телефонного звонка нет в течение трех дней. Теперь мы хотим узнать вероятность того, что наша гипотеза верна, с учетом предоставленных фактов. Как бы решили выше, у нас есть вероятность P(A) = 20%.

Время переворачивать все с ног на голову! Мы используем P(Evidence|Hypothesis), чтобы посмотреть на задачу с другой стороны и спрашиваем: «Какова вероятность наступления этих событий-доказательств в мире, где наша гипотеза верна?». Итак, если вернуться к нашему примеру, мы хотим знать, насколько вероятно, что, если нам не звонят в течение трех дней, нас все равно возьмут на работу. В изображении выше я пометил P(Evidence|Hypothesis), как “scaler” (скейлер), потому что это слово хорошо отражает суть значения. Когда мы умножаем его на априорное значение, он уменьшает или увеличивает вероятность события, в зависимости от того «вредит» ли какое-либо событие-доказательство нашей гипотезе. В нашем случае, чем больше дней проходит без звонка, тем меньше вероятность того, что нас позовут на работу. 3 дня тишины – это уже плохо (они сокращают нашу априорную вероятность на 60%), тогда как 20 дней без звонка полностью уничтожат надежду на получение работы. Таким образом, чем больше накапливается событий-доказательств (больше дней проходит без телефонного звонка), тем быстрее скейлер уменьшает вероятность. Скейлер – это механизм, который теорема Байеса использует для корректировки наших суждений.

Есть одна вещь, с которой я боролся в оригинальной версии этой статьи. Это была формулировка того, почему P(Evidence|Hypothesis) легче оценить, чем P(Hypothesis|Evidence). Причина этого заключается в том, что P(Evidence|Hypothesis) – это гораздо более ограниченная область суждений о мире. Сужая область, мы упрощаем задачу. Можно провести аналогию с огнем и дымом, где огонь – это наша гипотеза, а наблюдение дыма – событие, доказывающее наличие огня. P(огонь|дым) оценить сложнее, поскольку много чего может вызвать дым – выхлопные газы автомобилей, фабрики, человек, который жарит гамбургеры на углях. При этом P(дым|огонь) оценить проще, поскольку в мире, где есть огонь, почти наверняка будет и дым.

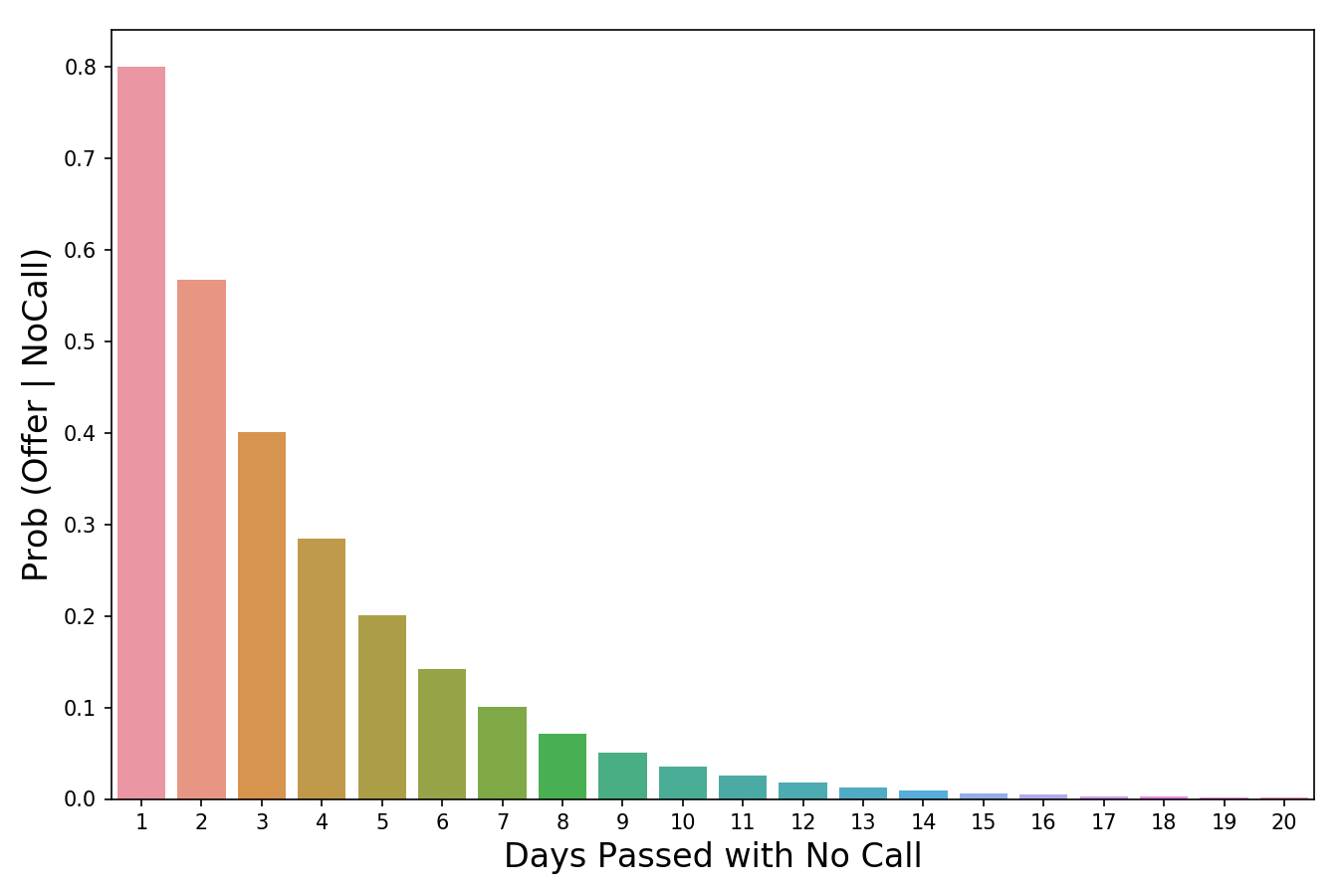
Значение вероятности уменьшается по мере того, сколько проходит дней без звонка.

Последняя часть формулы, P(B) или же P(Evidence) – это нормализатор. Как следует из названия, его цель – нормализовать произведение априорной вероятности и скейлера. Если бы у на не было нормализатора, мы бы имели следующее выражение:

Заметим, что произведение априорной вероятности и скейлера равно совместной вероятности. И поскольку одно из составляющих в нем P(Evidence), то на совместную вероятность повлияла бы маленькая частота событий.

Это проблема, поскольку совместная вероятность – это значение, включающее в себя все состояния мира. Но нам то не нужны все состояния, нам нужны только те состояния, которые были подтверждены событиями-доказательствами. Другими словами, мы живем в мире, где события – доказательства уже произошли, и их количество уже не имеет значения (поэтому мы не хотим, чтобы они влияли на наши расчеты в принципе). Деление произведения априорной вероятности и скейлера на P(Evidence) меняет его с совместной вероятности на условную(апостериорную). Условная вероятность учитывает только те состояния мира, в которых произошло событие-доказательство, именно этого мы и добиваемся.

Еще одна точка зрения, с которой можно взглянуть на то, почему мы делим скейлер на нормализатор, заключается в том, что они отвечают на два важных вопроса – и их отношение объединяет эту информацию. Давайте возьмем пример из моей недавней статьи про Байеса. Предположим, мы пытаемся выяснить, является ли наблюдаемое животное кошкой, основываясь на единственном признаке – ловкости. Все, что мы знаем, так это то, что животное, о котором мы говорим, проворное.

Скейлер говорит нам о том, у какого процента кошек хорошо с ловкостью. Это значение должно быть довольно высоким, допустим, 0.90.
Нормализатор говорит нам, какой процент животных ловок в принципе. Это значение должно быть средним, скажем, 0.50.
Отношение 0.90/0.50 = 1.8 говорит о том, что нужно изменить априорную вероятность, поскольку, если вы раньше считали иначе, настало время изменить свое мнение, поскольку вы скорее всего имеете дело с кошкой. Причина, по которой так можно считать заключается в том, что мы наблюдали некоторые доказательство того, что животное ловкое. Затем мы выяснили, что доля ловких кошек больше, чем доля ловких животных в целом. Учитывая, что на данный момент мы знаем только такую доказательную часть и ничего больше, разумно было бы пересмотреть наши убеждения в сторону мыслей о том, что мы все-таки наблюдаем кошку.

Подведем итог

Теперь, когда мы знаем, как трактовать каждую часть формулы, мы можем наконец собрать все воедино и посмотреть на то, что получилось:

Сразу после собеседования, мы устанавливаем априорную вероятность – шанс того, что нас возьмут на работу равен 20%.
Чем больше дней без звонка проходит, тем меньше становится вероятность того, что нас возьмут на работу. Например, после трех дней без звонка, мы считаем, что в мире, где мы эту работу можем получить, есть всего 40% вероятность того, что компания будет тянуть так долго, прежде чем вам позвонит. Умножаем скейлер на априорную вероятность и получаем 20% * 40% = 8%
Наконец, мы понимаем, что 8% было рассчитано для всех состояний, в которых может находиться мир. Но нас волнуют только те состояния, где нам не позвонили в течение трех дней. Для того, чтобы работать только с этими состояниями, мы принимаем за 90% априорную вероятность того, что в течение трех дней звонка не будет и получаем нормализатор. Мы делим ранее полученные 8% на нормализатор 8% / 90% = 8.9% и получаем окончательный ответ. Итого, при всех состояниях мира, если вы не получили звонка от компании в течение трех дней, вероятность получить работу составляет всего 8.9%.

Надеюсь, эта статья оказалась для вас полезной!

Источник

Начнем с примера. В урне, стоящей перед вами, с равной вероятностью могут быть (1) два белых шара, (2) один белый и один черный, (3) два черных. Вы тащите шар, и он оказывается белым. Как теперь вы оцените вероятность этих трех вариантов (гипотез)? Очевидно, что вероятность гипотезы (3) с двумя черными шарами = 0. А вот как подсчитать вероятности двух оставшихся гипотез!? Это позволяет сделать формула Байеса, которая в нашем случае имеет вид (номер формулы соответствует номеру проверяемой гипотезы):

Скачать заметку в формате Word или pdf

х – случайная величина (гипотеза), принимающая значения: х₁ – два белых, х₂ – один белый, один черный; х₃ – два черных; у – случайная величина (событие), принимающая значения: у₁ – вытащен белый шар и у₂ – вытащен чёрный шар; Р(х₁) – вероятность первой гипотезы до вытаскивания шара (априорная вероятность или вероятность до опыта) = 1/3; Р(х₂) – вероятность второй гипотезы до вытаскивания шара = 1/3; Р(х₃) – вероятность третьей гипотезы до вытаскивания шара = 1/3; Р(у₁|х₁) – условная вероятность вытащить белый шар, в случае, если верна первая гипотеза (шары белые) = 1; Р(у₁|х₂) – вероятность вытащить белый шар, в случае, если верна вторая гипотеза (один шар белый, второй – черный) = ½; Р(у₁|х₃) – вероятность вытащить белый шар, в случае, если верна третья гипотеза (оба черных) = 0; Р(у₁) – вероятность вытащить белый шар = ½; Р(у₂) – вероятность вытащить черный шар = ½; и, наконец, то, что мы ищем – Р(х₁|у₁) – вероятность того, что верна первая гипотеза (оба шара белых), при условии, что мы вытащили белый шар (апостериорная вероятность или вероятность после опыта); Р(х₂|у₁) – вероятность того, что верна вторая гипотеза (один шар белый, второй – черный), при условии, что мы вытащили белый шар.

Вероятность того, что верна первая гипотеза (два белых), при условии, что мы вытащили белый шар:

Вероятность того, что верна вторая гипотеза (один белый, второй – черный), при условии, что мы вытащили белый шар:

Вероятность того, что верна третья гипотеза (два черных), при условии, что мы вытащили белый шар:

Что делает формула Байеса? Она дает возможность на основании априорных вероятностей гипотез – Р(х₁), Р(х₂), Р(х₃) – и вероятностей наступления событий – Р(у₁), Р(у₂) – подсчитать апостериорные вероятности гипотез, например, вероятность первой гипотезы, при условии, что вытащили белый шар – Р(х₁|у₁).

Вернемся еще раз к формуле (1). Первоначальная вероятность первой гипотезы была Р(х₁) = 1/3. С вероятностью Р(у₁) = 1/2 мы могли вытащить белый шар, и с вероятностью Р(у₂) = 1/2 – черный. Мы вытащили белый. Вероятность вытащить белый при условии, что верна первая гипотеза Р(у₁|х₁) = 1. Формула Байеса говорит, что так как вытащили белый, то вероятность первой гипотезы возросла до 2/3, вероятность второй гипотезы по-прежнему равна 1/3, а вероятность третьей гипотезы обратилась в ноль.

Легко проверить, что вытащи мы черный шар, апостериорные вероятности изменились бы симметрично: Р(х₁|у₂) = 0, Р(х₂|у₂) = 1/3, Р(х₃|у₂) = 2/3.

Вот что писал Пьер Симон Лаплас о формуле Байеса в работе Опыт философии теории вероятностей, вышедшей в 1814 г.:

Это основной принцип той отрасли анализа случайностей, которая занимается переходами от событий к причинам.

Почему формула Байеса так сложна для понимания!? На мой взгляд, потому, что наш обычный подход – это рассуждения от причин к следствиям. Например, если в урне 36 шаров из которых 6 черных, а остальные белые. Какова вероятность вытащить белый шар? Формула Байеса позволяет идти от событий к причинам (гипотезам). Если у нас было три гипотезы, и произошло событие, то как именно это событие (а не альтернативное) повлияло на первоначальные вероятности гипотез? Как изменились эти вероятности?

Я считаю, что формула Байеса не просто о вероятностях. Она изменяет парадигму восприятия. Каков ход мыслей при использовании детерминистской парадигмы? Если произошло событие, какова его причина? Если произошло ДТП, чрезвычайное происшествие, военный конфликт. Кто или что явилось их виной? Как думает байесовский наблюдатель? Какова структура реальности, приведшая в данном случае к такому-то проявлению… Байесовец понимает, что в ином случае результат мог быть иным…

Немного иначе разместим символы в формулах (1) и (2):

Давайте еще раз проговорим, что же мы видим. С равной исходной (априорной) вероятностью могла быть истинной одна из трех гипотез. С равной вероятностью мы могли вытащить белый или черный шар. Мы вытащили белый. В свете этой новой дополнительной информации следует пересмотреть нашу оценку гипотез. Формула Байеса позволяет это сделать численно. Априорная вероятность первой гипотезы (формула 7) была Р(х₁), вытащили белый шар, апостериорная вероятность первой гипотезы стала Р(х₁|у₁). Эти вероятности отличаются на коэффициент .

Событие у₁ называется свидетельством, в большей или меньшей степени подтверждающим или опровергающим гипотезу х₁. Указанный коэффициент иногда называют мощностью свидетельства. Чем мощнее свидетельство (чем больше коэффициент отличается от единицы), тем больше факт наблюдения у₁ изменяет априорную вероятность, тем больше апостериорная вероятность отличается от априорной. Если свидетельство слабое (коэффициент ~ 1), апостериорная вероятность почти равна априорной.

Свидетельство у₁ в = 2 раза изменило априорную вероятность гипотезы х₁ (формула 4). В то же время свидетельство у₁ не изменило вероятность гипотезы х₂, так как его мощность = 1 (формула 5).

В общем случае формула Байеса имеет следующий вид:

х – случайная величина (набор взаимоисключающих гипотез), принимающая значения: х₁, х₂, … , х_n. у – случайная величина (набор взаимоисключающих событий), принимающая значения: у₁, у₂, … , у_n. Формула Байеса позволяет найти апостериорную вероятность гипотезы х_i при наступлении события y_j. В числителе – произведение априорной вероятности гипотезы х_i – Р(х_i) на вероятность наступления события y_j, если верна гипотеза х_i – Р(y_j|х_i). В знаменателе – сумма произведений того же, что и в числителе, но для всех гипотез. Если вычислить знаменатель, то получим суммарную вероятность наступления события у_j (если верна любая из гипотез) – Р(y_j) (как в формулах 1–3).

Еще раз о свидетельстве. Событие y_j дает дополнительную информацию, что позволяет пересмотреть априорную вероятность гипотезы х_i. Мощность свидетельства – – содержит в числителе вероятность наступления события y_j, если верна гипотеза х_i. В знаменателе – суммарная вероятность наступления события у_j (или вероятность наступления события у_j усредненная по всем гипотезам). Если вероятность наступления события у_j выше для гипотезы x_i, чем в среднем для всех гипотез, то свидетельство играет на руку гипотезе x_i, увеличивая ее апостериорную вероятность Р(y_j|х_i). Если вероятность наступления события у_j ниже для гипотезы x_i, чем в среднем для всех гипотез, то свидетельство понижает, апостериорную вероятность Р(y_j|х_i) для гипотезы x_i. Если вероятность наступления события у_j для гипотезы x_i такая же, как в среднем для всех гипотез, то свидетельство не изменяет апостериорную вероятность Р(y_j|х_i) для гипотезы x_i.

Предлагаю вашему вниманию несколько примеров, которые, надеюсь, закрепят ваше понимание формулы Байеса.

Задача 1.[1] Имеется 3 урны; в первой 3 белых шара и 1 черный; во второй — 2 белых шара и 3 черных; в третьей — 3 белых шара. Некто подходит наугад к одной из урн и вынимает из нее 1 шар. Этот шар оказался белым. Найдите апостериорные вероятности того, что шар вынут из 1-й, 2-й, 3-й урны. Ответ 1.

Задача 2. Два стрелка независимо друг от друга стреляют по одной и той же мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8, для второго — 0,4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что эта пробоина принадлежит первому стрелку. Ответ 2.

Задача 3. Объект, за которым ведется наблюдение, может быть в одном из двух состояний: Н₁ = {функционирует} и Н₂ = {не функционирует}. Априорные вероятности этих состояний Р(Н₁) = 0,7, Р(Н₂) = 0,3. Имеется два источника информации, которые приносят разноречивые сведения о состоянии объекта; первый источник сообщает, что объект не функционирует, второй — что функционирует. Известно, что первый источник дает правильные сведения с вероятностью 0,9, а с вероятностью 0,1 — ошибочные. Второй источник менее надежен: он дает правильные сведения с вероятностью 0,7, а с вероятностью 0,3 — ошибочные. Найдите апостериорные вероятности гипотез. Ответ 3.

Задача 4.[2] Вероятность того, что человек страдает от определенного заболевания, равна 0,03. Медицинский тест позволяет проверить, так ли это. Если человек действительно болен, вероятность точного диагноза (утверждающего, что человек болен, когда он действительно болен) равна 0,9. Если человек здоров, вероятность ложноположительного диагноза (утверждающего, что человек болен, когда он здоров) равна 0,02. Допустим, что медицинский тест дал положительный результат. Какова вероятность того, что человек действительно болен? Ответ 4.

[1] Задачи 1–3 взяты из учебника Е.С.Вентцель, Л.А.Овчаров. Теория вероятностей и ее инженерные приложения, раздел 2.6 Теорема гипотез (формула Байеса).

[2] Задача 4 взята из книги Левин. Статистика для менеджеров с использованием Microsoft Excel, раздел 4.3 Теорема Байеса.

Источник

Понравилось? Добавьте в закладки

Если событие А может произойти только при выполнении одного из событий , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле

Эта формула называется формулой полной вероятности.

Вновь рассмотрим полную группу несовместных событий , вероятности появления которых . Событие А может произойти только вместе с каким-либо из событий , которые будем называть гипотезами. Тогда по формуле полной вероятности

Если событие А произошло, то это может изменить вероятности гипотез .

По теореме умножения вероятностей

откуда

Аналогично, для остальных гипотез

Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез называются апостериорными вероятностями, тогда как – априорными вероятностями.

Пример. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% – продукция первого предприятия, 30% – продукция второго предприятия, 50% – продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии – 5% и на третьем – 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.

Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.

Можно применить формулу полной вероятности, причем в наших обозначениях:

Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:

Пример. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго – 0,5; для третьего – 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Решение. Возможны три гипотезы:

– на линию огня вызван первый стрелок,

– на линию огня вызван второй стрелок,

– на линию огня вызван третий стрелок.

Так как вызов на линию огня любого стрелка равновозможен, то

В результате опыта наблюдалось событие В – после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:

по формуле Байеса находим вероятность гипотезы после опыта:

Пример. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго.

а) Каков процент брака на конвейере?

б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере?

Решение. Возьмем с конвейера наудачу одну деталь и рассмотрим событие А – деталь бракованная. Оно связано с гипотезами относительно того, где была обработана эта деталь: – взятая наудачу деталь обработана на -ом станке, .