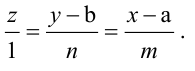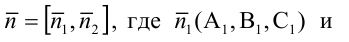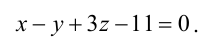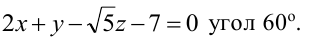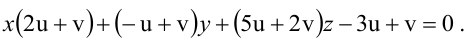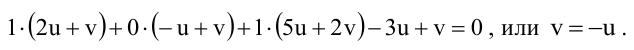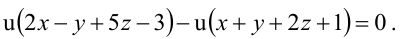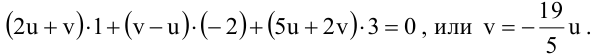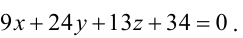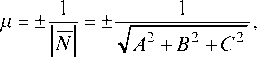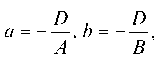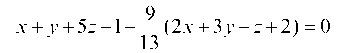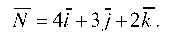Содержание:
Плоскость в пространстве
Общее уравнение плоскости
Определение: Уравнение вида
Определение: Порядок поверхности определяется по высшему показателю степени переменных х, у и z или по сумме показателей степени в произведении этих величин.
Определение: Уравнение вида Ax+By+Cz+D=O называется общим уравнением плоскости.
Рассмотрим частные случаи приведенного уравнения:
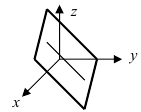
1. D = 0; Ах + By + Сz = 0. Из этого уравнения видно, что точка О(0; 0; 0) удов- летворяет этому уравнению, следовательно, это уравнение описывает плоскость, проходящую через начало координат (Рис. 36).
Рис. 36. Плоскость, проходящая через начало координат.
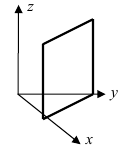
2. С = 0; Ах + Ву + D = 0. Этому уравнению удовлетворяет любое значение переменной z, поэтому данное уравнение описывает плоскость, которая параллельна оси аппликат (Oz) (Рис. 37).
Рис. 37. Плоскость, проходящая параллельно оси аппликат.
– плоскость параллельна оси ординат (Оу);
– плоскость параллельна оси абсцисс (Ох).
Замечание: При отсутствии в уравнении плоскости одной из переменных величин говорит о том, что плоскость параллельна соответствующей координатной оси.
3. С=0; D=0; Ах+ By=0 – плоскость проходит через начало отсчета параллельно оси аппликат (Рис. 38).
Рис. 38. Плоскость, проходящая через начало координат параллельно оси аппликат.
– плоскость проходит через начало координат параллельно оси ординат;
– плоскость проходит через начало координат параллельно оси абсцисс.
4. 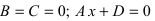
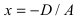
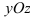
Рис. 39. Плоскость, проходящая параллельно координатной плоскости
5. В = С = D = 0; Ах = 0=>х = 0 – уравнение описывает плоскость 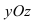
Рис. 40. Координатная плоскость 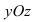
Другие уравнения плоскости
1. Уравнение плоскости в отрезках. Пусть в уравнении 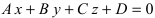
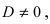
Введем следующие обозначения 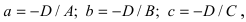
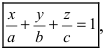
Откладывая на координатных осях точки М, N и Р, соединяя их прямыми лучим изображение данной плоскости (для определенности принято, что параметры а, b, с положительные) (Рис. 41):
Рис. 41. Отрезки, отсекаемые плоскостью на координатных осях.
Из рисунка видно, что числа а, b, с показывают отрезки, отсекаемые плоскостью на координатных осях, считая от начала координат.
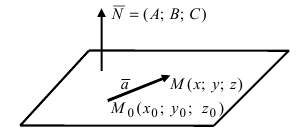
2. Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданному вектору. Пусть задана точка 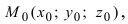
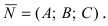
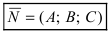
Возьмем на плоскости произвольную точку 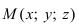
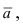
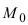
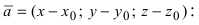
Рис. 42. Плоскость, проходящая через заданную точку перпендикулярно к нормальному вектору.
В силу того, вектор 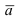
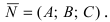
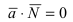
Пример:
Составить уравнение плоскости, проходящей через т. 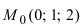
Решение:
Так как искомая плоскость параллельна плоскости (Q), то нормальный вектор этой плоскости 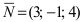
Пример:
Составить уравнение плоскости, проходящей через точки А(—1; 1 ;2) и В(0; —1; —1) параллельно вектору 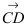
Решение:
Построим на искомой плоскости вектор 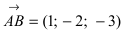
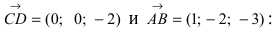
Уравнение плоскости, проходящей через заданную точку 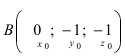
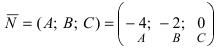
Отметим, что при выборе точки, через которую проходит искомая плоскость из точек 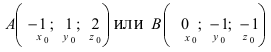
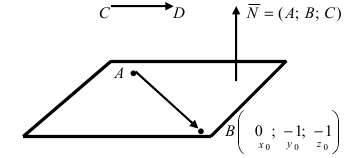
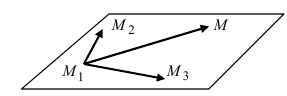
3. Уравнение плоскости, проходящей через три заданные точки. Пусть плоскость проходит через 3 известные точки 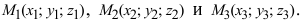
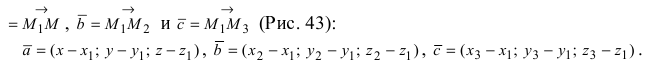
Рис. 43. Плоскость, проходящая через три заданные точки.
Вектора 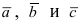
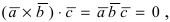
Замечание: Полученный определитель третьего порядка раскрывается по элементам первой строки.
Пример:
Составить уравнение плоскости, проходящей через три заданные точки
Решение:
Составим определитель третьего порядка 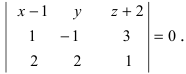
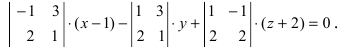
Основные задачи о плоскости в пространстве
1. Угол между пересекающимися плоскостями. Пусть даны две пересекающиеся плоскости 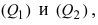
Пусть линия пересечения плоскостей определяется прямой (l). Из одной точки этой прямой проведем два перпендикулярных к прямой вектора 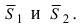
Рис.44. Угол между плоскостями.
В силу того, что 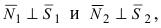
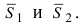
Следствие: Если плоскости перпендикулярны (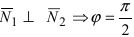
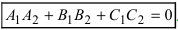
Следствие: Если плоскости параллельны, то нормальные вектора коллинеарны, следовательно, условие параллельности плоскостей:
2. Расстояние от данной точки до заданной плоскости. Расстояние от данной точки 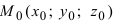
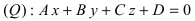
Пример:
На каком расстоянии от плоскости 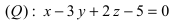
Решение:
Воспользуемся приведенной формулой:
Прямая в пространстве
Общее уравнение прямой
Прямая в пространстве может быть задана как пересечение двух плоскостей:
Определение: Геометрическое место точек пространства, удовлетворяющих системе уравнений (1), называется прямой в пространстве, а система уравнений (1) называется общим уравнением прямой.
Замечание: Для того чтобы система уравнений (1) определяла прямую в пространстве необходимо и достаточно, чтобы нормальные вектора плоскостей, определяющих прямую, 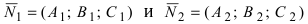
Пусть прямая проходит через точку 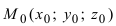
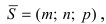
Замечание: Если в уравнении (2) одна из проекций направляющего вектора равна 0, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Пример:
Как расположена прямая 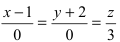
Решение:
Согласно замечанию эта прямая будет перпендикулярна осям абсцисс и ординат (параллельна оси аппликат) и будет проходить через точку 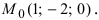
Пример:
Записать уравнение прямой 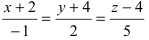
Решение:
Приравняем каждую дробь к параметру t: 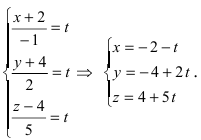
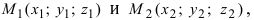
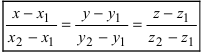
Пример:
Составить канонические и параметрические уравнения прямых, проходящих через точки А (— 1; 1; 2 ), В (0; -1; -1) И С (1; 0; -1), D (l; 0; 1 ).
Решение:
Составим каноническое уравнение прямой линии, проходящей через точки
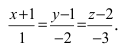
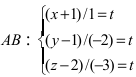
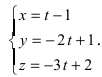
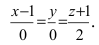
Основные задачи о прямой в пространстве
1. Переход от общего уравнения прямой к каноническому. Пусть прямая задана общим уравнением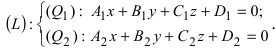
Пример:
Записать уравнение прямой 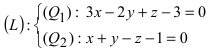
Решение:
Положив х = 0, получим СЛАУ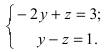
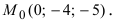
Запишем каноническое 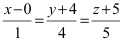
Угол между пересекающимися прямыми
Угол между двумя пересекающимися прямыми определяется как угол между их направляющими векторами. Если прямые 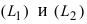
соответственно, то угол между прямыми определяется по формуле:
Следствие: Если прямые перпендикулярны (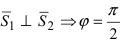
Следствие: Если прямые параллельны, то направляющие вектора коллинеарны, следовательно, условие параллельности прямых:
Координаты точки пересечения прямой и плоскости
Пусть прямая (L) задана общим уравнением 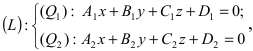
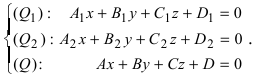
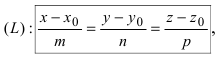
Рассмотрим возможные случаи:
- если выполняются условия
, то прямая не пересекает плоскость (прямая параллельна плоскости);
- при условиях
прямая лежит на плоскости;
- если
, прямая пересекает плоскость в одной точке.
Пример:
Найти координаты точки пересечения прямой (L), заданной уравнением 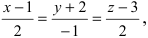
Решение:
Перепишем уравнение прямой (L) в параметрическом виде 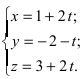
Найденное значение параметра 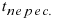
- Заказать решение задач по высшей математике
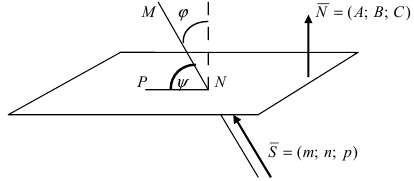
Угол между прямой и плоскостью
Пусть дана плоскость (Q) с нормальным вектором 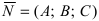
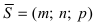
Рис. 45. Угол между прямой и плоскостью.
Угол 
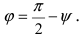
Следствие: Если прямая перпендикулярна плоскости (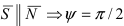
Следствие: Если прямая параллельна плоскости (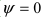
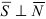
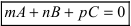
Плоскость и прямая в пространстве
Всякое уравнение первой степени относительно координат 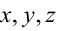

Вектор 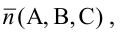
Особые случаи уравнения (3.1):
- D = 0, Ах + By + Cz = 0 – плоскость проходит через начало координат.
- С = 0, Ах + By + D = 0 – плоскость параллельна оси Oz.
- С = D = 0, Ах + By = 0 – плоскость проходит через ось Oz.
- С = В = 0, Ах + D = 0 – плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей:
Прямая в пространстве может быть задана:
- как линия пересечения двух плоскостей, т.е. системой уравнений:
- двумя своими точками
тогда прямая, через них проходящая, задается уравнениями:
- точкой
ей принадлежащей, и вектором
ей коллинеарным.
Тогда прямая определяется уравнениями:
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор 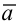
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t: 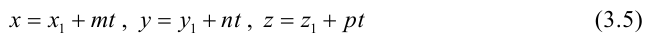
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор 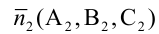
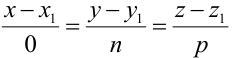
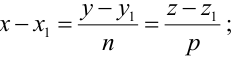
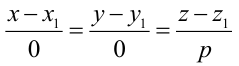
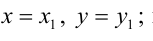
Пример:
Составьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение:
По условию задачи вектор 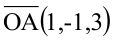
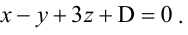
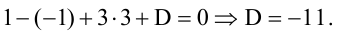
Пример:
Составьте уравнение плоскости, проходящей через ось Oz и образующей с плоскостью
Решение:
Плоскость, проходящая через ось Oz, задается уравнением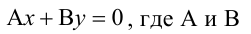
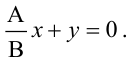
Решая квадратное уравнение 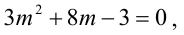
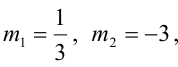
Пример:
Составьте канонические уравнения прямой: 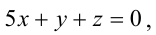
Решение:
Канонические уравнения прямой имеют вид:
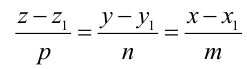
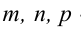
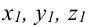
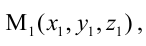
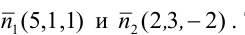
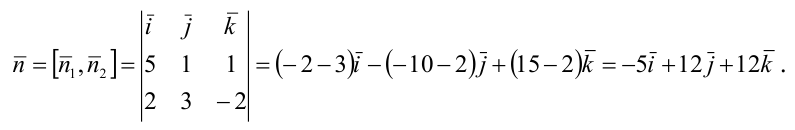
Пример:
В пучке, определяемом плоскостями 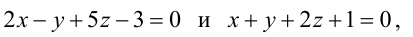
Решение:
Уравнение пучка, определяемого данными плоскостями, имеет вид 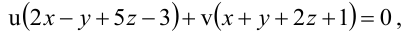
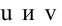
Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим:
Тогда уравнение плоскости, содержащей М, найдем, подставив 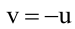
Т.к. и 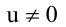
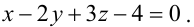
Значит, уравнение второй плоскости имеет вид: 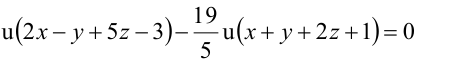
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
- Уравнения прямых и кривых на плоскости
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
72
Добавлен:
10.06.2015
Размер:
3.02 Mб
Скачать
A(x x0 ) B( y y0 ) C(z z0 ) 0
– уравнение называют – уравнением плоскости, проходящей
через заданную точку M0 (x0 , y0 , z0 ) .
Отметим, что вектор n A, B,C называют нормальным
|
вектором |
плоскости и в качестве нормального |
вектора |
|
плоскости |
может быть взят любой ненулевой |
вектор, |
|
перпендикулярный плоскости. |
||
|
Легко доказывается и обратное: |
||
|
Дано |
уравнение Ax By Cz D 0 |
и нужно |
|
убедиться, |
что оно описывает плоскость в пространстве R3 . |
|
|
Пусть (x0 , y0 , z0 ) – какое-либо решение данного уравнения. |
||
|
Тогда |
Ax0 By0 Cz0 D 0 . Отсюда |
получаем |
|
D Ax0 |
By0 Cz0 и, подставляя в исходное уравнение, |
получаем: Ax By Cz Ax0 By0 Cz0 0 ,
Или A(x x0 ) B( y y0 ) C(z z0 ) 0 .
а это есть уравнение плоскости, проходящей через точку
(x0 , y0 , z0 ) и имеющую нормальный вектор n A, B,C . Следовательно, и равносильное ему уравнение
Ax By Cz D 0 определяет плоскость.
Теорема доказана.
Рассмотрим важный частный случай построения уравнения плоскости, когда известны три точки M1(x1 , y1, z1) ,
M2 (x2 , y2 , z2 ) , M3 (x3 , y3, z3 ) принадлежащие плоскости и не лежащие на одной прямой.
Возьмем текущую точку M (x, y, z) плоскости и организуем три вектора
M1M2 x2 x1, y2 y1, z2 z1
M1M3 x3 x1, y3 y1, z3 z1
91

M1M x1 x, y1 y, z1 z
Эти векторы лежат в одной плоскости, уравнение которой и определяется. Следовательно, их смешанное произведение равно нулю, то есть
x x1
M1M M1M2 M1M3 x2 x1 x3 x1
|
y y1 |
z z1 |
|
|
y2 y1 |
z2 z1 |
0 |
|
y3 y1 |
z3 z1 |
есть уравнение плоскости, проходящей через три заданные точки M1 , M 2 , M3 .
При решении задач часто используется так называемое
|
уравнение плоскости в отрезках на осях. |
|||||||||
|
Пусть |
в |
общем |
уравнении |
плоскости |
|||||
|
Ax By Cz D 0, A B C D 0. |
|||||||||
|
Перенесем свободный член |
D в правую часть и разделим |
||||||||
|
обе части уравнения на –, D тогда получим: |
|||||||||
|
x |
y |
z |
1 |
||||||
|
a |
b |
c |
|||||||
|
где a D |
, b |
D , с |
D . |
||||||
|
A |
B |
С |
Уравнение называют уравнением плоскости в отрезках на осях, т.к. числа a,b,c имеют простой геометрический смысл:
a – абсцисса точки пересечения плоскости с осью Ox , b – ордината точки пересечения плоскости с осью Oy , с –
аппликата точки пересечения плоскости с осью Oz . Действительно, точка пересечения плоскости с осью,
|
скажем, Ox |
имеет ординату y 0 |
и аппликату z 0 . Но |
|
|
координаты |
этой точки |
x,0,0 |
должны удовлетворять |
|
уравнению плоскости, т.е. |
Ax B 0 C 0 D 0 |
92
Отсюда получаем x D .
A
Рассмотрим особенность расположения плоскости, заданной общим уравнением, если некоторые коэффициенты этого уравнения обращаются в нуль.
A 0 , By Cz D 0 – плоскость параллельна оси Ox
|
B 0 , |
Ax Cz D 0 – плоскость параллельна оси Oy |
||||||
|
C 0 , |
Ax By D 0 – плоскость параллельна оси Oz |
||||||
|
D 0 , |
Ax By Cz 0 |
– |
плоскость |
проходит |
через |
||
|
начало координат. |
|||||||
|
A 0 , B 0 , |
Cz D 0 плоскость параллельна плоскости |
||||||
|
OXY |
|||||||
|
B 0 , C 0 , |
Ax D 0 |
– |
плоскость параллельна |
||||
|
плоскости OYZ |
|||||||
|
A 0 , C 0 , |
By D 0 плоскость параллельна плоскости |
||||||
|
XOZ |
|||||||
|
D 0 , C 0 , |
Ax By 0 |
плоскость |
проходит |
через |
|||
|
координатную ось Oz |
|||||||
|
D 0 , B 0 , |
Ax Cz 0 |
– |
плоскость |
проходит |
через |
||
|
координатную ось Oy |
|||||||
|
D 0 , A 0 |
, By Cz 0 – |
плоскость |
проходит |
через |
|||
|
координатную ось Ox |
|||||||
|
D 0 , A 0 , |
B 0 |
– z 0 плоскость XOY |
|||||
|
D 0 , C 0 , |
B 0 |
– x 0 плоскость YOZ |
|||||
|
D 0 , A 0 , |
C 0 |
y 0 плоскость XOZ |
Замечание Если плоскость параллельна какой-нибудь координатной оси, то в ее уравнении отсутствует член, содержащий координату, одноименную с этой осью.

93
|
Решение |
||||
|
По условию уравнение плоскости имеет вид |
||||
|
Ax By D 0 |
(*) |
|||
|
– плоскость параллельна оси Oz . |
||||
|
Подставим |
координаты |
заданных точек в |
(*), |
получим |
|
2A 3B D 0 |
A t,B 3t,D 7t |
как |
решение |
|
|
, или |
||||
|
A 2B D 0 |
системы двух уравнений с тремя неизвестными, подставляя в (*), получаем x 3y 7 0
Нормальное уравнение плоскости
Пусть дана плоскость, проведем через начало координат прямую, перпендикулярно к плоскости – эта прямая нормаль, точка P – точка в которой прямая пересекает плоскость.
На нормали введем положительное направление от точки О к
|
точке P , , , – |
углы, |
которые |
составляют |
направленная |
|||||||||||||
|
нормаль с осями координат, |
p – длина отрезка OP . |
||||||||||||||||
|
cos x cos y cos z p 0 |
|||||||||||||||||
|
нормальное уравнение плоскости |
|||||||||||||||||
|
где |
|||||||||||||||||
|
cos |
A |
cos |
B |
||||||||||||||
|
A2 B2 C2 |
A2 B2 C2 |
||||||||||||||||
|
cos |
С |
p |
D |
||||||||||||||
|
A2 B2 C2 |
A2 B2 C2 |
||||||||||||||||
|
Знак “плюс” или знак “минус” выбирается так, чтобы |
p 0 . |
||||||||||||||||
|
Углы , , |
– это углы между вектором нормали n и |
||||||||||||||||
|
осями координат соответственно. |
|||||||||||||||||
|
Замечание |
В нормальном |
уравнении |
прямой |
сумма |
квадратов коэффициентов при текущих координатах должна быть равна 1, а свободный член должен быть отрицателен.
Умножим общее уравнение на множитель
Ax By Cz D 0
94

A cos , B cos , C cos D p ,
|
Возведем первые три уравнения в квадрат и сложим |
||||||
|
2 A2 B2 |
C2 |
1,отсюда, |
||||
|
1 |
– нормирующий множитель. |
|||||

Из уравнения D p , следует, что знак нормирующего
множителя противоположен знаку свободного члена нормируемого уравнения.
Для приведения общего уравнения плоскости к нормальному виду обе части его умножают на нормирующий множитель, знак выбирают противоположный знаку свободного члена в общем уравнении плоскости.
Если D 0 знак выбирается произвольно.
Расстояние от точки до плоскости
Определение Отклонением точки M * от данной
плоскости называется число d , если M * лежит по ту сторону от плоскости, куда идет положительное направление нормали, и
|
d , |
если |
M * |
лежит |
с |
другой |
стороны |
от |
данной |
|
плоскости. d . |
||||||||
|
d , |
когда |
точка M * |
и |
начало |
координат |
лежат |
по |
|
|
разные |
стороны от плоскости, |
и |
d , когда точка |
M * |
и |
|||
|
начало координат лежат по одну |
сторону от плоскости, 0 |
|||||||
|
для точек лежащих на плоскости. |
Чтобы найти отклонение какой-либо точки M * от некоторой прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки M* .
x* cos x* cos x* cos
x* cos y* cos z* cos p
95

|
Расстояние d от |
точки |
x0 ,y0 ,z0 до плоскости |
|||||||
|
Ax By Cz D 0 определяется по формуле |
|||||||||
|
d |
Ax0 By0 Cz0 D |
||||||||
|
A2 |
B2 C |
2 |
|||||||
|
Пример Дана |
плоскость |
3x 4y 1z 14 0 и точка |
M 4,3,1 . Найти отклонение точки от плоскости.
|
Решение |
||||||||
|
1 |
, |
1 |
3 4 4 3 12 114 2 точка |
|||||
|
13 |
13 |
|||||||
удалена от плоскости на расстояние 2.
Взаимное расположение двух плоскостей Угол между двумя плоскостями
Линейный угол, являющейся мерой двугранного угла между плоскостями, равен углу между перпендикулярами к этим плоскостям.
Для двух плоскостей, заданных уравнениями
A1x B1 y C1z D1 0, A2 x B2 y C2 z D2 0
|
направления перпендикуляров к ним совпадают с |
|||||||||||||||||||||||||||||
|
направлениями векторов N1 |
A1 , B1 ,C1 , N2 |
A2 , B2 ,C2 . |
|||||||||||||||||||||||||||
|
Определение Углом между плоскостями называется |
|||||||||||||||||||||||||||||
|
угол между их нормальными векторами |
|||||||||||||||||||||||||||||
|
N |
и |
N |
2 |
, то есть |
|||||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||||||||
|
2 |
N |
N |
2 |
||||||||||||||||||||||||||
|
1 |
1 |
||||||||||||||||||||||||||||
|
Поэтому угол между векторами равен углу между их |
|||||||||||||||||||||||||||||
|
нормальными векторами |
|||||||||||||||||||||||||||||
|
cos |
N1 N2 |
||||||||||||||||||||||||||||
|
или |
N1 |
N2 |
|||||||||||||||||||||||||||
|
cos |
A1 A2 B1 B2 C1 C2 |
||||||||||||||||||||||||||||
|
A2 B |
2 |
C 2 |
A2 |
B2 |
C 2 |
||||||||||||||||||||||||
|
1 |
1 |
1 |
2 |
2 |
2 |
96
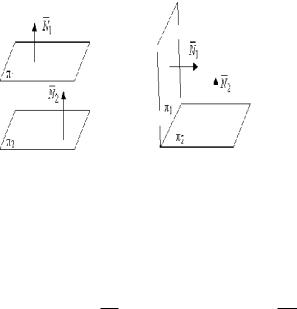
Угол между двумя плоскостями, точнее, один из двух смежных углов между двумя плоскостями, может быть вычислен как угол между нормальными векторами этих плоскостей.
Условие параллельности двух плоскостей
Пусть даны две плоскости
A1 x B1 y C1 z D1 0A1 x B1 y C1 z D2 0
Данные плоскости параллельны, когда их нормальные векторы
N1 A1 , B1 , C1 , N2 A2, B2,C2 коллинеарны.
|
A2 |
B2 |
C2 |
|||
|
A |
B |
C |
|||
|
1 |
1 |
1 |
Условие перпендикулярности двух плоскостей
Данные плоскости перпендикулярны, когда их нормальные
векторы N1 A1 , B1 , C1 , N2 A2 , B2 , C2 ,
перпендикулярны.
Условие перпендикулярности двух плоскостей
|
A A B B C C 0 . |
|||||
|
1 |
2 |
1 |
2 |
1 |
2 |
97
Контрольные вопросы по теме «Плоскость»
1.Написать векторное уравнение плоскости и объяснить смысл величин, входящих в это уравнение.
2.Написать общее уравнение плоскости
3.Написать уравнение плоскости, проходящей через заданную точку. Объяснить смысл величин, входящих в это уравнение.
4.Как вычислить угол между плоскостями?
5.Условия параллельности и перпендикулярности двух плоскостей.
|
Задачи для самостоятельного изучения |
||||||||||||
|
1. |
Построить плоскости: |
|||||||||||
|
а) 5x 2y 3z 10 0 , |
||||||||||||
|
б) 2z 7 0 , |
||||||||||||
|
в) 3x 2y z 0 , |
||||||||||||
|
г) 3x 2y 6 0 . |
||||||||||||
|
2. |
Построить плоскость |
2x 3y 6z 12 0 и найти углы |
||||||||||
|
нормали к плоскости с осями координат. |
||||||||||||
|
3. |
Даны точки M1 0, 1,3 |
и |
M 2 1,3,5 . |
Написать |
||||||||
|
уравнение |
плоскости, |
проходящей |
через |
точку |
M1 и |
|||||||
|
перпендикулярной к вектору M1M 2 . |
||||||||||||
|
4. |
Написать |
уравнение |
геометрического |
места |
точек, |
|||||||
|
3 |
||||||||||||
|
равноудаленных от точек A |
3; |
,3 |
и В ( 0; |
3 |
0 ). |
|||||||
|
2 |
2 |
5.Написать уравнение плоскости, проходящей через ось Ох и точку М1 (0;- 2;3).
6.Найти угол между плоскостями:
а) x 2y 2z 8 0 и x z 6 0 , б) x 2z 6 0 и x 2y 4 0 ,
в) x 3z 8 0 и 2x 6z 7 0,
г) 2x 3y z 3 0 и x y z 5 0 .
7. Написать уравнение плоскости, проходящей через точку M1 1, 1,2 и перпендикулярной к плоскостям x 2y x 4 0 и x 2y 2z 4 0 .
98

8.Написать уравнение плоскости, проходящей через точки M1 1, 2,0 и M 2 1,1,2 и перпендикулярной к
|
плоскости x 2y 2z 4 0 . |
||||||
|
9. |
Найти |
расстояние |
от точки |
M 5,1, 1 |
до |
плоскости |
|
x 2y 2z 4 0 . |
||||||
|
10. |
Найти |
расстояние |
точки |
M 4,3,0 |
от |
плоскости, |
|
проходящей |
через |
точки |
||||
|
M1 1,3,0 , M 2 4, 1,2 и M 3 3,0,1 . |
11.Найти расстояние между параллельными плоскостями
4x 3y 5z 12 0 и 4x 3y 5z 8 0 .
12.Написать уравнение плоскости, проходящей через
|
линию |
пересечения |
|
плоскостей 2x y 3z 6 0 и |
x 2y z 3 0 и |
|
через точку M 1,2,4 . |
13.Найти точку пересечения плоскостей 2x y 3z 9 0 ,
x2y 2z 3 0 , 3x y 4z 6 0 .
14.Написать уравнение плоскости, проходящей через точки0, 5,0 , M 2 0,0,2 и перпендикулярной к
плоскости x 5y 2z 10 0 . Построить ее.
Ответы к задачам для самостоятельного изучения
1.cos 72 , cos 34 , cos 76 ;
2.x 4y 2z 2 0 ;
3.x y z 3 0 ;
4.3y 2z 0 ;
5.а) 450 , б) 78030 , в) 00 , г) 900 ;
6.2x 3y 4z 3 0 ;
7.2x 2y z 2 0 ;
8.3;
9.
10.2
99
11.x 8y 9z 21 0 ;
12.1, 1,2 ;
13.2y 5z 10 0 .
100
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Плоскость.
1. Всякая плоскость в координатном пространстве OXYZ имеет векторное уравнение следующего вида: r ¦ п = p. Здесь
r = xi + yj + zk — радиус-вектор текущей точки плоскости
M(x, у, z); п = i cosa + j cos b + k cosg — единичный вектор, имеющий направление перпендикуляра, опущенного на плоскость из начала координат, a, b, g — углы, образованные этим перпендикуляром с осями координат OX, OY, OZ, и р — длина этого перпендикуляра.
При переходе к координатам это уравнение принимает вид xcos a + ycos b + zcos g – p = 0 (нормальное уравнение плоскости).
2. Уравнение всякой плоскости может быть записано также в виде Ах + Ву +Cz + D = 0 (общее уравнение). Здесь А, B, C можно рассматривать как координаты некоторого вектора
N = Ai + Bj + Ck, перпендикулярного к плоскости. Для приведения общего уравнения плоскости к нормальному виду все члены уравнения надо умножить на нормирующий множитель
где знак перед радикалом противоположен знаку свободного члена D в общем уравнении плоскости.
3. Частные случаи расположения плоскости, определяемой уравнением Ах + Ву +Cz + D = 0:
А = 0; плоскость параллельна оси ОХ;
В = 0; плоскость параллельна оси О^
C = 0; плоскость параллельна оси ОZ;
D = 0; плоскость проходит через начало координат;
А = В = 0; плоскость перпендикулярна оси ОZ (параллельна плоскости ХОY);
А = C = 0; плоскость перпендикулярна оси ОY (параллельна плоскости ХОZ);
В = C = 0; плоскость перпендикулярна оси ОХ (параллельна плоскости YОZ);
А = D = 0; плоскость проходит через ось ОХ;
В = D = 0; плоскость проходит через ось OY;
C = D = 0; плоскость проходит через ось OZ;
А = В = D = 0; плоскость совпадает с плоскостью XOY (z = 0);
А = C = D = 0; плоскость совпадает с плоскостью XOZ (у = 0);
B = C = D = 0; плоскость совпадает с плоскостью YOZ (х = 0).
Если в общем уравнении Ах + By +Cz + D = 0 коэффициент D ф 0, то, разделив все члены уравнения на – D, можно уравнение
плоскости привести к виду
. Это уравнение плоскости называется уравнением в отрезках: в нем а — абсцисса точки пересечения плоскости с осью OX, b и с — соответственно ордината и аппликата точек пересечения плоскости с осями OY и OZ.
4. Угол j между плоскостями А1х + В1У + Qz + D1 = 0 и А2х + В2У +C2z + D2 = 0 определяется по формуле
Условие параллельности плоскостей:
Условие перпендикулярности плоскостей:
5. Расстояние от точки М0(х0; у0; z0) до плоскости, определяемой уравнением
Оно равно взятому по абсолютной величине результату подстановки координат точки в нормальное уравнение плоскости; знак результата этой подстановки характеризует взаимное расположение точки M0 и начала координат относительно данной плоскости: этот знак положителен, если точка M0 и начало координат расположены по разные стороны от плоскости, и отрицателен, если они расположены по одну сторону от плоскости.
6. Уравнение плоскости, проходящей через точку М0(х0; у0; z0)
и перпендикулярной к вектору N = Ai + Bj + Ck, имеет вид А(х – х0) + B(y – у0) + C(z – z0) = 0. При произвольных А, В и C последнее уравнение определяет некоторую плоскость, принадлежащую к связке плоскостей, проходящих через точку М0. Его часто поэтому называют уравнением связки плоскостей.
7. Уравнение А1х + B1y +C1z + D1 + А(А2х + B^y +C2z + D2) = 0 при произвольном I определяет некоторую плоскость, проходящую через прямую, по которой пересекаются плоскости, определяемые уравнениями
и
некоторую плоскость, принадлежащую пучку плоскостей, проходящих через эту прямую (в силу чего такое уравнение часто называют уравнением пучка плоскостей). Если плоскости, определяемые уравнениями I и II, параллельны, то пучок плоскостей превращается в совокупность плоскостей, параллельных этим плоскостям.
8. Уравнение плоскости, проходящей через три заданные точки M1(r 1Х M1(Jj), M3(r 3) (Л = x1i + yd + z1k; r2 = x2i + У2 j + z2k; r3 = x3i + y3 j + z3 к), проще всего найти из условия компланарности векторов r – T1, r2 – rl, r3 – rl, где r = xi + yj+zk — радиус-вектор текущей точки искомой плоскости M:
или в координатной форме:
Пример 1.21. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + у + 5z – 1 = 0, 2x + 3у – z + 2 = 0 и через точку М(3, 2, 1).
Решение. Воспользуемся уравнением пучка плоскостей
Значение I определяем из условия, что координаты точки М должны удовлетворять этому уравнению:
Получаем искомое уравнение в виде:
или, умножая на 13 и приводя подобные члены, в виде:
Пример 1.22. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + 3у + 5z – 4 = 0 и X – у – 2z + 7 = 0 и параллельной оси оу.
Решение. Воспользуемся уравнением пучка x + 3у + 5z – 4 + + l(x – у – 2z + 7) = 0, преобразуем уравнение к виду (1 + Х)х + (3 -1)у + (5 – 2l)z + (71 – 4) = 0.
Так как искомая плоскость параллельна оси ординат, то коэффициент при у должен равняться нулю, т. е. 3 – l = 0, I = 3. Подставив значение I в уравнение пучка, получаем
Пример 1.23. Найти уравнение плоскости, проходящей через точки М (2; -1; 4) и N(3; 2; -1) перпендикулярно к плоскости X + у + z – 3 = 0.
Решение. Воспользуемся уравнением плоскости, проходящей через первую из данных точек:
Условие прохождения этой плоскости через вторую точку и условие перпендикулярности определяются равенствами:
Исключая коэффициенты А, В и C из системы уравнений
получаем искомое уравнение в виде:
или
Пример 1.24. Из точки P(2; 3; -5) на координатные плоскости опущены перпендикуляры. Найти уравнение плоскости, проходящей через их основания.
Решение. Основаниями перпендикуляров, опущенных на координатные плоскости, будут следующие точки М1(2; 3; 0), М2(2; 0; -5), М3(0; 3; -5). Напишем уравнение плоскости, проходящей через точки М1, М2, М3, для чего воспользуемся уравнением
находим
или
Пример 1.25. Составить уравнение плоскости, проходящей через точку M (2; 3; 5) и перпендикулярной к вектору
Решение. Достаточно воспользоваться уравнением плоскости, проходящей через данную точку и перпендикулярной к данному вектору:
Прямая.
1. Прямая может быть задана уравнениями 2-х плоскостей
пересекающихся по этой прямой.
2. Исключив поочередно х и у из предыдущих уравнений, получим уравнения х = аz + с, у = bz + d. Здесь прямая определена двумя плоскостями, проектирующими ее на плоскости хoz и yoz.
3. Если даны две точки M(x1, у1, z1) и N(x2, у2, z2), то уравнения прямой, проходящей через них, будут иметь вид:
4. Так называемые канонические уравнения
определяют прямую, проходящую через точку M(x1, у1, z1)
и параллельную вектору S = li + mj + nk. В частности, эти уравнения могут быть записаны в виде:
где a, b и g — углы, образованные прямой с осями координат.
5. От канонических уравнений прямой, вводя параметр t, нетрудно перейти к параметрическим уравнениям прямой:
6. Угол между двумя прямыми, заданными их каноническими
уравнениями
опре-
деляется по формуле
перпендикулярности двух прямых:
условие параллельности двух прямых:
7. Необходимое и достаточное условие расположения двух прямых, заданных их каноническими уравнениями, в одной плоскости (условие компланарности двух прямых):
Если величины /1, т, П1 непропорциональны величинам /2, m2, «2, то указанное соотношение является необходимым и достаточным условием пересечения двух прямых в пространстве.
условие параллельности прямой и плоскости: 



9. Для определения точки пересечения прямой

а) если А/ + Вт + Cn ф 0, то прямая пересекает плоскость в одной точке;
б) если А/ + Вт + Cn = 0 и Ах0 + Ву0 + Cz0 + D ф 0, то прямая параллельна плоскости;
в) если А/ + Вт + Cn = 0 и Ах0 + Ву0 + Cz0 + D = 0, то прямая лежит в плоскости.
Пример 1.26. Привести к каноническому виду уравнения прямой 2х – у + 3z – 1 = 0 и 5х + 4у – z – 7 = 0.
Решение. Исключив вначале у, а затем z, получим:
Если разрешим каждое из уравнений относительно х, то будем иметь:
отсюда
Второй способ: найдем вектор S = li + mj + nk, параллельный искомой прямой. Так как он должен быть перпендикулярен к нормальным векторам заданных плоскостей N1 = 2i – j + 3k и N2= 5i + 4 j – k, то за него можно принять векторное произведение векторов N1 и N2.
Таким образом, l = -11; m = 17; n = 13.
За точку M1(x1, у1, z1), через которую проходит искомая прямая, можно принять точку пересечения ее с любой из координатных плоскостей, например с плоскостью yoz. Т ак как при этом x1 = 0, то координаты y1 и z1 этой точки определятся из системы уравнений заданных плоскостей, если в них положить х = 0:
Решая эту систему, находим у1 = 2; z1 = 1.
Итак, искомая прямая определяется уравнениями:
Мы получили прежний ответ.
Пример 1.27. Построить прямую
Решение. Искомую прямую можно построить как линию пересечения плоскостей. Для этого напишем уравнения плоскостей, которыми определена прямая, в отрезках на осях:
Пример 1.28. Из начала координат опустить перпендикуляр на прямую
Решение. Составим уравнение плоскости, проходящей через начало координат и перпендикулярной заданной прямой: 2х + 3у + z = 0. (Для этой плоскости можно принять А = l; B = m; C = n; D = 0; использовано условие перпендикулярности прямой и плоскости, см. п. 8 введения к настоящему разделу).
Найдем точку пересечения этой плоскости и данной прямой. Параметрические уравнения прямой имеют вид:
Построив данные плоскости, мы получим искомую прямую как линию пересечения этих плоскостей (рис. 20).
Для определения t имеем уравнение:
Остается составить уравнения прямой, проходящей через начало координат и через точку М (см. п. 3 введения к настоящему разделу):
Пример 1.29. В уравнениях прямой
параметр n так, чтобы эта прямая пересекалась с прямой

Решение. Для нахождения параметра n используем условие пересечения 2-х прямых:
Отсюда следует:
или
Следовательно, уравнения пересекающихся прямых таковы: искомой:
заданной:
Для вычисления координат точки пересечения этих прямых выразим из первого уравнения х и у через z: х = 2z, у = -3z. Подставляя их значения в равенство

отсюда z = 1. Зная z, находим х и у: х = 2z = 2, у = -3z = -3. Следовательно M(2; -3; 1).
Пример 1.30. Прямая задана каноническими уравнениями
Составить общие уравнения этой прямой.
Решение. Канонические уравнения прямой можно записать в виде системы двух независимых уравнений:
Получили общие уравнения прямой, которая теперь задана пересечением 2-х плоскостей, одна из которых 5х – 3у – 13 = 0 параллельна оси Oz, а другая х + 3z – 11 = 0 параллельна оси Oy.
Пример 1.31. Найти координаты точки M, делящей попалам отрезок прямой
заключенный между плоскостями хoz и xoy.
Решение. Найдем точку А пересечения прямой с плоскостью хoz, полагая в уравнениях прямой у = 0. Тогда получим:
отсюда x = 2,6; z = 2,8. Тогда А(2,6; 0; 2,8).
отсюда X = 11, у = 14, или В(11; 14; 0).
Определяем координаты точки М, делящей отрезок АВ пополам:
Следовательно, координаты искомой точки М будут: М(6,8; 7; 1,4).
Пример 1.32. Составить уравнение плоскости, проходящей через прямую
параллельной прямой
Решение. Составим уравнение пучка плоскостей, проходящих через первую из данных прямых:
которое делим на а ф 0, и пусть b /а = I:
Аналогично, полагая в уравнениях прямой z = 0, найдем координаты точки В пересечения прямой с плоскостью хоу:
69
В этом пучке нужно выбрать плоскость, параллельную 2-й данной прямой. Из условия параллельности плоскости и прямой, имеем:
Отсюда l = 1.
Подставляя I = 1 в уравнение пучка плоскостей, получим: 
Пример 1.33. Дана прямая 
Решение. Нужно найти плоскость, которая проходит через данную прямую перпендикулярно к данной плоскости; тогда искомая проекция определится как пересечение этой плоскости с данной.
Составим уравнение пучка плоскостей, проходящих через данную прямую:
Эта плоскость должна быть перпендикулярной к данной плоскости, что можно записать как:
отсюда I = 1.
70
Тогда уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости, будет:
или
Проекция данной прямой на данную плоскость определяется как прямая пересечения плоскостей:
Запишем эту прямую в каноническом виде. Найдем на прямой какую-либо точку. Для этого положим, например х0 = 1, и система запишется в виде:
Отсюда, у0 = 1, z0 = 0, т. е. точка M(1; 1; 0) принадлежит искомой прямой.
Направляющий вектор прямой S = (l; m; n) найдем из того условия, что он перпендикулярен нормальным векторам
N1 = (2; -3; -2) и N2 = (5; 2; 2) плоскостей, определяющих искомую прямую.
В качестве S берем векторное произведение векторов N1 и N2 , т. е.
Тогда искомое уравнение в каноническом виде будет:
Раздел 2
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
| < Предыдущая | Следующая > |
|---|
11 класс. Геометрия. Метод координат в пространстве. Прямоугольная система координат.
11 класс. Геометрия. Метод координат в пространстве. Прямоугольная система координат.
- Оглавление
- Занятия
- Обсуждение
- О курсе
Вопросы
Поделись с друзьями
Комментарии преподавателя
1. Введение
Если через точку О в пространстве мы проведем три перпендикулярные прямые, назовем их, выберем направление, обозначим единичные отрезки, то мы получим прямоугольную систему координат в пространстве. Оси координат называются так: Ох – ось абсцисс, Оy – ось ординат и Оz – ось аппликат. Вся система координат обозначается – Oxyz. Таким образом, появляются три координатные плоскости: Оxy, Оxz, Оyz.
Приведем пример построения точки В(4;3;5) в прямоугольной системе координат (см. Рис. 1).
Рис. 1. Построение точки B в пространстве
Первая координата точки B – 4, поэтому откладываем на Ox 4, проводим прямую параллельно оси Oy до пересечения с прямой, проходящей через у=3. Таким образом, мы получаем точку K. Эта точка лежит в плоскости Oxy и имеет координаты K(4;3;0). Теперь нужно провести прямую параллельно оси Oz. И прямую, которая проходит через точку с аппликатой 5 и параллельна диагонали параллелограмма в плоскости Oxy. На их пересечении мы получим искомую точку B.
Рассмотрим расположение точек, у которых одна или две координаты равны 0 (см. Рис. 2).
Например, точка A(3;-1;0). Нужно продолжить ось Oy влево до значения -1, найти точку 3 на оси Ox, и на пересечении линий, проходящих через эти значения, получаем точку А. Эта точка имеет аппликату 0, а значит, она лежит в плоскости Oxy.
Точка C(0;2;0) имеет абсциссу и аппликату 0 – не отмечаем. Ордината равна 2, значит точка C лежит только на оси Oy, которая является пересечением плоскостей Oxy и Oyz.
Чтобы отложить точку D(-4;0;3) продолжаем ось Ox назад за начало координат до точки -4. Теперь восстанавливаем из этой точки перпендикуляр – прямую, параллельную оси Oz до пересечения с прямой, параллельной оси Ox и проходящей через значение 3 на оси Oz. Получаем току D(-4;0;3). Так как ордината точки равна 0, значит точка D лежит в плоскости Oxz.
Следующая точка E(0;5;-3). Ордината точки 5, аппликата -3, проводим прямые проходящие через эти значения на соответствующих осях, и на их пересечении получаем точку E(0;5;-3). Эта точка имеет первую координату 0, значит она лежит в плоскости Oyz.
2. Координаты вектора
Начертим прямоугольную систему координат в пространстве Oxyz. Зададим в пространстве прямоугольную систему координат Oxyz. На каждой из положительных полуосей отложим от начала координат единичный вектор, т. е. вектор, длина которого равна единице. Обозначим единичный вектор оси абсцисс, единичный вектор оси ординат , и единичный вектор оси аппликат (см. рис. 1). Эти векторы сонаправлены с направлениями осей, имеют единичную длину и ортогональны – попарно перпендикулярны. Такие вектора называют координатными векторами или базисом.
Рис. 1. Разложение вектора по трем координатным векторам
Возьмем вектор , поместим его в начало координат, и разложим этот вектор по трем некомпланарным – лежащим в разных плоскостях – векторам. Для этого опустим проекцию точки M на плоскость Oxy, и найдем координаты векторов , и . Получаем: . Рассмотрим по отдельности каждый из этих векторов. Вектор лежит на оси Ox, значит, согласно свойству умножения вектора на число, его можно представить как какое-то число x умноженное на координатный вектор . , а длина вектора ровно в x раз больше длины . Так же поступим и с векторами и , и получаем разложение вектора по трем координатным векторам:
Коэффициенты этого разложения x, y и z называются координатами вектора в пространстве.
Рассмотрим правила, которые позволяют по координатам данных векторов найти координаты их суммы и разности, а также координаты произведения данного вектора на данное число.
;
1) Сложение:
2) Вычитание:
3) Умножение на число: ,
Вектор, начало которого совпадает с началом координат, называется радиус–вектором. (Рис. 2). Вектор – радиус-вектор, где x, y и z – это коэффициенты разложения этого вектора по координатным векторам , , . В данном случае x – это первая координата точки A на оси Ox, y – координата точки B на оси Oy, z – координата точки C на оси Oz. По рисунку видно, что координаты радиус-вектора одновременно являются координатами точки М.
Возьмем точку A(x1;y1;z1) и точку B(x2;y2;z2) (см. рис. 3). Представим вектор как разность векторов и по свойству векторов. Причем, и – радиус-векторы, и их координаты совпадают с координатами концов этих векторов. Тогда мы можем представить координаты вектора как разность соответствующих координат векторов и : . Таким образом, координаты вектора мы можем выразить через координаты конца и начала вектора.
Рассмотрим примеры, иллюстрирующие свойства векторов и их выражение через координаты. Возьмем векторы , , . Нас спрашивают вектор . В данном случае найти это значит найти координаты вектора , которые полностью его определяют. Подставляем в выражение вместо векторов соответственно их координаты. Получаем:
Теперь умножаем число 3 на каждую координату в скобках, и то же самое делаем с 2:
У нас получилась сумма трех векторов, складываем их по изученному выше свойству:
Ответ:
Дано: Треугольная пирамида AOBC (см. рис. 4). Плоскости AOB, AOC и OCB – попарно перпендикулярны. OA=3, OB=7, OC=4; M – сер.AC; N – сер.OC; P – сер. CB.
Найти: ,,,,,,,.
Решение: Введем прямоугольную систему координат Oxyz с началом отсчета в точке O. По условию обозначаем точки A, B и C на осях и середины ребер пирамиды – M, P и N. По рисунку находим координаты вершин пирамиды: A(3;0;0), B(0;7;0), C(0;0;4).
Так как координаты вектора – это разность координат его конца и начала, получаем:. Таким же образом находим координаты векторов и . ; .
Чтобы найти координаты вектора , нужно сначала найти координаты точек M и N. По рисунку видно, что точка N имеет координаты, так как она лежит на оси аппликат. Рассмотрим . MN – средняя линия, . Значит координата точки M по оси Oz 2. Теперь проведем из точки M перпендикуляр к оси Ox, координата 1,5. Точка M лежит в плоскости Oxz, значит по оси Oy координата 0. Получаем M(1,5;0;2). Теперь зная координаты точек M и N, считаем их разность: .
Теперь найдем координаты точки P. Опустим перпендикуляр на плоскость Oxy, получаем значение 3,5 по оси ординат. И проведя перпендикуляр к оси Oz, получаем значение 2 по оси аппликат. Точка P имеет координаты (0;3,5;2). Зная координаты нужных точек, найдем координаты оставшихся векторов.
;
.
Вектора и – радиус-векторы, значит, их координаты равны координатам концов этих векторов: , .
Раздел 2. Векторная алгебра
Абсолютная величина вектора см. Модуль вектора.
Абсцисса – первая координата вектора или точки в декартовой системе координат.
Антикоммутативное свойство (Антикоммутативность) векторного произведения двух векторов: при перестановке сомножителей векторное произведение меняет знак на противоположный, т.е. a´b = – b´a.
Аппликата – третья координата вектора или точки в декартовой системе координат.
Базис n-мерного векторного пространства (Базисные векторы) – совокупность n линейно независимых векторов этого пространства, линейными комбинациями которых можно представить любой вектор пространства.
См. Ортонормированный базис.
Базис трехмерного пространства (Базис в пространстве) – упорядоченная тройка некомпланарных векторов.
Базис на плоскости – упорядоченная пара неколлинеарных векторов.
Базисные векторы см. Базис n-мерного пространства.
Базисные векторы декартовой прямоугольной системы координат – единичные ортогональные векторы i, j на плоскости и единичные попарно ортогональные векторы i, j, k в пространстве.
Вектор (Векторная величина, геометрический вектор) – направленный отрезок прямой. Пояснение. Вектор является величиной, полностью определенной своим направлением и длиной. Обозначение: a, 
См. Единичный, нулевой, свободный, связанный вектор; коллинеарные, компланарные, линейно зависимые, линейно независимые векторы.
Векторная алгебра – раздел математики, изучающий алгебраические операции над векторами.
Векторная величина см. Вектор.
Векторное произведениедвух векторов a и b – вектор c, определяемый следующими тремя условиями:
а) модуль вектора c, численно равен площади параллелограмма, построенного на векторах a и b как на сторонах, т.е. |c| = |a|×|b|×sin j, где j = Ð(a,b);
б) вектор c ортогонален векторам a и b;
в) вектор c направлен так, что векторы a, b, c образуют правую тройку.
Обозначения: a´b = c, [a, b] = c, [ab] = c.
Векторно-скалярное произведение векторов см. Смешанное произведение векторов.
Вектор-столбец – запись вектора, при которой его координаты располагаются вертикально.
Вектор-строка– запись вектора, при которой его координаты располагаются горизонтально.
Геометрический вектор см. Вектор.
Граничные точки отрезка см. Концевые точки отрезка.
Декартова прямоугольная система координат в пространстве– система координат, заданная тремя взаимно ортогональными единичными векторами, называемыми ортами.
Декартова прямоугольная система координат на плоскости– система координат, заданная двумя взаимно ортогональными единичными векторами, называемыми ортами.
Декартовы координаты вектора– проекции вектора на оси координат декартовой системы координат.
Длина вектора см. Модуль вектора.
Единичный вектор – вектор, модуль которого равен единице.
Обозначение: a o , e. См. Орт.
Квадрант – одна из четырех областей, на которые плоскость делится двумя взаимно перпендикулярными прямыми.
Коллинеарность векторов– свойство векторов быть коллинеарными.
Коллинеарные векторы – векторы, расположенные на одной прямой или на параллельных прямых. Обозначение: a||b.
Компланарность– свойство векторов быть компланарными.
Компланарные векторы– векторы, расположенные в одной плоскости или в параллельных плоскостях.
Компонента см. Координата.
Концевые точки отрезка(Граничные точки отрезка) – точки, между которыми заключен отрезок прямой.
Координата (компонента, составляющая) вектора в декартовой системе координат – проекция вектора на соответствующую ось координат.
Координатная плоскость – плоскость, проходящая через две координатные оси из трех.
Координатные оси (Оси координат) – числовые прямые, имеющие общую нулевую точку (начало координат).
Координаты точки – 1) числа, определяющие положение точки на плоскости или в пространстве; 2) координаты радиус-вектора этой точки.
Левая тройка векторов – тройка векторов, не являющаяся правой.
Линейная комбинация n векторов – сумма произведений этих векторов на произвольные скаляры (числа), называемые коэффициентами:
Линейно зависимые векторы – векторы, линейная комбинация которых равна нулю, если не все коэффициенты равны нулю.
Линейно независимые векторы – векторы, линейная комбинация которых равна нулю только при условии, когда все коэффициенты равны нулю.
Линейные операции над векторами – это операции сложения векторов и умножения вектора на число.
Многогранник (Многогранная поверхность) – поверхность, образованная из многоугольников (граней поверхности) так, что каждая сторона любого из этих многоугольников (ребро поверхности) является стороной еще одного многоугольника.
Многоугольник – замкнутая ломаная линия на плоскости.
Модуль вектора (Длина вектора, Абсолютная величина вектора) – число, равное расстоянию между его началом и концом. Обозначение: |a|, | 
Направляющий косинус вектора– косинус соответствующего направляющего угла.
Направляющий угол вектора– угол, образуемый вектором и соответствующей осью координат декартовой системы.
Начало координат– точка пересечения координатных осей, являющаяся началом отсчета. Обозначение: O.
Нулевой вектор– вектор, модуль которого равен нулю.
Пояснение. Начало и конец нулевого вектора совпадают. Обозначение: o.
Объем тела – мера пространственных тел, не меняющая своего значения при движении тела и равная единице на единичном кубе.
Октант – одна из восьми областей, на которые трехмерное пространство делится тремя взаимно перпендикулярными плоскостями.
Ордината– вторая координата вектора или точки в декартовой системе координат.
Ориентация векторов– взаимное расположение трех векторов в пространстве; три вектора могут быть с правой или левой ориентацией. Такие векторы образуют правую или левую тройку векторов соответственно.
См. Правая тройка векторов.
Орт – единичный вектор, направление которого совпадает с направлением вектора a. Обозначение: a o .
Ортогональность– свойство векторов быть ортогональными.
Ортогональные векторы– 1) векторы, угол между которыми является прямым; 2) векторы, скалярное произведение которых равно нулю.
Ортонормированный базис – базис векторного пространства, образованный единичными попарно ортогональными векторами.
Острый угол между векторами– угол, значение которого меньше 90 о .
Оси координат см. Координатные оси.
Ось– прямая, на которой указаны начало отсчета, единица и положительное направление.
Ось абсцисс (Ось x) – первая ось в декартовой системе координат на плоскости или в пространстве.
Ось аппликат (Ось z) – третья ось в декартовой системе координат в пространстве.
Ось ординат (Ось y) – вторая ось в декартовой системе координат на плоскости или в пространстве.
Отрезок прямой(Отрезок) – часть прямой, заключенная между двумя ее точками и включающая обе эти точки.
Параллелепипед– призма, основаниями которой являются параллелограммы.
Параллелограмм – плоский четырехугольник, противоположные стороны которого попарно параллельны.
Параллельный перенос (сдвиг) – перемещение фигуры, при котором каждая точка перемещается на один и тот же вектор.
Параллельный сдвиг см. Параллельный перенос.
Пирамида– многогранник, одной их граней которого является многоугольник (обычно это основание), а остальные грани – треугольники с общей вершиной.
Площадь плоской фигуры – неотрицательная функция геометрической фигуры на плоскости, сохраняющая свое значение при движениях и удовлетворяющая условию, что единичный квадрат имеет площадь, равную единице.
Полный угол – угол, равный 360 о .
Правая (Правоориентированная) тройка векторов – три некомпланарных вектора, удовлетворяющих условиям:
1) они упорядочены, и третий вектор направлен по направлению осевого движения правого винта при повороте по наименьшему углу от первого вектора ко второму;
2) они упорядочены и наблюдателю, находящемуся внутри телесного угла, образованного этими векторами, кратчайшие повороты от первого вектора ко второму и от второго к третьему кажутся происходящими против часовой стрелки;
3) они упорядочены и из конца третьего вектора кратчайший поворот от первого вектора ко второму виден совершающимся против часовой стрелки.
Пояснение. Приведены три равносильных условия (определения) правой тройки векторов.
Правило параллелограмма– графическое правило образования суммы двух векторов.
Правило треугольника– графическое правило образования суммы двух векторов.
Призма – многогранник, две грани (основания) которого – равные многоугольники, лежащие в параллельных плоскостях, а остальные грани (боковые грани) – параллелограммы.
Проекция вектора на вектор– число, равное модулю вектора, проекция которого находится, умноженному на косинус угла между векторами.
Произведение вектора a на скаляр (число) l – вектор, обозначаемый la, такой что:
а) его модуль равен произведению модулей исходного вектора и скаляра, т.е.
|la| = |l|×|a|;
б) новый вектор и исходный вектор коллинеарны, т.е. a || la;
в) векторы a и la сонаправлены, если l > 0, и противоположно направлены, если l o , в радианной мере p/2.
Прямоугольные декартовы координаты – координаты, базис которых состоит из попарно ортогональных единичных векторов.
Равные векторы – векторы, являющиеся коллинеарными, одинаково направленными и имеющие равные модули.
Радиус-вектор точки P – вектор 
Развернутый угол – угол, стороны которого составляют одну прямую; в градусной мере равен 180 o , в радианной мере p.
Свободный вектор– множество всех векторов, равных данному вектору, т.е. множество всех векторов с одинаковым модулем и направлением, но с различными начальными точками.
Связанный вектор– вектор с фиксированной начальной точкой.
Скаляр (Скалярная величина) – величина, которая полностью характеризуется одним числом.
Скалярная величинасм. Скаляр.
Скалярное произведение двух векторов– число, равное произведению модулей этих векторов на косинус угла между ними.
Обозначение: ab, a×b, (a,b).
Скалярный квадрат– скалярное произведение вектора на самого себя.
Обозначение: a 2 .
Сложение векторовсм. Сумма двух векторов.
Смешанное (Векторно-скалярное) произведение трех векторов – число, полученное по правилу: (a´b)×c), т.е. первые два вектора перемножаются векторно, а результат умножается на третий вектор скалярно. Обозначение: abc, (abc).
Составляющаясм. Координата.
Сумма двух векторов – новый вектор, получаемый по правилу треугольника или параллелограмма. Обозначение: a + b = c.
Тетраэдр– треугольная пирамида, т.е. пирамида, основанием которой является треугольник.
Пояснение. Тетраэдр имеет четыре треугольных грани, шесть ребер и четыре вершины.
Треугольная призма – призма, основания которой – треугольники.
Треугольник– многоугольник, имеющий три вершины и три стороны.
Тупой угол– угол, больший прямого, но меньший развернутого.
Угол между двумя векторами– наименьший угол, на который нужно повернуть один из векторов до совмещения с другим.
См. Острый, полный, прямой, развернутый, тупой угол.
Умножение вектора на скаляр – операция отыскания произведения вектора на скаляр. Обозначение: la = b.
Упорядоченная тройка векторов – три вектора, если указано, какой из них является первым, какой – вторым и какой – третьим.
Ортогональные векторы и условие ортогональности
В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.
Ортогональные векторы: определение и условие
Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .
Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.
Примеры решения задач на ортогональность векторов
Плоские задачи на ортогональность векторов
Если дана плоская задача, то ортогональность для векторов a ¯ = < a x × a y >и b ¯ = < b x × b y >записывают следующим образом:
a ¯ × b ¯ = a x × b x + a y × b y = 0
Задача 1. Докажем, что векторы a ¯ = < 1 ; 2 >и b ¯ = < 2 ; – 1 >ортогональны.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 1 × 2 + 2 × ( – 1 ) = 2 – 2 = 0
Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.
Задача 2. Докажем, что векторы a ¯ = < 3 ; – 1 >и b ¯ = < 7 ; 5 >ортогональны.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 3 × 7 + ( – 1 ) × 5 = 21 – 5 = 16
Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.
Задача 3. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 >и b ¯ = < n ; 1 >будут ортогональными.
Как решить?
Найдем скалярное произведение данных векторов:
a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = – 4 n = – 2
Ответ: векторы являются ортогональными при значении n = 2 .
Примеры пространственных задач на ортогональность векторов
При решении пространственной задачи на ортогональность векторов a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; – 1 ; 10 >условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .
Задача 4. Докажем, что векторы a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; – 1 ; 10 >являются ортогональными.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 1 × 2 + 2 × ( – 1 ) + 0 × 10 = 2 – 2 = 0
Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.
Задача 5. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 ; 1 >и b ¯ = < n ; 1 ; – 8 >будут являться ортогональными.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( – 8 ) = 2 n + 4 – 8 = 2 n – 4 2 n – 4 = 0 2 n = 4 n = 2
Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .
[spoiler title=”источники:”]
http://lektsii.org/1-77669.html
http://zaochnik.com/spravochnik/matematika/vektory/ortogonalnye-vektory-i-uslovie-ortogonalnosti/
[/spoiler]
Привожу то, что понял. Получилась система из трех уравнений:
[math]{2A+B+D=0[/math]
[math]{-B+2C+D=0[/math]
[math]{A+2B+frac{C}{2}=0[/math]
Кстати, не подскажете, как можно здесь показать, что уравнения являются системой координат (не знаю, как поставить слева от них одну общую фигурную скобку)?
Далее решаю получившуюся матрицу
[math]2[/math] [math]1[/math] [math]0[/math] [math]-D[/math]
[math]0[/math] [math]-1[/math] [math]2[/math] [math]-D[/math]
[math]1[/math] [math]2[/math] [math]frac{1}{2}[/math] [math]0[/math]
Получаются координаты
[math](-frac{8}{7}D;frac{9}{7}D;frac{D}{7})[/math]
Выношу коэффициент [math]frac{D}{7}[/math] за скобки.
В итоге ответ [math](-8;9;1)[/math]. Правильно?
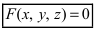
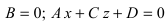 – плоскость параллельна оси ординат (Оу);
– плоскость параллельна оси ординат (Оу);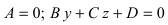 – плоскость параллельна оси абсцисс (Ох).
– плоскость параллельна оси абсцисс (Ох).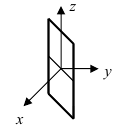
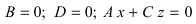 – плоскость проходит через начало координат параллельно оси ординат;
– плоскость проходит через начало координат параллельно оси ординат;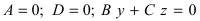 – плоскость проходит через начало координат параллельно оси абсцисс.
– плоскость проходит через начало координат параллельно оси абсцисс.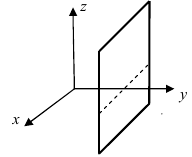
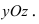
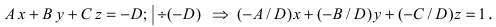
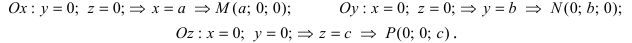
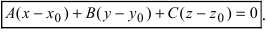
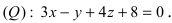
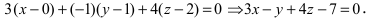
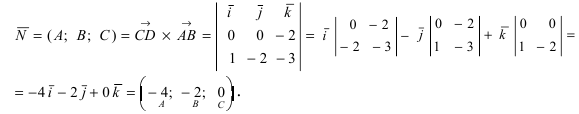
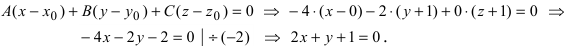
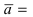

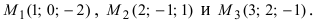
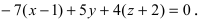
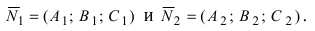
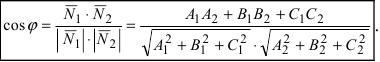
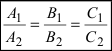
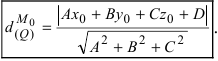
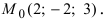
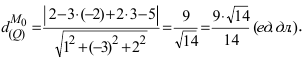
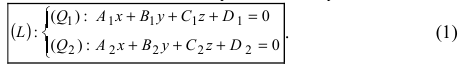
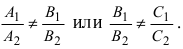

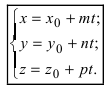
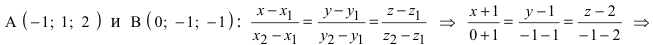
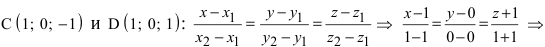
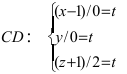
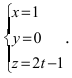
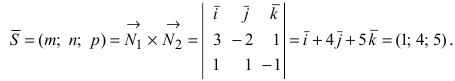
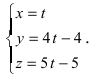
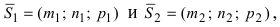

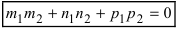
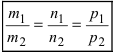
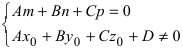 , то прямая не пересекает плоскость (прямая параллельна плоскости);
, то прямая не пересекает плоскость (прямая параллельна плоскости);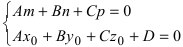 прямая лежит на плоскости;
прямая лежит на плоскости;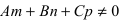 , прямая пересекает плоскость в одной точке.
, прямая пересекает плоскость в одной точке.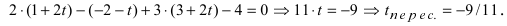
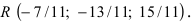
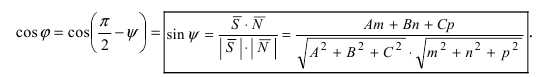
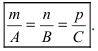
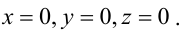
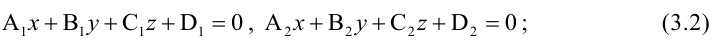
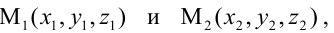 тогда прямая, через них проходящая, задается уравнениями:
тогда прямая, через них проходящая, задается уравнениями: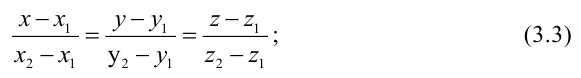
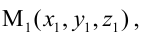 ей принадлежащей, и вектором
ей принадлежащей, и вектором 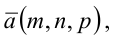 ей коллинеарным.
ей коллинеарным.