Как найти аппликату точки принадлежащей плоскости

Уравнение плоскости

Электронный урок по ЕН.01 Элементы высшей математики

Просмотр содержимого документа
«Уравнение плоскости»

• Всякое уравнение первой степени относительно координат x, y, z

• Ax + By + Cz +D=0

• задает плоскость, и наоборот:

всякая плоскость может быть представлена уравнением, которое называется уравнением плоскости.

Составить уравнение какой-нибудь плоскости, в которой лежит точка (2; -1; 3)

• Ax + By + Cz +D=0
• 3x + 4y + 5z +D=0 (3,4,5-любые числа)
• 3·2 + 4·(-1) + 5·3 +D=0
• 6- 4+ 15+D=0
• 17+D=0
• D=-17
• Ответ: 3x + 4y + 5z -17=0-уравнение плоскости на которой лежит точка (2; -1; 3)

Особые случаи уравнения плоскости

• 1. D = 0, Ax+By+Cz = 0 — плоскость проходит через начало координат.
• 2. C = 0, Ax+By+D = 0 — плоскость параллельна оси Oz.
• 3. C = D = 0, Ax +By = 0 — плоскость проходит через ось Oz.
• 4. B = C = 0, Ax + D = 0 — плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей:

• x = 0, y = 0, z = 0.

• 1) Найдите аппликату точки А(1;-3; z) , если она принадлежит плоскости, заданной уравнением 5х-2у+3z-1=0.
• 2) Принадлежит, ли точка В (-1; 2; 7) плоскости, заданной уравнением 2х+3у-z+3=0
• 3) Принадлежит, ли точка Е (0; 4; -6) плоскости, заданной уравнением х-5у-4z+2=0
• 4) При каком D точка А(1; 5;-2) принадлежит плоскости -3х+2у-z+D=0

• Сколько точек достаточно для построения плоскости?

• Через три точки не лежащие на одной прямой, можно провести плоскость, и притом только одну.

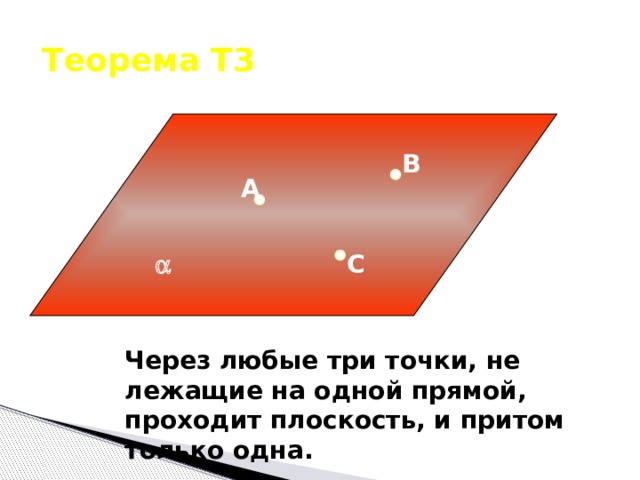
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Составьте уравнение плоскости, проходящей через точки

• А(1; 2;-3)
• В (0; 4; 2)
• С (2;-3;5)

Решение системы находим по формулам:

которые называют формулами Крамера

из коэффициентов при неизвестных

Если Δ≠0, то система совместна

Далее составим три вспомогательных определителя:

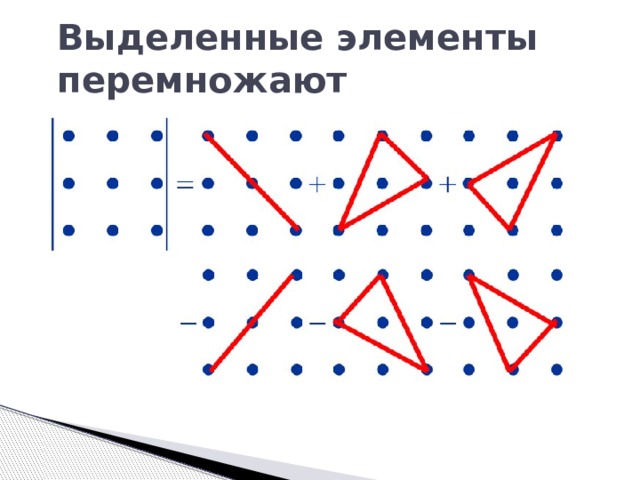
Выделенные элементы перемножают

• Если плоскость задана уравнением

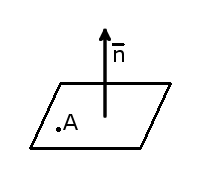
Ax + By + Cz +D=0, то вектор n= <А, В,С>перпендикулярен этой плоскости.

Этот вектор называется вектором нормали к плоскости или нормальным вектором к данной плоскости.

Дан вектор нормали некоторой плоскости n=<2; -3;1>, проходящей через точку А(-1;0;2) Составьте общее уравнение этой плоскости.

Общее уравнение плоскости

В данной статье мы рассмотрим общее уравнение плоскости в пространстве. Определим понятия полного и неполного уравнения плоскости. Для построения общего уравнения плоскости пользуйтесь калькулятором уравнение плоскости онлайн.

Пусть задана произвольная декартова прямоугольная система координат Oxyz. Общим уравнением плоскости называется линейное уравнение вида:

где A, B, C, D − некоторые постоянные, причем хотя бы один из элементов A , B и C отлично от нуля.

Мы покажем, что линейное уравнение (1) в пространстве определяет плоскость и любой плоскость в пространстве можно представить линейным уравнением (1). Докажем следующую теорему.

Теорема 1. В произвольной декартовой прямоугольной системе координат в пространстве каждая плоскость α может быть задана линейным уравнением (1). Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат в пространстве определяет плоскость.

Доказательство. Достаточно доказать, что плоскость α определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.

Пусть в пространстве задана плоскость α. Выберем оси Ox и Oy так, чтобы они располагались на плоскости α, а ось Oz направим перпендикулярно к этой плоскости. Тогда линейное уравнение z=0 будет уравнением плоскости, т.к. координаты любой точки, принадлежащей этой плоскости удовлетворяют уравнению z=0, а координаты любой точки, не лежащей на этой плоскости − нет. Первая часть теоремы доказана.

Пусть фиксирована произвольная декартова прямоугольная система координат Oxyz. Рассмотрим линейное уравнение (1), где хотя бы один из элементов A , B и C отлично от нуля. Тогда уравнение (1) имеет хотя бы одно решение x₀, y₀, z₀. Действительно. Пусть из коэффициентов A≠0. Возьмем произвольные числа y₀, z₀. Тогда

.

Таким образом, существует точка M₀(x₀, y₀, z₀), координаты которой удовлетворяют уравнению (1):

Вычитая из уравнения (1) тождество (2), получим

A(x−x0)+B(y−y0)+С(z−z0)=0,

(3)

которая эквивалентна уравнению (1).

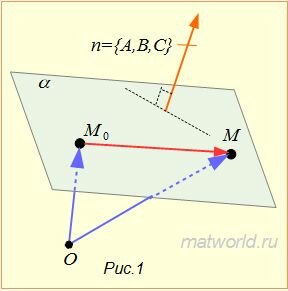
Покажем, что (3) определяет некоторую плоскость, проходящую через точку M₀(x₀, y₀, z₀) и перпендикулярную вектору n=<A,B,C> (n≠0, так как хотя бы один из чисел A,B,C отлично от нуля).

Если точка M₀(x₀, y₀, z₀) принадлежит плоскости α, то ее координаты удовлетворяют уравнению (3), т.к. векторы n=<A,B,C> и перпендикулярны (Рис.1) и их скалярное произведение равно нулю:

Если же точка M(x, y, z) не лежит на плоскости α, то векторы n=<A,B,C> и не ортогональны. Тогда их скалярное произведение не равно нулю, т.е. координаты точки M(x, y, z) не удовлетворяют условию (3). Теорема доказана.

Одновременно с доказательством теоремы 1 мы получили следующее утверждение.

Утверждение 1. В декартовой прямоугольной системе координат вектор с компонентами (A,B,C) перпендикулярен плоскости Ax+By+Cz+D=0.

Вектор n=(A,B,C) называется нормальным вектором плоскости , определяемой линейным уравнением (1).

Утверждение 2. Если два общих уравнения плоскости

определяют одну и ту же плоскость, то найдется такое число λ, что выпонены равенства

A2=A1λ, B2=B1λ, C2=C1λ, D2=D1λ.

(6)

Умножая уравнение (7) на λ и вычитая из него уравнение (8) получим:

(A₁λ−A₂)x₀+(B₁λ−B₂)y₀+(C₁λ−C₂)z₀+(D₁λ−D₂)=0.

Так как выполнены первые три равенства из выражений (6), то D₁λ−D₂=0. Т.е. D₂=D₁λ. Утверждение доказано.

Неполные уравнения плоскости

Определение 1. Общее уравнение плоскости (1) называется полным , если все коэффициенты A, B, C, D отличны от нуля. Если же хотя бы один из коэффициентов A, B, C, D равен нулю, то общее уравнение плоскости называется неполным .

Рассмотрим все возможные варианты неполных уравнений плоскости:

При D=0, имеем уравнение плоскости Ax+By+Cz=0, проходящей через начало координат (Рис.2). Действительно, точка O(0,0,0) удовлетворяет этой системы линейных уравнений.

При A=0, имеем уравнение плоскости By+Cz+D=0, которая параллельна оси Ox (Рис.3). В этом случае нормальный вектор плоскости n=<0,B,C> лежит на координатной плоскости Oyz.

При B=0, имеем уравнение плоскости Ax+Cz+D=0, которая параллельна оси Oy (Рис.4).

При C=0, имеем уравнение плоскости Ax+By+D=0, которая параллельна оси Oz (Рис.5).

При A=0,B=0 имеем уравнение плоскости Cz+D=0, которая параллельна координатной плоскости Oxy (Рис.6).

При B=0,C=0 имеем уравнение плоскости Ax+D=0, которая параллельна координатной плоскости Oyz (Рис.7).

При A=0,C=0 имеем уравнение плоскости By+D=0, которая параллельна координатной плоскости Oxz (Рис.8).

При A=0,B=0,D=0 имеем уравнение плоскости Cz=0, которая совпадает с координатной плоскостью Oxy (Рис.9).

При B=0,C=0,D=0 имеем уравнение плоскости Ax=0, которая совпадает с координатной плоскостью Oyz (Рис.10).

При A=0,C=0,D=0 имеем уравнение плоскости By=0, которая совпадает с координатной плоскостью Oxz (Рис.11).

Рассмотрим примеры построения общего уравнения плоскости.

Пример 1. Построить общее уравнение плоскости, проходящей через точку M(4,−1,2) параллельной координатной плоскости Oxy.

Решение. Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя координаты точки M в (3), получим:

A(x−4)+B(y−(−1))+C(z−2)=0

(9)

Так как плоскость параллельна координатной плоскости Oxy, то направляющий вектор имеет следующий вид n=<A,B,C>=<0,0,1>, т.е. A=0, B=0, C=1.

Подставляя коэффициенты A,B,C в (9), получим:

0(x−4)+0(y−(−1))+1(z−2)=0

(9)

Пример 2. Построить общее уравнение плоскости, проходящей через начало координат и имеющий нормальный вектор n==<2,3,1>.

Решение. Начало координат имеет коэффициенты (0,0,0). Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя коэффициенты начальной точки в (3), получим:

A(x−0)+B(y−0)+C(z−0)=0

(10)

Так как плоскость имеет нормальный вектор n=<A,B,C>=<2,3,1>, т.е. A=2, B=3, C=1, подставляя коэффициенты A,B,C в (10), получим:

2(x−0)+3(y−0)+1(z−0)=0

(9)

Онлайн калькулятор для построения общего уравнения плоскости находится здесь. Там же вы найдете примеры построения общего уравнения плоскости, если известны три точки этой плоскости или если известна одна точка и нормальный вектор этой плоскости.

Онлайн калькулятор. Уравнение плоскости

Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.

Найти уравнение плоскости

Выберите метод решения исходя из имеющихся в задаче данных:

В задаче известны:

Ввод данных в калькулятор для составления уравнения плоскости

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления уравнения плоскости

• Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория. Уравнение плоскости.

Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки

В зависимости от условий задачи уравнение плоскости можно составить следующими способами:

Если заданы координаты трех точек A( x ₁, y ₁, z ₁), B( x ₂, y ₂, z ₂) и C( x ₃, y ₃, z ₃), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле

x — x 1	y — y 1	z — z 1	= 0
x 2 — x 1	y 2 — y 1	z 2 — z 1
x 3 — x 1	y 3 — y 1	z 3 — z 1

Если заданы координаты точки A( x ₁, y ₁, z ₁) лежащей на плоскости и вектор нормали n = , то уравнение плоскости можно составить по следующей формуле:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Уравнение плоскости

Уравнение плоскости

• Всякое уравнение первой степени относительно координат x, y, z

• Ax + By + Cz +D=0  

• задает плоскость, и наоборот:

всякая плоскость может быть представлена уравнением, которое называется уравнением плоскости.

Уравнение плоскости

• Ax + By + Cz +D=0  

Составить уравнение какой-нибудь плоскости, в которой лежит точка (2; -1; 3)

• Ax + By + Cz +D=0
• 3x + 4y + 5z +D=0 (3,4,5-любые числа)
• 3·2 + 4·(-1) + 5·3 +D=0
• 6- 4+ 15+D=0
• 17+D=0
• D=-17
• Ответ: 3x + 4y + 5z -17=0-уравнение плоскости на которой лежит точка (2; -1; 3)

Особые случаи уравнения плоскости

• 1. D = 0, Ax+By+Cz = 0 – плоскость проходит через начало координат.
• 2. C = 0, Ax+By+D = 0 – плоскость параллельна оси Oz.
• 3. C = D = 0, Ax +By = 0 – плоскость проходит через ось Oz.
• 4. B = C = 0, Ax + D = 0 – плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей:

• x = 0, y = 0, z = 0.

Задания

• 1) Найдите аппликату точки А(1;-3; z) , если она принадлежит плоскости, заданной уравнением 5х-2у+3z-1=0.
• 2) Принадлежит, ли точка В (-1; 2; 7) плоскости, заданной уравнением 2х+3у-z+3=0
• 3) Принадлежит, ли точка Е (0; 4; -6) плоскости, заданной уравнением х-5у-4z+2=0
• 4) При каком D точка А(1; 5;-2) принадлежит плоскости -3х+2у-z+D=0

• Сколько точек достаточно для построения плоскости?

Теорема стереометрии

• Через три точки не лежащие на одной прямой, можно провести плоскость, и притом только одну.

Теорема Т3

В

A

С



Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Составьте уравнение плоскости, проходящей через точки

• А(1; 2;-3)
• В (0; 4; 2)
• С (2;-3;5)

Решение системы находим по формулам:

которые называют формулами Крамера

Составим определитель

из коэффициентов при неизвестных

Если Δ≠0, то система совместна

Далее составим три вспомогательных определителя:

, ,

Выделенные элементы перемножают

Вектор нормали

• Если плоскость задана уравнением

Ax + By + Cz +D=0, то вектор n={А, В,С} перпендикулярен этой плоскости.

Этот вектор называется вектором нормали к плоскости или нормальным вектором к данной плоскости.

Дан вектор нормали некоторой плоскости n={2; -3;1}, проходящей через точку А(-1;0;2) Составьте общее уравнение этой плоскости.

Уравнение плоскости

Электронный урок по ЕН.01 Элементы высшей математики

Просмотр содержимого документа
«Уравнение плоскости»

• Всякое уравнение первой степени относительно координат x, y, z

• Ax + By + Cz +D=0

• задает плоскость, и наоборот:

всякая плоскость может быть представлена уравнением, которое называется уравнением плоскости.

Составить уравнение какой-нибудь плоскости, в которой лежит точка (2; -1; 3)

• Ax + By + Cz +D=0
• 3x + 4y + 5z +D=0 (3,4,5-любые числа)
• 3·2 + 4·(-1) + 5·3 +D=0
• 6- 4+ 15+D=0
• 17+D=0
• D=-17
• Ответ: 3x + 4y + 5z -17=0-уравнение плоскости на которой лежит точка (2; -1; 3)

Особые случаи уравнения плоскости

• 1. D = 0, Ax+By+Cz = 0 – плоскость проходит через начало координат.
• 2. C = 0, Ax+By+D = 0 – плоскость параллельна оси Oz.
• 3. C = D = 0, Ax +By = 0 – плоскость проходит через ось Oz.
• 4. B = C = 0, Ax + D = 0 – плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей:

• x = 0, y = 0, z = 0.

• 1) Найдите аппликату точки А(1;-3; z) , если она принадлежит плоскости, заданной уравнением 5х-2у+3z-1=0.
• 2) Принадлежит, ли точка В (-1; 2; 7) плоскости, заданной уравнением 2х+3у-z+3=0
• 3) Принадлежит, ли точка Е (0; 4; -6) плоскости, заданной уравнением х-5у-4z+2=0
• 4) При каком D точка А(1; 5;-2) принадлежит плоскости -3х+2у-z+D=0

• Сколько точек достаточно для построения плоскости?

• Через три точки не лежащие на одной прямой, можно провести плоскость, и притом только одну.

Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Составьте уравнение плоскости, проходящей через точки

• А(1; 2;-3)
• В (0; 4; 2)
• С (2;-3;5)

Решение системы находим по формулам:

которые называют формулами Крамера

из коэффициентов при неизвестных

Если Δ≠0, то система совместна

Далее составим три вспомогательных определителя:

Выделенные элементы перемножают

• Если плоскость задана уравнением

Ax + By + Cz +D=0, то вектор n= <А, В,С>перпендикулярен этой плоскости.

Этот вектор называется вектором нормали к плоскости или нормальным вектором к данной плоскости.

Дан вектор нормали некоторой плоскости n=<2; -3;1>, проходящей через точку А(-1;0;2) Составьте общее уравнение этой плоскости.

Список вопросов базы знаний

Линейная алгебра с элементами аналитической геометрии

• Страница:
• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Левая часть	Правая часть

Верны ли определения?

А) Скалярное произведение вектора на вектор – это число, равное произведению их модулей на косинус угла между ними

В) Скалярное произведение вектора на вектор – это число, равное произведению их модулей

Подберите правильный ответ

Верны ли утверждения?

А) В пространстве многочленов степени n ≤ 2 система векторов f 1 = 1, f 2 = x + 1, f 3 = 2x образует базис

В) В пространстве многочленов степени n ≤ 2 система векторов f 1 = 1, f 2 = x, f 3 = x 2 образует стандартный базис

Подберите правильный ответ

Верны ли утверждения?

А) Вектор , перпендикулярный данной прямой, называется направляющим вектором прямой в пространстве

В) Если вектор нормали к плоскости коллинеарен направляющему вектору прямой, то плоскость и прямая параллельны

Подберите правильный ответ

Верны ли утверждения?

А) Вектор = (1, 2) является свобственным вектором матрицы А =

В) Собственный вектор = (1, 2) матрицы А = отвечает собственному значению l = 3

Подберите правильный ответ

Верны ли утверждения?

А) Векторы = (1, 1, 1), = (1, 1, 0), = (2, 2, 1) образуют базис в R 3

В) Векторы = (1, 1, 1), = (1, 1, 0), = (2, 2, 1) образуют базис линейной оболочки L( , )

Подберите правильный ответ

Верны ли утверждения?

А) Выражение a + bi называется алгебраической формой записи комплексного числа

В) Модуль комплекстного числа z = 1 – i равен |z| = 0

Подберите правильный ответ

Верны ли утверждения?

А) Гипербола – это геометрическое место точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная

В) Гипербола – это геометрическое место точек плоскости, модуль разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная

Подберите правильный ответ

Верны ли утверждения?

А) Две плоскости перпендикулярны, если скалярное произведение их нормальных векторов равно нулю

В) Две плоскости параллельны, если их нормальные векторы коллинеарны

Уравнение плоскости, виды уравнения плоскости

В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.

Определение уравнения плоскости

Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.

Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.

Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.

Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.

Общее уравнение плоскости

Сформулируем теорему, а затем запишем уравнение плоскости.

Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве

Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.

Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ – это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.

Общим уравнениям плоскости x – 2 · y + 3 · z – 7 = 0 и – 2 · x + 4 · y – 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.

Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .

Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.

Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.

Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y – 5 · z + 1 = 0 .

Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x – y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.

Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.

Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.

Нормальное уравнение плоскости

Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .

Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z – p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ – это направляющие косинусы нормального вектора данной плоскости единичной длины.

n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1

То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.

Плоскость задана общим уравнением плоскости вида – 1 4 · x – 3 4 · y + 6 4 · z – 7 = 0 . D = – 7 ≤ 0 , нормальный вектор этой плоскости n → = – 1 4 , – 3 4 , 6 4 имеет длину, равную единице, так как n → = – 1 4 2 + – 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.

Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.

Уравнение плоскости в отрезках

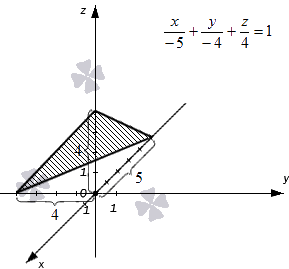
Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.

Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x – 5 + y – 4 + z 4 = 1 .

Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.

Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x – 5 + y – 4 + z 4 = 1 .

Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.

[spoiler title=”источники:”]

http://testserver.pro/kb/index/4007?p=10

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-ploskosti-vidy-uravnenija-ploskosti/

[/spoiler]

Левая часть	Правая часть

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из которых выбрано направление и единичный отрезок, то говорят, что задана прямоугольная система координат в пространстве.

Прямые с выбранными на них направлениями называются осями координат и обозначаются так: Ох, Оy, Оz, имеют свои названия: ось абсцисс, ось ординат и ось аппликат соответственно, а их общая точка – началом координат. Обычно она обозначается буквой О.

Вся система координат обозначается Охуz.

Если через оси координат Ох и Оу, Оу и Оz, Оz  и Ох провести плоскости,  то такие плоскости будут называться координатными плоскостями и обозначаться: Оху, Оуz, Оzх соответственно.

Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч — отрицательной полуосью.

В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами. Они определяются аналогично координатам точек на плоскости.

 Посмотрим, как это делается.

Проведем через точку М три плоскости, перпендикулярные осям координат, и обозначим через М₁, М₂ и М₃ точки пересечения этих плоскостей соответственно с осями абсцисс, ординат и аппликат.

Первая координата точки М (она называется абсциссой и обозначается обычно буквой х) определяется так: х = ОМ₁, если М₁ – точка положительной полуоси;

х= – ОМ₁, если М₁ – точка отрицательной полуоси; х =0, если М₁ совпадает с точкой О.

Аналогично с помощью точки М₂ определяется вторая координата (ордината) у точки М,

а с помощью точки М₃ — третья координата (аппликата) z точки М.

Координаты точки М записываются в скобках после обозначения точки М (х; у; z).

Запомните, что  первой указывают абсциссу, второй – ординату, третьей — аппликату.

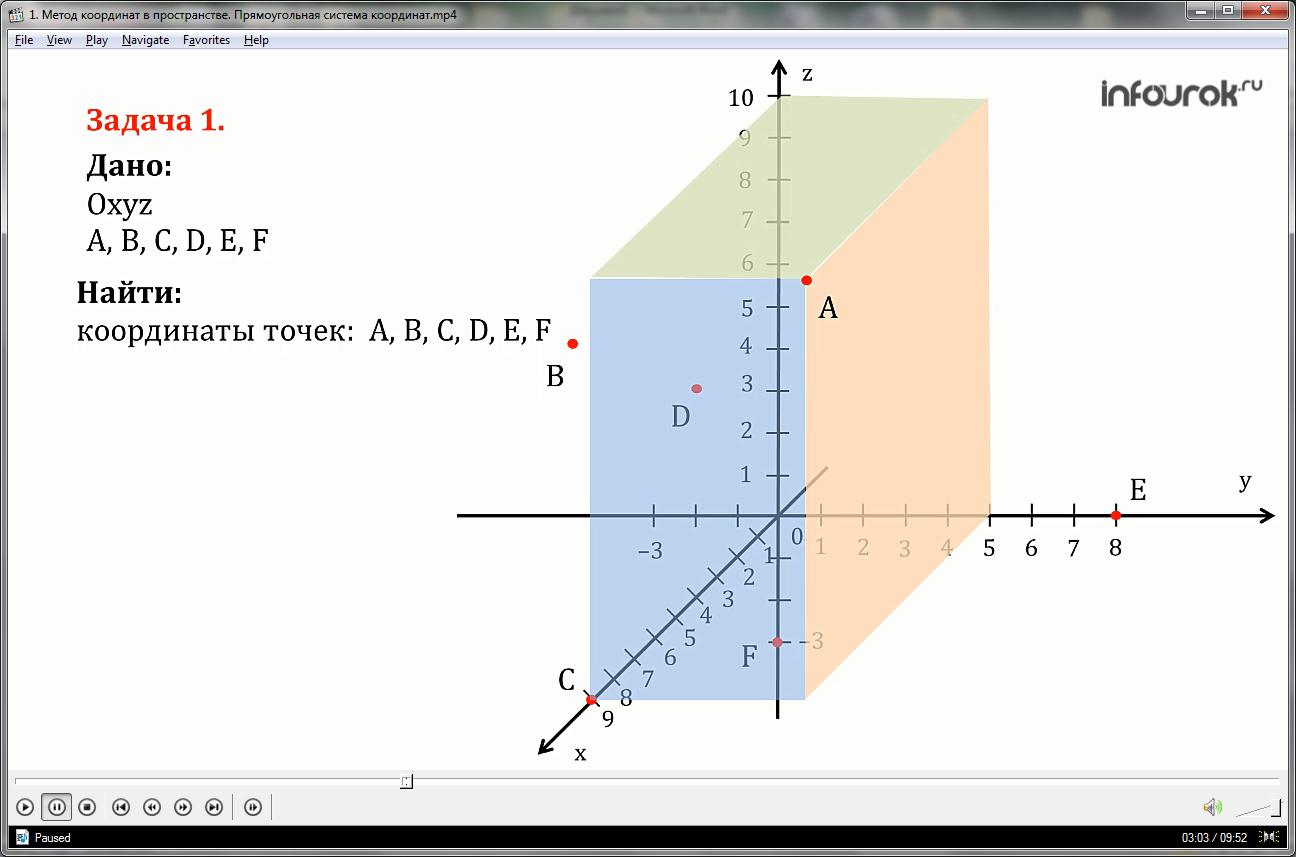
Задача 1.

Найдем координаты точек А, В, С, D, E, F, представленные на рисунке.

Проведем через точку А три плоскости, перпендикулярные к осям координат, тогда  точки пересечения этих плоскостей соответственно с осями абсцисс, ординат и аппликат будут координатами точки А. Точка А имеет координаты: абсцисса = 9, ордината = 5, аппликата = 10 и записывается это так: А (9; 5;10).

Аналогично записываются координаты следующих точек:

 Точка В имеет координаты: абсцисса = 4, ордината = -3, аппликата = 6 

Точка С имеет координаты: абсцисса = 9, ордината = 0, аппликата = 0

Точка  имеет D  координаты: абсцисса = 4, ордината = 0, аппликата = 5 

Точка Е имеет координаты: абсцисса = 0, ордината = 8, аппликата = 0

Точка F имеет координаты: абсцисса = 0, ордината = 0, аппликата = -3  

В (4; -3; 6),

С (9; 0; 0),

D (4; 0; 5),

Е (0; 8; 0),

F (0; 0; -3).

Если точка М (х; у; z) лежит на координатной плоскости на оси координат, то некоторые ее координаты равны нулю.

Если МЄОху (точка М принадлежит плоскости Оху), то аппликата точки М равна нулю: z=0.

Аналогично, если МЄОхz (точка М принадлежит плоскости Оxz), то у = 0, а если МЄОуz (точка М принадлежит плоскости Oyz), то х = 0.

Если МЄОх (точка М лежит на оси абсцисс) ордината и аппликата точки М равны нулю: у=о и z=0. В нашем примере это точка С.

Если МЄОу (точка М лежит на оси ординат), то х=0 и z=0. В нашем примере это точка Е.

Если МЄОz (точка М лежит на оси аппликат), то х = 0 и у = 0. В нашем примере это точка F.

Если все три координаты точки М равны нулю, то это значит, что М=О (0; 0; 0) – начало координат.

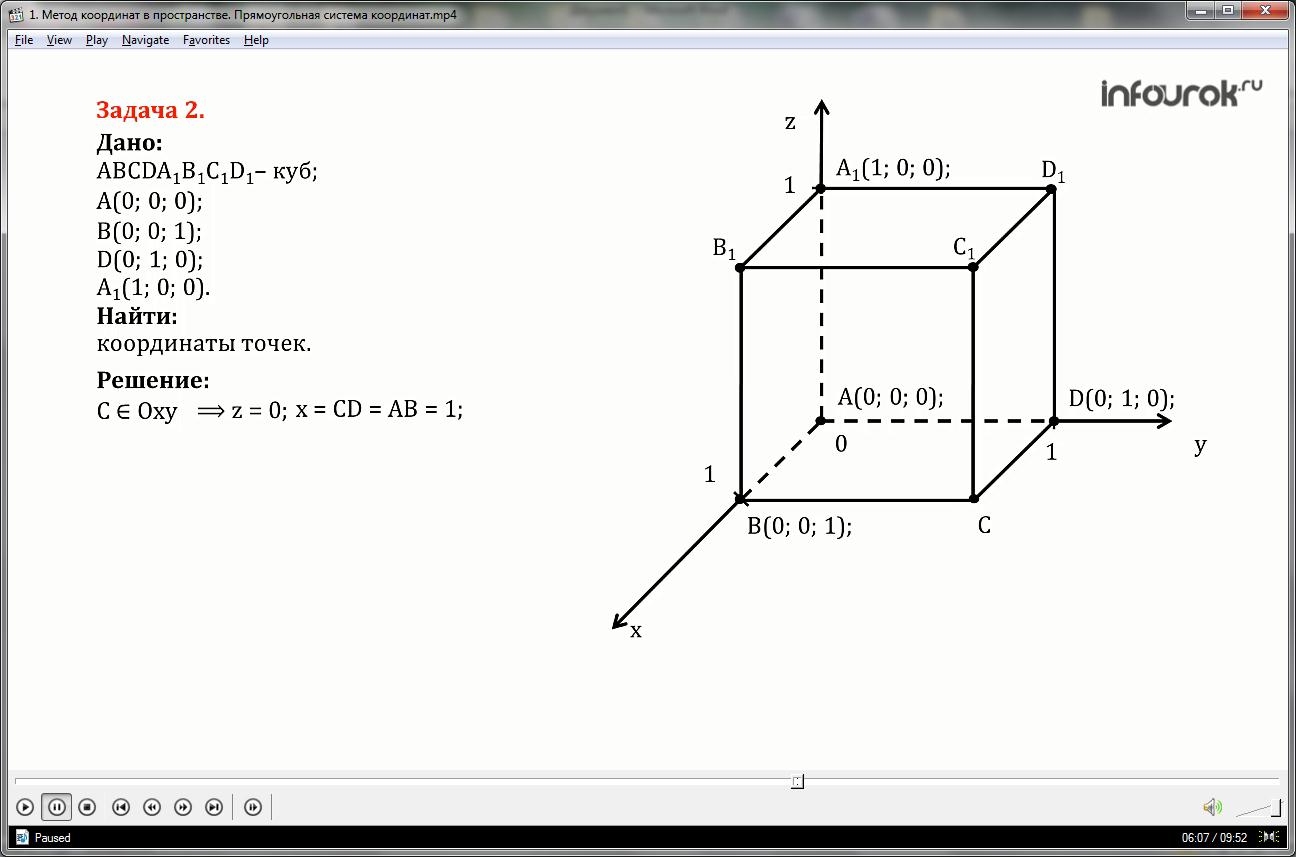
Задача 2

Даны координаты четырех вершин куба ABCDA₁B₁C₁D₁: A(0; 0; 0); B(0; 0; 1); D(0; 1; 0); A₁(1; 0; 0). Найдите координаты остальных вершин куба.

Решение:

Так как фигура — куб, то все стороны равны единице, все грани являются квадратами.

Точка С принадлежит плоскости Оху, то есть ее координата z равна нулю, координата х равна стороне СД и равна АВ, значит равна единице, координата игрек равна стороне куба СВ, значит равна АД и равна единице.

Аналогично, Точка В₁ принадлежи плоскости Охz, то еcть ее координата y равна нулю, координата х равна стороне координата х равна стороне А1B1 и равна АВ значит равна единице, координата зет равна стороне куба В В1значит равна АА1 и равна единице.

Точка Д₁ принадлежи плоскости Оуz, то еcть ее координата х равна нулю, координата у равна стороне А₁Д₁ и равна АД, значит равна единице, координата зет равна стороне куба А₁В₁ , значит равна АВ и равна единице.

Точка С₁ не принадлежит никакой плоскости, то еcть все координаты отличны от нуля, координата х равна стороне C₁D₁ и равна АB, значит равна единице, координата игрек равна стороне куба В₁С₁ , значит равна АД и равна единице, и координата зет равна стороне CC₁ , то есть AA₁ и также равна единице.

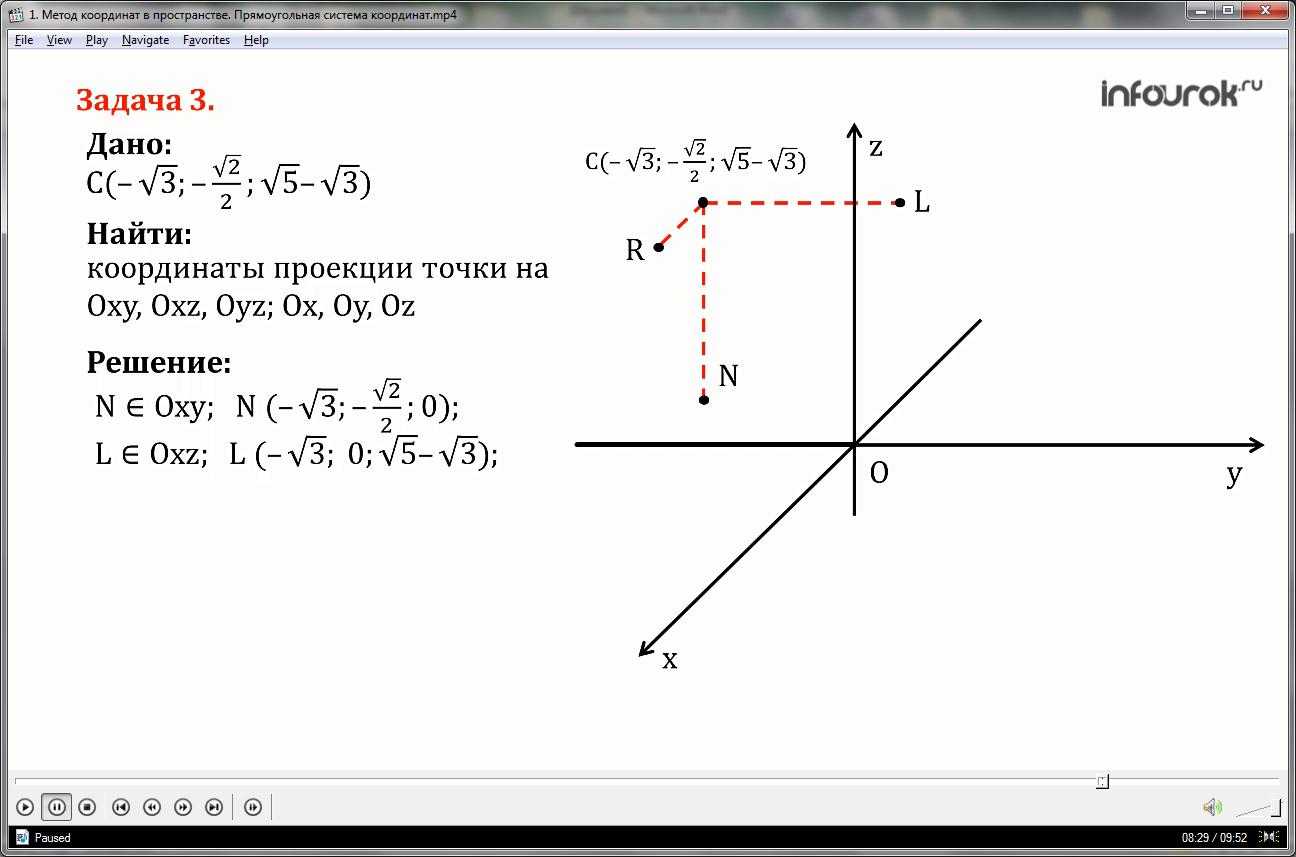
Задача 3.

Найдите координаты проекций точки C(; ; ) на координатные плоскости Oxy, Oxz, Oyz и координатные оси Ox, Oy, Oz.

Решение:

1) опустим перпендикуляры на плоскость Oxy— это CN, на плоскость Oxz – CL, и на плоскость Oyz прямая CR.

Таким образом, проекция точки С на плоскость Oxy это точка N и она имеет координаты икс равный минус корень из трех, игрек равен минус корень из двух на два, зет равнен нулю.

Проекция точки С на плоскость Oxz – это точка L и она имеет координаты икс равен минус корень из трех, игрек равен нулю, зет равен корень из пяти минус корень из трех.

 Проекция точки С на плоскость Oyz– это точка R и она имеет координаты икс равен нулю, игрек равен минус корень из двух на два, зет равен корень из пяти минус корень из трех.

2)Из точки N проводим перпендикуляры на ось Ох – прямая NK, а на Оу – прямая NG, и на ось Оz проводим перпендикуляр из точки R– это прямая RP.

Проекция точки С на ось Ох – точка К имеет координаты икс равный минус корень из трех, а игрек и зет равны нулю.

Проекция точки С на ось Оy– точка G имеет координаты икс и зет равны нулю, игрек равен минус корень из двух на два.

Проекция точки С на ось Оz– точка P имеет координаты икс и игрек равны нулю, зет равный корень из пяти минус корень из трех.

Решение типовых задач по теме “Задание плоскости в пространстве”. Часть 3
Задача №1. Даны две параллельные плоскости 3x + 4y-2z-1=0 и 6x+8y-4z-3=0.
Найти среднюю плоскость (т.е. параллельную данным плоскостям и расположенную между ними на равных расстояниях от них).
Решение. Пусть точка принадлежит искомой плоскости. Определим ее отклонение от каждой из данных плоскостей по формуле:

Так как точка М лежит между данными плоскостями, а плоскости расположены по одну сторону от начала координат.
, то отклонения и будут противоположных знаков:

— искомое уравнение.
Ответ: .
Задача №2. Найти плоскость, параллельную двум данным параллельным плоскостям
2х+3y-z-1=0 и 4x+6y-2z+3=0 и делящую расстояние между ними в отношении 2:3.
Решения задач №1 и №2 подробно изложены в следующем видео

Задача №3. Найти плоскость, проходящую через точку (2;-1;1) перпендикулярно к линии пересечения двух плоскостей: 3x-y-z+1=0, x-y+2z+1=0.
Задача №4. На оси Ох найти точку, равноудаленную от точки М(0;1;-2) и от плоскости бх+Зy-2z-9=0.
Решение. Точка, лежащая на оси Ох, имеет ординату и аппликату, равными 0. Таким образом, искомая точка N(х;0;0). Ее расстояние до точки М:
ее расстояние до плоскости:

Согласно условию Имеем:

Условию удовлетворяют две точки:
Ответ:
Решения задач №3 и №4 подробно изложены в следующем видео

Задача №5. Найти геометрическое место точек, отклонения которых от плоскости 12x-15y+16z-10=0 равно ±5.
Решение. Возьмем произвольную точку М(x;у;z) и определим ее отклонение до данной плоскости:

Согласно условию это отклонение равно ±5. Получим два уравнения:

или после упрощения

Мы получили две плоскости, параллельные данной плоскости и расположенные по разные стороны от нее на расстоянии 5 единиц.
Ответ:
Задача №6. Составить уравнение геометрического места точек, равноудаленных от двух параллельных плоскостей: x-5y+3z+5=0 и 2х-10y+6z+9=0.
Решения задач №3 и №4 подробно изложены в следующем видео

Задача №7. Составить уравнения плоскостей, делящих по¬полам двугранные углы, образованные двумя пересекающимися плоскостями: 5x-2y+5z-3=0 и 2x+y-7z+2=0.
Задача №8. Определить, лежат ли точки М(1;2;-1) и N(-3;1;2) в одном, в смежных или вертикальных двугранных углах, образованных при пересечении двух плоскостей:
1) 2х-3y+z-3=0, х-у-2z+4=0;
2) 5х-2y+z-1=0, 6x-Зу+2z-1=0;
3) 3х+у+ 11z-3=0, 4х+2y-5z+1=0.
Решения задач №5 и №6 подробно изложены в следующем видео

Задача №9. Установить, какие из следующих пар плоскостей пересекаются, параллельны или совпадают:
1) Зх+у-5z-12=0 и 2x+6z-3=0;
2) 2х-Зу+z+8=0 и 4х-6у-Зz-7=0;
3) 5х+2у-3z-5=0 и 10x+4y-6z+5=0;
4) Зx+7y+z+4=0 и 9x+21y+3z+12=0.
Задача №10. Даны уравнения трех граней параллелепипеда x-3y+4z-12=0, y+2z-5=0, x+4=0, и одна из его вершин (4;-3;2). Найти уравнения трех других граней параллелепипеда.
Решения задач №7 и №8 подробно изложены в следующем видео