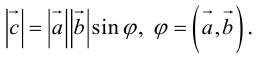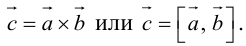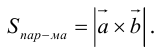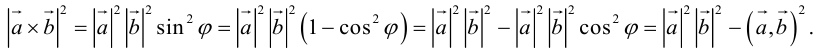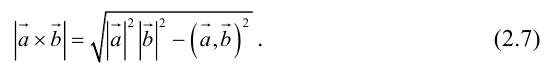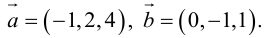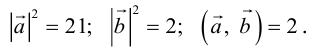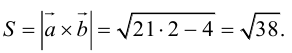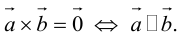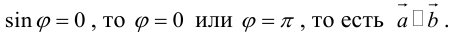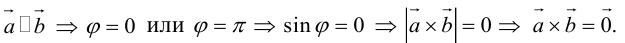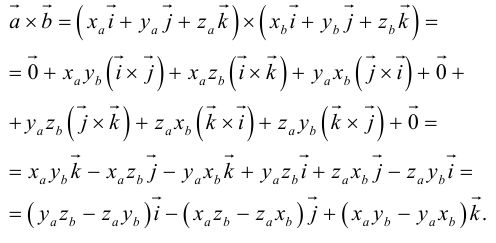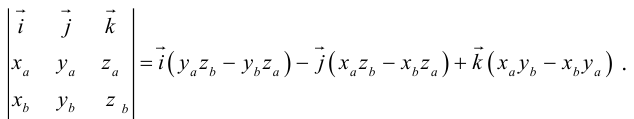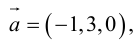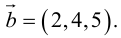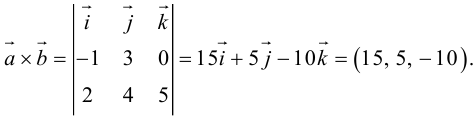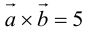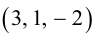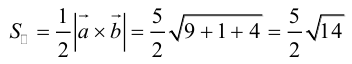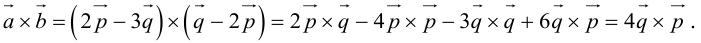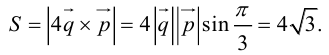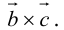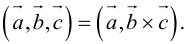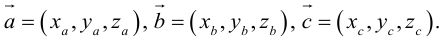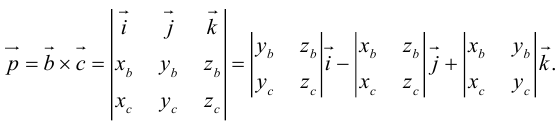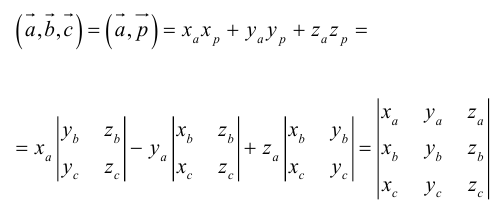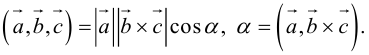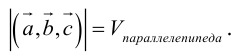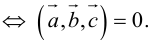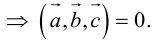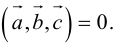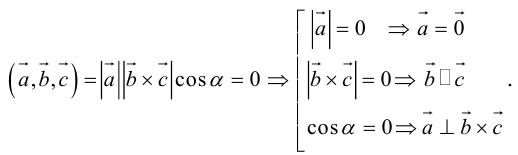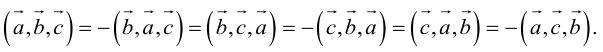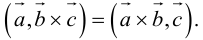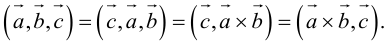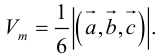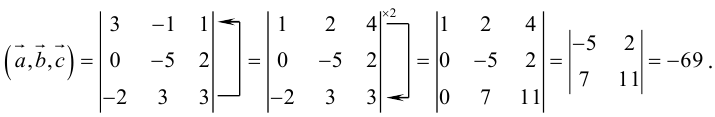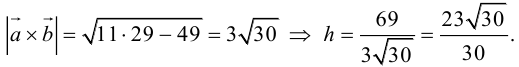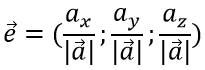Раздел 2. Векторная алгебра
Абсолютная величина вектора см. Модуль вектора.
Абсцисса – первая координата вектора или точки в декартовой системе координат.
Антикоммутативное свойство (Антикоммутативность) векторного произведения двух векторов: при перестановке сомножителей векторное произведение меняет знак на противоположный, т.е. a´b = – b´a.
Аппликата – третья координата вектора или точки в декартовой системе координат.
Базис n-мерного векторного пространства (Базисные векторы) – совокупность n линейно независимых векторов этого пространства, линейными комбинациями которых можно представить любой вектор пространства.
См. Ортонормированный базис.
Базис трехмерного пространства (Базис в пространстве) – упорядоченная тройка некомпланарных векторов.
Базис на плоскости – упорядоченная пара неколлинеарных векторов.
Базисные векторы см. Базис n-мерного пространства.
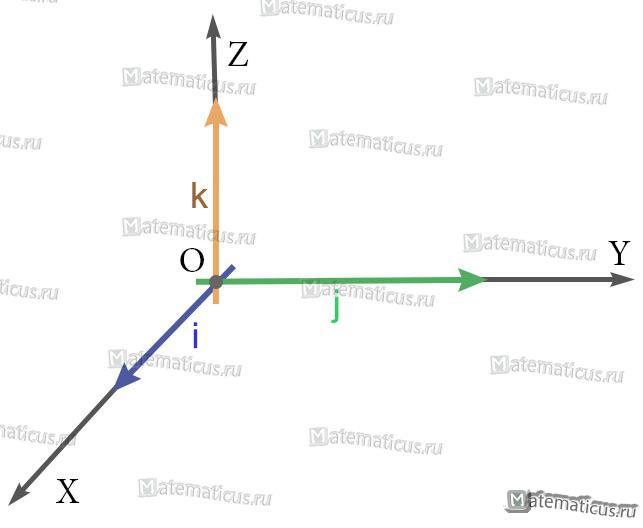
Базисные векторы декартовой прямоугольной системы координат – единичные ортогональные векторы i, j на плоскости и единичные попарно ортогональные векторы i, j, k в пространстве.
Вектор (Векторная величина, геометрический вектор) – направленный отрезок прямой. Пояснение. Вектор является величиной, полностью определенной своим направлением и длиной. Обозначение: a, 
См. Единичный, нулевой, свободный, связанный вектор; коллинеарные, компланарные, линейно зависимые, линейно независимые векторы.
Векторная алгебра – раздел математики, изучающий алгебраические операции над векторами.
Векторная величина см. Вектор.
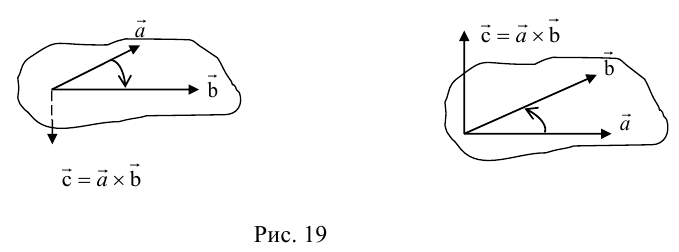
Векторное произведениедвух векторов a и b – вектор c, определяемый следующими тремя условиями:
а) модуль вектора c, численно равен площади параллелограмма, построенного на векторах a и b как на сторонах, т.е. |c| = |a|×|b|×sin j, где j = Ð(a,b);
б) вектор c ортогонален векторам a и b;
в) вектор c направлен так, что векторы a, b, c образуют правую тройку.
Обозначения: a´b = c, [a, b] = c, [ab] = c.
Векторно-скалярное произведение векторов см. Смешанное произведение векторов.
Вектор-столбец – запись вектора, при которой его координаты располагаются вертикально.
Вектор-строка– запись вектора, при которой его координаты располагаются горизонтально.
Геометрический вектор см. Вектор.
Граничные точки отрезка см. Концевые точки отрезка.
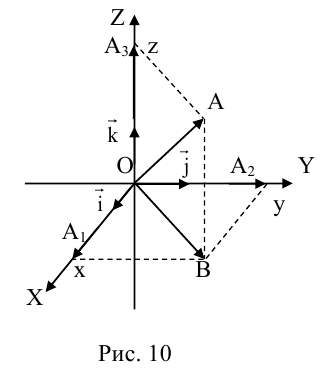
Декартова прямоугольная система координат в пространстве– система координат, заданная тремя взаимно ортогональными единичными векторами, называемыми ортами.
Декартова прямоугольная система координат на плоскости– система координат, заданная двумя взаимно ортогональными единичными векторами, называемыми ортами.
Декартовы координаты вектора– проекции вектора на оси координат декартовой системы координат.
Длина вектора см. Модуль вектора.
Единичный вектор – вектор, модуль которого равен единице.
Обозначение: a o , e. См. Орт.
Квадрант – одна из четырех областей, на которые плоскость делится двумя взаимно перпендикулярными прямыми.
Коллинеарность векторов– свойство векторов быть коллинеарными.
Коллинеарные векторы – векторы, расположенные на одной прямой или на параллельных прямых. Обозначение: a||b.
Компланарность– свойство векторов быть компланарными.
Компланарные векторы– векторы, расположенные в одной плоскости или в параллельных плоскостях.
Компонента см. Координата.
Концевые точки отрезка(Граничные точки отрезка) – точки, между которыми заключен отрезок прямой.
Координата (компонента, составляющая) вектора в декартовой системе координат – проекция вектора на соответствующую ось координат.
Координатная плоскость – плоскость, проходящая через две координатные оси из трех.
Координатные оси (Оси координат) – числовые прямые, имеющие общую нулевую точку (начало координат).
Координаты точки – 1) числа, определяющие положение точки на плоскости или в пространстве; 2) координаты радиус-вектора этой точки.
Левая тройка векторов – тройка векторов, не являющаяся правой.
Линейная комбинация n векторов – сумма произведений этих векторов на произвольные скаляры (числа), называемые коэффициентами:
Линейно зависимые векторы – векторы, линейная комбинация которых равна нулю, если не все коэффициенты равны нулю.
Линейно независимые векторы – векторы, линейная комбинация которых равна нулю только при условии, когда все коэффициенты равны нулю.
Линейные операции над векторами – это операции сложения векторов и умножения вектора на число.
Многогранник (Многогранная поверхность) – поверхность, образованная из многоугольников (граней поверхности) так, что каждая сторона любого из этих многоугольников (ребро поверхности) является стороной еще одного многоугольника.
Многоугольник – замкнутая ломаная линия на плоскости.
Модуль вектора (Длина вектора, Абсолютная величина вектора) – число, равное расстоянию между его началом и концом. Обозначение: |a|, | 
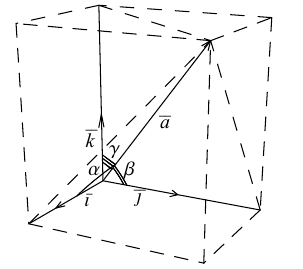
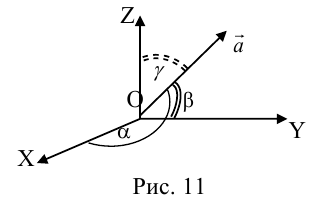
Направляющий косинус вектора– косинус соответствующего направляющего угла.
Направляющий угол вектора– угол, образуемый вектором и соответствующей осью координат декартовой системы.
Начало координат– точка пересечения координатных осей, являющаяся началом отсчета. Обозначение: O.
Нулевой вектор– вектор, модуль которого равен нулю.
Пояснение. Начало и конец нулевого вектора совпадают. Обозначение: o.
Объем тела – мера пространственных тел, не меняющая своего значения при движении тела и равная единице на единичном кубе.
Октант – одна из восьми областей, на которые трехмерное пространство делится тремя взаимно перпендикулярными плоскостями.
Ордината– вторая координата вектора или точки в декартовой системе координат.
Ориентация векторов– взаимное расположение трех векторов в пространстве; три вектора могут быть с правой или левой ориентацией. Такие векторы образуют правую или левую тройку векторов соответственно.
См. Правая тройка векторов.
Орт – единичный вектор, направление которого совпадает с направлением вектора a. Обозначение: a o .
Ортогональность– свойство векторов быть ортогональными.
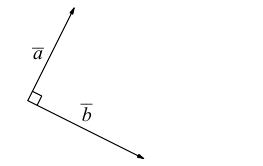
Ортогональные векторы– 1) векторы, угол между которыми является прямым; 2) векторы, скалярное произведение которых равно нулю.
Ортонормированный базис – базис векторного пространства, образованный единичными попарно ортогональными векторами.
Острый угол между векторами– угол, значение которого меньше 90 о .
Оси координат см. Координатные оси.
Ось– прямая, на которой указаны начало отсчета, единица и положительное направление.
Ось абсцисс (Ось x) – первая ось в декартовой системе координат на плоскости или в пространстве.
Ось аппликат (Ось z) – третья ось в декартовой системе координат в пространстве.
Ось ординат (Ось y) – вторая ось в декартовой системе координат на плоскости или в пространстве.
Отрезок прямой(Отрезок) – часть прямой, заключенная между двумя ее точками и включающая обе эти точки.
Параллелепипед– призма, основаниями которой являются параллелограммы.
Параллелограмм – плоский четырехугольник, противоположные стороны которого попарно параллельны.
Параллельный перенос (сдвиг) – перемещение фигуры, при котором каждая точка перемещается на один и тот же вектор.
Параллельный сдвиг см. Параллельный перенос.
Пирамида– многогранник, одной их граней которого является многоугольник (обычно это основание), а остальные грани – треугольники с общей вершиной.
Площадь плоской фигуры – неотрицательная функция геометрической фигуры на плоскости, сохраняющая свое значение при движениях и удовлетворяющая условию, что единичный квадрат имеет площадь, равную единице.
Полный угол – угол, равный 360 о .
Правая (Правоориентированная) тройка векторов – три некомпланарных вектора, удовлетворяющих условиям:
1) они упорядочены, и третий вектор направлен по направлению осевого движения правого винта при повороте по наименьшему углу от первого вектора ко второму;
2) они упорядочены и наблюдателю, находящемуся внутри телесного угла, образованного этими векторами, кратчайшие повороты от первого вектора ко второму и от второго к третьему кажутся происходящими против часовой стрелки;
3) они упорядочены и из конца третьего вектора кратчайший поворот от первого вектора ко второму виден совершающимся против часовой стрелки.
Пояснение. Приведены три равносильных условия (определения) правой тройки векторов.
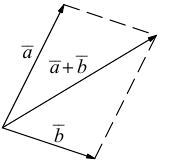
Правило параллелограмма– графическое правило образования суммы двух векторов.
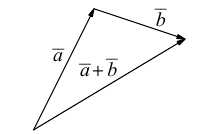
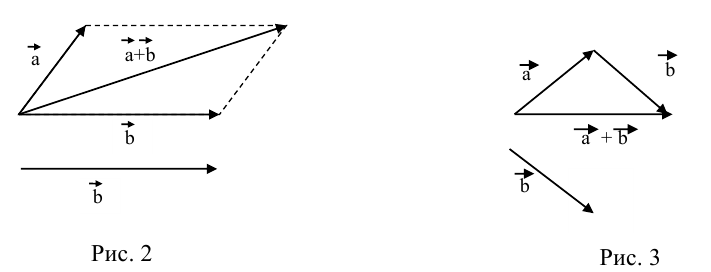
Правило треугольника– графическое правило образования суммы двух векторов.
Призма – многогранник, две грани (основания) которого – равные многоугольники, лежащие в параллельных плоскостях, а остальные грани (боковые грани) – параллелограммы.
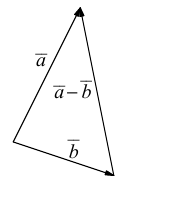
Проекция вектора на вектор– число, равное модулю вектора, проекция которого находится, умноженному на косинус угла между векторами.
Произведение вектора a на скаляр (число) l – вектор, обозначаемый la, такой что:
а) его модуль равен произведению модулей исходного вектора и скаляра, т.е.
|la| = |l|×|a|;
б) новый вектор и исходный вектор коллинеарны, т.е. a || la;
в) векторы a и la сонаправлены, если l > 0, и противоположно направлены, если l o , в радианной мере p/2.
Прямоугольные декартовы координаты – координаты, базис которых состоит из попарно ортогональных единичных векторов.
Равные векторы – векторы, являющиеся коллинеарными, одинаково направленными и имеющие равные модули.
Радиус-вектор точки P – вектор 
Развернутый угол – угол, стороны которого составляют одну прямую; в градусной мере равен 180 o , в радианной мере p.
Свободный вектор– множество всех векторов, равных данному вектору, т.е. множество всех векторов с одинаковым модулем и направлением, но с различными начальными точками.
Связанный вектор– вектор с фиксированной начальной точкой.
Скаляр (Скалярная величина) – величина, которая полностью характеризуется одним числом.
Скалярная величинасм. Скаляр.
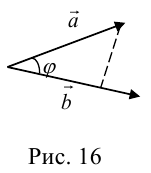
Скалярное произведение двух векторов– число, равное произведению модулей этих векторов на косинус угла между ними.
Обозначение: ab, a×b, (a,b).
Скалярный квадрат– скалярное произведение вектора на самого себя.
Обозначение: a 2 .
Сложение векторовсм. Сумма двух векторов.
Смешанное (Векторно-скалярное) произведение трех векторов – число, полученное по правилу: (a´b)×c), т.е. первые два вектора перемножаются векторно, а результат умножается на третий вектор скалярно. Обозначение: abc, (abc).
Составляющаясм. Координата.
Сумма двух векторов – новый вектор, получаемый по правилу треугольника или параллелограмма. Обозначение: a + b = c.
Тетраэдр– треугольная пирамида, т.е. пирамида, основанием которой является треугольник.
Пояснение. Тетраэдр имеет четыре треугольных грани, шесть ребер и четыре вершины.
Треугольная призма – призма, основания которой – треугольники.
Треугольник– многоугольник, имеющий три вершины и три стороны.
Тупой угол– угол, больший прямого, но меньший развернутого.
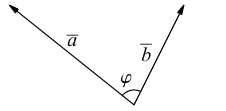
Угол между двумя векторами– наименьший угол, на который нужно повернуть один из векторов до совмещения с другим.
См. Острый, полный, прямой, развернутый, тупой угол.
Умножение вектора на скаляр – операция отыскания произведения вектора на скаляр. Обозначение: la = b.
Упорядоченная тройка векторов – три вектора, если указано, какой из них является первым, какой – вторым и какой – третьим.
Векторное произведение векторов
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
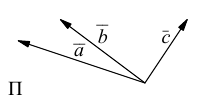
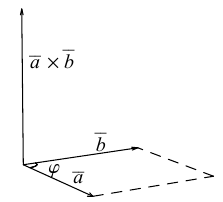
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
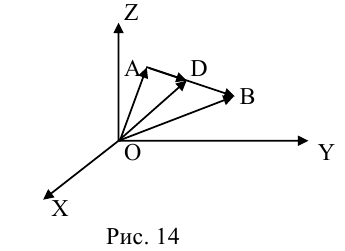
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
- он является нулевым, если векторы →a и →b коллинеарны;
- он перпендикулярен и вектору →a и вектору →b;
- длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
- тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a = и b = в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:
Векторное произведение векторов →a и →b обозначается как [→a • →b].
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
- Антикоммутативность
- Свойство дистрибутивности
Сочетательное свойство
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
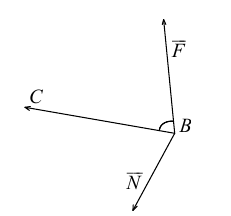
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
3.1.7. Примеры решения задач по теме «Линейные операции над векторами. Скалярное произведение»
Даны векторы А = (-2; 3; 5) и B = (4; -1; 7). Найти координаты вектора
При умножении вектора на число все его координаты
Умножаются на это число, при сложении векторов складываются их соответствующие координаты.
Координаты коллинеарных векторов пропорциональны.
Если A || B, то 
Ответ: 
Найти направляющие косинусы вектора А = <-2; -1; 2>.
Направляющие косинусы являются координатами орта (единичного вектора) данного направления.
Найдем модуль вектора А:
Разделив все координаты вектора А на его модуль, получим координаты орта:
Ответ:
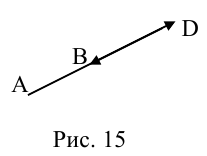
Тогда AA + BB + GC = <2A + B– 3G; –A + B+ G; 3A – B+ 2G>, причем координаты этого вектора должны равняться соответствующим координатам вектора D. Приравнивая эти координаты, получаем систему уравнений для определения A, B, G:
Для векторов A = <1; -2; 3>, B = <-1; 1; -2>, C = <3; 2; 1>, D = < 15; 7; 4>найти такие числа A, B, G, чтобы векторы AA, BB, GC и D образовали замкнутую ломаную линию, если начало каждого последующего вектора совместить с концом предыдущего.
C = <1; -4; 3>линейно зависимой или линейно независимой.
Система векторов называется линейно независимой, если равенство
Вычислим главный определитель Δ системы уравнений
По правилу Крамера система имеет единственное решение, но для однородной системы всегда существует нулевое решение (A = B = G = 0).
Поскольку других решений нет, данная система векторов линейно независима.
Ответ: Система векторов линейно независима.
Найти координаты какого-либо вектора, направленного по биссектрисе угла между векторами А = (-4; 3; 0) и B = (12; -15; 16).
Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.
Вектор A + B направлен по диагонали параллелограмма, построенного на векторах А и B как на смежных сторонах и выходящей из общего начала векторов А и B.
Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.
Следовательно, |5A| = |B|. Значит, параллелограмм со сторонами, совпадающими с векторами 5A и B, является ромбом, поэтому вектор 5A + B будет иметь заданное направление.
При каких значениях X, Y, Z точки А(Х; -1; 3), В(5; -4; Z), C(-2; Y; 9), D(-5; 1; 7) являются вершинами параллелограмма?
Для выполнения условия задачи требуется коллинеарность векторов 



Для выполнения условия задачи требуется коллинеарность векторов 



Найдем координаты этих векторов:
Из последней пропорции получаем, что Z = 1 – 2Y. Тогда
Но при этих значениях неизвестных
Условие задачи выполнено.
Используйте определение скалярного произведения:
Используем свойства скалярного произведения:
По определению скалярного произведения
Сложим левые и правые части полученных равенств:
Даны векторы А = <2; -3; 1>и B = <-1; 2; 1>. Найти скалярное произведение
Найдите координаты векторов 3А – B и A + 2B или используйте свойства скалярного произведения.
Используем свойства скалярного произведения:
Используйте формулу, выражающую косинус угла между векторами через их скалярное произведение.
Ответ: 
Координаты вектора B пропорциональны координатам А. Если K – коэффициент пропорциональности, то B = <2K; -2K; 3K>.
Координаты вектора B пропорциональны координатам А. Если K – коэффициент пропорциональности, то B = <2K; -2K; 3K>.
Известно, что |A| = 2, |B| = 7. Найти значения K, при которых векторы
Если векторы перпендикулярны, то их скалярное произведение равно нулю.
Если векторы перпендикулярны, то их скалярное произведение равно нулю.
Ответ: K = 
Найти проекцию вектора А = <7; 0; -5>на ось, образующую с координатными осями Ох и Оу углы 60о и 45о, а с осью Oz – тупой угол γ.
Используйте свойство направляющих косинусов:
Найдем cosγ: cos260o + cos245o + cos2γ = 1,
Тогда проекция А на заданную ось равна:
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/vektornoe-proizvedenie-vektorov
http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-i-analiticheskaia-geometriia/3-1-7-primery-resheniia-zadach-po-teme-lineinye-operatcii-nad-vektorami-skaliarnoe-proizvedenie
[/spoiler]
Как найти аппликата вектора
Адиль Айжанов
Ученик
(95),
на голосовании
1 год назад
Здравствуйте! Ищу в интернете и не могу найти формулу и нормальное разъяснение что такое аппликата и как её найти. Сама задача:
Заданы координаты точек А(-4, 6, 3), В(-5, -2, 6). Найдите аппликату вектора .
Голосование за лучший ответ
- Основные определения.
- Вектор (геометрический вектор) — это направленный отрезок (отрезок, у которого одна граничная точка считается начальной, другая – конечной).
На чертеже вектор обозначается стрелкой
над буквенным обозначением вектора также ставится стрелка.
Вектор, фигурирующий в определении, носит название связанного, или закрепленного вектора. - Закрепленный вектор
— это направленный отрезок АВ, началом которого является точка А, а концом — точка В.
Свободный вектор — это множество всех закрепленных векторов, получающихся из фиксированного закрепленного вектора с помощью параллельного переноса. Обозначается.
Если же точка приложения вектора (точка A для вектора) может быть выбрана произвольно, вектор называется свободным.
Если точка приложения может двигаться по линии действия вектора, говорят о скользящем векторе. Иначе говоря, свободный вектор является представителем бесконечного множества связанных или скользящих векторов. - Нулевой вектор — это вектор, у которого начало и конец совпадают:
- Коллинеарные векторы — это векторы, которые лежат на одной прямой, либо на параллельных прямых.
Нулевой вектор коллинеарен любому вектору. - Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Если тройка векторов содержит нулевой вектор или пару коллинеарных векторов, то эти векторы компланарны. - Длина вектора (модуль) — это расстояние между началом и концом вектора. Обозначение:
или
- Два вектора равны, если они коллинеарны, имеют одинаковую длину и направление. Например,
- Алгебраические операции над векторами.
- Операция сложения.
Суммой двух свободных векторови
называется свободный вектор
, начало которого совпадает с началом первого, а конец — с концом второго, если совмещены конец вектора
и начало вектора
.
Сумма двух векторови
(
) — это вектор, идущий из начала вектора
в конец вектора
при условии, что начало вектора
приложено к концу вектора
(правило треугольника).
Свойства операции сложения векторов:
1) Переместительное свойство:(коммутативность).
2) Сочетательное свойство:(ассоциативность).
3) Существует нулевой вектор, такой, что
для любого вектора
(особая роль нулевого вектора).
Нулевой векторпорождается нулевым закрепленным вектором, то есть точкой.
4) Для каждого векторасуществует противоположный ему вектор
, такой, что
. Вектор
называется вектором, противоположным вектору
.
Правило параллелограмма (правило сложения векторов): если векторыи
приложены к общему началу и на них построен параллелограмм, то сумма
этих векторов представляет собой диагональ параллелограмма, идущую из общего начала векторов
и
Вычитание векторов определяется через сложение:.
Другими словами, если векторыи
приложены к общему началу, то разностью векторов
и
будет вектор
, идущий из конца вектора
к концу вектора
.
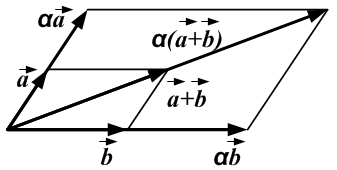
- Операция умножения вектора на число.
Произведением векторана число
называется вектор
такой, что:
1) если λ > 0,≠
, то
получается из
растяжением в λ раз:
;
2) если λ < 0,≠
, то
получается из
растяжением в |λ| раз и последующим отражением:
;
3) если λ = 0 или, то
.
Свойства операции умножения:
1) Распределительное свойство относительно суммы чисел:для любых действительных
и всех
(дистрибутивность).
2) Распределительное свойство относительно суммы векторов:(дистрибутивность).
3) Сочетательное свойство числовых сомножителей:(ассоциативность).
4) Существование единицы:.
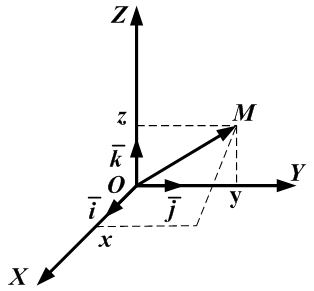
- Ортонормированный базис. Декартова прямоугольная система координат.
- Ортонормированный базис (ОНБ) — это три взаимно перпендикулярных вектора с длинами, равными единице.
Обозначения: - Базисные орты — это векторы
.
- Зафиксированная точка О – это начало координат.
Отложим от точки O векторы.
Полученная система координат — это прямоугольная декартова система координат. - Декартовы координаты вектора — это координаты любого вектора в этом базисе:
Пример 11. - Координатные оси — это прямые линии, проведенные через начало координат (точку O) по направлениям базисных векторов:
– порождает Ox;
– порождает Oy;
– порождает Oz.
- Абсцисса — это координата точки M (вектора
в декартовой системе координат по оси Ox.
Ордината — это координата точки M (векторав декартовой системе координат по оси Oy.
Аппликата — это координата точки M (вектора) в декартовой системе координат по оси Oz.
- Декартовы прямоугольные координаты x, y, z вектора
равны проекциям этого вектора на оси Ox, Oy, Oz, соответственно. Иначе:
где α, β, γ – углы, которые составляет векторс координатными осями Ox, Oy, Oz, соответственно, при этом cosα, cosβ, cosγ называются направляющими косинусами вектора
. Пример 12.
Для направляющих косинусов справедливо соотношение:
- Орт направления — это вектор
единичной длины данного направления.
Формулы, уравнения, теоремы, примеры решения задач
Содержание:
Векторная алгебра
Векторная алгебра – это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая – конечной.
Обозначать векторы мы будем строчными латинскими буквами
Длина отрезка, изображающего вектор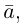
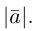
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
Два вектора 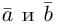
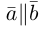
Аналогично, векторы а и b называются ортогональными (обозначение 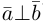
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
Углом между векторами 
Два ненулевых вектора 
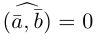
Введем теперь линейные операции над векторами.
а) Умножение числа на вектор.
Произведением действительного числа 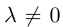
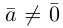
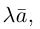
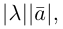
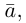
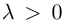
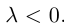
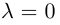
В частности, вектор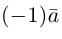
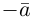
Если 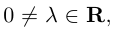
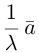
Из приведенного определения сразу же следует, что коллинеарные векторы 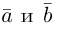
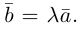
взять число 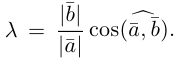
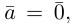
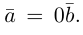
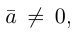
b) Сложение векторов.
Суммой двух векторов 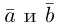
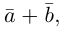
или по равносильному ему правилу параллелограмма
Вектор 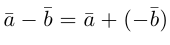
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
Проекцией вектора 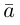
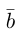
Геометрически очевидны следующие свойства проекции:
Пример №1
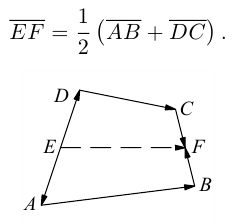
Пусть Е и F – середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
Сложив данные равенства и учитывая, что 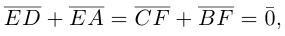
что и требовалось.
Базис и декартова система координат
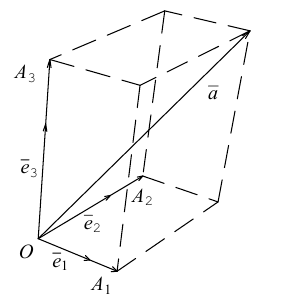
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 
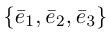
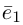
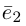
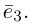
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 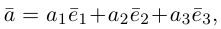
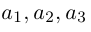
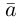
Приведем геометрическое доказательство этого утверждения.
Вектор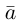
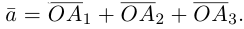
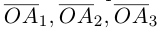
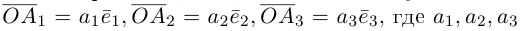
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 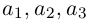
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 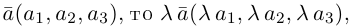
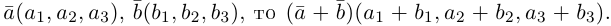
Рассмотрим теперь ортонормированный базис 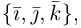
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
Величины 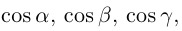
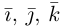
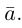
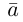
Очевидно также, что
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта 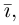
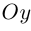
В выбранной системе координат координаты радиуса-вектора 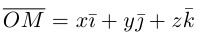
Если известны координаты начальной 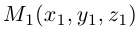
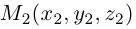
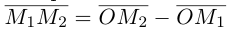
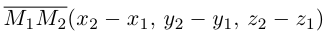
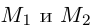
Найдем теперь координаты точки М, делящей отрезок с концами в точках 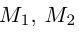
отношении 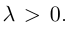
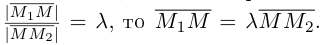
Следовательно, координаты искомой точки вычисляются по формулам:
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
Пример №2
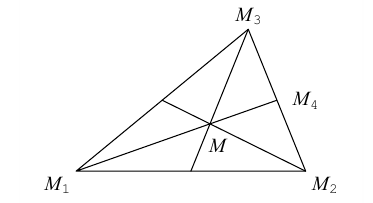
Треугольник задан координатами своих вершин 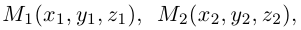
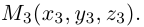
Пусть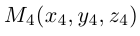
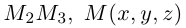
По известному свойству точки пересечения медиан 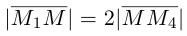
Подставив сюда найденные координаты точки 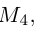
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
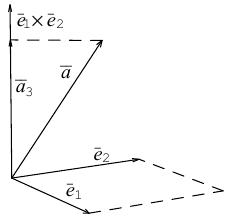
Замечание. Базисом n-мерного пространства 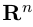
обладающая тем свойством, что любой вектор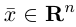
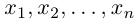
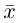
В качестве базиса в 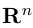
так как, очевидно, любой вектор 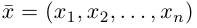
Скалярное произведение векторов
Определение: Скалярным произведением векторов 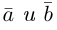
Из этого определения сразу же следует, что
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое – из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе 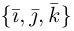
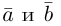
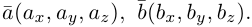
перемножим векторы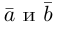
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
Пример №3
Разложить вектор 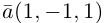
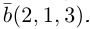
Решение.
Из чертежа следует, что 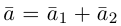
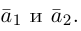
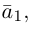
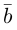
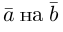
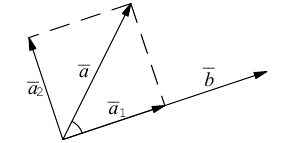
Тогда вторая ортогональная составляющая вектора 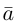
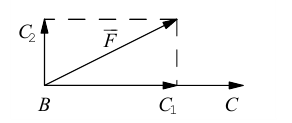
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы 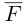
Найдем работу этой силы. Для этого разложим вектор силы 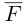
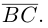
Составляющая 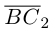
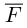
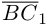
Окончательно, работа силы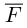
Замечание. Скалярным произведением векторов 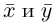
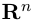
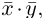
то
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в 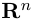
Длиной вектора 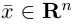
Векторы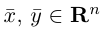
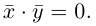
составляют ортонормированный базис пространства 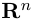
Любой вектор 
n-мерного пространства с координатами
Взяв еще одну точку 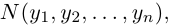
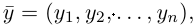
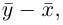
Таким образом переопределенное пространство 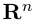
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R”. Точка 0(0,0,… ,0) называется, естественно, началом координат.
Векторное произведение векторов
Определение: Векторным произведением некоялинеарных векторов 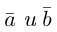

Из этого определения следует, что площадь параллелограмма, построенного на векторах 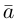
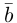

Сформулируем основные свойства векторного произведения.
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы 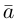
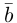
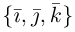
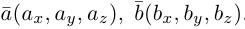
раскроем скобки в векторном произведении 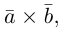
Полученный вектор мы можем записать в виде следующего символического определителя.
вычислять который удобно разложением по первой строке.
Пример №4
Найти составляющую вектора 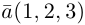
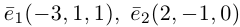
Решение.
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора 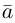

Переходим к вычислениям:
Тогда
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
Итак, пусть сила 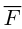
Смешанное произведение векторов
Определение: Смешанным произведением трех векторов 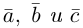
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
По определению смешанного произведения
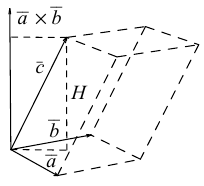
Поскольку 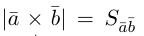
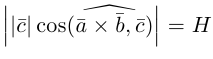
– объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе 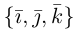
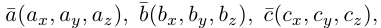
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение 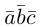
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 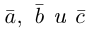
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 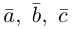
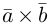
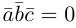
Следствие. Три вектора 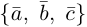
Заметим, кроме того, что, если 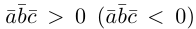
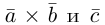
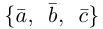
Пример №5
Доказать, что пять точек
расположены в одной плоскости.
Решение. Рассмотрим векторы 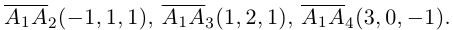
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки 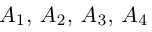
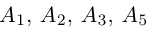
так как первая и третья строки в определителе пропорциональны. Плоскости 
Векторы и линейные операции над ними
Определение: Вектором называется направленный отрезок (рис. 1).
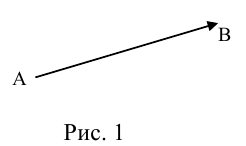
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 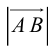
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
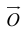
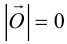
Определение: Векторы 
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
Сложение
а) Правило параллелограмма (рис.2): начала 
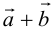
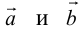
б) Правило треугольника (рис. 3): начало 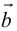
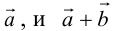
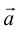
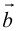
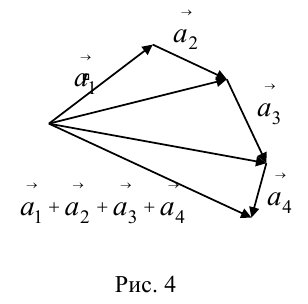
в) Правило сложения нескольких векторов (рис. 4).
Вектор 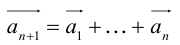
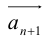
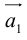
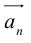
Умножение на число
Определение: Произведением вектора 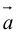
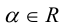
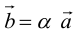
а) 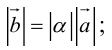
б) 
в)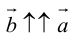
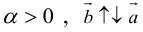
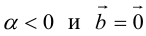
Произведение 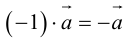
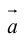
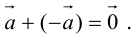
Определение: Разностью 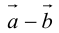
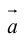
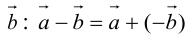
Начала 
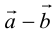
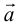
Свойства линейных операций
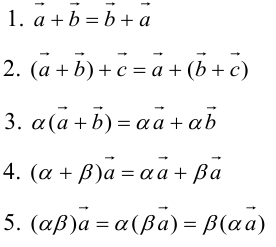
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией: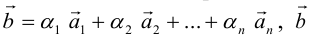
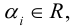
Пример №6
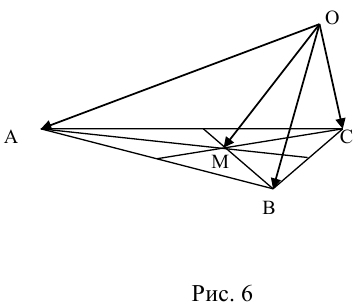
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить 
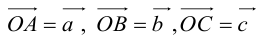
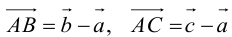
По правилу треугольника 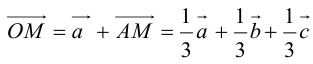
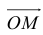
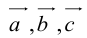
Теорема: Пусть 
где коэффициенты (2.1) определяются единственным образом.
Представление вектора 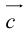
Доказательство:
- Пусть среди
есть два коллинеарных, например:
- Пусть среди
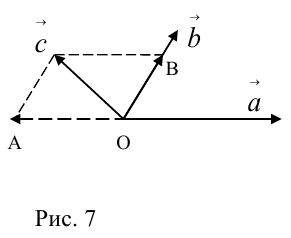
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
, а стороны параллельны прямым, на которых лежат
(рис. 7).
Тогда c 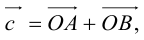
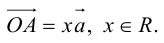
Докажем единственность разложения. Предположим, что 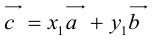
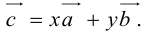
Если 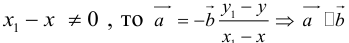
Теорема: Пусть 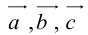
причем единственным образом.
Представление вектора 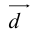
Доказать самостоятельно.
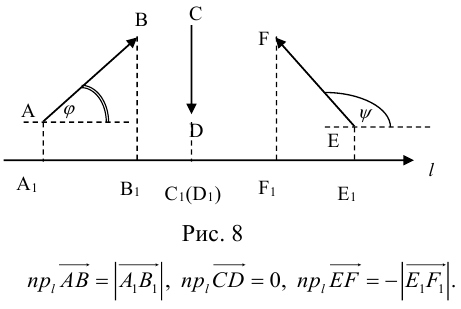
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси 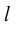
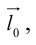
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось 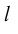
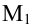
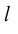
Определение: Ортогональной проекцией вектора 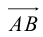
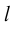
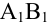
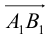
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
Очевидно, проекцию вектора на ось можно найти по формуле
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
В частности, проекция суммы векторов равна сумме их проекций:
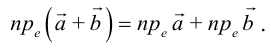
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим 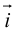
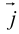

Аналогично в пространственной системе OXYZ 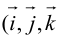
– разложение 
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором 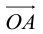
Определение: Координатами вектора 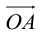
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если 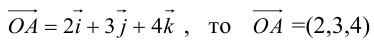
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
Из этих формул очевидно следует основное свойство направляющих косинусов:
Если известны длина 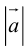
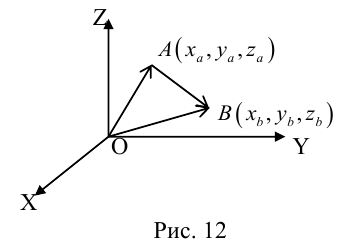
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
Тогда
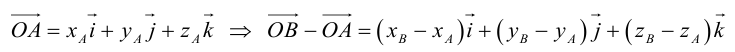
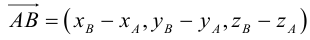
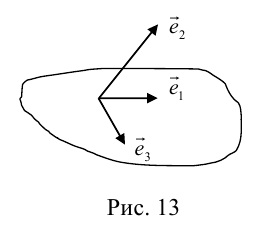
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
Если 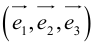
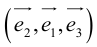
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать
Из теоремы 2 следует, что всякий вектор 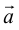
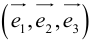
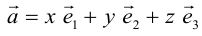
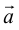
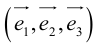
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 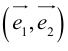
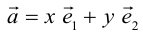
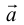
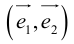
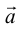
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 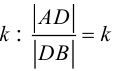
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
Обозначим
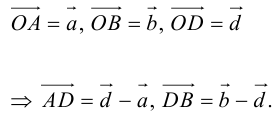
Так как 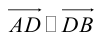
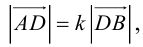
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
ЗАМЕЧАНИЕ 2. Если k < 0, 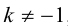
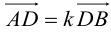
В этом случае
Скалярное произведение векторов
Определение: Скалярным произведением векторов 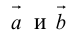
Скалярное произведение обозначается так: 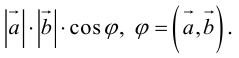
Так как 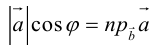
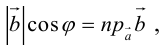
Свойства скалярного произведения
1.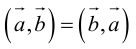
2.
Доказательство:
3.
Доказательство:
а) 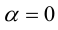
б)
в) 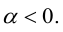
4.
Отсюда следует, что
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.
Доказательство:
а) пусть
б) пусть
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 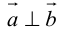
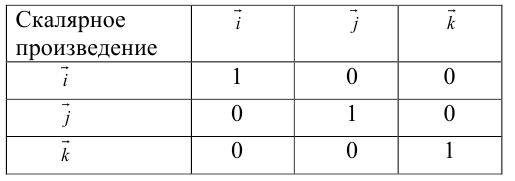
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов
Пусть в некоторой пдск 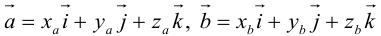
Таким образом,
Пример №8
Найти, при каком значении x векторы 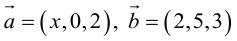
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5):
Пример №9
Найти угол между биссектрисой AD и медианой 
Так как 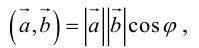
то
Найдем координаты векторов 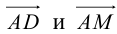
По теореме о биссектрисе внутреннего угла треугольника
Чтобы найти k , вычислим длины AC и AB :
Разделим отрезок CB в данном отношении по формулам (2.3):
отсюда
Заметим, что 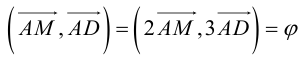
Пример №10
Найти
Воспользуемся свойствами 1–4 скалярного произведения:
Отсюда
ЗАМЕЧАНИЕ. Так как работа силы 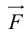
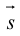
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов 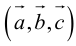
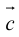
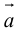
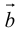
Определение: Векторным произведением вектора 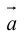
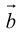
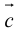
(
перпендикулярен плоскости векторов
и
).
- Направление
таково, что тройка
– правая.
Векторное произведение обозначается так:
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
Пример №11
Найти площадь параллелограмма, построенного на векторах
По формуле (2.7):
ЗАМЕЧАНИЕ 2. Направление вектора 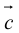
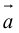
Свойства векторного произведения
1.
Доказательство:
а)пусть 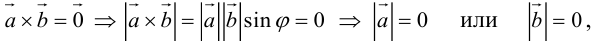
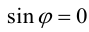
Его направление не определено, поэтому можно считать, что 
б)пусть
2. 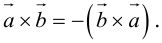
Доказательство: По определению направления векторов 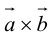
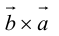
3.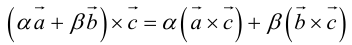
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов 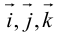
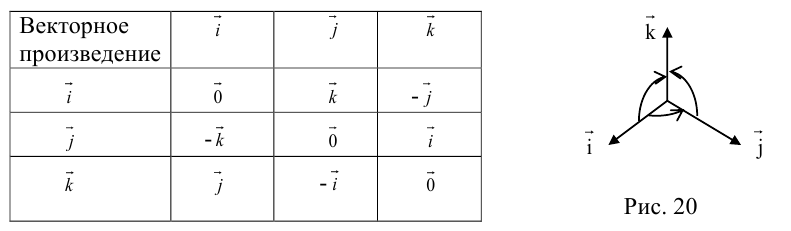
Пусть в некоторой пдск 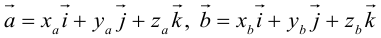
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
Таким образом,
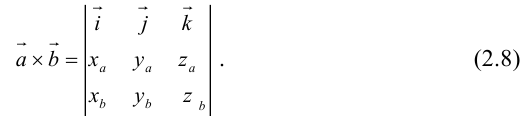
Пример №12
Вычислить векторное произведение векторов
По формуле (2.8):
Заметим, что площадь треугольника, построенного на векторах 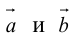
или
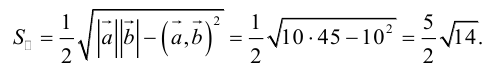
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 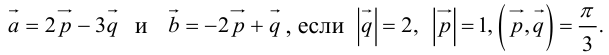
Так как 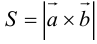
Отсюда
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов 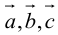
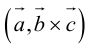
Смешанное произведение обозначается так:
Пусть в некоторой пдск
Обозначим
Тогда
по 7 свойству определителей.
Таким образом,
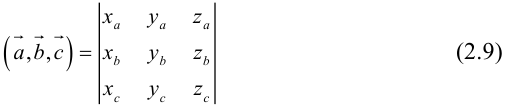
По определению скалярного произведения
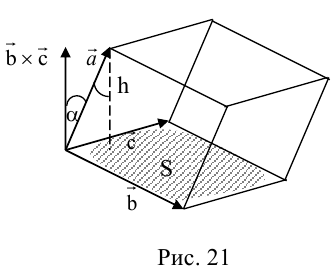
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
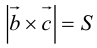
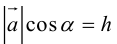
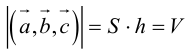
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 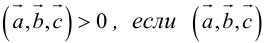
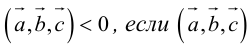
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 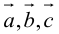
Доказательство: а) 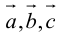
Если 
б)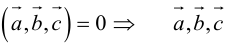
Во всех трех случаях 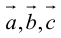
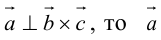
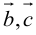
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами:
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим:
4. Смешанное произведение линейно по каждому из трех сомножителей.
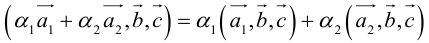
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
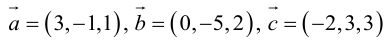
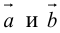
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому
Отсюда 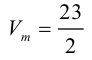

Чтобы найти высоту, воспользуемся формулой
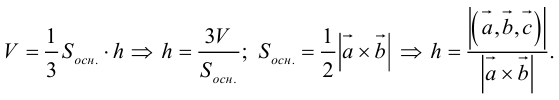
По формуле (2.7)
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.
i — единичный вектор оси абсцисс;
j — единичный вектор оси ординат;
k — единичный вектор оси аппликат.
i⊥j⊥k, i=j=k=1
В прямоугольной системе координат в пространстве координаты векторов равны:
i(1;0;0);j(0;1;0); k(0;0;1);
Замечание 1
Единичные векторы являются некомпланарными.
Замечание 2
Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.
a=xi+уj+zk
где x, y, z — координаты вектора проекции на соответствующие координатные оси.
Эта формула называется разложением вектора по ортам координатных осей.
Единичный вектор определяется по формуле:
Пример
Дан вектор а = (1; 2; -2)
Требуется найти длину (модуль) и единичный вектор e направления вектора а
Решение
Находим длину вектора a
$left| {vec a} right| = sqrt {{1^2} + {2^2} + {{left( { — 2} right)}^2}} = 3$
затем вычисляем единичный вектор e
$vec e = left( {frac{1}{3};frac{2}{3}; — frac{2}{3}} right)$
Векторное произведения единичных векторов
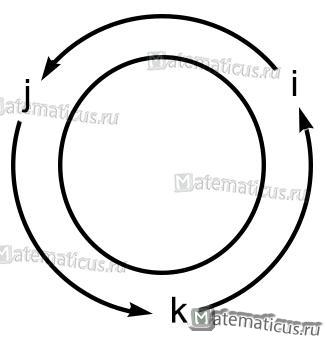
Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус». Смотрите схему 1.
Схема 1
На основании схемы получаем таблицу векторного произведения единичных векторов
i×i=0 i×j=k i×k=-j
j×i=-k j×j=0 j×k=i
k×i=j k×j=-i k×k=0
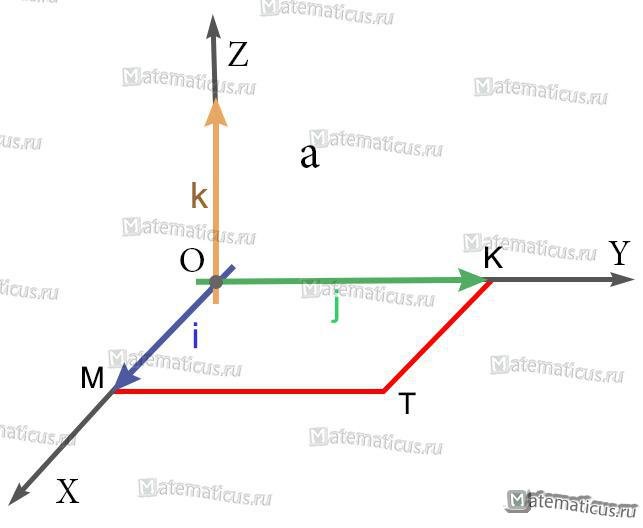
Пример 1
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.
Решение
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).
iхj=k
Пример 2
Найти векторное произведение jхi.
Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k
20798





















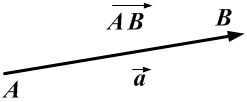
 .
. — это направленный отрезок АВ, началом которого является точка А, а концом — точка В.
— это направленный отрезок АВ, началом которого является точка А, а концом — точка В. .
.
 или
или 

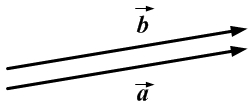
 называется свободный вектор
называется свободный вектор  , начало которого совпадает с началом первого, а конец — с концом второго, если совмещены конец вектора
, начало которого совпадает с началом первого, а конец — с концом второго, если совмещены конец вектора  ) — это вектор, идущий из начала вектора
) — это вектор, идущий из начала вектора 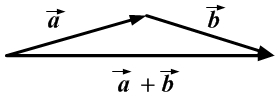
 (коммутативность).
(коммутативность). (ассоциативность).
(ассоциативность). , такой, что
, такой, что  для любого вектора
для любого вектора  , такой, что
, такой, что  . Вектор
. Вектор  называется вектором, противоположным вектору
называется вектором, противоположным вектору  этих векторов представляет собой диагональ параллелограмма, идущую из общего начала векторов
этих векторов представляет собой диагональ параллелограмма, идущую из общего начала векторов 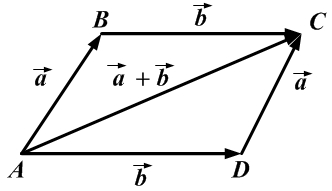
 .
. , идущий из конца вектора
, идущий из конца вектора 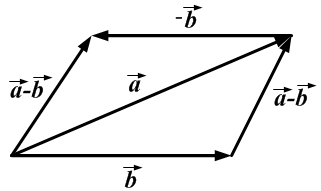
 называется вектор
называется вектор  такой, что:
такой, что: ≠
≠  , то
, то  получается из
получается из  ;
; ;
; , то
, то  .
. для любых действительных
для любых действительных  и всех
и всех  (дистрибутивность).
(дистрибутивность). (ассоциативность).
(ассоциативность). .
.

 .
.
 – порождает Ox;
– порождает Ox; – порождает Oy;
– порождает Oy; – порождает Oz.
– порождает Oz. в декартовой системе координат по оси Ox.
в декартовой системе координат по оси Ox.

 единичной длины данного направления.
единичной длины данного направления.
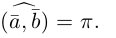
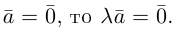
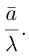
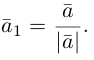
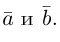
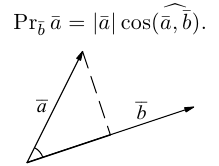
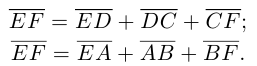
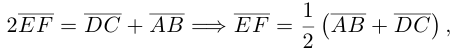
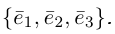
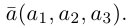
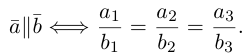
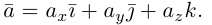
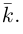

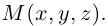
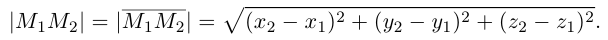
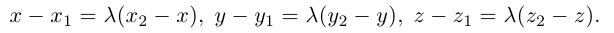
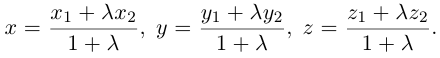
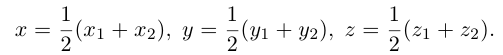
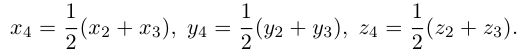
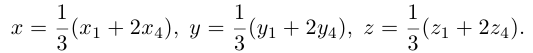
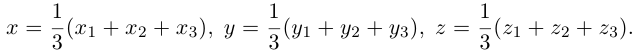


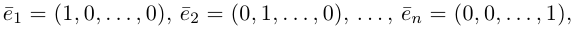
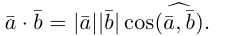
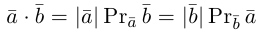
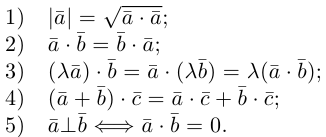
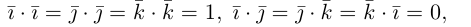
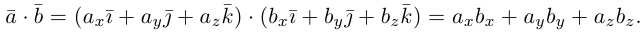
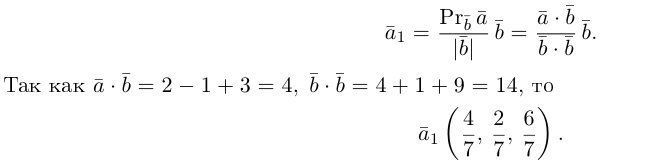
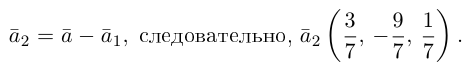
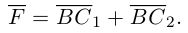
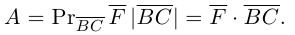
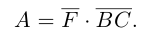
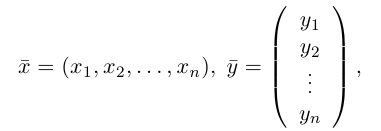
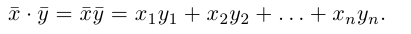
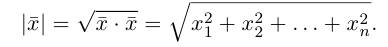
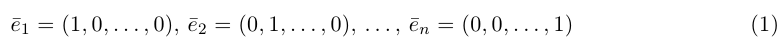
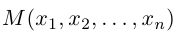

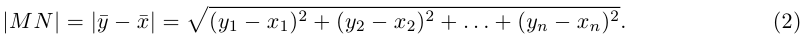
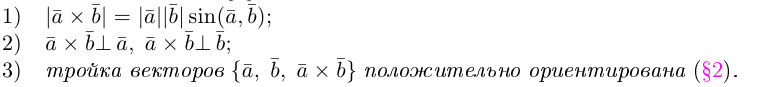
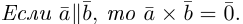
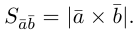
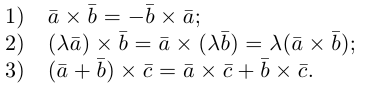
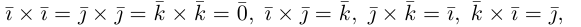
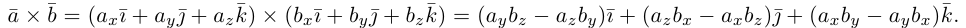
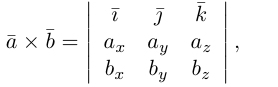
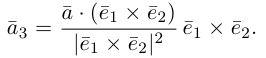
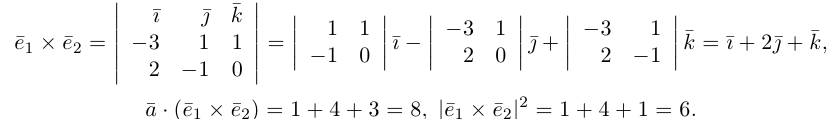
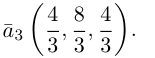
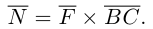
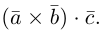
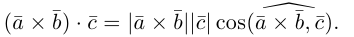
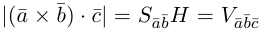
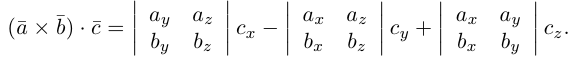
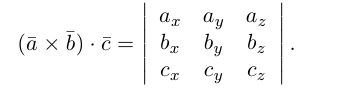
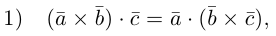
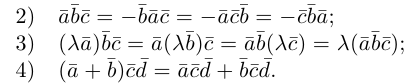
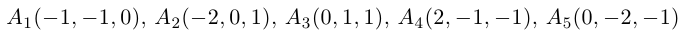
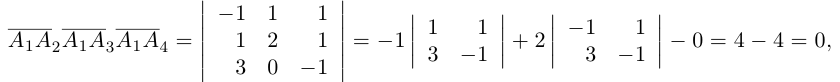
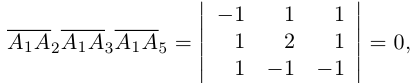
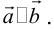

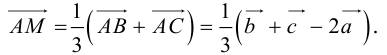
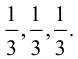
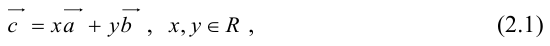
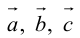 есть два коллинеарных, например:
есть два коллинеарных, например: 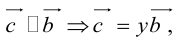
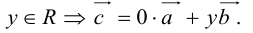
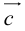 , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат  (рис. 7).
(рис. 7). 
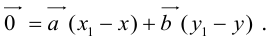
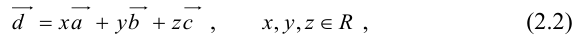
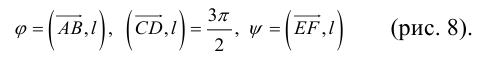
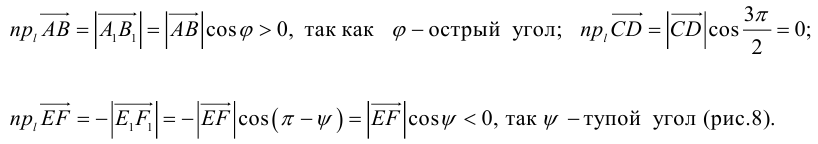
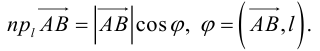
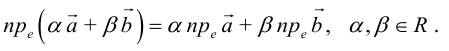
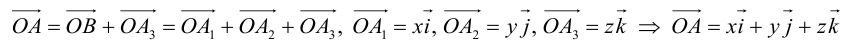
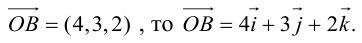
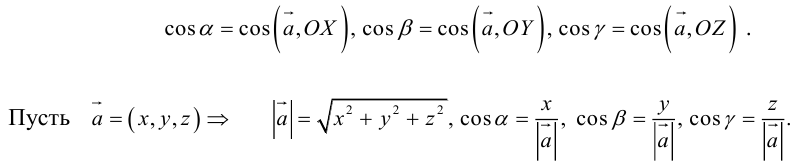
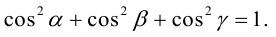
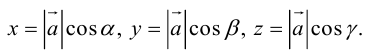
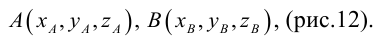
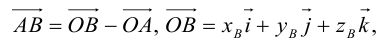
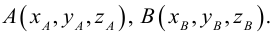

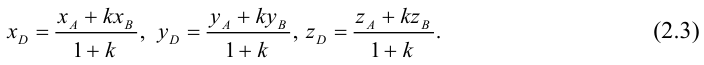
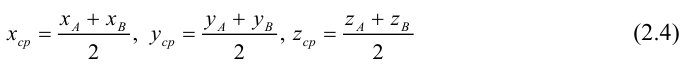
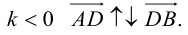
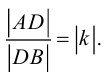
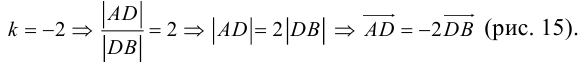
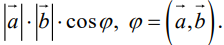
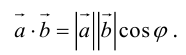
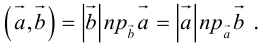
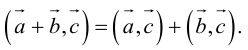
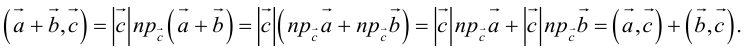
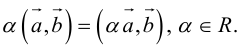
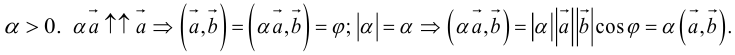
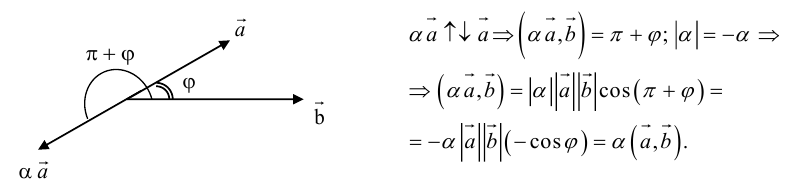
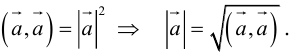
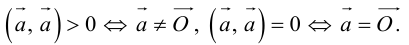
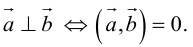
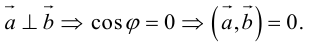
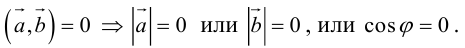
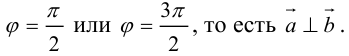
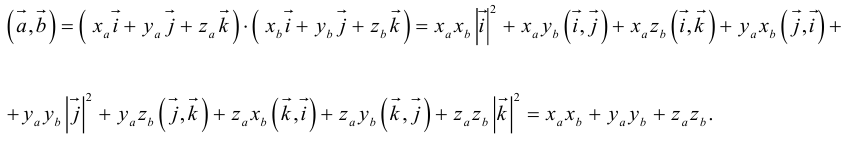

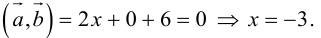
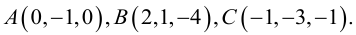

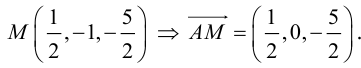
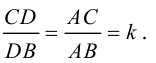
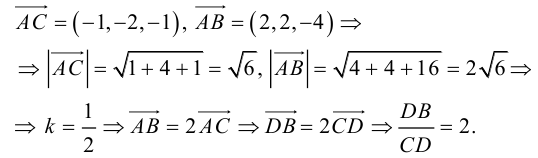
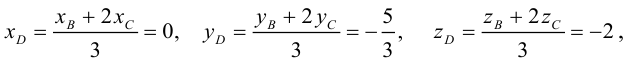
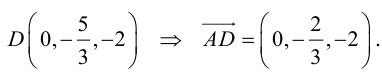
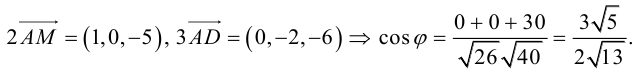
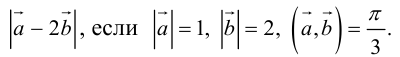
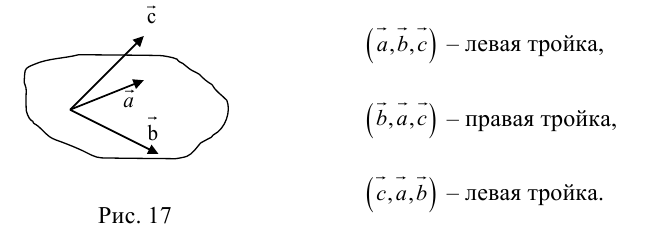
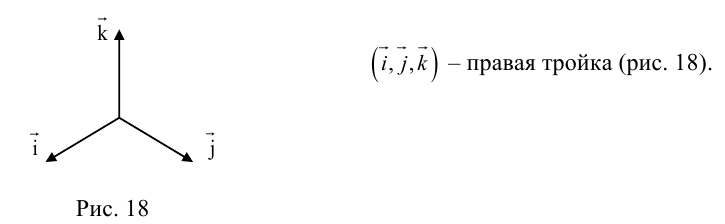
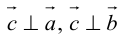 (
(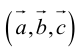 – правая.
– правая.