Как найти аппроксимирующую кривую

Пусть функция f(x)
задана таблицей:

x	x0	x1	x2	…	xn
f(x)	y0	y1	y2	…	yn

Требуется найти аппроксимирующую
кривую y(x)
в диапазоне [x₀,x_n].

В
случае, когда исходные данные носят
случайный характер, и для всех табличных
значений известна некоторая погрешность
или доверительный интервал, строят
сравнительно простую аппроксимирующую
функцию, не обязательно проходящую
через все точки. Данный подход называют
подгонкой кривой, которую стремятся
провести так, чтобы ее отклонения
табличных данных были минимальными,
т.е. получаемая функция должна отклоняться
от табличных значений незначительно
(проходить внутри доверительного
интервала). Обычно стремятся свести к
минимуму сумму квадратов разностей
между значениями функции, определяемыми
выбранной кривой и таблицей.

Такой метод подгонки называют методом
наименьших квадратов.

Пусть

(23)

искомый полином (m<n,
т.к. меньшая степень более удобна для
использования и не всегда полином
степени n является
наиболее подходящим для данной функции).

Отклонение полинома Q_m
от функции f(x)
принимает величину:

Необходимо, чтобы величина R_m
была наименьшей.

Найдем частные производные R_m
по неизвестным коэффициентам a_i.

Приравнивая производно к нулю, получим
систему из m+1
уравнения с m+1
неизвестными для определения неизвестных
коэффициентов a₀,
a₁, …,
a_m:

Введем обозначения:

Преобразуем систему, используя
обозначения:

(24)

Если среди точек

нет совпадающих и m≤n,
то определитель системы (24) отличен от
нуля и, следовательно, эта система
имеет единственное решение.

Многочлен (23) с такими коэффициентами
будет обладать минимальными квадратичными
отклонениями.

Пример

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

 

Аппроксимация линейной функцией

Пример реализации

Для примера реализации воспользуемся набором значений, полученных в соответствии с уравнением прямой

y = 8 · x — 3

Результат выполнения
Запуск без случайной составляющей

Запуск со случайной составляющей

Построение графика функции

Результат выполнения

Аппроксимация с фиксированной точкой пересечения с осью y

Результат выполнения программы поиска коэффициента угла наклона аппроксимирующей прямой при фиксированном значении b=0:

Назад: Алгоритмизация

Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.

Выполнение аппроксимации

Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.

Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.

Но она может быть построена с применением одного из пяти видов аппроксимации:

• Линейной;
• Экспоненциальной;
• Логарифмической;
• Полиномиальной;
• Степенной.

Рассмотрим каждый из вариантов более подробно в отдельности.

Урок: Как построить линию тренда в Excel

Способ 1: линейное сглаживание

Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.

Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.

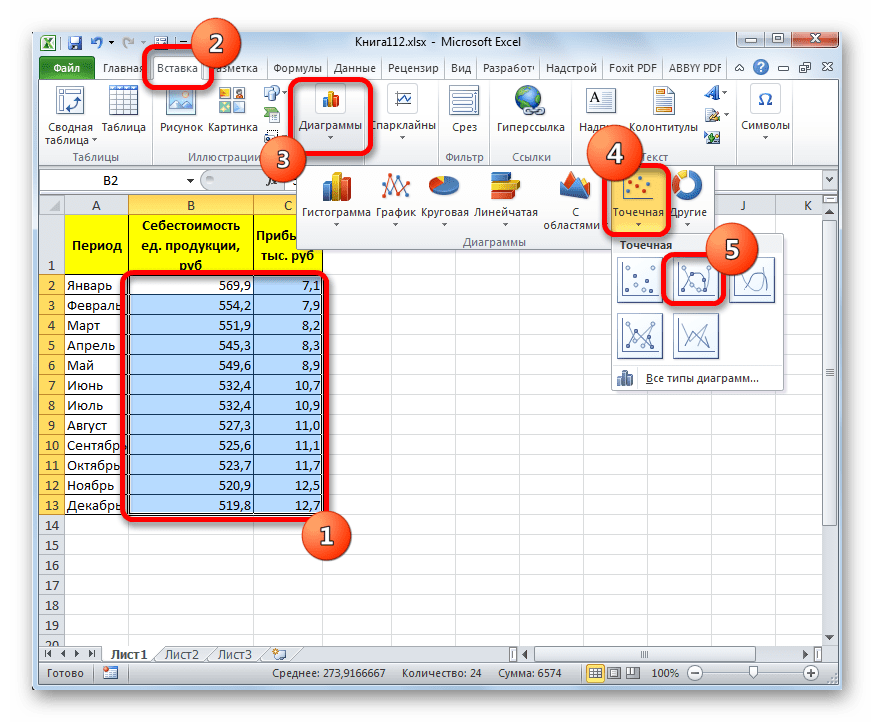
1. Для построения графика, прежде всего, выделяем столбцы «Себестоимость единицы продукции» и «Прибыль». После этого перемещаемся во вкладку «Вставка». Далее на ленте в блоке инструментов «Диаграммы» щелкаем по кнопке «Точечная». В открывшемся списке выбираем наименование «Точечная с гладкими кривыми и маркерами». Именно данный вид диаграмм наиболее подходит для работы с линией тренда, а значит, и для применения метода аппроксимации в Excel.



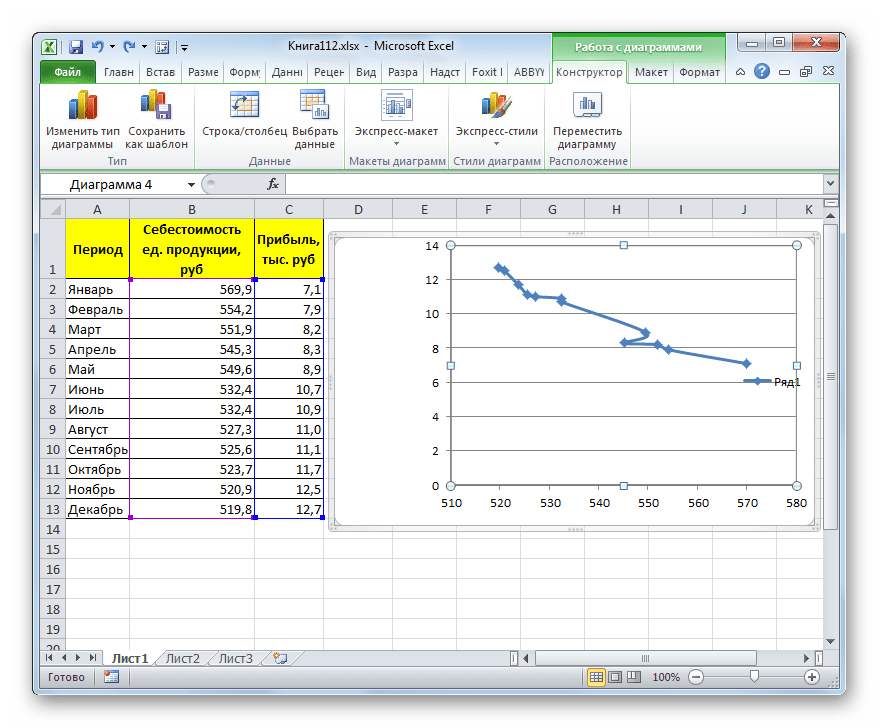
2. График построен.



3. Для добавления линии тренда выделяем его кликом правой кнопки мыши. Появляется контекстное меню. Выбираем в нем пункт «Добавить линию тренда…».
   

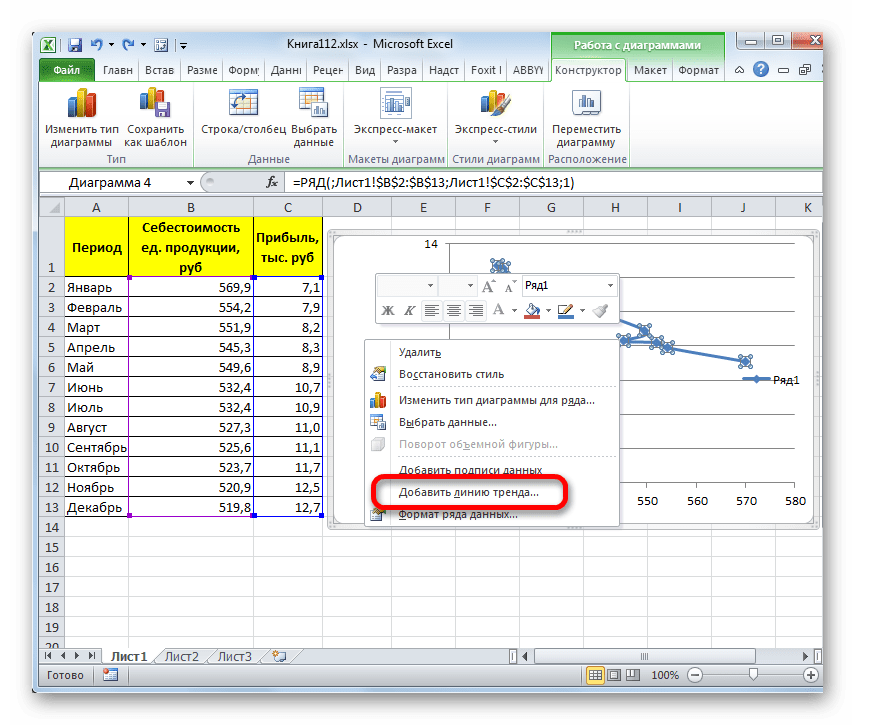
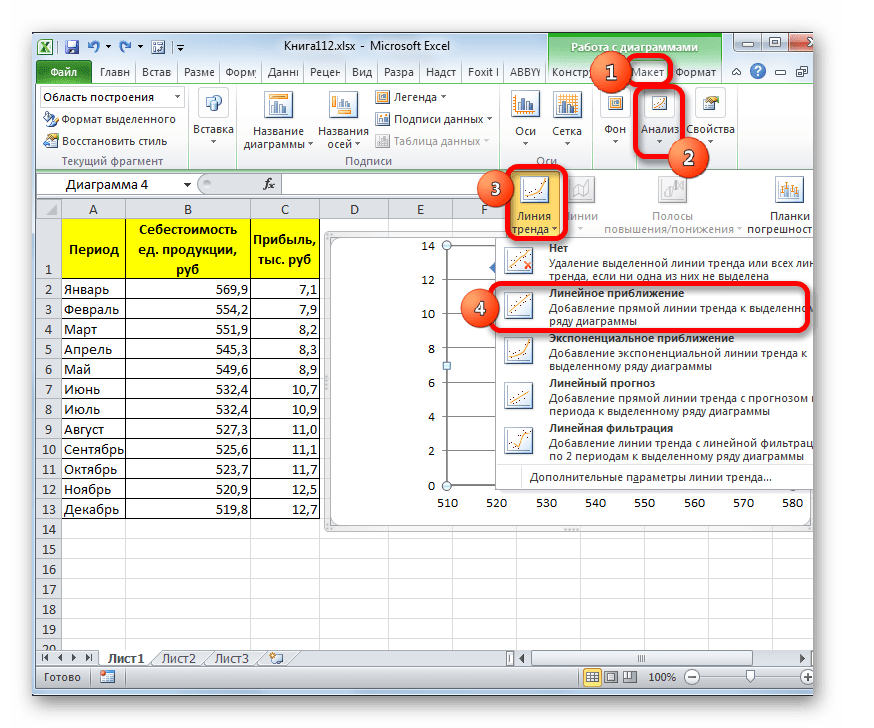
   Существует ещё один вариант её добавления. В дополнительной группе вкладок на ленте «Работа с диаграммами» перемещаемся во вкладку «Макет». Далее в блоке инструментов «Анализ» щелкаем по кнопке «Линия тренда». Открывается список. Так как нам нужно применить линейную аппроксимацию, то из представленных позиций выбираем «Линейное приближение».



4. Если же вы выбрали все-таки первый вариант действий с добавлением через контекстное меню, то откроется окно формата.

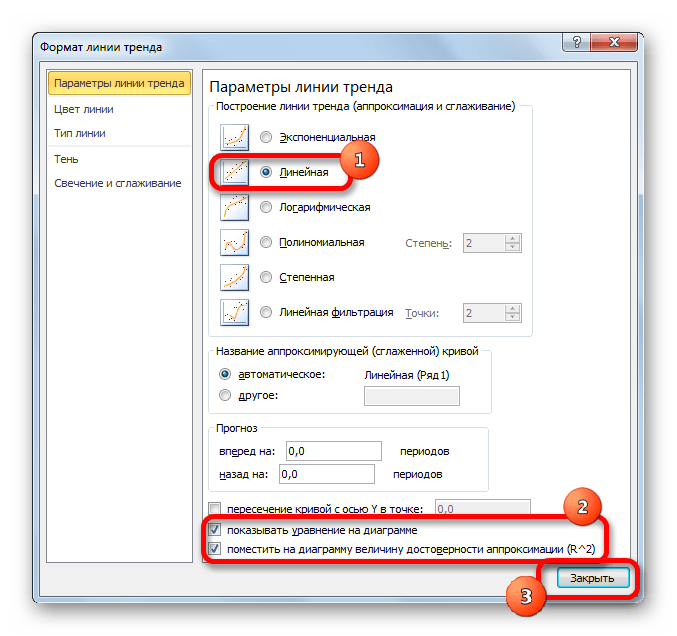
   В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
   При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.

   Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.

   После того, как провели все вышеуказанные настройки. Жмем на кнопку «Закрыть», размещенную в нижней части окна.



5. Как видим, на графике линия тренда построена. При линейной аппроксимации она обозначается черной прямой полосой. Указанный вид сглаживания можно применять в наиболее простых случаях, когда данные изменяются довольно быстро и зависимость значения функции от аргумента очевидна.

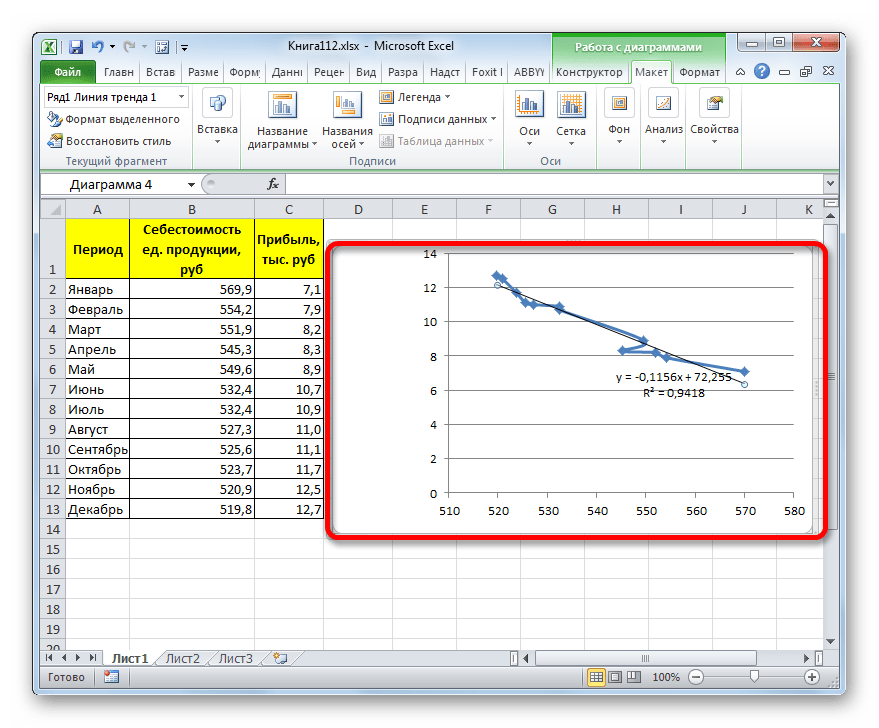
Сглаживание, которое используется в данном случае, описывается следующей формулой:

y=ax+b

В конкретно нашем случае формула принимает такой вид:

y=-0,1156x+72,255

Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.

Способ 2: экспоненциальная аппроксимация

Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.

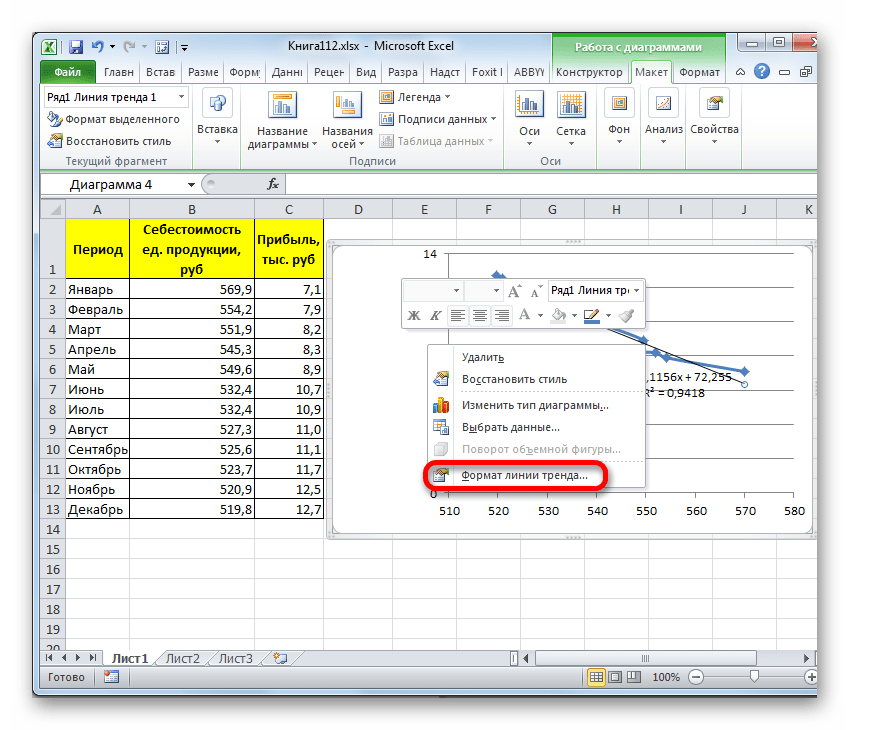
1. Для того, чтобы изменить тип линии тренда, выделяем её кликом правой кнопки мыши и в раскрывшемся меню выбираем пункт «Формат линии тренда…».



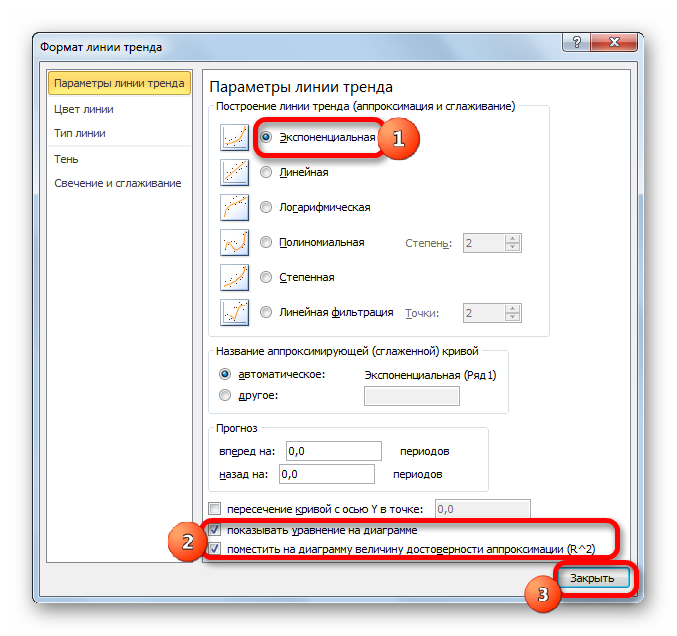
2. После этого запускается уже знакомое нам окно формата. В блоке выбора типа аппроксимации устанавливаем переключатель в положение «Экспоненциальная». Остальные настройки оставим такими же, как и в первом случае. Щелкаем по кнопке «Закрыть».



3. После этого линия тренда будет построена на графике. Как видим, при использовании данного метода она имеет несколько изогнутую форму. При этом уровень достоверности равен 0,9592, что выше, чем при использовании линейной аппроксимации. Экспоненциальный метод лучше всего использовать в том случае, когда сначала значения быстро изменяются, а потом принимают сбалансированную форму.

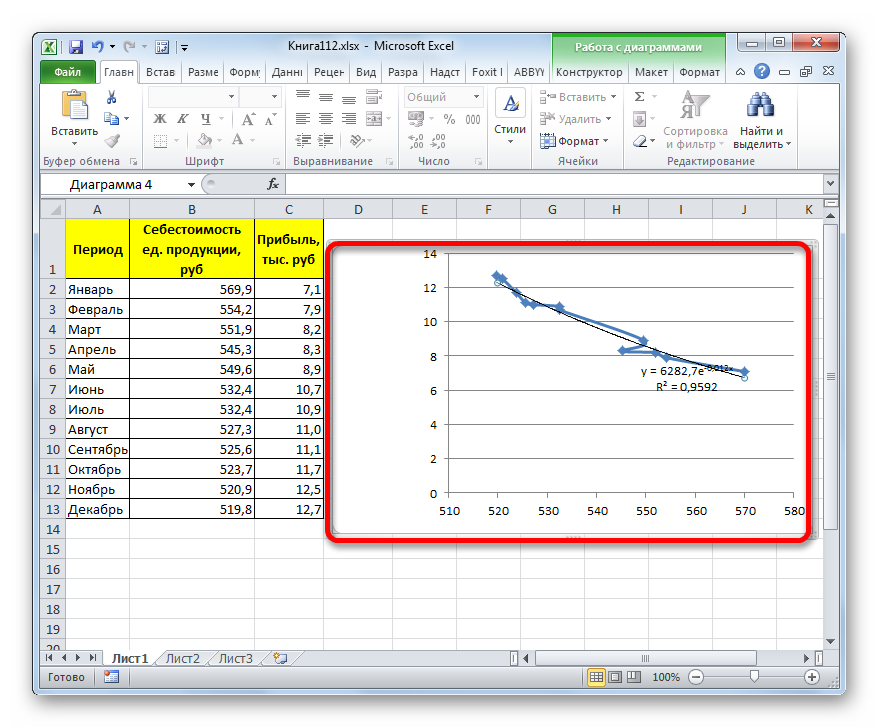
Общий вид функции сглаживания при этом такой:

y=be^x

где e – это основание натурального логарифма.

В конкретно нашем случае формула приняла следующую форму:

y=6282,7*e^(-0,012*x)

Способ 3: логарифмическое сглаживание

Теперь настала очередь рассмотреть метод логарифмической аппроксимации.

1. Тем же способом, что и в предыдущий раз через контекстное меню запускаем окно формата линии тренда. Устанавливаем переключатель в позицию «Логарифмическая» и жмем на кнопку «Закрыть».



2. Происходит процедура построения линии тренда с логарифмической аппроксимацией. Как и в предыдущем случае, такой вариант лучше использовать тогда, когда изначально данные быстро изменяются, а потом принимают сбалансированный вид. Как видим, уровень достоверности равен 0,946. Это выше, чем при использовании линейного метода, но ниже, чем качество линии тренда при экспоненциальном сглаживании.

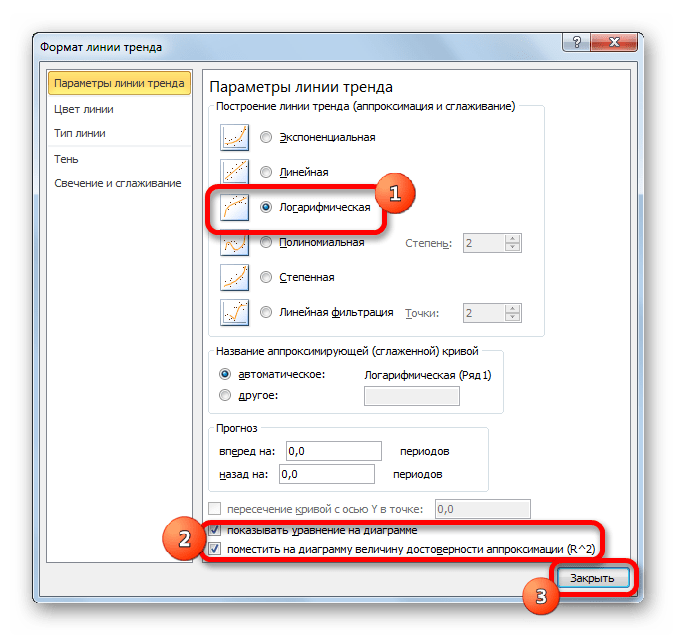
В общем виде формула сглаживания выглядит так:

y=a*ln(x)+b

где ln – это величина натурального логарифма. Отсюда и наименование метода.

В нашем случае формула принимает следующий вид:

y=-62,81ln(x)+404,96

Способ 4: полиномиальное сглаживание

Настал черед рассмотреть метод полиномиального сглаживания.

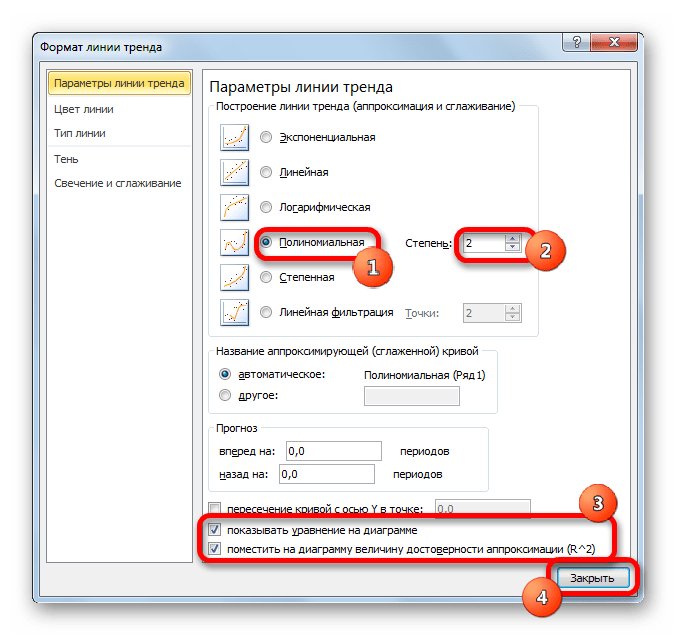
1. Переходим в окно формата линии тренда, как уже делали не раз. В блоке «Построение линии тренда» устанавливаем переключатель в позицию «Полиномиальная». Справа от данного пункта расположено поле «Степень». При выборе значения «Полиномиальная» оно становится активным. Здесь можно указать любое степенное значение от 2 (установлено по умолчанию) до 6. Данный показатель определяет число максимумов и минимумов функции. При установке полинома второй степени описывается только один максимум, а при установке полинома шестой степени может быть описано до пяти максимумов. Для начала оставим настройки по умолчанию, то есть, укажем вторую степень. Остальные настройки оставляем такими же, какими мы выставляли их в предыдущих способах. Жмем на кнопку «Закрыть».



2. Линия тренда с использованием данного метода построена. Как видим, она ещё более изогнута, чем при использовании экспоненциальной аппроксимации. Уровень достоверности выше, чем при любом из использованных ранее способов, и составляет 0,9724.
   

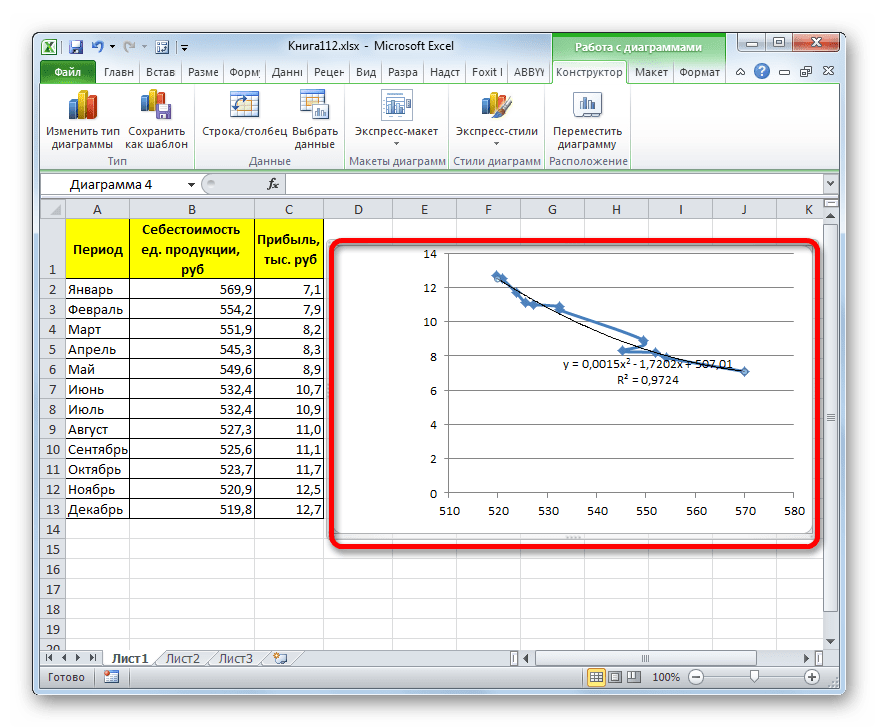
   Данный метод наиболее успешно можно применять в том случае, если данные носят постоянно изменчивый характер. Функция, описывающая данный вид сглаживания, выглядит таким образом:

   y=a1+a1*x+a2*x^2+…+an*x^n

   В нашем случае формула приняла такой вид:

   y=0,0015*x^2-1,7202*x+507,01

3. Теперь давайте изменим степень полиномов, чтобы увидеть, будет ли отличаться результат. Возвращаемся в окно формата. Тип аппроксимации оставляем полиномиальным, но напротив него в окне степени устанавливаем максимально возможное значение – 6.



4. Как видим, после этого наша линия тренда приняла форму ярко выраженной кривой, у которой число максимумов равно шести. Уровень достоверности повысился ещё больше, составив 0,9844.

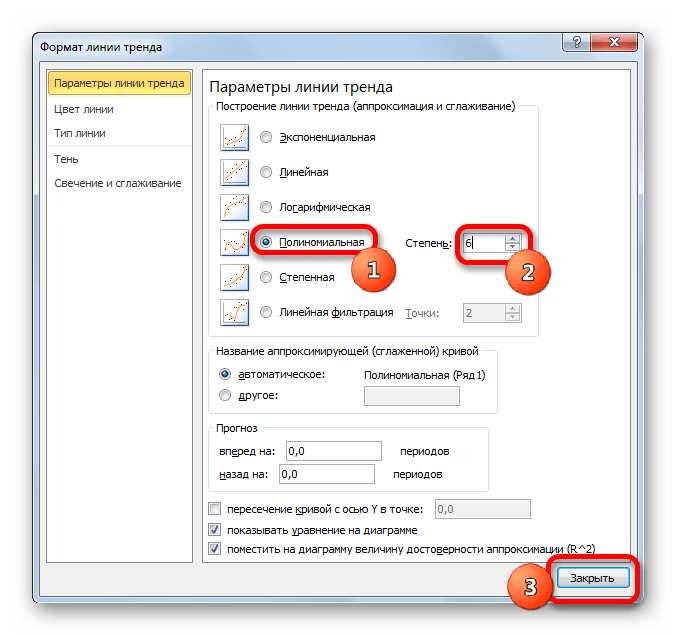
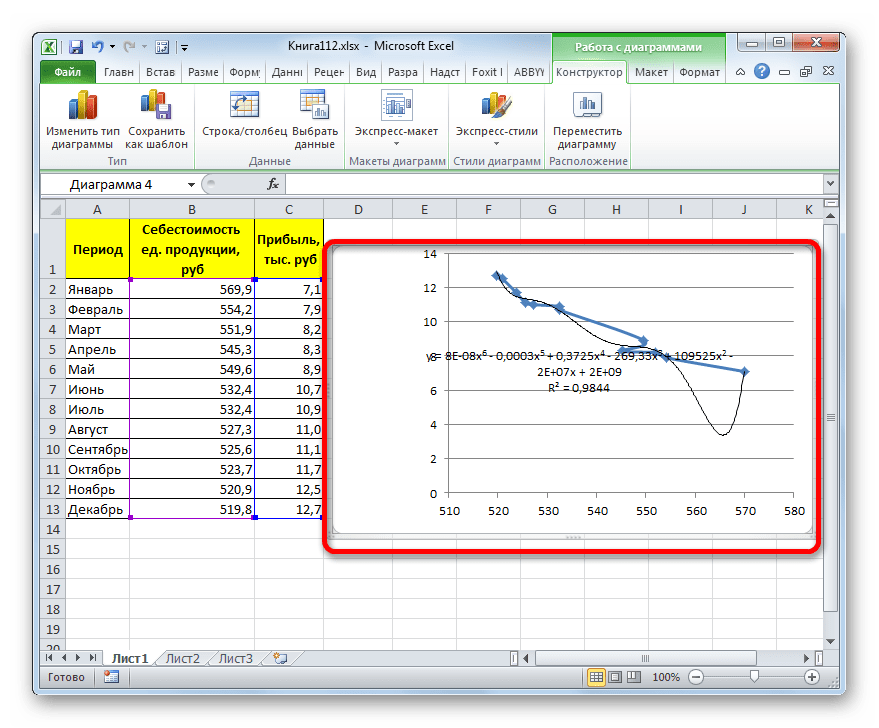
Формула, которая описывает данный тип сглаживания, приняла следующий вид:

y=8E-08x^6-0,0003x^5+0,3725x^4-269,33x^3+109525x^2-2E+07x+2E+09

Способ 5: степенное сглаживание

В завершении рассмотрим метод степенной аппроксимации в Excel.

1. Перемещаемся в окно «Формат линии тренда». Устанавливаем переключатель вида сглаживания в позицию «Степенная». Показ уравнения и уровня достоверности, как всегда, оставляем включенными. Жмем на кнопку «Закрыть».



2. Программа формирует линию тренда. Как видим, в нашем случае она представляет собой линию с небольшим изгибом. Уровень достоверности равен 0,9618, что является довольно высоким показателем. Из всех вышеописанных способов уровень достоверности был выше только при использовании полиномиального метода.

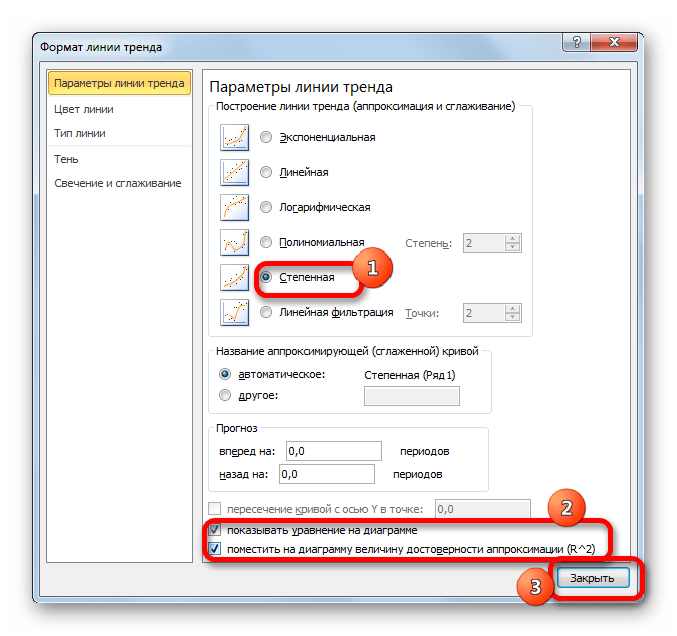
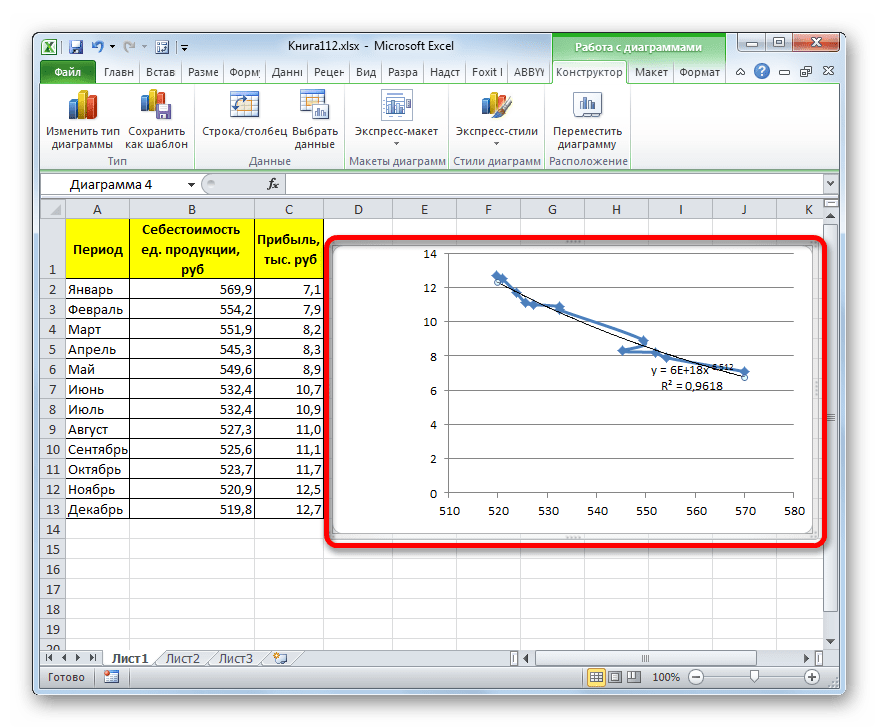
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.

Общая формула, описывающая данный метод имеет такой вид:

y=bx^n

В конкретно нашем случае она выглядит так:

y = 6E+18x^(-6,512)

Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.

Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.

Введение

В статье Ретеншен — основная метрика F2P игры, вероятностный подход я рассматривал ретеншен как биномиально распределенную случайную величину и показал, что точность оценки его отдельных измерений невысока.

Однако, можно получить более точную оценку, если использовать данные за несколько дней наблюдений и применить их, используя известные закономерности поведения метрики. В частности, можно отметить следующие доступные средства:

1. Если рассматривать все измеренные данные как временной ряд с некоторыми известными свойствами, можно построить аппроксимирующую кривую, которая будет являться точечной оценкой матожидания метрики.

2. Часто можно показать, что мы имеем дело не с биномальной случайной величиной, а с суммой нескольких случайных величин, что сужает ее дисперсию.

3. Как правило, известны не только данные о возвратах пользователей в один конкретный день после инсталла, но другие данных об их поведении, используя которые, можно гипотетически повысить точность оценки. Например, можно использовать измеренные данные о ретеншене глубины i, для уточнения оценки ретеншена глубины k.

4. Если мы располагаем большим объемом данных о значениях метрики от большого количества проектов, это, потенциально, позволяет более точно подобрать гиперпараметры аппроксимирующей модели и также повысить точность оценки метрики.

В данной статье рассматривается первый пункт из этого списка.

Постановка задачи

Рассмотрим классический ретеншн N-го (например, 1-го дня) дня как случайный временной ряд, значения которого мы определяем экспериментально. На графике этот процесс выглядит примерно так.

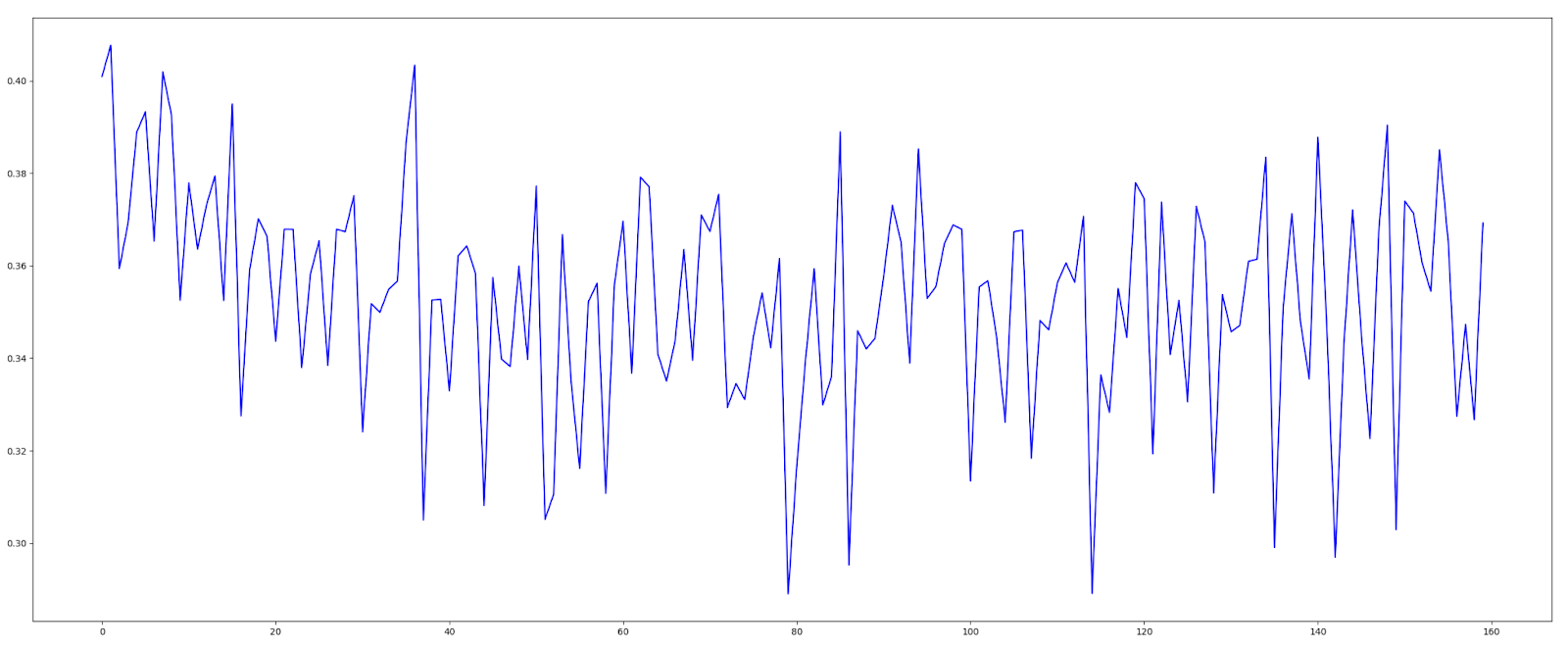
Задача – оценить параметры этого случайного ряда, а именно:

1. Получить точечную оценку математического ожидания в каждой точке ряда.

2. Получить интервальную оценку математического ожидания в каждой точке.

Задача по определению является задачей анализа временных рядов. Существуют специализированные фреймворки для решения задач подобного класса, например Prophet, Neural Prophet, Nixtla/statsforecast, о которых также можно найти информацию на хабре: 

Но сегодня я не буду использовать подобный фреймворк, а решаю задачу в общем виде, как задачу нелинейной аппроксимации процесса с некоторыми известными априори свойствами, подробно обосновывая принципы создания аппроксимирующей функции.

К слову, попытка использовать готовый фреймворк как черный ящик для данной задачи, не вникая в суть его работы и не вникая в суть аппроксимируемого процесса, может привести к провалу из-за некоторых особенностей задачи, в частности:

1. Процесс не стационарный. Метрика убывает со временем, на что накладывается выпуск патчей, дисперсия тоже меняется вследствие изменения количества установок приложения.

2. Исходных данных мало. Например, если проект находится в релизе целый год, у нас есть не более 365 точек наблюдения. Зачастую же надо измерить показатели патча, выпущенного только что или даже проекта только что выпущенного в релиз.

3. Данные очень сильно зашумлены.  Например тут автор рассматривает вопрос анализа временного ряда метрики CCU при количестве активных пользователей ~20к-60к в час. Я же говорю о необходимости исследования метрики проекта с тысячей инсталлов в день.

4. Метрика меняется не только вследствие изменения качества игры (что мы хотим измерить), но и-за изменения трафика.

В общем, сегодня и здесь будет деконструкция метрики и последующая нелинейная аппроксимация, а Prophet и его друзья будут потом, в одной из следующих публикаций.

Рисунок 2 иллюстрирует ожидаемый результат аппроксимации.

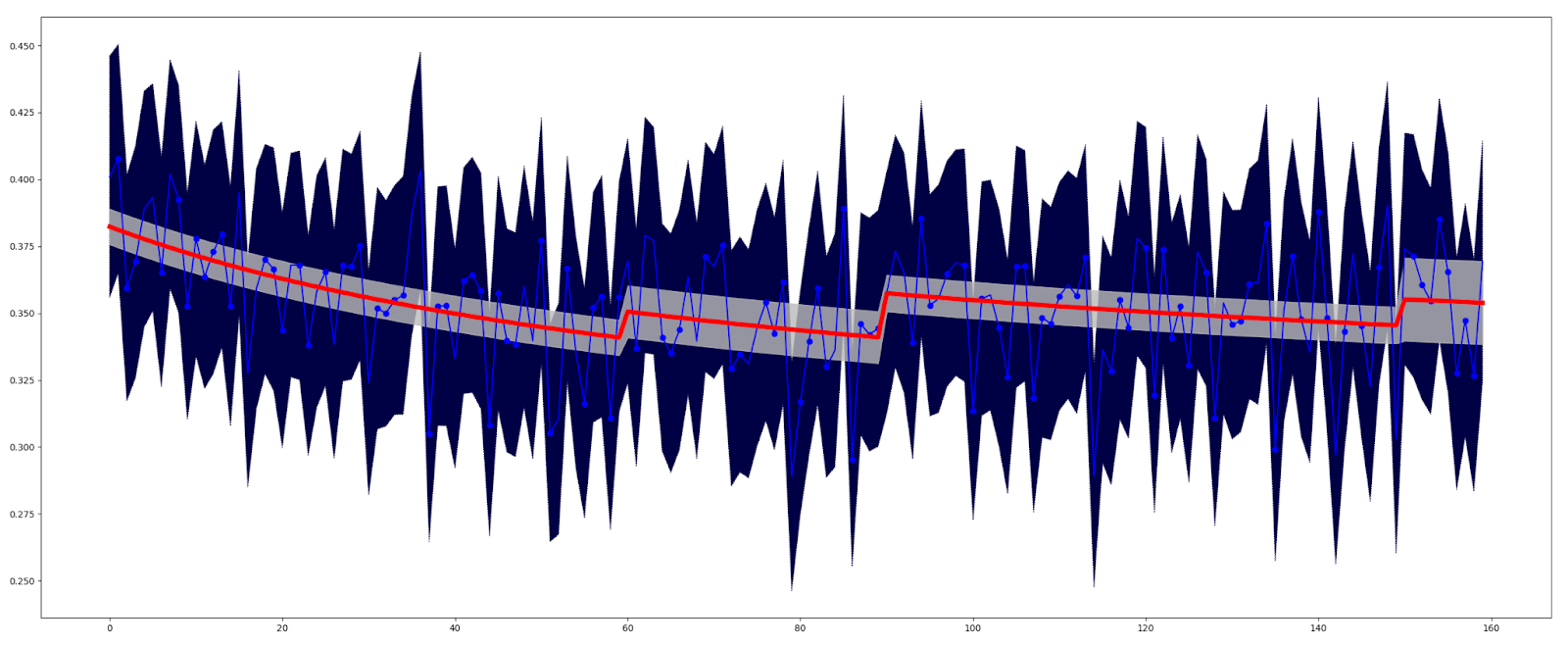
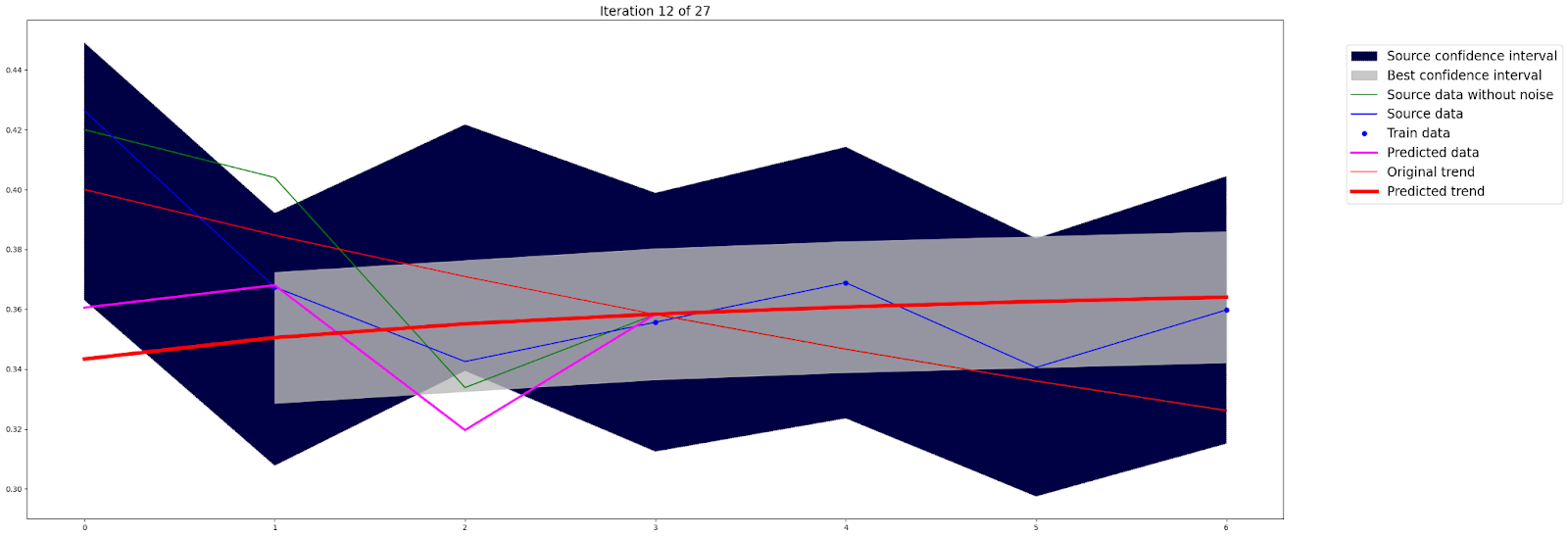
Обозначения на графике:

• Исходные измеренные данные изображены тонкой линией синего цвета

• Исходная интервальная оценка каждой точки наблюдения изображена плавающим коридором темно-синего цвета

• Аппроксимирующая кривая изображена как сплошная линия красного цвета.

• Новая интервальная оценка, полученная при помощи аппроксимации – коридор серого цвета.

Примечание. Здесь и далее я буду показывать не настоящие данные, а смоделированные. К сожалению, у меня нет возможности публиковать данные с реальных проектов.

Анализ задачи

В задаче анализа временных радов часто используется так называемая аддитивная модель, которая представляет аппроксимируемый случайный процесс в виде суммы:

r_i = g(t_i) + s(t_i) + a(t_i) + e(t_i) (1)

где

r_i , t_i – исходный временной ряд случайной функции

g(t) – линия общего тренда, одномерная функция

s(t) – сезонные явления, одномерная функция

h(t) – аномальные выбросы, случайная функция

e(t) – ошибка, нормально-распределенная случайная величина с нулевым матожиданием

В некоторых случаях корректнее соединять линию тренда и сезонные явления не аддитивно, а мультипликативно.

r_i = g(t_i) * s(t_i) + a(t_i) + e(t_i) (2)

Обе эти математические модели являются традиционными в задаче анализа временных рядов и я буду их использовать.

Покажем, что подобные модели могут быть применены к рассматриваемой здесь метрике “ретеншен”.

В конце первой статьи я привел список некоторых хорошо известных закономерностей поведения ретеншна. Большинство из них (но не все!) действительно можно разложить по четырем перечисленным выше составляющим. Рассмотрим это подробнее.

Линия тренда g(t)

Линия тренда – это и есть то, что мы хотим измерить. Это и есть среднее значение метрики, отражающее качество проекта.

Из практики известно, что ретеншен всегда плавно снижается снижается от момента релиза, но также может резко изменить значение в момент выпуска патча. Таким образом линию тренда удобно представить в виде двух слагаемых

g(t) = d(t) + p(t) (3)

где

d(t) – линия общего тренда, показывающая общую тенденцию поведения метрики – постоянное монотонное снижение.

p(t) – влияние патчей. Эта функция – кусочная, потому что она состоит из нескольких участков, каждый из которых соответствует одному конкретному патчу, и патчи не пересекаются.

Функции соединены аддитивно, поскольку это удобнее в работе, и, кроме того, в пределах действия одного патча значения функции d(t) существенно не меняются, следовательно мы сможем подобрать такой вид p(x), чтобы применять его аддитивно.

На рисунке 3 показана линия общего тренда (зеленая линия), линия патчей (черные линии) и их сумма – красная линия.

Ошибка e(t)

В первой статье показано, что ретеншен можно считать биномиально-распределенной случайной величиной, а также, одновременно, нормально-распределенной величиной, потому что при большом количестве установок, согласно центральной предельной теореме, биномиальное распределение становится нормальным. По правде сказать, утверждение о биномиальности взято несколько с потолка, скорее мы имеем дело с суммой нескольких распределений, вероятно, биномиальных. Но, в любом случае, количество установок большое, сотни как минимум, поэтому центральная предельная теорема работает и мы получим распределение, близкое к нормальному.

Ошибка e(t) является случайной функцией от времени, поскольку дисперсия ошибки, в общем случае, не является постоянной, а должна быть вычислена как дисперсия биномиального распределения с известными матожиданием и количеством экспериментов Бернулли (то есть установок приложения). То есть

e(t) = N(0,σ(t)) (4)

где

(5)

σ(t) – дисперсия биномиального распределения ретенешна с матожиданием M(r(t)) и количеством установок (количеством экспериментов Бернулли) I(t)

Аномальные выбросы a(t)

Помимо нормально распределенной ошибки формулах (1) и (2) присутствует еще одна случайная величина – a(t), аномальные выбросы.

Дело в том, что существует ряд аномальных факторов, существенно влияющих на метрику и не подчиняющихся закону биномиального распределения, основанному на количестве установок. Например, технические сбои, выпуск патчей – они приводят к существенным выбросам метрики, это уже не просто нормальный шум! И это надо как-то учитывать!

Оценка метрики в момент действия аномалии – сложная задача, выходящая за рамки настоящей статьи. Но и игнорировать факт существования аномалий нельзя, ведь они происходят действительно очень часто и сильно искажают измерения.

Буду действовать максимально просто:

1. Данные с большими аномалиями – выбрасывать из выборки.

2. Мелкие аномалии, незаметные на фоне шума, можно попробовать игнорировать – делать вид, что ничего не было.

В литературе по машинному обучению пишут, что задача обнаружения аномалий довольно сложна. К счастью, у нас не тот случай! Обнаружить аномалии можно, и не очень и сложно. Да аномалии (как правило) непредсказуемы – мы ведь не знаем (как правило), когда произойдет сбой и как количественно он повлияет на метрики. Но мы, к счастью, анализируем метрику постфактум и обладаем данными не только об этой метрике, но и огромным объемом других данных. Есть, например, метрика CCU, показывающая количество пользователей в игре в текущий момент с точностью до секунд, есть системные логи с ошибками – это отличные индикаторы аномалий. Современные средства машинного обучения отлично справятся с задачей их обнаружения. Кстати, аномальными днями зачастую следует считать и дни выпуска патчей, ведь патч тоже имеет признаки технического сбоя, о чем я писал в статье 1.

Сезонность s(t)

Функция s(t) показывает зависимость метрики от сезона. Сезонные изменения могут отражать недельные, месячные и годовые периодические процессы.

Недельная сезонность наиболее ярко выражена и хорошо объясняется поведением пользователей в разные дни недели, о чем я писал в первой статье.

Месячная сезонность как правило, очень слабо выражена, хотя иногда, в некоторых регионах, заметна. Например, в странах, где законодательно жестко зафиксирован день выплаты зарплаты, существует явная сезонность метрик, связанных с продажами, что влияет и на игровые метрики.

Годовая сезонность выражается факторами двух типов: краткосрочные события, соответствующие коротким праздникам (причем, в каждой стране – свои праздники) и долгосрочные сезонные изменения, связанные со сменой времен года. Годовая сезонность также может изменять паттерн недельной и месячной сезонности. Например, во время длинных каникул, все дни ведут себя как выходные дни.

Я не буду рассматривать здесь годовую и месячную сезонность, ограничившись недельной, как наиболее ярко выраженной.

Изменение метрики из-за изменения трафика

В формулах (1) и (2) нет очень важной составляющей  – метрика меняется из-за изменения качественного состава пользователей, то есть из-за изменения траффика.

Некорректно включать это в состав функции тренда g(x), поскольку мы измеряем ретеншен как показатель качества продукта, а не влияние состава пользователей на эту метрику. Считать изменения трафика аномалией и относить их в слагаемое a(t) тоже некорректно –  это не какое-то разовое событие, нельзя просто отбросить данные за 1-2 дня и успокоиться. 

Хороший и простой способ исключить фактор траффика – производить все измерения на некотором эталонном трафике – из эталонного источника, эталонного региона, эталонного объема. Это позволяет, с определенной натяжкой, утверждать, что мы будем измерять качество продукта на некоторых унифицированных пользователях, следовательно состав этих пользователей уже не влияет на метрику, и, следовательно, мы измеряем именно качество продукта. Такой подход требует определенной дисциплины в маркетинге и уменьшает размер ежедневной выборки, но это едва ли не единственное, что действительно можно сделать. Именно так мы и поступим.

Если вы плохо знаете о траффике и маркетинге F2P игры, и не понимаете, в чем проблема, под катом я поместил чуть более подробную информацию о ней.

Чуть подробнее о проблеме трафика

Глобальные факторы несезонного характера

Некоторые факторы, очень сильно влияющие на метрику, не носят какой-то сезонный характер. Например, ковидный локдаун. Каждый такой фактор надо рассматривать индивидуально. 

В настоящей статье эти факторы не рассматриваются.

Метод наименьших квадратов

Традиционно для оценки математического ожидания случайного процесса используют аппроксимацию по методу наименьших квадратов (или МНК). Я тоже буду использовать МНК, но прежде хотелось бы обосновать возможность применения этого метода, потому что он вообще-то может быть использован не всегда.

МНК используется и дает максимально точный результат в том случае, если:

1. Аппроксимируемый случайный процесс является серией нормально-распределенных испытаний.

2. Изматывания независимы.

3. Дисперсия испытаний постоянна.

4. Кроме того также делается предположение, что исследователь знает аналитически точно функцию математического ожидания этой случайной функции как обычную одномерную функцию с некоторыми коэффициентами, однако не знает значения некоторых коэффициентов, входящих в эту функцию. Задача аппроксимации (также именуемой, кстати задачей регрессии) – определить эти коэффициенты.

Рассмотрим каждое исходное требование. 

Условие 1. Нормальная форма распределения

Выше мы уже договорились исключить из выборки аномальные выбросы и объяснили, что функция ошибки, присутствующая в формулах (1) и (2) – нормально распределенная величина. Условие выполнено.

Уловия 2. Независимость испытаний

В литературе по регрессии условие независимости испытаний часто называют самым натянутым и спорным. Однако, на практике все вынуждены допускать независимость испытаний, чтобы не переусложнять задачу. Что касается именно ретеншена, то требование независимости интуитивно кажется довольно правильным. Метрика складывается из поведения совершенно различных людей, слабо связанных между собой. Теоретически можно предположить, что в течении некоторого промежутка времени в игру приходят тысячи людей, которые активно общаются между собой. Первые пришедшие люди из этой группы передают свое впечатление об игре другим и таким образом влияют на их поведение. Но такая организованная группа совершенно маловероятна.

Таким образом, да, будем считать условие выполненным.

Условие 3. Дисперсия во всех точках постоянна

В общем виде требования нарушено, ведь количество инсталлов ежедневно меняется, и, следовательно, согласно формуле дисперсии биномиальной случайной величины, дисперсия тоже будет постоянно меняться. К счастью, это легко решается введением весовых коэффициентов в метод наименьших квадратов.

Итак, это условие немного нарушено, но существует простое решение.

Условие 4. Формула математического ожидания известна.

Требование звучит довольно жестко. Необходимо заранее знать формулу функции, которую мы хотим найти! Как же так? Мы хотим заранее знать то, что хотим найти.

Ну да, выбор аппроксимирующей функции – этот процесс не простой, и, отчасти искусство. Нельзя взять одну аппроксимирующую функцию, скажем линейную, и применять ее во всех случаях жизни. Здесь необходимо использовать техническую эрудицию, обобщить все априорные данные об исследуемом процессе, а также учитывать объем обучающей выборки, чтобы аппроксимируемая функция не оказалась слишком сложной.

Таким образом, необходимо выбрать хороший вид аппроксимирующей функции, которая будет качественно отражать природу рассматриваемого процесса. Конечно, нельзя гарантировать, что функция выбрана идеально точно, и это неверный выбор будет вносить некоторую погрешность в измерения.

Методика аппроксимации

Итак, подытожу все написанное выше и сформулирую методику аппроксимации.

Исходные данные задачи

• фактические измеренные значения ретеншена – временной ряд {r_i}, {t_i}, i = 1…n

• фактическое количество установок приложения – временной ряд {I_i}, {t_i}, i = 1…n

Значения измерены в течении максимально доступного нам количества дней после релиза на некотором эталонном трафике, не меняющемся в течении всего периода наблюдений

Математическая модель

Будем рассматривать r_i как функцию вида:

r_i = d(t_i) + p(t_i) + s(t_i) + a(t_i) + N(0,σ(t_i)) (6)

или

r(t_i) = ( d(t_i) + p(t_i) ) * s(t_i) + a(t_i) + N(0,σ(t_i)) (7)

где:

d(t_i) – линия общего тренда,

p(t_i) – влияние патчей,

s(t_i) – недельная сезонность,

a(t_i) – аномальные выбросы,

N(0,σ(t_i)) – нормально-распределенная ошибка с нулевым матожиданием и дисперсией σ(t)

– дисперсия биномиального распределения ретенешна

с матожиданием M(r(t_i)) и количеством установок i(t_i)

Задачи

1. Определить функцию общей линии тренда d(t_i), как при условии известной функции сезонности s(t), так и при неизвестной.

2. Определить линию тренда с учетом воздействия патчей, то есть d(t) + p(t), как при условии известной сезонности s(t), так и при неизвестной.

3. Определить функцию недельной сезонности s(t)

4. Определить общий вид аппроксимирующей функции, тое есть функцию:

   R(t) = d(t) + p(t) + s(t) (аддитивная модель) (8)

   R(t) = ( d(t) + p(t) ) * s(t) (мультипликативная модель) (9)

Методика аппроксимации

1. Выбрасываем из исходной выборки аномальные дни, для обнаружения которых используем какие-то другие, дополнительные, данные.  

2. Создаем аппроксимирующую функцию, состоящую из трех составляющих

   d(t) – линия общего тренда,

   p(t) – влияние патчей,

   s(t) – недельная сезонность,

3. Для построения аппроксимации применяем метод взвешенных наименьших квадратов с учетом меняющейся дисперсии σ(t)

4. Качество работы модели будем оценивать грубо аналитически, а также статистически на основе предыдущего опыта ее применения, поскольку наша обучающая выборка слишком мала, чтобы выделять из нее тестовую и валидационную.

Предложенная методика реализована в виде Jupyter-ноутбука retention-rate-approximator, выложенного на github в открытый доступ

Аппроксимирующая функция

Ключевой момент рассматриваемого метода аппроксимации – это, конечно, вид аппроксимирующей функции.

Аппроксимирующая функция состоит из трех функций

1. Линия общего тренда d(t)

2. Линии патчей p(t)

3. Сезонность s(t)

Как я уже писал выше, линия тренда и линия патчей объединяются аддитивно, а сезонность может быть применена аддитивно или мультипликативно. Мне кажется более корректно применять сезонность мультипликативно, но, на всякий случай, в retention-rate-approximator я реализовал оба варианта, поскольку это было не сложно.

Линия общего тренда – убывающая функция

Из практики известно, что в момент релиза игры метрика максимальна, далее снижается с убывающей скоростью, но не доходит до нуля никогда. Из этих простых соображений сформулируем требования к линии общего тренда d(t).

1. Функция определена на значениях аргумента >= 0.

2. Функция непрерывная, монотонно убывающая, первая производная всегда отрицательна.

3. На бесконечных значениях аргумента функция медленно приближается к ассимптоте.

4. Функция вогнутая, то есть вторая производная всегда положительна.

Множество функций удовлетворяет этим требованиям. Например, можно использовать варианты предложенные в главе “Как моделировать удержание” книги Василия Сабирова. “Игра в цифры” (правда, автор их применяет для аппроксимации несколько другого процесса – он рассматривает ретеншен как функцию от количества дней, прошедших с момента установки, а не как функцию времени от момента релиза проекта). Можно попробовать использовать экспоненту, гиперболический тангенс и сигмоиду – все эти функции формально удовлетворяют заявленным требованиям в диапазонах значений x > 0 и правильно выбранных коэффициентах. Также при небольшом количестве наблюдений можно использовать линейную функцию и просто константу.

Список некоторых возможных кандидатов приведен в таблице 1

Недостатком всех этих функций (за исключением первых двух) является их нелинейность как по отношению к аргументу так и весам. Следовательно, регрессия будет нелинейная, свойства ее документированы плохо, сходимость может быть плохой.

Есть способ перейти от нелинейной регрессии к линейной, если вместо одной простой функции использовать ряд из нескольких базисных функций без весов в знаменателе. Однако, в этом случае количество весов будет большое, и, следовательно, на нашем небольшом объеме данных мы не сможем правильно обучить модель. Целесообразнее использовать одну нелинейную функцию но с малым количеством весов.

В Jupyter-ноутбуке retention-rate-approximator я реализовал несколько функций из предложенного выше набора, и вы можете их попробовать на практике. Также можете реализовать свою функцию по аналогии с уже реализованными, создав класс из 3-х простых методов, это совсем нетрудно.

Ниже по тексту я напишу немного о своих собственных экспериментах с аппроксимирующей функцией и сделанных мною выводах.

Линия патча

Мы хотим проанализировать результаты внедрения патча как можно скорее, поэтому аппроксимирующая функция должна быть максимально проста.

В большинстве случаев единственно возможным вариантом аппроксимации патча будет просто константа – у каждого патча один весовой коэффициент. То есть, патч добавляет просто постоянное смещение к линии тренда. p(t) = w₀

Если данных много и они слабо зашумлены вместо константы можно использовать линейную функцию. Два весовых коэффициента на каждый патч. p(t) = w₀ + w_{1 *} t

В ряде случаев, наверное, можно использовать и функцию с 3-мя и 4-мя коэффициентами из числа рассмотренных выше. Но для этого необходимо гигантское количество инсталлов.

Аппроксимация недельной сезонности

Для аппроксимации недельной сезонности часто использую для каждого дня недели свой весовой коэффициент, задающий смещение этого дня недели. Мне это подход кажется разумным, так и поступлю без дополнительных обоснований.

Нетрудно заметить, что, если каждому дню недели будет соответствовать свой вес, то есть отдельное отдельное слагаемое в аппроксимирующей функции, и мы применяем функцию недельной сезонности аддитивно (формула (6)), то один из этих 7-ми весовых коэффициентов будет являться линейной комбинации 6-ти других значений. Метод оптимизации никогда никогда не сможет найти оптимальное значение весов такой модели, ведь если увеличивать смещение w₀ линии тренда, и одновременно, на такую же величину уменьшать все недельные коэффициенты, результирующая функция не меняется.

Если функция сезонности применяется мультипликативно (формула (7)), то указанная проблема тоже присутствует, но она будет применена не аддитивно, а мультипликативно.

Проблема решается двумя способами.

1. Выбрать некоторый эталонный день недели, в который вес модели должен будет не настраиваемым, а равен нейтральному значению (ноль при аддитивном объединении и единица – при мультипликативном). Остальные другие веса сезонной функции будут задавать отклонения от этого эталонного дня.

2. Потребовать, чтобы среднее значение весов недельной модели равнялось нейтральному значению (ноль при аддитивном объединении и единица – при мультипликативном).

Мне больше нравится второй вариант, поскольку мы не знаем априори, какой именно день недели следует считать эталонным.

Для того, чтобы реализовать это требование при обучении модели я использую функцию регуляризации. Возможно, это несколько нестандартный случай применения регуляризатора (обычно используются функции L1 и L2), но ведь я хочу установить динамическое ограничение на веса модели, а именно это и делают регуляризаторы.

Чуть более подробно объясняю, причем здесь регуляризаторы.

Функция регуляризации будет такая:

(10)

Здесь N – это требуемое нейтральное среднее значение весов, зависящее от способа объединения убывающей и периодической функций. 

Если функции объединяются аддитивно, N = 0.

Если функции объединяются мультипликативно, N = 1.

Как учесть меняющуюся дисперсию

Дисперсия биномиального распределения ретеншна рассчитывается по формуле (5), повторю ее длянаглядгнсти

(5)

где

I_i = I(t_i) – известное нам количество установок приложения в момент времени t_i

M(r_i) – математическое ожидание ретеншена в момент времени t_i

В качестве функции M(r_i) наиболее корректно использовать вычисленное значение аппроксимирущей функции, то есть:

M(r_i) ≈ R(t) = d(t_i) + s(t_i) + p(t_i) (аддитивная модель) (11)

или

M(r_i) ≈ R(t) = (d(t_i) + s(t_i)) * p(t_i) (мультипликативная модель) (12)

На начальных итерациях градиентного спуска такая величина может быть очень далека от реального значения, она может даже не попадать в диапазон [0,1], поэтому можно попробовать использовать величину r(t).

M(r_i) ≈ r_i (на начальных итерациях градиентного спуска) (13)

Итак, дисперсия в каждой точке известна, поэтому можно использовать так называемый взвешенный метод наименьших квадратов. Как указано в [6] функция потерь этого метода имеет вид:

(14)

Где e(t_i) – ошибка, поученная как разность аппроксимирующей и аппроксимируемой функции.

Подставив сюда формулу дисперсии, получим

(15)

Где

{ t_i }_, {r_i } = аппроксимируемый временной ряд значений ретеншена

{ t_i }_, { I_i } – временной ряд соответствующего количества установок

R(t) – аппроксимирующая функция, вычисляемая по формуле (8) или (9)

M(r_i) – математическое ожидание ретеншена в точке i.

Заметим, что значение, получаемое с помощью этой формулы, будет зависеть от количества установок каждый день и от количества дней наблюдений. Это плохо, поскольку мы будем суммировать эту величину с функцией регуляризации весов сезонной функции, не зависящей от количества установок и рассматриваемого промежутка времени. Поэтому разделим полученное значение на общее количество установок за рассматриваемый период и получим итоговую нормированную формулу:

(16)

Реализация. Пользовательский интерфейс

Рассмотренная выше методика реализована мною на Python + PyTorch в виде колаб ноутбука retention-rate-approximator, который я выкладываю в открытый доступ на github.

В первую очередь коротко распишу его структуру, чтобы вы могли уже его потрогать руками.

Ноутбук состоит из трех блоков:

1. “В первом блоке “Import libraries, define classes and functions” содержится описание классов и функций, которые используются ниже. Вам следует просто выполнить этот блок, наивно надеясь, что он не сольет в сеть ваши персональные данные.

2. Второй блок – пользовательский интерфейс. Этот блок надо тоже выполнить, чтобы этот интерфейс увидеть. Интерфейс состоит из двух частей. Слева – генератор временных рядов, похожих на ретеншен, справа – настройки аппроксиматора. Все параметры уже инициализированы некоторыми не абсурдными начальными значениями, поэтому при первом запуске вы можете просто нажать кнопку Genetate dataset в левой части экрана. Также можно сохранить сгенерированные данные в csv-файл, нажав кнопку Save dataset и загрузить свои собственные обучающие данные в формате csv, нажав кнопку Upload dataset

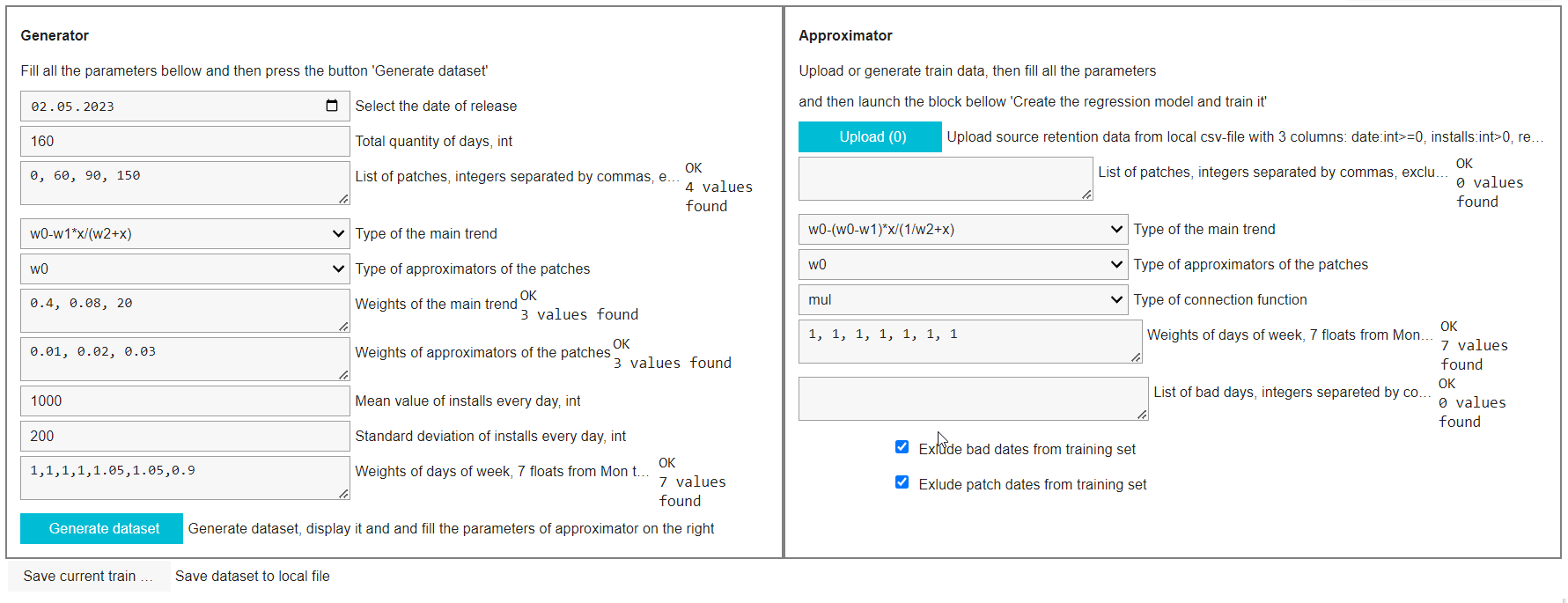
1. Третий блок “Create the regression model and train it” – собственно создание и обучение аппроксимирующей модели. Если вы заполнили все параметры параметры аппроксимирующей функции в правом блоке настройки аппроксиматора, просто запустите этот блок.

Реализация. Технические детали

Не буду подробно расписывать код ноутбука, он довольно простой и немного прокомментирован, все видно наглядно.

Конечно в процессе возникло работы, как обычно, множество нюансов, все не упомнишь, перечислю лишь несколько моментов.

1. Использован PyTorch а не Tensorflow/Kers поскольку первый более удобен для создания кастомных регуляризаторов и для создания кастомных моделей со сложными конструкциями внутри функции forward, что мне и требовалось.

2. Хотелось добиться в результате некоего подобия продукта, легко распространяемого и удобного в использовании, поэтому был выбран формат Jupyter-ноутбука, который можно запустить на любом компьютере, в любом браузере в Google Colab. Пришлось помучаться с пользовательским интерфейсом на базе библиотеки ipywidgets, с которой работаю впервые. Результатом не вполне доволен, но, грубо, желаемый результат достигнут – получилось доступно и более-менее удобно.

3. Весь код собран в одном ноутбуке и это конечно очень громоздко и неудобно в разработке. Следовало бы отделить 1-2 py-файла, держать их на гитхабе и загружать их в первом блоке ноутбука. Но я таких больших ноутбуков еще не создавал, и не знаю, как правильнее организовать такой проект. Возможно, кто-нибудь даст дельный совет. 

4. Помимо собственно аппроксиматора в ноутбуке есть генератор процессов, похожих на ретеншен, о чем я уже писал выше. Генератор довольно простой, и использует для генерации ту же самую математическую модель ретеншена, которая используется для аппроксимации.

5. Я попробовал реализовать и поэкспериментировал с несколькими вариантами функции для аппроксимации линии тренда, однако, больше всего работал только дробно-линейными функциями y(x) = w0-w1*x/(w2+x) (класс LinearFractionalFunction) и y(x) = w0-(w0-w1)*x/(1/w2+x)(класс LinearFractionalFunction_new). Именно эти классы реализованы лучше других. В частности, для качественного обучения модели имеет смысл предварительно инициализировать веса примерно подходящими подходящими значениями, используя данные обучающей выборки, этим занимается метод init_weights_from_train_data. Этот метод более-менее неплохо реализован в классах LinearFractionalFunction, LinearFractionalFunction_new и SigmoidFunction, но в остальных классах – совсем грубо.

6. Настройки стратегии обучения модели в текущий момент еще не вынесены в пользовательский интерфейс, их необходимо менять непосредственно в коде третьего блока ноутбука в переменных training_strateg, loss_function, regualizer_lambda,
   number_of_sigmas_for_plotting. Что означают эти переменные написано в комментариях в коде.

7. Я пробовал экспериментировать с различными типами оптимизаторов, в том числе использовал LBFGS, часто рекомендуемый для нелинейной регрессии, однако самый распространенный и популярный оптимизатор Adam, по моим наблюдениям, дает результаты как минимум не хуже большинства других. В настройках обучения, через константы, можно настроить оптимизатор Adam или LBFGS. Любой другой, разумеется тоже можно добавить, поменяв одну строчку в коде.

Эксперименты с функцией линии тренда

Выше был приведен список возможных кандидатов в функции аппроксимации тренда, он не много пугает разнообразием. Сейчас его немного отфильтруем.

Явно следует сразу исключить экспоненту – она убывает слишком быстро, совершенно не соответствует природе процесса. Гиперболический тангенс тоже выглядит не слишком удачным решением – у него есть два практически прямых участка – центральный, наклонный, и горизонтальная асимптота, соединенные перегибом – это слабо похоже на реальный процесс. Насчет других вариантов настолько однозначно сказать уже нельзя, нужно экспериментировать.

У меня нет, к сожалению, доступа к большому объему данных реальных проектов чтобы делать выводы, претендующие на объективность но по моим субъективным наблюдениям неплохо ведет себя обратная функция вида d(t) = w₀ + w₁ / (w₂ +t) и дробно-линейная функция вида d(t) = w₀ + w₁ * t / (w₂ +t).

В процесс экспериментов я остановился на функции вида d(t) = w₀ + w₁ * t / (w₂ +t), но далее, в процессе многих последующих экспериментов немного ее видоизменил, выполнив небольшое преобразование ее коэффициентов и получил итоговую функцию, которую считаю наиболее удачной:

d(t) = w₀ + ( w₀ – w₁ )* t / (1/w₂ +t ) (17)

С точки зрения зависимости от входной переменной это так же формула
d(t) = w₀ + w₁ * t / (w₂ +t), но для градиентного спуска важна зависимость не от входа, а от параметров. По поим наблюдениям, такой вид функции благотворно сказывается на результатах градиентного спуска, и у меня есть для этого объяснение. Аргументы в пользу функции такие:

1. Мало весов (3, а не 4 и не 5), что важно при небольшом объеме сильно зашумленных данных.

2. Не слишком быстро убывает, и, по моим наблюдениям, неплохо аппроксимирует ретеншн в течении довольно продолжительного количества дней после релиза.

3. Хороший физический смысл каждого параметра и они независимы друг от друга:

   1. Коэффициент w₀ задает начальное значение функции в нулевой момент времени.

   2. Коэффициент w₁ задает значений функции на бесконечном значении аргумента.

   3. Коэффициент w₂ задает скорость убывания функции.

4. Все 3 параметра имеют значения примерно одного порядка в диапазоне от 0 до 1. По моим наблюдениям, это свойство позволяет оптимизатору наиболее точно находить минимум функции ошибки.

5. При определенных значениях параметров превращается в линейную функцию или константу.

6. Вычислительная простота.

Вовсе не утверждаю, что такая функция единственно правильная. У меня даже нет достаточного количества данных для анализа, чтобы делать такие выводы. Если исследователь располагает большой историей развития метрики за большой промежуток времени, можно попробовать функции с 4-ю или 5- коэффициентами, можно составить функцию из нескольких звеньев. Если же данных наоборот слишком мало единственным возможным вариантом является линейная функция или, даже, константа.

Также я провел эксперименты с разными видами функции аппроксимации патчей.

При рассматриваемых условиях – ежедневное количество установок приложения ~1000 хороший результат можно получить только при использовании простейшего варианта функции p_i(t) = w0_i

Если использовать линейную функцию с двумя коэффициентами или еще более сложную функцию, получается полный провал получается полная ерунда – график ведет себя совершенно противоестественно. Необходимо гораздо больше инсталлов для такой аппроксимации. 

Грубая оценка доверительного интервала

А сейчас самое интересное – оценка доверительного интервала. Ради чего все и затевалось.

Непростая задача, совсем непростая. Регрессия нелинейная, теория тут сложная. Данных в обучающей выборке мало, поэтому не может быть и речи о том, чтобы ее разделить на обучающую тестовую и валидационную. У меня нет доступа к большому объему данных от множества проектов, чтобы проверить методику на большом объеме данных. Кроме того, существует огромное количеств факторов, влияющих на оценку доверительного интервала, это просто трудоемко. Например, известна или нет заранее форма сезонной функции, сколько дней прошло от момента релиза и т.д. Все эти варианты надо продумывать, прорабатывать. Большая работа, а времени у меня не так и много. И, кроме того, это не научное исследование, а практическая работа, надеюсь, полезная не только мне. Мне важнее опубликовать текущие результаты, чем тянуть время.

Ну вы поняли. Закапываться в жесткую теорию, не имея возможности проверить метод на большом объеме реальных данных совершенно глупо, не буду сейчас этого делать.

Но грубую оценку можно сделать, отталкиваясь от грубой теории и от фактических результатов измерений на моделированных данных.

Теория

Установим лучший идеальный доверительный интервал, который может быть получен при помощи такой регрессии. Доверительный интервал нашего метода не может быть лучше этого идеального.

Предположим, ретеншен не меняется в течении каждого патча, то есть линия тренда состоит из горизонтальных отрезков прямых – каждому патчу соответствует свой горизонтальный участок. Нам известна дисперсия в каждый момент времени (это биномиально-распределенная величина с известными параметрами), следовательно, полагая испытания в каждый день независимыми, мы можем посчитать дисперсию величины для каждого участка кривой (то есть для каждого патча) как взвешенное среднее значений дисперсии в каждый момент времени, а стандартное отклонение – как корень из этой дисперсии

(18)

где

k>=0 – номер патча

σ_k – оценка дисперсии k-го патча

n_k– количество измеренных дней в патче k

σ_kj – дисперсия в j-й день k-го патча (посчитанная как дисперсия биномиального распределения)

I_kj – количество установок приложения в j-й день k-го патча

В эту формулу, конечно, должны входить только те точки, которые использовались для аппроксимации. Точки, отброшенные как аномальные, необходимо исключить.

Таким образом, можно построить доверительный интервал аппроксимирующей кривой в каждой точке наблюдений. На графике это доверительный интервал изображается в виде полосы вокруг полученной аппроксимирующей кривой. Ширину полосы можно установить равной 2 сигмы (что должно соответствовать 95% точности аппроксимации) или 3 сигмы (точность аппроксимации – 99.7%)

Таким образом, лучшая точность, которую мы можем требовать от нашего метода аппроксимации,  – это стопроцентное попадание в такой коридор шириной 3 сигмы. Более высокой точности требовать нельзя.

На рисунке 4 коридор такого доверительного интервала показан полосой серого цвета. Видно, что ширина коридора на различных участках различна. Чем шире участок, тем больше в ней точек наблюдений, поэтому коридор уже.

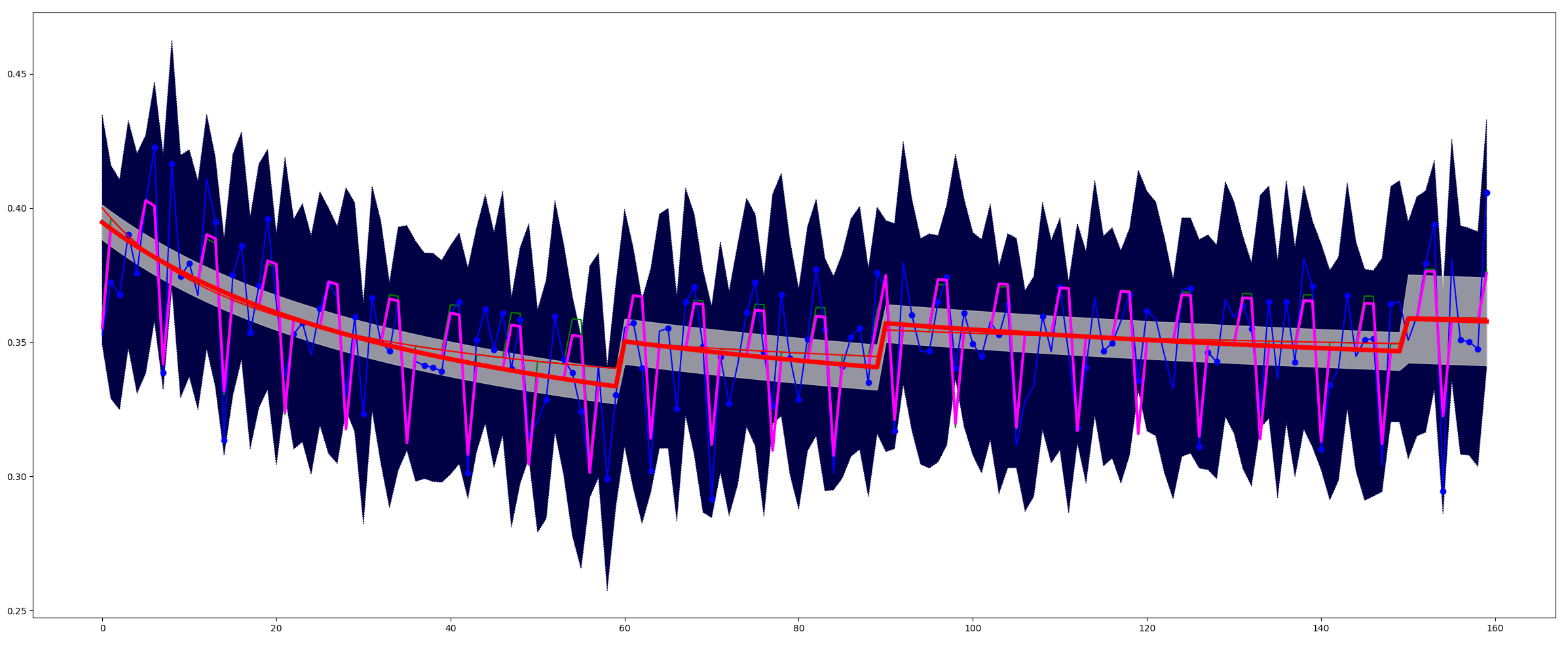
Практика

Не могу проверить адекватность предложенной модели применительно к большому объему реальных данных. Это плохо, но факт. Но можно проверить модель на аппроксимации искусственных данных, сгенерированных при помощи функции, аналогичной аппроксимирующей с добавлением биномиально-распределенного шума. Преимуществом такого метода является точное знание изначальной формы процесса, следовательно, можно точно оценить результат аппроксимации.

Я  провел моделирование 1000 случайных процессов, и оценил их результаты. Во всех случаях я предполагал, что интервал между патчами – около 30 дней, и с момента релиза прошло довольно много времени, от 32 до 365 дней. Во всех экспериментах среднее количество установок в день равнялось 1000. Во всех экспериментах 30% случайных данных от выборки а также все даты старта патчей и дата релиза было отброшено из выборки как якобы аномальные. Во всех случаях сезонная функция была примерно известна заранее. Довольно много допущений, но они не очень недалеки от практики

В качестве генерирующей и аппроксимирующей функции линии тренда использовал функцию вида d(t) = w₀ + ( w₀ – w₁ )* t / (1/w₂ +t )

В качестве линии каждого патча использовал простейшую функцию вида p_i(t) = w0_i

В качестве критерия оценки качества модели  я рассматривал простой бинарный факт – попадает ли кривая полностью в идеальный доверительный интервал 3-сигмы, полученный при помощи описанного выше метода или нет.

Полученные результаты 

1. Во всех испытаниях аппроксимируемая функция попала в идеальный доверительный интервал 3 сигмы в 100% случаях при аппроксимации всех патчей, кроме релизного.(при условии, что хотя бы одна точка наблюдений использовалась для аппроксимации патча – в редких случаях все точки патча отбрасывались как анамальные).

2. Примерно в 25% экспериментов кривая выходит из коридора доверительного интервала в первом сегменте, в начальных 2-3 точках.

Результаты грубо объясняю так:

1. В начальной стадии кривой на ее форму влияет все 3 основных веса, но, поскольку точек в этой начальной части кривой достаточно мало, такого количества недостаточно для правильного подбора всех 3-х коэффициентов. Кроме того, из рассмотрения всегда была выброшена самая первая точка наблюдений – нулевой день, как, потенциально, анормальная, но именно эта первая точка должна вносить максимальный вклад в нелинейную форму кривой. Таким образом, для моделирования кривой на ее начальном участке, до первого патча, аппроксиматор использовал только ~20 точек, чего, вероятно, мало для правильного подбора 3-х коэффициентов.

2. Что же касается аппроксимации патчей – уже через месяц после выпуска игры наиболее существенное значение на форму тренда имеет ее асимптотическое значение, а также коэффициент патча, и, следовательно, процесс приближен к рассмотренному выше идеальному случаю, и, следовательно, доверительный интервал определяется весьма точно.

Наверняка, имеют место и традиционные проблемы нелинейной регрессии – несколько локальным минимумов функции потерь, а также близость функции градиента к нулю в широком диапазоне значений параметров.

Все это , конечно, не настоящее исследование, это все сделано на глазок, но я не вижу смысла для столь грубой модели проводить исследование более полноценное без экспериментов над большими объемами реальных данных.

Критика

Самое время поговорить о недостатках методики. Они очевидны.

Необходимо весьма много данных, за большое количество дней наблюдений, чтобы аппроксимируемый процесс становился похож на реальный. Если, скажем, мы располагаем только лишь неделей наблюдений после релиза проекта, то во многих случаях о нелинейной регрессии не может идти и речи, лучше использовать обычную линейную. Или даже скалярную оценку. Попытка применить к такому процессу нелинейную регрессию приводит к неожиданным значениям коэффициентов. Ниже я привел 2 примера неверной нелинейной аппроксимации. В первом примере мы видим огромный провал в нулевой точке. Во втором примере нет такого гигантского провала, но наблюдается возрастающий процесс. Оба примера являются следствием того, что для аппроксимации были использованы только 4 из 7-ми точек – нулевая точка и еще 2 случайных были отброшены как аномальные.

Это вполне реалистичные кейсы. После выхода игры в софтланч вполне возможны сбои и действительно из 7-ми дней наблюдений у нас вполне может остаться только 4 хороших дня. Количество инсталлов также вполне может быть около 1000 в день, как в рассмотренных примерах. 

Хотелось бы иметь модель, обеспечивающую более точные измерения даже в таких сложных ситуациях.

Что дальше?

Существует ли возможность повысить точность наблюдений?

Да, несомненно. Во введении я уже упоминал несколько потенциальных способов, и сейчас остановлюсь на этом вопросе чуть подробное.

1. Можно улучшить текущую методику, тщательнее проработав детали реализации, тщательнее подобрать гиперпараметры модели. Например, использовать другую, более точную, аппроксимирующую функцию, поэкспериментировать с разными оптимизаторами и видом функции потерь, более точно инициализировать начальные веса модели, добавить какие-нибудь эвристические ограничения на значения весов и т.д. 

2. Более точно оценить вид исходного распределения и его дисперсию и за счет этого сузить доверительный интервал. Например, известно, что дисперсия суммы нескольких независимых биномиально-распределенных величин меньше дисперсии одного биномиального распределения (статья в википеии), этот факт можно попробовать использовать. Ретеншен действительно легко представить в виде суммы нескольких случайных величин, каждая из которых соответствует одной стране или региону, однако независимость этих величин будет под вопросом, это еще следует доказать. Кроме того, этот метод даст заметный эффект только если матожидания у разных сегментов сильно отличаются между собой, поэтому общий выигрыш будет, вероятно, небольшим. Но зато он достается практически бесплатно, без какого-либо усовершенствования метода, только теоретическим обоснованием.

Кстати, я не встречал никаких работ, посвященных исследованию функции распределения ретеншена. Ни теоретических , ни практических. Если у читателей есть информация о подобной работе, был бы очень рад получить ссылочку.

1. Следующий, потенциальный способ повысить точность – использовать для аппроксимации какие-то дополнительные данные. Например, пусть мы хотим аппроксимировать ретеншен 1 дня, располагая данными за 7 дней. Однако, в таком случае, у нас есть также данные о ретеншене 2-го дня за 6 дней измерений, данные о ретеншене 3 дня за 5 дней… , данные о ретеншене 7-го дня за 1 день. Таким образом, можно говорить о ретеншене как о двумерной функции, в координатах (время от релиза, время от инсталла) или как о некоторой поверхности в 3d пространстве. Форма этой поверхности будет довольно сложной, поскольку на нее будут накладываться и сезонные явления и выпуск патчей и аномалии, кроме того существует явная корреляция между ретеншеном N дня и ретеншеном M дня. Но, зато, такой способ позволяет увеличить количество точек наблюдения квадратично! Линия общего тренда такой поверхности должна быть непрерывной и, следовательно, может быть представлена моделью с небольшим числом коэффициентов, количество которых возрастет не квадратично.

   Можно еще выше поднять размерность функции ретеншена и добавить еще больше обучающих данных, рассматривая не классический ретеншен, а роллинг ретеншен ограниченной глубины. Действительно, роллинг ретеншен – это 3d-функция в координатах (время от релиза, время от инсталла, глубина роллинга). Классический ретеншен тут является частным случаем роллинга, когда глубина роллинга равняется нулю. Такую трехмерную модель еще сложнее построить, необходимо преодолеть еще больше проблем, однако количество исходных данных увеличивается уже в кубе!

2. Следующий потенциальный способ поднять точность измерений – учесть данные, наблюдаемые в момент аномалий. Выше я отбросил все анормальные дни, однако, можно рассмотреть эти данные более детально. Тщательный анализ аномалий может позволить сохранить как минимум часть наблюдений. Например, можно заметить, что технический сбой длится не весь день, и охватывает не всех пользователей, и как минимум часть данных в аномальные дни мы сможем использовать. 

3. Построить сложную модель, использующую данных с других проектов.
   Вероятно, это самый мощный способ создать максимально точную аппроксимацию. Крупные паблишеры и аналитические компании располагают огромными датасетами, накопленными от проектов, ранее выпущенных в релиз. Наличие такого датасета позволяет применять сложные модели с большим количеством весов. С этой точки зрения задача аппроксимации ретеншена представляется уже как задача восстановления из помех некоторого сигнала с известными нам свойствами и подобна, например, задаче восстановления зашумленной картинки. Можно построить модель, решающую подобную задачу и обучить его на этом датасете. Такая модель будет способна спрогнозировать значение метрики проекта, возможно, уже по одной двум точкам наблюдения сразу после релиза.

4. Использовать готовые фрймворки для предсказания временных рядов, например Prophet, Neural Prophet, Nixtla/statsforecast. Я только лишь поверхностно знаком с возможностями Prophet и пока не берусь судить, насколько он хорош для данной задачи. С другими фреймворками я пока совсем не сталкивался. В лоб получить заметный эффект Prophet не получилось, ведь он не знает ничего о природе нашего процесса. Однако, если можно задать ему правильный вид нашей аппроксимирующей функции, мы несомненно получим более качественное предсказание, как минимум потому, что он хорошо умеет учитывать сезонные явления – не только недельные, но и годовые, а также нацелен на нелинейную аппроксимацию и учитывает ее тонкости.  Способен ли Prophet на большее, например, рассматривать процесс как двумерную функцию или трехмерную функцию, я пока не знаю, но планирую разобраться.

Заключение и выводы

Итак, подведу краткие итоги

1. Рассмотрена методика нелинейной регрессии метрики “ретеншен”, учитывающий недельную сезонность и выпуск патчей.

2. Произведены эксперименты с различными видами аппроксимирующей функции и сделана субъективная рекомендация о выборе вида функции.

3. Методика реализована в виде ноутбука Jupyter-ноутбука retention-rate-approximator, выложено в открытый доступ на Githab

4. Дальнейшие планируемые направления работ – использовать для решения задачи специализированные фреймворки для анализа временных рядов, построить нейросеть с большим количеством весов, обучить ее на большом объеме данных (возможно, частично, искусственно сгенерированных), построить модель для двумерной и трехмерной аппроксимации процесса.

5. Отдельно следует рассмотреть задачу обнаружения аномалий, а также вопросы использования в аппроксимации метрики данных, полученных в аномальные дни.

6. При разработки более сложных моделей уделить больше внимания построению интервальной оценки.

Источники

1. Binomial sum variance inequality https://en.wikipedia.org/wiki/Binomial_sum_variance_inequality

2. Василий Сабиров: Игра в цифры. Как аналитика позволяет видеоиграм жить лучше

3. В.П. Лисьев ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА: Учебное пособие/ Московский государственный университет экономики, статистики и информатики. – М., 2006. – 199 с.

4. Дмитрий Балтин. Ретеншен — основная метрика F2P игры, вероятностный подход. https://habr.com/ru/articles/726396/

5. К.В. Воронцов,  Машинное обучение. Нелинейная регрессия. Школа анализа данных, Яндекс. https://www.youtube.com/watch?v=–gJR8pd-jg 

6. Филипп Картаев. Дружелюбная эконометрика https://books.econ.msu.ru/Introduction-to-Econometrics/

7. Биномиальное распределение https://ru.wikipedia.org/wiki/Биномиальное_распределение

8. Метрика Retention. Что означает, как ее рассчитать и как ее улучшить https://gopractice.ru/product/retention/

9. Нормальное распределение https://ru.wikipedia.org/wiki/Нормальное_распределение

Центральная предельная теорема https://ru.wikipedia.org/wiki/Центральная_предельная_теорема

Мы часто обрабатываем в COMSOL Multiphysics экспериментальные данные. Обычно они характеризуют свойства материалов или другие входные параметры модели. Однако экспериментальные данные часто бывают зашумленными; они содержат погрешности эксперимента, которые мы не хотели бы вносить в модель. В этой статье мы расскажем, как подбирать гладкие кривые и поверхности под экспериментальные данные, используя базовые функциональные возможности COMSOL Multiphysics.

Подбор кривой как задача минимизации функции

Давайте посмотрим на график с экспериментальными точками, представленный ниже. Мы видим, что данные зашумлены, а выборка по оси x неравномерна. Эти экспериментальные данные могут характеризовать материал. Если характеристика материала зависит от переменной, расчитываемой в ходе решения, (например, теплопроводность, зависящая от температуры), то эти изначальные данные обычно не желательно напрямую использовать для конечно-элементного анализа. Такие зашумленные входные данные часто могут вызывать проблемы со сходимостью решателя по причинам, рассмотренным здесь. Если же мы аппроксимируем данные гладкой кривой, то сходимость модели, как правило, улучшается, а характеристика материала будет представлена более простой функцией.

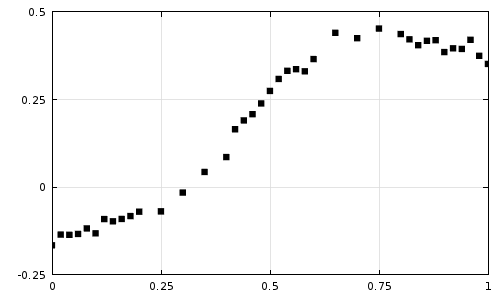
Экспериментальные данные, которые мы хотим аппроксимировать простой функцией.

Нам требуется найти функцию F(x), которая является наиболее точным приближением экспериментальных данных D(x). “Наиболее точное приближение” здесь означает функцию, минимизирующую интеграл квадрата разности экспериментальных данных и значений нашей приближенной функции, взятый по всему набору данных. Другими словами, мы хотим минимизировать

int_a^b (D(x)- F(x))^2 dx

В первую очередь мы должны решить, каким классом функций мы хотим аппроксимировать данные. Мы можем выбирать самые разные классы функций, при этом выбранная аппроксимирующая функция должна достаточно просто вычисляться. Опуская подробное обоснование, для максимальной устойчивости выберем следующую функцию:

F(x) = c_0left(frac{b-x}{b-a}right)^3 + c_1 left(frac{x-a}{b-a}right)left(frac{b-x}{b-a}right)^2 + c_2 left(frac{x-a}{b-a}right)^2left(frac{b-x}{b-a}right) + c_3 left(frac{x-a}{b-a}right)^3

В частном случае, когда a = 0, а b = 1, она имеет упрощенный вид:

F(x) = c_0(1-x)^3 + c_1 x(1-x)^2 + c_2 x^2(1-x) + c_3 x^3

Теперь требуется найти четыре коэффициента, обеспечивающих минимальное значение выражения:

R(c_0,c_1,c_2,c_3,x)= int_a^b (D(x)- F(c_0,c_1,c_2,c_3,x))^2 dx

Это похоже на задачу оптимизации, но мы не вводим ограничений на коэффициенты и предполагаем, что функция имеет единственный минимум. В точке этого минимума производные функции по коэффициентам будут равны нулю. Поэтому для подбора наилучшей функции мы должны найти такие значения коэффициентов, что

frac{partial R} {partial c_0} = frac{partial R} {partial c_1} = frac{partial R} {partial c_2} =frac{partial R} {partial c_3} = 0

Оказывается, эту задачу можно решить с помощью базовых функций COMSOL Multiphysics. Давайте посмотрим, как это сделать.

Решение задачи в COMSOL

Мы начинаем с создания нового файла с одномерным компонентом. Мы воспользуемся интерфейсом физики Global ODEs and DAEs (Глобальные обыкновенные дифференциальные уравнения и алгебраические дифференциальные уравнения), чтобы найти искомые коэффициенты, и будем использовать стационарный решатель. Для простоты выберем безразмерную единицу длины, как показано на снимке экрана ниже.

В настройках узла 1D component (Одномерный компонент) в поле Unit system (Система единиц) выберите None (Безразмерная).

Далее зададим геометрию. Геометрия задачи состоит из интервала (экспериментальные точки в нашем случае лежат в интервале от 0 до 1) и множества точек по оси x для каждой экспериментальной точки. Вы можете просто скопировать этот набор точек из электронной таблицы и вставить в поле Point (Точка), как показано ниже.

Добавьте точки, соответствующие экспериментальным данным, в интервал.

Считайте экспериментальные данные с помощью функции Interpolation (Интерполяция). Присвойте набору данных удобное имя (на снимке экрана внизу использовано просто D), активируйте опцию Use spatial coordinates as arguments (Использовать пространственные координаты в качестве аргументов) и убедитесь, что выбран вариант интерполяции между точками данных по умолчанию — Linear (Линейная).

Настройки импорта экспериментальных данных.

Задайте оператор интегрирования (Integration) на всех областях. Вы можете оставить наименование по умолчанию, intop1. Он будет использоваться для вычисления указанного выше интеграла.

Оператор интегрирования задан на всех областях.

Теперь задайте две переменных. Одна из них будет вашей функцией F, а другая — функцией R, которую требуется минимизировать. Так как в поле Geometric Entity Level (Уровень геометрических объектов) выбран вариант Entire Model (Вся модель), функция F будет задана на всей области как функция пространственной переменной x. С другой стороны, R везде задана скалярным значением и также доступна по всей модели. Как показано на снимке экрана ниже, мы можем ввести F как функцию c_0, c_1, c_2, c_3, а сами коэффициенты определим позднее.

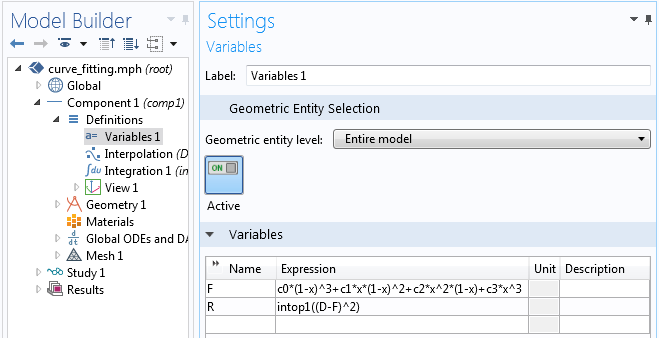
Определение подбираемой функции и целевой функции минимизации.

Далее мы используем интерфейс Global Equations (Глобальные уравнения), чтобы определить четыре уравнения, которым удовлетворяют четыре наших коэффициента. Если вы помните, мы хотим, чтобы производная функции R по каждому коэффициенту обращалась в нуль. Используя дифференциальный оператор d(f(x),x), мы можем ввести это условие так:

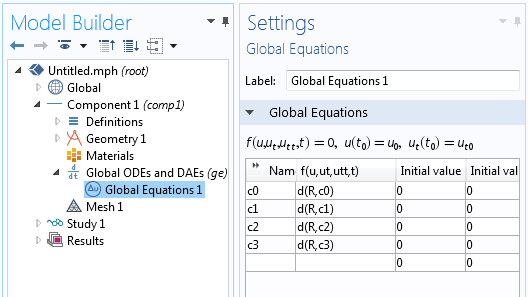
Глобальные уравнения используются для нахождения коэффициентов подбираемой функции.

Наконец, мы должны наложить на нашу одномерную область подходящую сетку. Как вы помните, ранее мы разместили в каждой точке экспериментальных данных геометрическую точку. С помощью подфункции Distribution (Распределение) функции Edge Mesh (Сетка на ребрах) мы можем разместить ровно один элемент между каждой парой точек данных. Дополнительных элементов не требуется, так как мы предполагаем, что интерполяция между точками набора данных линейная, но и меньшим числом элементов мы не обойдемся, не пропустив некоторые экспериментальные точки данных.

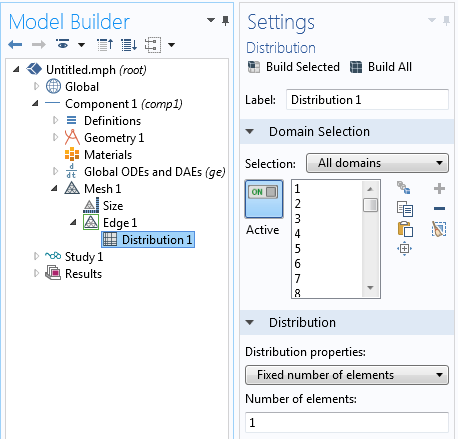
На каждом интервале данных должен располагаться один элемент.

Теперь мы можем решить стационарную задачу для нахождения численных значений коэффициентов, а затем построить результаты. На графике ниже мы видим построенный набор начальных точек, линейную интерполяцию между ними и подобранную функцию, полученную при расчете. Мы минимизировали интеграл от квадрата разности между этими кривыми на данном интервале и получили гладкую и простую функцию, достаточно хорошо аппроксимирующую наши данные.

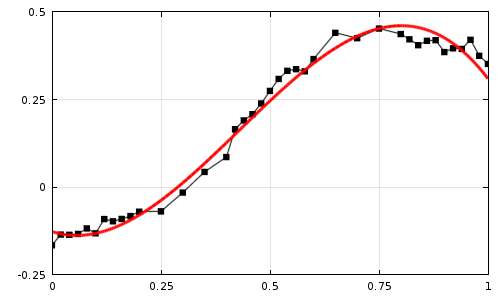
Экспериментальные данные с линейной интерполяцией (черный) и подобранная функция (красный).

Дальнейшие расширения

Проделанная нами работа на самом деле достаточно проста, и подобные кривые можно рассчитать в любом редакторе электронных таблиц и во многих других программных инструментах. Но этот же подход позволяет достичь гораздо большего. Мы не ограничены использованием данной подобранной функции. Вы можете выбрать любую функцию, но лучше выбирать функцию, являющуюся суммой набора ортогональных функций. Например, можно попробовать следующую функцию:

F(x) = c_0 + c_1sin ( pi x /4 ) + c_2cos ( pi x /4 ) + c_3sin ( pi x /2 ) + c_4cos ( pi x /2 )

Имейте в виду, что вычисляемые коэффициенты, входящие в подбираемую функцию, должны быть линейными. Следует избегать нелинейных коэффициентов аппроксимации, таких как F(x) = c_0 + c_1sin ( pi x /c_3 ) + c_2cos ( pi x /c_4), поскольку такая задача может оказаться слишком нелинейной, чтобы сходиться.

Но что делать, если у вас есть двухмерный или трехмерный набор данных? Вы можете применить к ним точно такой же подход. Разница в том, что теперь мы задаем двухмерную или трехмерную область. Области не обязательно должны быть декартовыми, вы можете переключиться на другую систему координат.

Давайте посмотрим на некоторый набор данных, измеренных на показанной ниже области.

Набор данных на двухмерной области. Мы хотим подобрать поверхность, наиболее соответствующую высотам этих точек.

Так как данные собраны на этой кольцеобразной области и, по видимости, изменяются в зависимости от радиальной и азимутальной координат (r, theta), а не от декартовых координат, мы можем подобрать такую функцию:

F(x) = c_0 + c_1r cos ( theta ) +c_2 r sin ( theta )+ c_3(2r^2-1) + c_4 r^2 cos ( 2theta ) +c_5 r^2 sin ( 2theta )

Мы можем следовать такой же процедуре, как и раньше. Теперь мы будем интегрировать по двухмерной области, а не по кривой, и запишем выражение с использованием цилиндрической системы координат.

Рассчитанная поверхность наилучшего приближения показана выше.

Заключение

Вы видите, что базовые функци пакета COMSOL Multiphysics предоставляют чрезвычайно гибкие возможности для поиска кривых наилучшего приближения в одномерном, двухмерном и трехмерном пространствах с помощью описанных методов.

В некоторых случаях может потребоваться не ограничиваться простым подбором кривых и вводить дополнительные ограничения. Тогда вы можете воспользоваться модулем Оптимизация, который также может подбирать эти кривые и решать множество других задач. Введение в подбор кривых с помощью модуля Оптимизация и в связанную задачу оценки параметров вы найдете здесь:

• Подбор кривой данных модели материала для экспериментальных данных