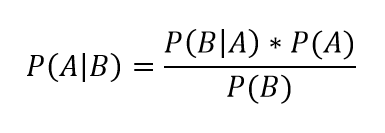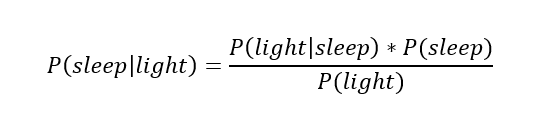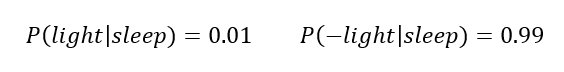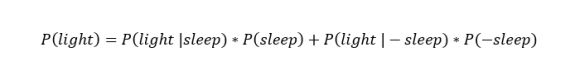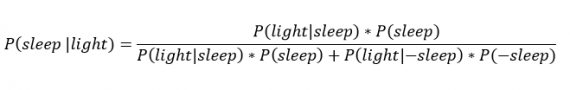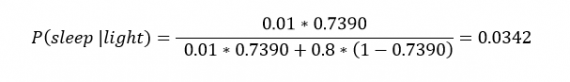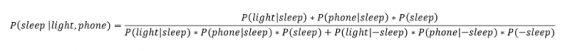Как найти априорную вероятность

Понимаем теорему Байеса

Перевод статьи подготовлен специально для студентов базового и продвинутого курсов «Математика для Data Science».

---

Теорема Байеса – одна из самых известных теорем в статистике и теории вероятности. Даже если вы не работаете с расчетами количественных показателей, вероятно, вам в какой-то момент пришлось познакомиться с этой теоремой во время подготовки к экзамену.

P(A|B) = P(B|A) * P(A)/P(B)

Вот так она выглядит, но что это значит и как работает? Сегодня мы это узнаем и углубимся в теорему Байеса.

Основания для подтверждения наших суждений

В чем вообще заключается смысл теории вероятности и статистики? Одно из наиболее важных применений относится к принятию решений в условиях неопределенности. Когда вы принимаете решение совершить какое-либо действие (если, конечно, вы человек разумный), вы делаете ставку на то, что после завершения этого действия оно повлечет за собой результат лучший, чем если бы этого действия не произошло… Но ставки – это вещь ненадежная, как же вы в конечном итоге принимаете решение делать ли тот или иной шаг или нет?

Так или иначе вы оцениваете вероятность успешного исхода, и, если эта вероятность выше определенного порогового значения, вы предпринимаете шаг.

Таким образом, возможность точно оценить вероятность успеха имеет решающее значение для принятия правильных решений. Несмотря на то, что случайность всегда будет играть определенную роль в конечном исходе, вам следует учиться правильно использовать эти случайности и оборачивать их в свою пользу с течением времени.

Именно здесь вступает в силу теорема Байеса – она дает нам количественную основу для сохранения нашей веры в исход действия по мере изменений окружающих факторов, что, в свою очередь, позволяет нам со временем совершенствовать процесс принятия решений.

Разберем формулу

Давайте еще раз посмотрим на формулу:

P(A|B) = P(B|A) * P(A)/P(B)

Здесь:

• P(A|B) – вероятность наступления события А, при условии, что событие В уже случилось;
• P(B|A) – вероятность наступления события В, при условии, что событие А уже случилось. Сейчас это выглядит как какой-то замкнутый круг, но мы скоро поймем, почему формула работает;
• P(A) – априорная (безусловная) вероятность наступления события А;
• P(B) – априорная (безусловная) вероятность наступления события В.

P(A|B) – это пример апостериорной (условной) вероятности, то есть такой, которая измеряет вероятность какого-то определенного состояния окружающего мира (а именно состояния, при котором произошло событие В). Тогда как P(A) – это пример априорная вероятности, которая может быть измерена при любом состоянии окружающего мира.

Давайте посмотрим на теорему Байеса в действии на примере. Предположим, что недавно вы закончили курс по анализу данных от bootcamp. Вы еще не получили ответа от некоторых компаний, в которых вы проходили собеседование, и начинаете волноваться. Итак, вы хотите рассчитать вероятность того, что конкретная компания сделает вам предложение об устройстве на работу, при условии, что уже прошло три дня, а они вам так и не перезвонили.

Перепишем формулу в терминах нашего примера. В данном случае, исход А (Offer) – это получения предложения о работе, а исход В (NoCall) – «отсутствие телефонного звонка в течение трех дней». Исходя из этого, нашу формулу можно переписать так:

P(Offer|NoCall) = P(NoCall|Offer) * P(Offer) / P(NoCall)

Значение P(Offer|NoCall) — это вероятность получения предложения при условии, что звонка нет в течение трех дней. Эту вероятность оценить крайне сложно.

Однако обратной вероятности, P(NoCall|Offer), то есть отсутствию телефонного звонка в течение трех дней, при учете, что в итоге вы получили предложение о работе от компании, вполне можно привязать какое-то значение. Из разговоров с друзьями, рекрутерами и консультантами вы узнаете, что эта вероятность небольшая, но иногда компания все же может сохранять тишину в течение трех дней, если она все еще планирует пригласить вас на работу. Итак, вы оцениваете:

P(NoCall|Offer) = 40%

40% — это неплохо и кажется, еще есть надежда! Но мы еще не закончили. Теперь нам нужно оценить P(Offer), вероятность выхода на работу. Все знают, что поиск работы – это долгий и трудный процесс, и возможно вам придется проходить собеседование несколько раз, прежде чем вы получите это предложение, поэтому вы оцениваете:

P(Offer) = 20%

Теперь нам осталось оценить P(NoCall), вероятность, что вы не получите звонок от компании в течение трех дней. Существует множество причин, по которым вам могут не перезвонить в течение трех дней – они могут отклонить вашу кандидатуру или до сих пор проводить собеседования с другими кандидатами, или рекрутер просто заболел и поэтому не звонит. Что ж, есть множество причин, по которым вам могли не позвонить, так что эту вероятность вы оцениваете как:

P(NoCall) = 90%

А теперь собрав это все вместе, мы можем рассчитать P(Offer|NoCall):

P(Offer|NoCall) = 40% * 20%/90% = 8.9%

Это довольно мало, так что, к сожалению, рациональнее оставить надежду на эту компанию (и продолжать отправлять резюме в другие). Если это все еще кажется немного абстрактным, не переживайте. Я чувствовал то же самое, когда впервые узнал про теорему Байеса. Теперь давайте разберемся, как мы пришли к этим 8,9% (имейте в виду, что ваша изначальная оценка в 20% уже была низкой).

Интуиция, стоящая за формулой

Помните, мы говорили о том, что теорема Байеса дает основания для подтверждения наших суждений? Так откуда же они берутся? Они берутся из априорной вероятности P(A), которая в нашем примере зовется P(Offer), по сути, это и есть наше изначальное суждение том, насколько вероятно, что человек получит предложение о работе. В нашем примере вы можете считать, что априорная вероятность – это вероятность того, что вы получите предложение о работе в тот же момент, когда покинете собеседование.

Появляется новая информация – прошло 3 дня, а компания вам так и не перезвонила. Таким образом мы используем другие части уравнения, чтобы скорректировать нашу априорную вероятность нового события.

Давайте рассмотрим вероятность P(B|A), которая в нашем примере называется P(NoCall|Offer). Когда вы впервые видите теорему Байеса, вы задаетесь вопросом: Как понять откуда взять вероятность P(B|A)? Если я не знаю, чему равна вероятность P(A|B), то каким магическом образом я должен узнать, чему равна вероятность P(B|A)? Я вспоминаю фразу, которую однажды сказал Чарльз Мангер:

«Переворачивайте, всегда переворачивайте!»
— Чарльз Мангер

Он имел в виду, что, когда вы пытаетесь решить сложную задачу, ее нужно перевернуть с ног на голову и посмотреть на нее под других углом. Именно это и делает теорема Байеса. Давайте переформулируем теорему Байеса в терминах статистики, чтобы сделать ее более понятной (об это я узнал отсюда):

Для меня, например, такая запись выглядит понятнее. У нас есть априорная гипотеза (Hypothesis) — о том, что мы получили работу, и наблюдаемые факты — доказательства (Evidence) – телефонного звонка нет в течение трех дней. Теперь мы хотим узнать вероятность того, что наша гипотеза верна, с учетом предоставленных фактов. Как бы решили выше, у нас есть вероятность P(A) = 20%.

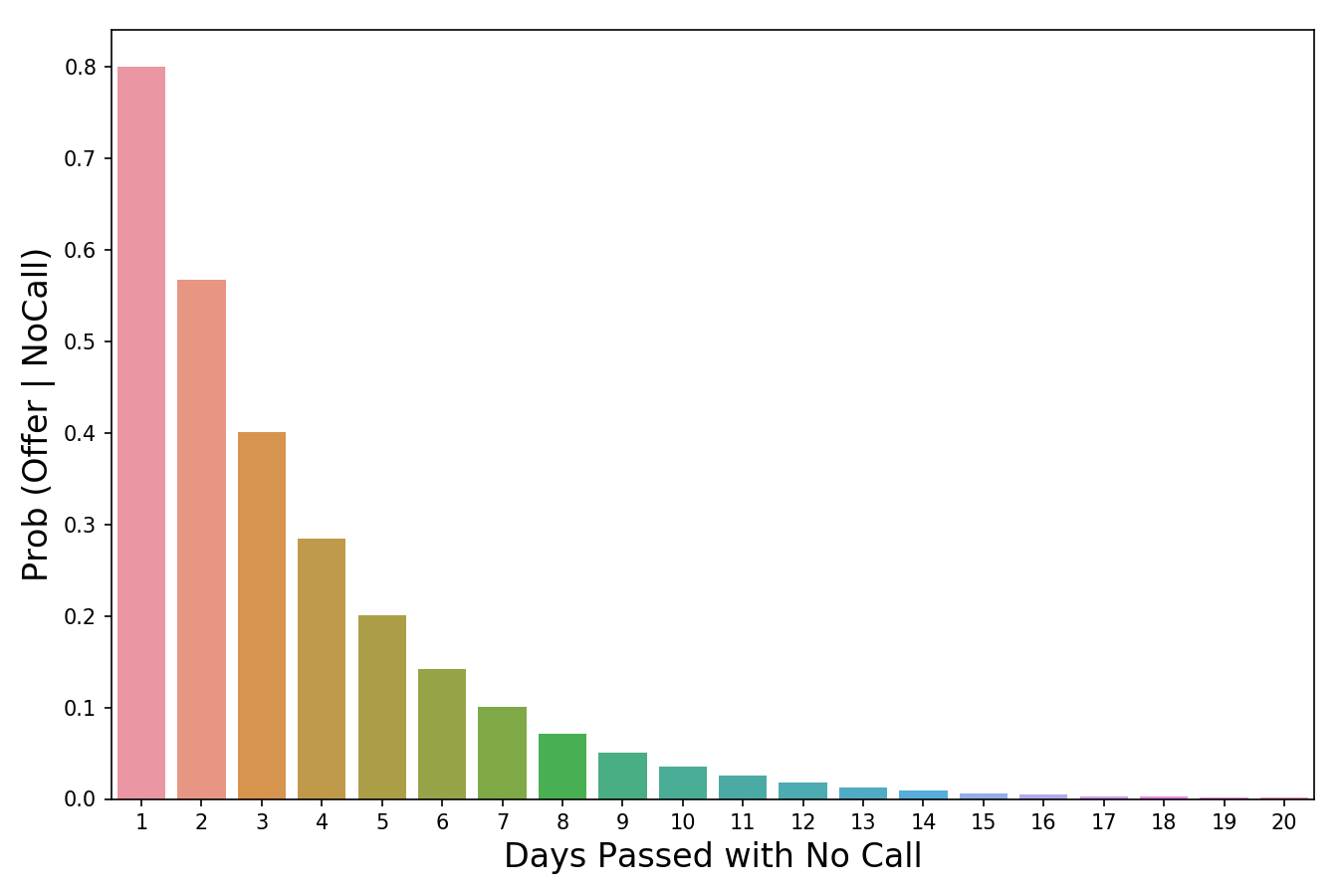
Время переворачивать все с ног на голову! Мы используем P(Evidence|Hypothesis), чтобы посмотреть на задачу с другой стороны и спрашиваем: «Какова вероятность наступления этих событий-доказательств в мире, где наша гипотеза верна?». Итак, если вернуться к нашему примеру, мы хотим знать, насколько вероятно, что, если нам не звонят в течение трех дней, нас все равно возьмут на работу. В изображении выше я пометил P(Evidence|Hypothesis), как “scaler” (скейлер), потому что это слово хорошо отражает суть значения. Когда мы умножаем его на априорное значение, он уменьшает или увеличивает вероятность события, в зависимости от того «вредит» ли какое-либо событие-доказательство нашей гипотезе. В нашем случае, чем больше дней проходит без звонка, тем меньше вероятность того, что нас позовут на работу. 3 дня тишины – это уже плохо (они сокращают нашу априорную вероятность на 60%), тогда как 20 дней без звонка полностью уничтожат надежду на получение работы. Таким образом, чем больше накапливается событий-доказательств (больше дней проходит без телефонного звонка), тем быстрее скейлер уменьшает вероятность. Скейлер – это механизм, который теорема Байеса использует для корректировки наших суждений.

Есть одна вещь, с которой я боролся в оригинальной версии этой статьи. Это была формулировка того, почему P(Evidence|Hypothesis) легче оценить, чем P(Hypothesis|Evidence). Причина этого заключается в том, что P(Evidence|Hypothesis) – это гораздо более ограниченная область суждений о мире. Сужая область, мы упрощаем задачу. Можно провести аналогию с огнем и дымом, где огонь – это наша гипотеза, а наблюдение дыма – событие, доказывающее наличие огня. P(огонь|дым) оценить сложнее, поскольку много чего может вызвать дым – выхлопные газы автомобилей, фабрики, человек, который жарит гамбургеры на углях. При этом P(дым|огонь) оценить проще, поскольку в мире, где есть огонь, почти наверняка будет и дым.

Значение вероятности уменьшается по мере того, сколько проходит дней без звонка.

Последняя часть формулы, P(B) или же P(Evidence) – это нормализатор. Как следует из названия, его цель – нормализовать произведение априорной вероятности и скейлера. Если бы у на не было нормализатора, мы бы имели следующее выражение:

Заметим, что произведение априорной вероятности и скейлера равно совместной вероятности. И поскольку одно из составляющих в нем P(Evidence), то на совместную вероятность повлияла бы маленькая частота событий.

Это проблема, поскольку совместная вероятность – это значение, включающее в себя все состояния мира. Но нам то не нужны все состояния, нам нужны только те состояния, которые были подтверждены событиями-доказательствами. Другими словами, мы живем в мире, где события – доказательства уже произошли, и их количество уже не имеет значения (поэтому мы не хотим, чтобы они влияли на наши расчеты в принципе). Деление произведения априорной вероятности и скейлера на P(Evidence) меняет его с совместной вероятности на условную(апостериорную). Условная вероятность учитывает только те состояния мира, в которых произошло событие-доказательство, именно этого мы и добиваемся.

Еще одна точка зрения, с которой можно взглянуть на то, почему мы делим скейлер на нормализатор, заключается в том, что они отвечают на два важных вопроса – и их отношение объединяет эту информацию. Давайте возьмем пример из моей недавней статьи про Байеса. Предположим, мы пытаемся выяснить, является ли наблюдаемое животное кошкой, основываясь на единственном признаке – ловкости. Все, что мы знаем, так это то, что животное, о котором мы говорим, проворное.

1. Скейлер говорит нам о том, у какого процента кошек хорошо с ловкостью. Это значение должно быть довольно высоким, допустим, 0.90.
2. Нормализатор говорит нам, какой процент животных ловок в принципе. Это значение должно быть средним, скажем, 0.50.
3. Отношение 0.90/0.50 = 1.8 говорит о том, что нужно изменить априорную вероятность, поскольку, если вы раньше считали иначе, настало время изменить свое мнение, поскольку вы скорее всего имеете дело с кошкой. Причина, по которой так можно считать заключается в том, что мы наблюдали некоторые доказательство того, что животное ловкое. Затем мы выяснили, что доля ловких кошек больше, чем доля ловких животных в целом. Учитывая, что на данный момент мы знаем только такую доказательную часть и ничего больше, разумно было бы пересмотреть наши убеждения в сторону мыслей о том, что мы все-таки наблюдаем кошку.

Подведем итог

Теперь, когда мы знаем, как трактовать каждую часть формулы, мы можем наконец собрать все воедино и посмотреть на то, что получилось:

• Сразу после собеседования, мы устанавливаем априорную вероятность – шанс того, что нас возьмут на работу равен 20%.
• Чем больше дней без звонка проходит, тем меньше становится вероятность того, что нас возьмут на работу. Например, после трех дней без звонка, мы считаем, что в мире, где мы эту работу можем получить, есть всего 40% вероятность того, что компания будет тянуть так долго, прежде чем вам позвонит. Умножаем скейлер на априорную вероятность и получаем 20% * 40% = 8%
• Наконец, мы понимаем, что 8% было рассчитано для всех состояний, в которых может находиться мир. Но нас волнуют только те состояния, где нам не позвонили в течение трех дней. Для того, чтобы работать только с этими состояниями, мы принимаем за 90% априорную вероятность того, что в течение трех дней звонка не будет и получаем нормализатор. Мы делим ранее полученные 8% на нормализатор 8% / 90% = 8.9% и получаем окончательный ответ. Итого, при всех состояниях мира, если вы не получили звонка от компании в течение трех дней, вероятность получить работу составляет всего 8.9%.

Надеюсь, эта статья оказалась для вас полезной!

What Is Prior Probability?

Prior probability, in Bayesian statistics, is the probability of an event before new data is collected. This is the best rational assessment of the probability of an outcome based on the current knowledge before an experiment is performed.

Prior probability can be compared with posterior probability.

Understanding Prior Probability

The prior probability of an event will be revised as new data or information becomes available, to produce a more accurate measure of a potential outcome. That revised probability becomes the posterior probability and is calculated using Bayes’ theorem. In statistical terms, the posterior probability is the probability of event A occurring given that event B has occurred.

Example

For example, three acres of land have the labels A, B, and C. One acre has reserves of oil below its surface, while the other two do not. The prior probability of oil being found on acre C is one third, or 0.333. But if a drilling test is conducted on acre B, and the results indicate that no oil is present at the location, then the posterior probability of oil being found on acres A and C become 0.5, as each acre has one out of two chances.

Bayes’ Theorem



P

(

A

∣

B

)

 

=

 

P

(

A

∩

B

)

P

(

B

)

 

=

 

P

(

A

)

 

×

 

P

(

B

∣

A

)

P

(

B

)

where:

P

(

A

)

 

=

 

the prior probability of 

A

 occurring

P

(

A

∣

B

)

=

 

the conditional probability of 

A

 

 given that 

B

 occurs

P

(

B

∣

A

)

 

=

 

the conditional probability of 

B

 

 

 given that 

A

 occurs

begin{aligned}&P(Amid B) = frac{P(Acap B)}{P(B)} = frac{P(A) times P(Bmid A)}{P(B)}\&textbf{where:}\&P(A) = text{the prior probability of }Atext{ occurring}\&P(Amid B)= text{the conditional probability of }A\&qquadqquadquad text{ given that }Btext{ occurs}\&P(Bmid A) = text{the conditional probability of }B\&qquadqquadquad text{ given that }Atext{ occurs}\&P(B) = text{the probability of }Btext{ occurring}end{aligned}

​P(A∣B) = P(B)P(A∩B)​ = P(B)P(A) × P(B∣A)​where:P(A) = the prior probability of A occurringP(A∣B)= the conditional probability of A  given that B occursP(B∣A) = the conditional probability of B   given that A occurs​

If we are interested in the probability of an event of which we have prior observations; we call this the prior probability. We’ll deem this event A, and its probability P(A). If there is a second event that affects P(A), which we’ll call event B, then we want to know what the probability of A is given B has occurred. In probabilistic notation, this is P(A|B), and is known as posterior probability or revised probability. This is because it has occurred after the original event, hence the post in posterior. This is how Baye’s theorem uniquely allows us to update our previous beliefs with new information.

В байесовском статистическом выводе априорное распределение вероятностей (англ. prior probability distribution, или просто prior) неопределённой величины  — распределение вероятностей, которое выражает предположения о до учёта экспериментальных данных. Например, если  — доля избирателей, готовых голосовать за определённого кандидата, то априорным распределением будет предположение о до учёта результатов опросов или выборов. Противопоставляется апостериорной вероятности.

Согласно теореме Байеса, нормализованное произведение априорного распределения на функцию правдоподобия является условным распределением неопределённой величины согласно учтённым данным.

Априорное распределение часто задается субъективно опытным экспертом. При возможности используют сопряжённое априорное распределение, что упрощает вычисления.

Параметры априорного распределения называют гиперпараметрами, чтобы отличить их от параметров модели данных. Например, если используется бета-распределение для моделирования распределения параметра распределения Бернулли, то:

Информативное априорное распределение[править | править код]

Информативное априорное распределение выражает конкретную информацию о переменной.

Например, подходящим априорным распределением для температуры воздуха завтра в полдень будет нормальное распределение со средним значением, равным температуре сегодня в полдень, и дисперсией, равной ежедневной дисперсии температуры.

Таким образом, апостериорное распределение для одной задачи (температуры сегодня) становится априорным для другой задачи (температуры завтра); чем больше свидетельств накапливается в таком априори, тем менее оно зависит от исходного предположения и более — от накопленных данных.

Неинформативное априорное распределение[править | править код]

Неинформативное априорное распределение выражает размытую или общую информацию о переменной.

Такое название не очень точно, более точным было бы не очень информативное априори или объективное априори, так как свойства распределения не назначаются субъективно.

Например, такое априори может выражать «объективную» информацию о том, что «переменная может быть только положительной» или «переменная лежит в интервале».

Простейшим и старейшим правилом назначения неинформативного априори является принцип безразличия, который назначает равные вероятности для всех возможностей.

В задачах оценки параметра использование неинформативных априори обычно приносит результаты, которые мало отличаются от традиционных, так как функция правдоподобия часто приносит больше информации, чем неинформативные априори.

Были предприняты попытки найти логические априори (англ. a priori probability), которые бы следовали из самой природы вероятности. Это является предметом философской дискуссии, которая разделила последователей байесовского подхода на две группы: «объективных» (которые верят, что такое априори существует во многих прикладных ситуациях) и «субъективных» (которые верят, что априорные распределения обычно представляют субъективные мнения и не могут быть строго обоснованы (Williamson 2010)). Возможно, сильнейший аргумент в пользу объективного байесизма был дан Эдвином Томпсоном Джейнсом.

В качестве примера естественного априори, следуя Джейнсу (2003), рассмотрим ситуацию, когда известно, что мяч спрятан под одной из трех чашек A, B или C, но нет никакой другой информации. В этом случае равномерное распределение интуитивно кажется единственно обоснованным. Более формально, проблема не изменится, если поменять местами названия чашек. Поэтому стоит выбрать такое априорное распределение, чтобы перестановка названий его не изменяла. И равномерное распределение является единственным подходящим.

Некорректное априорное распределение[править | править код]

Если теорема Байеса записана в виде:

то очевидно, что она останется верной, если все априорные вероятности P(A_i) и P(A_j) будут умножены на одну и ту же константу; то же верно для непрерывных случайных величин. Апостериорные вероятности останутся нормированными на сумму (или интеграл) 1, даже если априорные не были нормированными. Таким образом, априорное распределение должно задавать только верные пропорции вероятностей.

См. также[править | править код]

• Априорная вероятность Джеффри
• Апостериорная вероятность
• Теорема Байеса
• Байесианизм

Литература[править | править код]

• Williamson, Jon (2010). “review of Bruno di Finetti. Philosophical Lectures on Probability” (PDF). Philosophia Mathematica. 18 (1): 130&ndash, 135. DOI:10.1093/philmat/nkp019. Архивировано из оригинала (PDF) 2011-06-09. Дата обращения 2010-07-02.

Возможно, вы никогда не слышали про теорему Байеса, но пользовались ей постоянно. Например, изначально вы оценили вероятность получения прибавки к зарплате как 50%. Получив положительные отзывы от менеджера, вы скорректировали оценку в лучшую сторону, и, наоборот, уменьшили ее, если сломали кофеварку на работе. Так происходит уточнение значения вероятности по мере аккумулирования информации.

Основная идея теоремы Байеса состоит в том, чтобы получить большую точность оценки вероятности события путем учета дополнительных данных.

Принцип прост: есть первоначальная основная оценка вероятности, которую уточняют c получением большего количества информации.

Формула Байеса

Интуитивные действия формализуются в простом, но мощном уравнении (формула вероятности Байеса):

Левая часть уравнения — апостериорная оценка вероятности события А при условии наступления события В (т. н. условная вероятность).

• P(A)  — вероятность события А (основная, априорная оценка);
• P(B|A) — вероятность (также условная), которую мы получаем из наших данных;
• а P(B) — константа нормировки, которая ограничивает вероятность значением 1.

Это короткое уравнение является основой байесовского метода.

Абстрактность событий А и В не позволяет четко осознать смысл этой формулы. Для понимания сути теоремы Байеса рассмотрим реальную задачу.

Пример

Одной из тем, над которой я работаю, является изучение моделей сна. У меня есть данные за два месяца, записанные с помощью моих часов Garmin Vivosmart, показывающие, во сколько я засыпаю и просыпаюсь. Окончательная модель, показывающая наиболее вероятное распределение вероятности сна как функцию времени (MCMC — приблизительный метод), приведена ниже.

На графике приведена вероятность того, что я сплю, в зависимости лишь от времени. Как она изменится, если учесть время, в течение которого включен свет в спальне? Для уточнения оценки и нужна теорема Байеса. Уточненная оценка основана на априорной и имеет вид:

Выражение слева — вероятность того, что я сплю, при условии, что известно, включен ли свет в моей спальне. Априорная оценка в данный момент времени (приведена на графике выше) обозначена как P(sleep). Например, в 10:00 вечера априорная вероятность того, что я сплю, равна 27,34%.

Добавим больше информации, используя вероятность P(bedroom light|sleep), полученную из наблюдаемых данных.

Из собственных наблюдений мне известно следующее: вероятность того, что я сплю, когда свет включен, равна 1%.

Вероятность того, что свет выключен во время сна, равна 1-0,01 = 0,99 (знак «-» в формуле означает противоположное событие), потому что сумма вероятностей противоположных событий равна 1. Когда я сплю, то свет в спальне либо включен, либо выключен.

Наконец, уравнение также включает в себя константу нормировки P(light) — вероятность того, что свет включен. Свет бывает включен и когда я сплю, и когда бодрствую. Поэтому, зная априорную вероятность сна, вычислим константу нормировки так:

Вероятность того, что свет включен, учтена в обоих вариантах: либо я сплю, либо нет (P (-sleep) = 1 — P (sleep) — это вероятность того, что я не сплю.)

Вероятность того, что свет включен в тот момент, когда я не сплю, равна P(light|-sleep), и определяется путем наблюдения. Мне известно, что свет горит, когда я бодрствую, с вероятностью 80% (это означает, что есть 20% вероятность того, что свет не включен, если я бодрствую).

Окончательное уравнение Байеса принимает вид:

Оно позволяет вычислить вероятность того, что я сплю, при условии, что свет включен. Если нас интересует вероятность того, что свет выключен, нужно каждую конструкцию P(light|… заменить на P(-light|….

Давайте посмотрим, как используют полученные символьные уравнения на практике.

Применим формулу к моменту времени 22:30 и учтем, что свет включен. Мы знаем, вероятность того, что я спал, равна 73,90%. Это число — отправная точка для нашей оценки.

Уточним его, учтя информацию об освещении. Зная, что свет включен, подставим числа в формулу Байеса:

Дополнительные данные резко изменили оценку вероятности: от более 70% до 3,42%. Это показывает силу теоремы Байеса: мы смогли уточнить нашу первоначальную оценку ситуации, включив в нее больше информации. Возможно, мы уже интуитивно делали это раньше, но теперь, рассуждая об этом в терминах формальных уравнений, мы смогли подтвердить наши прогнозы.

Python

Рассмотрим еще один пример. Что если на часах 21:45 и свет выключен? Попытайте рассчитать вероятность самостоятельно, считая априорную оценку равной 0.1206.

Вместо того, чтобы каждый раз считать вручную, я написал простой код на Python для выполнения этих вычислений, который вы можете попробовать в Jupyter Notebook. Вы получите следующий ответ:

Time: 09:45:00 PM            Light is OFF.

The prior probability of sleep: 12.06%
The updated probability of sleep: 40.44%

И снова дополнительная информация меняет нашу оценку. Теперь, если моя сестра захочет позвонить мне в 21:45 зная, что мой свет включен, она может воспользоваться этим уравнением, чтобы определить, смогу ли я взять трубку (предполагая, что я беру трубку только бодрствующим)! Кто говорит, что статистика неприменима повседневной жизни?

Визуализация вероятности

Наблюдение за вычислениями полезно, но визуализация помогает добиться более глубокого понимания результата. Я всегда стараюсь использовать графики, чтобы генерировать идеи, если они сами не приходят при простом изучении уравнений. Мы можем визуализировать априорное и апостериорное распределения вероятности сна с использованием дополнительных данных:

Когда свет включен, график смещается вправо, указывая на то, что я с меньшей вероятностью сплю в данный момент времени. Аналогично, график смещается влево, если мой свет выключен. Понять смысл теоремы Байеса непросто, но эта иллюстрация наглядно демонстрирует, зачем ее нужно использовать. Формула Байеса — инструмент для уточнения прогнозов с помощью дополнительных данных.

Что, если есть еще больше данных?

Зачем останавливаться на освещении в спальне? Мы можем использовать еще больше данных в нашей модели для дальнейшего уточнения оценки (пока данные остаются полезными для рассматриваемого случая). Например, я знаю, что если мой телефон заряжается, то я сплю с вероятностью 95%. Этот факт можно учесть в нашей модели.

Предположим, что вероятность того, что мой телефон заряжается, не зависит от освещения в спальне (независимость событий — это достаточно сильное упрощение, но оно позволит сильно облегчить задачу). Составим новое, еще более точное выражение для вероятности:

Получившаяся формула выглядит громоздко, но, используя код на Python, мы можем написать функцию, которая будет производить расчет. Для любого момента времени и любой комбинации наличия освещения/зарядки телефона эта функция возвращает уточненную вероятность того, что я сплю.

Пропустим математику (все равно считать будет компьютер) и перейдем к результатам:

Time is 11:00:00           PM Light is ON           Phone IS NOT charging.

The prior probability of sleep: 95.52%
The updated probability of sleep: 1.74%

В 23:00 без дополнительной информации мы могли почти с полной вероятностью сказать, что я сплю. Однако, как только у нас будет дополнительная информация о том, что свет включен, а телефон не заряжается, мы заключаем, что вероятность того, что я сплю, практически равна нулю. Вот еще один пример:

Time is 10:15:00 PM           Light is OFF           Phone IS charging.

The prior probability of sleep: 50.79%
The updated probability of sleep: 95.10%

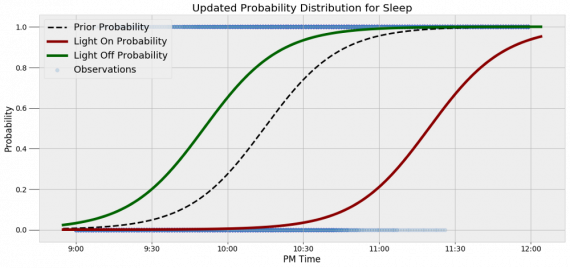
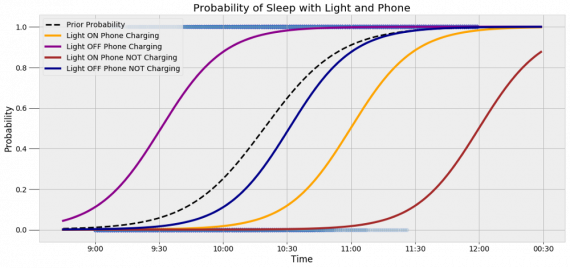
Вероятность смещается вниз или вверх в зависимости от конкретной ситуации. Чтобы продемонстрировать это, рассмотрим четыре конфигурации дополнительных данных и то, как они изменяют распределение вероятности:

На этом графике представлено много информации, но главный смысл состоит в том, что кривая вероятности изменяется в зависимости от дополнительных факторов. По мере добавления других данных мы будем  получать более точную оценку.

Заключение

Теорема Байеса и другие статистические понятия могут быть трудными для понимания, когда они представлены абстрактными уравнениями, использующими только буквы или выдуманные ситуации. Настоящее обучение приходит, когда мы применяем абстрактные понятия в реальных задачах.

Успех в области data science — это непрерывное обучение, добавление новых методов в набор навыков и поиск оптимального метода для решения задач. Теорема Байеса позволяет уточнять наши оценки вероятности с помощью дополнительной информации для более качественного моделирования реальности. Увеличение количества информации позволяет получать более точные прогнозы, и метод Байеса оказывается полезным инструментом для решения этой задачи.

Я приветствую обратную связь, дискуссию и конструктивную критику. Связаться со мной можно в Twitter: @koehrsen_will.

Оригинал

---

Может быть интересно:

• Недавно ученые смоделировали поведение религиозных групп, и предсказали вероятность этнического конфликта европейцев с беженцами с Ближнего востока.
• Как работать с векторными представлениями слов;
• Как работает нейронная сеть — алгоримы, обучение, активация

Что такое априорная вероятность?

Априорная вероятность относится к вероятности возникновения события, когда существует конечное количество исходов, и каждый из них имеет одинаковую вероятность. Исходы с априорной вероятностью не зависят от предшествующего исхода. Или, другими словами, любые результаты на сегодняшний день не дадут вам преимущества в прогнозировании будущих результатов. Подбрасывание монеты обычно используется для объяснения априорной вероятности. Вероятность завершения игры орлом или решкой составляет 50% при каждом подбрасывании монеты, независимо от того, выпадет ли у вас решка или орел. Самый большой недостаток этого метода определения вероятностей заключается в том, что он может применяться только к конечному набору событий, поскольку большинство реальных событий, которые нас волнуют, подвержены условной вероятности, по крайней мере, в некоторой степени. Априорная вероятность также называется классической вероятностью.

Понимание априорной вероятности

Априорная вероятность — это в значительной степени теоретическая основа для вероятностей, которые могут быть ограничены небольшим количеством результатов. Формула для вычисления априорной вероятности очень проста:

Априорная вероятность = желаемый результат (ы) / общее количество результатов

Таким образом, априорная вероятность выпадения шестерки на шестигранной кости равна единице (желаемый результат — шесть), деленной на шесть. Таким образом, у вас есть 16% шанс выпадения шестерки и точно такой же шанс с любым другим числом, которое вы выберете на кубике. Конечно, априорные вероятности можно складывать в набор результатов, поэтому ваши шансы выпадения четного числа на одном кубике увеличиваются до 50% просто потому, что желаемых результатов больше.

Пример априорной вероятности из реального мира

Повседневный пример априорной вероятности — это ваши шансы на выигрыш в числовой лотерее. Формула для расчета вероятности становится намного более сложной, поскольку ваши шансы основаны на комбинации чисел на билете, выбранной случайным образом в правильном порядке, и вы можете купить несколько билетов с несколькими комбинациями чисел. Тем не менее, существует ограниченный набор комбинаций, которые приведут к победе. К сожалению, количество возможных результатов затмевает количество желаемых результатов — ваш конкретный набор билетов. Вероятность выиграть главный приз в лотерее, такой как лотерея Powerball в США, составляет одну к сотням миллионов. Более того, шансы выиграть только главный приз (а не разделить его) снижаются по мере увеличения банка и увеличения числа игроков.

Априорная вероятность и финансы

Применение априорной вероятности к финансам ограничено. Помимо того, что люди не хотят отдавать свою финансовую судьбу в руки лотереи, большинство результатов, о которых заботятся финансовые сотрудники, не имеют конечного числа результатов. Вы не можете сказать, что цена акции имеет три возможных исхода: рост, падение или сохранение неизменной цены, если на эти результаты влияет ряд внешних факторов, которые изменяют вероятность каждого исхода.

В финансах люди чаще используют эмпирическую или субъективную вероятность, а не классическую. При эмпирической вероятности вы смотрите на прошлые данные, чтобы понять, какими будут результаты в будущем. С субъективной вероятностью вы накладываете на данные свой личный опыт и взгляды, чтобы сделать звонок, который является уникальным для вас. Если акция росла в течение трех дней после того, как превзошла рекомендации аналитиков, инвестор может разумно ожидать, что она продолжится, основываясь на недавнем ценовом движении. Однако другой инвестор может увидеть то же ценовое движение и вспомнить, что консолидация последовала за резким ростом этих акций два года назад, принимая противоположный смысл из тех же данных о ценах. В зависимости от рынка, оба инвестора могут быть не более точными, чем прогноз, основанный на априорной вероятности, но мы лучше относимся к решениям, которые можем обосновать, используя хотя бы некоторую логику, выходящую за рамки случайности.