Формулы с обратными тригонометрическими функциями: arcsin, arccos, arctg и arcctg
Ранее мы рассматривали обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс. Как и в случае с другими функциями, между ними существуют связи и зависимости, реализуемые в виде формул, которые можно использовать для решения задач.
Сейчас мы будем рассматривать основные формулы с использованием этих функций: какие они бывают, на какие группы их можно разделить, как их доказать и как решать задачи с их помощью.
Формулы котангенса арккотангенса, тангенса арктангенса, синуса арксинуса и косинуса арккосинуса
Для начала сгруппируем формулы, в которых содержатся основные свойства обратных тригонометрических функций. Мы уже обсуждали и доказывали их ранее, а здесь приведем, чтобы логика объяснения была более понятной и все формулы были в одной статье.
для α∈-1, 1 sin(arccis α)=α, cos(arccos α)=α,для α∈(-∞, ∞) tg(arctg α)=α, ctg(arcctg α)=α
Указанное в них легко сформулировать из самих определений обратных тригонометрических функций числа. Если вы забыли, как найти, например, тангенс арктангенса, все можно посмотреть в этой формуле.
Формулы арккотангенса котангенса, арктангенса тангенса и арксинуса синуса и арккосинуса косинуса
для -π2≤α≤π2 arcsin (sin α)=α,для 0≤α≤π arccos(cos α)=α,для -π2<α<π2 arctg (tg α)=α,для 0<α<π arcctg (ctg α)=α
Здесь все также более-менее очевидно, как и в предыдущем пункте: эти формулы можно вывести из определений арксинуса, арккосинуса и др. Единственное, на что нужно обратить пристальное внимание: они будут верны только в том случае, если a (число или угол) будут входить в указанный предел. В противном случае расчет по формуле будет ошибочен, и применять ее нельзя.
Как соотносятся между собой арксинусы, арккосинусы, арктангенсы и арккотангенсы противоположных чисел
В этом блоке мы сформулируем важное утверждение:
Обратные тригонометрические функции отрицательного числа можно выразить через арксинус, арккосинус, арктангенс и арккотангенс противоположного ему положительного числа.
для α∈-1, 1 arccis (-α)=-arcsin α, arccos (-α)=π-arccos α,для α∈(-∞, ∞) arctg (-α)=-arctg α, arcctg (-α)=π-arcctg α
Таким образом, если в расчетах нам встречаются эти функции для отрицательных чисел, мы можем от них избавиться, преобразовав их в аркфункции положительных чисел, с которыми иметь дело проще.
Формулы суммы: арксинус + арккосинус, арктангенс + арккотангенс
Они выглядят следующим образом:
для α∈-1, 1 arccis α+arccos α=π2,для α∈(-∞, ∞) arctg α+arcctg α=π2
Из написанного видно, что арксинус некоторого числа можно вывести с помощью его арккосинуса, и наоборот. С арктангенсом и арккотангенсом аналогично – они соотносятся между собой аналогичным образом.
Формулы связи между прямыми и обратными тригонометрическими функциями
Знать связи между прямыми функциями и их аркфункциями очень важно для решения многих практических задач. Как же быть, если у нас есть необходимость вычислить, к примеру, тангенс арксинуса? Ниже приведен список основных формул для этого, которые полезно выписать себе.
| -1≤α≤1,sin (arcsin α)=α | -1≤α≤1,sin (arccos α)=1-α2 | -∞≤α≤+∞,sin (arctg α)=α1+α2 | -∞≤α≤+∞, sin (arcctg α)=11+α2 |
| -1≤α≤1,cos (arcsin α)=1-α2 | -1≤α≤1,cos (arccos α)=α | -∞≤α≤+∞,cos (arctg α)=11+α2 | -∞≤α≤+∞, cos (arcctg α)=11+α2 |
| -1<α<1,tg (arcsin α) =α1-α2 | α∈(-1, 0)∪(0, 1),tg (arccos α) =1-α2α | -∞≤α≤+∞,tg (arctg α)=α | α≠0 ,tg (arcctg α)=1α |
| α∈(-1, 0)∪(0, 1),ctg (arcsin α)=1-α2α | -1<α<1,ctg (arccos α)=α1-α2 | α≠0,ctg (arctg α)=1α | -∞≤α≤+∞, ctg (arcctg α)=α |
Теперь разберем примеры, как они применяются в задачах.
Вычислите косинус арктангенса из 5.
Решение
У нас для этого есть подходящая формула следующего вида: cos(arctg α)=11+α2
Подставляем нужное значение: cos(arctg5)=11+(5)2=26
Вычислить синус арккосинуса 12.
Решение
Для этого нам понадобится формула: sin (arccos α)=1-a2
Подставляем в нее значения и получаем: sin (arccos 12)=1-(12)2=32
Обратите внимание, что непосредственные вычисления приводят к аналогичному ответу: sin(arccos 12)=sin π3=32
Если вы забыли, как правильно вычислять значения прямых и обратных функций, вы всегда можете вернуться к нашим предыдущим материалам, где мы разбирали это.
Доказательства формул синусов арккосинуса, арккотангенса и арктангенса
Для того, чтобы наглядно вывести полученные формулы, нам понадобятся основные тригонометрические тождества и собственно формулы основных обратных функций – косинуса арккосинуса и др. Мы их уже выводили ранее, поэтому тратить время на их доказательства не будем. Начнем сразу с формул синусов арккосинуса, арккотангенса и арктангенса. Используя тождество, получим:
sin2α+cos2α=11+ctg2α=1sin2α
Вспомним, что tgα·ctgα=1. Из этого можно получить:
sinα=1-cos2α, 0≤α≤π sinα=tgα1+tg2α, -π2<α<π2sinα=11+ctg2α, 0<α<π
У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.
Теперь в первой формуле вместо a мы добавим arccos a. Итог – формула синуса арккосинуса.
Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.
Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.
Все наши расчеты можно сформулировать более емко:
- sinα=1-cos2α, 0≤α≤π
Следовательно, sin(arccosα)=1-cos2(arccosα)=1-a2
- sinα=tgα1+tgα, -π2<α<π2,
Следовательно, sin(arctgα)=tg(arctgα)1+tg2(arctgα)=α1+α2
- sinα=11+ctg2α, 0<α<π
Следовательно, sin(arctgα)=11+tg2(arctgα)=11+α2
Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.
Их мы выведем по имеющемуся шаблону:
- Из cosα=1-sin2α, -π2≤α≤π2 следует, что
cos(arcsin α)=1-sin2(arcsin α)=1-a2
- Из cosα=11+tg2α, -π2<α<π2 следует, что
- Из cosα=ctgα1+ctg2α, 0<α<πcos(arctgα)=11+tg2(arctgα)=11+α2
следует, что cos(arctgα)=ctg(arcctgα)1+ctg2(arcctgα)=α1+α2
Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса
- Исходим из tgα=sin α1-sin2α, -π2<α<π2. Получаем tg(arcsin α)=sin(arcsinα)1-sin2(arcsinα)=α1-α2 при условии, что -1<α<1.
- Исходим из tgα=1-cos2αcosα, α∈[0, π2)∪(π2, π], получаем
tg(arccosα)=1-cos2(arccosα)cos(arccosα)=1-α2α при условии α∈(-1, 0)∪(0, 1).
- Исходим из tgα=1ctgα, α∈(0, π2)∪(π2, π), получаем tg(arcctgα)=1ctg(arcctgα)=1α при условии, что α≠0.
Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:
ctgα=1tgα
Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса. Для этого понадобится поменять в них местами числитель и знаменатель.
Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее
Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции. Разберем примеры.
Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:
arcsinα=arccos1-α2, 0≤α≤1-arccos1-a2, -1≤α<0arcsinα=arctgα1-α2, -1<α<1arcsinα=arcctg1-α2α, 0<α≤1arcctg1-α2α-π, -1≤α≤0
А так мы выразим арккосинус через остальные обратные функции:
arccosα=arcsin1-α2, 0≤α≤1π-arcsin1-α2, -1≤α<0arccosα=arctg1-α2α, 0<α≤1π+arctg1-α2α, -1<α<0arccosα=arcctgα1-α2, -1<α<1
Формула выражения арктангенса:
arctgα=arcsinα1+α2, -∞<α<+∞arctgα=arccos11+α2, α≥0-arccos11+α2, α<0arctgα=arcctg1α, α≠0
Последняя часть – выражение арккотангенса через другие обратные функции:
arcctgα=arcsin11+α2, α≥0π-arcsin11+α2, α<0arcctgα=arccosα1+α2, -∞<α<+∞arcctgα=arctg1α, α≠0
Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.
Возьмём arcsinα=arctgα1-α2, -1<α<1 и постараемся вывести доказательство.
Мы знаем, что arctgα1-α2 – это число, величина которого составляет от минус половины пи до плюс половины пи. Из формулы синуса арктангенса получим:
sin(arctgα1-α2)=α1-α21+(α1-α2)2=α1-α21+α21-α2=α1-α21+α21-α2=α1-α211-α2=α
Получается, что arctgα1-α2 при условии 1<a<1 – это и есть арксинус числа a.
Вывод: arcsina=arctga1-a2, -1<a<1
Прочие формулы доказываются по аналогии.
В завершение разберем один пример применения формул на практике.
Условие Вычислить синус арккотангенса минус корня из 3.
Решение
Нам понадобится формула выражения арккотангенса через арксинус: arcctgα=arcsin11+a2, α≥0π-arcsin 11+a2, α<0
Подставим в нее α=-3 и получим ответ – 12. Непосредственное вычисление дало бы нам те же результаты: sin(arcctg(-3))=sin5π6=12 Для решения задачи можно взять и другую формулу, выражающую синус через котангенс: sinα=11+ctg2α, 0<α<π
В итоге у нас бы вышло: sin(arcctg(-3))=11+ctg2(arcctg(-3))=11+(-3)2=12
Или возьмем формулу синуса арккотангенса и получим тот же ответ: sin(arcctgα)=11+α2 sin(arcctg(-3))=11+(-3)2=12
Прочие формулы с обратными функциями
Мы рассмотрели самые основные формулы, которые понадобятся вам при решении задач. Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.
Разберем одну из них, называемую формулой половинного угла. Она выглядит следующим образом:
sin2α2=1-cosα2
Если угол альфа при этом больше нуля, но меньше числа пи, то у нас выходит:
sinα2=1-cosα2
Учитывая данное условие, заменяем упомянутый угол на arccos. В итоге наша предварительная формула выглядит так:
sinarccosα2=1-cos(arccosα)2⇔sinarccosα2=1-α2
Отсюда мы выводим итоговую формулу, в которой арксинус выведен через арккосинус:
arccosα2=arcsin1-α2
Мы перечислили не все связи, которые имеются между обратными тригонометрическими функциями, а лишь наиболее употребляемые из них. Важно подчеркнуть, что ценность имеют не столько сами сложные формулы, что мы привели в статье: заучивать их наизусть не нужно. Гораздо важнее уметь самому делать нужные преобразования, и тогда сложные вычисления не потребуется хранить в голове.
В продолжение темы в следующей статье мы рассмотрим преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
- Определение
- График арккосинуса
-
Свойства арккосинуса
- Таблица арккосинусов
Определение
Арккосинус (arccos) – это обратная тригонометрическая функция.
Арккосинус x определяется как функция, обратная к косинусу x, при -1≤x≤1.
Если косинус угла у равен х (cos y = x), значит арккосинус x равняется y:
arccos x = cos-1 x = y
Примечание: cos-1x означает обратный косинус, а не косинус в степени -1.
Например:
arccos 1 = cos-1 1 = 0° (0 рад)
График арккосинуса
Функция арккосинуса пишется как y = arccos (x). График в общем виде выглядит следующим образом:
Свойства арккосинуса
Ниже в табличном виде представлены основные свойства арккосинуса с формулами.
Таблица арккосинусов
| x | arccos x (рад) | arccos x (°) |
| -1 | π | 180° |
| -√3/2 | 5π/6 | 150° |
| -√2/2 | 3π/4 | 135° |
| -1/2 | 2π/3 | 120° |
| 0 | π/2 | 90° |
| 1/2 | π/3 | 60° |
| √2/2 | π/4 | 45° |
| √3/2 | π/6 | 30° |
| 1 | 0 | 0° |
microexcel.ru
Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arcus — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Так, обычный синус позволяет по дуге окружности найти стягивающую её хорду, а обратная функция решает противоположную задачу. Манера обозначать таким образом обратные тригонометрических функции появилась у австрийского математика XVIII века Карла Шерфера и закрепилась благодаря Лагранжу. Впервые специальный символ для обратной тригонометрической функции использовал Даниил Бернулли в 1729 году. Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: 
но они не прижились[1].
Лишь изредка в иностранной литературе, также как и в научных/инженерных калькуляторах, пользуются обозначениями типа sin−1, cos−1 для арксинуса, арккосинуса и т. п.[2], — такая запись считается не очень удобной, так как возможна путаница с возведением функции в степень −1.
Тригонометрические функции периодичны, поэтому функции, обратные к ним, многозначны. То есть, значение аркфункции представляет собой множество углов (дуг), для которых соответствующая прямая тригонометрическая функция равна заданному числу. Например, 
означает множество углов 
, синус которых равен 
. Из множества значений каждой аркфункции выделяют её главные значения (см. графики главных значений аркфункций ниже), которые обычно и имеют в виду, говоря об арксинусе, арккосинусе и т. д.
В общем случае при условии 
все решения уравнения 
можно представить в виде 
[3]
Основное соотношение[править | править код]
Функция arcsin[править | править код]
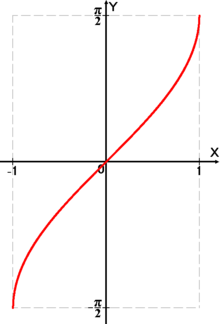
График функции 
Аркси́нусом числа x называется такое значение угла y, выраженного в радианах, для которого 
Функция непрерывна и ограничена на всей своей области определения. Она является строго возрастающей.
Свойства функции arcsin[править | править код]
Получение функции arcsin[править | править код]
Дана функция 
. На всей своей области определения она является кусочно-монотонной, и, значит, на всей числовой прямой обратное соответствие функцией не является. Поэтому рассмотрим отрезок ![{displaystyle [-pi /2;pi /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e194f6091eb1b362d19112a5bffdab91ef2a07df)
, на котором функция строго монотонно возрастает и принимает все значения своей области значений только один раз. Тогда на отрезке существует обратная функция , график которой симметричен графику функции относительно прямой 
.
Функция arccos[править | править код]
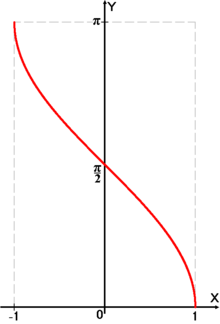
График функции 
Аркко́синусом числа x называется такое значение угла y в радианной мере, для которого 
Функция непрерывна и ограничена на всей своей области определения. Она является строго убывающей и неотрицательной.
Свойства функции arccos[править | править код]
Получение функции arccos[править | править код]
Дана функция 
. На всей своей области определения она является кусочно-монотонной, и, значит, на всей числовой прямой обратное соответствие функцией не является. Поэтому рассмотрим отрезок ![[0;pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/45ba33419dc889bf6c0c684b11285afda3437c95)
, на котором функция строго монотонно убывает и принимает все значения своей области значений только один раз. Тогда на отрезке существует обратная функция , график которой симметричен графику функции относительно прямой .
Функция arctg[править | править код]
График функции 
Аркта́нгенсом числа x называется такое значение угла 
выраженное в радианах, для которого 
Функция 
определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго возрастающей.
Свойства функции arctg[править | править код]
Получение функции arctg[править | править код]
Дана функция 
. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим интервал 
, на котором функция строго монотонно возрастает и принимает все значения своей области значений только один раз. Тогда на интервале существует обратная функция , график которой симметричен графику функции относительно прямой .
Функция arcctg[править | править код]
График функции 
Арккота́нгенсом числа x называется такое значение угла y (в радианной мере измерения углов), для которого 
Функция 
определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго убывающей и всюду положительной.
Свойства функции arcctg[править | править код]
Получение функции arcctg[править | править код]
Дана функция 
. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим интервал 
, на котором функция строго монотонно убывает и принимает все значения своей области значений только один раз. Тогда на интервале существует обратная функция , график которой симметричен графику функции относительно прямой .
График арккотангенса получается из графика арктангенса, если последний отразить относительно оси ординат (то есть заменить знак аргумента, 
) и сместить вверх на π/2; это вытекает из вышеупомянутой формулы 
Функция arcsec[править | править код]
График функции 
Арксе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого 
Функция непрерывна и ограничена на всей своей области определения. Она является строго возрастающей и всюду неотрицательной.
Свойства функции arcsec[править | править код]
Функция arccosec[править | править код]
График функции 
Арккосе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого 
Функция непрерывна и ограничена на всей своей области определения. Она является строго убывающей.
Свойства функции arccosec[править | править код]
Разложение в ряды[править | править код]
Производные от обратных тригонометрических функций[править | править код]
Все обратные тригонометрические функции бесконечно дифференцируемы в каждой точке своей области определения. Первые производные:
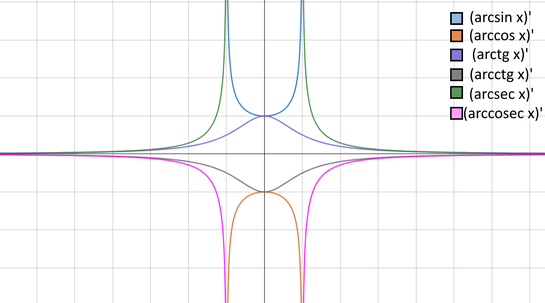
производные обратных тригонометрических функций
Функция  |
Производная  |
Примечание |
|---|---|---|
 |
 |
Доказательство Найти производную арксинуса можно при помощи взаимно обратных функций. |
 |
 |
Доказательство Найти производную арккосинуса можно при помощи данного тождества: |
 |
 |
Доказательство Найти производную арктангенса можно при помощи взаимнообратной функции: |
 |
 |
Доказательство Найти производную арккотангенса можно при помощи данного тождества: |
 |
 |
Доказательство Найти производную арксеканса можно при помощи тождества:
Теперь находим производную обеих частей этого тождества.
Получается.
|
 |
 |
Доказательство Найти производную арккосеканса можно при помощи данного тождества: |
![{displaystyle [sin(arcsin((x))]'=x'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be684108880964393fc7a90ba55f07de0e6d659a)
![{displaystyle D(cos(x))=[{frac {pi }{2}};-{frac {pi }{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1cb9db2cfdfe382a787aa5288735756e8dcb12e)
![{displaystyle [arcsin(x)+arccos(x)]'=({frac {pi }{2}})'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3606594a168f2f06eb6faddfaac18f1c85324466)
![{displaystyle [tg(arctg(x))]'=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ce9406b214a5266d0bf8282fd6aae4b59602c66)
![{displaystyle [arctg(x)+arcctg(x)]'=({frac {pi }{2}})'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f84cee67adf89ef76bfaa5c415907cce038d455)
![{displaystyle [arccosec(x)+arcsec(x)]'=({frac {pi }{2}})'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4847d93af2226f3ab5e1ba20940ec8530526b49e)
Интегралы от обратных тригонометрических функций[править | править код]
Неопределённые интегралы[править | править код]
Для действительных и комплексных x:
Для действительных x ≥ 1:
- См. также Список интегралов от обратных тригонометрических функций
Использование в геометрии[править | править код]
Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например, с помощью теоремы косинусов.
В прямоугольном треугольнике эти функции от отношений сторон сразу дают угол.
Так, если катет длины 
является противолежащим для угла 
, то
Связь с натуральным логарифмом[править | править код]
Для вычисления значений обратных тригонометрических функций от комплексного аргумента удобно использовать формулы, выражающие их через натуральный логарифм:
См. также[править | править код]
- Обратные гиперболические функции
- Теорема Данжуа — Лузина
Примечания[править | править код]
Ссылки[править | править код]
- Weisstein, Eric W. Обратные тригонометрические функции (англ.) на сайте Wolfram MathWorld.
- Математическая энциклопедия / Гл. ред. И. М. Виноградов. — М.: «Советская Энциклопедия», 1982. — [dic.academic.ru/dic.nsf/enc_mathematics/3612/%D0%9E%D0%91%D0%A0%D0%90%D0%A2%D0%9D%D0%AB%D0%95 Т. 3. — с. 1135].
- Обратные тригонометрические функции — статья из Большой советской энциклопедии. — М.: «Советская Энциклопедия», 1974. — Т. 18. — с. 225.
- Обратные тригонометрические функции // Энциклопедический словарь юного математика / Савин А.П. — М.: Педагогика, 1985. — С. 220—221. — 352 с.
- Построение графиков обратных тригонометрических функций онлайн
- Онлайн калькулятор: обратные тригонометрические функции
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных доменов
|
Сферы применения правил обратных тригонометрических функций
Определение
Тригонометрия — раздел математики, объясняющий зависимость между сторонами и углами треугольника, правила используют для расчета углов.
Изучая постулаты тригонометрических функций, ученики и студенты часто задаются вопросом, где эти знания могут пригодиться. Сфер применения достаточно много. Астрономы используют понятия для расчёта положения небесных объектов, тригонометрия помогает выполнять чертежи и создавать архитектурные шедевры, выстраивать модель биологических ритмов. В морской и воздушной навигации, акустике и оптике, в анализе финансового рынка, статистике, медицине, химии, во многих областях используются тригонометрические вычисления. Поэтому так важно научиться применять и выводить формулы самостоятельно.
Обратные функции тригонометрии
Обратными называются функции, которые ещё называют арксинус, арккосинус, арктангенс, арккотангенс.
Название данный вид тригонометрической зависимости, получил от соответствующей прямой функции с приставкой арк — дуга. Взаимосвязь просматривается между длиной дуги единичной окружности и соответствующим определённым отрезком.
Правила обратной функции справедливы в пределах интервалов, например,
формула арксинуса возможна при:
[arcsin (sin mathrm{x})=mathrm{x} text { при }-frac{pi}{2} leq mathrm{x} leq frac{pi}{2}]
[arccos (cos mathrm{x})=mathrm{x} text { при } 0 leq mathrm{x} leq pi]
и так далее.
Формулы с обратными функциями тригонометрии
Уже были рассмотрены обратные тригонометрические функции. Они, как и другие функции имеют между собой связи и зависимости, которые можно выразить в виде формул и использовать для решения задач.
В данной работе мы рассмотрим основные формулы, в которых применяются функции тригонометрии. Разберём их виды, деление на группы, доказательства и способы решения задач с их помощью.
Группировка основных понятий
Сначала проведём группировку формул, для того чтобы сделать более понятной логику объяснений. И объединим все правила и доказательства в одну статью.
Синус от арксинуса для [alpha in(-1 ; 1) sin (arcsin alpha)=alpha, cos (arccos alpha)=alpha]
Тангенса от арктангенса для [alpha in(-infty, infty) operatorname{tg}(operatorname{arctg} alpha)=alpha, operatorname{ctg}(operatorname{arctg} alpha)=alpha].
Указанное в данных выражениях легко выводится из самих определений обратных функций тригонометрии. При необходимости найти arcsin tg, можно использовать приведённые формулы.
Тангенс, арктангенс, котангенс, арккотангенс, синус, арксинус, косинус, арккосинус и формулы
[text{Для }-frac{pi}{2} leq alpha leq frac{pi}{2} arcsin (sin alpha)=alpha],
[text{Для } leq alpha leq pi arccos (cos alpha)=alpha],
[text{Для }-frac{pi}{2}<alpha<frac{pi}{2} operatorname{arctg}(operatorname{tg} alpha)=alpha],
[text{Для } 0<alpha<pi operatorname{arcctg}(operatorname{ctg} alpha)=alpha].
В данном примере собраны тригонометрические выражения, достаточно очевидные, которые можно вывести из определений функций тригонометрии. Необходимо обратить внимание, на то, что высказывания будут верны, если «а» (угол, или числовое значение) будет входить в определённый предел. Если условие не выполняется, расчёт будет не верен и формулу использовать нельзя.
Соотношение между собой обратных тригонометрических функций противоположных чисел
Рассмотрим важное определение:
Обратные функции тригонометрии можно выразить через аркфункции противоположного положительного числа.
[text{Для }alpha in operatorname{open}-1,1] text { arccis }(-alpha)= -operatorname{arc} sin alpha, quad operatorname{arc} cos (-alpha)=pi -a r c cos alpha]
[text { Для } alpha in(-infty, infty) operatorname{arctg}(-alpha)= -operatorname{arctg} alpha, operatorname{arcctg}(-alpha)=pi-operatorname{arcctg} alpha]
Это значит, если расчёты имеют функции отрицательного числа, от них можно избавиться. Для этого необходимо преобразовать их в аркфункции положительных чисел. Такие вычисления проводить проще.
Формулы суммы: arcsin + arccos, arctg +arcctg
Правила суммы выглядят так:
Для [alpha in[-1,1] arcsin alpha+arccos alpha=frac{pi}{2}],
Для [alpha in[-infty, infty] operatorname{arctg} alpha+operatorname{arctg} alpha=frac{pi}{2}].
Отсюда видно, что arcsin определённого числа можно выразить через его arccos , и наоборот. Тоже правило касается и arctg и arcctg, которые выражаются аналогично.
Формулы связи между обратными и прямыми тригонометрическими функциями
Чтобы иметь возможность решить множество задач, требуется знание связей между прямыми тригонометрическими функциями, и их аркфункциями. Рассмотрим, как необходимо поступить, если нужно вычислить тангенс арксинуса. Ниже представлен список основных формул, которые помогут в решении таких задач.
| [-1 leq alpha leq 1], [sin (arcsin alpha)=alpha] |
[-1 leq alpha leq 1], [sin (arccos alpha) =sqrt{1-alpha^{2}}] |
[-infty leq alpha leq+infty], [sin (operatorname{arctg} alpha)=frac{alpha}{sqrt{1+alpha^{2}}}] |
[-infty leq alpha leq+infty], [sin (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}] |
| [-1 leq alpha leq 1], [cos (arcsin alpha)=sqrt{1-alpha^{2}}] |
[-1 leq alpha leq 1], [cos (arccos alpha)=alpha] |
[-infty leq alpha leq+infty], [cos (operatorname{arctg} alpha)=frac{1}{sqrt{1+a^{2}}}] |
[-infty leq alpha leq+infty], [cos (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}] |
| [-1<alpha<1], [operatorname{tg}(arcsin alpha)=frac{alpha}{sqrt{1-alpha^{2}}}] |
[alpha in(-1,0) cup(0,1)], [operatorname{tg}(arccos alpha)=frac{sqrt{1-a^{2}}}{alpha}] |
[-infty leq alpha leq+infty], [operatorname{tg}(operatorname{arctg} alpha)=alpha] |
[alpha neq 0], [operatorname{tg}(operatorname{arcctg} alpha)=frac{1}{alpha}] |
| [alpha in(-1,0) cup(0,1)], [operatorname{ctg}(arcsin alpha)=frac{sqrt{1-alpha^{2}}}{alpha}] |
[-1<alpha<1], [operatorname{ctg}(arccos alpha)=frac{alpha}{sqrt{1-a^{2}}}] |
[alpha neq 0], [operatorname{ctg}(operatorname{arctg} alpha)=frac{1}{alpha}] |
[-infty leq alpha leq+infty], [operatorname{ctg}(operatorname{arcctg} alpha)=alpha] |
Примеры 1 — 2
Нужно найти косинус арктангенса из 5.
Решение. Для этого необходимо воспользоваться формулой следующего вида: [cos (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}]
Подставим необходимое значение: [cos (operatorname{arctg} sqrt{5})=frac{1}{sqrt{1+sqrt{5^{2}}}}=frac{2}{sqrt{6}}]
Определить синус арккосинуса [frac{1}{2}]
Решение. Реализовать решение нам поможет формула: [sin (arccos alpha)=sqrt{1-alpha^{2}}]
Ставим значение и получаем: [sin left(arccos frac{1}{2}right)=sqrt{1-left(frac{1}{2}right)^{2}}=frac{sqrt{3}}{2}]
Заметим, что непосредственное вычисление приведёт к тому же ответу: [sin left(arccos frac{1}{2}right)=sin frac{pi}{3}=frac{sqrt{3}}{2}]
Для правильного вычисления значений прямых и обратных тригонометрических функций, стоит вспомнить начальные материалы.
Доказательство формул синуса от арккосинуса, арккотангенса и арктангенса
Чтобы вывести формулы и разобрать их более наглядно, необходимо применить основные тригонометрические тождества и правила обратных тригонометрических функций, которые были выведены ранее.
Доказательство формул 1
Используя тождества получим:
[sin ^{2} alpha+cos ^{2} alpha=1]
[1+operatorname{ctg}^{2} alpha=frac{1}{sin ^{2} alpha}]
Вспомним тот факт, что tg α *ctg α= 1, следовательно
[sin alpha=sqrt{1-cos ^{2} alpha}, 0 leq alpha leq pi]
[sin alpha=frac{operatorname{tg} alpha}{sqrt{1+operatorname{tg}^{2} alpha}},-frac{pi}{2}<alpha<frac{pi}{2}]
[sin alpha=frac{1}{sqrt{1+c t g^{2} alpha}}, 0<alpha<pi]
Результатом станет вывод синуса через подходящие аркфункции в заданном условии.
В математическое выражение вместо α, ставим arccos α, получаем в итоге формулу синуса арккосинуса.
Во втором случае вместо α подставляем arctg α, соответственно получаем формулу синуса арктангенса.
В третьем варианте проводим аналогичную операцию и подставляем arcctg α для выражения формулы синуса арккотангенса.
Нет времени решать самому?
Наши эксперты помогут!
Доказательство формул для тангенса, обратных функций(arcsin, arccos, arcctg)
В данном разделе рассмотрим доказательство закона тангенса обратных функций тригонометрии.
Доказательство формул 2
- Исходя из: [frac{sin alpha}{sqrt{1-sin alpha^{2}}},-frac{pi}{2}<alpha<frac{pi}{2}]Получим [operatorname{tg}(arcsin alpha)=frac{sin (arcsin alpha)}{sqrt{1-sin ^{2}(arcsin alpha)}}=frac{alpha}{sqrt{1-alpha^{2}}}]При условии [-1<alpha<1]
- Из выражения [operatorname{tg} alpha=frac{sqrt{1-cos ^{2} alpha}}{cos alpha}, alpha inleft[0, frac{pi}{2}right) cupleft(frac{pi}{2}, piright]]
Получаем [operatorname{tg}(arccos alpha)=frac{sqrt{1-cos ^{2}(arccos alpha)}}{cos (arccos alpha)}=frac{sqrt{1-alpha^{2}}}{alpha}] при условии [alpha in(-1,0) cup(0,1)]. - Исходя из [operatorname{tg} alpha=frac{1}{operatorname{ctg} alpha}, alpha inleft(0, frac{pi}{2}right) cupleft(frac{pi}{2}, piright)] получаем [operatorname{tg}(operatorname{arcctg} alpha)=frac{1}{operatorname{ctg}(operatorname{arcctg} alpha)}=frac{1}{alpha}] при условии, что [alpha neq 0].
Далее нам понадобятся понятия котангенсов арксинуса, арккосинуса, арктангенса. Напомним такое тригонометрическое равенство:
[operatorname{ctg} alpha=frac{1}{operatorname{tg} alpha}]
Применяя данное выражение можно вывести необходимые формулы, вставляя выражения тангенса обратных функций тригонометрии. Практически необходимо поменять местами числитель и знаменатель.
Выражение арксинуса с помощью арккосинуса, арктангенса и арккотангенса
Прямые и обратные функции в тригонометрии связаны между собой. Полученные в результате выведения формулы помогут найти связь и между обратными функциями тригонометрии, выразив одни аркфункции через другие. Рассмотрим примеры.
В первом случае меняем арксинус на арккосинус, а арктангенс на арккотангенс, получим следующие формулы арксинуса и арккосинуса:
[begin{aligned}
&arcsin a=left{begin{array}{l}
arccos sqrt{1-a^{2}}, 0 leq a leq 1 \
-arccos sqrt{1-a^{2}},-1 leq a<0
end{array}right. \
&arcsin a=operatorname{arctg} frac{a}{sqrt{1-a^{2}}},-1<a<1 \
&arcsin a=left{begin{array}{l}
operatorname{arcctg} frac{sqrt{1-a^{2}}}{a}, 0<a leq 1 \
operatorname{arcctg} frac{sqrt{1-a^{2}}}{a}-pi,-1 leq a<0
end{array}right.
end{aligned}]
Для арккосинуса также есть свои формулы:
[begin{aligned}
&arccos a=left{begin{array}{l}
arcsin sqrt{1-a^{2}}, 0 leq a leq 1 \
pi-arcsin sqrt{1-a^{2}},-1 leq a<0
end{array}right. \
&arccos a=left{begin{array}{l}
operatorname{arctg} frac{sqrt{1-a^{2}}}{a}, 0<a leq 1 \
pi+operatorname{arctg} frac{sqrt{1-a^{2}}}{a},-1 leq a<0
end{array}right. \
&arccos a=operatorname{arcctg} frac{a}{sqrt{1-a^{2}}},-1<a<1
end{aligned}]
Выражения для арктангенса:
[begin{aligned}
&operatorname{arctg} a=arcsin frac{a}{sqrt{1+a^{2}}},-infty<a<+infty\
&operatorname{arctg} a=left{begin{array}{l}
arccos frac{1}{sqrt{1+a^{2}}}, a geq 0 \
-arccos frac{1}{sqrt{1+a^{2}}}, a<0
end{array}right.\
&operatorname{arctg} a=operatorname{arcctg} frac{1}{a}, a neq 0
end{aligned}]
Последний блок формул покажет преобразование арккотангенса через другие обратные функции тригонометрии:
[begin{aligned}
&operatorname{arcctg} a=left{begin{array}{l}
arcsin frac{1}{sqrt{1+a^{2}}}, a geq 0 \
pi-arcsin frac{1}{sqrt{1+a^{2}}}, a<0
end{array}right.\
&operatorname{arctg} a=arccos frac{a}{sqrt{1+a^{2}}},-infty<a<+infty\
&operatorname{arcctg} a=operatorname{arctg} frac{1}{a}, a neq 0
end{aligned}]
Рассмотренные формулы арксинуса, арккосинуса, арктангенса помогут в решении различных задач. Разберём доказательство с использованием основных определений обратных функций и ранее рассмотренных правил.
Возьмём arcsin [alpha=operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}},-1<alpha<1] для выведения доказательства.
Мы имеем выражение [operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}] — число, которое имеет значение от минус половины [pi] до плюс половины [pi]. Используя выражение синуса арктангенса, получаем следующее:
[sin left(operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}right)=frac{frac{alpha}{sqrt{1-alpha^{2}}}}{sqrt{1+left(frac{alpha}{sqrt{1-alpha^{2}}}right)^{2}}}=frac{frac{alpha}{sqrt{1-alpha^{2}}}}{sqrt{1+frac{alpha^{2}}{1-alpha^{2}}}}=frac{frac{alpha}{sqrt{1-alpha^{2}}}}{frac{1}{sqrt{1-alpha^{2}}}}=alpha]
Получается, что [operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}] с условием [-1<alpha<1] — арксинус числа [alpha].
Вывод: [arcsin alpha=operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}},-1<alpha<1].
Другие подобные формулы доказываются по аналогичной схеме.
Рассмотрим пример применения полученных истин.
Пример 3
Необходимо вычислить синус арккотангенса — [sqrt{3}]
Решение. Для того чтобы провести решение задачи, необходимо использовать формулу связи арккотангенса и арксинуса: [arcsin alpha=operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}]
Подставим в неё [alpha=-sqrt{3}] и получим [-frac{1}{2}].
Используя непосредственное вычисление ответ был бы такой же: [sin (operatorname{arcctg}(-sqrt{3}))=sin frac{5 pi}{6}=frac{1}{2}]
Можно использовать и следующую формулу:
[sin (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}]
[sin (operatorname{arcctg}(-sqrt{3}))=frac{1}{sqrt{1+(-sqrt{3})^{2}}}=frac{1}{2}]
Другие формулы, в которых используются обратные функции тригонометрии
Разобраны основные функции, которые чаще всего используются для решения задач. Но представлены не все формулы с обратными тригонометрическими функциями, есть некоторые специфичные, употребляемые редко, но они тоже полезны. Учить их нет смысла, лучше вывести при необходимости.
Пример 4
Разберём для примера одну такую формулу. Выглядит она так:
[sin ^{2} frac{alpha}{2}=sqrt{frac{1-cos alpha}{2}}]
Если представленный угол имеет значение больше нуля, но меньше Пи, то получаем:
[sin frac{arccos alpha}{2}=sqrt{frac{1-cos (arccos alpha)}{2}}]
[Leftrightarrow sin frac{arccos alpha}{2}=frac{sqrt{1-alpha}}{2}]
Здесь мы выводим следующую готовую формулировку, арксинус которой выведен через арккосинус:
[frac{arccos alpha}{2}=arcsin sqrt{frac{1-alpha}{2}}]
В тексте рассмотрены лишь некоторые, самые популярные виды связей между прямыми и обратными функциями тригонометрии. Главное не выучить наизусть данные постулаты, а научиться их применять и выводить, исходя из уже известных определений.
Удобно использовать инженерный вид калькулятора, на котором есть, необходимые для вычислений тригонометрические формулы и функции.
План урока:
Арккосинус
Арксинус
Арктангенс
Решение уравнения cosx = a
Решение уравнения sinx = a
Решение уравнений tgx = a и ctgx = a
Арккосинус
Напомним, что на единичной окружности косинус угла – это координата х точки А, соответствующей этому углу:
Можно утверждать, что косинус – это ф-ция, которая ставит каждому углу в соответствие некоторую координату х. Теперь предположим, что нам известна эта координата (пусть она будет равна величине а), и по ней надо определить значение угла. Отложим на оси Ох отрезок длиной а, проведем через него вертикальную прямую и отметим ее точки пересечения с единичной окружностью. Если – 1<а < 1, то должно получиться две точки, которым соответствуют два противоположных угла:
Получается, что каждому значению числа а соответствует некоторый угол α. А если есть соответствие, то есть и функция:
α = f (a)
В математике ее называют арккосинусом. Записывается она так:
Вертикальная прямая может пересекать единичную окружность в двух разных точках. Им соответствуют разные углы. Принято считать, что арккосинус – это значение того угла, который лежит в первой или второй четверти, то есть ему соответствует точка, лежащая выше оси Ох. Тогда другая точка пересечения будет соответствовать углу (– arccosa):
Выходит, что арккосинус может принимать только значения из отрезка [0; π]. Дадим определение арккосинуса:
Задание. Вычислите арккосинус числа 1/2.
Решение. Мы помним, что косинус угла π/3 равен 1/2:
Следовательно, arccos 1/2 – это и есть угол π/3:
Ответ: π/3.
Обратим внимание, что если число а равно 1 или (– 1), то его арккосинус равен нулю в первом случае и π во втором:
В тех случаях, когда а > 1 либо а <– 1, то соответствующая прямая не пересечет единичную окружность. Это значит, что эти значения не входят в область определения арккосинуса:
Получается, что область определения арккосинуса – это промежуток [– 1; 1].
Для вычисления арккосинусов от отрицательных величин удобно пользоваться формулой
Действительно, если отложить на координатной прямой числа а и (– а), то вертикальные прямые, проходящие через них, пересекут окружность в некоторых точках А и С:
Дополнительно обозначим буквой В точку с координатами (1; 0) и буквой D точку с координатами (– 1; 0). Эти точки располагаются на пересечении оси Ох и единичной окружности. Тогда можно записать, что
ведь эти два угла образуют вместе развернутый угол ВОD, равный π. С другой стороны, из симметрии очевидно, что углы ∠COD и ∠АОВ равны друг другу, значит, ∠COD = ∠АОВ = arccosa. Тогда
Но ∠СОВ – это арккосинус от (– а), поэтому
Задание. Вычислите arccos (– 1/2).
Решение. Используем только что полученную формулу:
Ответ: 2π/3.
Арксинус
Арккосинус – это ф-ция, обратная косинусу. Аналогично можно вести и другие обратные тригонометрические ф-ции. Пусть нам требуется узнать, синус какого угла равен числу а. Так как синус – это координата у точки на единичной окружности, то достаточно провести горизонтальную линию у = а:
Прямая может пересечь окружность сразу в двух точках. За арксинус принимают угол, соответствующей точке, расположенной правее оси Оу. Вторая же точка соответствует углу π – arcsin α:
Арксинус может быть вычислен и для отрицательного значения а. В этом случае точка пересечения прямой и окружности будет располагаться в IV четверти, а соответствующий ему угол окажется отрицательным:
При значениях а, равных (– 1) и 1, точка пересечения будет только одна. В этих случаях арксинус окажется равным либо углу π/2, либо углу (– π/2):
Таким образом, арксинус может принимать значения из отрезка [– π/2; π/2], а вычислить его можно для чисел а, принадлежащих отрезку [– 1; 1]. Если же число а выходит за пределы этого промежутка, то горизонтальная прямая не пересекает единичную окружность, а потому ф-ция арксинуса становится неопределенной:
Получается, что областью определения арксинуса является промежуток [– 1; 1], а областью значений – промежуток [– π/2; π/2].
Дадим определение арксинусу:
Задание. Чему равен arcsin0,5?
Решение. Мы знаем, что sinπ/6 = 1/2 = 0,5. Следовательно, арксинус 0,5 равен π/6.
Для вычисления арксинусов отрицательных углов используется формула
Справедливость этой формулы очевидна из картинки:
Задание. Вычислите arcsin (– 0,5).
Решение. Используем формулу для арксинуса отрицательного числа:
Арктангенс
Введем ф-цию, обратную тангенсу. Она называется арктангенс.
Напомним, что величину тангенса на координатной плоскости можно получить, если продолжить угол до его пересечения с вертикальной прямой х = 1. Аналогично, чтобы определить арктангенс некоторого числа а, надо отметить на этой прямой точку с координатами (1; а) и соединить её с началом координат:
Несложно видеть, что, какое бы число а нами не было выбрано, мы с помощью построения всегда сможем соединить точку А с началом координат и получить некоторый угол arctga. Это значит, что область определения арктангенса – это вся числовая прямая, то есть промежуток (– ∞; + ∞).
Ещё раз уточним, что вводимые нами функции arcos, arcsin, arctg называются ОБРАТНЫМИ тригонометрическими функциями. C их помощью можно определить угол, если известно значение его синуса, косинуса или тангенса.Образно говоря, обратные триг-кие функции играют в тригонометрии ту же роль, что и квадратные корни при исследовании квадратных ур-ний. Как без квадратных корней невозможно решать квадратные ур-ния, так и без знания об обратных триг-ких функций нельзя решать уже тригом-кие уравнения.
Теперь вернемся к понятию арктангенса. При положительном значении числа а угол arctga будет принадлежать I четверти. Если же а – отрицательное число, то угол arctga окажется также отрицательным и будет принадлежать IV четверти:
Получается, что величина arctgа может принадлежать промежутку (– π/2; π/2). Обратите внимание, что в данном случае у промежутка круглые скобки. Действительно для углов (– π/2) и π/2 тангенс не определен, а потому арктангенс не может принимать эти два значения.
Задание. Чему равен arctg 1?
Решение. Из таблицы тангенсов мы знаем, что tgπ/4 = 1. Это значит, что
Для вычисления арктангенсов отрицательных чисел используют формулу
В ее справедливости можно убедиться, взглянув на рисунок:
Задание. Вычислите arctg (– 1).
Решение.
Ответ: – 1
В принципе можно ввести ещё ф-цию, обратную котангенсу – арккотангенс. Однако для решения тригонометрических уравнений, как мы убедимся далее, она не требуется, а поэтому в рамках школьного курса математики ее можно не изучать.
В заключение приведем таблицы, которые помогают вычислять значение обратных тригон-ких функций:
Решение уравнения cosx = a
Рассмотрим тригонометрическое уравнение, в левой части которого стоит ф-ция cosx, а в правой – число, например, 0,5:
По определению арккосинуса очевидно, что arccos 0,5 будет его решением, ведь
Так как arccos 0,5 = π/3, то мы находим очевидный корень х = π/3. И действительно, если подставить это значение в исходное ур-ние, то получится верное равенство:
Значит ли это, что мы решили ур-ние? Нет, ведь мы нашли только один корень, а их может быть несколько. Проведем на единичной окружности вертикальную прямую х = 0,5 и посмотрим, где она пересечет окружность:
Видно, что есть ещё одна точка пересечения, соответствующая углу (– arccos 0,5). Это значит, что этот угол также является решением ур-ния. Проверим это:
Здесь мы использовали тот факт, косинус – четная функция, то есть
Итак, число – π/3 также является корнем ур-ния. Есть ли ещё какие-нибудь корни? Оказывается, есть. Построим график ф-ции у = cosx и посмотрим, где ее пересекает прямая у = 0,5:
Оказывается, прямая пересекает график в бесконечном количестве точек! Это связано с периодичностью ф-ции у = cosx. Период этой ф-ции равен 2π, то есть
Поэтому, если число π/3 является решением ур-ния, то так же решением будут и число π/3 + 2π. Но к этому числу можно ещё раз добавить 2π и получить число π/3 + 4π. И оно тоже будет корнем. С другой стороны, период можно не только добавлять, но и вычитать, поэтому корнями ур-ния окажутся числа π/3 – 2π, π/3 – 4π и т.д. Как же записать все эти бесчисленные решения? Для этого используется такая запись:
Запись «π/3+ 2πn» называется серией решений. Она включает в себя бесконечное количество значений х, которые обращают ур-ние в справедливое равенство. Достаточно выбрать любое целое число и подставить его в серию решений. Например, при n = 0 получим решение
При n = 5 получим корень
При n = – 10 у нас получится решение
Однако помимо серии х = π/3 + 2πn решениями ур-ния будет определять ещё одна серия:
Действительно, число (– π/3) является корнем, но не входит в первую серию. Поэтому оно порождает собственную серию корней. Так, подставив в эту серию n = 4, получим корень
Итак, решением ур-ния являются две серии решений. Заметим, что каждой серии решений с периодом 2π соответствует ровно одна точка на единичной окружности:
Объединить же обе серии можно одной записью:
Напомним, что мы решали ур-ние
и получили для него решение
Число π/3 появилось в записи по той причине, что arccos 0,5 = π/3. Поэтому в общем случае, когда ур-ние имеет вид
где а – некоторое число, его решением будут все такие х, что
Для краткости запись «n– целое число» заменяют эквивалентной записью
«n ∈ Z»
Напомним, что буквой Z обозначают множество целых чисел.
Задание. Решите ур-ние
Решение. Вспомним, что
Задание. Решите ур-ние
Решение. В таблице стандартных углов нет такого числа, у которого косинус равен 0,25. Поэтому вычислить значение arccos 0,25 мы не сможем. Но для записи решения и не нужно его вычислять:
Иногда встречаются задачи, в которых надо не просто решить ур-ние, но и выбрать некоторые его корни, удовлетворяющие определенному условию. Процедуру выбора корней, удовлетворяющих условию задачи, часто называют отбором корней. Заметим, что иногда при отборе корней удобнее записывать решение ур-ние не в виде одной серии, а в виде двух серий, у каждой из которых период равен 2π. Рассмотрим отбор корней на примере.
Задание. Укажите три наименьших положительных корня ур-ния
Решение. Так как
то все решения образуют две серии:
Начнем подставлять вместо n целые числа и выпишем из каждой серии несколько чисел. Так мы сможем найти наименьшие положительные числа в каждой серии.
Для первой серии:
Для второй серии:
Отметим все найденные корни на координатной прямой (схематично, не выдерживая масштаб):
Видно, что тремя наименьшими положительными корнями являются числа π/4, 7π/4 и 9π/4
Ответ: π/4, 7π/4 и 9π/4.
Отметим, что возможны три частных случая, когда две серии решений сливаются в одну. Для ур-ния
На графике видно, что этим значениям х соответствуют вершины синусоиды. Решениями же ур-ния
являются точки, в которых график пересекает ось Ох:
Отдельно отметим, что если правая часть в ур-нии – это число, большее единицы или меньшее (– 1), то ур-ние корней не имеет, ведь область определения косинуса – это отрезок [– 1; 1].
Решение уравнения sinx = a
Ур-ние cosx = a называют простейшим тригонометрическим уравнением, ведь, ведь для его решения не требуется проводить никаких преобразований. Аналогично простейшими являются ур-ния sinx = a, tgx = a и ctgx = a.
Ситуация с ур-нием sinx = a аналогична ситуации с косинусом. Если число а не принадлежит промежутку [– 1; 1], то корней у ур-ния не будет. Если же число а будет принадлежать этому промежутку, то у ур-ния окажется бесконечное число решений.
Рассмотрим случай, когда 0<а< 1. Тогда решениями ур-ния окажутся числа arcsina и π – arcsina:
В свою очередь каждое из этих двух решений порождает свою собственную бесконечную серию решений
Однако, как и в случае с косинусом, существует способ записать одной формулой сразу оба этих решения. Для этого перепишем первую серию таким образом:
Действительно, если n окажется четным, то, то выражение (– 1)n,будет равно единице, и мы получим первую серию. Если же n – нечетное число, то, то выражение (– 1)n окажется равным (– 1), и мы получим вторую серию.
Задание. Решите ур-ние
Задание. Запишите корни ур-ния
Теперь будем подставлять в это решение значения n, чтобы найти конкретные значения х. Нас интересуют корни, которые больше π, но меньше 4π, поэтому будем сразу сравнивать полученные результаты с этими числами.
Получили два корня, относящихся к промежутку – это 7π/3 и 8π/3. Нет смысла проверять другие возможные значения n, ведь они будут давать корни, заведомо меньшие 2π/3 или большие 13π/3:
Ответ: 7π/3 и 8π/3.
Как и в случае с косинусом, есть несколько частных случаев, когда решение ур-ния записывается проще. Ур-ние
Это видно из графика, где корням ур-ния соответствуют точки пересечения синусоиды с осью Ох:
Решениями ур-ния
Наконец, решениями ур-ния
Решение уравнений tgx = a и ctgx = a
Ур-ния вида tgx = a отличаются тем, что имеют решение при любом значении а. Действительно, построим одну тангенсоиду и проведем горизонтальную линии у = а. При любом а прямая пересечет тангенсоиду, причем ровно в одной точке, которая имеет координаты (arctga; a):
Таким образом, у ур-ния tgx = a существует очевидное решение
x = arctg a
Однако напомним, что тангенс является периодической ф-цией, его график представляет собой бесконечное множество тангенсоид, расстояние между которыми равно π. Поэтому корень х = arctga порождает целую серию корней, которую можно записать так:
Задание. Решите ур-ние
Задание. Запишите формулу корней ур-ния
Далее рассмотрим ур-ние вида
Задание. Решите ур-ние
Существует особый случай, когда нельзя заменить котангенс на тангенс. В ур-нии
Из сегодняшнего урока мы узнали про обратные тригонометрические ф-ции – арксинус, арккосинус и арктангенс. Также мы научились находить решения простейших тригонометрических уравнений. Это поможет нам в будущем при изучении более сложных ур-ний.
