uni
Сообщение uni » Вт сен 06, 2005 6:42 pm
Отвечу пока кратко, т.к. ещё не вошёл в тему.
> 1. Каким образом у Вас получается выводить на график вертикальные линии? Хотелось бы вывести прямые ff и fff на графике (Рис 1).
Двойным щелчком вызовите окно свойств графика. На вкладке X-Y Axes включите галочки напротив Show markers для оси X. Выйдите из окна свойств. На графике появятся 2 placeholder’а так называемых, как вы догадались какое значение вы туда введёте туда линии и встанут по оси X.
> 2. Что обозначает N?
У меня N – это количество отсчётов, т.е. я сначала задал сигнал в математической форме, потом его продискретизировал (s1=s(ii*delta_t-tи)), а потом выполнил БПФ (S=fft(s1)). Так вот, БПФ в Mathcad’е быстрое преобразование делает только для степени двойки, поэтому N=2^8.
> 3. … (пропущу)
Объяснение ниже.
> 4. Существует математическая модель фильтра Найквиста. Рис 1 …
Ещё не вводил, но думаю попозже нарисуем так как по теории.
> Возможно, что интересуемые меня значения необходимо искать относительно этого фильтра. (Рис 4)
Вот я тоже так подумал. Позволю прокомментировать ваши картинки. Итак, у нас есть некий сигнал с цифровой модуляцией. Поскольку сигнал на выходе передатчика имеет вероятностный характер, то спектральное представление обобщают функцией вида sin(t/T)/(t/T). Импульс Найквиста тоже имеет такое представление. Вообще в книжке, которую я тут отыскал у себя на полке, приведена чуть более общая формула для этого фильтра. Он я так понял называется выравгивающим, а конкретнее – приподнятым косинусом (raised-cosine). Только вот у меня в книже нет сомножителя у косинуса, который появился у вас. В программном блоке посередине должен стоять один только косинус в квадрате, а всё остальное – его аргумент. Если мы пропустим сигнал через такой фильтр, то огибающая его спектра на выходе будет выглядеть как приплюснутый косинус, поэтому видимо не важно какая была ширина спектра у сигнала по уровню половинной мощности или ещё как, если мы посчитаем ширину у квадрата косинуса, то это будет оценка сверху. Поэтому вы как мне кажется правильно сказали, что нужно исходить из формулы для фильтра Найквиста. Таким образом, я думаю не трудно будет отыскать агрумент по значению ![]() В моей книжке в формуле есть два коэффициента: W – максимальная ширина полосы, Wo=1/(2T) – минимальная ширина полосы по Найквисту, а коэффициент сглаживания альфа равен (W-Wo)/Wo. Видимо эти значения используются в программе (или вычисляются по параметрам сигнала). Посмотрю поподробней позже. Формул для оценки ширины спектра по виду цифровой модуляции пока не имею. Кстати, а что за сигнал такой DSSS?
В моей книжке в формуле есть два коэффициента: W – максимальная ширина полосы, Wo=1/(2T) – минимальная ширина полосы по Найквисту, а коэффициент сглаживания альфа равен (W-Wo)/Wo. Видимо эти значения используются в программе (или вычисляются по параметрам сигнала). Посмотрю поподробней позже. Формул для оценки ширины спектра по виду цифровой модуляции пока не имею. Кстати, а что за сигнал такой DSSS?
Решение уравнения в mathcad root
Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.
| root( f(z), z) | Возвращает значение z, при котором выражение или функция f(z) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр. |
Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.
Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.
Рассмотрим пример, как найти a — решение уравнения e x = x 3 . Для этого выполните следующие шаги:
- Определите начальное значение переменной x. Введите x:3. Выбор начального приближения влияет на корень, возвращаемый Mathcad (если выражение имеет несколько корней).
- Определите выражение, которое должно быть обращено в ноль. Для этого перепишите уравнение e x = x 3 в виде x 3 – e x = 0. Левая часть этого выражения и является вторым аргументом функции root
- Определите переменную a как корень уравнения. Для этого введите a:root(x^3[Space]-e^x[Space],x).
- Напечатайте a=, чтобы увидеть значение корня.
При использовании функции root имейте в виду следующее:
- Удостоверьтесь, что переменной присвоено начальное значение до начала использования функции root.
- Для выражения с несколькими корнями, например x 2 – 1 = 0, начальное значение определяет корень, который будет найден Mathcad. На Рисунке 1 приведен пример, в котором функция root возвращает различные значения, каждое из которых зависит от начального приближения.
- Mathcad позволяет находить как комплексные, так и вещественные корни. Для поиска комплексного корня следует взять в качестве начального приближения комплексное число.
- Задача решения уравнения вида f(x) = g(x) эквивалентна задаче поиска корня выражения f(x) – g(x) =0. Для этого функция root может быть использована следующим образом:
Функция root предназначена для решения одного уравнения с одним неизвестным. Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 1: Использование графика и функции root для поиска корней уравнения.
Что делать, когда функция root не сходится
Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.
Если после многих итераций Mathcad не может найти подходящего приближения, то появляется сообщение об ошибке “отсутствует сходимость”. Эта ошибка может быть вызвана следующими причинами:
- Уравнение не имеет корней.
- Корни уравнения расположены далеко от начального приближения.
- Выражение имеет локальные максимумы или минимумы между начальным приближением и корнями.
- Выражение имеет разрывы между начальным приближением и корнями.
- Выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find
Некоторые советы по использованию функции root
В этом разделе приведены несколько советов по использованию функции root:
- Для изменения точности, с которой функция root ищет корень, можно изменить значение встроенной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL := 0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите из меню Математика команду Встроенные переменные и введите подходящее значение в поле TOL. Нажав “OK”, выберите из меню Математика команду Пересчитать всё, чтобы обновить все вычисления в рабочем документе с использованием нового значения переменной TOL.
- Если уравнение имеет несколько корней, пробуйте использовать различные начальные приближения, чтобы найти их. Использование графика функции полезно для нахождения числа корней выражения, их расположения и определения подходящих начальных приближений. Рисунок 1 показывает пример. Если два корня расположены близко друг от друга, можно уменьшить TOL, чтобы различить их.
- Если f(x) имеет малый наклон около искомого корня, функция может сходиться к значению r, отстоящему от корня достаточно далеко . В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f(x)=0 на g(x)=0, где
Решение уравнений с параметром
Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции
Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.
Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.
Рисунок 2: Определение функции пользователя с функцией root.
Нахождение корней полинома
Для нахождения корней выражения, имеющего вид
лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.
| polyroots(v) | Возвращает корни полинома степени . Коэффициенты полинома находятся в векторе v длины n+1. Возвращает вектор длины n, состоящий из корней полинома. |
Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.
Рисунок 4: Использование функции polyroots для поиска корней полинома.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Решение уравнения в mathcad root
Глава 4. Решение уравнений
4.1 Функция root
Функция root используется для решения одного уравнения с одним неизвестным. Перед началом решения желательно построить график функции, чтобы проверить, есть ли корни, то есть пересекает ли график ось абсцисс. Начальное приближение лучше всего выбрать по графику поближе к корню, так как итерационные методы весьма чувствительны к выбору начального приближения.
Обращение к функции осуществляется следующим образом:
root ( f ( x ), x ), где f ( x ) – выражение, равное нулю; x – аргумент, варьируя который, система ищет значение, обращающее в нуль ( рис. 4.1 ).
Уравнение
начальное приближение
решение
или
другие корни
Задан интервал поиска корней
Рис. 4. 1 Использование функции root
Функция f ( x ) и аргумент x должны быть скалярами, то есть результат вычисления функции – число, а не вектор или матрица. Функция root использует метод секущих. Корень уравнения – ближайшее к начальному приближению значение x , обращающее функцию f ( x ) в нуль. Если корней несколько, то для отыскания каждого корня необходимо задавать свое начальное приближение.
Mathcad позволяет вместо начального приближения задавать диапазон значений аргумента, в котором лежит значение искомого корня. В этом случае обращение к функции root должно иметь четыре параметра:
root ( f ( x ), x , а, b ),
где a и b – границы интервала, в котором лежит один корень уравнения. Внутри интервала не должно быть больше одного корня, так как Mathcad выводит на экран лишь один корень, лежащий внутри интервала.
Значение функции на границах интервала должно быть разного знака, иначе, возможно, корень не будет найден.
Если уравнение не имеет действительных корней, то есть на графике функция f ( x ) нигде не равна нулю, то для вывода комплексных корней надо ввести начальное приближение в комплексной форме (рис. 4.2) .
Если функция имеет мнимый корень,
то начальное приближение задается комплексным числом
– начальное приближение
Рис. 4. 2 Решение уравнения с комплексными корнями
Для ввода мнимой единицы надо ввести с клавиатуры 1 i или 1 j .
Если уравнение имеет несколько корней, то для их нахождения можно использовать разложение функции f ( x ) на простые множители:
где x 1, x 2 , , xn – корни уравнения. Начальное приближение можно задать только для первого корня. В качестве функции f ( x ) нужно взять
,
где ,
и т. д. (рис. 4.3)
у этой функции 3 корня
диапазон значений х для вывода графика
Рис. 4. 3 Определение трех корней уравнения
Если функция f ( x ) имеет малый наклон вблизи искомого корня, то функция root ( f ( x ), x ) может сходиться к значению, довольно далеко отстоящему от корня. В таком случае для уточнения корня необходимо уменьшить значение погрешности вычислений, задаваемое встроенной переменной TOL . Для этого:
1) в стандартном меню Mathcad выберите команду Tools → Worksheet Options → Built – In Variables (Инструменты → Параметры документов → Встроенные переменные);
2) в открывшемся окне поменяйте значение Convergence Tolerance ( TOL ) (Погрешность сходимости).
Чем меньше константа TOL , тем ближе к нулю будет значение функции при найденном корне уравнения, но тем больше будет время вычисления корня.
Для повышения точности расчета корня можно заменить f ( x ) на
.
Корень можно найти и по графику, увеличив масштаб. Для этого необходимо:
1) выделить график, щелкнув левой кнопкой мыши внутри графика;
2)в главном меню Mathcad выбрать команду Format → Graph → Zoom (Формат→График→Масштаб);
3) при нажатии левой кнопки мыши обвести пунктирной линией область графика вблизи искомого корня, которую надо увеличить;
4) в открытом окне X – Y Zoom (Масштаб по осям X – Y ) нажать кнопку Zoom .
Прямо с графика можно передать в буфер обмена численное значение корня. Для этого выполните следующие действия:
1) Выделите график, щелкнув левой кнопкой мыши внутри графика,
2) в главном меню Mathcad выберите команду Format → Graph → Trace (Формат→График→Трассировка),
3) щелкните левой кнопкой мыши внутри графика – появится перекрестье осей,
4) двигая мышь при нажатой левой кнопке, установите перекрестье на пересечении графика с осью абсцисс. При этом численные значения координат перекрестья появляются в открытом окне X – Y Trace (Трассировка X и Y ).
5) правильно выбрав положение перекрестья, нажмите кнопки Copy X и Copy Y – численные значения будут помещены в буфер
6) вне поля графика запишите имя, которое хотите дать корню, и оператор присваивания :=. Нажмите кнопку Paste (Вставить) в стандартном меню Mathcad или в контекстном меню, открывающемся при нажатии правой кнопки мыши.
Рис. 4. 4 Определение корня уравнения по графику
В окне X – Y Trace есть пункт Track Data Points (Отмечать расчетные точки). Если установить этот флажок, при перемещении мыши пунктирное перекрестье на графике будет перемещаться скачками, отмечая расчетные значения функции. Если флажок снять, движение перекрестья становится плавным.
При работе с Mathcad постоянно пользуйтесь правой кнопкой мыши (в контекстном меню каждый раз появляются новые, наиболее нужные в данный момент функции). Щелкните правой кнопкой мыши на графике: в открывшемся контекстном меню есть пункты Zoom и Trace .
Решение уравнения в mathcad root
РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ
4 Решение уравнений и систем средствами Mathcad
Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.
Функция root, блоки Given…Find, Given…Minerr
В ходе численного решения обычно выделяют два этапа:
- отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
- уточнение корней – нахождение численного значения корня с указанной точностью.
Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.
Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается
root(f(x), x, [a, b])
и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:
- f(x) – функция левой части уравнения f(x) = 0;
- x – переменная, относительно которой требуется решить уравнение;
- a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде
Этот прием используется в Mathcad так:
- задается матрица коэффициентов при неизвестных системы A;
- задается столбец свободных членов b;
- вводится формула для нахождения решения системы X:=A -1 b;
- выводится вектор решений системы X=.
Кроме того, пакет Mathcad имеет встроенную функцию
lsolve(A, b),
возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).
Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.
Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.
Порядок выполнения лабораторной работы
- Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
- Сохранить в личной папке на диске z: новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
- Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:
Лабораторная работа № 4
Решение уравнений и систем в Mathcad.
- В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
- Выполнить задание 1.
Задание 1. Решить уравнение .
Решение.
Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.
Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:
Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:
Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).
Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).
Для появления графика щелкнем левой клавишей мыши вне графической области.
Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.
Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.
После указанных преобразований график функции f(x) будет выглядеть следующим образом:
Из графика функции f(x) видно, что уравнение имеет три корня, которые приблизительно равны: x1 ≈ -1; x2 ≈ 1; x3 ≈ 2,5.
Этап отделения корней завершен.
Уточним теперь корни уравнения с помощью функции root.
Присвоим начальное приближение переменной x и укажем точность поиска корня:
Уточним заданное приближение к значению корня с помощью функции root:
Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:
Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:
Задание 2. Решить уравнение .
Решение.
Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:
Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.
Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.
Для получения результата напечатаем polyroots(v) =:
Задание 3. Решить систему линейных уравнений Сделать проверку.
Решение.
1-й способ. Использование блока Given … Find.
Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:
Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).
После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:
Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом
После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.
2-й способ. Использование блока Given…Minerr.
Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:
3-й способ. Решение системы линейных уравнений матричным способом.
Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:
Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:
Решим систему матричным способом по формуле
Решим систему с помощью функции lsolve:
Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:
[spoiler title=”источники:”]
http://www.math.mrsu.ru/text/courses/mcad/4.1.htm
http://zf.bsut.by/it/fbo/zc/lab2_mc.htm
[/spoiler]
Функции.
Функции в Mathcad
записываются в обычной для математика
форме:
f(x,
…) – функция;
f –
имя функции;
x, …
– список переменных.
В Mathcad
формально можно разделить функции на
два типа:
-
Встроенные
функции (например, sin(x)); -
Функции,
определенные пользователем (например,
f(x,y)=x2cos(x+y)).
Система Mathcad
содержит расширенный набор встроенных
элементарных функций. Имя функции
отождествляется с выполняемой ей
математической функцией, например:
sin(x) –
функция, вычисляющая синус аргумента
х, где sin – имя функции.
Полный перечень вычисляемых функций
можно просмотреть, нажав на пользовательской
панели инструментов на кнопку f(x)
или выбрав пункт меню Вставка подменю
Функция.
Аргумент и значение
функции могут быть действительным или
комплексным числом z.
Ниже приведены функции разбитые на 6
групп.
Тригонометрические:
sin(z), cos(z),
tan(z), sec(z),
csc(z), cot(z).
Гиперболические:
sinh(z), cosh(z), tanh(z), sech(z), csch(z), coth(z).
Обратные
тригонометрические: asin(z), acos(z), atan(z).
Обратные
гиперболические: asinh(z), acosh(z), atanh(z).
Показательные
и логарифмические: exp(z), ln(z), log(z).
Функции комплексного
аргумента: Re(z) – выделение действительной
части z, lm(z) – выделение мнимой части z,
arg(z) – вычисление аргумента (фазы).
Символьный вывод.
Наряду с численным
выводом, в Mathcad имеется
возможность символьного, или аналитического,
вычисления значения выражения. Для
символьных вычислений имеется ряд
специальных средств, самое простое из
них – это оператор символьного вывода
(). Если численный
вывод – это «запрограммированный»
расчет по формулам, то символьный вывод
– это результат работы символьного
процессора. Работа символьного процессора
заключается в анализе самого текста
математических выражений.
Чтобы вычислить
символьно математическое выражение,
необходимо выполнить следующее:
-
Ввести
это выражение; -
Ввести
оператор символьного вывода нажатием
соответствующей кнопки

на панели Символы.
После этого справа
от символа оператора символьного вывода
появится определенное аналитически
значение выражения. Если символьному
процессору Mathcad не удается
аналитически упростить выражение, то
оно будет выдано справа от знака
в том же виде, что и слева.
Пример:

Вычислительные
операторы.
Вычислительные
операторы вставляются в документы при
помощи панели инструментов Вычисления.
При нажатии любой из кнопок в документе
появляется символ соответствующего
математического действия, снабженный
несколькими местозаполнителями (рис.3).
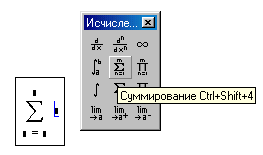
Рис.3 Вставка
оператора суммирования
После ввода
какого-либо вычислительного оператора
имеется возможность вычислить его
значение либо численно, нажатием клавиши
<=>, либо символьно, с помощью оператора
символьного вывода.
Задание:
Перед
выполнением каждого задания, необходимо
сначала писать само задание.
Например:

1. Задайте переменным
а и b
числовые значения и выполните над ними
элементарные операции: сложение,
вычитание, умноже6ние, деление, возведение
а
в степень b,
корень из а.
2. Вычислить
тригонометрические функции при заданном
самостоятельно значении x,
используя пункт Меню Вставить /
Функция
![]()
3. Вычислить
натуральный и десятичный логарифмы при
заданном х.
4. Вычислить
производные первого, второго и третьего
порядка от заданной функции
f(x)=2x+3+cos(x)2
5. Вычислить
определенный (пределы интегрирования
задать самостоятельно) и неопределенный
интегралы двух функций:
f(x)=2x+3+cos(x)2
f(x)=ex
cos(x)
6. Вычислить пределы
функций
![]()

7. Найти сумму и
произведение. Число m –
задать самостоятельно.

Для присвоения n
значений от 1 до 5 использовать Булево
равенство
![]()
из панели Булевы операторы.

8.
Пользуясь мастером функций получить
значение синуса и гиперболического
арккосинуса

5
1.5. Некоторые стандартные функции MathCAD
Рассмотрим некоторые стандартные функции системы MathCAD. Введем специальные обозначения для аргументов функций. Пусть первый символ имени аргумента обозначает его тип:
M – квадратная матрица;
V – вектор (матрица из одного столбца);
A – произвольная матрица;
S – симметричная матрица;
G – произвольная матрица или число;
X – вектор или число;
Z – комплексная матрица или число;
z – комплексное число;
прочие символы – скалярные величины.
Экспоненциальные и логарифмические функции
exp(X) – экспонента от X;
ln(X) – натуральный логарифм от X;
log(X) – десятичный логарифм от X;
log(X,b) – логарифм от X по основанию b.
Гиперболические и тригонометрические (прямые и обратные) функции
sin(X), cos(X), tan(X), cot(X), sec(X), csc(X) – соответственно синус, косинус, тангенс, котангенс, секанс, косеканс от X, причем аргументы указываются в радианах;
sinh(X), cosh(X), tanh(X), coth(X), sech(X), csch(X) – аналогичные гиперболические функции;
asin(z), acos(z), atan(z), acot(z), asec(z), acsc(z) – соответственно арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс от z.
Функции для работы с комплексными числами
Re(Z), Im(Z) – соответственно вещественная и мнимая части комплексного числа Z;
arg(z) – аргумент комплексного числа z (в радианах).
Матричные функции
length(V) – возвращает число элементов вектора V;
cols(A) – возвращает число столбцов матрицы A;
rows(A) – возвращает число строк матрицы A;
matrix(m, n, f) – матрица размером mxn, значения элементов матрицы определяются f – функцией f (i, j) от двух переменных (номера строки и номера столбца). Эта функция должна быть предварительно определена пользователем;
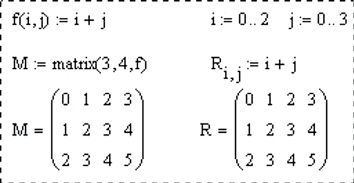
identity(n) – единичная матрица n×n;
tr(M) – след матрицы M (сумма элементов главной диагонали);
rank(A) – ранг матрицы M;
norme(M) – эвклидова норма матрицы M, то есть корень квадратный из суммы квадратов всех элементов;
eigenvals(M) – вектор, элементы которого являются собственными числами матрицы M;
eigenvecs(M) – матрица, состоящая из нормализованных собственных векторов матрицы M;
cholesky(S) – возвращает нижнетреугольную матрицу L – результат разложения Холецкого вида L∙LT = S;
lu(M) – возвращает матрицу размера n×3n, состоящую из трех соединенных матриц P, L, U, являющихся результатом LU-разложения вида P∙M = L∙U.
Пример вычислений с матричными функциями: нахождение собственного числа путем решения матричного уравнения det(M – λE) = 0 и с помощью функции eigenvals.

Элементы статистического анализа данных
gmean(G1,G2,G3…) – среднее геометрическое аргументов;
mean(G1,G2,G3…) – среднее арифметическое аргументов;
var(G1,G2,G3…) – дисперсия;
stdev(G1,G2,G3…) – среднеквадратичное отклонение.
Дискретные преобразования
fft(V1), ifft(V2) – прямое и обратное быстрые преобразования Фурье над вещественными данными. V1 – вектор из 2m элементов, V2 – вектор из 1 + 2m–1 элементов, m > 2;
cfft(A), icfft(A) – прямое и обратное преобразования Фурье над вещественными и комплексными векторами и матрицами;
wave(V), iwave(V) – прямое и обратное вейвлет-преобразования, V – вектор из 2m элементов, m – целое число.
Аппроксимация, интерполяция и экстраполяция
Аппроксимация – поиск функции, которая с заданной степенью точности описывает исходные данные.
Интерполяция – определение наиболее правдоподобных промежуточных значений в интервале между известными значениями (подбор гладкой кривой, проходящей через заданные точки или максимально близко к ним).
Экстраполяция – определение наиболее правдоподобных последующих значений на основании анализа предыдущих значений (предсказание дальнейшего поведения неизвестной функции).
Применяются следующие функции MathCAD:
regress(VX,VY,k) – возвращает вектор данных, используемый для поиска интерполирующего полинома (a0 + a1x + a2x2 + … + akxk) порядка k. Полином должен описывать данные, состоящие из упорядоченных значений аргумента (VX) и соответствующих значений неизвестной функции (VY), то есть график полинома должен проходить через все точки, заданные координатами (VX, VY), или максимально близко к этим точкам;
interp(VS,VX,VY,x) – возвращает интерполированное значение неизвестной функции при значении аргумента x. VS – вектор значений, который вернула функция regress. VX,VY – те же данные, что и для regress. Функции interp и regress используются в паре;
predict(V,m,n) – возвращает вектор из n предсказанных значений на основании анализа m предыдущих значений из вектора V. Предполагается, что значения функции в векторе V были получены при значениях аргумента, взятых последовательно, с одинаковым шагом. Используется алгоритм линейной предикции. Наиболее целесообразно использовать predict для предсказания значений по данным, в которых отмечены колебания.
Для интерполяции система MathCAD использует подход, основанный на применении метода наименьших квадратов.
Примеры интерполяции и экстраполяции:
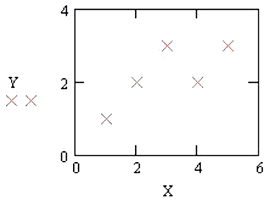
1.5.1. Пусть заданы координаты пяти точек (1; 1), (2; 2), (3; 3), (4; 2), (5; 3), представляющих результаты измерения значений некоторой неизвестной функции при различных значениях x. Необходимо подобрать интерполирующую функцию (гладкую кривую), проходящую через заданные точки.
1.5.2. Дана функция y(i) = e–i/10∙sin (i). Известны значения данной функции при i = 0, 1, …, 10. Основываясь на десяти последних значениях, необходимо предсказать последующие десять значений.
Решения показаны на рис. 19.
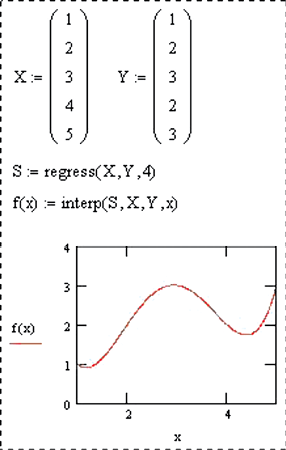
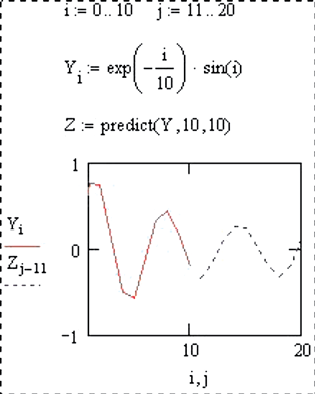
а б
Рис. 19. Решения в MathCAD первой (а) и второй (б) задач
Нахождение корней полинома
polyroots(V) – возвращает вектор, содержащий все корни полинома a0 + a1x + a2x2 + … + akxk, заданного вектором-столбцом коэффициентов
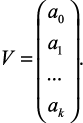
Прочие функции
max(G1,G2,…) – максимальное значение среди аргументов;
min(G1,G2,…) – минимальное значение среди аргументов;
if(a,b,c) – возвращает b, если a ≠ 0, иначе возвращает c;
sign(a) – возвращает –1, 0 или 1 в зависимости от знака числа a.
На рис. 20 показан пример применения функции if.
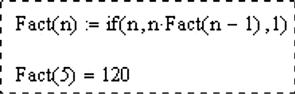
Рис. 20. Функция, вычисляющая факториал
Mathcad: получаем вектор значений функции
Часто задаваемый вопрос – как получить из значений функции, посчитанной в заданных пределах с заданным шагом именно вектор значений (а не ранжированную переменную, она же переменная-диапазон, она же дискретный аргумент).
Допустим, нам нужно табулировать функцию f(x) в интервале изменения значений x от a до b включительно с известным шагом по x, равным h.
Решить задачу с помощью дискретного аргумента очень просто, достаточно задать нужный дискретный аргумент и взять от него функцию:

табулирование функции в Mathcad с помощью ранжированной переменной (нижняя часть списка значений отрезана)
Оператор “равно” не сработает в одном действии с “присвоить” для аргумента-диапазона.
Важней здесь другое – в диапазоне величины не занумерованы, как в массиве, соответственно, нельзя по номеру “вытащить” нужную величину и нельзя воспользоваться стандартными функциями для обработки векторов.
Чтобы получить вектор значений функции, рассчитаем требуемое количество узлов сетки по формуле
n = (b-a)/h + 1, затем сформируем вектор t из требуемых значений аргумента (не будем переопределять уже занятое ранжированной переменной наименование “x“, хотя это и возможно), а затем вычислим значения функции по формуле yi = f(ti), все эти действия показаны на втором рисунке:

табулирование функции в Mathcad с сохранением вектора значений (показаны только первые элементы вектора)
Замечания.
1. Предполагаем, что количество узлов сетки n = (b-a)/h + 1 получается целым, если это не так, всегда можно взять вместо n величину ceil(n) (значение, округлённое вверх), как и сделано на скрине, правда, мы рискуем при этом “прихватить” лишнюю область определения, например, при a = 1, b = 3, h = 0.3, имеем n = 7.667, ceil(n) = 8, а последнее вычисленное значение x будет равно a + h * (ceil(n)-1) = 3.1.
2. Также предполагается, что системная переменная ORIGIN (начало нумерации элементов для векторов и матриц) не менялась и равна нулю.
Код проверялся в актуальной сборке Mathcad 15 под Windows 10.
![]() Скачать этот документ Mathcad 14/15 .xmcd в архиве .zip (12 Кб)
Скачать этот документ Mathcad 14/15 .xmcd в архиве .zip (12 Кб)
Примечание. В новой линейке Mathcad Prime вектору уже можно непосредственно присваивать диапазон, если сразу выполнить “:=” и “=”, хотя различие по контексту между векторами и диапазонами остаётся:

Mathcad Prime – присваиваем диапазон вектору
08.06.2020, 19:47 [4035 просмотров]
К этой статье пока нет комментариев, Ваш будет первым
