Как найти аргумент в матлабе

Main Content

Real and imaginary components, phase angles

In MATLAB^®, i and j represent the basic imaginary
unit. You can use them to create complex numbers such as 2i+5. You can also
determine the real and imaginary parts of complex numbers and compute other common values such
as phase and angle.

Functions

abs	Absolute value and complex magnitude
angle	Phase angle
complex	Create complex array
conj	Complex conjugate
cplxpair	Sort complex numbers into complex conjugate pairs
i	Imaginary unit
imag	Imaginary part of complex number
isreal	Determine whether array uses complex storage
j	Imaginary unit
real	Real part of complex number
sign	Sign function (signum function)
unwrap	Shift phase angles

Topics

• Plot Imaginary and Complex Data

  Plot the imaginary part versus the real part of a complex vector.

При
наборе комплексных чисел в командной
строке MatLab
можно использовать либо i,
либо j,
а сами числа при умножении, делении и
возведении в степень
необходимо заключать в круглые скобки:

»(2.1+3.2i)*2+(4.2+1.7i)^2

ans
=

18.9500
+20.6800i

Если не использовать
скобки, то умножаться или возводиться
в степень будет только мнимая часть и
получится неверный результат:

»
2.1+3.2i*2+4.2+1.7i^2

ans
=

3.4100
+ 6.4000i

Для
вычисления комплексно-сопряженного
числа применяется апостроф, который
следует набирать сразу за числом, без
пробела:

»
23i’

ans
=

2.0000
+ 3.0000i

Если необходимо
найти комплексно-сопряженное выражение,
то исходное выражение должно быть
заключено в круглые скобки:

»((3.2+1.5i)*2+4.2+7.9i)’

ans
=

10.6000
10.9000i

MatLab позволяет
использовать комплексные числа в
качестве аргументов встроенных
элементарных функций:

»
sin(2+3i)

ans
=

9.1545

4.1689i

Конструирование
комплексного числа по его действительной
и мнимой части выполняется с помощью
функции complex:

»
complex(2.3,
5.8)

ans
=
2.3000
+ 5.8000i

Как
узнать, какие встроенные элементарные
функции можно использовать и
как их вызывать? Наберите в командной
строке команду help
eifun,
при этом
в командное окно выводится список всех
встроенных элементарных функций
с их кратким описанием.

3. Простейшие вычисления в пакете MatLab с использованием переменных и векторов

3.1. Использование переменных в пакете MatLab

Как
и во всех языках программирования, в
MatLab
предусмотрена возможность работы с
переменными. Причем пользователь не
должен заботиться о том,
какие значения будет принимать переменная
(комплексные, вещественные
или только целые). Для того чтобы
присвоить, например, переменной
z
значение 1.45, достаточно написать в
командной строке z
= 1.45, при этом
MatLab
сразу же выведет значение z:

»
z
= 1.45

z
=

1.4500

Здесь
знак равенства используется в качестве
оператора
присваивания. Часто
не
очень удобно после каждого присваивания
получать еще и результат. Поэтому в
MatLab
предусмотрена возможность завершать
оператор присваивания
точкой с запятой для подавления вывода
результата в командное окно. Именем
переменной может быть любая
последовательность букв и цифр без
пробела,
начинающаяся с буквы. Строчные и прописные
буквы различаются,
например MZ
и mz
являются двумя разными переменными.
Количество воспринимаемых
MatLab
символов в имени переменной составляет
31.

В
качестве упражнения на использование
переменных найдите значение следующего
выражения:

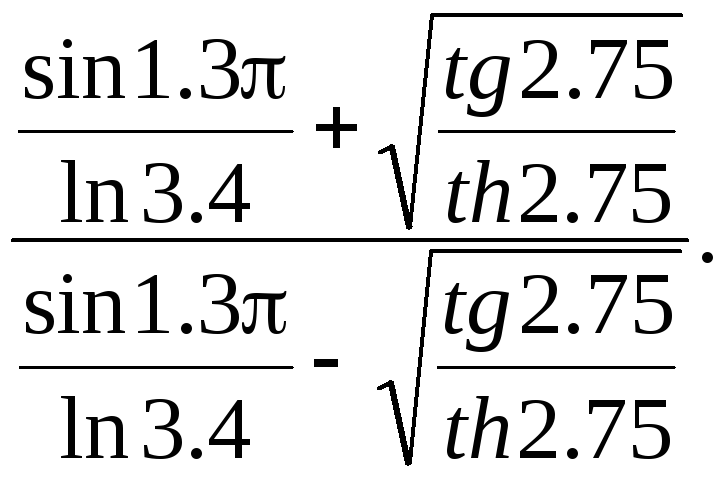
Наберите
последовательность команд, приведенную
ниже (обратите внимание
на точку с запятой в первых двух операторах
присваивания для подавления вывода
промежуточных значений на экран):

»
х
= sin(1.3*pi)/log(3.4);

»
у
= sqrt(tan(2.75)/tanh(2.75));

»
z
=
(х+у)/(х-у)

Z
=

0.0243
– 0.9997i

Последний
оператор присваивания не завершается
точкой с запятой для того,
чтобы сразу получить значение исходного
выражения. Конечно, можно
было бы ввести сразу всю формулу и
получить тот же результат:

»(sin(1.3*pi)/log(3.4)+sqrt(tan(2.75)/tanh(2.75)))/…

(sin(1.3*pi)/log(3.4)-sqrt(tan(2.75)/tanh(2.75)))
ans
=

0.0243
– 0.9997i

Обратите
внимание, насколько первая запись
компактнее и яснее второй! Во
втором варианте формула не помещалась
в командном окне на одной строке, и
пришлось записать ее в две строки, для
чего в конце первой строки
поставлены три точки.

Замечание
1

Для
ввода длинных формул или команд в
командную строку следует поставить три
точки (подряд, без пробелов), нажать
клавишу <Enter>
и продолжить набор формулы на следующей
строке. Так можно разместить выражение
на нескольких строках. MatLab
вычислит все выражение или выполнит
команду после нажатия
на <Enter>
в последней строке (в которой нет трех
идущих подряд точек).

MatLab
запоминает значения всех переменных,
определенных во время сеанса
работы. Если после ввода примера,
приведенного выше, были проделаны
еще какие-либо вычисления, и возникла
необходимость вывести значение х,
то следует просто набрать
х
в командной строке и нажать <Enter>:

»
x

-0.6611

Переменные,
определенные выше, можно использовать
и в других формулах.
Например, если теперь необходимо
вычислить выражение

,

то достаточно
ввести следующую команду:

»
(x-y)^(3/2)

ans
=

-0.8139
+ 0.3547i

Вызов
функций в MatLab
обладает достаточной гибкостью. Например,
вычислить е^3.5
можно, вызвав функцию ехр из командной
строки:

»
ехр(3.5)

ans
=

33.1155

Другой способ
состоит в использовании оператора
присваивания:

»
t
= ехр(3.5)

t
=

33.1155

Предположим,
что часть вычислений с переменными
выполнена, а остальные
придется доделать во время следующего
сеанса работы с MatLab.
В этом случае
понадобится сохранить переменные,
определенные в рабочей среде.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Main Content

Accept a variable number of inputs or outputs, check for valid
values

Since MATLAB^® is an untyped language, most functions do not require argument
declarations or validation. However, if your function has wide usage and you
need to verify the type, size, or other aspects of inputs to ensure that
your code works as expected, you can define an arguments block (since R2019b). For details, see Function Argument Validation.

Additionally, you can check how many inputs or outputs your function
receives, the names of input variables, and more.

Functions

expand all

Declare and Validate Arguments

Arguments Block

arguments

Declare function argument validation

Numeric Value Validation

Comparisons

Data Types

Size

Range and Set Membership

Names

Name-Value Arguments Structure

namedargs2cell

Convert structure containing name-value pairs to cell array

Variable-Length Argument Lists

Inputs

varargin	Variable-length input argument list
nargin	Number of function input arguments
narginchk	Validate number of input arguments

Outputs

varargout	Variable-length output argument list
nargout	Number of function output arguments
nargoutchk	Validate number of output arguments

Additional Checks

Topics

Argument Validation

• Function Argument Validation

  Declare argument class and size, and enforce restrictions on argument values.

  • Validate Required and Optional Positional Arguments
  • Validate Repeating Arguments
  • Validate Name-Value Arguments
• Argument Validation Functions

  Validate specific requirements of arguments using validation functions. Write your own
  functions to check for specific argument requirements.

  • Use Validation Functions to Avoid Unwanted Class and Size Conversions
  • Use nargin Functions During Argument Validation
• Check Function Inputs with validateattributes
  This example shows how to verify that the inputs to
  your function conform to a set of requirements using the validateattributes function.
• Parse Function Inputs

  Define required and optional inputs, assign defaults
  to optional inputs, and validate all inputs to a custom function using
  the Input Parser.

  • Input Parser Validation Functions

Number of Arguments

• Support Variable Number of Inputs
  Define a function that accepts a variable number of
  input arguments using varargin. The varargin argument
  is a cell array that contains the function inputs, where each input
  is in its own cell.
• Support Variable Number of Outputs
  Define a function that returns a variable number of
  output arguments using varargout. Output varargout is
  a cell array that contains the function outputs, where each output
  is in its own cell.
• Find Number of Function Arguments

  Use nargin and nargout to
  determine how many input or output arguments your function receives.

  • Validate Number of Function Arguments
  • Checking Number of Arguments in Nested Functions

Pass-Through Inputs

• Ignore Inputs in Function Definitions
  If your function accepts a predefined set of inputs, but does not use all the
  inputs, use the tilde (~) operator to ignore them in your
  function definition.