Как найти аргумент вектора

Заказать задачи по любым предметам можно здесь от 10 минут

Комплексные числа

В математике кроме натуральных, рациональных и вещественных чисел имеется ещё один вид, называемый комплексными числами. Такое множество принято обозначать символом $ mathbb{C} $.

Рассмотрим, что из себя представляет комплексное число. Запишем его таким образом: $ z = a + ib $, в котором мнимая единица $ i = sqrt{-1} $, числа $ a,b in mathbb{R} $ вещественные. 

Если положить $ b = 0 $, то комплексное число превращается в вещественное. Таким образом, можно сделать вывод, что действительные числа это частный случай комплексных и записать это в виде подмножества $ mathbb{R} subset mathbb{C} $. К слову говоря также возможно, что $ a = 0 $.

Принято записывать мнимую часть комплексного числа как $ Im(z) = b $, а действительную $ Re(z) = a $.

Введем понятие комплексно-сопряженных чисел. К каждому комплексному числу $ z = a+ib $ существует такое, что $ overline{z} = a-ib $, которое и называется сопряженным. Такие числа отличаются друг от друга только знаками между действительной и мнимой частью.

Формы

Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:

1. Алгебраическая $ z = a+ib $
2. Показательная $ z = |z|e^{ivarphi} $
3. Тригонометрическая $ z = |z|cdot(cos(varphi)+isin(varphi)) $

Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.

Изображение

Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:

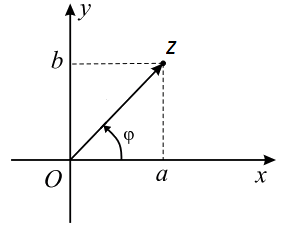Видим, что $ a,b in mathbb{R} $ расположены на соответствующих осях плоскости. 

Комплексное число $ z = a+ib $ представляется в виде вектора $ overline{z} $.

Аргумент обозначается $ varphi $.

Модуль $ |z| $ равняется длине вектора  $ overline{z} $ и находится по формуле $ |z| = sqrt{a^2+b^2} $

Аргумент комплексного числа $ varphi $ нужно находить по различным формулам в зависимости от полуплоскости, в которой лежит само число.

Если:

1. $ a>0 $, то $ varphi = arctgfrac{b}{a} $
2. $ a<0, b>0 $, то $ varphi = pi + arctgfrac{b}{a} $
3. $ a<0, b<0 $, то $ varphi = -pi + arctgfrac{b}{a} $

Операции

Над комплексными числами можно проводить различные операции, а именно:

• Складывать и вычитать
• Умножать и делить
• Извлекать корни и возводить в степень
• Переводить из одной формы в другую 

Для нахождения суммы и разности складывается и вычитаются только соответствующие друг другу члены. Мнимая часть только с мнимой, а действительная только с действительной:

$$ z_1 + z_2 = (a_1+ib_1) + (a_2+ib_2) = (a_1 + a_2)+i(b_1 + b_2) $$

$$ z_1 – z_2 = (a_1+ib_1) – (a_2+ib_2) = (a_1 – a_2)+i(b_1 – b_2) $$

Умножение в алгебраической форме:

$$ z_1 cdot z_2 = (a_1+ib_1) cdot (a_2+ib_2) = (a_1 a_2 – b_1 b_2)+i(a_1 b_2 + a_2 b_1) $$

Умножение в показательной форме:

$$ z_1 cdot z_2 = |z_1|e^{ivarphi_1} cdot |z_2|e^{ivarphi_2} = |z_1|cdot|z_2|cdot e^{i(varphi_1 + varphi_2)} $$

Деление в алгебраической форме:

$$ frac{z_1}{z_2} = frac{a_1+ib_1}{a_2+ib_2} = frac{a_1 a_2 + b_1 b_2 }{a_2 ^2 + b_2 ^2} + i frac{a_2 b_1 – a_1 b_2}{a_2 ^2 + b_2 ^2} $$

Деление в показательной форме:

$$ frac{z_1}{z_2} = frac{|z_1|e^{ivarphi_1}}{|z_2|e^{ivarphi_2}} = frac{|z_1|}{|z_2|}e^{i(varphi_1 – varphi_2)} $$

Для возведения в степень необходимо умножить комплексное число само на себя необходимое количество раз, либо воспользоваться формулой Муавра:

$$ z^n = |z|^n(cos nvarphi+isin nvarphi) $$

Для извлечения корней необходимо также воспользоваться формулой Муавра:

$$ z^frac{1}{n} = |z|^frac{1}{n}bigg(cos frac{varphi + 2pi k}{n}+isin frac{varphi + 2pi k}{n}bigg), k=0,1,…,n-1 $$

Так же теория комплексных чисел помогает находить корни многочленов. Например, в квадратном уравнении, если $ D<0 $, то вещественных корней нет, но есть комплексные. В последнем примере рассмотрен данный случай.

Рассмотрим на практике комплексные числа: примеры с решением.

Примеры с решением

Пример 1

Перевести из алгебраической в тригонометрическую и показательную форму:$$ z = 4-4i $$

Решение

Для начала приступим к нахождению модуля комплексного числа: $$ |z| = sqrt{4^2 + (-4)^2} = sqrt{16 + 16} = sqrt{32} = 4sqrt{2} $$ Осталось найти аргумент: $$ varphi = arctg frac{b}{a} = arctg frac{-4}{4} = arctg (-1) = -frac{pi}{4} $$ Теперь составляем тригонометрическую запись комплексного числа, указанного в условии примера: $$ z = 4sqrt{2}bigg(sin(-frac{pi}{4}) + isin(-frac{pi}{4}) bigg) $$ Тут же можно записать показательную форму: $$ z = 4sqrt{2} e^{-frac{pi}{4}i} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ z = 4sqrt{2}bigg(sin(-frac{pi}{4}) + isin(-frac{pi}{4}) bigg) $$ $$ z = 4sqrt{2} e^{-frac{pi}{4}i} $$

Пример 2

Вычислить сумму и разность заданных комплексных чисел: $$ z_1 = 3+i, z_2 = 5-2i $$

Решение

Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел: $$ z_1 + z_2 = (3+i) + (5-2i) = (3+5)+(i-2i) = 8 – i $$ Аналогично выполним вычитание чисел: $$ z_1 – z_2 = (3+i) – (5-2i) = (3-5)+(i+2i) = -2 + 3i $$

Ответ

$$ z_1 + z_2 = 8 – i; z_1 – z_2 = -2 + 3i $$

Пример 3

Выполнить умножение и деление комплексных чисел: $$ z_1 = 3+i, z_2 = 5-2i $$

Решение

$$ z_1 cdot z_2 = (3+i) cdot (5-2i) = $$ Просто на просто раскроем скобки и произведем приведение подобных слагаемых, так же учтем, что $ i^2 = -1 $: $$ = 15 – 6i + 5i -2i^2 = 15 – i – 2cdot(-1) = $$ $$ = 15 – i + 2 = 17 – i $$ Так, теперь разделим первое число на второе: $$ frac{z_1}{z_2} = frac{3+i}{5-2i} = $$ Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки: $$ = frac{(3+i)(5+2i)}{(5-2i)(5+2i)} = frac{15 + 6i + 5i + 2i^2}{25 + 10i – 10i -4i^2} = $$ $$ = frac{15 + 11i -2}{25 + 4} = frac{13 + 11i}{29} $$ Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы: $$ frac{z_1}{z_2} = frac{13}{29} + frac{11}{29}i $$

Ответ

$$ z_1 cdot z_2 = 17 – i; frac{z_1}{z_2} = frac{13}{29} + frac{11}{29}i $$

Пример 4

Возвести комплексное число $ z = 3+3i $ в степень: a) $ n=2 $ б) $ n=7 $

Решение

1) $ n = 2 $ Для возведения в квадрат достаточно умножить число само на себя: $$ z^2 = (3+3i)^2 = (3+3i)cdot (3+3i) = $$ Пользуемся формулой для умножения, раскрываем скобки и приводим подобные: $$ =9 + 9i + 3icdot 3 + 9i^2 = 9 + 18i – 9 = 18i $$ Получили ответ, что $$ z^2 = (3+i)^2 = 18i $$ 2) $ n = 7 $ В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую. Вычисляем значение модуля: $$ |z| = sqrt{3^2 + 3^2} = sqrt{9 + 9} = sqrt{18} = 3sqrt{2} $$ Найдем чем равен аргумент: $$ varphi = arctg frac{3}{3} = arctg(1) = frac{pi}{4} $$ Записываем в тригонометрическом виде: $$ z = 3sqrt{2}(cos frac{pi}{4} + isin frac{pi}{4}) $$ Возводим в степень $ n = 7 $: $$ z^7 = (3sqrt{2})^7 (cos frac{7pi}{4} + isin frac{7pi}{4}) = $$ Преобразуем в алгебраическую форму для наглядности: $$ =(3sqrt{2})^7 (frac{1}{sqrt{2}}-ifrac{1}{sqrt{2}}) = $$ $$ = 3^7 sqrt{2}^7 (frac{1}{sqrt{2}}-ifrac{1}{sqrt{2}}) = $$ $$ = 3^7 sqrt{2}^6 (1-i) = 3^7 cdot 8(1-i) = $$ $$ = 2187 cdot 8 (1-i) = 17496(1-i) $$

Ответ

$$ z^2 = (3+i)^2 = 18i $$ $$ z^7 = 17496(1-i) $$

Пример 5

Извлечь корень $ sqrt[3]{-1} $ над множеством $ mathbb{C} $

Решение

Представим число в тригонометрической форме. Найдем модуль и аргумент: $$ |z| = sqrt{(-1)^2 + 0^2} = sqrt{1+0} = sqrt{1}=1 $$ $$ varphi = arctg frac{0}{-1} +pi = arctg 0 + pi = pi $$ Получаем: $$ z = (cos pi + isin pi) $$ Используем знакомую формулу Муавра для вычисления корней любой степени: $$ z^frac{1}{n} = r^frac{1}{n}bigg(cos frac{varphi + 2pi k}{n}+isin frac{varphi + 2pi k}{n}bigg), k=0,1,…,n-1 $$ Так как степень $ n = 3 $, то по формуле $ k = 0,1,2 $: $$ z_0 = sqrt[3]{1} (cos frac{pi}{3}+isin frac{pi}{3}) = frac{1}{2}+ifrac{sqrt{3}}{2} $$ $$ z_1 = sqrt[3]{1} (cos frac{3pi}{3}+isin frac{3pi}{3}) = -1 $$ $$ z_2 = sqrt[3]{1} (cos frac{5pi}{3}+isin frac{5pi}{3}) = frac{1}{2} – ifrac{sqrt{3}}{2} $$

Ответ

$$ z_0 = frac{1}{2}+ifrac{sqrt{3}}{2} $$ $$ z_1 = -1 $$ $$ z_2 = frac{1}{2} – ifrac{sqrt{3}}{2} $$

Пример 6

Решить квадратное уравнение $ x^2 + 2x + 2 = 0 $ над $ mathbb{C} $

Решение

Решать будем по общей формуле, которую все выучили в 8 классе. Находим дискриминант $$ D = b^2 – 4ac = 2^2 – 4cdot 1 cdot 2 = 4-8 = -4 $$ Получили, что $ D=-4<0 $ и казалось бы, что решение можно заканчивать. Но нет! В нашем задании требуется решить уравнение над комплексным множеством, а то что дискриминант отрицательный означает только лишь отсутствие вещественных корней. А комплексные корни есть! Найдем их продолжив решение: $$ x_{1,2} = frac{-bpm sqrt{D}}{2a} = frac{-2pm sqrt{-4}}{2} = $$ Заметим, что $ sqrt{-4} = 2sqrt{-1} = 2i $ и продолжим вычисление: $$ = frac{-2 pm 2i}{2} = -1 pm i $$ Получили комплексно-сопряженные корни: $$ x_1 = -1 – i; x_2 = -1 – i $$ Как видите любой многочлен можно решить благодаря комплексным числам.

Ответ

$$ x_1 = -1 – i; x_2 = -1 – i $$

В статье “Комплексные числа: примеры с решением” было дано определение, основные понятия, формы записи, алгебраические операции и решение практических примеров.

Модуль и аргумент комплексного числа, формулы

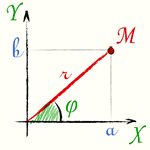Длина вектора, изображающего комплексное число, называется модулем комплексного числа. Модуль любого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа a + i·b обозначается |a + i·b|, а также буквой r. Из чертежа видно, что:

[r = vert a + htmlStyle{color: MediumPurple;}{i} b vert = sqrt{a^2+b^2}]

Модуль действительного числа, совпадает с его абсолютным значением. Сопряженные комплексные числа a + i·b и a – i·b имеют один и тот же модуль.

Угол φ между осью абсцисс и вектором OM, изображающим комплексное число a + i·b, называется аргументом комплексного числа a + i·b

Каждое не равное нулю комплексное число имеет бесчисленное множество аргументов, отличающихся друг от друга на целое число полных оборотов (т.е. на 360°·k, где k – любое целое число). Аргумент комплексного числа связан с его координатами следующими формулами:

[ tg(φ) = frac{b}{a} ]

[ cos(φ) = frac{a}{sqrt{a^2+b^2}}]

[ sin(φ) = frac{b}{sqrt{a^2+b^2}}]

Однако ни одна из этих формул в отдельности не позволяет найти аргумент.
Для того чтобы найти аргумент комплексного числа, эти формулы надо использовать в совокупности,
а также учитывать номер четверти, на координатной плоскости,
в которой находится комплексное число.

Вычислить, найти модуль и аргумент комплексного числа по формулам (1, 2, 3, 4)

Модуль и аргумент комплексного числа	стр. 75

VII.1. Формы записи комплексных чисел и действия над ними

(схема
43)

Комплексным числом называется выражение вида z=x+iy,                                                                                            (7.1) 

 где x и y – действительные числа, а  i так называемая мнимая единица. Соотношение для
мнимой единицы  

i²=–1.                                                                                                                                                                                                          (7.2)

Если x=0, то число 0+iy=iy
называется чисто мнимым; если y=0, то число x+i∙0=x
отождествляется с действительным числом x, а это означает, что множество R всех действительных чисел является подмножеством
множества C  всех
комплексных чисел, то есть .

Число x называется действительной частью комплексного
числа  z и обозначается 
x=Re z, а y – мнимой частью комплексного числа  z и
обозначается  y=Im z.

Два  комплексных
числа z₁=x₁+iy₁  и z₂=x₂+iy₂
называются равными (z₁=z₂) тогда, когда равны их действительные и мнимые части: x₁=x₂, y₁=y₂. В частности, комплексное число z=x+iy равно
нулю, когда  x=y=0.

Понятия «больше» и «меньше» для комплексных чисел не
вводятся.

Числа  z=x+iy и  называются комплексно сопряженными.

Всякое комплексное число z=x+iy можно изобразить точкой M(x;y) плоскости x0y такой,
что x=Re z, y=Im z.
Верно и обратное: каждую точку M(x;y) координатной
плоскости можно рассматривать как образ комплексного числа  z=x+iy (рис. 7.1).

Плоскость, на которой изображаются  комплексные числа, называется комплексной
плоскостью. Ось абсцисс называется действительной осью, так как на ней
лежат действительные числа z=x+0∙y=x. Ось ординат –  мнимой осью,  на ней лежат чисто мнимые комплексные числа z=0+iy.

 Комплексное
число z=x+iy можно задавать с помощью радиус-вектора . Длина вектора , изображающего комплексное число z, называется модулем этого числа и обозначается |z| или r. Величина
угла между положительным направлением действительной оси и вектором  называется
аргументом  комплексного
числа, обозначается Arg z или  φ.

Для комплексного числа z=0 аргумент не определен. Аргумент комплексного числа   – величина
многозначная и определяется с точностью до слагаемого 2πk (k=0;–1;1;–2;2…): , где arg z – главное  значение аргумента,
заключенное в промежутке (–π;π).
Иногда в качестве главного значения аргумента берут величину, принадлежащую
промежутку  [0;2π).

 Алгебраической
формой комплексного числа называется запись числа z в виде z=x+iy.

    Модуль r и
аргумент φ можно рассматривать как
полярные координаты вектора , изображающего комплексное число z=x+iy (см. рис. 7.1). Тогда из соотно­шений сторон в прямоугольном треугольнике получа­ем

. Следовательно, комплексное число
z=x+iy можно
записать в виде  или

 .                                                                                                                                                           (7.3)

Равенство
(7.3) есть тригонометрическая форма
комплексного числа. Модуль r=|z| однозначно
определяется по формуле

            .                                                                                                                                                                               (7.4)

Аргумент  определяется из формул: 

 .                                                                                                                                                       (7.5)

При переходе от
алгебраической формы комплексного числа к тригонометрической достаточно
определить главное значение аргумента комплексного числа z, то есть
считать  φ=arg z. Знаки полученных значений cos φ и sin φ по
формулам (7.5), дают возможность определить, какой координатной четверти
принадлежит угол φ.

Используя формулу
Эйлера

 ,                                                                                                                                                                      (7.6)

комплексное число  можно записать в так
назы­ваемой показательной (или
экспоненциальной) форме  

           z=re^iφ,                                                                                                                                                                                            (7.7)

где r=|z| — модуль комплексного числа, а угол   (k=0;–1;1;–2;2…).

Функция e^iφ – периодическая с основным пери­одом 2π, поэтому для записи комплексного числа  в показательной форме по формуле 7.7 достаточно найти главное значение его аргумента, то есть считать φ=arg z.

Пример 7.1. Записать
комплексные числа  в 
тригонометрической и показательной формах.     

Решение. Для z₁ имеем   . Поэтому .

Для действительного числа  . Поэтому 

 На множестве комплексных чисел определен ряд операций.

1.    
Суммой двух
комплексных чисел z₁=x₁+iy₁ и z₂=x₂+iy₂
называется комплексное число, определяемое равенством

 .                                                                                                                                                        (7.8)

Из (7.8) следует, что геометрически комплексные числа складываются как
векторы, причем сумма комплексных чисел интерпретируется как диагональ
параллелограмма, построенного на векторах, представляющих слагаемые (рис. 7.2).

2.    
Вычитание
комплексных чисел определяется
как действие, обратное сложению. Разностью двух комплексных чисел z₁ и z₂
называется такое комплексное число z, которое, будучи сложенным с z₂, дает число z₁, то есть
z= z₁ – z₂, если z+z₂=z₁. Если  z₁=x₁+iy₁, z₂=x₂+iy₂, то из
этого определения получаем:

                                                            (7.9)

Из равенства (7.9) следует, что геометрически
комплексные числа вычитаются как векторы. При этом число z= z₁ – z₂
изображается вектором, соединяющим концы векторов ,  и исходящим из конца
вычитаемого в конец уменьшаемого (см. рис. 7.2). 
Таким образом, модуль разности двух комплексных чисел равен расстоянию d между
точками, изображающими эти числа на плоскости:

.                                                                                                                                (7.10)

3.    
Произведением  комплексных чисел z₁=x₁+iy₁ и z₂=x₂+iy₂ называется 
комплексное число, определяемое равенством

.                                                                                                                             (7.11)

Из (7.11) следует важнейшее соотношение i²= –1.
Действительно, 

. 

Найдем произведение комплексных чисел  и . Производя все необходимые выкладки согласно формуле (7.11),
получим формулу произведения комплексных чисел, заданных в тригонометрической форме:

.                                                                                                                          (7.12)

Видно, что при умножении комплексных чисел в
тригонометрической форме их модули перемножаются, а аргументы складываются. Это
правило распространяется на любое конечное число множителей. Нетрудно видеть,
что если есть n множителей и все они одинаковые, то частным случаем
равенства (7.12) является формула возведения комплексного числа в
натуральную
степень:

.                                                                                                                        (7.13)

(7.13)
называется первой  формулой  Муавра.

Произведение двух комплексных чисел в показательной
(экспоненциальной) форме имеет вид:

.                                                                                                                           (7.14)

4.    
Частным двух
комплексных чисел z₁ и  называется комплексное
число z, которое, будучи умноженным на z₂, дает число z₁,  то есть , если .

Пусть , тогда с использованием этого определения получаем:

.                                                                                                                                         (7.15)

На практике при  нахождении частного двух комплексных чисел
удобно умножить числитель и знаменатель дроби  на число, сопряженное
знаменателю, с дальнейшим применением равенства i²= –1 и формулы разности квадратов.

Деление комплексных чисел осуществляется также и в
тригонометрической форме, при этом имеет место формула:

.                                                                                      (7.16)

Видно, что при делении
комплексных чисел их модули  делятся, а
аргументы вычитаются соответственно.

Частное двух комплексных чисел в показательной
(экспоненциальной) форме имеет вид:

.                                                                                                                     (7.17)

Пример 7.2. Найти
сумму, разность, произведение и частное комплексных чисел .

Решение. По
формуле (7.8) сумма заданных чисел равна .

Согласно формуле (7.9) разность заданных чисел равна .

Пользуясь формулой (7.11), вычислим их произведение

 .

На основании формулы (7.14) вычислим их частное

Пример 7.3. Найти
произведение и частное комплексных чисел  , представив их в тригонометрической и показательной форме.

Решение.
Используя (7.4) и (7.5), получаем:

. Следовательно, на основе формул
(7.3) и (7.7) число z₁ имеет
тригонометрическую и показательную форму

 .

Аналогично, для z₂ можно
записать:

 . Отсюда .

По формулам (7.12) и (7.16) получим в
тригонометрической форме:

Пользуясь формулами (7.14) и (7.17), получим в
показательной форме:

5.    
 Извлечение 
корня  n-ой 
степени  –  операция,  обратная возведению

в натуральную степень, определенному ранее формулой  (7.13).

Корнем n-ой степени из комплексного числа z называется комплексное число ω, удовлетворяющее равенству ωⁿ=z, то есть , если ωⁿ=z.

Пусть , тогда  по данному
определению и формуле (7.13) Муавра можно записать: . Сравнивания части этого равенства, получим: . Отсюда  (корень
арифметический). Окончательно получаем:

.                                                   (7.18)

(7.18) называется второй формулой Муавра.

Видно, что для
любого   корень n-ой степени
из комплексного числа z имеет равно n различных значений.

Пример 7.4.  Найти все корни уравнения  z⁴+16=0.

Решение.
Запишем уравнение в виде z⁴=–16+0∙i. Отсюда по
формуле (7.18) получим:

. 

Рассмотрим различные значения  k=0;1;2;3.

Корни z₁ и z₄, а также
z₂ и z₃ являются
комплексно сопряженными. Таким образом, корнями заданного уравнения  z⁴+16=0
являются комплексные числа    

Сформулируем несколько иначе основную теорему алгебры 3.2 над полем комплексных чисел.

Теорема 7.1 (основная теорема алгебры).  Для всякого
многочлена с комплексными коэффициентами

 степени n>0
существует  точка , в которой P(z₀)=0

Приведем еще
одну теорему, имеющую место над множеством комплексных чисел.

Теорема 7.2. Если
многочлен P_n(x) с действительными коэффициентами имеет комплексный
корень a+ib, то он
имеет и сопряженный корень a–ib

В разложение
многочлена  комплексные корни
входят сопряженными парами. Пусть корни многочлена x₁=a+ib и x₂=a–ib. Перемножив линейные множители 
разложения , получим трехчлен второй степени с действительными
коэффициентами x²+px+q и
отрицательным дискриминантом. Действительно,

Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.

Вопросы
для самопроверки

Определение.
Модулем
комплексного числа
называется длина вектора, изображающего
это число, и обозначается
.

Модуль
числа z
= x
+ iy
определяется однозначно и может быть
найден по формуле
=

.

Нетрудно
видеть, что z
∙
=

и
.

Если
z
= 0 , то
.

Определение.
Аргументом
комплексного числа
z
≠ 0 называется любой угол ,
отсчитываемый от положительного луча
оси ОХ до радиус-вектора z.
Этот угол считается положительным, если
отсчет производится против часовой
стрелки, и отрицательным – в противоположном
случае. Для числа z
= 0 аргумент не определен.

В
отличие от модуля, аргумент комплексного
числа определяется неоднозначно.

Пример
6.1 Найти
аргумент комплексного числа 1 + i.

Решение.

Аргументами
числа 1 + i
являются углы

(рисунок 4),

(рисунок 5),

(рисунок 6) и, вообще, любой из углов.

,
k

Z.

Рисунок
4 Рисунок 5
Рисунок
6

Все
множество аргументов числа z
обозначается Arg
z,
(фр. Ar-gument
– аргумент). Такое значение 

Arg
z,
которое принадлежит промежутку –
< 
≤ 
либо 0 ≤ 
< 2
и называется главным
аргументом.
Он обозначается arg
z
и определяется однозначно

Arg
z = arg z + 2k,
k 
Z,
– 
< arg z ≤ .

Упражнения

7 Отметить на
плоскости точки, изображающие следующие
комплексные числа:

а)
2i
– 3; б)
;
в)
–6 + 2i;

г)
–2 – 2i; д)
(1 – i)⁴;
е)

.

8 Найти модуль и
аргумент комплексного числа:

а)
–
;
б)
;
в) 3 – 2;

г)
(i + 1)(i – 2); д)

.

§ 7 Тригонометрическая (полярная) форма

комплексного
числа

Модуль

и аргумент 
комплексного числа z
= x
+ iy
≠ 0 – это, по существу, полярные координаты
(r;
)
точки М(х; у) – рису- нок 7.

Используя
связь между декартовыми и полярными
координатами точки М (рисунок 8)

,

можно
любое комплексное число z
≠ 0 представить в виде:

z
= x + iy = r ∙ cos 
+ ir ∙ sin 
= r(cos 
+ i sin ).

Рисунок
7 Рисунок 8

Запись
z
= r(cos

+ i
sin
)
называется тригонометрической
или полярной
формой
комплексного числа.

Чтобы
записать число z
= x
+ iy
≠ 0 в тригонометрической форме, следует
найти его модуль по формуле

и один из аргументов, решив систему
.

Аргумент
комплексного числа можно определить
из соотношения
,
являющегося следствием последней
системы. Откуда 

.

Однако
не все решения этого соотношения являются
решением системы. Напомним, что период
функции y
= tg
x равен .
При с 
R
одно из решений уравнения tg

= c,
удовлетворяющее условию
,
обозначается arctg
c.
Таким образом, в промежутке (– ;
]
имеются два угла, тангенсы которых равны

.
Для определения четверти, в которой
лежит угол ,
нужно еще учесть знаки х, у – координат
точки z:

1. если
   точка z
   лежит в I
   и IV
   четверти, x
   > 0, то

 =
arg
z
=
(рисунок 9);

2)
если точка z
лежит во II
четверти, т.е. x
< 0, y
> 0, то
и
arg
z
=
(рисунок 10);

3)
Если точка z
лежит в III
четверти, т.е. x
< 0, y
< 0, то

и

(рисунок
11).

Рисунок 9
Рисунок 10

Рисунок 11

Для главного
аргумента справедливы формулы:

Пример
7.1 Записать
числа в тригонометрической форме:

1)
z = 4 + 4i.

Решение.

x
= 4, y
= 4 (I
четверть);
.

Так
как arg
z
=

,
то

z
= 4 + 4i =

2)
z =
–
i.

Решение.

x
=,
y
= –1 (IVчетверть);

Так
как x
> 0, 
= arg
z
= arctg

=

Поэтому

– i
= 2

3)
z = – 2 –
i.

Решение.

x
= –2, y = –

(III четверть);

Так
как x
< 0 и y
< 0, 
= arg
z
= –

–2
–
i
=

4)
z = –+
i.

Решение.

x
= –,
y
= 1 (II
четверть);

.
Так как x
< 0, y
> 0,

 =
arg z =

–+
i =

5)
z = 5.

Решение.

Так
как число z
= 5 действительное и 5 > 0, то


= 0.

6)
z = –.

Решение.

,

= 
(так как –<
0).

).

7)
z = 3i.

Решение.

Так
как число z
= 3i
– мнимое (х = 0, у = 3), причем y
= Im
z
=

=
3 > 0, то
,

= arg
z
=.

8)
z = –i.

Решение.

x
= 0, y = –<
0;
,

= arg
z
= –
.

9)
z = cos
– isin
.

Решение.

Данная
запись числа не является тригонометрической.
Это чис-ло записано в алгебраической
форме, где

, у = –
.

Искомая
запись имеет вид z
= cos

+ isin
.

;

;
arg z = –.

–

Данное представление
могло быть получено, учитывая чет-ность
функции y = cos x и нечетность функции y =
sin x.

10)
z = –

Решение.

,
поэтому искомая запись имеет вид: z
= cos 
+ i sin .

Так
как
,
то –

– sin

Соседние файлы в папке КЧ

• #
• #

Содержание:

• Модуль комплексного числа
• Аргумент комплексного числа

Комплексные числа изображаются на так называемой комплексной плоскости. Ось, соответствующая в прямоугольной декартовой
системе координат оси абсцисс, называется действительной осью, а оси ординат – мнимой осью (рис. 1).

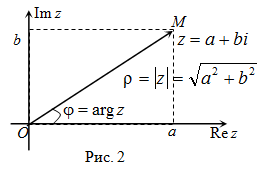
Комплексному числу $z=a+b i$ будет однозначно соответствовать
на комплексной плоскости точка
$(a ; b)$:
$z=a+b i leftrightarrow(a ; b)$ (рис. 2). То есть на действительной оси
откладывается действительная часть комплексного числа, а на мнимой – мнимая.

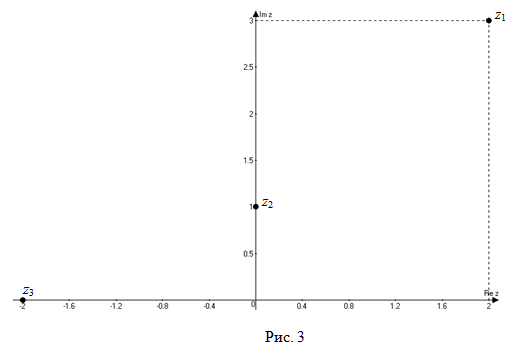
Например. На рисунке 3 на комплексной плоскости изображены числа
$z_{1}=2+3 i$,
$z_{2}=i$ и
$z_{3}=-2$ .

Модуль комплексного числа

Комплексное число также можно изображать радиус-вектором
$overline{O M}$ (рис. 2). Длина радиус-вектора, изображающего
комплексное число $z=a+b i$, называется модулем
этого комплексного числа.

Модуль любого ненулевого комплексного числа есть положительное число. Модули
комплексно сопряженных чисел равны.
Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.

Модуль вычисляется по формуле:

То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.

Аргумент комплексного числа

Угол $phi$ между положительным направлением
действительной оси и радиус-вектора $overline{O M}$, соответствующим
комплексному числу $z=a+b i$, называется аргументом
этого числа и обозначается $arg z$ .

Аргумент $phi$ комплексного числа
$z=a+b i$ связан с его
действительной и мнимой частями соотношениями:

$phi=operatorname{tg} frac{b}{a}, cos phi=frac{a}{sqrt{a^{2}+b^{2}}}, sin phi=frac{b}{sqrt{a^{2}+b^{2}}}$

На практике для вычисления аргумента комплексного числа обычно пользуются формулой:

$phi=arg z=arg (a+b i)=left{begin{array}{l}{operatorname{arctg} frac{b}{a}, a geq 0} \ {operatorname{arctg} frac{b}{a}+pi, a lt 0}end{array}right.$

Аргумент действительного положительного числа равен
$0^{circ}$, действительного отрицательного –
$pi$ или
$180^{circ}$. Чисто мнимые числа с положительной мнимой частью имеют
аргумент равный $frac{pi}{2}$, с отрицательной мнимой частью –
$frac{3 pi}{2}$ .

У комплексно сопряженных чисел аргументы отличаются знаком (рис. 3).

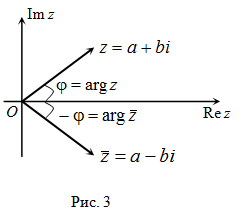
Читать дальше: комплексно сопряженные числа.