import numpy as np
from collections import deque
from itertools import combinations
# data = np.array([1487, 1847, 4817, 4871, 7481, 7841, 8147, 8741])
np.random.seed(42)
data = np.random.randint(0, 100000, 1000)
data.sort()
# Интуитивный подход (baseline), O(n^3)
def find_evenly_spaced_v1(data):
for a, b, c in combinations(data, 3):
if b - a == c - b:
yield a, b, c
# Эмпирическая оптимизация, O(n^2)
def find_evenly_spaced_v2(data):
dataset = set(data)
for a, c in combinations(data, 2):
b, mod = divmod(a + c, 2)
if (mod == 0) and (b in dataset):
yield a, b, c
# Векторный вариант
def find_evenly_spaced_v3(data):
grid = data.reshape(-1, 1) + data.reshape(1, -1)
divs, mods = np.divmod(grid, 2)
mask = np.tri(*grid.shape, -1, dtype='bool') & np.isin(divs, data) & ~ mods.astype('bool')
for c, a in zip(*np.where(mask)):
b = divs[a, c]
a, c = data[[a, c]]
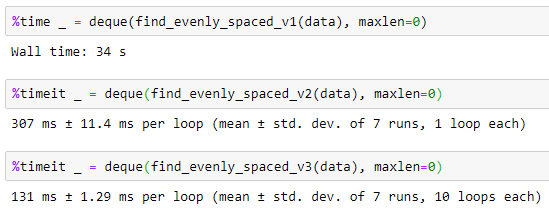
yield a, b, cИзмерения скорости для 1000 элементов:
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given an array A[] of N integers. Consider an integer num such that num occurs in the array A[] and all the positions of num, sorted in increasing order forms an arithmetic progression. The task is to print all such pairs of num along with the common difference of the arithmetic progressions they form.
Examples :
Input: N = 8, A = {1, 2, 1, 3, 1, 2, 1, 5}
Output: {1, 2}, {2, 4}, {3, 0}, {5, 0}
Explanation: Positions at which 1 occurs are: 0, 2, 4, 6
It can be easily seen all the positions have same difference between consecutive elements (i.e. 2).
Hence, positions of 1 forms arithmetic progression with common difference 2.
Similarly, all positions of 2 forms arithmetic progression with common difference 4.
And, 3 and 5 are present once only.
According to the definition of arithmetic progression (or A.P.), single element sequences are also A.P. with common difference 0.Input: N = 1, A = {1}
Output: {1, 0}
Approach: The idea to solve the problem is by using Hashing.
Follow the steps to solve the problem:
- Create a map having integer as key and vector of integers as value of key.
- Traverse the array and store all positions of each element present in array into the map.
- Iterate through the map and check if all the positions of the current element in the map forms A.P.
- If so, insert that element along with the common difference into the answer.
- Else, continue to iterate through the map
Below is the implementation for the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void printAP(int N, int A[])
{
unordered_map<int, vector<int> > pos;
for (int i = 0; i < N; i++) {
pos[A[i]].push_back(i);
}
map<int, int> ans;
for (auto x : pos) {
if (x.second.size() == 1) {
ans[x.first] = 0;
}
else {
bool flag = 1;
int diff = x.second[1] - x.second[0];
int prev = x.second[1];
int curr;
for (auto it = 2;
it < x.second.size(); it++) {
curr = x.second[it];
if (curr - prev != diff) {
flag = 0;
break;
}
prev = x.second[it];
}
if (flag == 1) {
ans[x.first] = diff;
}
}
}
for (auto it : ans) {
cout << it.first << " "
<< it.second << endl;
}
}
int main()
{
int N = 8;
int A[] = { 1, 2, 1, 3, 1, 2, 1, 5 };
printAP(N, A);
}
Java
import java.io.*;
import java.util.*;
class GFG {
public static void printAP(int N, int[] A)
{
HashMap<Integer, List<Integer> > pos
= new HashMap<Integer, List<Integer> >();
for (int i = 0; i < N; i++) {
pos.put(A[i], new ArrayList<Integer>());
}
for (int i = 0; i < N; i++)
{
pos.get(A[i]).add(i);
}
Map<Integer, Integer> ans
= new HashMap<Integer, Integer>();
for (Integer x : pos.keySet()) {
Integer key = x;
List<Integer> value = pos.get(x);
if (value.size() == 1) {
ans.put(key, 0);
}
else {
int flag = 1;
int diff = value.get(1) - value.get(0);
int prev = value.get(1);
int curr;
for (int it = 2; it < value.size(); it++) {
curr = value.get(it);
if (curr - prev != diff) {
flag = 0;
break;
}
prev = value.get(it);
}
if (flag == 1) {
ans.put(key, diff);
}
}
}
for (Integer it : ans.keySet()) {
int key = it;
int value = ans.get(it);
System.out.println(key + " " + value);
}
}
public static void main(String[] args)
{
int N = 8;
int[] A = { 1, 2, 1, 3, 1, 2, 1, 5 };
printAP(N, A);
}
}
Python3
def printAP(N, A):
pos = {}
for i in range(N):
if(A[i] not in pos):
pos[A[i]] = []
pos[A[i]].append(i)
ans = {}
for x in pos:
if (len(pos[x]) == 1):
ans[x] = 0
else:
flag = 1
diff = pos[x][1]-pos[x][0]
prev = pos[x][1];
curr = 0
length = len(pos[x])
for it in range(2, length):
curr = pos[x][it];
if (curr - prev != diff):
flag = 0;
break;
prev = curr
if (flag == 1):
ans[x] = diff
for x in ans:
print(x, ans[x])
if __name__=='__main__':
N = 8
A = [1, 2, 1, 3, 1, 2, 1, 5]
printAP(N, A)
C#
using System;
using System.Collections.Generic;
class GFG {
public static void printAP(int N, int[] A)
{
Dictionary<int, List<int> > pos
= new Dictionary<int, List<int> >();
for (int i = 0; i < N; i++) {
pos[A[i]] = new List<int>();
}
for (int i = 0; i < N; i++)
{
pos[A[i]].Add(i);
}
Dictionary<int, int> ans
= new Dictionary<int, int>();
foreach (int x in pos.Keys) {
int key = x;
List<int> value = pos[x];
if (value.Count == 1) {
ans[key] = 0;
}
else {
int flag = 1;
int diff = value[1] - value[0];
int prev = value[1];
int curr;
for (int it = 2; it < value.Count; it++) {
curr = value[it];
if (curr - prev != diff) {
flag = 0;
break;
}
prev = value[it];
}
if (flag == 1) {
ans[key] = diff;
}
}
}
foreach (int it in ans.Keys) {
int key = it;
int value = ans[it];
Console.WriteLine(key + " " + value);
}
}
public static void Main()
{
int N = 8;
int[] A = { 1, 2, 1, 3, 1, 2, 1, 5 };
printAP(N, A);
}
}
Javascript
<script>
const printAP = (N, A) => {
let pos = {};
for (let i = 0; i < N; i++) {
if (A[i] in pos) pos[A[i]].push(i);
else pos[A[i]] = [i];
}
let ans = {};
for (let x in pos) {
if (pos[x].length == 1) {
ans[x] = 0;
}
else {
let flag = 1;
let diff = pos[x][1] - pos[x][0];
let prev = pos[x][1];
let curr;
for (let it = 2; it < pos[x].length; it++) {
curr = pos[x][it];
if (curr - prev != diff) {
flag = 0;
break;
}
prev = pos[x][it];
}
if (flag == 1) {
ans[x] = diff;
}
}
}
for (let it in ans) {
document.write(`${it} ${ans[it]}<br/>`);
}
}
let N = 8;
let A = [1, 2, 1, 3, 1, 2, 1, 5];
printAP(N, A);
</script>
Time Complexity: O(N*log(N))
Auxiliary Space: O(N)
Last Updated :
27 Oct, 2022
Like Article
Save Article
|
302 / 160 / 62 Регистрация: 27.02.2010 Сообщений: 317 |
|
|
1 |
|
как найти наибольшую арифметическую прогрессию в массиве12.03.2010, 16:31. Показов 2132. Ответов 4
Здравствуйте! Подскажите, пожалуйста, как можно найти в массиве арифметическую прогрессию наибольшей длины, вывести на печать эту прогрессию и разность прогрессии. Массив вводится пользователем. Желательно выполнить с помощью функций и без указателей.
0 |
|
2505 / 1480 / 37 Регистрация: 14.09.2009 Сообщений: 2,740 |
|
|
12.03.2010, 16:46 |
2 |
|
Задача не очень понятна. Элементы прогрессии должны быть в том же порядке, что и в массиве?
0 |
|
302 / 160 / 62 Регистрация: 27.02.2010 Сообщений: 317 |
|
|
12.03.2010, 16:51 [ТС] |
3 |
|
Да, элементы не могут разделяться другими элементами. Например, если массив: 1 2 3 4 5 7 9 11 13 15 17 6 , то в нем 2 арифметические прогрессии, но большая из них: 5 7 9 11 13 15 17, она должна быть выведена на печать и зазность прогрессии, т.е 2
0 |
|
Грымзик 2505 / 1480 / 37 Регистрация: 14.09.2009 Сообщений: 2,740 |
||||
|
12.03.2010, 17:21 |
4 |
|||
|
Считывание сами добавьте. И надо рассмотреть случай, если всего 1 элемент, у меня тогда работать не будет.
1 |
|
302 / 160 / 62 Регистрация: 27.02.2010 Сообщений: 317 |
|
|
12.03.2010, 17:29 [ТС] |
5 |
|
Спасибо большое!
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
12.03.2010, 17:29 |
|
Помогаю со студенческими работами здесь Найти числа, образующие арифметическую прогрессию Найти числа, образующие арифметическую прогрессию Найти арифметическую прогрессию максимальной длины и ее количество Найти среди чисел хотя бы одну арифметическую прогрессию Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 5 |
Какой способ найти, если массив содержит арифметическую прогрессию (последовательность)
Я отсортировал массив чисел, как
1, 4, 5 , 6, 8
Как узнать, содержит ли этот массив арифметическую прогрессию (последовательность)?
как в этом примере
4,6,8
или же
4,5,6
примечание: минимальное число в последовательности равно 3
2010-11-02 07:18
6
ответов
Решение
Вы можете решить эту проблему рекурсивно, разбив ее на более мелкие проблемы:
- Определите пары {1,4},{1,5}…{6,8}
- Для каждой пары ищите последовательности с одинаковым интервалом
Сначала создайте леса для решения проблем:
Dim number(7) As Integer
Dim result() As Integer
Dim numbers As Integer
Sub FindThem()
number(1) = 1
number(2) = 4
number(3) = 5
number(4) = 6
number(5) = 8
number(6) = 10
number(7) = 15
numbers = UBound(number)
ReDim result(numbers)
Dim i As Integer
For i = 1 To numbers - 2
FindPairs i
Next
End Sub
Теперь перебираем пары
Sub FindPairs(start As Integer)
Dim delta As Integer
Dim j As Integer
result(1) = number(start)
For j = start + 1 To numbers
result(2) = number(j)
delta = result(2) - result(1)
FindMore j, 2, delta
Next
End Sub
Поиск последовательности по ходу дела
Sub FindMore(start As Integer, count As Integer, delta As Integer)
Dim k As Integer
For k = start + 1 To numbers
step = number(k) - result(count)
result(count + 1) = number(k) ' should be after the if statement
' but here makes debugging easier
If step = delta Then
PrintSeq "Found ", count + 1
FindMore k, count + 1, delta
ElseIf step > delta Then ' Pointless to search further
Exit Sub
End If
Next
End Sub
Это просто чтобы показать результаты
Sub PrintSeq(text As String, count As Integer)
ans = ""
For t = 1 To count
ans = ans & "," & result(t)
Next
ans = text & " " & Mid(ans, 2)
Debug.Print ans
End Sub
Результаты
findthem
Found 1,8,15
Found 4,5,6
Found 4,6,8
Found 4,6,8,10
Found 5,10,15
Found 6,8,10
Изменить: Да, и, конечно, массив должен быть отсортирован!
НТН
2010-11-02 13:28
Общая идея состоит в том, чтобы выбрать элемент в качестве вашего a_1, затем любой элемент после этого в качестве вашего a_2, вычислить разницу, а затем посмотреть, соответствуют ли другие элементы впоследствии этой разнице. Пока есть как минимум 3 элемента с одинаковой разницей, мы считаем это прогрессией.
progression (A, n)
for i = 1 ... n - 2
a_1 = A[i]
for j = i + 1 ... n - 1
a_2 = A[j]
d = a_2 - a_1
S = [ i, j ]
for k = j + 1 ... n
if ( d == ( a[k] - a[S.last] ) )
/* Append the element index to the sequence so far. */
S += k
if ( |s| > 2 )
/* We define a progression to have at least 3 numbers. */
return true
return false
Вы можете изменить алгоритм для сохранения каждого набора S до его потери, чтобы вычислить все прогрессии для данного массива A. Алгоритм работает в O(n^3), предполагая, что добавление и получение последнего элемента набора S находятся в постоянное время
Хотя я чувствую, что может быть более эффективное решение…
2010-11-02 08:07
Во-первых, я предполагаю, что вам нужны только арифметические последовательности из трех или более терминов.
Я бы предложил проверить каждый номер a[i] в качестве начала арифметической последовательности, и a[i+n] как следующий.
Теперь, когда у вас есть первые два термина в вашей серии, вы можете найти следующий. Как правило, если x – это ваш первый термин, а y – второй, ваши условия будут x + i*(y-x)с первым членом при i = 0. Следующим будет x + 2*(yx). Найдите в вашем массиве это значение. Если это значение находится в вашем массиве, у вас есть арифметическая последовательность из трех или более элементов!
Вы можете продолжить с i=3, i=4 и т. Д., Пока не достигнете того, которое не найдено в вашем массиве.
Если l размер вашего массива, сделайте это для всех i от 0 до l-2, и все n от 0 в l-i-1
Единственное серьезное предостережение заключается в том, что в этом примере будут найдены обе последовательности 4,6,8 так же как 6,8, Технически, оба они являются арифметическими последовательностями в вашей серии. Вам нужно будет более конкретно определить, что вы хотите там. В вашем случае, может быть тривиально просто проверить и устранить все прогрессии, которые полностью содержатся внутри других.
2010-11-02 07:37
Конечно, не оптимальный способ решить вашу проблему, но вы можете сделать следующее:
Перебирайте все пары чисел в вашем массиве – каждые 2 числа полностью определяют арифметическую последовательность, если мы предположим, что они 1-й и 2-й члены прогрессии. Итак, зная эти 2 числа, вы можете создать дополнительные элементы прогрессии и проверить, есть ли они в вашем массиве.
Если вы хотите просто найти 3 числа, образующие арифметическую прогрессию, то вы можете перебрать все пары несмежных чисел a[i] и a[j], j > i+1 и проверить, принадлежит ли их среднее арифметическое к массиву – вы можете сделать что с помощью бинарного поиска на интервале] I, J [.
2010-11-02 07:30
Что я пытаюсь сделать, это найти все комбинации из 3 чисел, которые находятся в этом массиве.
и найти расстояние между ними, если оно равно, мы нашли
лайк:
for ($i = 1; $i <= $countArray - 2; $i++) {
for ($j = $i+1; $j <= $countArray - 1; $j++) {
for ($k = $j+1; $k <= $countArray; $k++) {
if($array[$j]-$array[$i] == $array[$k]-$array[$j]){
# found
}
}
}
}
user74314
02 ноя ’10 в 07:56
2010-11-02 07:56
2010-11-02 07:56
Вот код в Swift 4:
extension Array where Element == Int {
var isArithmeticSequence: Bool {
let difference = self[1] - self[0]
for (index, _) in self.enumerated() {
if index < self.count-1 {
if self[index + 1] - self[index] != difference {
return false
}
}
}
return true
}
var arithmeticSlices: [[Int]] {
var arithmeticSlices = [[Int]]()
var sliceSize = 3
while sliceSize < self.count+1 {
for (index, _) in self.enumerated() {
if (index + sliceSize-1) <= self.count - 1 {
let currentSlice = Array(self[index...index + sliceSize-1])
if currentSlice.isArithmeticSequence {
arithmeticSlices.append(currentSlice)
}
}
}
sliceSize+=1
}
return arithmeticSlices
}
}
let A = [23, 24, 98, 1, 2, 5]
print(A.arithmeticSlices) // []
let B = [4, 7, 10, 4,5]
print(B.arithmeticSlices) //[[1, 2, 3], [2, 3, 4], [3, 4, 5], [1, 2, 3, 4], [2, 3, 4, 5], [1, 2, 3, 4, 5]]
let C = [4, 7, 10, 23, 11, 12, 13]
print(C.arithmeticSlices) // [[4, 7, 10], [11, 12, 13]]
2017-10-11 21:21
Ученик
(3),
закрыт
10 лет назад
Jurii
Высший разум
(175098)
11 лет назад
Сортировать не нужно! − По условию он уже должен либо образовывать, либо не образовывать.
По определению арифметической последовательности: каждый следующий элемент получается прибавлением к текущему некоторого значения (одного и того-же) .
Значит всё просто:
1) ищем разность 1 и 2 элементов массива D = A[1] – A[2]
2) начиная со второго элемента N = 2
3) предполагаем, что последовательность является арифметической прогрессией Arifm = true
4) пока выполняются оба условия N < ArrSize и Arifm = true
5) проверяем правильность утверждения Arifm = (A[N] – A[N + 1) = D
6) увеличивем счётчик N = N + 1
7) конец цикла
8) выводим результат: “Элементы массива образуют арифметическую последовательность = “, Arifm