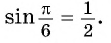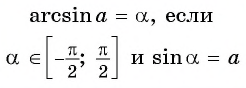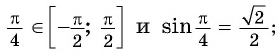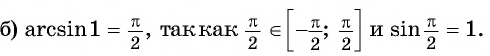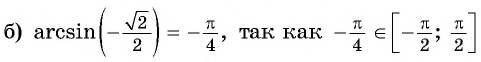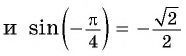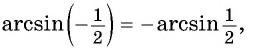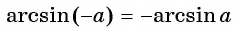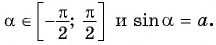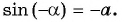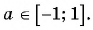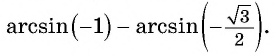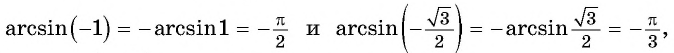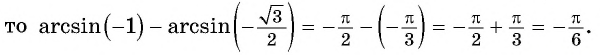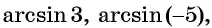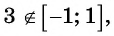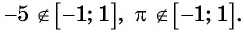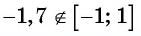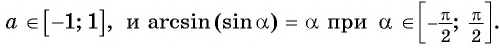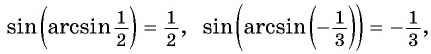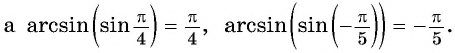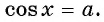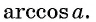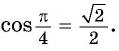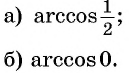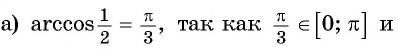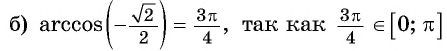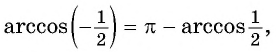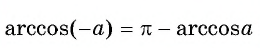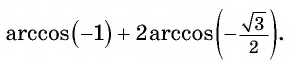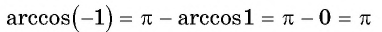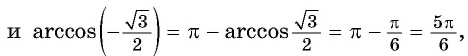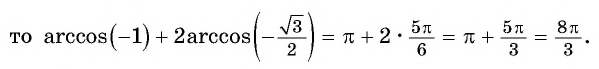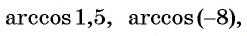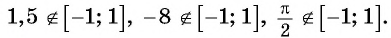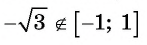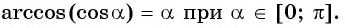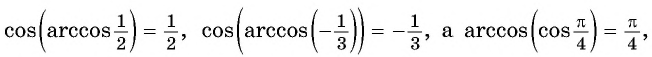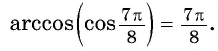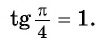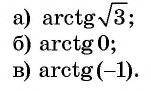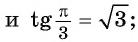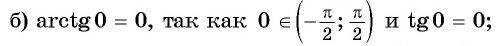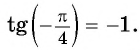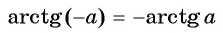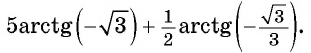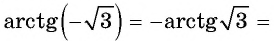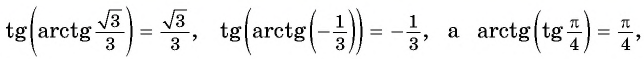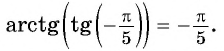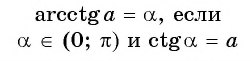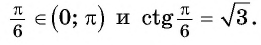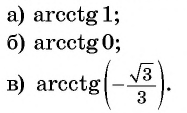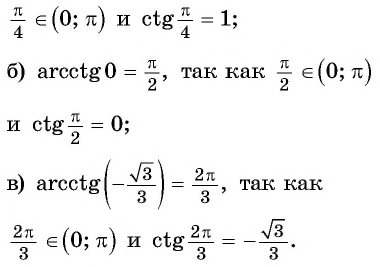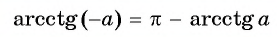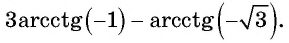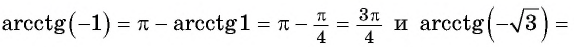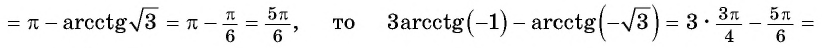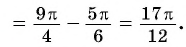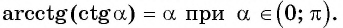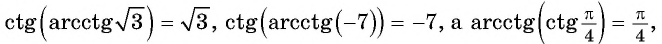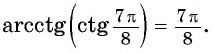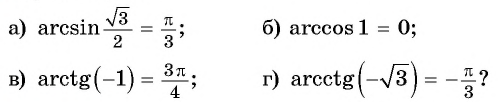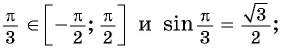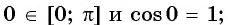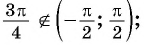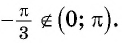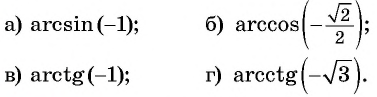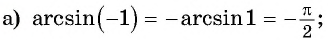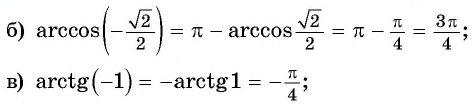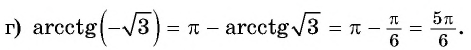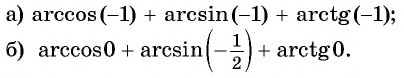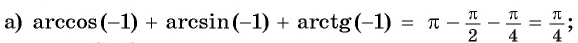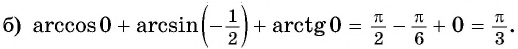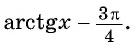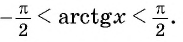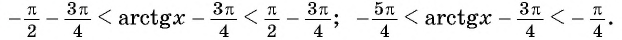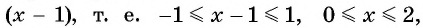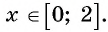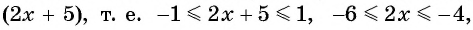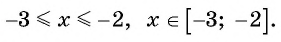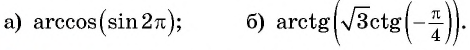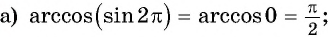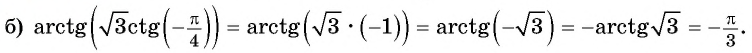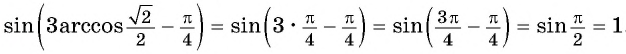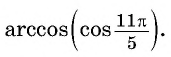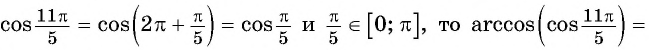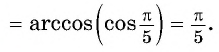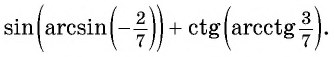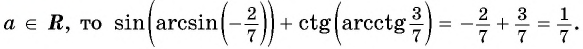Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arcus — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Так, обычный синус позволяет по дуге окружности найти стягивающую её хорду, а обратная функция решает противоположную задачу. Манера обозначать таким образом обратные тригонометрических функции появилась у австрийского математика XVIII века Карла Шерфера и закрепилась благодаря Лагранжу. Впервые специальный символ для обратной тригонометрической функции использовал Даниил Бернулли в 1729 году. Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: 
но они не прижились[1].
Лишь изредка в иностранной литературе, также как и в научных/инженерных калькуляторах, пользуются обозначениями типа sin−1, cos−1 для арксинуса, арккосинуса и т. п.[2], — такая запись считается не очень удобной, так как возможна путаница с возведением функции в степень −1.
Тригонометрические функции периодичны, поэтому функции, обратные к ним, многозначны. То есть, значение аркфункции представляет собой множество углов (дуг), для которых соответствующая прямая тригонометрическая функция равна заданному числу. Например, 
означает множество углов 
, синус которых равен 
. Из множества значений каждой аркфункции выделяют её главные значения (см. графики главных значений аркфункций ниже), которые обычно и имеют в виду, говоря об арксинусе, арккосинусе и т. д.
В общем случае при условии 
все решения уравнения 
можно представить в виде 
[3]
Основное соотношение[править | править код]
Функция arcsin[править | править код]
График функции 
Аркси́нусом числа x называется такое значение угла y, выраженного в радианах, для которого 
Функция непрерывна и ограничена на всей своей области определения. Она является строго возрастающей.
Свойства функции arcsin[править | править код]
Получение функции arcsin[править | править код]
Дана функция 
. На всей своей области определения она является кусочно-монотонной, и, значит, на всей числовой прямой обратное соответствие функцией не является. Поэтому рассмотрим отрезок ![{displaystyle [-pi /2;pi /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e194f6091eb1b362d19112a5bffdab91ef2a07df)
, на котором функция строго монотонно возрастает и принимает все значения своей области значений только один раз. Тогда на отрезке существует обратная функция , график которой симметричен графику функции относительно прямой 
.
Функция arccos[править | править код]
График функции 
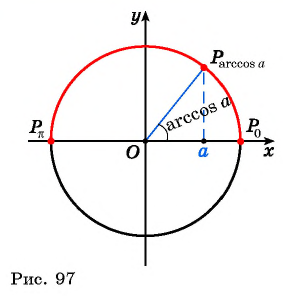
Аркко́синусом числа x называется такое значение угла y в радианной мере, для которого 
Функция непрерывна и ограничена на всей своей области определения. Она является строго убывающей и неотрицательной.
Свойства функции arccos[править | править код]
Получение функции arccos[править | править код]
Дана функция 
. На всей своей области определения она является кусочно-монотонной, и, значит, на всей числовой прямой обратное соответствие функцией не является. Поэтому рассмотрим отрезок ![[0;pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/45ba33419dc889bf6c0c684b11285afda3437c95)
, на котором функция строго монотонно убывает и принимает все значения своей области значений только один раз. Тогда на отрезке существует обратная функция , график которой симметричен графику функции относительно прямой .
Функция arctg[править | править код]
График функции 
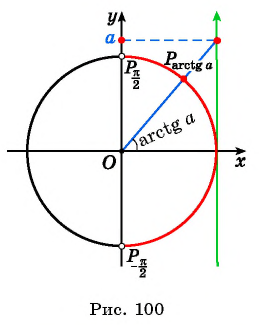
Аркта́нгенсом числа x называется такое значение угла 
выраженное в радианах, для которого 
Функция 
определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго возрастающей.
Свойства функции arctg[править | править код]
Получение функции arctg[править | править код]
Дана функция 
. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим интервал 
, на котором функция строго монотонно возрастает и принимает все значения своей области значений только один раз. Тогда на интервале существует обратная функция , график которой симметричен графику функции относительно прямой .
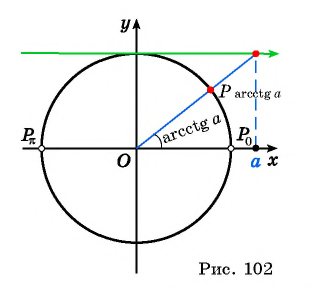
Функция arcctg[править | править код]
График функции 
Арккота́нгенсом числа x называется такое значение угла y (в радианной мере измерения углов), для которого 
Функция 
определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго убывающей и всюду положительной.
Свойства функции arcctg[править | править код]
Получение функции arcctg[править | править код]
Дана функция 
. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим интервал 
, на котором функция строго монотонно убывает и принимает все значения своей области значений только один раз. Тогда на интервале существует обратная функция , график которой симметричен графику функции относительно прямой .
График арккотангенса получается из графика арктангенса, если последний отразить относительно оси ординат (то есть заменить знак аргумента, 
) и сместить вверх на π/2; это вытекает из вышеупомянутой формулы 
Функция arcsec[править | править код]
График функции 
Арксе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого 
Функция непрерывна и ограничена на всей своей области определения. Она является строго возрастающей и всюду неотрицательной.
Свойства функции arcsec[править | править код]
Функция arccosec[править | править код]
График функции 
Арккосе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого 
Функция непрерывна и ограничена на всей своей области определения. Она является строго убывающей.
Свойства функции arccosec[править | править код]
Разложение в ряды[править | править код]
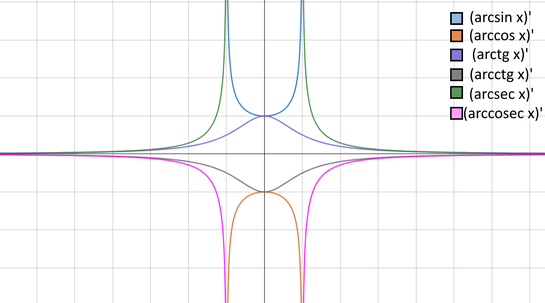
Производные от обратных тригонометрических функций[править | править код]
Все обратные тригонометрические функции бесконечно дифференцируемы в каждой точке своей области определения. Первые производные:
производные обратных тригонометрических функций
Функция  |
Производная  |
Примечание |
|---|---|---|
 |
 |
Доказательство Найти производную арксинуса можно при помощи взаимно обратных функций. |
 |
 |
Доказательство Найти производную арккосинуса можно при помощи данного тождества: |
 |
 |
Доказательство Найти производную арктангенса можно при помощи взаимнообратной функции: |
 |
 |
Доказательство Найти производную арккотангенса можно при помощи данного тождества: |
 |
 |
Доказательство Найти производную арксеканса можно при помощи тождества:
Теперь находим производную обеих частей этого тождества.
Получается.
|
 |
 |
Доказательство Найти производную арккосеканса можно при помощи данного тождества: |
![{displaystyle [sin(arcsin((x))]'=x'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be684108880964393fc7a90ba55f07de0e6d659a)
![{displaystyle D(cos(x))=[{frac {pi }{2}};-{frac {pi }{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1cb9db2cfdfe382a787aa5288735756e8dcb12e)
![{displaystyle [arcsin(x)+arccos(x)]'=({frac {pi }{2}})'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3606594a168f2f06eb6faddfaac18f1c85324466)
![{displaystyle [tg(arctg(x))]'=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ce9406b214a5266d0bf8282fd6aae4b59602c66)
![{displaystyle [arctg(x)+arcctg(x)]'=({frac {pi }{2}})'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f84cee67adf89ef76bfaa5c415907cce038d455)
![{displaystyle [arccosec(x)+arcsec(x)]'=({frac {pi }{2}})'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4847d93af2226f3ab5e1ba20940ec8530526b49e)
Интегралы от обратных тригонометрических функций[править | править код]
Неопределённые интегралы[править | править код]
Для действительных и комплексных x:
Для действительных x ≥ 1:
- См. также Список интегралов от обратных тригонометрических функций
Использование в геометрии[править | править код]
Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например, с помощью теоремы косинусов.
В прямоугольном треугольнике эти функции от отношений сторон сразу дают угол.
Так, если катет длины 
является противолежащим для угла 
, то
Связь с натуральным логарифмом[править | править код]
Для вычисления значений обратных тригонометрических функций от комплексного аргумента удобно использовать формулы, выражающие их через натуральный логарифм:
См. также[править | править код]
- Обратные гиперболические функции
- Теорема Данжуа — Лузина
Примечания[править | править код]
Ссылки[править | править код]
- Weisstein, Eric W. Обратные тригонометрические функции (англ.) на сайте Wolfram MathWorld.
- Математическая энциклопедия / Гл. ред. И. М. Виноградов. — М.: «Советская Энциклопедия», 1982. — [dic.academic.ru/dic.nsf/enc_mathematics/3612/%D0%9E%D0%91%D0%A0%D0%90%D0%A2%D0%9D%D0%AB%D0%95 Т. 3. — с. 1135].
- Обратные тригонометрические функции — статья из Большой советской энциклопедии. — М.: «Советская Энциклопедия», 1974. — Т. 18. — с. 225.
- Обратные тригонометрические функции // Энциклопедический словарь юного математика / Савин А.П. — М.: Педагогика, 1985. — С. 220—221. — 352 с.
- Построение графиков обратных тригонометрических функций онлайн
- Онлайн калькулятор: обратные тригонометрические функции
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных доменов
|
- Определение
- График арксинуса
- Свойства арксинуса
- Таблица арксинусов
Определение
Арксинус (arcsin) – это обратная тригонометрическая функция.
Арксинус x определяется как функция, обратная к синусу x, при -1≤x≤1.
Если синус угла у равен х (sin y = x), значит арксинус x равняется y:
arcsin x = sin-1 x = y
Примечание: sin-1x означает обратный синус, а не синус в степени -1.
Например:
arcsin 1 = sin-1 1 = 90° (π/2 рад)
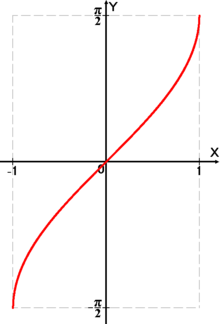
График арксинуса
Функция арксинуса пишется как y = arcsin (x). График в общем виде выглядит следующим образом (-1≤x≤1, -π/2≤y≤π/2):
Свойства арксинуса
Ниже в табличном виде представлены основные свойства арксинуса с формулами.
Таблица арксинусов
| x | arcsin x (рад) | arcsin x (°) |
| -1 | -π/2 | -90° |
| -√3/2 | -π/3 | -60° |
| -√2/2 | -π/4 | -45° |
| -1/2 | -π/6 | -30° |
| 0 | 0 | 0° |
| 1/2 | π/6 | 30° |
| √2/2 | π/4 | 45° |
| √3/2 | π/3 | 60° |
| 1 | π/2 | 90° |
microexcel.ru
Как найти арксинус: формула, свойства, функция
Содержание:
- Понятие арксинуса
- Зачем нужен арксинус
- Получение функции arcsin с пояснением на примерах
- Свойства функции arcsin
- График арксинуса
Понятие арксинуса
Обратные тригонометрические функции называют по соответствующим им тригонометрическим функциям. Формулировка наименования заключается в приписывании приставки «арк», что является производным от латинского слова «дуга» (arcus).
Такая методика объясняется тем, что в геометрии функцию, обратную тригонометрической, связывают с длиной, которую имеет дуга единичной окружности, равной какому-то отрезку, либо с углом, стягивающим данную дугу. В результате с помощью синуса можно, учитывая дугу окружности, определить хорду, которая ее стягивает.
Обратная функция под названием арксинус призвана решить противоположную задачу. Арксинус обозначают (arcsin x) и определяют, как угол с синусом, равным х.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для тригонометрических функций характерна периодичность. В связи с этим, обратные тригонометрические функции являются многозначными. Аркфункция обладает значением в виде множества из углов, для которых прямая тригонометрическая функция соответствует заданному числу.
Пример 1
Рассмотрим функцию: (arcsin ½). Данная аркфункция обозначает множество из углов:
(left ( frac{pi}{6}, frac{5 pi}{6}, frac{13 pi}{6}, frac{17 pi}{6} dots ~ (30^circ, 150^circ, 390^circ, 510^circ dots) right ))
Значение синуса при этом: ½
Как правило, под обратными тригонометрическими функциями понимают ключевые значения каждой аркфункции, выделенные из ее множества значений.
Если (-1leqslant alpha leqslant 1), то любое решение уравнения (sin x=alpha) записывают в такой форме: ( x=(-1)^{n}arcsin alpha +pi n,~n=0,pm 1,pm 2,dots )~
Арксинус числа х — значение для угла у, определенного в радианах, для которого (sin y=x,quad -{frac {pi }{2}}leqslant yleqslant {frac {pi }{2}},quad |x|leqslant 1).
Зачем нужен арксинус
С помощью аркфункций, в том числе — арккосинуса, арктангенса, арккотангенса, арксинуса — определяют углы треугольника. Подобное действие доступно при наличии информации о сторонах данной геометрической фигуры.
В том случае, когда имеется некий прямоугольный треугольник, обратные тригонометрические функции от отношений сторон позволяют определить угол. Например, длина катета составляет «а». Этот катет определяется, как противолежащий для угла (alpha), то:
(alpha =arcsin(a/c)=arccos(b/c)=operatorname {arctg} (a/b)=operatorname {arccosec} (c/a)=operatorname {arcsec}(c/b)=operatorname {arcctg} (b/a))
Получение функции arcsin с пояснением на примерах
Предположим, что существует некая функция:
(y=sin x)
Записанная функция обладает областью определения. В ее рамках она приобретает кусочно-монотонный вид. По этой причине обратное выражение y=arcsin x нельзя причислить к функциям.
В результате целесообразно проанализировать отрезок, где наблюдается строгое возрастание функции, и все значения относятся к ряду из области значений:
(left[-{frac {pi }{2}};{frac {pi }{2}}right])
Функция (y=sin x ) на отрезке (left[-{frac {pi }{2}};{frac {pi }{2}}right]) обладает следующей особенностью: какое-либо из значений этой функции возможно только при одном значении аргумента. По этой причине на данном интервале может существовать обратная функция с формулой (y=arcsin x.)
График обратной функции является симметричным графику функции (y=sin x) в рамках интервала (left[-{frac {pi }{2}};{frac {pi }{2}}right]) по отношению к прямой y=x. Можно наблюдать симметричность в расположении графиков функций, которые являются взаимно обратными, по отношению к биссектрисе первого и третьего координатных углов на плоскости координат Oxy.
Пример 2
Определим значение выражение:
(arcsin 0,4)
По определению обратной тригонометрической функции можно сделать вывод, что запись означает угол с синусом, равным 0,4. В данном выводе заключается смысл понятия арксинус.
Пример 3
Требуется найти, что означает (arcsin 0,5).
Если знать определение, эта простая обратная тригонометрическая функция является обозначением угла с синусом, равным 0,5. Таким синусом обладает угол в 30°. Таким образом:
(arcsin 0,5 = 30°)
Общий ответ можно высчитать не в градусах, а в радианах:
Свойства функции arcsin
Рассмотрим функцию (y=arcsin x). Она является непрерывной в тригонометрии и ограничивается на протяжении всей своей области определения. Данная функция строго возрастает.
Область определения, в которой функцию можно вычислить:
(D(arcsin x)=[-1;1]qquad) (от минус единицы до плюс единицы)
Область значений:
(E(arcsin x)=left[-{frac {pi }{2}};{frac {pi }{2}}right]qquad )
Значения функций можно посчитать таким образом:
- (sin(arcsin x)=xqquad), если (-1leqslant xleqslant 1)
- (arcsin(sin y)=yqquad), если (-{frac {pi }{2}}leqslant yleqslant {frac {pi }{2}})
Функция arcsin обладает следующими свойствами:
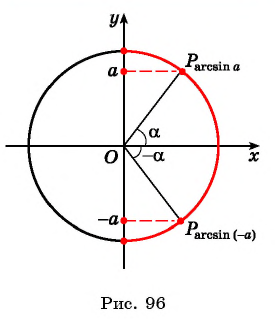
- (arcsin(-x)=-arcsin xqquad )(нечетная функция);
- (arcsin x>0, когда 0<xleqslant 1);
- (arcsin x=0, когда x=0);
- (arcsin x<0, если -1leqslant x<0);
- (arcsin x=left{{begin{matrix}arccos {sqrt {1-x^{2}}},qquad 0leqslant xleqslant 1\-arccos {sqrt {1-x^{2}}},qquad -1leqslant x<0end{matrix}}right.)
- (arcsin x=operatorname {arctg}{frac {x}{{sqrt {1-x^{2}}}}});
- (arcsin x=left{{begin{matrix}operatorname {arcctg},{frac {{sqrt {1-x^{2}}}}{x}},qquad 0<xleqslant 1\operatorname {arcctg},{frac {{sqrt {1-x^{2}}}}{x}}-pi ,qquad -1leqslant x<0end{matrix}}right.)
График арксинуса
График функции (y=arcsin x):
Содержание:
При изучении тригонометрических функций часто возникает вопрос о нахождении значения аргумента, при котором значение функции равно заданному числу.
Нахождение значения аргумента
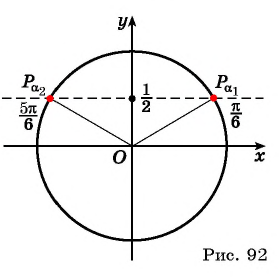
Например, найдем все значения аргумента, при которых значение функции 
На единичной окружности найдем точки 
ординаты которых равны 
Этим точкам соответствуют углы 
и 
и таких углов бесконечно много. Однако, если рассмотреть промежуток 
то на нем функция 
возрастает и принимает все значения от -1 до 1. Поэтому для любого числа 
из промежутка 
существует единственное число 
такое что 
Так на промежутке 
существует единственное значение аргумента, при котором значение функции 
равно 
— это угол равный 
( рис.93)
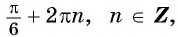
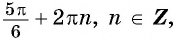
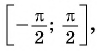
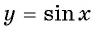
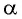
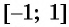
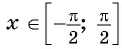
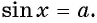
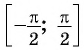
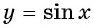
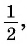
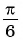
Определение Арксинуса
Определение:
Арксинусом числа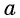 
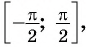
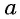
называется угол, принадлежащий промежутку 
синус которого равен 
(рис. 94).
Этот угол обозначают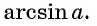 
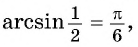
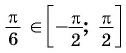
Так, 
поскольку 
и 
Пример №1
Вычислите:
Решение:
так как 
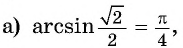
Пример №2
Найдите значение выражения:
Решение:
так как
(рис. 95, б).
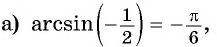
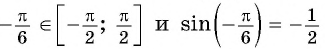
Заметим, что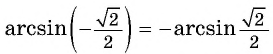 
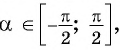
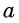
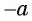
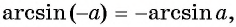
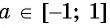
( рис.95) Так как углы, соответствующие точкам 
и 
где 
с ординатами 
и 
отличаются только знаком, то 
для любого числа 
(рис. 96).
Пусть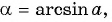 
тогда 
Так как точки
имеют противоположные ординаты, то 
Поскольку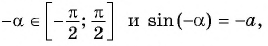 
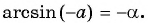
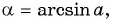
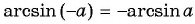
то по определению арксинуса 
Так как 
то 
для любого числа 
Воспользуемся полученным равенством и найдем значение выражения
Так как 
Отметим, что областью определения выражения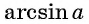 
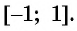
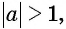
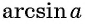
является отрезок 
Если 
то выражение 
не имеет смысла.
Например, выражения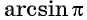 
не имеют смысла, так как 
Выражение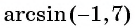 
не имеет смысла, так как 
Из определения арксинуса числа следует, что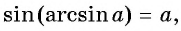 
если 
Например, 
Рассмотрим промежуток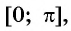 
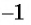
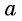
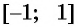
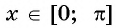
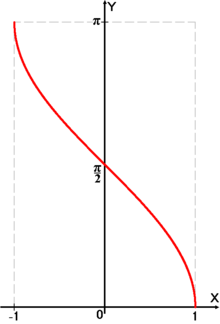
на котором функция 
возрастает и принимает все значения от 
до 1. Для любого числа 
из промежутка 
существует единственное число 
такое, что 
Определение Арккосинуса
Определение:
Арккосинусом числа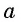 
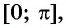
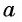
называется угол, принадлежащий промежутку 
косинус которого равен 
(рис. 97).
Этот угол обозначают 
Например: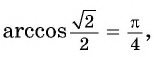 
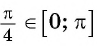
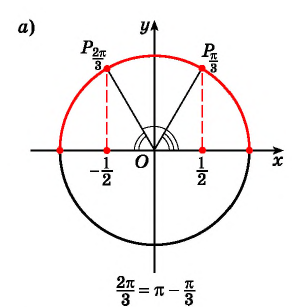
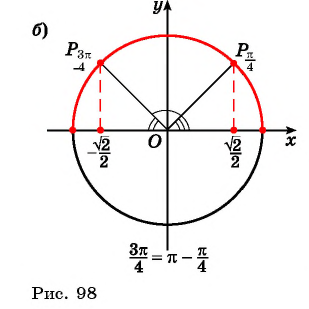
поскольку 
и 
Пример №3
Вычислите:
Решение:
Пример №4
Найдите значение выражения:
Решение:
так как 
( рис. 98.а)
( рис.98.б)
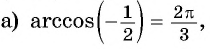
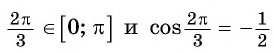
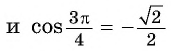
Заметим, что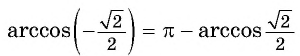 
( см.98)
Пусть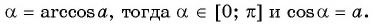 
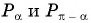
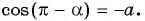
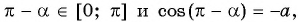
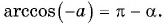
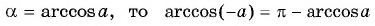
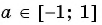
Так как точки 
имеют противоположные абсциссы, то 
Поскольку 
то по определению арккосинуса 
Так как 
для любого числа 
(рис. 99).
Воспользуемся полученным равенством и найдем значение выражения
Так как 
Областью определения выражения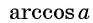 
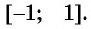
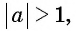
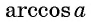
является отрезок 
Если 
то выражение 
не имеет смысла.
Так, выражения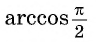 
не имеют смысла, поскольку
Выражение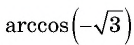 
не имеет смысла, так как 
Из определения арккосинуса числа следует, что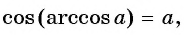 
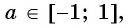
если 
и 
Например, 
На промежутке монотонности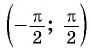 
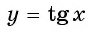
функции 
существует единственный угол, тангенс которого равен некоторому данному числу 
Определение Арктангенса
Определение:
Арктангенсом числа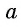 
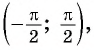
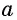
называется угол, принадлежащий промежутку 
тангенс которого равен 
(рис. 100).
Этот угол обозначают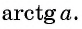 
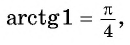
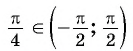
Так, 
поскольку 
и 
Пример №5
Вычислите:
Решение:
так как 
и 
и 
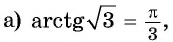
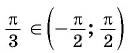
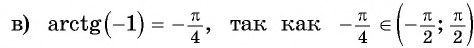
Для любого числа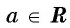 
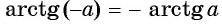
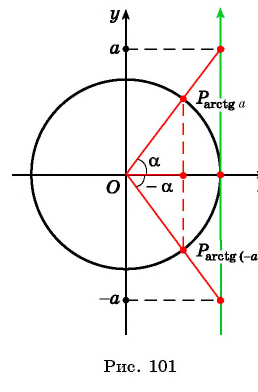
верно равенство 
(рис. 101).
Пример №6
Найдите значение выражения
Решение:
Так как 
Из определения арктангенса числа следует, что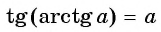 
при 
Например, 
На промежутке монотонности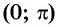 
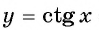
функции 
существует единственный угол, котангенс которого равен некоторому данному числу 
Определение Арккотангенса
Определение:
Арккотангенсом числа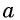 
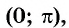
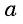
называется угол, принадлежащий промежутку 
котангенс которого равен 
(рис. 102).
Этот угол обозначают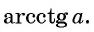 
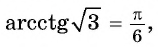
Например, 
поскольку
- Заказать решение задач по высшей математике
Пример №7
Вычислите:
Решение:
так как
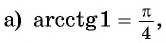
Для любого числа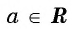 
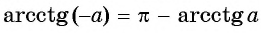
верно равенство 
(рис. 103).
Пример №8
Найдите значение выражения 
Решение:
Так как 
Из определения арккотангенса числа следует, что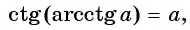 
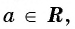
если 
и 
Например, 
Примеры заданий и их решения
Пример №9
Верно ли, что:
Решение:
а) Верно, так как 
б) верно, так как 
в) неверно, так как 
г) неверно, так как 
Пример №10
Вычислите:
Решение:
Пример №11
Найдите значение выражения:
Решение:
Пример №12
Оцените значение выражения 
Решение:
По определению арктангенса числа 
Воспользуемся свойствами числовых неравенств и получим: 
Пример №13
Найдите область определения выражения:
Решение:
а) По определению арксинуса числа 
это угол, синус которого равен 
б) По определению арккосинуса числа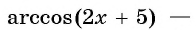 
это угол, косинус которого равен 
Пример №14
Найдите значение выражения:
Решение:
Пример №15
Вычислите 
Решение:
Пример №16
Найдите значение выражения 
Решение:
Воспользуемся формулой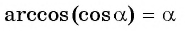 
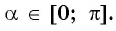
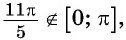
при 
Поскольку 
то эту формулу сразу применить нельзя.
Так как 
Пример №17
Найдите значение выражения 
Решение:
Так как 
при 
при 
- Тригонометрические уравнения
- Тригонометрические неравенства
- Формулы приведения
- Синус, косинус, тангенс суммы и разности
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x – их свойства, графики
Арксинус, арккосинус, арктангенс и арккотангенс – начальные сведения
Задача, обратная нахождению значения синуса, косинуса, тангенса и котангенса данного угла (числа), подразумевает нахождение угла (числа) по известным значениям тригонометрических функций. Она приводит к понятиям арксинуса, арккосинуса, арктангенса и арккотангенса числа.
В этой статье мы дадим определения арксинуса, арккосинуса, арктангенса и арккотангенса числа, введем принятые обозначения, а также приведем примеры арксинуса, арккосинуса, арктангенса и арккотангенса. В заключение упомянем про аркфункции и покажем, как арксинус, арккосинус, арктангенс и арккотангенс связаны с единичной окружностью.
Навигация по странице.
Определения, обозначения, примеры
Арксинус, арккосинус, арктангенс и арккотангенс можно определить как угол и как число. Это связано с тем, что мы определили синус, косинус, тангенс и котангенс как угла, так и числа (смотрите синус, косинус, тангенс и котангенс в тригонометрии). Остановимся на обоих подходах к определению арксинуса, арккосинуса, арктангенса и арккотангенса.
Арксинус, арккосинус, арктангенс и арккотангенс как угол
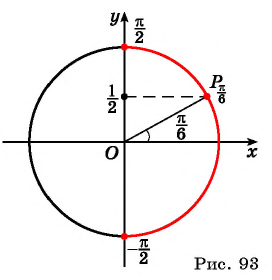
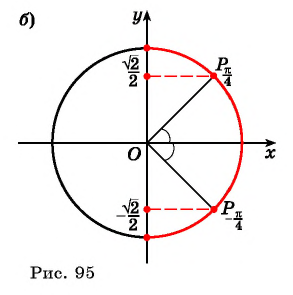
Пусть про угол альфа α известно лишь то, что его синус равен числу 1/2 , то есть, sinα=1/2 . Последнее равенство определяет угол α неоднозначно, так как ему удовлетворяет бесконечное множество углов α=(−1) k ·30°+180°·k ( α=(−1) k ·π/6+π·k ), где k∈Z . Однако, если потребовать, чтобы величина угла α в градусах принадлежала отрезку [−90, 90] (в радианах – отрезку [−π/2, π/2] ), то равенство sinα=1/2 будет определять угол альфа однозначно. При этом условии равенству удовлетворяет единственный угол в 30 градусов ( π/6 радианов).
Вообще, равенство sinα=a (не путайте a и альфа: a и α ) при любом числе a∈[−1, 1] и условии −90°≤α≤90° ( −π/2≤α≤π/2 ) определяет единственный угол α . Этот угол называют арксинусом числа a .
Арксинус числа a∈[−1, 1] – это угол −90°≤α≤90° ( −π/2≤α≤π/2 ), синус которого равен a .
Аналогично определяются арккосинус, арктангенс и арккотангенс.
Арккосинус числа a∈[−1, 1] – это угол 0°≤α≤180° ( 0≤α≤π ), косинус которого равен a .
Арктангенс числа a∈(−∞, +∞) – это угол −90° ( −π/2 ), тангенс которого равен a .
Арккотангенс числа a∈(−∞, +∞) – это угол 0° ( 0 ), котангенс которого равен a .
Для записи арксинуса, арккосинуса, арктангенса и арккотангенса приняты следующие обозначения: arcsin , arccos , arctg и arcctg . То есть, арксинус числа a можно записать как arcsin a , арккосинус, арктангенс и арккотангенс числа a запишутся соответственно как arccos a , arctg a и arcctg a .
Также можно встретить обозначения arctan и arccot , они являются другой формой обозначения арктангенса и арккотангенса, которая принята в англоязычной литературе. Мы же арктангенс и арккотангенс будем обозначать как arctg и arcctg .
В свете введенных обозначений, определения арксинуса, арккосинуса, арктангенса и арккотангенса числа можно записать более формально:
arcsin a , a∈[−1, 1] , есть такой угол α , что −90°≤α≤90° ( −π/2≤α≤π/2 ) и sinα=a ;
arccos a , a∈[−1, 1] , есть такой угол α , что 0°≤α≤180° ( 0≤α≤π ) и cosα=a ;
arctg a , a∈(−∞, +∞) , есть такой угол α , что −90° ( −π/2 ) и tgα=a ;
arcctg a , a∈(−∞, +∞) , есть такой угол α , что 0° ( 0 ) и ctgα=a .
Подчеркнем, что арксинус и арккосинус числа определен для чисел, принадлежащих отрезку [−1, 1] , для остальных чисел арксинус и арккосинус не определен. Например, не имеет смысла запись arcsin2 . Аналогично не определен арксинус пяти, арксинус минус корня из трех, арккосинус семи целых двух третьих и арккосинус минус пи, так как числа 2 , 5 , , −π выходят за пределы числового отрезка от −1 до 1 . В свою очередь записи arctg a и arcctg a имеют смысл для любого действительного числа a , например, имеют смысл записи arctg0 , arctg(−500,2) , arcctg(6·π+1) и т.п.
Теперь можно привести примеры арксинуса, арккосинуса, арктангенса и арккотангенса числа.
Начнем с примеров арксинуса. Определение арксинуса позволяет утверждать, что угол π/3 является арксинусом числа , то есть, (здесь и α=π/3 ). Действительно, число принадлежит отрезку [−1, 1] , угол π/3 лежит в пределах от −π/2 до π/2 и . Приведем еще несколько примеров арксинуса числа: arcsin(−1)=−90° , arcsin(0,5)=π/6 , .
А вот π/10 не является арксинусом 1/2 , так как sin(π/10)≠1/2 . Еще пример: несмотря на то, что синус 270 градусов равен −1 , угол 270 градусов не является арксинусом минус единицы, так как 270 градусов не является углом в пределах от −90 до 90 градусов. Более того, угол 270 градусов вообще не может быть арксинусом какого-либо числа, так как арксинус числа должен лежать в пределах от −90 до 90 градусов.
Для полноты картины приведем примеры арккосинуса, арктангенса и арккотангенса числа. Например, угол 0 радианов является арккосинусом единицы, то есть, arccos1=0 (так как выполняются все условия из определения арккосинуса: число 1 принадлежит отрезку от −1 до 1 , угол нуль радианов лежит в пределах от нуля до пи включительно и cos0=1 ). Аналогично, угол π/2 есть арккосинус нуля: arccos0=π/2 . По определению арктангенса числа arctg(−1)=−π/4 или arctg(−1)=−45° . Арктангенс корня из трех равен 60 градусам ( π/3 рад). А из определения арккотангенса можно заключить, что arcctg0=π/2 , так как угол π/2 лежит в рамках от 0 до пи и ctg(π/2)=0 .
Подобный подход к определению арксинуса, арккосинуса, арктангенса и арккотангенса описан в учебнике Кочеткова [1, с. 260-278] .
Арксинус, арккосинус, арктангенс и арккотангенс как число
Когда мы имеем дело с синусом, косинусом, тангенсом и котангенсом угла, то естественно арксинус, арккосинус, арктангенс и арккотангенс определять как угол. Если же мы начинаем говорить про синус, косинус, тангенс и котангенс числа, а не угла, то естественно арксинус, арккосинус, арктангенс и арккотангенс определять уже как число.
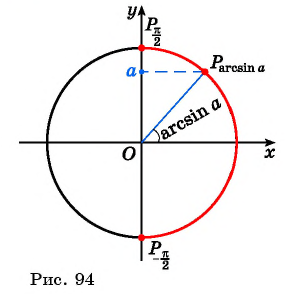
Арксинусом числа a∈[−1, 1] называется такое число t∈[−π/2, π/2] , синус которого равен a .
Алгебра
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Арккосинус
Напомним, что на единичной окружности косинус угла – это координата х точки А, соответствующей этому углу:
Можно утверждать, что косинус – это ф-ция, которая ставит каждому углу в соответствие некоторую координату х. Теперь предположим, что нам известна эта координата (пусть она будет равна величине а), и по ней надо определить значение угла. Отложим на оси Ох отрезок длиной а, проведем через него вертикальную прямую и отметим ее точки пересечения с единичной окружностью. Если – 1 1 либо а n ,будет равно единице, и мы получим первую серию. Если же n – нечетное число, то, то выражение (– 1) n окажется равным (– 1), и мы получим вторую серию.
Задание. Решите ур-ние
Задание. Запишите корни ур-ния
Теперь будем подставлять в это решение значения n, чтобы найти конкретные значения х. Нас интересуют корни, которые больше π, но меньше 4π, поэтому будем сразу сравнивать полученные результаты с этими числами.
Получили два корня, относящихся к промежутку – это 7π/3 и 8π/3. Нет смысла проверять другие возможные значения n, ведь они будут давать корни, заведомо меньшие 2π/3 или большие 13π/3:
Ответ: 7π/3 и 8π/3.
Как и в случае с косинусом, есть несколько частных случаев, когда решение ур-ния записывается проще. Ур-ние
Это видно из графика, где корням ур-ния соответствуют точки пересечения синусоиды с осью Ох:
Наконец, решениями ур-ния
Решение уравнений tgx = a и ctgx = a
Ур-ния вида tgx = a отличаются тем, что имеют решение при любом значении а. Действительно, построим одну тангенсоиду и проведем горизонтальную линии у = а. При любом а прямая пересечет тангенсоиду, причем ровно в одной точке, которая имеет координаты (arctga; a):
Таким образом, у ур-ния tgx = a существует очевидное решение
Однако напомним, что тангенс является периодической ф-цией, его график представляет собой бесконечное множество тангенсоид, расстояние между которыми равно π. Поэтому корень х = arctga порождает целую серию корней, которую можно записать так:
Задание. Решите ур-ние
Задание. Запишите формулу корней ур-ния
Далее рассмотрим ур-ние вида
Задание. Решите ур-ние
Существует особый случай, когда нельзя заменить котангенс на тангенс. В ур-нии
Из сегодняшнего урока мы узнали про обратные тригонометрические ф-ции – арксинус, арккосинус и арктангенс. Также мы научились находить решения простейших тригонометрических уравнений. Это поможет нам в будущем при изучении более сложных ур-ний.
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа помогут разобраться в вычислении заданных функций. Значение тригонометрических функций угла равняется числу a , тогда автоматически считается величиной этого угла. Если a – число, тогда это и есть значение функции.
Для четкого понимания рассмотрим пример.
Если имеем арккосинус угла равного π 3 , то значение косинуса отсюда равно 1 2 по таблице косинусов. Данный угол расположен в промежутке от нуля до пи, значит, значение арккосинуса 1 2 получим π на 3 . Такое тригонометрическое выражение записывается как a r cos ( 1 2 ) = π 3 .
Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °
Основные значения arcsin, arccos, arctg и arctg
Благодаря таблице синусов, косинусов, тангенсов и котангенсов, мы имеет точные значения угла при 0 , ± 30 , ± 45 , ± 60 , ± 90 , ± 120 , ± 135 , ± 150 , ± 180 градусов. Таблица достаточно удобна и из нее можно получать некоторые значения для аркфункций, которые имеют название как основные значения арксинуса, арккосинуса, арктангенса и арккотангенса.
Таблица синусов основных углов предлагает такие результаты значений углов:
sin ( – π 2 ) = – 1 , sin ( – π 3 ) = – 3 2 , sin ( – π 4 ) = – 2 2 , sin ( – π 6 ) = – 1 2 , sin 0 = 0 , sin π 6 = 1 2 , sin π 4 = 2 2 , sin π 3 = 3 2 , sin π 2 = 1
Учитывая их, можно легко высчитать арксинус числа всех стандартных значений, начиная от – 1 и заканчивая 1 , также значения от – π 2 до + π 2 радианов, следуя его основному значению определения. Это и является основными значениями арксинуса.
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
в р а д и а н а х
| α | – 1 | – 3 2 | – 2 2 | – 1 2 | 0 | 1 2 | 2 2 | 3 2 |
| a r c sin α к а к у г о л | – π 2 | – π 3 | – π 4 | – π 6 | 0 | π 6 | π 4 | π 3 |
| в г р а д у с а х | – 90 ° | – 60 ° | – 45 ° | – 30 ° | 0 ° | 30 ° | 45 ° | 60 ° |
| a r c sin α к а к ч и с л о | – π 2 | – π 3 | – π 4 | – π 6 | 0 | π 6 | π 4 | π 3 |
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
cos 0 = 1 , cos π 6 = 3 2 , cos π 4 = 2 2 , cos π 3 = 1 2 , cos π 2 = 0 , cos 2 π 3 = – 1 2 , cos 3 π 4 = – 2 2 , cos 5 π 6 = – 3 2 , cos π = – 1
Следуя из таблицы, находим значения арккосинуса:
a r c cos ( – 1 ) = π , arccos ( – 3 2 ) = 5 π 6 , arcocos ( – 2 2 ) = 3 π 4 , arccos – 1 2 = 2 π 3 , arccos 0 = π 2 , arccos 1 2 = π 3 , arccos 2 2 = π 4 , arccos 3 2 = π 6 , arccos 1 = 0
в р а д и а н а х
| α | – 1 | – 3 2 | – 2 2 | – 1 2 | 0 | 1 2 | 2 2 | 3 2 | 1 |
| a r c cos α к а к у г о л | π | 5 π 6 | 3 π 4 | 2 π 3 | π 2 | π 3 | π 4 | π 6 | 0 |
| в г р а д у с а х | 180 ° | 150 ° | 135 ° | 120 ° | 90 ° | 60 ° | 45 ° | 30 ° | 0 ° |
| a r c cos α к а к ч и с л о | π | 5 π 6 | 3 π 4 | 2 π 3 | π 2 | π 3 | π 4 | π 6 | 0 |
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.
| α | – 3 | – 1 | – 3 3 | 0 | 3 3 | 1 | 3 | |
| a r c t g a к а к у г о л | в р а д и а н а х | – π 3 | – π 4 | – π 6 | 0 | π 6 | π 4 | π 3 |
| в г р а д у с а х | – 60 ° | – 45 ° | – 30 ° | 0 ° | 30 ° | 45 ° | 60 ° | |
| a r c t g a к а к ч и с л о | – π 3 | – π 4 | – π 6 | 0 | π 6 | π 4 | π 3 |
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
a r c sin , a r c cos , a r c t g и a r c c t g
Для точного значения a r c sin , a r c cos , a r c t g и a r c c t g числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.
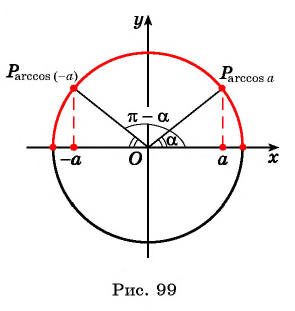
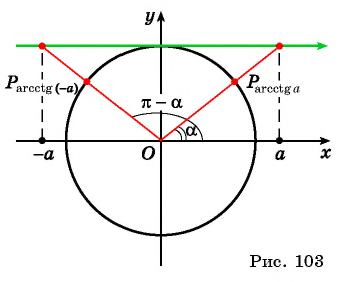
Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения a r c sin , a r c cos , a r c t g и a r c c t g отрицательных и положительных чисел сводится к нахождению формул a r c sin , a r c cos , a r c t g и a r c c t g противоположных чисел вида a r c sin ( – α ) = – a r c sin α , a r c cos ( – α ) = π – a r c cos α , a r c t g ( – α ) = – a r c t g α , a r c c t g ( – α ) = π – a r c c t g α .
Рассмотрим решение нахождения значений a r c sin , a r c cos , a r c t g и a r c c t g с помощью таблицы Брадиса.
Если нам необходимо найти значение арксинуса 0 , 2857 , ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0 , 2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.
Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0 , 2863 используется та самая поправка в 0 , 0006 , так как ближайшим числом будет 0 , 2857 . Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Таким образом находятся значения a r c sin , a r c cos , a r c t g и a r c c t g .
Нахождение значения arcsin, arccos, arctg и arcctg
Чтобы найти арксинус через известный арккосинус данного числа, нужно применить тригонометрические формулы a r c sin α + a r c cos α = π 2 , a r c t g α + a r c c t g α = π 2 (не обходимо просмотреть тему формул суммы арккосинуса и арксинуса, суммы арктангенса и арккотангенса).
При известном a r c sin α = – π 12 необходимо найти значение a r c cos α , тогда необходимо вычислить арккосинус по формуле:
a r c cos α = π 2 − a r c sin α = π 2 − ( − π 12 ) = 7 π 12 .
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Если дан арккосинус числа а равный π 10 , а вычислить арктангенс данного числа поможет таблица тангенсов. Угол π 10 радиан представляет собой 18 градусов, тогда по таблице косинусов видим, что косинус 18 градусов имеет значение 0 , 9511 , после чего заглядываем в таблицу Брадиса.
При поиске значения арктангенса 0 , 9511 определяем, что значение угла имеет 43 градуса и 34 минуты. Рассмотрим по таблице ниже.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.
[spoiler title=”источники:”]
http://100urokov.ru/predmety/urok-4-prostejshaya-trigonometriya
http://zaochnik.com/spravochnik/matematika/trigonometrija/nahozhdenie-znachenij-arksinusa-arkkosinusa-arktan/
[/spoiler]
