Салин Дмитрий
Профи
(720),
закрыт
13 лет назад
Лучший ответ
Ника
Высший разум
(181432)
13 лет назад
Решение: 
Салин ДмитрийПрофи (720)
13 лет назад
большое спасибо за решение 🙂
РизаевичПрофи (526)
10 лет назад
ошибочка) когда второй раз интегрируете по частям: v=-2(корень из (1-х^2))
Oksana PeshkovaУченик (180)
7 лет назад
ошибка во второй замене
Остальные ответы
Сергей Миронов
Профи
(552)
13 лет назад
Ну выглядит не сложно! Почти любой подобный пример с интегралами можно решить при
помощи зарубежного бесплатного сервиса wolframalpha либо российского Интегралотикон
Просто погуглите!
Похожие вопросы
Интеграл от арксинуса
Интеграл от арксинуса равен сумме произведения переменной интегрирования на этот арксинус и корню квадратному из разности единицы и переменной интегрирования в квадрате плюс константа интегрирования
(
int arcsin x d x=x arcsin x+sqrt{1-x^{2}}+C
)
Примеры решения задач
ПРИМЕР 1
Доказать, что (
int arcsin x d x=x arcsin x+sqrt{1-x^{2}}+C
)
Для доказательства применим формулу интегрирования по частям:
(
int arcsin x d x|u=underset{d x}{arcsin x}, d v=d x|=x arcsin x-int frac{x d x}{sqrt{1-x^{2}}}left|begin{array}{l}{1-x^{2}=t^{2}} \ {-2 x d x=2 t d t} \ {x d x=-t d t}end{array}right|=
)
(
=x arcsin x-int frac{-t d t}{sqrt{t^{2}}}=x arcsin x+int d t=x arcsin x+t+C=x arcsin x+sqrt{1-x^{2}}+C
)
ПРИМЕР 2
Найти интеграл (
int arcsin 4 x d x
)
Сведем данный интеграл к формуле, предварительно сделав в нем замену переменной:
(
int arcsin 4 x d xleft|begin{array}{l}{4 x=t} \ {4 d x=d t} \ {d x=frac{d t}{4}}end{array}right|=int arcsin t cdot frac{d t}{4}=frac{1}{4} int arcsin t d t=
)
(
=frac{1}{4}left(t arcsin t+sqrt{1-t^{2}}right)+C=frac{1}{4}left(4 x arcsin 4 x+sqrt{1-(4 x)^{2}}right)+C=
)
(
=x arcsin 4 x+frac{sqrt{1-16 x^{2}}}{4}+C
)
(
int arcsin 4 x d x=x arcsin 4 x+frac{sqrt{1-16 x^{2}}}{4}+C
)
-
Определение
- График арксинуса
- Свойства арксинуса
- Таблица арксинусов
Определение
Арксинус (arcsin) – это обратная тригонометрическая функция.
Арксинус x определяется как функция, обратная к синусу x, при -1≤x≤1.
Если синус угла у равен х (sin y = x), значит арксинус x равняется y:
arcsin x = sin-1 x = y
Примечание: sin-1x означает обратный синус, а не синус в степени -1.
Например:
arcsin 1 = sin-1 1 = 90° (π/2 рад)
График арксинуса
Функция арксинуса пишется как y = arcsin (x). График в общем виде выглядит следующим образом (-1≤x≤1, -π/2≤y≤π/2):

Свойства арксинуса
Ниже в табличном виде представлены основные свойства арксинуса с формулами.
Таблица арксинусов
| x | arcsin x (рад) | arcsin x (°) |
| -1 | -π/2 | -90° |
| -√3/2 | -π/3 | -60° |
| -√2/2 | -π/4 | -45° |
| -1/2 | -π/6 | -30° |
| 0 | 0 | 0° |
| 1/2 | π/6 | 30° |
| √2/2 | π/4 | 45° |
| √3/2 | π/3 | 60° |
| 1 | π/2 | 90° |
microexcel.ru
Решение
$$operatorname{asin}^{2}{left(t right)}$$
$$frac{d}{d t} operatorname{asin}^{2}{left(t right)}$$
Первая производная
[src]
2*asin(t) ----------- ________ / 2 / 1 - t
$$frac{2 operatorname{asin}{left(t right)}}{sqrt{- t^{2} + 1}}$$
Вторая производная
[src]
/ 1 t*asin(t)
2*|- ------- + -----------|
| 2 3/2|
| -1 + t / 2 |
1 - t / /
$$2 left(frac{t operatorname{asin}{left(t right)}}{left(- t^{2} + 1right)^{frac{3}{2}}} – frac{1}{t^{2} – 1}right)$$
Третья производная
[src]
/ 2 | asin(t) 3*t 3*t *asin(t)| 2*|----------- + ---------- + ------------| | 3/2 2 5/2 | |/ 2 / 2 / 2 | \1 - t / -1 + t / 1 - t / /
$$2 cdot left(frac{3 t}{left(t^{2} – 1right)^{2}} + frac{3 t^{2} operatorname{asin}{left(t right)}}{left(- t^{2} + 1right)^{frac{5}{2}}} + frac{operatorname{asin}{left(t right)}}{left(- t^{2} + 1right)^{frac{3}{2}}}right)$$
График
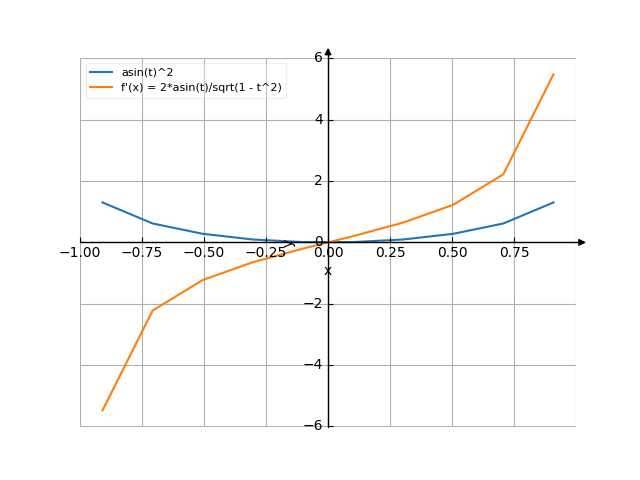
Хочу вычислить квадрат арксинуса от аргумента X
from math import pow, asin
pow(asin, 2)(x)
но я понимаю, что это не работает, потому что pow вернет число
задан 17 мар 2022 в 22:16
1
1 ответ
Ну как в школе на алгебре – сначала вычисляем арксинус от X, потом результат возводим
в квадрат
y = pow(asin(x), 2)
ещё в степень можно возвести с помощью оператора **
y = (asin(x))**2
ответ дан 18 мар 2022 в 6:09
MBoMBo
47.8k1 золотой знак17 серебряных знаков40 бронзовых знаков
