Арктангенс(y = arctg(x)) – это обратная тригонометрическая функция к тангенсу x = tg(y). Область определения -∞ ≤ x ≤ +∞ и множество значений -π/2 ≤ y ≤ +π/2.
| arctg(0) = 0° | arctg(-1.732050808) = 120° | arctg(1.732050808) = 240° |
| arctg(0.01745506493) = 1° | arctg(-1.664279482) = 121° | arctg(1.804047755) = 241° |
| arctg(0.03492076949) = 2° | arctg(-1.600334529) = 122° | arctg(1.880726465) = 242° |
| arctg(0.05240777928) = 3° | arctg(-1.539864964) = 123° | arctg(1.962610506) = 243° |
| arctg(0.06992681194) = 4° | arctg(-1.482560969) = 124° | arctg(2.050303842) = 244° |
| arctg(0.08748866353) = 5° | arctg(-1.428148007) = 125° | arctg(2.144506921) = 245° |
| arctg(0.1051042353) = 6° | arctg(-1.37638192) = 126° | arctg(2.246036774) = 246° |
| arctg(0.1227845609) = 7° | arctg(-1.327044822) = 127° | arctg(2.355852366) = 247° |
| arctg(0.1405408347) = 8° | arctg(-1.279941632) = 128° | arctg(2.475086853) = 248° |
| arctg(0.1583844403) = 9° | arctg(-1.234897157) = 129° | arctg(2.605089065) = 249° |
| arctg(0.1763269807) = 10° | arctg(-1.191753593) = 130° | arctg(2.747477419) = 250° |
| arctg(0.1943803091) = 11° | arctg(-1.150368407) = 131° | arctg(2.904210878) = 251° |
| arctg(0.2125565617) = 12° | arctg(-1.110612515) = 132° | arctg(3.077683537) = 252° |
| arctg(0.2308681911) = 13° | arctg(-1.07236871) = 133° | arctg(3.270852618) = 253° |
| arctg(0.2493280028) = 14° | arctg(-1.035530314) = 134° | arctg(3.487414444) = 254° |
| arctg(0.2679491924) = 15° | arctg(-1) = 135° | arctg(3.732050808) = 255° |
| arctg(0.2867453858) = 16° | arctg(-0.9656887748) = 136° | arctg(4.010780934) = 256° |
| arctg(0.3057306815) = 17° | arctg(-0.9325150861) = 137° | arctg(4.331475874) = 257° |
| arctg(0.3249196962) = 18° | arctg(-0.9004040443) = 138° | arctg(4.704630109) = 258° |
| arctg(0.3443276133) = 19° | arctg(-0.8692867378) = 139° | arctg(5.144554016) = 259° |
| arctg(0.3639702343) = 20° | arctg(-0.8390996312) = 140° | arctg(5.67128182) = 260° |
| arctg(0.383864035) = 21° | arctg(-0.8097840332) = 141° | arctg(6.313751515) = 261° |
| arctg(0.4040262258) = 22° | arctg(-0.7812856265) = 142° | arctg(7.115369722) = 262° |
| arctg(0.4244748162) = 23° | arctg(-0.7535540501) = 143° | arctg(8.144346428) = 263° |
| arctg(0.4452286853) = 24° | arctg(-0.726542528) = 144° | arctg(9.514364454) = 264° |
| arctg(0.4663076582) = 25° | arctg(-0.7002075382) = 145° | arctg(11.4300523) = 265° |
| arctg(0.4877325886) = 26° | arctg(-0.6745085168) = 146° | arctg(14.30066626) = 266° |
| arctg(0.5095254495) = 27° | arctg(-0.6494075932) = 147° | arctg(19.08113669) = 267° |
| arctg(0.5317094317) = 28° | arctg(-0.6248693519) = 148° | arctg(28.63625328) = 268° |
| arctg(0.5543090515) = 29° | arctg(-0.600860619) = 149° | arctg(57.28996163) = 269° |
| arctg(0.5773502692) = 30° | arctg(-0.5773502692) = 150° | arctg(∞) = 270° |
| arctg(0.600860619) = 31° | arctg(-0.5543090515) = 151° | arctg(-57.28996163) = 271° |
| arctg(0.6248693519) = 32° | arctg(-0.5317094317) = 152° | arctg(-28.63625328) = 272° |
| arctg(0.6494075932) = 33° | arctg(-0.5095254495) = 153° | arctg(-19.08113669) = 273° |
| arctg(0.6745085168) = 34° | arctg(-0.4877325886) = 154° | arctg(-14.30066626) = 274° |
| arctg(0.7002075382) = 35° | arctg(-0.4663076582) = 155° | arctg(-11.4300523) = 275° |
| arctg(0.726542528) = 36° | arctg(-0.4452286853) = 156° | arctg(-9.514364454) = 276° |
| arctg(0.7535540501) = 37° | arctg(-0.4244748162) = 157° | arctg(-8.144346428) = 277° |
| arctg(0.7812856265) = 38° | arctg(-0.4040262258) = 158° | arctg(-7.115369722) = 278° |
| arctg(0.8097840332) = 39° | arctg(-0.383864035) = 159° | arctg(-6.313751515) = 279° |
| arctg(0.8390996312) = 40° | arctg(-0.3639702343) = 160° | arctg(-5.67128182) = 280° |
| arctg(0.8692867378) = 41° | arctg(-0.3443276133) = 161° | arctg(-5.144554016) = 281° |
| arctg(0.9004040443) = 42° | arctg(-0.3249196962) = 162° | arctg(-4.704630109) = 282° |
| arctg(0.9325150861) = 43° | arctg(-0.3057306815) = 163° | arctg(-4.331475874) = 283° |
| arctg(0.9656887748) = 44° | arctg(-0.2867453858) = 164° | arctg(-4.010780934) = 284° |
| arctg(1) = 45° | arctg(-0.2679491924) = 165° | arctg(-3.732050808) = 285° |
| arctg(1.035530314) = 46° | arctg(-0.2493280028) = 166° | arctg(-3.487414444) = 286° |
| arctg(1.07236871) = 47° | arctg(-0.2308681911) = 167° | arctg(-3.270852618) = 287° |
| arctg(1.110612515) = 48° | arctg(-0.2125565617) = 168° | arctg(-3.077683537) = 288° |
| arctg(1.150368407) = 49° | arctg(-0.1943803091) = 169° | arctg(-2.904210878) = 289° |
| arctg(1.191753593) = 50° | arctg(-0.1763269807) = 170° | arctg(-2.747477419) = 290° |
| arctg(1.234897157) = 51° | arctg(-0.1583844403) = 171° | arctg(-2.605089065) = 291° |
| arctg(1.279941632) = 52° | arctg(-0.1405408347) = 172° | arctg(-2.475086853) = 292° |
| arctg(1.327044822) = 53° | arctg(-0.1227845609) = 173° | arctg(-2.355852366) = 293° |
| arctg(1.37638192) = 54° | arctg(-0.1051042353) = 174° | arctg(-2.246036774) = 294° |
| arctg(1.428148007) = 55° | arctg(-0.08748866353) = 175° | arctg(-2.144506921) = 295° |
| arctg(1.482560969) = 56° | arctg(-0.06992681194) = 176° | arctg(-2.050303842) = 296° |
| arctg(1.539864964) = 57° | arctg(-0.05240777928) = 177° | arctg(-1.962610506) = 297° |
| arctg(1.600334529) = 58° | arctg(-0.03492076949) = 178° | arctg(-1.880726465) = 298° |
| arctg(1.664279482) = 59° | arctg(-0.01745506493) = 179° | arctg(-1.804047755) = 299° |
| arctg(1.732050808) = 60° | arctg(0) = 180° | arctg(-1.732050808) = 300° |
| arctg(1.804047755) = 61° | arctg(0.01745506493) = 181° | arctg(-1.664279482) = 301° |
| arctg(1.880726465) = 62° | arctg(0.03492076949) = 182° | arctg(-1.600334529) = 302° |
| arctg(1.962610506) = 63° | arctg(0.05240777928) = 183° | arctg(-1.539864964) = 303° |
| arctg(2.050303842) = 64° | arctg(0.06992681194) = 184° | arctg(-1.482560969) = 304° |
| arctg(2.144506921) = 65° | arctg(0.08748866353) = 185° | arctg(-1.428148007) = 305° |
| arctg(2.246036774) = 66° | arctg(0.1051042353) = 186° | arctg(-1.37638192) = 306° |
| arctg(2.355852366) = 67° | arctg(0.1227845609) = 187° | arctg(-1.327044822) = 307° |
| arctg(2.475086853) = 68° | arctg(0.1405408347) = 188° | arctg(-1.279941632) = 308° |
| arctg(2.605089065) = 69° | arctg(0.1583844403) = 189° | arctg(-1.234897157) = 309° |
| arctg(2.747477419) = 70° | arctg(0.1763269807) = 190° | arctg(-1.191753593) = 310° |
| arctg(2.904210878) = 71° | arctg(0.1943803091) = 191° | arctg(-1.150368407) = 311° |
| arctg(3.077683537) = 72° | arctg(0.2125565617) = 192° | arctg(-1.110612515) = 312° |
| arctg(3.270852618) = 73° | arctg(0.2308681911) = 193° | arctg(-1.07236871) = 313° |
| arctg(3.487414444) = 74° | arctg(0.2493280028) = 194° | arctg(-1.035530314) = 314° |
| arctg(3.732050808) = 75° | arctg(0.2679491924) = 195° | arctg(-1) = 315° |
| arctg(4.010780934) = 76° | arctg(0.2867453858) = 196° | arctg(-0.9656887748) = 316° |
| arctg(4.331475874) = 77° | arctg(0.3057306815) = 197° | arctg(-0.9325150861) = 317° |
| arctg(4.704630109) = 78° | arctg(0.3249196962) = 198° | arctg(-0.9004040443) = 318° |
| arctg(5.144554016) = 79° | arctg(0.3443276133) = 199° | arctg(-0.8692867378) = 319° |
| arctg(5.67128182) = 80° | arctg(0.3639702343) = 200° | arctg(-0.8390996312) = 320° |
| arctg(6.313751515) = 81° | arctg(0.383864035) = 201° | arctg(-0.8097840332) = 321° |
| arctg(7.115369722) = 82° | arctg(0.4040262258) = 202° | arctg(-0.7812856265) = 322° |
| arctg(8.144346428) = 83° | arctg(0.4244748162) = 203° | arctg(-0.7535540501) = 323° |
| arctg(9.514364454) = 84° | arctg(0.4452286853) = 204° | arctg(-0.726542528) = 324° |
| arctg(11.4300523) = 85° | arctg(0.4663076582) = 205° | arctg(-0.7002075382) = 325° |
| arctg(14.30066626) = 86° | arctg(0.4877325886) = 206° | arctg(-0.6745085168) = 326° |
| arctg(19.08113669) = 87° | arctg(0.5095254495) = 207° | arctg(-0.6494075932) = 327° |
| arctg(28.63625328) = 88° | arctg(0.5317094317) = 208° | arctg(-0.6248693519) = 328° |
| arctg(57.28996163) = 89° | arctg(0.5543090515) = 209° | arctg(-0.600860619) = 329° |
| arctg(∞) = 90° | arctg(0.5773502692) = 210° | arctg(-0.5773502692) = 330° |
| arctg(-57.28996163) = 91° | arctg(0.600860619) = 211° | arctg(-0.5543090515) = 331° |
| arctg(-28.63625328) = 92° | arctg(0.6248693519) = 212° | arctg(-0.5317094317) = 332° |
| arctg(-19.08113669) = 93° | arctg(0.6494075932) = 213° | arctg(-0.5095254495) = 333° |
| arctg(-14.30066626) = 94° | arctg(0.6745085168) = 214° | arctg(-0.4877325886) = 334° |
| arctg(-11.4300523) = 95° | arctg(0.7002075382) = 215° | arctg(-0.4663076582) = 335° |
| arctg(-9.514364454) = 96° | arctg(0.726542528) = 216° | arctg(-0.4452286853) = 336° |
| arctg(-8.144346428) = 97° | arctg(0.7535540501) = 217° | arctg(-0.4244748162) = 337° |
| arctg(-7.115369722) = 98° | arctg(0.7812856265) = 218° | arctg(-0.4040262258) = 338° |
| arctg(-6.313751515) = 99° | arctg(0.8097840332) = 219° | arctg(-0.383864035) = 339° |
| arctg(-5.67128182) = 100° | arctg(0.8390996312) = 220° | arctg(-0.3639702343) = 340° |
| arctg(-5.144554016) = 101° | arctg(0.8692867378) = 221° | arctg(-0.3443276133) = 341° |
| arctg(-4.704630109) = 102° | arctg(0.9004040443) = 222° | arctg(-0.3249196962) = 342° |
| arctg(-4.331475874) = 103° | arctg(0.9325150861) = 223° | arctg(-0.3057306815) = 343° |
| arctg(-4.010780934) = 104° | arctg(0.9656887748) = 224° | arctg(-0.2867453858) = 344° |
| arctg(-3.732050808) = 105° | arctg(1) = 225° | arctg(-0.2679491924) = 345° |
| arctg(-3.487414444) = 106° | arctg(1.035530314) = 226° | arctg(-0.2493280028) = 346° |
| arctg(-3.270852618) = 107° | arctg(1.07236871) = 227° | arctg(-0.2308681911) = 347° |
| arctg(-3.077683537) = 108° | arctg(1.110612515) = 228° | arctg(-0.2125565617) = 348° |
| arctg(-2.904210878) = 109° | arctg(1.150368407) = 229° | arctg(-0.1943803091) = 349° |
| arctg(-2.747477419) = 110° | arctg(1.191753593) = 230° | arctg(-0.1763269807) = 350° |
| arctg(-2.605089065) = 111° | arctg(1.234897157) = 231° | arctg(-0.1583844403) = 351° |
| arctg(-2.475086853) = 112° | arctg(1.279941632) = 232° | arctg(-0.1405408347) = 352° |
| arctg(-2.355852366) = 113° | arctg(1.327044822) = 233° | arctg(-0.1227845609) = 353° |
| arctg(-2.246036774) = 114° | arctg(1.37638192) = 234° | arctg(-0.1051042353) = 354° |
| arctg(-2.144506921) = 115° | arctg(1.428148007) = 235° | arctg(-0.08748866353) = 355° |
| arctg(-2.050303842) = 116° | arctg(1.482560969) = 236° | arctg(-0.06992681194) = 356° |
| arctg(-1.962610506) = 117° | arctg(1.539864964) = 237° | arctg(-0.05240777928) = 357° |
| arctg(-1.880726465) = 118° | arctg(1.600334529) = 238° | arctg(-0.03492076949) = 358° |
| arctg(-1.804047755) = 119° | arctg(1.664279482) = 239° | arctg(-0.01745506493) = 359° |
Формулы с обратными тригонометрическими функциями: arcsin, arccos, arctg и arcctg
Ранее мы рассматривали обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс. Как и в случае с другими функциями, между ними существуют связи и зависимости, реализуемые в виде формул, которые можно использовать для решения задач.
Сейчас мы будем рассматривать основные формулы с использованием этих функций: какие они бывают, на какие группы их можно разделить, как их доказать и как решать задачи с их помощью.
Формулы котангенса арккотангенса, тангенса арктангенса, синуса арксинуса и косинуса арккосинуса
Для начала сгруппируем формулы, в которых содержатся основные свойства обратных тригонометрических функций. Мы уже обсуждали и доказывали их ранее, а здесь приведем, чтобы логика объяснения была более понятной и все формулы были в одной статье.
для α∈-1, 1 sin(arccis α)=α, cos(arccos α)=α,для α∈(-∞, ∞) tg(arctg α)=α, ctg(arcctg α)=α
Указанное в них легко сформулировать из самих определений обратных тригонометрических функций числа. Если вы забыли, как найти, например, тангенс арктангенса, все можно посмотреть в этой формуле.
Формулы арккотангенса котангенса, арктангенса тангенса и арксинуса синуса и арккосинуса косинуса
для -π2≤α≤π2 arcsin (sin α)=α,для 0≤α≤π arccos(cos α)=α,для -π2<α<π2 arctg (tg α)=α,для 0<α<π arcctg (ctg α)=α
Здесь все также более-менее очевидно, как и в предыдущем пункте: эти формулы можно вывести из определений арксинуса, арккосинуса и др. Единственное, на что нужно обратить пристальное внимание: они будут верны только в том случае, если a (число или угол) будут входить в указанный предел. В противном случае расчет по формуле будет ошибочен, и применять ее нельзя.
Как соотносятся между собой арксинусы, арккосинусы, арктангенсы и арккотангенсы противоположных чисел
В этом блоке мы сформулируем важное утверждение:
Обратные тригонометрические функции отрицательного числа можно выразить через арксинус, арккосинус, арктангенс и арккотангенс противоположного ему положительного числа.
для α∈-1, 1 arccis (-α)=-arcsin α, arccos (-α)=π-arccos α,для α∈(-∞, ∞) arctg (-α)=-arctg α, arcctg (-α)=π-arcctg α
Таким образом, если в расчетах нам встречаются эти функции для отрицательных чисел, мы можем от них избавиться, преобразовав их в аркфункции положительных чисел, с которыми иметь дело проще.
Формулы суммы: арксинус + арккосинус, арктангенс + арккотангенс
Они выглядят следующим образом:
для α∈-1, 1 arccis α+arccos α=π2,для α∈(-∞, ∞) arctg α+arcctg α=π2
Из написанного видно, что арксинус некоторого числа можно вывести с помощью его арккосинуса, и наоборот. С арктангенсом и арккотангенсом аналогично – они соотносятся между собой аналогичным образом.
Формулы связи между прямыми и обратными тригонометрическими функциями
Знать связи между прямыми функциями и их аркфункциями очень важно для решения многих практических задач. Как же быть, если у нас есть необходимость вычислить, к примеру, тангенс арксинуса? Ниже приведен список основных формул для этого, которые полезно выписать себе.
| -1≤α≤1,sin (arcsin α)=α | -1≤α≤1,sin (arccos α)=1-α2 | -∞≤α≤+∞,sin (arctg α)=α1+α2 | -∞≤α≤+∞, sin (arcctg α)=11+α2 |
| -1≤α≤1,cos (arcsin α)=1-α2 | -1≤α≤1,cos (arccos α)=α | -∞≤α≤+∞,cos (arctg α)=11+α2 | -∞≤α≤+∞, cos (arcctg α)=11+α2 |
| -1<α<1,tg (arcsin α) =α1-α2 | α∈(-1, 0)∪(0, 1),tg (arccos α) =1-α2α | -∞≤α≤+∞,tg (arctg α)=α | α≠0 ,tg (arcctg α)=1α |
| α∈(-1, 0)∪(0, 1),ctg (arcsin α)=1-α2α | -1<α<1,ctg (arccos α)=α1-α2 | α≠0,ctg (arctg α)=1α | -∞≤α≤+∞, ctg (arcctg α)=α |
Теперь разберем примеры, как они применяются в задачах.
Вычислите косинус арктангенса из 5.
Решение
У нас для этого есть подходящая формула следующего вида: cos(arctg α)=11+α2
Подставляем нужное значение: cos(arctg5)=11+(5)2=26
Вычислить синус арккосинуса 12.
Решение
Для этого нам понадобится формула: sin (arccos α)=1-a2
Подставляем в нее значения и получаем: sin (arccos 12)=1-(12)2=32
Обратите внимание, что непосредственные вычисления приводят к аналогичному ответу: sin(arccos 12)=sin π3=32
Если вы забыли, как правильно вычислять значения прямых и обратных функций, вы всегда можете вернуться к нашим предыдущим материалам, где мы разбирали это.
Доказательства формул синусов арккосинуса, арккотангенса и арктангенса
Для того, чтобы наглядно вывести полученные формулы, нам понадобятся основные тригонометрические тождества и собственно формулы основных обратных функций – косинуса арккосинуса и др. Мы их уже выводили ранее, поэтому тратить время на их доказательства не будем. Начнем сразу с формул синусов арккосинуса, арккотангенса и арктангенса. Используя тождество, получим:
sin2α+cos2α=11+ctg2α=1sin2α
Вспомним, что tgα·ctgα=1. Из этого можно получить:
sinα=1-cos2α, 0≤α≤π sinα=tgα1+tg2α, -π2<α<π2sinα=11+ctg2α, 0<α<π
У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.
Теперь в первой формуле вместо a мы добавим arccos a. Итог – формула синуса арккосинуса.
Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.
Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.
Все наши расчеты можно сформулировать более емко:
- sinα=1-cos2α, 0≤α≤π
Следовательно, sin(arccosα)=1-cos2(arccosα)=1-a2
- sinα=tgα1+tgα, -π2<α<π2,
Следовательно, sin(arctgα)=tg(arctgα)1+tg2(arctgα)=α1+α2
- sinα=11+ctg2α, 0<α<π
Следовательно, sin(arctgα)=11+tg2(arctgα)=11+α2
Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.
Их мы выведем по имеющемуся шаблону:
- Из cosα=1-sin2α, -π2≤α≤π2 следует, что
cos(arcsin α)=1-sin2(arcsin α)=1-a2
- Из cosα=11+tg2α, -π2<α<π2 следует, что
- Из cosα=ctgα1+ctg2α, 0<α<πcos(arctgα)=11+tg2(arctgα)=11+α2
следует, что cos(arctgα)=ctg(arcctgα)1+ctg2(arcctgα)=α1+α2
Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса
- Исходим из tgα=sin α1-sin2α, -π2<α<π2. Получаем tg(arcsin α)=sin(arcsinα)1-sin2(arcsinα)=α1-α2 при условии, что -1<α<1.
- Исходим из tgα=1-cos2αcosα, α∈[0, π2)∪(π2, π], получаем
tg(arccosα)=1-cos2(arccosα)cos(arccosα)=1-α2α при условии α∈(-1, 0)∪(0, 1).
- Исходим из tgα=1ctgα, α∈(0, π2)∪(π2, π), получаем tg(arcctgα)=1ctg(arcctgα)=1α при условии, что α≠0.
Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:
ctgα=1tgα
Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса. Для этого понадобится поменять в них местами числитель и знаменатель.
Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее
Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции. Разберем примеры.
Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:
arcsinα=arccos1-α2, 0≤α≤1-arccos1-a2, -1≤α<0arcsinα=arctgα1-α2, -1<α<1arcsinα=arcctg1-α2α, 0<α≤1arcctg1-α2α-π, -1≤α≤0
А так мы выразим арккосинус через остальные обратные функции:
arccosα=arcsin1-α2, 0≤α≤1π-arcsin1-α2, -1≤α<0arccosα=arctg1-α2α, 0<α≤1π+arctg1-α2α, -1<α<0arccosα=arcctgα1-α2, -1<α<1
Формула выражения арктангенса:
arctgα=arcsinα1+α2, -∞<α<+∞arctgα=arccos11+α2, α≥0-arccos11+α2, α<0arctgα=arcctg1α, α≠0
Последняя часть – выражение арккотангенса через другие обратные функции:
arcctgα=arcsin11+α2, α≥0π-arcsin11+α2, α<0arcctgα=arccosα1+α2, -∞<α<+∞arcctgα=arctg1α, α≠0
Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.
Возьмём arcsinα=arctgα1-α2, -1<α<1 и постараемся вывести доказательство.
Мы знаем, что arctgα1-α2 – это число, величина которого составляет от минус половины пи до плюс половины пи. Из формулы синуса арктангенса получим:
sin(arctgα1-α2)=α1-α21+(α1-α2)2=α1-α21+α21-α2=α1-α21+α21-α2=α1-α211-α2=α
Получается, что arctgα1-α2 при условии 1<a<1 – это и есть арксинус числа a.
Вывод: arcsina=arctga1-a2, -1<a<1
Прочие формулы доказываются по аналогии.
В завершение разберем один пример применения формул на практике.
Условие Вычислить синус арккотангенса минус корня из 3.
Решение
Нам понадобится формула выражения арккотангенса через арксинус: arcctgα=arcsin11+a2, α≥0π-arcsin 11+a2, α<0
Подставим в нее α=-3 и получим ответ – 12. Непосредственное вычисление дало бы нам те же результаты: sin(arcctg(-3))=sin5π6=12 Для решения задачи можно взять и другую формулу, выражающую синус через котангенс: sinα=11+ctg2α, 0<α<π
В итоге у нас бы вышло: sin(arcctg(-3))=11+ctg2(arcctg(-3))=11+(-3)2=12
Или возьмем формулу синуса арккотангенса и получим тот же ответ: sin(arcctgα)=11+α2 sin(arcctg(-3))=11+(-3)2=12
Прочие формулы с обратными функциями
Мы рассмотрели самые основные формулы, которые понадобятся вам при решении задач. Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.
Разберем одну из них, называемую формулой половинного угла. Она выглядит следующим образом:
sin2α2=1-cosα2
Если угол альфа при этом больше нуля, но меньше числа пи, то у нас выходит:
sinα2=1-cosα2
Учитывая данное условие, заменяем упомянутый угол на arccos. В итоге наша предварительная формула выглядит так:
sinarccosα2=1-cos(arccosα)2⇔sinarccosα2=1-α2
Отсюда мы выводим итоговую формулу, в которой арксинус выведен через арккосинус:
arccosα2=arcsin1-α2
Мы перечислили не все связи, которые имеются между обратными тригонометрическими функциями, а лишь наиболее употребляемые из них. Важно подчеркнуть, что ценность имеют не столько сами сложные формулы, что мы привели в статье: заучивать их наизусть не нужно. Гораздо важнее уметь самому делать нужные преобразования, и тогда сложные вычисления не потребуется хранить в голове.
В продолжение темы в следующей статье мы рассмотрим преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
- Понятие арктангенса
- График и свойства функции y=arctgx
- Уравнение tgx=a
- Понятие арккотангенса
- График и свойства функции y=arcctgx
- Уравнение ctgx=a
- Формулы преобразований аркфункци
- Примеры
Определение тангенса и котангенса через отношение сторон прямоугольника и с помощью касательной к числовой окружности – см. §3 данного справочника.
Свойства функции y=tgx на всей области определения (xinmathbb{R}) – см. §6 данного справочника.
Свойства функции y=ctgx на всей области определения (xinmathbb{R}) – см. §7 данного справочника.
Определение и свойства взаимно обратных функций – см. §2 справочника для 9 класса.
п.1. Понятие арктангенса
В записи (y=tgx) аргумент x – это значение угла (в градусах или радианах), функция y – тангенс угла, действительное число в пределах от (-infty;) до (+infty). Т.е., по заданному углу мы находим тангенс.
Можно поставить обратную задачу: по заданному тангенсу найти угол. Но одному значению тангенса соответствует бесконечное количество углов. Например, если (tgx=1), то (x=fracpi4+pi k, kinmathbb{Z}); если (tgx=0), то (x=pi k, kinmathbb{Z}) и т.д.
Поэтому, чтобы построить однозначную обратную функцию, ограничим значения углов x главной ветвью тангенса: (-fracpi2leq xleq fracpi2) (правая половина числовой окружности, вся ось тангенсов).
Арктангенсом числа (a (ainmathbb{R})) называется такое число (xin[-fracpi2; fracpi2]), тангенс которого равен (a). $$ arctg a=x Leftrightarrow begin{cases} tgx=a\ -fracpi2leq xleq fracpi2 end{cases} $$
Например:
(arctgfrac{1}{sqrt{3}}=fracpi6, arctg(-sqrt{3})=-frac{pi}{3}, arctg1=fracpi4).
п.2. График и свойства функции y=arctgx

1. Область определения (xinmathbb{R}).
2. Функция ограничена сверху и снизу асимптотами (-fracpi2leq arctgxleq fracpi2).
Область значений (yinleft(-fracpi2; fracpi2right))
3. Функция стремится к максимальному значению (y_{max}=fracpi2 text{при} xrightarrow +infty)
Функция стремится к минимальному значению (y_{min}=-fracpi2 text{при} xrightarrow -infty)
Функция имеет две горизонтальные асимптоты (y=pmfracpi2).
4. Функция возрастает на всей области определения.
5. Функция непрерывна на всей области определения.
6. Функция нечётная: (arctg(-x)=-arctg(x)).
п.3. Уравнение tgx=a
 |
На оси тангенсов каждому углу на числовой окружности в интервале (-fracpi2leq xleq fracpi2) соответствует одно действительное число.
Например: |
 |
2) Решим уравнение (tgx=2) Числу (frac{1}{sqrt{3}}) на оси тангенсов соответствует угол (arctg2) на числовой окружности. Учитывая период тангенса (pi), получаем ответ: (x=arctg2+pi k) |
В общем случае:
Уравнение (tgx=a) имеет решения $$ x=arctga+pi k, kinmathbb{Z}, ainmathbb{R} $$
п.4. Понятие арккотангенса
По аналогии с арктангенсом, арккотангенс определяется на главной ветви котангенса: (0lt xlt pi) (верхняя половина числовой окружности, вся ось котангенсов).
Арккотангенсом числа (a (ainmathbb{R})) называется такое число (xin(0;pi)), котангенс которого равен (a). $$ arcctg a=x Leftrightarrow begin{cases} ctgx=a\ 0lt xlt pi end{cases} $$
Например:
(arcctgfrac{1}{sqrt{3}}=fracpi3, arcctg(-sqrt{3})=-frac{pi}{6}, arcctg1=fracpi4).
п.5. График и свойства функции y=arcctgx

1. Область определения (xinmathbb{R}).
2. Функция ограничена сверху и снизу асимптотами (0lt arcctgxlt pi).
Область значений (yin(0;pi))
3. Функция стремится к максимальному значению (y_{max}=pi text{при} xrightarrow -infty)
Функция стремится к минимальному значению (y_{min}=0 text{при} xrightarrow +infty)
Функция имеет две горизонтальные асимптоты (y=0 text{и} y=pi).
4. Функция убывает на всей области определения.
5. Функция непрерывна на всей области определения.
6. Функция ни чётная, ни нечётная.
п.6. Уравнение ctgx=a

В общем случае:
Уравнение (ctgx=a) имеет решения $$ x=arcctga+pi k, kinmathbb{Z}, ainmathbb{R} $$
Часто уравнение (ctgx=a) преобразуют в уравнение (tgx=frac{1}{a}), и ищут его корни.
Например:
1) (ctgx=sqrt{3})
(x=fracpi6+pi k)
Можно также преобразовать уравнение в (tg x=frac{1}{sqrt{3}})
Получаем тот же ответ: (x=fracpi6+pi k)
2) (ctgx=2)
(x=arcctg2+pi k)
Можно также преобразовать уравнение в (tg x=frac{1}{2})
Получаем ответ: (x=arctgfrac12+pi k)
Очевидно, что (arcctg 2=arctgfrac{1}{2}) (см. ниже формулы для аркфункций).
п.7. Формулы преобразования аркфункций
begin{gather*} arcsin(sinalpha)=alpha, alphainleft[-fracpi2;fracpi2right], arccos(cosalpha)=alpha, alphain[0;pi]\ arctg(tgalpha)=alpha, alphainleft(-fracpi2;fracpi2right), arcctg(ctgalpha)=alpha, alphain(0;pi) end{gather*}
begin{gather*} arcsin(-alpha)=-arcsinalpha, arccos(-alpha)=pi-arccosalpha\ arctg(-alpha)=-arctgalpha, arcctg(-alpha)=pi-arcctgalpha end{gather*}
begin{gather*} arcsinalpha+arccosalpha=fracpi2, arctgalpha+arcctgalpha=fracpi2 end{gather*}
Сводная таблица тригонометрических функций от аркфункций
| arcsin | arccos | arctg | arcctg | |
| sin | begin{gather*} a\ ain[-1;1] end{gather*} | begin{gather*} sqrt{1-a^2}\ ain[-1;1] end{gather*} | begin{gather*} frac{a}{sqrt{1+a^2}}\ ainmathbb{R} end{gather*} | begin{gather*} frac{1}{sqrt{1+a^2}}\ ainmathbb{R} end{gather*} |
| cos | begin{gather*} sqrt{1-a^2}\ ain[-1;1] end{gather*} | begin{gather*} a\ ain[-1;1] end{gather*} | begin{gather*} frac{1}{sqrt{1+a^2}}\ ainmathbb{R} end{gather*} | begin{gather*} frac{a}{sqrt{1+a^2}}\ ainmathbb{R} end{gather*} |
| tg | begin{gather*} frac{a}{sqrt{1-a^2}}\ ain(-1;1) end{gather*} | begin{gather*} frac{sqrt{1-a^2}}{a}\ ain(-1;0)cup(0;1) end{gather*} | begin{gather*} a\ ainmathbb{R} end{gather*} | begin{gather*} frac{1}{a}\ ane 0 end{gather*} |
| ctg | begin{gather*} frac{sqrt{1-a^2}}{a}\ ain(-1;0)cup(0;1) end{gather*} | begin{gather*} frac{a}{sqrt{1-a^2}}\ ain(-1;1) end{gather*} | begin{gather*} frac{1}{a}\ ane 0 end{gather*} | begin{gather*} a\ ainmathbb{R} end{gather*} |
Аркфункции, выраженные через другие аркфункции
| arcsin | |
| arccos | $$ arcsina= begin{cases} arccossqrt{1-a^2}, 0leq aleq 1\ -arccossqrt{1-a^2}, -1leq alt 0 end{cases} $$ |
| arctg | $$ arcsina=arctgfrac{a}{sqrt{1-a^2}}, -1lt alt 1 $$ |
| arcctg | $$ arcsina= begin{cases} arcctgfrac{sqrt{1-a^2}}{a}, 0lt aleq 1\ -arcctgfrac{sqrt{1-a^2}}{a}-pi, -1leq alt 0 end{cases} $$ |
| arccos | |
| arcsin | $$ arccosa= begin{cases} arcsinsqrt{1-a^2}, 0leq aleq 1\ pi-arcsinsqrt{1-a^2}, -1leq alt 0 end{cases} $$ |
| arctg | $$ arccosa= begin{cases} arcctgfrac{sqrt{1-a^2}}{a}, 0lt aleq 1\ pi+arctgfrac{sqrt{1-a^2}}{a}, -1leq alt 0 end{cases} $$ |
| arcctg | $$ arccosa=arcctgfrac{a}{sqrt{1-a^2}}, -1lt alt 1 $$ |
| arctg | |
| arcsin | $$ arctga=arcsinfrac{a}{sqrt{1+a^2}}, ainmathbb{R} $$ |
| arccos | $$ arctga= begin{cases} arccosfrac{1}{sqrt{1+a^2}}, ageq 0\ -arccosfrac{1}{sqrt{1+a^2}}, alt 0 end{cases} $$ |
| arcctg | $$ arctga=arcctgfrac{1}{a}, ane 0 $$ |
| arcctg | |
| arcsin | $$ arcctga= begin{cases} arcsinfrac{1}{sqrt{1+a^2}}, ageq 0\ pi-arcsinfrac{1}{sqrt{1+a^2}}, alt 0 end{cases} $$ |
| arccos | $$ arcctga=arccosfrac{a}{sqrt{1+a^2}}, ainmathbb{R} $$ |
| arctg | $$ arcctga=arctgfrac{1}{a}, ane 0 $$ |
п.8. Примеры
Пример 1. Найдите функцию, обратную арктангенсу. Постройте графики арктангенса и найденной функции в одной системе координат.
Для (y=arctgx) область определения (xinmathbb{R}), область значений (-fracpi2leq yleq fracpi2).
Обратная функция (y=tgx) должна иметь ограниченную область определения (-fracpi2leq xleq fracpi2) (главная ветвь) и область значений (yinmathbb{R}).
Строим графики:
Графики симметричны относительно прямой y=x.
Обратная функция найдена верно.
Пример 2. Решите уравнения:
| a) (tg x=-1) (x=fracpi4+pi k) |
б) (ctgx=-1) (x=frac{3pi}{4}+pi k) Если решать через (tgx=-1) |
| в) (tg x=-5) (x=arctg(-5)+pi k=-arctg5+pi k) |
г) (ctgx=3) (x=arcctg3+pi k) Если решать через (tgx=frac13) |
Пример 3. Вычислите:
a) (2arccosleft(-frac12right)+arctg(-1)+arcsinfrac{sqrt{2}}{2}=2cdotfrac{2pi}{3}-fracpi4+fracpi4=frac{4pi}{3})
б) (arcsin1-arccosfrac{sqrt{3}}{2}-arctg(sqrt{-3})=arcsin1-fracpi3+fracpi3=arcsin1)
в) (arctg4+arcsin0-arccos1=arctg4+0-0=arctg4)
г) (5-2arccos0+arcsinfrac{sqrt{2}}{2}+3arccosfrac{sqrt{2}}{2}=5-2cdotfracpi2+fracpi4+3cdotfracpi4=5)
Пример 4. Постройте графики функций:
(a) y=arccosleft(frac{1}{x}right)+arccosleft(-frac{1}{x}right))
Сумма арккосинусов (arccosa+arccos(-a)=pi), где (-1leq aleq 1).
Получаем систему для определения ОДЗ: begin{gather*} -1leq frac{1}{x}leq 1Rightarrow 0leq frac{1}{x}+1leq 2Rightarrow begin{cases} frac{x+1}{x}geq 0\ frac{x+1}{x}leq 2 end{cases} Rightarrow begin{cases} frac{x+1}{x}geq 0\ frac{-x+1}{x}leq 0 end{cases} Rightarrow begin{cases} frac{x+1}{x}geq 0\ frac{x-1}{x}geq 0 end{cases} Rightarrow\ Rightarrow left[ begin{array}{l l} begin{cases} xgt 0\ x+1geq 0\ x-1geq 0 end{cases} \ begin{cases} xlt 0\ x+1leq 0\ x-1leq 0 end{cases} end{array} right. Rightarrow left[ begin{array}{l l} begin{cases} xgt 0\ xgeq 1 end{cases} \ begin{cases} xlt 0\ xleq -1 end{cases} end{array} right. Rightarrow xleq -1cup xgeq 1 end{gather*} Заметим, что используя модуль, тот же результат можно получить значительно быстрей: $$ -1leqfrac{1}{x}leq 1Leftrightarrow |frac{1}{x}|leq 1Leftrightarrow |x|geq 1 $$ Таким образом, ОДЗ – вся числовая прямая, кроме (xnotin(-1;1).) $$ y=arccosleft(frac{1}{x}right)+arccosleft(-frac{1}{x}right)Leftrightarrow begin{cases} y=pi\ xnotin (-1;1) end{cases} $$ Строим график:
(б) y=arcctg(sqrt{x})+arcctg(-sqrt{x}))
Сумма арккотангенсов (arcctga+arcctg(-a)=pi), где (ainmathbb{R})
ОДЗ ограничено требованием к подкоренному выражению: (xgeq 0)
$$ y=arcctgleft(sqrt{x}right)+arcctgleft(-sqrt{x}right)Leftrightarrow begin{cases} y=pi\ xgeq 0 end{cases} $$ Строим график:
Пример 5*. Запищите в порядке возрастания:
$$ arctgleft(fracpi4right), arcsinleft(fracpi4right), arctg1 $$
 |
Способ 1. С помощью числовой окружности.
Отмечаем точку (fracpi4) на оси синусов (ось OY) и точки (fracpi4) и 1 на оси тангенсов (касательная к окружности). |
| Способ 2. Аналитический Арктангенс – функция возрастающая: (fracpi4approx 0,79lt 1Rightarrow arctgleft(fracpi4right)lt arctg 1) Сравним (arctg1=fracpi4=arcsinleft(frac{sqrt{2}}{2}right)) и (arcsinleft(fracpi4right)) (frac{sqrt{2}}{2} ? fracpi4) – возведем в квадрат обе части (frac12 ? frac{pi^2}{16}Leftrightarrow 8 ? pi^2) (8ltpi^2Rightarrowfrac{sqrt{2}}{2}ltfracpi4 Rightarrow arcsinleft(frac{sqrt{2}}{2}right)lt arcsinleft(fracpi4right)Rightarrow 1lt arcsinleft(fracpi4right)) Получаем: $$ arctgleft(fracpi4right)lt underbrace{arctg1}_{=fracpi4} lt arcsinleft(fracpi4right) $$ |
Пример 6*. Решите уравнения:
a) (arccosx=arctgx)
ОДЗ определяется ограничением для арккосинуса: (-1leq xleq 1)
Арккосинус ограничен (0leq arccosxleq pi), арктангенс (-fracpi2leq arctgxltfracpi2)
Т.к. по условию они равны, ограничение сужается до (0leq arctgxlt fracpi2) и (0leq arccos xlt fracpi2) $$ arccosx=arctgxLeftrightarrow begin{cases} x=cos(arctgx)\ -1leq xleq 1\ 0leq arctgxltfracpi2\ 0leq arccosxltfracpi2 end{cases} Leftrightarrow begin{cases} x=cos(arctgx)\ -1leq xleq 1\ 0leq x\ 0lt xleq 1 end{cases} Leftrightarrow begin{cases} x=cos(arctgx)\ 0lt xlt 1 end{cases} $$ Для решения можно воспользоваться готовой формулой для (cos(arctgx)).
Выведем её. Пуcть (arctgx=varphi). Тогда (x=tgvarphi) и $$ cos(arctgx)=cosvarphi=sqrt{frac{1}{1+tg^2varphi}}=sqrt{frac{1}{1+x^2}} $$ Получаем уравнение: $$ x=sqrt{frac{1}{1+x^2}}Rightarrow x^2=frac{1}{1+x^2}Rightarrow x^2(1+x^2)=1Rightarrow x^4+x^2-1=0 $$ $$ D=1+4=5, x^2=frac{-1pmsqrt{5}}{2} $$ Квадрат числа не может быть отрицательным. Остаётся корень (x^2=frac{sqrt{5}-1}{2})
Откуда (x=pmsqrt{frac{sqrt{5}-1}{2}})
По условию (0lt xlt 1). Получаем (x=sqrt{frac{sqrt{5}-1}{2}})
Ответ: (sqrt{frac{sqrt{5}-1}{2}})
б) (arccos^2x+arcsin^2x=frac{5pi^2}{36})
Используем формулу для суммы: (arccosx+arcsinx=fracpi2)
Получаем: begin{gather*} arccos^2x+left(fracpi2-arccosxright)^2=frac{5pi^2}{36}\ arccos^2x+frac{pi^2}{4}-pi arccosx+arccos^2x=frac{5pi^2}{36}\ 2arccos^2x-pi arccosx+frac{pi^2}{9}=0\ D=(-pi)^2-4cdot 2cdot frac{pi^2}{9}=pi^2-frac89pi^2=frac{pi^2}{9}\ arccosx=frac{pipmfracpi3}{4}Rightarrow left[ begin{array} {l l} arccosx_1=fracpi6\ arccosx_2=fracpi3 end{array} right. Rightarrow left[ begin{array} {l l} x_1=cosfracpi6=frac{sqrt{3}}{2}\ x_2=cosfracpi3=frac12 end{array} right. end{gather*} Ответ: (left{frac12; frac{sqrt{3}}{2}right})
в) (arcsinfrac{sqrt{3x+2}}{2}=arcctgsqrt{frac{2}{x+1}})
ОДЗ определяется ограничением для арксинуса: ( -1leq frac{sqrt{3x+2}}{2}leq 1)
Арксинус ограничен (-fracpi2leq arcsinfrac{sqrt{3x+2}}{2}leqfracpi2), арккотангенс (0leq arcctgsqrt{frac{2}{x+1}}ltpi)
Т.к. по условию они равны, ограничение сужается до (0leq arcctgsqrt{frac{2}{x+1}}ltfracpi2) и (0leq arcsinfrac{sqrt{3x+2}}{2}ltfracpi2). begin{gather*} arcsinfrac{sqrt{3x+2}}{2}=arcctgsqrt{frac{2}{x+1}}Leftrightarrow begin{cases} frac{sqrt{3x+2}}{2}=sinleft(arcctgsqrt{frac{2}{x+1}}right)\ -1leqfrac{sqrt{3x+2}}{2}leq 1\ 0leq arcsinfrac{sqrt{3x+2}}{2}ltfracpi2\ 0leq arcctgsqrt{frac{2}{x+1}}ltfracpi2 end{cases} Leftrightarrow\ Leftrightarrow begin{cases} frac{sqrt{3x+2}}{2}=sinleft(arcctgsqrt{frac{2}{x+1}}right)\ -1leqfrac{sqrt{3x+2}}{2}leq 1\ 0leq frac{sqrt{3x+2}}{2}lt 1\ 0leq sqrt{frac{2}{x+1}} end{cases} Leftrightarrow begin{cases} frac{sqrt{3x+2}}{2}=sinleft(arcctgsqrt{frac{2}{x+1}}right)\ 0leq frac{sqrt{3x+2}}{4}lt 1\ frac{4}{x+1}geq 0 end{cases} end{gather*} Для ОДЗ получаем: $$ begin{cases} 0leq 3x+2lt 4\ x+1gt 0 end{cases} Rightarrow begin{cases} -2leq 3x lt 2\ xgt -1 end{cases} Rightarrow begin{cases} -frac23leq x lt frac23\ xgt -1 end{cases} Rightarrow -frac23leq xltfrac23 $$ ОДЗ: (-frac23leq xlt frac23)
Выведем формулу для синуса арккотангенса.
Пусть (arcctgx=varphi Rightarrow x=ctgvarphi)
Тогда (sin(arcctgx)=sinvarphi=sqrt{frac{1}{1+ctg^2varphi}}=sqrt{frac{1}{1+x^2}})
Правая часть уравнения: $$ sinleft(arcctgsqrt{frac{2}{x+1}}right)= sqrt{frac{1}{1+left(sqrt{frac{2}{x+1}}right)}}= sqrt{frac{1}{1+frac{2}{x+1}}}=sqrt{frac{x+1}{x+3}} $$ Подставляем: begin{gather*} frac{sqrt{3x+2}}{2}=sqrt{frac{x+1}{x+3}}Rightarrow frac{3x+2}{4}=frac{x+1}{x+3}Rightarrow (3x+2)(x+3)=4(x+1)Rightarrow\ Rightarrow 3x^2+11x+6=4x+4Rightarrow 3x^2+7x+2=0\ D=49-4cdot 3cdot 2=25\ x=frac{-7pm5}{6}Rightarrow left[ begin{array} {l l} x_1=-2 – text{ не подходит по ОДЗ}\ x_2=-frac13 end{array} right. end{gather*} Ответ: (-frac13)
- Определение
- График арктангенса
- Свойства арктангенса
- Таблица арктангенсов
Определение
Арктангенс (arctg или arctan) – это обратная тригонометрическая функция.
Арктангенс x определяется как функция, обратная к тангенсу x, где x – любое число (x∈ℝ).
Если тангенс угла у равен х (tg y = x), значит арктангенс x равняется y:
arctg x = tg-1 x = y, причем -π/2<y<π/2
Примечание: tg-1x означает обратный тангенс, а не тангенс в степени -1.
Например:
arctg 1 = tg-1 1 = 45° = π/4 рад
График арктангенса
Функция арктангенса пишется как y = arctg (x). График в общем виде выглядит следующим образом:

Свойства арктангенса
Ниже в табличном виде представлены основные свойства арктангенса с формулами.
Таблица арктангенсов
| arctg x (°) | arctg x (рад) | x |
| -90° | -π/2 | -∞ |
| -71.565° | -1.2490 | -3 |
| -63.435° | -1.1071 | -2 |
| -60° | -π/3 | -√3 |
| -45° | -π/4 | -1 |
| -30° | -π/6 | -1/√3 |
| -26.565° | -0.4636 | -0.5 |
| 0° | 0 | 0 |
| 26.565° | 0.4636 | 0.5 |
| 30° | π/6 | 1/√3 |
| 45° | π/4 | 1 |
| 60° | π/3 | √3 |
| 63.435° | 1.1071 | 2 |
| 71.565° | 1.2490 | 3 |
| 90° | π/2 | ∞ |
microexcel.ru
Чётность и возрастание
Чтобы получить график арктангенса, используется кривая тангенса путём замены местами осей ординат и абсцисс. Для устранения многозначности используется интервал, на котором функция монотонна. Это определение считается основным значением арктангенса. Если показатель отрицательный, значит функция нечётная.
Главное свойство arctg — бесконечность на его области определения (для числа х). Так как y = arctg x, где y равен нулю, тогда x = 0, значит и arctg 0. При выполнении расчётов используется таблица арктангенсов.
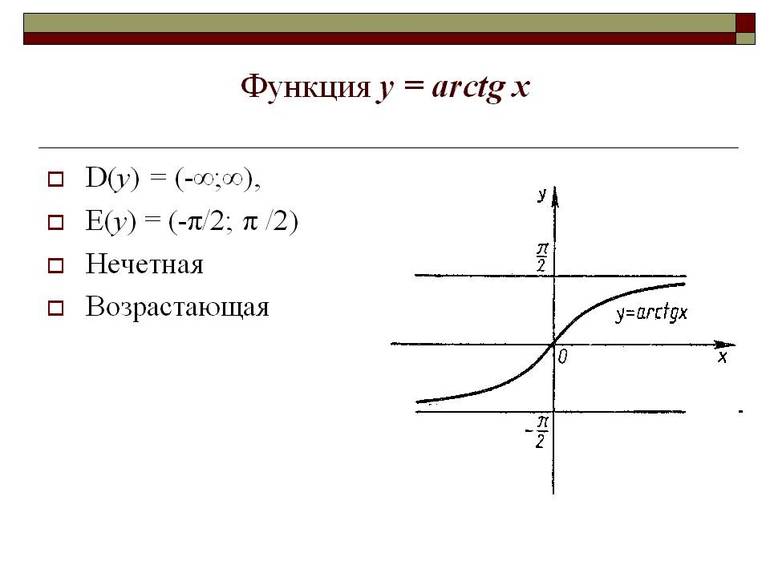
В ней указаны значения в градусах и радианах, при определённых данных аргумента. Если вычисления выполняются на математическом веб-ресурсе, пользователю предоставляется возможность бесплатно использовать онлайн-калькулятор и таблицу Брадиса. Можно вычислить синус, косинус, производную арктангенса в экселе либо с помощью языка программирования Паскаль.
Чтобы посчитать величину правильно, используются свойства функций. При помощи определения арксинуса выполняется уравнение sin (arcsin a)=a. Свойства других величин:
- косинус: cos (arccos a)=a;
- тангенс: tg (arctg a)=a;
- катангенс: ctg (arcctg a)=a.
В первых двух свойствах соблюдается условие −1≤a≤1. Если значение а выходит за указанные пределы, тогда функции нет смысла определять. Учитывая свойства синуса арксинуса, нельзя записать sin (arcsin8)=8, так как выражение sin (arcsin8) не имеет смысла. Аналогичный ответ получается, если необходимо определить разность арккосинуса sqrt (квадратный корень) из пяти.
Противоположные числа
Формулы, с помощью которых производится расчёт связи между производными: arcsin (-a)=-arcsina, arccos (-a)=пи-arccosa, arctg (-a)=-arctga, arcctg (-a)=пи-arcctga. Должно соблюдаться условие −1≤a≤1. Если а принадлежит промежутку −∞ до +∞, тогда arctg (−a), и arcctg (−a).
Чтобы доказать первое отношение с противоположными числами, рассматривается определение arcsin (−a). Число либо угол находится в пределах −π/2-π/2 и синус, равный −a. Учитывая определение арксинуса, можно записать следующее равенство: −π/2≤arcsin a≤π/2.
На основе свойств неравенств, выполняется умножение составных частей на -а. Заменив знаки неравенств на противоположные, можно произвести умножение на -1: −π/2≤−arcsin a≤π/2.
Необходимо доказать, что sin (−arcsin a)=−a. Для этого рекомендуется придерживаться свойств противоположных углов. Из рассмотренных примеров можно сделать вывод: sin (−arcsin a)=−sin (arcsin a)=−a.
Аналогичным способом можно доказать, что arccos (−a)=π−arccos a. Используя определение производной функции, подтверждается, что π−arccos a — угол либо число, значение которого колеблется в пределах 0-π, а cos (π−arccos a)=−a. Придерживаясь определения арккосинуса числа, выполняется неравенство 0≤arccos a≤π.
Используя свойства неравенств, перемножаются поочерёдно его части на -1, сменяются знаки. Решается неравенство из сумм частей и числа пи, при этом сохраняются знаки: −π+π≤−arccosa+π≤0+π. Получается двойное выражение вида 0≤π−arccos a≤π.
Если средняя часть уравнения равняется −a, тогда, придерживаясь формулы приведения, записывается следующее равенство cos (π−arccos a)=−cos (arcos a). С помощью свойства производной косинуса завершается доказательство cos (π−arccos a)=−cos (arcos a)=−a. Аналогичной схемы рекомендуется придерживаться при рассмотрении свойств арккотангенсов и арктангенсов противоположных знаков. Плюс утверждения — возможность избавиться от вычисления производных функций отрицательных чисел.
Сложение величин
Свойство, согласно которому устанавливается связь между arccos arcsin числа а, и между arctg и arcctg переменной, записывается следующим образом: arcsina+arccosa=пи/2, arctga+arcctga=пи/2. Чтобы доказать первую часть равенства, где расписана сумма производных синуса и косинуса числа а, делённая на два, необходимо рассмотреть следующую запись: arcsin a=π/2−arccos a.
Основываясь на определение арксинуса, можно доказать, что выражение верно, когда π/2−arccos a — угол (цифровое значение), лежащий на промежутке −π/2 до π/2, а синус угла равен а. Чтобы показать такую действительность, используется определение арккосинуса и равенство 0≤arccos a≤π. Последнее выражение считается справедливым.

С учётом свойств неравенств, умножаются части на минус один, изменяются знаки. Полученные значения суммируются с числом π/2. Выполнив перечисленные действия, получается неравенство −π/2≤π/2−arccosa≤π/2. Чтобы показать, что sin (π/2−arccos a)=a, используется формула приведения, свойство производной функции косинус.
Доказано, что сумма arccos и arccos a равна π/2. Аналогично понадобится доказать, что сумма арккотангенса числа a и арктангенса равняется π/2. Главное предназначение таких свойств заключается в том, что они выражают арксинус через акрккосинус одного числа, а также арккотангенс через арктангенс и наоборот.
Примеры и задачи
Задания на свойства функций и их производных от числа либо угла можно решить с помощью разных программ: excel, pascal. Действия будут зависеть от условий задачи. Решение должно основываться на основные признаки, доказанные либо утверждённые равенства. Свойствам производных отвечают следующие выражения:
- arcsin (sinx)=x;
- arccos (cosx)=x;
- arctg (tgx)=x;
- arcctg (ctgx)=x.
Равенства при определённых условий следуют из определений функций числа. Чтобы понять утверждения, необходимо доказать: arcsin (sin α)=α, при этом должно выполняться требование −π/2≤α≤π/2. Аналогичным образом доказываются оставшиеся свойства. Если обозначить sin α=а, которое находится на отрезке [−1, 1], тогда получится выражение arcsin (sin α)=α, то есть arcsin a=α. Известно из условий задач, что −π/2≤α≤π/2. При решении через а обозначили sin α.
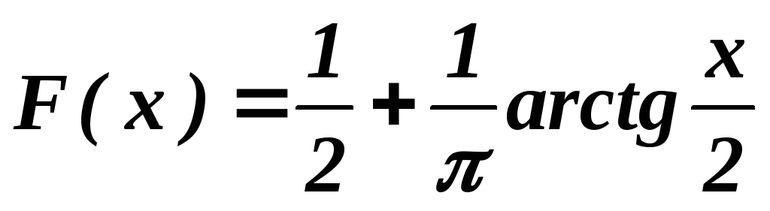
Поэтому можно записать, что arcsin a=α, что эквивалентно определению производной функции синуса. Вывод: arcsin (sin α)=α при условии, что −π/2≤α≤π/2. Разные свойства, связанные с синусом и косинусом, тангенсом и котангенсом, можно применить на практике.
Известно, аrcsin sin (-15)= -15 град., arccos (cos (2π/3))=2π/3, arctg (tg (0,2))=0,2. Нужно отметить, что выражение arcsin (sin α) справедливо на отрезке −π/2≤α≤π/2. Но равенство arcsin (sin α)=α имеет смысл только при соблюдении этого условия. Нельзя утверждать, что arcsin (sin (7π/4))=7π/4, так как 7π/4 не принадлежит указанному интервалу (−π/2-π/2).
Запись arccos (cos α) правдивая, не только при условии, что 0≤α≤π. Выражение arccos (cos α)=α считается справедливым только при таком условии. Поэтому arccos (cos (−3π))=−3π не верно, так как −3π не принадлежит указанному отрезку. Схожие утверждения логичны и для arcctg (ctg α), arctg (tg α).
Используя определение всех функций, их признаки, тригонометрические формула можно получить другие равенства и уравнения, в которых отображается связь между arcsin, arcctg, arctg и arccos. Чтобы быстро решать задачи на данную тематику, рекомендуется выучить некоторые утверждённые равенства (arcsin 0=0, arccos 1=0, как угол arccos (-1)=180 градусов). Они описаны в специальных таблицах, которые можно найти в глобальной сети либо в учебниках по математике.
