Как найти асимптотическую формулу

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 марта 2020 года; проверки требуют 3 правки.

Эта статья — о поведении функций при стремлении их аргументов к некоторым предельным значениям. Об асимптотах в геометрии см. Асимптота.

Асимптотический анализ — метод описания предельного поведения функций.

Например, в функции при стремлении к бесконечности слагаемое становится пренебрежимо малым по сравнению с , поэтому про функцию говорят, что она «асимптотически эквивалентна при », что зачастую также записывают как . Примером важного асимптотического результата является теорема о распределении простых чисел. Пусть обозначает функцию распределения простых чисел, то есть, равна количеству простых чисел, которые меньше либо равны , тогда теорема может быть сформулирована как .

Асимптотическое равенство[править | править код]

Пусть и  — некоторые функции. Тогда бинарное отношение определяется таким образом, что

если и только если^[1]

Функции и при этом называются асимптотически эквивалентными, так как является отношением эквивалентности для функций над . Областью определения и при этом может быть любое множество, в котором имеет смысл понятие предела: вещественные числа, комплексные числа, натуральные и т. д. Те же обозначения также используются для других предельных ограничений на , таких как . Конкретный предел обычно не указывают если он понятен из контекста.

Определение выше распространено в литературе, однако оно теряет смысл если принимает значение бесконечное число раз. Поэтому некоторые авторы используют альтернативное определение в терминах O-нотации:

Данное определение эквивалентно приведённому выше если отлично от нуля в некоторой окрестности предельной точки^[2][3].

Свойства[править | править код]

Если и , то при некоторых естественных ограничениях верно следующее:

Указанные свойства позволяют свободно менять асимптотически эквивалентные функции друг на друга в некоторых алгебраических выражениях.

Примеры асимптотических формул[править | править код]

• Формула Стирлинга для факториалов

• Количество способов разбить натуральное число в неупорядоченную сумму натуральных чисел

• Функции Ганкеля

Асимптотическое разложение[править | править код]

Асимптотическим разложением функции называют выражение функции в виде ряда, чьи частичные суммы могут не сходиться, но при этом любая частичная сумма даёт правильную асимптотическую оценку . Таким образом, каждый следующий элемент асимптотического разложения даёт чуть более точное описание порядка роста . Другими словами, если  — асимптотическое разложение , то и, в общем случае, для любого . В соответствии с определением это значит, что , то есть, растёт асимптотически значительно медленнее

Если асимптотическое разложение не сходится, то для любого аргумента найдётся некоторая частичная сумма, которая наилучшим образом приближает функцию в этой точке, а дальнейшее добавление слагаемых к ней будет лишь уменьшать точность. Как правило, число слагаемых в такой оптимальной сумме будет увеличиваться с приближением к предельной точке.

Примеры асимптотических разложений[править | править код]

• Гамма-функция

• Интегральная экспонента

• Функция ошибок

где (2n − 1)!! — двойной факториал.

Применения[править | править код]

Асимптотический анализ используется:

• В прикладной математике для построения численных методов решения уравнений.
• В математической статистике и теории вероятностей для определения предельных свойств случайных величин и статистических оценок.
• В информатике при анализе алгоритмов и их времени работы.
• В статистической физике при анализе поведения физических систем.
• В анализе катастроф при определении причин катастрофы моделированием множества катастроф в том же месте.

Асимптотический анализ является ключевым инструментом изучения дифференциальных уравнений, возникающих в математическом моделировании явлений реального мира^[4]. Как правило, применение асимптотического анализа направлено на исследование зависимости модели от некоторого безразмерного параметра, который предполагается пренебрежимо малым в масштабах решаемой задачи.

Асимптотические разложения, как правило, возникают при приближенных вычислениях некоторых интегралов (метод Лапласа, метод перевала) или распределений вероятности (ряд Эджворта). Примером расходящегося асимптотического разложения являются графы Фейнмана в квантовой теории поля.

См. также[править | править код]

• Асимптота
• Асимптотическая плотность (в теории чисел)
• «O» большое и «o» малое
• Асимптотически достоверное событие

Примечания[править | править код]

Литература[править | править код]

• Федорюк М. В. Асимптотика: Интегралы и ряды. — М.: Наука, 1987. — 544 с. — (Справочная математическая библиотека).
• Олвер, Ф. Введение в асимптотические методы и специальные функции. — М.: Наука, 1978. — 386 с.
• Balser, W. (1994), From Divergent Power Series To Analytic Functions, Springer-Verlag, <https://books.google.com/books?id=V-17CwAAQBAJ&printsec=frontcover#v=onepage&q&f=false>
• de Bruijn, N. G. (1981), Asymptotic Methods in Analysis, Dover Publications, <https://books.google.com/books?id=Oqj9AgAAQBAJ&printsec=frontcover>
• Estrada, R. & Kanwal, R. P. (2002), A Distributional Approach to Asymptotics, Birkhäuser, <https://books.google.com/books?id=X3cECAAAQBAJ&printsec=frontcover#v=onepage&q&f=false>
• Miller, P. D. (2006), Applied Asymptotic Analysis, American Mathematical Society, <https://books.google.com/books?id=KQvqBwAAQBAJ&printsec=frontcover#v=onepage&q&f=false>
• Murray, J. D. (1984), Asymptotic Analysis, Springer, <https://books.google.com/books?id=PC3rBwAAQBAJ&printsec=frontcover#v=onepage&q&f=false>
• Paris, R. B. & Kaminsky, D. (2001), Asymptotics and Mellin-Barnes Integrals, Cambridge University Press, <https://www.researchgate.net/profile/Richard_Paris/publication/39064661_Asymptotics_and_Mellin-Barnes_Integrals/links/00b495295c15197336000000/Asymptotics-and-Mellin-Barnes-Integrals.pdf>

Ссылки[править | править код]

• Asymptotic Analysis  — home page of the journal, which is published by IOS Press
• A paper on time series analysis using asymptotic distribution

СЕМИНАР 16

Вычисление пределов функций с помощью
замечательных пределов, получение
асимптотических формул и применение
их к вычислению пределов, непрерывность
функции, классификация точек разрыва.

Вводная информация

Замечательные
пределы.

Замечательными
пределами являются:

первый
замечательный предел

и второй
замечательный предел

.

Асимптотические
формулы.

Теорема. Если
,
то
,
где
,
т.е. функция

является бесконечно малой функцией при
.
Верно и обратное утверждение: если
,
где

– бесконечно малая функция при
,
то
.

Рассмотрим первый
замечательный предел
.
Тогда
,
при этом
.
Используя полученную формулу, представим
функцию

в виде
.
Так как

(действительно
),
перепишем найденную формулу в виде
.

Подобные формулы,
которые называют асимптотическими
формулами

(или асимптотическими
разложениями,
или асимптотическими
представлениями функций),
можно получить для многих функций. Для
простейших элементарных функций
справедливы оценки:

1)
;

2)
;

3)
,

;

4)
;

5)
;

6)
;

7)
;
8)
;

9)
;

10)
;

11)
.

Эти формулы удобно
использовать при нахождении пределов
функций вида
.

Непрерывность
функции.

Определение.
Функция

называется непрерывной
в точке
,
если
.

Приведем эквивалентное
определение. Функция

называется непрерывной
в точке
,
если: 1) она определена в точке
;
2)

такое, что при
.

Определение.
Точка
,
в которой функция

не является непрерывной, называется
точкой
разрыва этой
функции.

Определение.
Точка

называется точкой
разрыва первого рода функции
,
если существуют конечные односторонние
пределы

и

и выполняются условия: 1)

или 2)
.

Разность

называется скачком
функции

в точке
.
Точка разрыва первого рода, удовлетворяющая
условию 2), называется точкой устранимого
разрыва
(разрыв устраняется переопределением
значения функции в этой точке
).

Определение.
Точку

называют точкой
разрыва второго рода,
если в этой точке имеется разрыв функции,
не являющийся разрывом первого рода.

ЗАДАЧИ

1. Задачи
удовлетворительного уровня сложности.

Вычислить пределы,
используя первый замечательный предел.

16.1
.
16.2.
.
16.3.
.
16.4.
.

16.5.
.
16.6.
.
16.7.
.
16.8.
.

16.9.
.
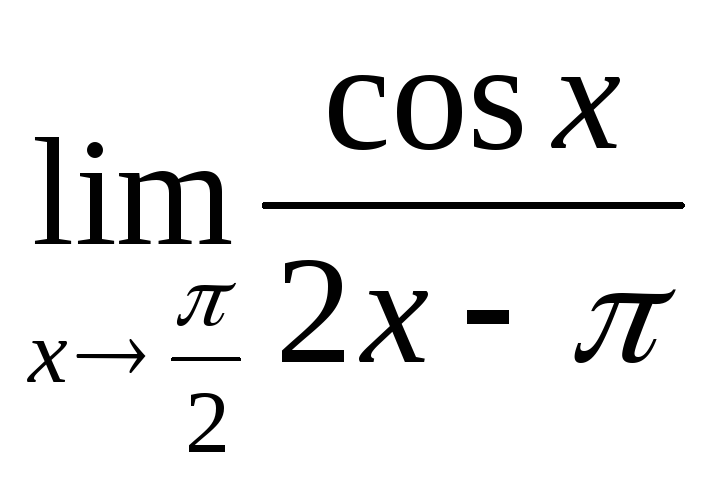16.10.
.
16.11.
.
16.12.
.

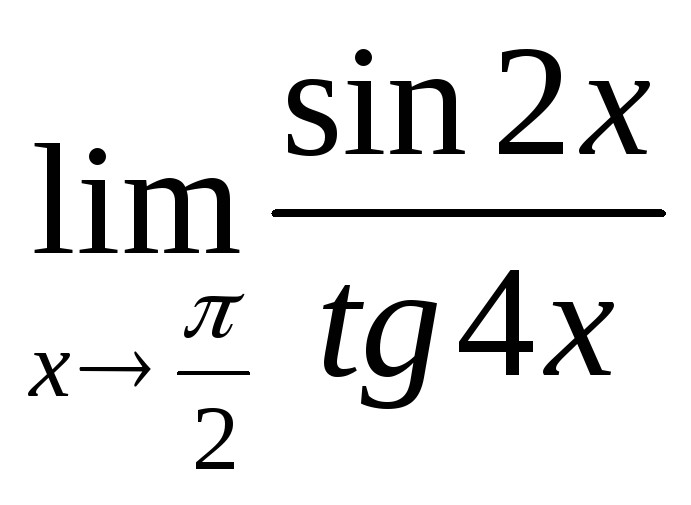16.13.
.
16.14.
.
16.15.
.

16.16.
.
16.17.
.
16.18.
.

2. Вычислить
пределы, используя второй замечательный
предел.

16.19.
.
16.20.
.
16.21.
.

16.22.
.
16.23.
.
16.24.
.

16.25.
.
16.26.
.
16.27.
.

16.28. Вычислить
предел

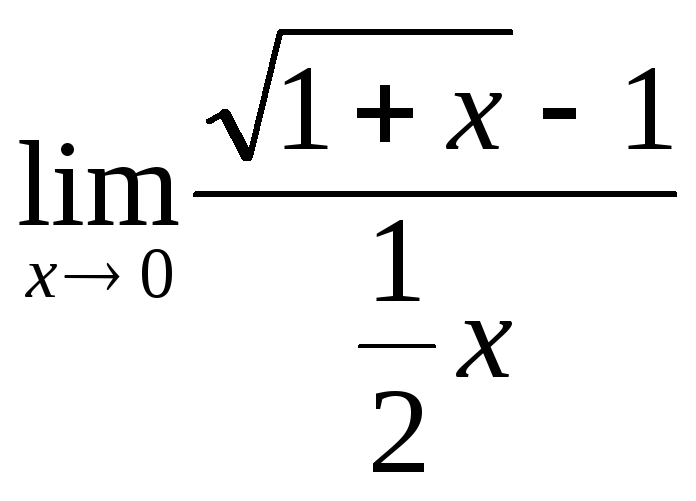
и, используя результат вычисления, найти
асимптотическую формулу для функции
.

16.29. Вычислить
предел

и, используя результат вычисления,
найти асимптотическую формулу для
функции
.

16.30. Вычислить
предел

и, используя результат вычисления, найти
асимптотическую формулу для функции
.

16.31. Вычислить
предел

и, используя результат вычисления, найти
асимптотическую формулу для функции
.

16.32. Вычислить
предел

и, используя результат вычисления, найти
асимптотическую формулу для функции
.

Используя
асимптотические формулы вычислить
пределы.

16.33.
.
16.34.
.
16.35.
.

16.36.
.
16.37.
.
16.38.
.

16.39.
.
16.40.
.
16.41.
.

16.42.
.
16.43.
.
16.44.
.

16.45.
.
16.46.
.
16.47.

Исследовать на
непрерывность функции. Определить род
точек разрыва при их наличии.

16.48.
.
16.49.
.
16.50.
.

16.51.
.
16.52.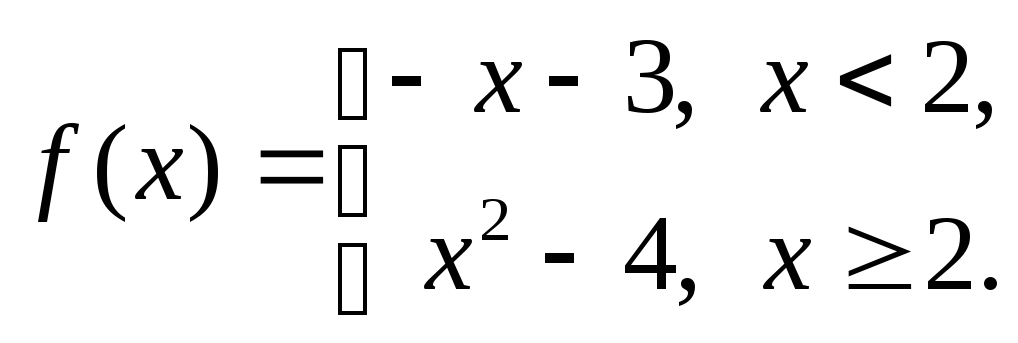

16.53.

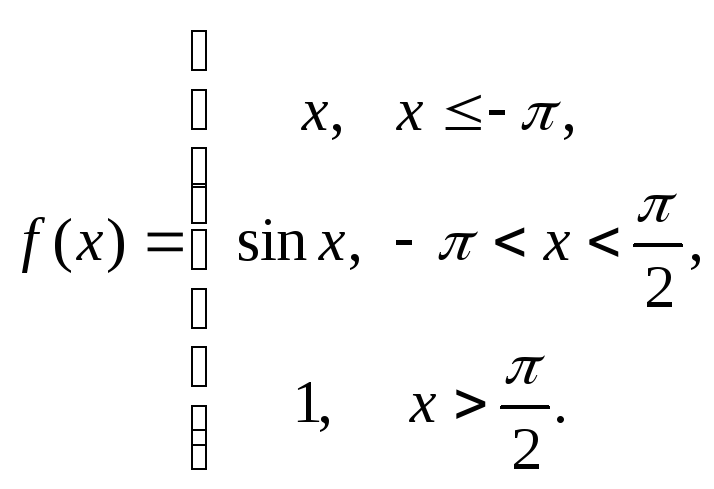
16.54.

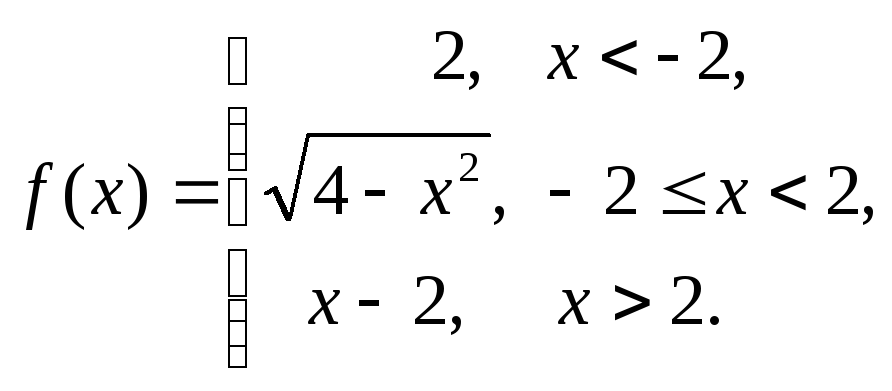
16.55.

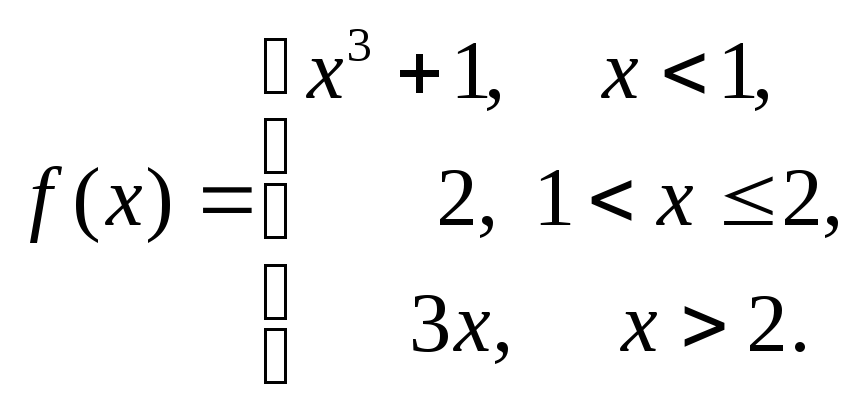
16.56.
.
16.57.
.

16.58.
.
16.59.
.
16.60.

2. Задачи повышенного
уровня сложности.

Вычислить пределы,
используя первый замечательный предел.

16.61..
16.62.
.
16.63.
.

16.64.
.
16.65.
.
16.66.
.

Вычислить пределы,
используя второй замечательный предел.

16.67.
.
16.68.
.
16.69.
.

16.70.
.
16.71.
.

16.72. Вычислить
предел

и, используя результат вычисления, найти
асимптотическую формулу для функции
.

16.73. Вычислить
предел

и, используя результат вычисления, найти
асимптотическую формулу для функции
.

16.74. Вычислить
предел

и, используя результат вычисления, найти
асимптотическую формулу для функции
.

Используя
асимптотические формулы вычислить
пределы.

16.75.
.
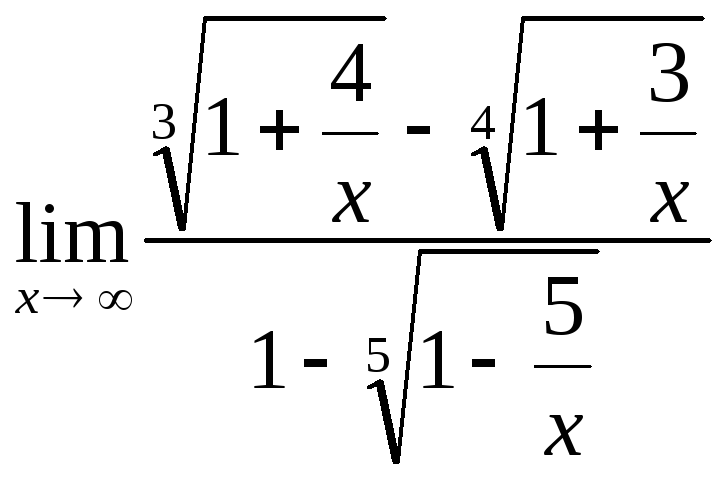16.76.
.

16.77.
.
16.78.
.
6.79.
.
16.80.
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Описание предельного поведения функции

В математическом анализе, асимптотика Анализ, также известный как асимптотика, представляет собой метод описания ограничивающего поведения.

В качестве иллюстрации предположим, что нас интересуют свойства функции f (n), когда n становится очень большим. Если f (n) = n + 3n, то, когда n становится очень большим, член 3n становится незначимым по сравнению с n. Функция f (n) называется «асимптотически эквивалентной n при n → ∞». Это часто символически записывается как f (n) ~ n, что читается как «f (n) асимптотичен n».

Примером важного асимптотического результата является теорема о простых числах. Пусть π (x) обозначает функцию подсчета простых чисел (которая не имеет прямого отношения к константе pi ), то есть π (x) – это количество простых чисел, которые меньше или равны x. Тогда теорема утверждает, что

π (x) ∼ x ln ⁡ x. { displaystyle pi (x) sim { frac {x} { ln x}}.}

Содержание

• 1 Определение
• 2 Свойства
• 3 Примеры асимптотических формул
• 4 Конструкция
  • 4.1 Общие положения
  • 4.2 Асимптотика двух различных многочленов
• 5 Асимптотическое разложение
  • 5.1 Примеры асимптотических разложений
  • 5.2 Рабочий пример
• 6 Асимптотическое распределение
• 7 Приложения
• 8 См. Также
• 9 Примечания
• 10 Ссылки
• 11 Внешние ссылки

Определение

Формально, учитывая функции f (x) и g (x), мы определяем бинарное отношение

е (x) ∼ g (x) (как x → ∞) { displaystyle f (x) sim g (x) quad ({ text {as}} x to infty)}

если и только если (де Брюйн 1981, §1.4)

lim x → ∞ f (x) g (x) = 1. { displaystyle lim _ {x to infty} { frac {f (x)} {g (x)}} = 1.}

Символ ~ – это тильда. Отношение является отношением эквивалентности на множестве функций от x; функции f и g называются асимптотически эквивалентными. домен для f и g может быть любым набором, для которого определен предел: например, действительные числа, комплексные числа, положительные целые числа.

То же обозначение используется и для других способов перехода к пределу: например, x → 0, x ↓ 0, | x | → 0. Способ предельного перехода часто явно не указывается, если это понятно из контекста.

Хотя приведенное выше определение широко используется в литературе, это проблематично, если g (x) бесконечно часто равен нулю, когда x стремится к предельному значению. По этой причине некоторые авторы используют альтернативное определение. Альтернативное определение в небольшой нотации состоит в том, что f ~ g тогда и только тогда, когда

f (x) = g (x) (1 + o (x)). { displaystyle f (x) = g (x) (1 + o (x)).}

Это определение эквивалентно предыдущему определению, если g (x) не равно нулю в некоторой окрестности предельного значения.

Свойства

Если f ∼ g { displaystyle f sim g}и a ∼ b { displaystyle a sim b}, то при некоторых мягких условиях выполняется следующее.

Такие свойства позволяют свободно обмениваться асимптотически эквивалентными функциями во многих алгебраических выражениях.

Примеры асимптотических формул

n! ∼ 2 π N (ne) n { displaystyle n! Sim { sqrt {2 pi n}} left ({ frac {n} {e}} right) ^ {n}}

– это приближение Стирлинга

Для положительного целого числа n функция распределения p (n) дает количество способов записать целое число n как сумму положительных целых чисел, где порядок дополнений не рассматривается.

п (п) ∼ 1 4 N 3 е π 2 N 3 { Displaystyle р (п) sim { frac {1} {4n { sqrt {3}}}} e ^ { pi { sqrt { frac {2n} {3}}}}}

Функция Эйри, Ai (x), является решением дифференциального уравнения y ” – xy = 0; он имеет множество приложений в физике.

Ai ⁡ (x) ∼ e – 2 3 x 3 2 2 π x 1/4 { displaystyle operatorname {Ai} (x) sim { frac {e ^ {- { frac {2} { 3}} x ^ { frac {3} {2}}}} {2 { sqrt { pi}} x ^ {1/4}}}}

H α (1) (z) ∼ 2 π zei (z – 2 π α – π 4) H α (2) (z) ∼ 2 π ze – i (z – 2 π α – π 4) { displaystyle { begin {align} H _ { alpha} ^ {(1)} (z) sim { sqrt { frac {2} { pi z}}} e ^ {i left (z – { frac {2 pi альфа – pi} {4}} right)} \ H _ { alpha} ^ {(2)} (z) sim { sqrt { frac {2} { pi z}}} e ^ {-i left (z – { frac {2 pi alpha – pi} {4}} right)} end {align}}}

Строительство

Общие

Рассмотрим:

час (x) = f (x) (1 – F (x)) + g (x) F (x) { displaystyle h (x) = f (x) (1-F (x)) + g (x) F (x)}

где f (x) { displaystyle f (x)}и g (x) { displaystyle g (x)}– вещественные аналитические функции, а F (x) { displaystyle F (x)}– Кумулятивная функция распределения.

Тогда h (x) { displaystyle h (x)}асимптотичен f ( x) { displaystyle f (x)}as x → (- ∞) { displaystyle x to (- infty)}и асимптотика до g (x) { displaystyle g (x)}as x → (+ ∞) { displaystyle x to (+ infty)}.

Асимптотика двух разных многочленов

Предположим, нам нужна функция с действительным знаком, которая асимптотична (a 0 + a 1 x) { displaystyle (a_ {0} + a_ {1} x)}как x → (- ∞) { displaystyle x to (- infty)}и асимптотичен (b 0 + b 1 x) { displaystyle (b_ {0}) + b_ {1} x)}как x → (+ ∞) { displaystyle x to (+ infty)}. Тогда

час (x) = (a 0 + a 1 x) (1 – F (x)) + (b 0 + b 1 x) F (x) { displaystyle h (x) = (a_ {0 } + a_ {1} x) (1-F (x)) + (b_ {0} + b_ {1} x) F (x)}

сделает это.

Асимптотическое разложение

Асимптотическое разложение функции f (x) на практике является выражением этой функции в терминах серии , частичные суммы из которых не обязательно сходятся, но такие, что взятие любой начальной частичной суммы дает асимптотическую формулу для f. Идея состоит в том, что последовательные члены обеспечивают все более точное описание порядка роста f.

В символах это означает, что мы имеем f ∼ g 1, { displaystyle f sim g_ {1},}, но также f – g 1 ∼ g 2 { displaystyle f-g_ {1} sim g_ {2}}и f – g 1 – ⋯ – gk – 1 ∼ gk { displaystyle f-g_ {1} – cdots -g_ {k-1} sim g_ {k}}для каждого фиксированного k. С учетом определения символа ∼ { displaystyle sim}последнее уравнение означает f – (g 1 + ⋯ + gk) = o (gk) { displaystyle f- (g_ {1} + cdots + g_ {k}) = o (g_ {k})}в маленькой нотации o, т. е. f – (г 1 + ⋯ + gk) { displaystyle f- (g_ {1} + cdots + g_ {k})}намного меньше, чем gk. { displaystyle g_ {k}.}

Отношение f – g 1 – ⋯ – gk – 1 ∼ gk { displaystyle f-g_ {1} – cdots -g_ {k-1} sim g_ {k}}принимает свое полное значение, если gk + 1 = o (gk) { displaystyle g_ {k + 1} = o (g_ {k})}для всех k, что означает, что gk { displaystyle g_ {k}}образуют асимптотическую шкалу. В этом случае некоторые авторы могут оскорбительно написать f ∼ g 1 + ⋯ + gk { displaystyle f sim g_ {1} + cdots + g_ {k}}для обозначения утверждения f – (g 1 + ⋯ + gk) = o (gk). { displaystyle f- (g_ {1} + cdots + g_ {k}) = o (g_ {k}).}Однако следует быть осторожным, чтобы это не стандартное использование ∼ { displaystyle sim}символ, и что он не соответствует определению, данному в § Определение.

В данной ситуации это отношение gk = o ( gk – 1) { displaystyle g_ {k} = o (g_ {k-1})}фактически следует из объединения шагов k и k − 1; вычитая f – g 1 – ⋯ – gk – 2 = gk – 1 + o (gk – 1) { displaystyle f-g_ {1} – cdots -g_ {k-2} = g_ {k- 1} + o (g_ {k-1})}из f – g 1 – ⋯ – gk – 2 – gk – 1 = gk + o (gk), { displaystyle f- g_ {1} – cdots -g_ {k-2} -g_ {k-1} = g_ {k} + o (g_ {k}),}получается gk + o (gk) = o (gk – 1), { displaystyle g_ {k} + o (g_ {k}) = o (g_ {k-1}),}т.е. g k = o (g k – 1). { displaystyle g_ {k} = o (g_ {k-1}).}

В случае, если асимптотическое разложение не сходится, для любого конкретного значения аргумента будет определенная частичная сумма, которая обеспечивает наилучшее приближение а добавление дополнительных условий снизит точность. Эта оптимальная частичная сумма обычно будет содержать больше членов по мере приближения аргумента к предельному значению.

Примеры асимптотических разложений

exxx 2 π x Γ (x + 1) ∼ 1 + 1 12 x + 1 288 x 2 – 139 51840 x 3 – ⋯ (x → ∞) { displaystyle { frac {e ^ {x}} {x ^ {x} { sqrt {2 pi x}}}} Gamma (x + 1) sim 1 + { frac {1} { 12x}} + { frac {1} {288x ^ {2}}} – { frac {139} {51840x ^ {3}}} – cdots (x to infty)}

xex E 1 (x) ∼ n знак равно 0 ∞ (- 1) nn! xn (x → ∞) { displaystyle xe ^ {x} E_ {1} (x) sim sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} n! } {x ^ {n}}} (x to infty)}

π xex 2 erfc (x) ∼ 1 + ∑ n = 1 ∞ (- 1) n (2 n – 1)! ! п! (2 Икс 2) N (Икс → ∞) { Displaystyle { sqrt { pi}} xe ^ {x ^ {2}} { rm {erfc}} (х) sim 1+ сумма _ {п = 1} ^ { infty} (- 1) ^ {n} { frac {(2n-1) !!} {n! (2x ^ {2}) ^ {n}}} (x to infty)}

где (2n – 1) !! является двойным факториалом.

Рабочий пример

Асимптотические разложения часто возникают, когда обычный ряд используется в формальном выражении, которое вынуждает принимать значения вне области сходимости. Например, мы можем начать с обычного ряда

1 1 – w = ∑ n = 0 ∞ wn { displaystyle { frac {1} {1-w}} = sum _ {n = 0} ^ { infty} w ^ {n}}

Выражение слева действительно на всей комплексной плоскости w ≠ 1 { displaystyle w neq 1}, а правая часть сходится только для | w | < 1 {displaystyle |w|<1}. Умножение на e – w / t { displaystyle e ^ {- w / t}}и интегрирование обеих сторон дает

∫ 0 ∞ e – wt 1 – wdw = ∑ n = 0 ∞ tn + 1 ∫ 0 ∞ е – uundu { displaystyle int _ {0} ^ { infty} { frac {e ^ {- { frac {w} {t}}}} {1-w}} , dw = sum _ {n = 0} ^ { infty} t ^ {n + 1} int _ {0} ^ { infty} e ^ {- u} u ^ {n} , du}

Интеграл в левой части может быть выражен через экспоненциальный интеграл . Интеграл в правой части после замены u = w / t { displaystyle u = w / t}может быть распознан как гамма-функция. Оценивая оба, получаем асимптотическое разложение

e – 1 t Ei ⁡ (1 t) = ∑ n = 0 ∞ n! tn + 1 { displaystyle e ^ {- { frac {1} {t}}} operatorname {Ei} left ({ frac {1} {t}} right) = sum _ {n = 0 } ^ { infty} n! ; t ^ {n + 1}}

Здесь правая часть явно не сходится ни при каком ненулевом значении t. Однако, сохраняя t маленьким и усекая ряд справа до конечного числа членов, можно получить довольно хорошее приближение к значению Ei ⁡ (1 / t) { displaystyle operatorname {Ei} (1 / т)}. Подставив x = – 1 / t { displaystyle x = -1 / t}и отметив, что Ei ⁡ (x) = – E 1 (- x) { displaystyle operatorname {Ei} (x) = – E_ {1} (- x)}приводит к асимптотическому разложению, приведенному ранее в этой статье.

Асимптотическое распределение

В математической статистике асимптотическое распределение – это гипотетическое распределение, которое в некотором смысле является ” предельное »распределение последовательности распределений. Распределение – это упорядоченный набор случайных величин Z i для i = 1,…, n для некоторого положительного целого числа n. Асимптотическое распределение позволяет i иметь неограниченный диапазон, то есть n бесконечно.

Особым случаем асимптотического распределения является то, что поздние записи стремятся к нулю, то есть Z i стремятся к 0, когда i стремится к бесконечности. Некоторые примеры «асимптотического распределения» относятся только к этому частному случаю.

Это основано на понятии асимптотической функции, которая чисто приближается к постоянному значению (асимптоте), когда независимая переменная стремится к бесконечности; “чистый” в этом смысле означает, что для любой желаемой близости эпсилон существует некоторое значение независимой переменной, после которого функция никогда не отличается от константы более чем на эпсилон.

Асимптота – это прямая линия, к которой приближается кривая, но никогда не пересекает и не пересекает ее. Неформально можно говорить о кривой, пересекающей асимптоту «на бесконечности», хотя это не точное определение. В уравнении y = 1 x, { displaystyle y = { frac {1} {x}},}y становится произвольно малым по величине с увеличением x.

Приложения

Асимптотический анализ используется в нескольких математических науках. В статистике асимптотическая теория обеспечивает предельные аппроксимации распределения вероятностей для выборочной статистики, например, отношения правдоподобия статистика и ожидаемое значение отклонения . Однако асимптотическая теория не предоставляет метода оценки распределений выборочной статистики по конечной выборке. Неасимптотические границы обеспечиваются методами теории приближений.

Примеры приложений следующие.

• В прикладной математике асимптотический анализ используется для построения численных методов для аппроксимации уравнения решений.
• В математической статистике и теория вероятностей, асимптотики используются в анализе долгосрочного или большой выборки поведения случайных величин и оценок.
• в информатике в анализ алгоритмов с учетом производительности алгоритмов.
• поведение физических систем, примером является статистическая механика.
• в аварии анализ при выявлении причины сбоев посредством моделирования количества сбоев с большим количеством сбоев в заданном времени и пространстве.

Асимптотический анализ является ключевым инструментом для изучения обычных и частичных дифференциальные уравнения, возникающие при математическом моделировании реальных явлений. Наглядным примером является вывод уравнений пограничного слоя из полных уравнений Навье-Стокса, управляющих потоком жидкости. Во многих случаях асимптотическое разложение зависит от малого параметра ε: в случае пограничного слоя это безразмерное отношение толщины пограничного слоя к типичному масштабу длины задачи. В самом деле, приложения асимптотического анализа в математическом моделировании часто сосредотачиваются вокруг безразмерного параметра, который, как было показано или предположительно, мал благодаря рассмотрению масштабов рассматриваемой проблемы.

Асимптотические разложения обычно возникают при приближении некоторых интегралов (метод Лапласа, метод перевала, метод наискорейшего спуска ) или в аппроксимация вероятностных распределений (ряд Эджворта ). Графы Фейнмана в квантовой теории поля – еще один пример асимптотических разложений, которые часто не сходятся.

См. Также

Примечания

1. ^, Энциклопедия математики, EMS Press, 2001 [1994]
2. ^Эстрада и Канвал (2002, §1.2)
3. ^ Ховисон, С. (2005), Практическая прикладная математика, Кембридж University Press

Ссылки

• Balser, W. (1994), От дивергентных степенных рядов к аналитическим функциям, Springer-Verlag, ISBN 9783540485940
• де Брюйн, Н.Г. (1981), Асимптотические методы в анализе, Dover Publications, ISBN 9780486642215
• Estrada, R.; Канвал, Р.П. (2002), Дистрибутивный подход к асимптотике, Биркхойзер, ISBN 9780817681302
• Миллер, PD (2006), Прикладной асимптотический анализ, Американское математическое общество, ISBN 9780821840788
• Мюррей, Дж. Д. (1984), Асимптотический анализ, Springer, ISBN 9781461211228
• Париж, РБ; Каминский, Д. (2001), Асимптотика и интегралы Меллина-Барнса, Cambridge University Press

Внешние ссылки

From Wikipedia, the free encyclopedia

This article is about the behavior of functions as inputs approach infinity or some other limit value. For asymptotes in geometry, see Asymptote.

In mathematical analysis, asymptotic analysis, also known as asymptotics, is a method of describing limiting behavior.

As an illustration, suppose that we are interested in the properties of a function f (n) as n becomes very large. If f(n) = n² + 3n, then as n becomes very large, the term 3n becomes insignificant compared to n². The function f(n) is said to be “asymptotically equivalent to n², as n → ∞“. This is often written symbolically as f (n) ~ n², which is read as “f(n) is asymptotic to n²“.

An example of an important asymptotic result is the prime number theorem. Let π(x) denote the prime-counting function (which is not directly related to the constant pi), i.e. π(x) is the number of prime numbers that are less than or equal to x. Then the theorem states that

Asymptotic analysis is commonly used in computer science as part of the analysis of algorithms and is often expressed there in terms of big O notation.

Definition[edit]

Formally, given functions f (x) and g(x), we define a binary relation

if and only if (de Bruijn 1981, §1.4)

The symbol ~ is the tilde. The relation is an equivalence relation on the set of functions of x; the functions f and g are said to be asymptotically equivalent. The domain of f and g can be any set for which the limit is defined: e.g. real numbers, complex numbers, positive integers.

The same notation is also used for other ways of passing to a limit: e.g. x → 0, x ↓ 0, |x| → 0. The way of passing to the limit is often not stated explicitly, if it is clear from the context.

Although the above definition is common in the literature, it is problematic if g(x) is zero infinitely often as x goes to the limiting value. For that reason, some authors use an alternative definition. The alternative definition, in little-o notation, is that f ~ g if and only if

This definition is equivalent to the prior definition if g(x) is not zero in some neighbourhood of the limiting value.^[1][2]

Properties[edit]

If and , then, under some mild conditions,^{[further explanation needed]} the following hold:

Such properties allow asymptotically-equivalent functions to be freely exchanged in many algebraic expressions.

Examples of asymptotic formulas[edit]

• Factorial

  

  —this is Stirling’s approximation

• Partition function For a positive integer n, the partition function, p(n), gives the number of ways of writing the integer n as a sum of positive integers, where the order of addends is not considered.

  

• Airy function The Airy function, Ai(x), is a solution of the differential equation y″ − xy = 0; it has many applications in physics.

  

• Hankel functions

  

Asymptotic expansion[edit]

An asymptotic expansion of a function f(x) is in practice an expression of that function in terms of a series, the partial sums of which do not necessarily converge, but such that taking any initial partial sum provides an asymptotic formula for f. The idea is that successive terms provide an increasingly accurate description of the order of growth of f.

In symbols, it means we have but also and for each fixed k. In view of the definition of the symbol, the last equation means in the little o notation, i.e., is much smaller than

The relation takes its full meaning if for all k, which means the form an asymptotic scale. In that case, some authors may abusively write to denote the statement One should however be careful that this is not a standard use of the symbol, and that it does not correspond to the definition given in § Definition.

In the present situation, this relation actually follows from combining steps k and k−1; by subtracting from one gets i.e.

In case the asymptotic expansion does not converge, for any particular value of the argument there will be a particular partial sum which provides the best approximation and adding additional terms will decrease the accuracy. This optimal partial sum will usually have more terms as the argument approaches the limit value.

Examples of asymptotic expansions[edit]

• Gamma function

  

• Exponential integral

  

• Error function

  

  where m!! is the double factorial.

Worked example[edit]

Asymptotic expansions often occur when an ordinary series is used in a formal expression that forces the taking of values outside of its domain of convergence. For example, we might start with the ordinary series

The expression on the left is valid on the entire complex plane , while the right hand side converges only for . Multiplying by and integrating both sides yields

The integral on the left hand side can be expressed in terms of the exponential integral. The integral on the right hand side, after the substitution , may be recognized as the gamma function. Evaluating both, one obtains the asymptotic expansion

Here, the right hand side is clearly not convergent for any non-zero value of t. However, by keeping t small, and truncating the series on the right to a finite number of terms, one may obtain a fairly good approximation to the value of . Substituting and noting that results in the asymptotic expansion given earlier in this article.

Asymptotic distribution[edit]

In mathematical statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the “limiting” distribution of a sequence of distributions. A distribution is an ordered set of random variables Z_i for i = 1, …, n, for some positive integer n. An asymptotic distribution allows i to range without bound, that is, n is infinite.

A special case of an asymptotic distribution is when the late entries go to zero—that is, the Z_i go to 0 as i goes to infinity. Some instances of “asymptotic distribution” refer only to this special case.

This is based on the notion of an asymptotic function which cleanly approaches a constant value (the asymptote) as the independent variable goes to infinity; “clean” in this sense meaning that for any desired closeness epsilon there is some value of the independent variable after which the function never differs from the constant by more than epsilon.

An asymptote is a straight line that a curve approaches but never meets or crosses. Informally, one may speak of the curve meeting the asymptote “at infinity” although this is not a precise definition. In the equation y becomes arbitrarily small in magnitude as x increases.

Applications[edit]

Asymptotic analysis is used in several mathematical sciences. In statistics, asymptotic theory provides limiting approximations of the probability distribution of sample statistics, such as the likelihood ratio statistic and the expected value of the deviance. Asymptotic theory does not provide a method of evaluating the finite-sample distributions of sample statistics, however. Non-asymptotic bounds are provided by methods of approximation theory.

Examples of applications are the following.

• In applied mathematics, asymptotic analysis is used to build numerical methods to approximate equation solutions.
• In mathematical statistics and probability theory, asymptotics are used in analysis of long-run or large-sample behaviour of random variables and estimators.
• In computer science in the analysis of algorithms, considering the performance of algorithms.
• The behavior of physical systems, an example being statistical mechanics.
• In accident analysis when identifying the causation of crash through count modeling with large number of crash counts in a given time and space.

Asymptotic analysis is a key tool for exploring the ordinary and partial differential equations which arise in the mathematical modelling of real-world phenomena.^[3] An illustrative example is the derivation of the boundary layer equations from the full Navier-Stokes equations governing fluid flow. In many cases, the asymptotic expansion is in power of a small parameter, ε: in the boundary layer case, this is the nondimensional ratio of the boundary layer thickness to a typical length scale of the problem. Indeed, applications of asymptotic analysis in mathematical modelling often^[3] center around a nondimensional parameter which has been shown, or assumed, to be small through a consideration of the scales of the problem at hand.

Asymptotic expansions typically arise in the approximation of certain integrals (Laplace’s method, saddle-point method, method of steepest descent) or in the approximation of probability distributions (Edgeworth series). The Feynman graphs in quantum field theory are another example of asymptotic expansions which often do not converge.

See also[edit]

Notes[edit]

References[edit]

• Balser, W. (1994), From Divergent Power Series To Analytic Functions, Springer-Verlag, ISBN 9783540485940
• de Bruijn, N. G. (1981), Asymptotic Methods in Analysis, Dover Publications, ISBN 9780486642215
• Estrada, R.; Kanwal, R. P. (2002), A Distributional Approach to Asymptotics, Birkhäuser, ISBN 9780817681302
• Miller, P. D. (2006), Applied Asymptotic Analysis, American Mathematical Society, ISBN 9780821840788
• Murray, J. D. (1984), Asymptotic Analysis, Springer, ISBN 9781461211228
• Paris, R. B.; Kaminsky, D. (2001), Asymptotics and Mellin-Barnes Integrals, Cambridge University Press

External links[edit]

• Asymptotic Analysis  —home page of the journal, which is published by IOS Press
• A paper on time series analysis using asymptotic distribution