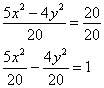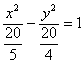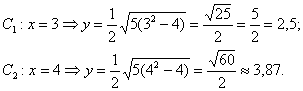Как найти асимптоты гиперболы по каноническому уравнению - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

Асимптоты гиперболы – это прямые, проходящие через центр гиперболы. Гипербола приближается к асимптотам, но никогда не пересекает (и даже не касается) их. Найти уравнения асимптот можно двумя способами, которые помогут понять саму концепцию асимптот.

1
Запишите каноническое уравнение гиперболы. Рассмотрим простейший пример – гиперболу, центр которой расположен в начале координат. В этом случае каноническое уравнение гиперболы имеет вид: ^x²/_a² – ^y²/_b² = 1 (когда ветви гиперболы направлены вправо или влево) или ^y²/_b² – ^x²/_a² = 1 (когда ветви гиперболы направлены вверх или вниз).^[1] Имейте в виду, что в этом уравнении «х» и «у» – это переменные, а «а» и «b» – постоянные (то есть числа).
- Пример 1: ^x²/₉ – ^y²/₁₆ = 1
- Некоторые преподаватели и авторы учебников меняют местами постоянные «а» и «b».^[2] Поэтому изучите данное вам уравнение, чтобы понять, что к чему. Не стоит просто запоминать уравнение – в этом случае вы ничего не поймете, если переменные и/или постоянные будут обозначены другими символами.
2
Приравняйте каноническое уравнение к нулю (а не к единице). Новое уравнение описывает обе асимптоты, но чтобы получить уравнение каждой асимптоты, придется приложить некоторые усилия.^[3]
- Пример 1: ^x²/₉ – ^y²/₁₆ = 0
3
Разложите на множители новое уравнение. Разложите на множители левую часть уравнения. Вспомните, как раскладывать на множители квадратное уравнение, и читайте дальше.
- Конечное уравнение (то есть уравнение, разложенное на множители) будет иметь вид (__ ± __)(__ ± __) = 0.
- При перемножении первых членов (внутри каждой пары скобок) должен получиться член ^x²/₉, поэтому из этого члена извлеките квадратный корень, и результат запишите вместо первого пробела внутри каждой пары скобок:(^x/₃ ± __)(^x/₃ ± __) = 0
- Аналогично извлеките квадратный корень из члена ^y²/₁₆, и результат запишите вместо второго пробела внутри каждой пары скобок: (^x/₃ ± ^y/₄)(^x/₃ ± ^y/₄) = 0
- Вы нашли все члены уравнения, поэтому внутри одной пары скобок между членами напишите знак плюс, а внутри второй – знак минус, чтобы при перемножении соответствующие члены сокращались: (^x/₃ + ^y/₄)(^x/₃ – ^y/₄) = 0
4
Приравняйте каждый двучлен (то есть выражение внутри каждой пары скобок) к нулю и вычислите «y». Так вы найдете два уравнения, которые описывают каждую асимптоту.
- Пример 1: Так как (^x/₃ + ^y/₄)(^x/₃ – ^y/₄) = 0, то ^x/₃ + ^y/₄ = 0 и ^x/₃ – ^y/₄ = 0
- Перепишите уравнение следующим образом: ^x/₃ + ^y/₄ = 0 → ^y/₄ = – ^x/₃ → y = – ^4x/₃
- Перепишите уравнение следующим образом: ^x/₃ – ^y/₄ = 0 → – ^y/₄ = – ^x/₃ → y = ^4x/₃
5
Выполните описанные действия с гиперболой, уравнение которой отличается от канонического. В предыдущем шаге вы нашли уравнения асимптот гиперболы с центром в начале координат. Если центр гиперболы находится в точке с координатами (h,k), то она описывается следующим уравнением: ^{(x – h)²}/_a² – ^{(y – k)²}/_b² = 1 или ^{(y – k)²}/_b² – ^{(x – h)²}/_a² = 1. Это уравнение также можно разложить на множители. Но в этом случае не трогайте двучлены (x – h) и (y – k) до тех пор, пока не придете к последнему шагу.
- Пример 2: ^{(x – 3)²}/₄ – ^{(y + 1)²}/₂₅ = 1
- Приравняйте это уравнение к 0 и разложите его на множители:
- (^{(x – 3)}/₂ + ^{(y + 1)}/₅)(^{(x – 3)}/₂ – ^{(y + 1)}/₅) = 0
- Приравняйте каждый двучлен (то есть выражение внутри каждой пары скобок) к нулю и вычислите «y», чтобы найти уравнения асимптот:
- ^{(x – 3)}/₂ + ^{(y + 1)}/₅ = 0 → y = –⁵/₂x + ¹³/₂
- (^{(x – 3)}/₂ – ^{(y + 1)}/₅) = 0 → y = ⁵/₂x – ¹⁷/₂
Реклама

1
Обособьте член y² на левой стороне уравнения гиперболы. Применяйте этот метод в том случае, когда уравнение гиперболы дано в квадратичной форме. Даже если дано каноническое уравнение гиперболы, этот метод позволит лучше понять концепцию асимптот. Обособьте y² или (y – k)² на левой стороне уравнения.
- Пример 3: ^{(y + 2)²}/₁₆ – ^{(x + 3)²}/₄ = 1
- К обеим частям уравнения прибавьте «х», а затем умножьте обе части на 16:
- (y + 2)² = 16(1 + ^{(x + 3)²}/₄)
- Упростите полученное уравнение:
- (y + 2)² = 16 + 4(x + 3)²
2
Извлеките квадратный корень из каждой части уравнения. При этом не упрощайте правую часть уравнения, так как при извлечении квадратного корня получаются два результата – положительный и отрицательный (например, -2 * -2 = 4, поэтому √4 = 2 и √4 = -2). Чтобы привести оба результата, используйте символ ±.
- √((y + 2)²) = √(16 + 4(x + 3)²)
- (y+2) = ± √(16 + 4(x + 3)²)
3

Уясните понятие асимптоты. Сделайте это до того, как перейти к следующему шагу. Асимптота – это прямая, к которой приближается гипербола с ростом значений «х». Гипербола никогда не пересечет асимптоту, но с увеличением «х» гипербола приблизится к асимптоте на бесконечно малое расстояние.
4
Преобразуйте уравнение с учетом больших значений «х». Как правило, при работе с уравнениями асимптот учитываются только большие значения «х» (то есть такие значения, которые стремятся к бесконечности). Поэтому в уравнении можно пренебречь определенными константами, так как по сравнению с «х» их вклад невелик. Например, если переменная «х» равна нескольким миллиардам, то прибавление числа (константы) 3 окажет мизерное влияние на значение «х».
- В уравнении (y+2) = ± √(16 + 4(x + 3)²) при стремлении «x» к бесконечности постоянной 16 можно пренебречь.
- При больших значениях «х» (y+2) ≈ ± √(4(x + 3)²)
5
Вычислите «у», чтобы найти уравнения асимптот. Избавившись от констант, можно упростить подкоренное выражение. Помните, что в ответе нужно записать два уравнения – одно со знаком плюс, а второе со знаком минус.
- y + 2 = ±√(4(x+3)^2)
- y + 2 = ±2(x+3)
- y + 2 = 2x + 6 и y + 2 = -2x – 6
- y = 2x + 4 и y = -2x – 8
Реклама

Советы

Помните, что уравнение гиперболы и уравнения ее асимптот всегда включают постоянные (константы).
Равносторонняя гипербола – это гипербола, в уравнении которой а = b = с (константа).
Если дано уравнение равносторонней гиперболы, сначала преобразуйте его в каноническую форму, а затем найдите уравнения асимптот.

Предупреждения

Помните, что ответ не всегда записывается в канонической форме.

Об этой статье

Эту страницу просматривали 91 599 раз.

Была ли эта статья полезной?

Источник

3.4.1. Каноническое уравнение и построение гиперболы

Общая структура изложения материала будет напоминать предыдущий параграф. Начнём с общего понятия гиперболы и задачи на её построение.

Каноническое уравнение гиперболы имеет вид , где – положительные действительные числа. Обратите внимание, что в отличие от эллипса, здесь не накладывается условие , то

есть, значение «а» может быть и меньше, чем «бэ».
Надо сказать, довольно неожиданно… – уравнение «школьной» гиперболы и

близко не напоминает каноническую запись. Но эта загадка нас ещё подождёт, а пока раскинем на экране своего воображения график функции …. Какие мысли?

У гиперболы две симметричные ветви.

У гиперболы две асимптоты.

Неплохой прогресс! Данными свойствами обладает любая гипербола, и сейчас вы с неподдельным восхищением заглянем в декольте этой линии:

Задача 99

Построить гиперболу, заданную уравнением

Решение: на первом шаге приведём данное уравнение к каноническому виду . Пожалуйста, запомните типовой порядок действий. Справа необходимо получить «единицу», поэтому

обе части исходного уравнения делим на 20:

Здесь можно сократить обе дроби, но технически грамотнее сделать каждую из них трёхэтажной (см. Приложение Школьные

материалы):

и только после этого провести сокращение:

Выделяем квадраты в знаменателях:

Готово.

Почему преобразования лучше проводить именно так? Ведь дроби левой части можно сразу сократить и получить .

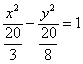
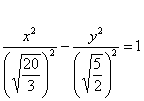
Дело в том, что в рассматриваемом примере немного повезло: число 20 делится и на 4 и на 5. В общем случае получится что-нибудь вроде и без 3-го этажа не обойтись: .

Воспользуемся плодом наших трудов – каноническим уравнением :

Как построить гиперболу?

Существует два подхода к построению гиперболы – геометрический и алгебраический. С практической точки зрения вычерчивание с помощью циркуля я бы

даже сказал утопично, поэтому гораздо выгоднее вновь привлечь на помощь нехитрые расчёты.

Целесообразно придерживаться следующего алгоритма (читайте и смотрите на чертёж ниже):

1) Сначала находим асимптоты. Если гипербола задана каноническим уравнением , то её асимптотами являются прямые . В нашем случае: . Данный пункт

обязателен! Это принципиальная особенность чертежа, и будет грубой ошибкой, если ветви гиперболы «вылезут» за свои асимптоты.

2) Теперь находим две вершины гиперболы, которые расположены на оси абсцисс в точках . Выводится элементарно: если , то каноническое уравнение превращается в , откуда и следует,

что . Наша гипербола имеет вершины

3) Ищем дополнительные точки. Обычно хватает двух-трёх. В каноническом положении гипербола симметрична относительно начала

координат и обеих координатных осей, поэтому вычисления достаточно провести для 1-й координатной четверти. Методика точно такая же, как и при построении эллипса. Из канонического уравнения на черновике выражаем:

и уравнение распадается на две функции:
– определяет верхние дуги гиперболы (то, что нам надо);
– определяет нижние дуги гиперболы.

Напрашивается нахождение точек с абсциссами :

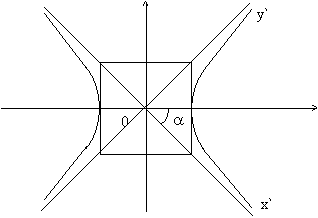
4) Изобразим асимптоты , вершины , дополнительные и

симметричные им точки в других координатных четвертях. Аккуратно соединим соответствующие точки у каждой ветви гиперболы:
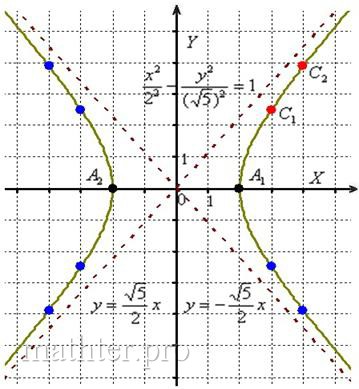
Техническая трудность может возникнуть с иррациональным угловым коэффициентом , но это вполне преодолимая проблема.

Отрезок называют действительной осью гиперболы;

Число называют действительной полуосью гиперболы;

число – мнимой полуосью.

В нашем случае: , , и, очевидно, если гиперболу повернуть вокруг центра симметрии и / или переместить, то эти значения не

изменятся.

3.4.2. Определение гиперболы

3.3.4. Поворот и параллельный перенос эллипса

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник

Асимптоты гиперболы

Пусть Г – какая-нибудь
линия, М – переменная точка на ней, а –
некоторая прямая. Если возможно такое
движение точки М по линии Г, что:

точка М уходит в
бесконечность;
при этом расстояние
от точки М до прямой а стремится к нулю,
–

то говорят, что линия
Г ассимптотически приближается к прямой
а. Прямая а в таком случае называется
асимптотой линии Г.

Асимптотами гиперболы
называются прямые, имеющие уравнения:

и
.
(3)

Эти прямые являются
диагоналями основного прямоугольника.
Построим гиперболу
и
рассмотрим какую-нибудь точку М(х;у),
лежащую на гиперболе в первом квадранте.

Выясним, как в первом
квадранте по мере возрастания х будет
изменяться расстояние от точки М
гиперболы до асимптоты
.
Обозначим через N точку асимптоты с
абсциссой х: N(x;Y), где Y=.
Тогда

(4)

Так как а 
х, то в скобках первое слагаемое всегда
больше второго, следовательно, Y-y>0, а
это означает, что при одной и той же
абсциссе точка гиперболы лежит под
соответствующей точкой асимптоты.

Преобразовав неравенство
(4):

,
(5)

убеждаемся, что длина
отрезка MN по мере возрастания х
уменьшается, и когда х неограниченно
растет, MN стремится к нулю. Так как MN
больше расстояния МК от точки M до
асимптоты, то при этом МК и подавно
стремится к нулю.

Аналогичное рассуждение
можно провести в любом квадранте.

Итак, прямые
в
смысле определения асимптот к графику
функции являются асимптотами гиперболы

При построении гиперболы
обычно строят основной прямоугольник
и проводят асимптоты, так как они
позволяют точнее вычерчивать гиперболу.

Равнобочная гипербола

Возьмем каноническое
уравнение гиперболы

В случае, когда а=b,
уравнение гиперболы имеет вид

или

х²
– у²
= а².
(6)

Гипербола, у которой
полуоси а и b равны, называется равнобочной
гиперболой.
Уравнение (6) называется уравнением
равнобочной гиперболы. Так как основной
прямоугольник этой гиперболы является
квадратом, то асимптоты равнобочной
гиперболы будут перпендикулярны друг
другу. (Рис. 5)

Рис. 5

Сопряженная гипербола

Рассмотрим уравнение

.
(7)

Представим уравнение
(7) в следующем виде:

.
(8)

Очевидно, что уравнение
(8) представляет собой уравнение гиперболы,
у которой действительной осью является
ось ординат, а мнимой – ось абсцисс.

Построим основной
прямоугольник, проведем асимптоты и
построим гиперболу (7). Далее в той же
системе координат построим (пунктиром)
(Рис. 6) гиперболу

Рис. 6

Очевидно, что гиперболы
и
имеют
общие асимптоты. Такие гиперболы
называются сопряженными.

Выведем теперь уравнение
гиперболы, асимптотами которой служат
оси координат. Возьмем уравнение
равнобочной гиперболы х²
– у²
= а²
и рассмотрим уравнение этой гиперболы
в новой системе координат Х`OY`, полученной
из старой поворотом осей координат на
угол =(Рис.
2).

Используя для этого
формулы поворота осей координат:

х = х`cos
– y`sin;

y = x`sin
+ y`cos,

подставим значения х,
у в уравнение гиперболы:

х²
– у²
= а².

Получим:

.
(9)

Обозначая
,
получим х`y`=c.

Уравнение равнобочной
гиперболы, для которой координатные
оси ОХ и OY являются асимптотами, будет
иметь вид:

ху = с

или

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Гипербола: определение, свойства, построение

Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек F_1 и F_2 есть величина постоянная (2a) , меньшая расстояния (2c) между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.

Фокальное свойство гиперболы

Точки F_1 и F_2 называются фокусами гиперболы, расстояние 2c=F_1F_2 между ними — фокусным расстоянием, середина отрезка F_1F_2 — центром гиперболы, число — длиной действительной оси гиперболы (соответственно, — действительной полуосью гиперболы). Отрезки F_1M и F_2M , соединяющие произвольную точку гиперболы с ее фокусами, называются фокальными радиусами точки . Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Отношение $e=frac{c}{a}$ , где $c=sqrt{a^2+b^2}$ , называется эксцентриситетом гиперболы. Из определения (2a<2c) следует, что e>1 .

Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:

$frac{x^2}{a^2}-frac{y^2}{b^2}=1.$

(3.50)

Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр гиперболы примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки F_1 к точке F_2 ); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).

Гипербола и фокальное свойство гипербол

Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов F_1(-c,0) и F_2(c,0) . Для произвольной точки M(x,y) , принадлежащей гиперболе, имеем:

$left||overrightarrow{F_1M}|-|overrightarrow{F_2M}|right|=2a.$

Записывая это уравнение в координатной форме, получаем:

$sqrt{(x+c)^2+y^2}-sqrt{(x-c)^2+y^2}=pm2a.$

Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:

$frac{x^2}{a^2}-frac{y^2}{b^2}=1,,$

где $b=sqrt{c^2-a^2}$ , т.е. выбранная система координат является канонической.

Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.

Директориальное свойство гиперболы

Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии $a^2!!not{phantom{|}},c$ от нее (рис.3.41,а). При a=0 , когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.

Гиперболу с эксцентриситетом e=1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету (директориальное свойство гиперболы). Здесь и — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.

Директрисы гиперболы и директориальное свойство

В самом деле, например, для фокуса F_2 и директрисы d_2 (рис.3.41,а) условие $frac{r_2}{rho_2}=e$ можно записать в координатной форме:

$sqrt{(x-c)^2+y^2}=eleft(x-frac{a^2}{c}right)$

Избавляясь от иррациональности и заменяя $e=frac{c}{a},~c^2-a^2=b^2$ , приходим к каноническому уравнению гиперболы (3.50). Аналогичные рассуждения можно провести для фокуса F_1 и директрисы d_1 :

$frac{r_1}{rho_1}=e quad Leftrightarrow quad sqrt{(x+c)^2+y^2}= eleft(x+frac{a^2}{c} right).$

Уравнение гиперболы в полярной системе координат

Уравнение правой ветви гиперболы в полярной системе координат F_2rvarphi (рис.3.41,б) имеет вид

$r=frac{p}{1-ecdotcosvarphi}$ , где $p=frac{p^2}{a}$ — фокальный параметр гиперболы.

В самом деле, выберем в качестве полюса полярной системы координат правый фокус F_2 гиперболы, а в качестве полярной оси — луч с началом в точке F_2 , принадлежащий прямой F_1F_2 , но не содержащий точки F_1 (рис.3.41,б). Тогда для произвольной точки M(r,varphi) , принадлежащей правой ветви гиперболы, согласно геометрическому определению (фокальному свойству) гиперболы, имеем F_1M-r=2a . Выражаем расстояние между точками M(r,varphi) и F_1(2c,pi) (см. пункт 2 замечаний 2.8):

$F_1M=sqrt{(2c)^2+r^2-2cdot(2c)^2cdot rcdotcos(varphi-pi)}=sqrt{r^2+4cdot ccdot rcdotcosvarphi+4cdot c^2}.$

Следовательно, в координатной форме уравнение гиперболы имеет вид

$sqrt{r^2+4cdot ccdot rcdotcosvarphi+4cdot c^2}-r=2a.$

Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:

$r^2+4crcdotcosvarphi+4c^2=4a^2+4ar+r^2 quad Leftrightarrow quad aleft(1-frac{c}{a}cosvarphiright)r=c^2-a^2.$

Выражаем полярный радиус и делаем замены $e=frac{c}{a},~b^2=c^2-a^2,~p=frac{b^2}{a}$ :

$r=frac{c^2-a^2}{a(1-ecosvarphi)} quad Leftrightarrow quad r=frac{b^2}{a(1-ecosvarphi)} quad Leftrightarrow quad r=frac{p}{1-ecosvarphi},$

что и требовалось доказать. Заметим, что в полярных координатах уравнения гиперболы и эллипса совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( e>1 для гиперболы, 0leqslant e<1 для эллипса).

Геометрический смысл коэффициентов в уравнении гиперболы

Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение y=0 , находим абсциссы точек пересечения: x=pm a . Следовательно, вершины имеют координаты (-a,0),,(a,0) . Длина отрезка, соединяющего вершины, равна . Этот отрезок называется действительной осью гиперболы, а число — действительной полуосью гиперболы. Подставляя x=0 , получаем y=pm ib . Длина отрезка оси ординат, соединяющего точки (0,-b),,(0,b) , равна . Этот отрезок называется мнимой осью гиперболы, а число — мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.

Замечания 3.10.

1. Прямые x=pm a,~y=pm b ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).

2. Прямые $y=pmfrac{b}{a},x$ , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).

Для равносторонней гиперболы, описываемой уравнением $frac{x^2}{a^2}-frac{y^2}{a^2}=1$ (т.е. при a=b ), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат Ox'y' (рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид $y'=frac{a^2}{2x'}$ (гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).

Асимптоты гиперболы и равносторонняя гипербола

В самом деле, повернем каноническую систему координат на угол $varphi=-frac{pi}{4}$ (рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами

$left{!begin{aligned}x&=frac{sqrt{2}}{2}cdot x'+frac{sqrt{2}}{2}cdot y',\ y&=-frac{sqrt{2}}{2}cdot x'+frac{sqrt{2}}{2}cdot y'end{aligned}right. quad Leftrightarrow quad left{!begin{aligned}x&=frac{sqrt{2}}{2}cdot(x'+y'),\ y&=frac{sqrt{2}}{2}cdot(y'-x')end{aligned}right.$

Подставляя эти выражения в уравнение $frac{x^2}{a^2}-frac{y^2}{a^2}=1$ равносторонней гиперболы и приводя подобные члены, получаем

$frac{frac{1}{2}(x'+y')^2}{a^2}-frac{frac{1}{2}(y'-x')^2}{a^2}=1 quad Leftrightarrow quad 2cdot x'cdot y'=a^2 quad Leftrightarrow quad y'=frac{a^2}{2cdot x'}.$

3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.

Действительно, если точка M(x,y) принадлежит гиперболе $frac{x^2}{a^2}-frac{y^2}{b^2}=1$ . то и точки M'(x,y) и M''(-x,y) , симметричные точке относительно координатных осей, также принадлежат той же гиперболе.

Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.

4. Из уравнения гиперболы в полярных координатах $r=frac{p}{1-ecosvarphi}$ (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси ( r=p при $varphi=frac{pi}{2}$ ).

5. Эксцентриситет характеризует форму гиперболы. Чем больше , тем шире ветви гиперболы, а чем ближе к единице, тем ветви гиперболы уже (рис.3.43,а).

Действительно, величина gamma угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника: $operatorname{tg}frac{gamma}{2}=frac{b}{2}$ . Учитывая, что $e=frac{c}{a}$ и c^2=a^2+b^2 , получаем

$e^2=frac{c^2}{a^2}=frac{a^2+b^2}{a^2}=1+{left(frac{b}{a}right)!}^2=1+operatorname{tg}^2frac{gamma}{2}.$

Чем больше , тем больше угол gamma . Для равносторонней гиперболы (a=b) имеем e=sqrt{2} и $gamma=frac{pi}{2}$ . Для e>sqrt{2} угол gamma тупой, а для 1<e<sqrt{2} угол gamma острый (рис.3.43,а).

Эксцентриситет гиперболы и сопряжённая гипербола

6. Две гиперболы, определяемые в одной и той же системе координат уравнениями $frac{x^2}{a^2}-frac{y^2}{b^2}=1$ и $-frac{x^2}{a^2}+frac{y^2}{b^2}=1$ называются сопряженными друг с другом. Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы $-frac{x^2}{a^2}+frac{y^2}{b^2}=1$ приводится к каноническому при помощи переименования координатных осей (3.38).

7. Уравнение $frac{(x-x_0)^2}{a^2}-frac{(y-y_0)^2}{b^2}=1$ определяет гиперболу с центром в точке O'(x_0,y_0) , оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение $-frac{(x-x_0)^2}{a^2}+frac{(y-y_0)^2}{b^2}=1$ определяет сопряженную гиперболу с центром в точке O'(x_0,y_0) .

Параметрическое уравнение гиперболы

Параметрическое уравнение гиперболы в канонической системе координат имеет вид

$begin{cases}x=acdotoperatorname{ch}t,\y=bcdotoperatorname{sh}t,end{cases}tinmathbb{R},$

где $operatorname{ch}t=frac{e^t+e^{-t}}{2}$ — гиперболический косинус, a $operatorname{sh}t=frac{e^t-e^{-t}}{2}$ гиперболический синус.

Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству $operatorname{ch}^2t-operatorname{sh}^2t=1$ .

Построение гиперболы в канонической системе координат

Пример 3.21. Изобразить гиперболу $frac{x^2}{2^2}-frac{y^2}{3^2}=1$ в канонической системе координат Oxy . Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.

Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: a=2 — действительная полуось, b=3 — мнимая полуось гиперболы. Строим основной прямоугольник со сторонами 2a=4,~2b=6 с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя x=4 в уравнение гиперболы, получаем

$frac{4^2}{2^2}-frac{y^2}{3^2}=1 quad Leftrightarrow quad y^2=27 quad Leftrightarrow quad y=pm3sqrt{3}.$

Следовательно, точки с координатами (4;3sqrt{3}) и (4;-3sqrt{3}) принадлежат гиперболе. Вычисляем фокусное расстояние

$2cdot c=2cdotsqrt{a^2+b^2}=2cdotsqrt{2^2+3^2}=2sqrt{13}$

эксцентриситет $e=frac{c}{a}=frac{sqrt{13}}{2}$ ; фокальныи параметр $p=frac{b^2}{a}=frac{3^2}{2}=4,!5$ . Составляем уравнения асимптот $y=pmfrac{b}{a},x$ , то есть $y=pmfrac{3}{2},x$ , и уравнения директрис: $x=pmfrac{a^2}{c}=frac{4}{sqrt{13}}$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Советы

Предупреждения

Об этой статье

Была ли эта статья полезной?

3.4.1. Каноническое уравнение и построение гиперболы

Как построить гиперболу?

Асимптоты гиперболы

Равнобочная гипербола

Сопряженная гипербола

Гипербола: определение, свойства, построение

Фокальное свойство гиперболы

Директориальное свойство гиперболы

Уравнение гиперболы в полярной системе координат

Геометрический смысл коэффициентов в уравнении гиперболы

Параметрическое уравнение гиперболы

Вам также может понравиться

Как найти ухаживающего за инвалидом

Как найти дрова для костра

Как найти читера в майнкрафт

Добавить комментарий Отменить ответ