Асимптоты графика функций: их виды, примеры решений
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Понятие асимптоты
Если предварительно построить асимптоты кривой, то многих случаях построение графика функции облегчается.
Судьба асимптоты полна трагизма. Представьте себе, каково это: всю жизнь двигаться по прямой к заветной цели, подойти к ней максимально близко, но так и не достигнуть её. Например, стремиться соединить свой жизненный путь с путём желанного человека, в какой-то момент приблизиться к нему почти вплотную, но даже не коснуться его. Или стремиться заработать миллиард, но до достижения этой цели и записи в книгу рекордов Гиннеса для своего случая не достаёт сотых долей цента. И тому подобное. Так и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное возможное расстояние, но так и не касается его.
Определение 1. Асимптотами называются такие прямые, к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.
Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Вертикальные асимптоты
Первое, что нужно узнать о вертикальных асимптотах: они параллельны оси Oy .
Определение. Прямая x = a является вертикальной асимптотой графика функции, если точка x = a является точкой разрыва второго рода для этой функции.
Из определения следует, что прямая x = a является вертикальной асимптотой графика функции f(x) , если выполняется хотя бы одно из условий:
- (предел функции при значении аргумента, стремящимся к некоторому значению a слева, равен плюс или минус бесконечности)
- (предел функции при значении аргумента, стремящимся к некоторому значению a справа, равен плюс или минус бесконечности).
- символом обозначается стремление x к a справа, причём x остаётся больше a;
- символом обозначается стремление x к a слева, причём x остаётся меньше a.
Из сказанного следует, что вертикальные асимптоты графика функции можно искать не только в точках разрыва, но и на границах области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет.
Пример 1. График функции y=lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy ) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения
Пример 2. Найти асимптоты графика функции .
Пример 3. Найти асимптоты графика функции
Пример 4. Найти асимптоты график функции .
Горизонтальные асимптоты
Первое, что нужно узнать о горизонтальных асимптотах: они параллельны оси Ox .
Если (предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b), то y = b – горизонтальная асимптота кривой y = f(x ) (правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности, и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).
Пример 5. График функции
при a > 1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осью Ox ), так как предел функции при стремлении “икса” к минус бесконечности равен нулю:
Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении “икса” к плюс бесконечности равен бесконечности:
Наклонные асимптоты
Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны осям координат, поэтому для их построения нам требовалось лишь определённое число – точка на оси абсцисс или ординат, через которую проходит асимптота. Для наклонной асимптоты необходимо больше – угловой коэффициент k, который показывает угол наклона прямой, и свободный член b, который показывает, насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию, а из неё – уравнения прямой, заметят, что для наклонной асимптоты находят уравнение прямой с угловым коэффициентом. Существование наклонной асимптоты определяется следующей теоремой, на основании которой и находят названные только что коэффициенты.
Теорема. Для того, чтобы кривая y = f(x) имела асимптоту y = kx + b , необходимо и достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции при стремлении переменной x к плюс бесконечности и минус бесконечности:
(1)
(2)
Найденные таким образом числа k и b и являются коэффициентами наклонной асимптоты.
В первом случае (при стремлении икса к плюс бесконечности) получается правая наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.
При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных, эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только один из них.
При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус бесконечности прямая y = kx + b является двусторонней асимптотой кривой.
Если хотя бы один из пределов, определяющих асимптоту y = kx + b , не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).
Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0 .
Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
Пример 6. Найти асимптоты графика функции
Решение. Функция определена на всей числовой прямой, кроме x = 0 , т.е.
Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:
Следовательно, x = 0 – вертикальная асимптота графика данной функции.
Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:
Выясним наличие наклонной асимптоты:
Получили конечные пределы k = 2 и b = 0 . Прямая y = 2x является двусторонней наклонной асимптотой графика данной функции (рис. внутри примера).
Пример 7. Найти асимптоты графика функции
Решение. Функция имеет одну точку разрыва x = −1 . Вычислим односторонние пределы и определим вид разрыва:
,
.
Заключение: x = −1 – точка разрыва второго рода, поэтому прямая x = −1 является вертикальной асимптотой графика данной функции.
Ищем наклонные асимптоты. Так как данная функция – дробно-рациональная, пределы при и при будут совпадать. Таким образом, находим коэффициенты для подстановки в уравнение прямой – наклонной асимптоты:
Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:
На рисунке график функции обозначен бордовым цветом, а асимптоты – чёрным.
Пример 8. Найти асимптоты графика функции
.
Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:
.
Таким образом, график данной функции имеет асимптоту y = 0 при и не имеет асиптоты при .
Пример 9. Найти асимптоты графика функции
.
Решение. Сначала ищем вертикальные асимптоты. Для этого найдём область определения функции. Функция определена, когда выполняется неравенство и при этом . Знак переменной x совпадает со знаком . Поэтому рассмотрим эквивалентное неравенство . Из этого получаем область определения функции: . Вертикальная асимптота может быть только на границе области определения функции. Но x = 0 не может быть вертикальной асимптотой, так как функция определена при x = 0 .
Рассмотрим правосторонний предел при (левосторонний предел не существует):
.
Точка x = 2 – точка разрыва второго рода, поэтому прямая x = 2 – вертикальная асимптота графика данной функции.
Ищем наклонные асимптоты:
Итак, y = x + 1 – наклонная асимптота графика данной функции при . Ищем наклонную асимптоту при :
Итак, y = −x − 1 – наклонная асимптота при .
Пример 10. Найти асимптоты графика функции
Решение. Функция имеет область определения . Так как вертикальная асимптота графика этой функции может быть только на границе области определения, найдём односторонние пределы функции при :
,
.
Оба предела нашли, используя первый замечательный предел. Заключение: x = 0 – точка устранимого разрыва, поэтому у графика функции нет вертикальных асимптот.
Ищем наклонные асимптоты:
Таким образом, при наклонной асимптотой графика данной функции является прямая y = x . Но при найденные пределы не изменяются. Поэтому при наклонной асимптотой графика данной функции также является y = x .
Пример 11. Найти асимптоты графика функции
.
Решение. Сначала найдём вертикальные асимптоты. Для этого найдём точки разрыва функции и их виды. Знаменатель не может быть равным нулю, поэтому должно соблюдаться условие . Функция имеет две точки разрыва: , . Чтобы установить вид разрыва, найдём односторонние пределы:
Так как все пределы равны бесконечности, обе точки разрыва – второго рода. Поэтому график данной функции имеет две вертикальные асимптоты: x = 2 и x = −2 .
Ищем наклонные асимптоты. Так как данная функция является дробно-рациональной, пределы при и при совпадают. Поэтому, определяя коэффициенты прямой, ищем просто пределы:
Подставляем найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты y = 2x . Таким образом, график данной функции имеет три асимптоты: x = 2 , x = −2 и y = 2x .
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения
Пример 12. Найти асимптоты графика функции .
Пример 13. Найти асимптоты графика функции .
Точки перегиба. Асимптоты
Кривая называется выпуклой в точке х=х0, если в некоторой окрестности этой точки кивая расположена под касательной, проведенной в этой точке (рис.6а), если же кривая лежит над касательной, то функция называется вогнутой (рис.6б).
В качестве достаточных условий выпуклости, вогнутости графика функций можно принять следующие: если y”>0, то кривая вогнутая, если y”
6. Найти точки пересечения графика с осями координат.
7. При необходимости вычислить значения функции в дополнительных точках.
1.5.1. Найти промежутки выпуклости, вогнутости, точки перегиба:
Ответ: а) (-∞;0) – выпуклая; (0;∞) – вогнутая;
б) р(5;2) – точка перегиба;
в) (-∞;-2) – выпуклая; (-2;∞) – вогнутая;
г) точек перегиба нет.
1.5.2. Найти асимптоты графика функций:
а) ; б) ;
в) ; г) y=-xarctgx.
г)
1.5.3. Исследовать функции и построить их графики:
а) ; б) ;
в) ; г) .
1.5.4. Найти промежутки выпуклости, вогнутости, точки перегиба:
а) ; б) ;
в) y=ln|x|; г) .
Ответ: а) (2;-8/3); б) ; в) точек перегиба нет;
г) .
1.5.5. Найти асимптоты графиков функций:
а) ; б) y=x-arctgx;
в) .
Ответ: а) х=0; у=1; б) ; в) у=2х; х=0.
1.5.6. Исследовать функции и построить графики:
а) ; б) .
Ответ: а) у=-х – наклонная асимптота; б) уmin(6)=13,5; (0;0) – точка перегиба; х=2; у=х+4 – асимптоты.
Параметрически заданные функции.
Векторная функция скалярного аргумента.
Кривизна плоской кривой
Пусть даны две функции переменной величины , рассматриваемые для одних и тех же значений t. Эти уравнения на плоскости задают некоторую кривую. Так как переменная t называется параметром, то и приведенная система называется параметрическимуравнениемкривой.
Если , то , а .
Пусть теперь некоторая кривая задана в пространстве R3своими параметрическими уравнениями: . Тогда каждому значению t можно поставить в соответствие вектор , который называется векторной функцией скалярного аргумента t. Линия с, описываемая концом радиуса – вектора , называется годографом.
Если рассматривать как траекторию движения материальной точки в пространстве, то законы изменения скорости и ускорения движения этой точки имеют вид:
Пусть задана плоская кривая уравнением y=f(x). Величина определяет ее кривизну.
Радиус кривизны есть . Для параметрически заданной кривой .
1.6.1. Найти , еслиx=arccost, y=arcsint.
Ответ: .
1.6.2. Исключить параметр t из уравнений x=acost, y=bsint. Построить кривую.
Ответ: .
1.6.3. Траектория движения материальной точки задана уравнением . Найти закон изменения скорости движения. Построить траекторию и векторы скорости при t=0; t=1.
Ответ: .
1.6.4. Определить кривизну кривой при t=1.
Ответ: .
Асимптоты
п.1. Понятие асимптоты
Различают вертикальные, горизонтальные и наклонные асимптоты.
Например:
| Вертикальная асимптота x=3 | Горизонтальная асимптота y=1 |
| Наклонная асимптота y=x |
п.2. Вертикальная асимптота
Таким образом, практически каждой точке разрыва 2-го рода (см. §40 данного справочника) соответствует вертикальная асимптота.
Вертикальных асимптот может быть сколько угодно, в том числе, бесконечное множество (например, как у тангенса – см. §6 данного справочника).
Например:
Исследуем непрерывность функции (y=frac<1><(x-1)(x+3)>)
ОДЗ: (xne left<-3;1right>)
(left\notin D) – точки не входят в ОДЗ, подозрительные на разрыв.
Исследуем (x_0=-3). Найдем односторонние пределы: begin lim_frac<1><(x-1)(x+3)>=frac<1><(-3-0-1)(-3-0+3)>=frac<1><-4cdot(-0)>=+infty\ lim_frac<1><(x-1)(x+3)>=frac<1><(-3+0-1)(-3+0+3)>=frac<1><-4cdot(+0)>=-infty end Односторонние пределы не равны и бесконечны.
Точка (x_0=-3) – точка разрыва 2-го рода.
Исследуем (x_1=1). Найдем односторонние пределы: begin lim_frac<1><(x-1)(x+3)>=frac<1><(1-0-1)(1-0+3)>=frac<1><-0cdot 4>=-infty\ lim_frac<1><(x-1)(x+3)>=frac<1><(1+0-1)(1+0+3)>=frac<1><+0cdot 4>=+infty end Односторонние пределы не равны и бесконечны.
Точка (x_1=1) – точка разрыва 2-го рода.
Вывод: у функции (y=frac<1><(x-1)(x+3)>) две точки разрыва 2-го рода (left\), соответственно – две вертикальные асимптоты с уравнениями (x=-3) и (x=1).
п.3. Горизонтальная асимптота
Число горизонтальных асимптот не может быть больше двух.
Например:
Исследуем наличие горизонтальных асимптот у функции (y=frac<1><(x-1)(x+3)>)
Ищем предел функции на минус бесконечности: begin lim_frac<1><(x-1)(x+3)>=frac<1><(-infty)(-infty)>=+0 end На минус бесконечности функция имеет конечный предел (b=0) и стремится к нему сверху (о чем свидетельствует символическая запись +0).
Ищем предел функции на плюс бесконечности: begin lim_frac<1><(x-1)(x+3)>=frac<1><(+infty)(+infty)>=+0 end На плюс бесконечности функция имеет тот же конечный предел (b=0) и также стремится к нему сверху.
Вывод: у функции (y=frac<1><(x-1)(x+3)>) одна горизонтальная асимптота (y=0). На плюс и минус бесконечности функция стремится к асимптоте сверху.
Итоговый график асимптотического поведения функции (y=frac<1><(x-1)(x+3)>):
п.4. Наклонная асимптота
Число наклонных асимптот не может быть больше двух.
Чтобы построить график асимптотического поведения, заметим, что у функции (y=frac), очевидно, есть вертикальная асимптота x=1. При этом: begin lim_frac=-infty, lim_frac=+infty end
График асимптотического поведения функции (y=frac):
п.5. Алгоритм исследования асимптотического поведения функции
На входе: функция (y=f(x))
Шаг 1. Поиск вертикальных асимптот
Исследовать функцию на непрерывность. Если обнаружены точки разрыва 2-го рода, у которых хотя бы один односторонний предел существует и бесконечен, сопоставить каждой такой точке вертикальную асимптоту. Если таких точек не обнаружено, вертикальных асимптот нет.
Шаг 2. Поиск горизонтальных асимптот
Найти пределы функции на плюс и минус бесконечности. Каждому конечному пределу сопоставить горизонтальную асимптоту. Если оба предела конечны и равны, у функции одна горизонтальная асимптота. Если оба предела бесконечны, горизонтальных асимптот нет.
Шаг 3. Поиск наклонных асимптот
Найти пределы отношения функции к аргументу на плюс и минус бесконечности.
Каждому конечному пределу k сопоставить наклонную асимптоту, найти b. Если только один предел конечен, у функции одна наклонная асимптота. Если оба значения k конечны и равны, и оба значения b равны, у функции одна наклонная асимптота. Если оба предела для k бесконечны, наклонных асимптот нет .
На выходе: множество всех асимптот данной функции.
п.6. Примеры
Пример 1. Исследовать асимптотическое поведение функции и построить схематический график:
a) ( y=frac<4x> )
1) Вертикальные асимптоты
Точки, подозрительные на разрыв: (x=pm 1)
Односторонние пределы в точке (x=-1) begin lim_frac<4x><(x+1)(x-1)>=frac<4(-1-0)><(-1-0+1)(-1-0-1)>=frac<-4><-0cdot(-2)>=-infty\ lim_frac<4x><(x+1)(x-1)>=frac<4(-1+0)><(-1+0+1)(-1+0-1)>=frac<-4><+0cdot(-2)>=+infty end Точка (x=-1) – точка разрыва 2-го рода
Односторонние пределы в точке (x=1) begin lim_frac<4x><(x+1)(x-1)>=frac<4(1-0)><(1-0+1)(1-0-1)>=frac<4><2cdot(-0)>=-infty\ lim_frac<4x><(x+1)(x-1)>=frac<4(1+0)><(1+0+1)(1+0-1)>=frac<4><2cdot(+0)>=+infty end Точка (x=1) – точка разрыва 2-го рода
Функция имеет две вертикальные асимптоты (x=pm 1)
График асимптотического поведения функции (y=frac<4x>)
2) Горизонтальные асимптоты
Пределы функции на бесконечности: begin b_1=lim_e^<frac<1>>=e^0=1\ b_2=lim_e^<frac<1>>=e^0=1\ b=b_1=b_2=1 end Функция имеет одну горизонтальную асимптоту (y=1). Функция стремится к этой асимптоте на минус и плюс бесконечности.
График асимптотического поведения функции (y=e^<frac<1>>)
в) ( y=frac )
Заметим, что ( frac=frac<(x+1)(x-1)>=frac<(x^2)(x+1)><(x+1)(x-1)>=frac ) $$ y=fracLeftrightarrow begin y=frac\ xne -1 end $$ График исходной функции совпадает с графиком функции (y=frac), из которого необходимо выколоть точку c абсциссой (x=-1).
3) Наклонные асимптоты
Ищем угловые коэффициенты: begin k_1=lim_frac=left[frac<infty><infty>right]=lim_fracright)>=frac<1+0><1-0>=1\ k_2=lim_frac=left[frac<infty><infty>right]=lim_fracright)>=frac<1+0><1-0>=1\ k=k_1=k_2=1 end У функции есть одна наклонная асимптота с (k=1).
Ищем свободный член: begin b=lim_(y-kx)= lim_left(frac-2right)= lim_frac= lim_frac=left[frac<infty><infty>right]=\ =lim_frac=frac<1+0><1-0>=1 end Функция имеет одну наклонную асимптоту (y=x+1).
График асимптотического поведения функции (y=frac)
2) Горизонтальные асимптоты
Пределы функции на бесконечности: begin b_1=lim_xe^<frac<1><2-x>>=-inftycdot e^0=-infty\ b_2=lim_xe^<frac<1><2-x>>=+inftycdot e^0=+infty end Оба предела бесконечны.
Функция не имеет горизонтальных асимптот.
График асимптотического поведения функции (y=xe^<frac<1><2-x>>)
[spoiler title=”источники:”]
http://poisk-ru.ru/s19964t1.html
http://reshator.com/sprav/algebra/10-11-klass/asimptoty/
[/spoiler]
Пусть
имеем две функции
![]()
и
![]()
,
где
![]()
– общей для
![]()
и
![]()
области определения. Вычисляя при
и
считаем, что полученное значение
![]()
есть функция от полученного
.
Тем самым получаем функцию
![]()
.
Такое приведение, параметрически
заданной, функции к явной не всегда
возможно и может быть потеряна часть
информации. Параметрически заданную
функцию удобно тракторвать как уравнение
движения точки на плоскости. В момент
времени
мы знаем координаты точки
![]()
.
Множество всех точек
,
где
,
называетя графиком функции или траекторией
движения точки. При построении графика
получаем направление движения точки.
Основной
метод построения графика функции,
заданной параметрически, состоит в том,
чтобы разбить весь график на монотонные
и непрерывные куски (ветви). Монотонную
и непрерывную ветвь можно строить по
точкам, используя при этом исследование
функции на концах промежутка, если на
концах хотя бы одна из функций
или
разрывна.
6.1. Порядок построения графика параметрически заданной функции
• Найти
– область определения по
![]()
общую для
и
и отметить её на числовой оси
,
там же отметить точки разрыва функций.
• Найти
производные
![]()
и
![]()
и их область определения и отметить её
на той же числовой оси
,
также отметить точки разрыва производных.
• Решить
уравнения
![]()
,
![]()
и нули производных отметить на той же
оси.
Тем
самым ось
будет разбита на промежутки, на каждом
из которых
,
и вместе с ними
![]()
будут монотонны и непрерывны.
Результат
исследования на монотонность функций
и
оформляют в виде таблицы (см. ниже в
решении примера). По таблице строится
черновик графика, который позже уточняется
нахождением асимптот, участков выпуклости
определённого знака и точек перегиба.
6. 2. Асимптоты параметрического графика
• Если
при некотором
![]()
![]()
или
![]()
и
![]()
,
то
![]()
– горизонтальная асимптота. Пределы
слева и справа вычисляются отдельно,
т.к. это могут быть две разные асимптоты.
Эти пределы уже бывают вычислены при
заполнении таблицы.
• Если
![]()
,
![]()
или
![]()
,
то
![]()
-вертикальная асимптота.
• Если
![]()
или
![]()
и
![]()
или
![]()
,
то возможно, у этой ветви есть наклонная
асимптота
![]()
,
где
![]()
Если
существует, то ищем
![]()
:
![]()
Если
– существует, то у соответствующей ветви
будет наклонная асимптота
.
6. 3. Точки перегиба
Для
нахождения участков выпуклости и точек
перегиба нужна производная
![]()
,
которая находится по формуле
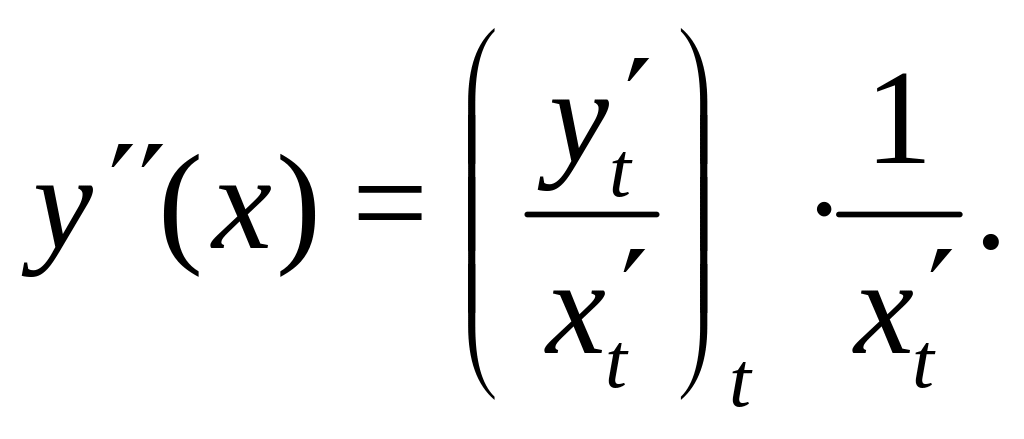
Исследуем
знак
,
определяем направдение выпуклости,
находим точки перегиба, если есть, и
корректируем черновик графика.
6.4. Пример построения графика параметрически заданной функции
Пример
18. 21
Построить
эскиз графика
![]()
,
![]()
.
Решение.
Совокупная область определения:
![]()
.
Найдем
,
:
![]()
Получаем,
что
не существует при
![]()
,
при
![]()
,
не существует при
![]()
и
в нуль не обращается.
На
ось
наносим точки
![]()
,
,
(см. рис. 40):
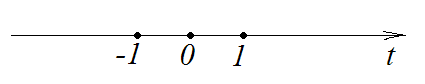
Рис.
40. Ось
.
Мы
получили четыре интервала. На каждом
интервале функции
,
,
а вместе с ними и
будут непрерывны и монотонны. Осталось
найти промежутки изменения функций
и
.
Другими словами, откуда и куда движется
точка по плоскости. Результат такого
иследования оформляем в виде таблицы.
Основных трок в таблице четыре, а столбцов
только, сколько отмечено интервалов на
оси
.
Таблица
14.
|
|
|
|
|
|
|
Знак |
||||
|
Убывает |
Убывает |
Возрастает |
Возрастает |
|
|
от до |
от до |
от до |
от до |
|
|
Знак |
||||
|
Возрастает |
Возрастает |
Возрастает |
Убывает |
|
|
от до |
от до |
от до |
от до |
Для
заполнения первой клетки изменения
функции
вычисляем
![]()
![]()
Для
первой клетки функции
вычисляем
![]()
![]()
Аналогично
заполняются остальные клетки. В точках
непрерывности вычисляем просто значение
функции.
Для
построения графика читаем таблицу по
столбцам. Получаем, что переменная точка
движется от точки
неограниченно влнво (
– убывает) и одновременно поднимается
от
до
.
В
данном случае при
![]()
имеем горизонтальную асимптоту
![]()
.
Получим монотонную ветвь по которой
точка движется влево (см. рис. 41). Правый
конец ветви на рис. 41 соответствует
![]()
,
левый –
![]()
.

Рис.
41. Ветвь графика функции
,
при
.
Остальные
три ветви строим аналогично как движение
точки в нужном направлении.
Для
уточнения графика на ветви
найдем хотя бы одну точку. Выберем
![]()
получим округлённо
![]()
.
На ветви
возьмем
![]()
получим
![]()
.
Исследуем
направление выпуклости. Находим
![]()
![]()
Наносим
на ось
точки разрыва функций
,
и нули
![]()
.
Находим и проставляем знаки
.
(см. рис. 42).
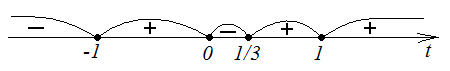
Рис.
42. Ось
и знаки
.
При
![]()
получаем точку перегиба
![]()
.
При
![]()
кривая будет выпукла вверх, при
![]()
– выпукла вниз, при
![]()
– выпукла вверх, при
![]()
– выпукла вниз, при
![]()
– выпукла вниз.
При
![]()
имеем
![]()
,
![]()
,
поэтому у ветви
может быть наклонная асимптота. Проверим
это:
![]()
Это
значит, что асимптоты не существует. У
ветви
при
![]()
проверка показывает отсутствие аимптоты.
При
![]()
– горизонтальная асимптота
.
Заметим также, что
![]()
при любых
,
поэтому график функции находится выше
оси
.
График
функции
![]()
,
![]()
изображен на рис. 43.
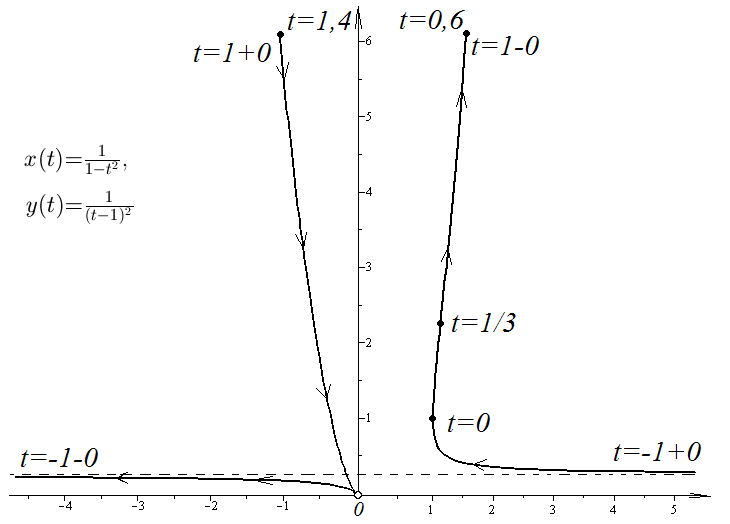
Рис.
43. График функции
,
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Наклонная асимптота параметрической функции
|
|
16/12/13 |
Доброго времени суток. Подскажите, пожалуйста, как найти наклонную асимптоту параметрической функции (как найти такую асимптоту в обычном графике я знаю, и гор/верт асимптоты параметрической функции – тоже).
|
|
|
|
|
ewert |
Re: Наклонная асимптота параметрической функции
|
||
11/05/08 |
Приведите пример задачи. Дело в том, что при обычном, явном задании функции роль параметра играет просто икс. В общем же случае вариантов получения асимптоты, вообще говоря, больше.
|
||
|
|
|||
|
provincialka |
Re: Наклонная асимптота параметрической функции
|
||
18/01/13 |
|||
|
|
|||
|
patzer2097 |
Re: Наклонная асимптота параметрической функции
|
||
14/03/10 |
|||
|
|
|||
|
provincialka |
Re: Наклонная асимптота параметрической функции
|
||
18/01/13 |
patzer2097 , да, конечно, спасибо. Поправлю.
|
||
|
|
|||
|
Desman |
Re: Наклонная асимптота параметрической функции
|
|
16/12/13 |
Сама функция:
|
|
|
|
|
provincialka |
Re: Наклонная асимптота параметрической функции
|
||
18/01/13 |
|||
|
|
|||
|
Desman |
Re: Наклонная асимптота параметрической функции
|
|
16/12/13 |
|
|
|
|
|
Aritaborian |
Re: Наклонная асимптота параметрической функции
|
|
11/06/12 |
Сначала найдём предел
|
|
|
|
|
Desman |
Re: Наклонная асимптота параметрической функции
|
|
16/12/13 |
|
|
|
|
|
provincialka |
Re: Наклонная асимптота параметрической функции
|
||
18/01/13 |
Теперь осталось в каждом случае найти — 19.12.2013, 23:01 — Там получается забавная фигура из трех кусков с 6 лучами.
|
||
|
|
|||
|
Aritaborian |
Re: Наклонная асимптота параметрической функции
|
|
11/06/12 |
(provincialka) Думал, что у вас нет проблем с ТеХом. Предел записывается так: lim limits _{n to infty} a_n.
|
|
|
|
|
provincialka |
Re: Наклонная асимптота параметрической функции
|
||
18/01/13 |
(Aritaborian) спасибо, я именно эту запись постоянно забываю. Пыталась так записать, но не знала, куда “сунуть” подчеркивание. Плюнула и записала по-школярски. Сейчас исправлю.
|
||
|
|
|||
|
Desman |
Re: Наклонная асимптота параметрической функции
|
|
16/12/13 |
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Нужно найти все значения параметра, в которых хотя бы одна из функций
$$x(t),;y(t)$$ бесконечна. После этого нужно проверить наличие асимптот у
графика функции $$y(x)$$.
Условия существования асимптот графика параметрически заданной
функции $$y(x)$$:
Если при $$tto S;;$$ $$xto x_{0},;;$$ а$$;;$$ $$yto infty,;$$ то
$$x=x_{0};-;$$ вертикальная асимптота кривой.
Если при $$tto S;;$$ $$xto infty,;;$$ а$$;;$$ $$yto y_{0},;$$ то
$$;y=y_{0};-;$$ горизонтальная асимптота кривой.
Если при $$tto S;;$$ $$xto infty;;$$ и$$;;$$ $$yto infty,;$$ то
возможна
наклонная асимптота кривой $$y=kx+b,;;k,bin
mathbb{R},;$$ где
$$k=lim_{tto S}frac{y(t)}{x(t)},;;$$ $$b=lim_{tto S}(y(t)-kx(t)),;;$$
$$S={t_{n},;t_{n}-0,;t_{n}+0,;$$$$infty,;-infty,;+infty}, ;;$$$$t_{n}in
mathbb{R}.$$
Как найти асимптоту функции заданной пармаетрически? Без перевода функции в обычный вид!
Сергей Коноплёв
Профи
(905),
закрыт
13 лет назад
ValKo
Высший разум
(112944)
13 лет назад
Сначала находят такое значение параметра to, при котором (t→to) lim(x(t)) = ∞.
Затем находят коэффициенты асимптоты через пределы:
a = (t→to) lim( y(t)/x(t) )
b = ((t→to) lim( y(t) – a x(t) )
Все это, конечно, при условии, что указанные пределы существуют.. . если же нет, значит и нет асимптот…


 (и второй, соотвественно)…
(и второй, соотвественно)… . Впрочем, функция четная, так что достаточно рассмотреть один случай.
. Впрочем, функция четная, так что достаточно рассмотреть один случай.