Как найти аттрактор системы

(с)

Среди ученых ходит байка о нетривиальном способе сделать свой доклад интересным и увлекательным. Во время выступления нужно выбрать в зале самого недоумевающего, самого потерянного слушателя, и рассказывать персонально ему, да так, чтобы зажечь в глазах огонек интереса.

Еще известен афоризм, приписываемый физику Ричарду Фейнману: «Если вы ученый, квантовый физик, и не можете в двух словах объяснить пятилетнему ребенку, чем вы занимаетесь, — вы шарлатан».

Доступно объяснять устройство сложных вещей — великий навык, однако бывают истории, о которые сломает язык даже самый искусный оратор. Теория динамических систем – вот та область, где без визуализации чувствуешь себя слепым садовником в окружении колючих, увенчанных шипами растений.

Сложные непериодические режимы поведения динамических систем можно описать непериодическими траекториями — так называемыми странными аттракторами, имеющими фрактальную структуру. Сегодня покажем, как визуализируют поведение странных и некоторых других аттракторов.

Great attractor

Если остановить на улице первого попавшегося человека, посветить ему в лицо фонариком и спросить, что он знает об аттракторах, то, скорее всего,

ничего не услышим

услышим о Великом аттракторе, притягивающем к себе в глубинах космоса сотни тысяч галактик, чтобы однажды перезапустить Матрицу.

На самом деле космологические аттракторы — это области гравитационной аномалии, вызванные, по всей видимости, особыми галактическими скоплениями, и не имеющие прямого отношения к теме статьи.

Безусловно, стоит отметить, что теория динамических систем особенно хорошо подходит для определения возможных асимптотических состояний различных космологических моделей. Да и видео интересное — посмотрите.

Lorenz attractor

Один из самых знаменитых аттракторов — аттрактор Лоренца, получивший известность благодаря массовому распространению термина «эффект бабочки». Помимо того, что при визуализации аттрактора его форма напоминает бабочку, он представляет собой набор хаотических решений системы Лоренца.

Демонстрация хаотических систем, подобных аттрактору Лоренца (можно сделать самому на C++).

Суть решений Эдварда Лоренца в нелинейной системе обыкновенных дифференциальных уравнений можно передать следующим образом: в любой физической системе при отсутствии совершенного знания начальных условий мы не способны в полной мере предсказать ее будущее. Физические системы могут быть полностью непредсказуемыми даже при отсутствии квантовых эффектов.

Hidden attractor

Аттрактор называется скрытым, если его область притяжения не пересекается с определенной открытой окрестностью точек равновесия. В противном случае он называется самовозбуждающимся аттрактором (self-excited attractor).

Классификация аттракторов (скрытые или самовозбуждающиеся) появилась только в 2009 году — после того как был обнаружен скрытый аттрактор в простейшей электрической цепи Чуа с одним нелинейным резистором, демонстрирующей режимы хаотических колебаний.

Multiscroll attractor

Это целое семейство многокомпонентных аттракторов, включающее в том числе модифицированный скрытый хаотический аттрактор Чуа.

Nonchaotic attractor

Помимо «обычных» хаотических аттракторов существуют периодические, квазипериодические, а также странные нехаотические аттракторы.

Один из основных критериев, по которому аттрактор можно причислить к нехаотическим, — расчет показателей Ляпунова. В этом типе аттракторов для системы экспоненты Ляпунова не являются положительными.

Hyperchaotic attractor

Hyperchaotic attractor — это визуализация дифференциальных уравнений Safieddine Bouali. Гиперхаотические аттракторы существуют только в динамических системах, размерность фазового пространства которых более или равна четырем. Модели гиперхаотических аттракторов могут использоваться в реальных приложениях, имеющих отношение к безопасной связи и шифрованию.

Limit Cycle

Непрерывная динамическая система с изолированной орбитой, подразумевающая самоподдерживающиеся колебания (например, колебания маятниковых часов или сердцебиение во время отдыха).

Rössler attractor

Хаотический аттрактор системы дифференциальных уравнений Рёсслера. В 1976 году врач Отто Рёсслер представил трехмерную модель динамики химических реакций, протекающих в некоторой смеси с перемешиванием. Для аттрактора Рёсслера характерна фрактальная структура в фазовой плоскости.

На аттракторе Рёсслера траектории не пересекают сами себя. Поверхности, образующие странный аттрактор, делятся на отдельные слои, создавая бесконечное множество поверхностей, каждая из которых находится чрезвычайно близко к соседней. Можно допустить, что лента, которая образует основание аттрактора, подобна многослойному листу Мёбиуса.

Spiral attractor

Spiral attractor — аттрактор, позволивший изучить жизнь амеб Dictyostelium discoideum. При истощении питательных ресурсов амебы секретируют циклический аденозинмонофосфат (цАМФ) — сигнальные молекулы, привлекающие соседние клетки к центральному местоположению. Голодные миксамёбы (одноклеточная стадия развития Dictyostelium), подчиняясь сигналам, сползаются к центру, который образовался в результате «склеивания» первых миксамёб, случайно оказавшихся рядом. Соединяясь с помощью молекул клеточной адгезии, они образуют агрегат из нескольких десятков тысяч клеток. Собственно, этот процесс и представлен на видео.

Tinkerbell attractor

Карта Тинкербелла — динамическая система с дискретным временем, демонстрирующая хаотическое поведение в двумерном пространстве. Форму Тинкербелла можно изменить, чтобы получить другие хаотические аттракторы в системах защищенных коммуникаций, использующих хаос связи.

Thomas’ cyclically symmetric attractor

Трехмерный аттрактор, предложенный биоинформатиком Рене Томасом, может рассматриваться как траектория демпфирующей частицы, движущейся в трехмерной решетке сил.

Ikeda attractor

Фрактальный набор, к которому притягивается орбита любой точки на плоскости, если мы продолжаем итерацию определенной карты от плоскости к самой себе.

Заключение

Мы рассмотрели лишь несколько известных типов аттракторов. Всего же вы можете найти упоминания о сотне различных аттракторов.

Надо отметить, что это очень молодая область науки, и поиск, начавшийся с идеи уйти от математической абстракции в сторону практического «создания» хаоса, продолжается по сей день.

Неизменно одно: наш интерес с силой Великого аттрактора притягивают системы, чрезвычайно чувствительные к небольшим отклонениям в описании начального состояния. Мы сталкиваемся с этими системами не из праздного любопытства — мы живем среди них и благодаря им.

Аттра́ктор (англ. attract — привлекать, притягивать) — компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности. Аттрактором может являться притягивающая неподвижная точка (к примеру, в задаче о маятнике с трением о воздух), периодическая траектория (пример — самовозбуждающиеся колебания в контуре с положительной обратной связью), или некоторая ограниченная область с неустойчивыми траекториями внутри (как у странного аттрактора).

Существуют различные формализации понятия стремления, что приводит к различным определениям аттрактора, задающим, соответственно, потенциально различные множества (зачастую — вложенные одно в другое). Наиболее употребительными определениями являются максимальный аттрактор (зачастую — в своей малой окрестности, см. ниже), аттрактор Милнора и неблуждающее множество.

Классификация[править | править код]

Аттракторы классифицируют по:

1. Формализации понятия стремления: различают максимальный аттрактор, неблуждающее множество, аттрактор Милнора, центр Биркгофа, статистический и минимальный аттрактор.
2. Регулярности самого аттрактора: аттракторы делят на регулярные (притягивающая неподвижная точка, притягивающая периодическая траектория, многообразие) и странные (нерегулярные — зачастую фрактальные и/или в каком-либо сечении устроенные как канторово множество; динамика на них обычно хаотична).
3. Локальности («притягивающее множество») и глобальности (здесь же — термин «минимальный» в значении «неделимый»).

Также, есть известные «именные» примеры аттракторов: Лоренца, Плыкина, соленоид Смейла-Вильямса, гетероклинический аттрактор (пример Боуэна).

Свойства и связанные определения[править | править код]

При всех определениях аттрактор полагается замкнутым и (полностью) инвариантным множеством.

С понятием аттрактора также тесно связано понятие меры Синая-Рюэлля-Боуэна: инвариантной меры на нём, к которой стремятся временные средние типичной (в смысле меры Лебега) начальной точки либо временные средние итераций меры Лебега. Впрочем, такая мера существует не всегда (что иллюстрирует, в частности, пример Боуэна).

Виды формализации определения[править | править код]

Поскольку всё фазовое пространство в любом случае сохраняется динамикой, формальное определение аттрактора можно давать, исходя из философии, что «аттрактор это наименьшее множество, к которому всё стремится» — иными словами, выкидывая из фазового пространства всё, что может быть выкинуто.

Максимальный аттрактор[править | править код]

Пусть для динамической системы задана область , которая переводится строго внутрь себя динамикой:

Тогда максимальным аттрактором системы в ограничении на U называется пересечение всех его образов под действием динамики:

То же самое определение можно применить и для потоков: в этом случае, необходимо потребовать, чтобы векторное поле, задающее поток, на границе области было направлено строго внутрь неё.

Это определение часто применяется как для характеризации множества как «естественного» аттрактора («является максимальным аттрактором своей окрестности»). Также его применяют в уравнениях с частными производными^[1].

У этого определения есть два недостатка. Во-первых, для его применения необходимо найти поглощающую область. Во-вторых, если такая область была выбрана неудачно — скажем, содержала отталкивающую неподвижную точку с её бассейном отталкивания — то в максимальном аттракторе будут «лишние» точки, около которых на самом деле несколько раз подряд оказаться нельзя, но текущий выбор области этого «не чувствует».

Аттрактор Милнора[править | править код]

По определению, аттрактором Милнора динамической системы называется наименьшее по включению замкнутое множество, содержащее ω-предельные множества почти всех начальных точек по мере Лебега. Иными словами — это наименьшее множество, к которому стремится траектория типичной начальной точки.

Неблуждающее множество[править | править код]

Точка x динамической системы называется блуждающей, если итерации некоторой её окрестности U никогда эту окрестность не пересекают:

Иными словами, точка блуждающая, если у неё есть окрестность, которую любая траектория может пересечь только один раз. Множество всех точек, не являющихся блуждающими, называется неблуждающим множеством.

Статистический аттрактор[править | править код]

Статистический аттрактор определяется как наименьшее по включению замкнутое множество , в окрестности которого почти все точки проводят почти всё время: для любой его окрестности для почти любой (в смысле меры Лебега) точки выполнено

Минимальный аттрактор[править | править код]

Минимальный аттрактор определяется как наименьшее по включению замкнутое множество , в окрестности которого почти вся мера Лебега проводит почти всё время: для любой его окрестности выполнено

Примеры несовпадений[править | править код]

Этот раздел статьи ещё не написан. Здесь может располагаться раздел, посвящённый примерам несовпадения задаваемых различными определениями аттракторов. Помогите Википедии, написав его. (30 июня 2016)

Локальность, минимальность и глобальность[править | править код]

Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (30 июня 2016)

Регулярные и странные аттракторы[править | править код]

Регулярные аттракторы[править | править код]

Притягивающая неподвижная точка[править | править код]

(пример: маятник с трением)

Предельный цикл[править | править код]

(пример: микрофон+колонки, осциллятор Ван дер Поля)

Странные аттракторы[править | править код]

(примеры: аттрактор Лоренца, аттрактор Рёсслера, соленоид Смейла-Вильямса; комментарий про эффект бабочки и про динамический хаос.)

Странный аттрактор — это притягивающее множество неустойчивых траекторий в фазовом пространстве диссипативной динамической системы^[2]. В отличие от аттрактора, не является многообразием, то есть не является кривой или поверхностью. Структура странного аттрактора фрактальна. Траектория такого аттрактора непериодическая (она не замыкается) и режим функционирования неустойчив (малые отклонения от режима нарастают). Основным критерием хаотичности аттрактора является экспоненциальное нарастание во времени малых возмущений. Следствием этого является «перемешивание» в системе, непериодичность во времени любой из координат системы, сплошной спектр мощности и убывающая во времени автокорреляционная функция.

Динамика на странных аттракторах часто бывает хаотической: прогнозирование траектории, попавшей в аттрактор, затруднено, поскольку малая неточность в начальных данных через некоторое время может привести к сильному расхождению прогноза с реальной траекторией. Непредсказуемость траектории в детерминированных динамических системах называют динамическим хаосом, отличая его от стохастического хаоса, возникающего в стохастических динамических системах. Это явление также называют эффектом бабочки, подразумевая возможность преобразования слабых турбулентных потоков воздуха, вызванных взмахом крыльев бабочки в одной точке планеты, в мощное торнадо на другой её стороне вследствие многократного их усиления в атмосфере за некоторое время. Но на самом деле взмах крыла бабочки обыкновенно не создает торнадо, так как на практике наблюдается такая тенденция, что такие маленькие колебания в среднем не меняют динамики таких сложных систем как атмосфера планеты, и сам Лоренц по этому поводу говорил: «Но в целом, я утверждаю, что в течение лет незначительные потрясения ни увеличивают, ни уменьшают частоту возникновения различных погодных явлений, таких как ураганы. Всё, что они могут сделать — это изменить порядок, в котором происходят эти явления.» И это, пожалуй, важная и удивительная вещь, без которой было бы трудно, а то и вообще невозможно изучать хаотическую динамику (динамику, которая чувствительна к малейшим изменениям начальных условий системы).

Среди странных аттракторов встречаются такие, хаусдорфова размерность которых отлична от топологической размерности и является дробной. Одним из наиболее известных среди подобных аттракторов является аттрактор Лоренца.

Именные примеры[править | править код]

Аттрактор Лоренца[править | править код]

Система дифференциальных уравнений, создающих аттрактор Лоренца, имеет вид:

при следующих значениях параметров: , , .
Аттрактор Лоренца не является классическим. Он также не является странным в смысле Смейла.^[3]

Соленоид Смейла-Вильямса[править | править код]

Соленоид Смейла-Вильямса — пример обратимой динамической системы, аналогичной по поведению траекторий отображению удвоения на окружности. Более точно, эта динамическая система определена на полнотории, и за одну её итерацию угловая координата удваивается; откуда автоматически возникает экспоненциальное разбегание траекторий и хаотичность динамики. Также соленоидом называют и максимальный аттрактор этой системы (откуда, собственно, и происходит название): он устроен как (несчётное) объединение «нитей», наматывающихся вдоль полнотория.

Аттрактор Плыкина[править | править код]

Аттрактор Плыкина — пример динамической системы на диске, максимальный аттрактор которой гиперболичен. В частности, этот пример структурно устойчив, как удовлетворяющий аксиоме A Смейла.

Этот раздел статьи ещё не написан. Здесь может располагаться раздел, посвящённый описанию аттрактора Плыкина (см. также [1]). Помогите Википедии, написав его. (9 ноября 2009)

Пример Боуэна, или гетероклинический аттрактор[править | править код]

Этот раздел статьи ещё не написан. Здесь может располагаться раздел, посвящённый примеру Боуэна. Помогите Википедии, написав его. (9 ноября 2009)

Аттрактор Эно[править | править код]

Этот раздел статьи ещё не написан. Здесь может располагаться раздел, посвящённый аттрактору Эно. Помогите Википедии, написав его. (9 ноября 2009)

https://web.archive.org/web/20101227004521/http://ibiblio.org/e-notes/Chaos/ru/strange_r.htm

Гипотезы[править | править код]

Гипотеза Палиса^[4][править | править код]

• Существует такое метрически плотное подмножество D пространства T, что аттрактор Милнора всякой динамической системы из множества D может быть разбит лишь на конечное количество транзитивных компонент;
• Транзитивные компоненты аттрактора обладают SRB-мерой;
• Транзитивные компоненты аттрактора стохастически устойчивы в своих бассейнах притяжения;
• Для типичной системы типичного семейства одномерной динамики компоненты аттрактора либо представляют собой притягивающие периодические траектории, либо обладают абсолютно непрерывной инвариантной мерой.^[5]

Этот раздел статьи ещё не написан. Здесь может располагаться раздел, посвящённый описанию гипотезы Палиса. Помогите Википедии, написав его. (9 ноября 2009)

Гипотезы Рюэля[править | править код]

Этот раздел статьи ещё не написан. Здесь может располагаться раздел, посвящённый описанию гипотезы Рюэля. Помогите Википедии, написав его. (9 ноября 2009)

См. также[править | править код]

• Мера Синая — Рюэлля — Боуэна
• Цепь Чуа

Примечания[править | править код]

Ссылки и литература[править | править код]

• A. Gorodetski, Yu. Ilyashenko. Minimal and strange attractors, International Journal of Bifurcation and Chaos, vol. 6, no. 6 (1996), pp. 1177—1183.
• А. С. Городецкий. Минимальные аттракторы и частично гиперболические множества динамических систем. Дисс. к. ф.-м. н., МГУ, 2001.
• Электронная библиотека по нелинейной динамике
• Статья Дж. Милнора «Аттрактор», Scholarpedia.
• Галерея самых странных аттракторов. LENTA.RU. Дата обращения: 28 марта 2013. Архивировано 4 апреля 2013 года.
• Е. В. Никульчев. Геометрический метод реконструкции систем по экспериментальным данным // Письма в ЖТФ. 2007. Т. 33. Вып. 6. С. 83-89.
• Е. В. Никульчев. Идентификация динамических систем на основе симметрий реконструированных аттракторов м. 2010.

In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve,^[2] for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed.

In finite-dimensional systems, the evolving variable may be represented algebraically as an n-dimensional vector. The attractor is a region in n-dimensional space. In physical systems, the n dimensions may be, for example, two or three positional coordinates for each of one or more physical entities; in economic systems, they may be separate variables such as the inflation rate and the unemployment rate.^{[not verified in body]}

If the evolving variable is two- or three-dimensional, the attractor of the dynamic process can be represented geometrically in two or three dimensions, (as for example in the three-dimensional case depicted to the right). An attractor can be a point, a finite set of points, a curve, a manifold, or even a complicated set with a fractal structure known as a strange attractor (see strange attractor below). If the variable is a scalar, the attractor is a subset of the real number line. Describing the attractors of chaotic dynamical systems has been one of the achievements of chaos theory.

A trajectory of the dynamical system in the attractor does not have to satisfy any special constraints except for remaining on the attractor, forward in time. The trajectory may be periodic or chaotic. If a set of points is periodic or chaotic, but the flow in the neighborhood is away from the set, the set is not an attractor, but instead is called a repeller (or repellor).

Motivation of attractors[edit]

A dynamical system is generally described by one or more differential or difference equations. The equations of a given dynamical system specify its behavior over any given short period of time. To determine the system’s behavior for a longer period, it is often necessary to integrate the equations, either through analytical means or through iteration, often with the aid of computers.

Dynamical systems in the physical world tend to arise from dissipative systems: if it were not for some driving force, the motion would cease. (Dissipation may come from internal friction, thermodynamic losses, or loss of material, among many causes.) The dissipation and the driving force tend to balance, killing off initial transients and settle the system into its typical behavior. The subset of the phase space of the dynamical system corresponding to the typical behavior is the attractor, also known as the attracting section or attractee.

Invariant sets and limit sets are similar to the attractor concept. An invariant set is a set that evolves to itself under the dynamics.^[3] Attractors may contain invariant sets. A limit set is a set of points such that there exists some initial state that ends up arbitrarily close to the limit set (i.e. to each point of the set) as time goes to infinity. Attractors are limit sets, but not all limit sets are attractors: It is possible to have some points of a system converge to a limit set, but different points when perturbed slightly off the limit set may get knocked off and never return to the vicinity of the limit set.

For example, the damped pendulum has two invariant points: the point x₀ of minimum height and the point x₁ of maximum height. The point x₀ is also a limit set, as trajectories converge to it; the point x₁ is not a limit set. Because of the dissipation due to air resistance, the point x₀ is also an attractor. If there was no dissipation, x₀ would not be an attractor. Aristotle believed that objects moved only as long as they were pushed, which is an early formulation of a dissipative attractor.

Some attractors are known to be chaotic (see strange attractor), in which case the evolution of any two distinct points of the attractor result in exponentially diverging trajectories, which complicates prediction when even the smallest noise is present in the system.^[4]

Mathematical definition[edit]

Let represent time and let be a function which specifies the dynamics of the system. That is, if is a point in an -dimensional phase space, representing the initial state of the system, then and, for a positive value of , is the result of the evolution of this state after units of time. For example, if the system describes the evolution of a free particle in one dimension then the phase space is the plane with coordinates , where is the position of the particle, is its velocity, , and the evolution is given by

An attractor is a subset of the phase space characterized by the following three conditions:

For any open neighborhood of , there is a positive constant such that for all real .

• There is no proper (non-empty) subset of having the first two properties.

Since the basin of attraction contains an open set containing , every point that is sufficiently close to is attracted to . The definition of an attractor uses a metric on the phase space, but the resulting notion usually depends only on the topology of the phase space. In the case of , the Euclidean norm is typically used.

Many other definitions of attractor occur in the literature. For example, some authors require that an attractor have positive measure (preventing a point from being an attractor), others relax the requirement that be a neighborhood.^[5]

Types of attractors[edit]

Attractors are portions or subsets of the phase space of a dynamical system. Until the 1960s, attractors were thought of as being simple geometric subsets of the phase space, like points, lines, surfaces, and simple regions of three-dimensional space. More complex attractors that cannot be categorized as simple geometric subsets, such as topologically wild sets, were known of at the time but were thought to be fragile anomalies. Stephen Smale was able to show that his horseshoe map was robust and that its attractor had the structure of a Cantor set.

Two simple attractors are a fixed point and the limit cycle. Attractors can take on many other geometric shapes (phase space subsets). But when these sets (or the motions within them) cannot be easily described as simple combinations (e.g. intersection and union) of fundamental geometric objects (e.g. lines, surfaces, spheres, toroids, manifolds), then the attractor is called a strange attractor.

Fixed point[edit]

A fixed point of a function or transformation is a point that is mapped to itself by the function or transformation. If we regard the evolution of a dynamical system as a series of transformations, then there may or may not be a point which remains fixed under each transformation. The final state that a dynamical system evolves towards corresponds to an attracting fixed point of the evolution function for that system, such as the center bottom position of a damped pendulum, the level and flat water line of sloshing water in a glass, or the bottom center of a bowl containing a rolling marble. But the fixed point(s) of a dynamic system is not necessarily an attractor of the system. For example, if the bowl containing a rolling marble was inverted and the marble was balanced on top of the bowl, the center bottom (now top) of the bowl is a fixed state, but not an attractor. This is equivalent to the difference between stable and unstable equilibria. In the case of a marble on top of an inverted bowl (a hill), that point at the top of the bowl (hill) is a fixed point (equilibrium), but not an attractor (unstable equilibrium).

In addition, physical dynamic systems with at least one fixed point invariably have multiple fixed points and attractors due to the reality of dynamics in the physical world, including the nonlinear dynamics of stiction, friction, surface roughness, deformation (both elastic and plasticity), and even quantum mechanics.^[6] In the case of a marble on top of an inverted bowl, even if the bowl seems perfectly hemispherical, and the marble’s spherical shape, are both much more complex surfaces when examined under a microscope, and their shapes change or deform during contact. Any physical surface can be seen to have a rough terrain of multiple peaks, valleys, saddle points, ridges, ravines, and plains.^[7] There are many points in this surface terrain (and the dynamic system of a similarly rough marble rolling around on this microscopic terrain) that are considered stationary or fixed points, some of which are categorized as attractors.

Finite number of points[edit]

In a discrete-time system, an attractor can take the form of a finite number of points that are visited in sequence. Each of these points is called a periodic point. This is illustrated by the logistic map, which depending on its specific parameter value can have an attractor consisting of 1 point, 2 points, 2ⁿ points, 3 points, 3×2ⁿ points, 4 points, 5 points, or any given positive integer number of points.

Limit cycle[edit]

A limit cycle is a periodic orbit of a continuous dynamical system that is isolated. It concerns a cyclic attractor. Examples include the swings of a pendulum clock, and the heartbeat while resting. The limit cycle of an ideal pendulum is not an example of a limit cycle attractor because its orbits are not isolated: in the phase space of the ideal pendulum, near any point of a periodic orbit there is another point that belongs to a different periodic orbit, so the former orbit is not attracting. For a physical pendulum under friction, the resting state will be a fixed-point attractor. The difference with the clock pendulum is that there, energy is injected by the escapement mechanism to maintain the cycle.

Limit torus[edit]

There may be more than one frequency in the periodic trajectory of the system through the state of a limit cycle. For example, in physics, one frequency may dictate the rate at which a planet orbits a star while a second frequency describes the oscillations in the distance between the two bodies. If two of these frequencies form an irrational fraction (i.e. they are incommensurate), the trajectory is no longer closed, and the limit cycle becomes a limit torus. This kind of attractor is called an N_t -torus if there are N_t incommensurate frequencies. For example, here is a 2-torus:

A time series corresponding to this attractor is a quasiperiodic series: A discretely sampled sum of N_t periodic functions (not necessarily sine waves) with incommensurate frequencies. Such a time series does not have a strict periodicity, but its power spectrum still consists only of sharp lines.

Strange attractor[edit]

An attractor is called strange if it has a fractal structure.^{[clarification needed]} This is often the case when the dynamics on it are chaotic, but strange nonchaotic attractors also exist. If a strange attractor is chaotic, exhibiting sensitive dependence on initial conditions, then any two arbitrarily close alternative initial points on the attractor, after any of various numbers of iterations, will lead to points that are arbitrarily far apart (subject to the confines of the attractor), and after any of various other numbers of iterations will lead to points that are arbitrarily close together. Thus a dynamic system with a chaotic attractor is locally unstable yet globally stable: once some sequences have entered the attractor, nearby points diverge from one another but never depart from the attractor.^[8]

The term strange attractor was coined by David Ruelle and Floris Takens to describe the attractor resulting from a series of bifurcations of a system describing fluid flow.^[9] Strange attractors are often differentiable in a few directions, but some are like a Cantor dust, and therefore not differentiable. Strange attractors may also be found in the presence of noise, where they may be shown to support invariant random probability measures of Sinai–Ruelle–Bowen type.^[10]

Examples of strange attractors include the double-scroll attractor, Hénon attractor, Rössler attractor, and Lorenz attractor.

Attractors characterize the evolution of a system[edit]

The parameters of a dynamic equation evolve as the equation is iterated, and the specific values may depend on the starting parameters. An example is the well-studied logistic map, , whose basins of attraction for various values of the parameter are shown in the figure. If , all starting values of will rapidly lead to function values that go to negative infinity; starting values of will also go to negative infinity. But for the values rapidly converge to , i.e. at this value of , a single value of is an attractor for the function’s behaviour. For other values of , more than one value of may be visited: if is 3.2, starting values of will lead to function values that alternate between and . At some values of , the attractor is a single point (a “fixed point”), at other values of two values of are visited in turn (a period-doubling bifurcation), or, as a result of further doubling, any number values of ; at yet other values of , any given number of values of are visited in turn; finally, for some values of , an infinitude of points are visited. Thus one and the same dynamic equation can have various types of attractors, depending on its starting parameters.

Basins of attraction[edit]

An attractor’s basin of attraction is the region of the phase space, over which iterations are defined, such that any point (any initial condition) in that region will asymptotically be iterated into the attractor. For a stable linear system, every point in the phase space is in the basin of attraction. However, in nonlinear systems, some points may map directly or asymptotically to infinity, while other points may lie in a different basin of attraction and map asymptotically into a different attractor; other initial conditions may be in or map directly into a non-attracting point or cycle.^[11]

Linear equation or system[edit]

A single-variable (univariate) linear difference equation of the homogeneous form diverges to infinity if from all initial points except 0; there is no attractor and therefore no basin of attraction. But if all points on the number line map asymptotically (or directly in the case of 0) to 0; 0 is the attractor, and the entire number line is the basin of attraction.

Likewise, a linear matrix difference equation in a dynamic vector , of the homogeneous form in terms of square matrix will have all elements of the dynamic vector diverge to infinity if the largesteigenvalues of is greater than 1 in absolute value; there is no attractor and no basin of attraction. But if the largest eigenvalue is less than 1 in magnitude, all initial vectors will asymptotically converge to the zero vector, which is the attractor; the entire -dimensional space of potential initial vectors is the basin of attraction.

Similar features apply to linear differential equations. The scalar equation causes all initial values of except zero to diverge to infinity if but to converge to an attractor at the value 0 if , making the entire number line the basin of attraction for 0. And the matrix system gives divergence from all initial points except the vector of zeroes if any eigenvalue of the matrix is positive; but if all the eigenvalues are negative the vector of zeroes is an attractor whose basin of attraction is the entire phase space.

Nonlinear equation or system[edit]

Equations or systems that are nonlinear can give rise to a richer variety of behavior than can linear systems. One example is Newton’s method of iterating to a root of a nonlinear expression. If the expression has more than one real root, some starting points for the iterative algorithm will lead to one of the roots asymptotically, and other starting points will lead to another. The basins of attraction for the expression’s roots are generally not simple—it is not simply that the points nearest one root all map there, giving a basin of attraction consisting of nearby points. The basins of attraction can be infinite in number and arbitrarily small. For example,^[12] for the function , the following initial conditions are in successive basins of attraction:

2.35287527 converges to 4;

2.35284172 converges to −3;

2.35283735 converges to 4;

2.352836327 converges to −3;

2.352836323 converges to 1.

Newton’s method can also be applied to complex functions to find their roots. Each root has a basin of attraction in the complex plane; these basins can be mapped as in the image shown. As can be seen, the combined basin of attraction for a particular root can have many disconnected regions. For many complex functions, the boundaries of the basins of attraction are fractals.

Partial differential equations[edit]

Parabolic partial differential equations may have finite-dimensional attractors. The diffusive part of the equation damps higher frequencies and in some cases leads to a global attractor. The Ginzburg–Landau, the Kuramoto–Sivashinsky, and the two-dimensional, forced Navier–Stokes equations are all known to have global attractors of finite dimension.

For the three-dimensional, incompressible Navier–Stokes equation with periodic boundary conditions, if it has a global attractor, then this attractor will be of finite dimensions.^[13]

See also[edit]

• Cycle detection
• Hyperbolic set
• Stable manifold
• Steady state
• Wada basin
• Hidden oscillation
• Rössler attractor
• Stable distribution
• Convergent evolution

References[edit]

Further reading[edit]

• John Milnor (ed.). “Attractor”. Scholarpedia.
• David Ruelle; Floris Takens (1971). “On the nature of turbulence”. Communications in Mathematical Physics. 20 (3): 167–192. Bibcode:1971CMaPh..20..167R. doi:10.1007/BF01646553. S2CID 17074317.
• D. Ruelle (1981). “Small random perturbations of dynamical systems and the definition of attractors” (PDF). Communications in Mathematical Physics. 82 (1): 137–151. Bibcode:1981CMaPh..82..137R. doi:10.1007/BF01206949. S2CID 55827557.
• David Ruelle (1989). Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press. ISBN 978-0-12-601710-6.
• Ruelle, David (August 2006). “What is…a Strange Attractor?” (PDF). Notices of the American Mathematical Society. 53 (7): 764–765. Retrieved 16 January 2008.
• Celso Grebogi; Edward Ott; Pelikan; Yorke (1984). “Strange attractors that are not chaotic”. Physica D. 13 (1–2): 261–268. Bibcode:1984PhyD…13..261G. doi:10.1016/0167-2789(84)90282-3.
• Chekroun, M. D.; E. Simonnet; M. Ghil (2011). “Stochastic climate dynamics: Random attractors and time-dependent invariant measures”. Physica D. 240 (21): 1685–1700. Bibcode:2011PhyD..240.1685C. CiteSeerX 10.1.1.156.5891. doi:10.1016/j.physd.2011.06.005.
• Edward N. Lorenz (1996) The Essence of Chaos ISBN 0-295-97514-8
• James Gleick (1988) Chaos: Making a New Science ISBN 0-14-009250-1

External links[edit]

• Basin of attraction on Scholarpedia
• A gallery of trigonometric strange attractors
• Double scroll attractor Chua’s circuit simulation
• A gallery of polynomial strange attractors
• Chaoscope, a 3D Strange Attractor rendering freeware
• Research abstract and software laboratory
• Online strange attractors generator
• Interactive trigonometric attractors generator
• Economic attractor

Построение аттракторов

Аттрактор– неподвижная точкасистемыназывается устойчивой (или аттрактором),
если для любой окрестности N точкисуществует
некоторая меньшая окрестность этой
точкитакая, что любая траектория, проходящая
через N ‘, остается в N при возрастании
t. Кроме того, под аттрактором понимают
совокупность всехустойчивыхточекфазового портретасистемы.

Для большинства систем можно наблюдать,
что облако исходных точек «конденсируется»
на некоторые предельные объекты. Это и
есть аттракторы. Динамические системы,
которые обладают аттракторами, называют
диссипативными. Существование аттрактором
приводит к весьма важным выводам о
поведении системы. В этом случае
исследование установившихся режимов
эквивалентно изучению геометрической
структуры аттрактора.

Фрактальная размерность и показатель Хёрста

Для того чтобы иметь возможность
сравнивать фрактальные свойства
различных природных процессов, таких,
как сток рек, отложение ила или рост
колец деревьев, Хёрст использовал при
анализе временных рядов наблюдений
безразмерный показатель в виде отношения
размаха (R) накопленного отклонения от
среднего к среднеквадратическому
отклонению (S) – R/S-метод.

Зависимость параметра (R/S) от времени
наблюдения, построенная в двойном
логарифмическом масштабе, представляет
исследуемый процесс в виде фрактальной
функции. При аппроксимации фрактальной
функции прямой линией определяется
угловой коэффициент Н, называемый
показателем Хёрста. Показатель
Хёрста используют для вычисления
основного фрактального параметра
процесса – размерности Хаусдорфа-Безиковича:

D = 2 – H.

Размерность Хаусдорфа-Безиковича или
фрактальная размерностьявляется
интегральной характеристикой объекта
или процесса. Она обобщает понятие
евклидовой геометрической размерности
и, в отличие от последней, может принимать
нецелочисленные значения. Вообще,размерность– число, характеризующее
скорость роста числа ячеек покрытия
данного множества при уменьшении размера
ячеек.

Познавательная сила понятия фрактальной
размерности состоит в том, что с его
помощью можно упорядочивать исследуемые
процессы по свойствам хаотичности или
сложности и, таким образом, классифицировать
их.

Общие закономерности связи степени
зашумленности сигналов и их фрактальных
свойств, выраженных показателем Хёрста,
проиллюстрированы на рис. 2, где изображены
реализации временных рядов наблюдений
(объем выборки N = 1000), имеющие различные
фрактальные свойства и, соответственно,
разные оценки показателя Хёрста.

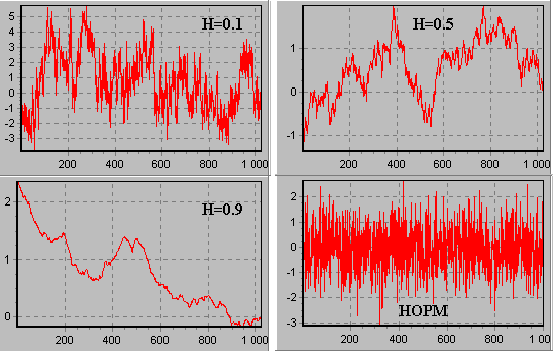
Рис.
7.2. Типовые реализации фрактальных
временных рядов наблюдений c H = 0,1; H =
0,5; H = 0,9 и белого шума с нормальным
распределением

Визуально можно определить, что
стационарные случайные сигналы (например,
шум с нормальным распределением) имеют
максимальную зашумленность, а зашумленность
фрактальных сигналов падает с увеличением
показателя Хёрста.

Задание на лабораторную работу

1. Ознакомиться с теоретическим введением
к лабораторной работе.

2. В среде MatLabнаписать
функции генерации синусоидального
сигнала, пилы, меандра. С помощью программыFractanпостроить фазовый
портрет сигнала, а также рассчитать для
этого сигнала показатель Хёрста.
Проанализировать и объяснить полученные
результаты.

3. Построить фазовый портрет логистической
функции для цикла периода 2, 3, 8, для
хаотического режима (подобрать параметры
логистической функции для необходимых
режимов можно с помощью программы
Chaos).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

в математический поле динамические системы, аттрактор представляет собой набор числовых значений, к которым система стремится развиваться для самых разных начальных условий системы. Системные значения, которые достаточно близки к значениям аттрактора, остаются близкими, даже если они слегка нарушены.

В конечномерных системах эволюционирующая переменная может быть представлена алгебраически как п-размерный вектор. Аттрактором является область в п-мерное пространство. В физические системы, то п размеры могут быть, например, двумя или тремя позиционными координатами для каждого из одного или нескольких физических объектов; в экономические системы, они могут быть отдельными переменными, такими как уровень инфляции и уровень безработицы.

Если эволюционирующая переменная двух- или трехмерная, аттрактор динамического процесса может быть представлен геометрически в двух или трех измерениях (как, например, в трехмерном случае, изображенном справа). Аттрактором может быть точка, конечный набор точек, a изгиб, а многообразие, или даже сложный набор с фрактал структура известная как странный аттрактор (увидеть странный аттрактор ниже). Если переменная скаляр, аттрактор – это подмножество прямой числовой линии. Описание аттракторов хаотических динамических систем было одним из достижений теория хаоса.

А траектория динамической системы в аттракторе не должен удовлетворять никаким специальным ограничениям, за исключением того, что остается на аттракторе вперед во времени. Траектория может быть периодический или хаотичный. Если набор точек периодический или хаотический, но поток в окрестности находится вдали от набора, набор не является аттрактором, а вместо этого называется отпугиватель (или же репеллент).

Мотивация аттракторов

А динамическая система обычно описывается одним или несколькими дифференциал или разностные уравнения. Уравнения данной динамической системы определяют ее поведение в течение любого заданного короткого периода времени. Чтобы определить поведение системы в течение более длительного периода, часто необходимо интегрировать уравнения, либо с помощью аналитических средств, либо с помощью итерация, часто с помощью компьютеров.

Динамические системы в физическом мире обычно возникают из диссипативные системы: если бы не какая-то движущая сила, движение прекратилось бы. (Рассеяние может происходить из внутреннее трение, термодинамические потери, или потеря материала, среди многих причин.) Рассеяние и движущая сила имеют тенденцию уравновешиваться, подавляя начальные переходные процессы и приводя систему в ее типичное поведение. Подмножество фазовое пространство динамической системы, соответствующей типичному поведению, является аттрактор, также известный как секция привлечения или аттракцион.

Инвариантные множества и предельные наборы аналогичны концепции аттрактора. An инвариантный набор – это набор, который эволюционирует под действием динамики.^[2] Аттракторы могут содержать инвариантные множества. А установленный предел – это набор точек, в котором существует некоторое начальное состояние, которое заканчивается произвольно близким к предельному набору (то есть к каждой точке набора) по мере того, как время стремится к бесконечности. Аттракторы – это предельные множества, но не все предельные множества являются аттракторами: возможно, что некоторые точки системы сходятся к предельному набору, но разные точки при незначительном отклонении от предельного набора могут быть сбиты с толку и никогда не вернуться в окрестности установленный предел.

Например, затухающий маятник имеет две инвариантные точки: точка Икс₀ минимальной высоты и точки Икс₁ максимальной высоты. Смысл Икс₀ также является предельным множеством, так как к нему сходятся траектории; смысл Икс₁ не является ограничением. Из-за рассеивания из-за сопротивления воздуха точка Икс₀ также является аттрактором. Если бы не было диссипации, Икс₀ не будет аттрактором. Аристотель считал, что объекты перемещаются только до тех пор, пока их толкают, что является ранней формулировкой диссипативного аттрактора.

Известно, что некоторые аттракторы хаотичны (см. # Странный аттрактор ), и в этом случае эволюция любых двух различных точек аттрактора приводит к экспоненциальному расходящиеся траектории, что усложняет прогноз, когда в системе присутствует даже самый маленький шум.^[3]

Математическое определение

Позволять т представляют время и пусть ж(т, •) – функция, задающая динамику системы. То есть, если а точка в п-мерное фазовое пространство, представляющее начальное состояние системы, то ж(0, а) = а а при положительном значении т, ж(т, а) является результатом эволюции этого состояния после т единиц времени. Например, если система описывает эволюцию свободной частицы в одном измерении, то фазовое пространство – это плоскость р² с координатами (Икс,v), где Икс – положение частицы, v его скорость, а = (Икс,v), а эволюция дается выражением

An аттрактор это подмножество А из фазовое пространство характеризуется следующими тремя состояниями:

• А является прямой инвариант под ж: если а является элементом А тогда так ж(т,а), для всехт > 0.
• Существует район из А, называется бассейн притяжения за А и обозначен B(А), который состоит из всех точек б что “войти А в пределе т → ∞ “. Более формально B(А) – множество всех точек б в фазовом пространстве со следующим свойством:

Для любого открытого района N из А, существует положительная постоянная Т такой, что ж(т,б) ∈ N для всех реальных т > Т.

• Не существует собственного (непустого) подмножества А имеющий первые два свойства.

Поскольку бассейн притяжения содержит открытый набор содержащий А, каждая точка, достаточно близкая к А привлекает А. В определении аттрактора используется метрика на фазовом пространстве, но результирующее понятие обычно зависит только от топологии фазового пространства. На случай, если р^п, обычно используется евклидова норма.

В литературе встречается множество других определений аттрактора. Например, некоторые авторы требуют, чтобы аттрактор имел положительный мера (предотвращая превращение точки в аттрактор), другие ослабляют требование, чтобы B(А) быть соседством. ^[4]

Типы аттракторов

Аттракторы – это порции или подмножества из фазовое пространство из динамическая система. До 1960-х годов аттракторы считались простые геометрические подмножества фазового пространства, как точки, линии, поверхности, и простые области трехмерное пространство. Более сложные аттракторы, которые нельзя отнести к категории простых геометрических подмножеств, например топологически дикие наборы, о которых было известно в то время, но считались хрупкими аномалиями. Стивен Смейл смог показать, что его карта подковы был крепкий и что его аттрактор имеет структуру Кантор набор.

Два простых аттрактора – это фиксированная точка и предельный цикл. Аттракторы могут принимать множество других геометрических форм (подмножества фазового пространства). Но когда эти множества (или движения внутри них) нельзя легко описать как простые комбинации (например, пересечение и союз ) из фундаментальные геометрические объекты (например. линии, поверхности, сферы, тороиды, коллекторы ), то аттрактор называется странный аттрактор.

Фиксированная точка

А фиксированная точка функции или преобразования – это точка, которая отображается сама на себя функцией или преобразованием. Если мы рассматриваем эволюцию динамической системы как серию преобразований, тогда может быть или не быть точка, которая остается фиксированной при каждом преобразовании. Конечное состояние, в котором развивается динамическая система, соответствует фиксированной точке притяжения функции эволюции для этой системы, такой как центральное нижнее положение затухающий маятник, уровень и плоская водная линия плещущейся воды в стакане или центр дна чаши содержат катящийся шарик. Но неподвижная точка (точки) динамической системы не обязательно является аттрактором системы. Например, если чаша, содержащая катящийся шарик, была перевернута, и шарик был уравновешен на верхней части чаши, центральное дно (теперь верх) чаши является фиксированным состоянием, но не аттрактором. Это эквивалентно разнице между стабильные и нестабильные равновесия. В случае шарика на вершине перевернутой чаши (холма) эта точка на вершине чаши (холма) является фиксированной точкой (равновесием), но не аттрактором (устойчивое равновесие).

Кроме того, физические динамические системы с хотя бы одной фиксированной точкой неизменно имеют несколько фиксированных точек и аттракторов из-за реальности динамики в физическом мире, включая нелинейная динамика из прикол, трение, шероховатость поверхности, деформация (обе эластичный и пластичность ), и даже квантовая механика.^[5] В случае мрамора на перевернутой чаше, даже если она кажется идеальной полусферический, и мрамор сферический формы, являются как гораздо более сложными поверхностями при исследовании под микроскопом, так и их формы меняются или деформировать во время контакта. Можно увидеть, что любая физическая поверхность имеет неровную местность с множеством пиков, долин, седловин, гребней, оврагов и равнин.^[6] На этой поверхности (и в динамической системе такого же грубого мрамора, катящегося по этой микроскопической местности) есть много точек, которые считаются стационарный или неподвижные точки, некоторые из которых классифицируются как аттракторы.

Конечное количество баллов

В дискретное время В системе аттрактор может принимать форму конечного числа точек, которые посещаются последовательно. Каждая из этих точек называется периодическая точка. Это иллюстрируется логистическая карта, который в зависимости от конкретного значения параметра может иметь аттрактор, состоящий из 2^п точки, 3 × 2^п баллов и т. д. для любого значения п.

Предельный цикл

А предельный цикл периодическая орбита непрерывной динамической системы, которая изолированные. Примеры включают колебания маятниковые часы, и сердцебиение в состоянии покоя. (Предельный цикл идеального маятника не является примером аттрактора предельного цикла, потому что его орбиты не изолированы: в фазовом пространстве идеального маятника около любой точки периодической орбиты есть другая точка, принадлежащая другой периодической орбите. орбита, поэтому прежняя орбита не привлекает).

Предельный тор

В периодической траектории системы через состояние предельного цикла может быть более одной частоты. Например, в физике одна частота может определять скорость, с которой планета вращается вокруг звезды, а вторая частота описывает колебания расстояния между двумя телами. Если две из этих частот образуют иррациональная дробь (т.е. они несоизмеримый ), траектория перестает быть замкнутой, и предельный цикл становится предельным тор. Такой аттрактор называется N_т -тор если есть N_т несоизмеримые частоты. Например, вот 2-тор:

Временной ряд, соответствующий этому аттрактору, есть квазипериодический серия: дискретно выбранная сумма N_т периодические функции (не обязательно синус волны) с несоизмеримыми частотами. Такой временной ряд не имеет строгой периодичности, но его спектр мощности по-прежнему состоит только из резких линий.

Странный аттрактор

Аттрактор называется странный если у него есть фрактал структура. Это часто бывает, когда динамика на нем хаотичный, но странные нехаотические аттракторы тоже существуют. Если странный аттрактор хаотичен, чувствительная зависимость от начальных условий, то любые две произвольно близкие альтернативные начальные точки на аттракторе после любого из различного числа итераций приведут к точкам, которые расположены произвольно далеко друг от друга (в зависимости от ограничений аттрактора), и после любого другого количества итераций приводят к точкам, которые расположены произвольно близко друг к другу. Таким образом, динамическая система с хаотическим аттрактором является локально нестабильной, но глобально устойчивой: как только некоторые последовательности входят в аттрактор, близлежащие точки расходятся друг от друга, но никогда не отходят от аттрактора.^[7]

Период, термин странный аттрактор был придуман Дэвид Рюэлль и Флорис Такенс описать аттрактор, возникающий в результате ряда бифуркации системы, описывающей течение жидкости.^[8] Странные аттракторы часто дифференцируемый в нескольких направлениях, но некоторые из них подобно а Канторовская пыль и поэтому не дифференцируемы. Странные аттракторы также могут быть обнаружены в присутствии шума, где они могут быть показаны как поддерживающие инвариантные случайные вероятностные меры типа Синая – Рюэля – Боуэна.^[9]

Примеры странных аттракторов включают аттрактор двойной прокрутки, Аттрактор Энона, Аттрактор Рёсслера, и Аттрактор Лоренца.

Аттракторы характеризуют эволюцию системы

Параметры динамического уравнения развиваются по мере повторения уравнения, и конкретные значения могут зависеть от начальных параметров. Примером может служить хорошо изученный логистическая карта, , бассейны притяжения которых при различных значениях параметра р показаны на рисунке. Если , все начинается Икс ценности быстро приведет к значениям функции, которые стремятся к отрицательной бесконечности; начало Икс ценности уйдет в бесконечность. Но для то Икс ценности быстро сходятся к , т.е. при этом значении р, одно значение Икс является аттрактором поведения функции. Для других значений р, может быть посещено более одного значения x: если р составляет 3,2, начальные значения приведет к значениям функции, которые чередуются между и . При некоторых значениях р, аттрактор – единственная точка (a “фиксированная точка” ), при других значениях р два значения Икс посещаются по очереди ( бифуркация удвоения периода ); при других значениях r, любом заданном количестве значений Икс посещаются по очереди; наконец, для некоторых значений р, посещается бесконечное количество точек. Таким образом, одно и то же динамическое уравнение может иметь различные типы аттракторов в зависимости от его исходных параметров.

Бассейны притяжения

Аттрактора бассейн притяжения это регион фазовое пространство, по которым определяются итерации, такая, что любая точка (любая начальное состояние ) в этом регионе будет асимптотически повторяться в аттрактор. Для стабильный линейная система, каждая точка фазового пространства находится в области притяжения. Однако в нелинейные системы некоторые точки могут отображаться прямо или асимптотически в бесконечность, в то время как другие точки могут находиться в другом бассейне притяжения и асимптотически отображаться в другой аттрактор; другие начальные условия могут быть в непривлекающей точке или цикле или отображаться непосредственно в ней.^[10]

Линейное уравнение или система

Однопеременная (одномерная) линейная разностное уравнение из однородная форма расходится в бесконечность, если |а| > 1 из всех начальных точек, кроме 0; нет аттрактора и, следовательно, нет области притяжения. Но если |а| <1 все точки на числовой прямой асимптотически (или непосредственно в случае 0) отображаются в 0; 0 – это аттрактор, а вся числовая линия – это область притяжения.

Аналогичным образом линейный матричное разностное уравнение в динамичном вектор Икс, однородной формы с точки зрения квадратная матрица А все элементы динамического вектора будут расходиться до бесконечности, если наибольший собственное значение из А больше 1 по модулю; нет ни аттрактора, ни притяжения. Но если наибольшее собственное значение меньше единицы по величине, все начальные векторы будут асимптотически сходиться к нулевому вектору, который является аттрактором; целиком п-мерное пространство потенциальных начальных векторов является областью притяжения.

Аналогичные функции применимы к линейным дифференциальные уравнения. Скалярное уравнение вызывает все начальные значения Икс кроме нуля расходиться до бесконечности, если а > 0, но сходиться к аттрактору при значении 0, если а <0, что делает всю числовую линию областью притяжения для 0. А матричная система дает расхождение со всеми начальными точками, кроме вектора нулей, если любое собственное значение матрицы А положительный; но если все собственные значения отрицательны, вектор нулей является аттрактором, чьей областью притяжения является все фазовое пространство.

Нелинейное уравнение или система

Уравнения или системы, которые нелинейный может привести к более разнообразному поведению, чем линейные системы. Одним из примеров является Метод Ньютона итерации до корня нелинейного выражения. Если в выражении более одного настоящий root, некоторые начальные точки для итеративного алгоритма приведут к одному из корней асимптотически, а другие начальные точки приведут к другому. Области притяжения для корней выражения, как правило, непростые – дело не просто в том, что все точки, ближайшие к одному корню, отображаются там, создавая область притяжения, состоящую из близлежащих точек. Области притяжения могут быть бесконечными и сколь угодно маленькими. Например,^[11] для функции , следующие начальные условия находятся в последовательных областях притяжения:

2.35287527 сходится к 4;

2,35284172 сходится к −3;

2.35283735 сходится к 4;

2,352836327 сходится к −3;

2.352836323 сходится к 1.

Метод Ньютона также может быть применен к сложные функции найти свои корни. У каждого корня есть бассейн притяжения в комплексная плоскость; эти бассейны можно нанести на карту, как показано на изображении. Как можно видеть, объединенная область притяжения для определенного корня может иметь много разрозненных областей. Для многих сложных функций границы областей притяжения фракталы.

Уравнения с частными производными

Параболические уравнения в частных производных могут иметь конечномерные аттракторы. Диффузионная часть уравнения подавляет более высокие частоты и в некоторых случаях приводит к глобальному аттрактору. В Гинзбург – Ландау, то Курамото – Сивашинский, а двумерная вынужденная Уравнения Навье – Стокса как известно, имеют глобальные аттракторы конечной размерности.

Для трехмерного несжимаемого уравнения Навье – Стокса с периодическим граничные условия, если он имеет глобальный аттрактор, то этот аттрактор будет конечных размеров.^[12]

Смотрите также

• Обнаружение цикла
• Гиперболический набор
• Стабильный коллектор
• Устойчивое состояние
• Бассейн Вада
• Скрытые колебания
• Аттрактор Росслера
• Стабильное распространение

Рекомендации

дальнейшее чтение

• Джон Милнор (ред.). «Аттрактор». Scholarpedia.
• Дэвид Рюэлль; Флорис Такенс (1971). «О природе турбулентности». Коммуникации по математической физике. 20 (3): 167–192. Дои:10.1007 / BF01646553. S2CID  17074317.
• Д. Рюэль (1981). «Малые случайные возмущения динамических систем и определение аттракторов». Коммуникации по математической физике. 82: 137–151. Дои:10.1007 / BF01206949. S2CID  55827557.
• Дэвид Рюэлль (1989). Элементы дифференцируемой динамики и теории бифуркаций. Академическая пресса. ISBN  978-0-12-601710-6.
• Руэль, Дэвид (Август 2006 г.). “Что такое … странный аттрактор?” (PDF). Уведомления Американского математического общества. 53 (7): 764–765. Получено 16 января 2008.
• Селсо Гребоги; Эдвард Отт; Пеликан; Йорк (1984). «Странные аттракторы, которые не хаотичны». Physica D. 13 (1–2): 261–268. Дои:10.1016/0167-2789(84)90282-3.
• Chekroun, M.D .; Э. Симонне; М. Гил (2011). «Стохастическая динамика климата: случайные аттракторы и инвариантные меры, зависящие от времени». Physica D. 240 (21): 1685–1700. CiteSeerX  10.1.1.156.5891. Дои:10.1016 / j.physd.2011.06.005.
• Эдвард Н. Лоренц (1996) Сущность Хаоса ISBN  0-295-97514-8
• Джеймс Глейк (1988) Хаос: создание новой науки ISBN  0-14-009250-1

внешняя ссылка

• Бассейн притяжения на Scholarpedia
• Галерея странных тригонометрических аттракторов
• Аттрактор двойной прокрутки Схематическое моделирование Чуа
• Галерея полиномиальных странных аттракторов
• Chaoscope, бесплатная программа для рендеринга 3D-странного аттрактора
• Аннотация исследования и лаборатория программного обеспечения
• Генератор странных аттракторов онлайн
• Генератор интерактивных тригонометрических аттракторов
• Экономический аттрактор