Как найти аванс в экселе

Что такое аванс и в какие сроки его необходимо выдавать?

Все, кто работал по найму, понимают, что такое аванс на практическом уровне. Во второй половине месяца работники получают определенную сумму. Как правило, она составляет какой-то процент от оклада. Эту часть оплаты труда, которую работники получают в течение расчетного месяца, и называют по традиции авансом.

Если же обратиться к трудовому законодательству, основой которого является ТК РФ, то там это понятие в явном виде отсутствует. Но сам порядок выплаты зарплаты ТК РФ регламентирует. Законом от 03.07.2016 № 272-ФЗ были внесены соответствующие изменения в ст. 136 кодекса. В действующей редакции указанной статьи определяется, что работники должны получать оплату труда не реже чем раз в 2 недели и не позднее 15 календарных дней со дня окончания расчетного периода.

Понятно, что полностью рассчитать зарплату за месяц сложнее, чем начислить аванс. Поэтому на практике в организации сначала определяют дату выплаты зарплаты. В соответствии со ст. 136 ТК РФ она должна быть установлена в период с 1 до 15 числа следующего месяца. Какое конкретно число выбрать в этом диапазоне, зависит от организации учета на предприятии. Чем лучше организован обмен информацией между службами и выше степень автоматизации учета, тем раньше можно начислить и выплатить зарплату.

После установления даты выплаты зарплаты к ней нужно прибавить полмесяца (15 дней). Так и определяется дата выплаты аванса в соответствии с требованиями ТК РФ. Например, если срок для выплаты зарплаты установлен 4 числа, то аванс нужно выдать не позднее 19, если 8, то не позднее 23 и т. д.

А если выдать аванс раньше, чем через 15 дней? Например, 12 числа при дате выплаты зарплаты 5. В этом случае от аванса до следующей выплаты зарплаты пройдет больше 20 дней, что превышает установленный ТК РФ срок. В этом случае организация может быть привлечена к ответственности за нарушение порядка выплаты.

Подробне об этом см. «Зарплата раньше срока может повлечь штраф».

Как правильно считать по новым правилам аванс в 2023 году?

Новые правила расчета аванса, не так давно прописанные в ТК РФ, коснулись главным образом только сроков. А при определении суммы аванса следует исходить из реально отработанного за первую половину месяца времени (письмо Минтруда от 10.08.2017 № 14-1/В-725).

См. также: «Аванс: сколько процентов платить работникам, объяснил Роструд».

Причем чиновники рекомендуют учитывать при расчете аванса только те составляющие зарплаты, которые прямо привязаны к рабочему времени (оклад, надбавки за совмещение и т. п.). Что же касается выплат, размер которых можно определить только по итогам месяца (например, премии за выполнение плана), то они, по мнению Минтруда, при расчете аванса использоваться не должны.

Подробнее о премии как составной части оплаты труда читайте в статье «Является ли премия частью заработной платы?».

Рассмотрим, как считать аванс с учетом разъяснений государственных органов.

Пример 1

Количество рабочих дней в расчетном месяце — 20, оклад инженера Петрова И. И. составляет 25 000 руб. в месяц. За первую половину месяца Петров И. И. отработал 9 дней. Таким образом, ему должен быть выплачен аванс в сумме:

А = 25 000 руб. / 20 дн. × 9 дн. = 11 250 руб.

Однако он не получит на руки эту сумму полностью, из нее работодателю придется удержать НДФЛ. Связано это с тем, что с 1 января 2023 года порядок удержания НДФЛ с заработной платы меняется. Об этом мы поговорим в следующем разделе.

Таким образом, новая формула расчета аванса учитывает реально отработанное время за период с 1 по 15 число расчетного месяца.

Подобная методика расчета является весьма трудоемкой. Фактически при этом удваивается объем работы бухгалтерских служб, занимающихся расчетом зарплаты. Поэтому на практике при определении того, как рассчитывается аванс по зарплате, его обычно устанавливают в виде определенного процента от суммы оклада.

Минздравсоцразвития в своем письме от 25.02.2009 № 22-2-709 рекомендует выдавать заработную плату и аванс в сопоставимых суммах. Т. к. ранее, когда при выплате аванса НДФЛ не удерживался, для обеспечения сопоставимости выплат оптимальным решением было установление аванса в размере 40–45% от оклада. С 2023 года чтобы обеспечить такую сопоставимость некоторым работодателям придется поднять процент аванса до 50%. Подробнее об этом читайте здесь.

Рассмотрим, как правильно рассчитать аванс при этом варианте его начисления.

Пример 2

Оклад Петрова И. И. составляет 25 000 руб. в месяц. На предприятии в 2022 году был установлен размер аванса — 40% от оклада. Вычетами по НДФЛ Петров И. И. не пользовался. В этом случае он получал аванс в сумме:

Ав. = 25 000 руб. × 40% = 10 000 руб.

И заработную плату в сумме:

З/п = 25 000 руб. – 25 000 руб. × 13% – 10 000 руб. = 11 750 руб.

В 2023 году суммы, полученные на руки, будут немного отличаться:

Ав. = 25 000 руб. х 40% = 10 000,00 руб. На руки = 10 000,00 – НДФЛ = 8 700,00 руб.

З/п = 25 000,00 – 10 000,00 = 15 000,00 руб. На руки = 15 000,00 – НДФЛ = 13 050,00 руб.

Видно, что зарплата за первую половину месяца при таком значении аванса оказывается гораздо меньшей. Если же в 2023 году закрепить аванс на уровне 50% от оклада, то за каждую часть месяца Петров будет получать 10 875,00 руб., что обеспечит равномерность получения доходов этим сотрудником.

Понятно, что в примере рассмотрен идеальный вариант. По факту работник может часть расчетного месяца отсутствовать на рабочем месте (по болезни, из-за отпуска и т. п.). В этом случае лучше рассчитывать аванс исходя из отработанного времени.

Как рассчитывать аванс по зарплате в том или ином случае, необходимо указать в локальных нормативных актах предприятия.

Платится ли НДФЛ при выдаче аванса?

При выплате зарплаты работодатель выполняет функции налогового агента, удерживая НДФЛ из дохода работника. Ранее до 31 декабря 2022 года зарплата становилась доходом с точки зрения налогообложения в последний день расчетного месяца (п. 2 ст. 223 НК РФ). А так как аванс выплачивается в течение расчетного периода, то на момент его выплаты доход за период еще не считался полученным и, соответственно, не было оснований для уплаты НДФЛ. Эта позиция, верная для предыдущей редакции Налогового кодекса, отражена, в частности, в письмах Минфина от 13.02.2019 № 03-04-06/8932, от 13.07.2017 № 03-04-05/44802.

Однако если на предприятии дата получения аванса установливалась на последний день месяца, то налоговики могли признать эту выплату доходом за истекший период. В этом случае предприятию приходилось рассчитывать и удерживать НДФЛ дважды в месяц. Позицию налоговых органов по данному вопросу поддерживал и Верховный суд (определение от 11.05.2016 № 309-КГ16-1804). Чтобы избежать подобных проблем, лучшим решением было не выдавать аванс в последний день месяца.

Нужно ли уплачивать страховые взносы с аванса по зарплате? Ответ на данный вопрос дала советник государственной гражданской службы РФ 1 класса Баландина Е. Б. Получите бесплатный пробный доступ к системе КонсультантПлюс и ознакомьтесь с точкой зрения чиновника.

Удержание НДФЛ с аванса в 2023 году – изменения

Закон от 14.07.2022 № 263-ФЗ скорректировал правила удержания и перечисления НДФЛ с заработной платы, действовавшие ранее в соответствии с НК РФ. С 1 января 2023 года датой получения физлицом дохода в виде зарплаты — и за первую и за вторую часть  месяца, а также  отпускных и больничных будет признаваться дата его фактической выплаты на руки или на счет сотрудника — по общему правилу, установленному подп. 1 п. 1 ст. 223 НК РФ. Удержание НДФЛ отныне будет происходить и в момент выплаты аванса в том числе, т.е. до завершения расчетов по основной части зарплаты.

Кроме того, значительно поменялись сроки перечисления удержанного налога в бюджет. Если раньше мы перечисляли налог до конца рабочего дня, следующего за днем выплаты зарплаты, по больничным и отпускным – до конца месяца, в котором они были выданы, то теперь НК РФ определил единые даты для всех без исключения выплат – это 28 число + дополнительные даты в декабре и январе. На какие даты следует ориентироваться при уплате НДФЛ в 2023 году, узнайте из этой статьи.

О порядке расчета и перечислении НДФЛ в бюджет с 1 января 2023 года налоговыми агентами мы рассказали здесь.

В 2023 году при переводе НДФЛ и всех прочих налогов в бюджет не нужно указывать КБК в платежке, ведь мы начнем погашать все налоговые обязательства одной суммой. Это связано с введением принципа единого налогового платежа. Но чтобы инспекторы не ошиблись при разноске сумм по видам налогов, хозяйствующие субъекты заранее, в срок до 25 числа, станут направлять уведомления в налоговую. Подробности, касающиеся уведомления по НДФЛ, ищите в этом материале. 

Отметим, что в 2023 году еще разрешат перечислять налоги по старому – платежками с прописанными КБК, без подачи уведомления. Однако для этого потребуется попасть под определенное условие.

О том, какие еще изменения ждут нас в налоговом законодательстве в 2023 году, расскажет Типовая ситуация от справочно-правовой системы КонсультантПлюс. Оформите бесплатный пробный доступ и переходите к просмотру материала.

Итоги

Сроки выплаты аванса и зарплаты в соответствии с ТК РФ устанавливаются так, чтобы выплаты работникам осуществлялись не реже чем раз в 2 недели. Порядок того, как рассчитывается аванс, ТК РФ в явном виде не определяет.

Государственные органы рекомендуют выдавать аванс на основании реально отработанного времени за первую половину месяца. При установлении аванса в процентах, по мнению чиновников, аванс и расчет по итогам месяца должны быть сопоставимы по сумме. Ранее НДФЛ при выдаче аванса не удерживался, однако с 2023 года данная норма Налогового кодекса утрачивает свою силу и налоговый агент станет обязан удерживать подоходный налог и при выплате аванса, и при выплате окончательного расчета.

Рассмотрим
ряд примеров, разбор которых позволит
читателю освоить основные средства
Excel. Кроме того, читатель, возможно,
обнаружит среди предложенных примеров
задачу, похожую на ту, что он решает
ежедневно на своем рабочем месте, но
делает это вручную. Представленный ниже
материал не следует воспринимать как
пособие по финансовой математике.
Тематика предлагаемых задач часто
связана с денежными расчетами просто
потому, что их постановка понятна любому
читателю. Это, конечно, совершенно не
означает, что для такого инструмента
не найдется множества технических
приложений. Отметим, что некоторые
задания могут быть исполнены несколькими,
иногда, возможно, и более эффективными,
способами. Цель предлагаемого далее
материала – не получение самого лучшего
решения в каждом конкретном случае, а
овладение техникой построения и
оформления таблиц.

Замечания.
1. Информация, используемая
в примерах, носит условный характер и
не отражает реального законодательства.
2. Таблицы представлены на
рисунках как в нормальном (“результативном”)
виде, так и, по возможности, – в формульном
виде. Номера рисунков в тексте совпадают
с номерами задач. 3. Следует иметь
в виду, что данные во многих примерах
сопровождаются единицами измерения
($, кг, шт и др.), которые не вводятся
непосредственно в клетки таблицы, но
устанавливаются с помощью форматирования.

 В
связи с тем, что во многих примерах
имеются “процентные” данные, напомним,
как их использовать. Проценты вводятся
в таблицу как десятичные коэффициенты,
которым затем придается формат %, либо
они сразу вводятся со знаком процента.
В Excel число, изображенное со знаком
процента, соответствует в сто раз меньшей
величине без знака %. То, что, например,
выглядит как 20%, на самом деле является
0,2, то, что выглядит как 100%, соответствует
1. Иными словами, это просто разные формы
представления одного и того же числа.

Пусть
нам нужно выделить часть числа,
определенную как его некоторый процент.
При вычислениях “на бумаге” следует
выполнить такие действия

искомая_часть_числа=исходное_число
_*
процент_от_числа/100%
.

В
Excel же достаточно формулы вида
искомая_часть_числа=исходное_число
* процент_от_
числа.

Т.е.
нужно умножить это число на процент.
Делить на 100% нет необходимости. Однако,
если это сделать, результат не измениться
ведь здесь 100%1.

Например,
нужно найти 20% от числа 500:
=500*20%=500*0,2=100.

Обе
формулы в Excel совершено идентичны.

Другая
ситуация. Пусть нужно вычислить новое
значение числа, уменьшенное на некоторый
процент (например, учесть скидку). Здесь
следует записать так

новое_число=исходное_число
– исходное_число
* процент или короче

новое_число=исходное_число
* (1–процент).

Например,
пусть старая цена товара составляет
500 руб., а новая цена имеет скидку в 20%.
Определить новую цену товара в рублях
=500(1–20%)=500(100%–20%)=500(1–0,2).
Все три записи в Excel идентичны.

Аналогичным
образом вычисляется наценка:
новое_число=исходное_число
* (1+процент).

Наценка
в 20% к 500 руб. даст такую новую цену
=500(1+20%)=500(100%+20%)=500(1+0,2).

Поскольку,
обычно, такие данные участвуют в формулах
не в качестве констант, а своими адресами
(например, А3
и В4),
вполне очевидны формулы вида =А3*(1–В4)
и =А3*(1+В4)
для скидки и наценки. Очевидно также,
что превратить одну функцию в другую
можно просто изменив знак непосредственно
при числе, находящемся в ячейке, содержащей
процент (здесь в В4).
Во всех случаях следует иметь в виду,
что нельзя складывать (вычитать)
процент с каким-либо иным значением,
кроме процента (коэффициента).

Замечание.
Владельцы калькуляторов
знают, что (при наличии на нем кнопки %)
правомочно действие, в котором с
собственно данными (например с деньгами)
складываются/вычитаются проценты.
Например, действие вида 200р+10% повлечет
результат равный 220р (т.е. будет начислен
желаемый процент), что, как будто,
противоречит вышесказанному. Здесь
следует учесть, что в калькуляторе
имеется специальная операция взятия
процента, которая на сам деле выполнила
действие вида 200+200*10%/100%. Поскольку в
Excel
отсутствует подобный механизм начисления
процента, мы
должны пользоваться известными школьными
правилами работы с процентами.



В
начале рассмотрим простенький пример,
который нам поможет выработать подход
к проектированию таблиц. На рис. 5.0а
слева изображена вся таблица, справа –
формулы для столбца D. Пусть требуется
выполнить расчет платы за квартиру.
Положим она состоит из оплаты за
коммунальные услуги (по 2 руб. за квадратный
метр площади) и оплаты за газоснабжение
(по 3 руб. с каждого проживающего в
квартире человека).

Здесь
реализован очевидный механизм расчета

квартплата=площадь
* тариф_за_коммунальные_услуги
+ человек * тариф_за_газ.

Или
в виде чисел для первой квартиры
D3=80*2+4*3.

	A	B	C	D		D
1	РАСЧЕТ КВАРТПЛАТЫ
2	Квартира	Площадь	Человек	Кв. плата		Кв. плата
3	№1	80	4	172		=B3*2+C3*3
4	№2	60	3	129		=B4*2+C4*3
5	№3	110	5	235		=B5*2+C5*3
6	№4	120	8	264		=B6*2+C6*3
7	ВСЕГО	370	20	800		=СУММ(D3:D6)
			Рис. 5.0а

Поскольку
квартир в доме может быть очень много,
непосредственный ввод таких формул для
каждой из них делает использование
компьютера малопродуктивным, если не
сказать бессмысленным. По существу, мы
применяем его как тривиальный калькулятор.
Конечно, этого и не требуется. Нужно
использовать не арифметическое, а
алгебраическое представление данных,
когда они участвуют в формуле не своими
непосредственными значениями, а адресами
ячеек (т.е. переменными), в которых они
находятся. В нашем случае D3=B3*2+
C3*3. Далее
следует просто скопировать (воспользовавшись
маркером заполнения клетки) первую
формулу D3=B3*2+C3*3
во все нижележащие ячейки. В следующей
снизу клетке она превратится в
D4=B4*2+C4*3,
затем в D5=B5*2+C5*3
и т.д. Здесь проявилось чрезвычайно
полезное свойство копируемых ссылок –
адаптируемость адресных ссылок под
новое положение.

	A	B	C	D		D
1	Тарифы оплаты
2	комм/уc:	2,0р/метр	газ:	3,0р/чел		3,0р/чел
3	РАСЧЕТ КВАРТПЛАТЫ
4	Квартира	Площадь	Человек	Кв. плата		Кв. плата
5	№1	80м	4	172,0р		=B5*B$2+C5*D$2
6	№2	60м	3	129,0р		=B6*B$2+C6*D$2
7	№3	110м	5	235,0р		=B7*B$2+C7*D$2
8	№4	120м	8	264,0р		=B8*B$2+C8*D$2
9	ВСЕГО	370м	20	800,0р		=СУММ(D5:D8)
			Рис. 5.0б

Очевидным
недостатком нашего решения является
его зависимость от изменения тарифов
– при их пересмотре придется изменять
множество формул. В виду этого, в
электронных таблицах все нормативные
данные выносят в отдельные области
листа (или даже на отдельные листы),
обычно, в верхней его части. В нашем
случае такими данными являются цены на
коммунальное услуги и газ. Разместим
их в клетках В2 и D2 (рис. 5.0б), а в формулах
вместо констант (2 руб. и 3 руб.) укажем
ссылки на эти ячейки. Как и ранее, введем
формулу только для первой квартиры
(D5=B5*B2+C5*D2),
скопировав затем
ее вниз. Если поступить таким образом,
мы обнаружим что в нижележащих клетках
D6,
D7
и т.п. получены выражения вида:

 
D5=B5*B2+C5*D2   

D6=B6*B3+C6*D3,

D7=B7*B4+C6*D4
и т.д.

Они
неверны (ошибочные значения подчеркнуты).
Поскольку при перемещении вниз изменились
также адреса, содержащие тарифы, то
площадь квартиры №2 перемножается уже
не на тариф коммунальных услуг из ячейки
В2, а на содержимое пустой клетки В3.
Аналогично с оплатой за газ. Это же
относится и ко всем другим квартирам.
Чтобы избежать нежелательного изменения
адресов тарифов, они фиксируются в
формулах (“замо­раживаются”) введением
знака $ перед номером строки (D5=B5*B$2+C5*
D$2). Копирование
такой формулы вниз

	A	B		B
1	Вклад:	1000		1000
2	ПРОСТЫЕ ПРОЦЕНТЫ
3	Норма	Прибыль		Прибыль
4	10%	100,00		=A4*$B$1
5	15%	150,00		=A5*$B$1
6	20%	200,00		=A6*$B$1
7	30%	300,00		=A7*$B$1
8		750,00		=СУММ(B4:B7)
		Рис. 5.1

 

D5=B5*B$2+C5*D$2   

D6=B6*B$2+C6*D$2,

D7=B7*B$2+C6*D$2
и т.д.

уже
не повлечет изменения цифры 2 в адресах
B$2
и D$2
(результаты
изображены на рис. 5.0б).

Ранее
нами уже обсуждался вопрос о возможности
вставки строк в таблицу и влияние этого
действия на поведение итоговых функции.
В нашем случае вставка новых данных
(новых квартир) между 4-ой и 5-ой и между
8-ой и 9-ой строками будет проигнорирована
функцией СУММ(D5:D8).
Обеспечить правильную реакцию функции
на верхнюю вставку можно, включив
заголовок таблицы в область суммирования,
т.е. сделать D9=СУММ(D4:D8).
Правильную реакцию на дополнение таблицы
в нижней ее части можно реализовать
(начиная с версии Excel-2000),
если установить флажок Расширять
форматы и формулы в списках (вкладка
Правка).
Однако, если (конечно, в сложных случаях)
этот механизм не срабатывает,
такое дополнение можно осуществлять
оставляя пустой самую последнюю (в нашем
случае девятую) строку между собственно
данными и десятой строкой, где теперь
будут вычисляться суммы. Тогда щелчок
мышью на строке 9 с последующей вставкой
новой строки опустит 9-ю и 10-ю строки
ниже и изменит в последней формулу на
D11=
СУММ(D4:D10), что
соответствует нашим целям.

Исключить
необходимость присутствия пустой строки
среди данных можно, если воспользоваться
более сложной функцией суммирования
(см. вставку 
после раздела 4.16 в главе
“Функции рабочего листа”) вида D9=
СУММ(D$4:ИНДЕКС(D:D;СТРОКА()–1)), а
если вы хотите изъять заголовок таблицы
из области суммирования, то

D9=СУММ(ИНДЕКС(D:D;5):ИНДЕКС(D:D;СТРОКА()–1)).

Теперь
допускается вставка новых строк в
произвольное место таблицы (например,
выделив любую строку и нажав Ctrl+Плюс)
не заботясь о правильности осуществления
суммирования – оно будет корректным.

Больше
этого вопроса мы касаться пока не будем
и, чтобы не загромождать таблицы,
ограничимся применением самой простой
функции СУММ( ),
полагая, что на практике пользователь
самостоятельно выберет и применит
удобное ему решение.

К
оформлению таблицы.
Для удобства восприятия информации
данные снабжены символами, указывающими
на единицы измерения. Так клетка В2 имеет
пользовательский формат 0,0”р/метр”,
клетка D2 – 0,0”р/чел”,
клетки В5-В9 – 0”м”,
клетки D5-D9 – 0,0”р”.

Пример 5.1.
Расчеты по вкладам. Построить таблицу
вычисления прибыли от инвестирования
суммы, равной 1000 (клетка В1), на четыре
года в некоторое производство или в
банк. Предполагаемая, выплачиваемая
ежегодно, норма прибыли должна составить
10%, 15%, 20% и 30% соответственно. Таблица в
числовом и формульном (только для столбца
В) видах приведена на рис. 5.1. Используемые
табличные функции очевидны и реализуют
выражение вида прибыль=вклад*норма.
Способ исчисления дохода
по вкладу здесь соответствует так
называемым простым процентам.

Пример 5.2.
Расчеты по вкладам (сложные проценты).
Аналогичная задача, но предполагается,
что инвестор не изымает прибыль, а
реинвестирует ее снова в дело. Такой
механизм начисления дохода определяется
термином “сложные проценты” или
“капитализа­ция дохода”. Здесь:

прибыль=норма*предыдущая_сумма_на_счету
сумма=предыдущая_сумма_на_счету
+ прибыль.

Замечание.
В этой задаче копирование формул возможно
только со второго года (со строки 5).
Именно с этого года формулы начинают
повторяться.

Значение
нарастающей суммы можно выяснить и с
помощью име­ющейся в Excel финансовой
функции вычисления будущего значения
прибыли с изменяющейся процентной
ставкой БЗРАСПИС()

сумма=БЗРАСПИС(вклад;
нормы_предшествующих_лет).

Так,
полное ее значение по завершении
последнего четвертого года составит
величину, равную выражению
B7=БЗРАСПИС(B1;A4:A7).
На рис. 5.2б изображена таблица с
решением той же задачи (и, естественно,
с теми же результатами), но с использованием
указанной функции. Если не требуется
знать значения накопленных вкладов в
конце каждого года, можно, вообще,
ограничиться только одной формулой из
последней ячейки =БЗРАСПИС(B$1;
A$4:A7).
А если не
нужна таблица, то и вообще
=БЗРАСПИС(1000;{0,1;0,15;0,2;0,3}).

	A	B	C		B	C		A	B
1	Вклад:	1000			1000			Вклад:	1000
2	СЛОЖНЫЕ ПРОЦЕНТЫ
3	Норма	Прибыль	Сумма		Прибыль	Сумма		Норма	Сумма
4	10%	100,0	1100,0		=A4*B1	=B1+B4		10%	=БЗРАСПИС(B$1;A$4:A4)
5	15%	165,0	1265,0		=A5*C4	=B5+C4		15%	=БЗРАСПИС(B$1;A$4:A5)
6	20%	253,0	1518,0		=A6*C5	=B6+C5		20%	=БЗРАСПИС(B$1;A$4:A6)
7	30%	455,4	1973,4		=A7*C6	=B7+C6		30%	=БЗРАСПИС(B$1;A$4:A7)
8		973,4			=СУММ(B4:B7)
	Рис. 5.2а		Рис. 5.2б

Пример 5.3.
Распределение фонда заработной платы.
Создать таблицу распределения фонда
заработной платы сотрудников подразделения
в соответствии с устанавливаемым
руководителем коэффициентом (индивидуальной
оценкой качества и ответственности
труда). Для определения
зарплаты здесь сначала нужно найти
“вес” единицы коэффициента в денежном
исчислении (т.е. фонд_зарплаты/сумма_коэффициентов),
а затем умножить его на индивидуальный
коэффициент работника

зарплата_работника=фонд/сумма_коэффициентов*коэффициент_работника.

Отсюда
следует, что прежде нужно найти сумму
всех коэффициентов В8=СУММ(B4:B7).
Тогда зарплата
Петра будет вычисляться по формуле
C4=B$1/B$8*B4.
И, наконец,
подсчитывается сумма всех установленных
зарплат C8=СУММ(C4:C7).
Как видим, она в точности равна фонду
зарплаты (1000), т.е. выражения записаны
верно. На рис. 5.3а таблица отображена в
числовом и в формульном форматах.

	A	B	C		B	C
1	Фонд:	1000			1000
2	РАСПРЕДЕЛЕНИЕ ЗАРПЛАТЫ
3	Имя	Коэфф.	Зарплата		Коэфф.	Зарплата
4	Петр	1	178,57		1	=B$1/B$8*B4
5	Иван	1,1	196,43		1,1	=B$1/B$8*B5
6	Сергей	2	357,14		2	=B$1/B$8*B6
7	Олег	1,5	267,86		1,5	=B$1/B$8*B7
8	ВСЕГО	5,6	1000,00		=СУММ(B4:B7)	=СУММ(C4:C7)
			Рис.	5.3а

	A	B	C	D
1	Фонд:	1000
2	РАСПРЕДЕЛЕНИЕ ЗАРПЛАТЫ
3	Имя	Прежняя зарплата	Коэфф.	Новая зарплата
4	Петр	100	1	173,21
5	Иван	130	1,1	210,54
6	Сергей	160	2	306,43
7	Олег	200	1,5	309,82
8	ВСЕГО	590	5,6	1000,00
		Рис.	5.3б

Усложним
задачу (рис. 5.3б). Пусть задается не только
коэффициент, но и минимальная зарплата
для каждого сотрудника.
Такая ситуация возможна в случае,
например, если фонд заработной платы
увеличен и прибавку следует распределить
среди сотрудников. При этом не должно
получиться так, что кто-то станет получать
зарплату меньшую, чем раньше. Эти данные
находятся в столбце Прежняя
зарплата.
Отсюда формула зарплаты работника

	A	B	C	D
1	Фонд:	1000
2	РАСПРЕДЕЛЕНИЕ ЗАРПЛАТЫ
3	Имя	Прежняя зарплата	Коэфф.	Новая зарплата
4	Петр	100	1	=(B$1–B$8)/C$8*C4+B4
5	Иван	130	1,1	=(B$1–B$8)/C$8*C5+B5
6	Сергей	160	2	=(B$1–B$8)/C$8*C6+B6
7	Олег	200	1,5	=(B$1–B$8)/C$8*C7+B7
8	ВСЕГО	=СУММ(B4:B7)	=СУММ(C4:C7)	=СУММ(D4:D7)
			Рис. 5.3в

=(фонд–сумма_прежних_зарплат)/сумма_коэффициентов*коэффициент_работника+прежняя_зарплата.
Таким образом,
здесь делится не весь фонд, а только та
его часть, которая больше суммы всех
прежних зарплат. Для Петра
это D4=(B$1–B$8)/C$8
*C4+B4.
Остальные формулы (рис. 5.3в)
очевидны. Такое решение подразумевает,
что выделенный фонд заработной платы
не может быть менее суммы прежних зарплат
(т.е. менее прежнего фонда оплаты труда).
В случае, если он окажется меньше (у нас
меньше 590), результаты будут бессмысленны.
Если такое обстоятельство возможно,
следует учесть его, например, следующим
образом

D4=ЕСЛИ(B$8>=B$1;

(B$1–B$8)/C$8*C4+B4;B$1/C$8*C4).

Здесь,
если сумма прежних зарплат больше
выделенного фонда, вычисления производятся
как и ранее, если нет – фонд делится
между всеми работниками пропорционально
их коэффициентам независимо от прежней
зарплаты.

	A	B	C	D	E		В	C	D	E
1	ПРИЕМ НО	ВЫХ	АКЦИОН	ЕРОВ			ВЫХ	АКЦИОН	ЕРОВ
2		Сум	ма	Сум	ма		Сум	ма	Сум	ма
3	Акционеры	старых	акций	новых	акций		старых	акций	новых	акций
4		530т.р	100,00%	1230т.р	100,00%		=СУММ (B5:B10	=СУММ (C5:C10)	=СУММ (D5:D10)	=СУММ (E5:E10)
5	Акционер1	100т.р	18,87%	100т.р	8,13%		100т.р	=B5/B$4	100т.р	=D5/D$4
6	Акционер2	150т.р	28,30%	150т.р	12,20%		150т.р	=B6/B$4	150т.р	=D6/D$4
7	Акционер3	200т.р	37,74%	200т.р	16,26%		200т.р	=B7/B$4	200т.р	=D7/D$4
8	Акционер4	80т.р	15,09%	80т.р	6,50%		80т.р	=B8/B$4	80т.р	=D8/D$4
9	Новый акционер1			400т.р	32,52%				400т.р	=D9/D$4
10	Новый акционер2			300т.р	24,39%	Рис. 5.4			300т.р	=D10/D$4

Пример 5.4.
Перераспределение собственности.
Создать таблицу перераспределения
собственности акционерного общества
при приеме новых пайщиков. Положим,
существующие (старые) акционеры имеют
голоса (столбец С) в управлении предприятием
и распределении прибыли в соответствии
со стоимостью их пакетов акций (столбец
В). Положим также, что фирма испытывает
финансовые затруднения (или хочет
расширяться) и ей нужны новые инвесторы,
которые готовы внести необходимую для
поддержания деятельности компании
сумму в 700 тыс. рублей (по 400 и 300 тыс. руб.
соответственно). Следует определить
новые права каждого из новых и старых
пайщиков. Строка 4 в таблице является
суммой соответствующих столбцов
(например, B4=СУММ(B5:B10)).
Относительная значимость каждого
акционера определяется по формуле вида
C5=B5/B$4
для старого пакета акций и формуле
E5=D5/D$4
для нового. Таким образом, новые акционеры
получают по 32,52% и 24,39% собственности АО,
а относительная собственность старых
акционеров соответственно уменьшается.
Правильность расчетов подтверждает
получение 100% в клетке Е4.

	A	B	C		C
1	ПРИЕМ НОВЫХ АКЦИОНЕРОВ
2	Акционеры	100%	100%		=СУММ(С3:C8)
3	Акционер1	20%	14%		=(1–(C$7+C$8))*B3
4	Акционер2	25%	18%		=(1–(C$7+C$8))*B4
5	Акционер3	20%	14%		=(1–(C$7+C$8))*B5
6	Акционер4	35%	25%		=(1–(C$7+C$8))*B6
7	Новый акционер1		20%		20%
8	Новый акционер2		10%	Рис. 5.5	10%

Пример 5.5. Перераспределение
собственности (относительное). Схожая
задача. Пусть абсолютная рыночная
стоимость акций неизвестна, поскольку
они не предлагаются на бирже, а покупная
их цена с истечением времени (из-за
инфляции и изменения состояния
предприятия) ни о чем больше не говорит.
Вообще, абсолютная стоимость акций до
тех пор, пока они не предлагаются к
продаже, и не имеет большого значения
– важно знать, какая часть собственности
кому принадлежит. Положим, новые акционеры
вносят какую-то сумму или другие активы
при условии, что им будет передано право
собственности на 20% и 10% соответственно.
Нам надо определить новые индивидуальные
права старых собственников, при условии,
что их собственность уменьшилась до
величины 100%–(20%+10%)=70%. Здесь новые права
(клетки С3, С4, С5, С6) старых собственников
вычисляются по формуле вида:

новые_права_старых_акционеров=(1–права_новых_акционеров)*старые_права_акционера.

Так
для первого акционера С3=(1–(C$7+C$8))*B3.
С целью проверки правильности вычислений
вверху таблицы все проценты просуммированы
(С2=100%).

Пример 5.6.
Взаиморасчеты акционеров. Еще одна
простая задача из “жизни акционеров”.
Положим, для деятельности АО потребовалось
срочно внести некоторую сумму (1200 т.
руб.), которую и внесли те из акционеров,
которые смогли быстро изыскать средства
(колонка Внесено
ранее). Нам нужно осуществить
последующие перерасчеты между акционерами
таким образом, чтобы все члены АО внесли
суммы пропорциональные
частям их собственности (колонка Внесено
потом).
С этой целью выполним следующие вычисления
для каждого из акционеров

=всего_внесено_ранее
*
его_часть_собственности
­– им_внесено_ранее.

	A	B	C	D	E		D	E
1		ВЗН	ОСЫ
2	Ф.И.О.	Часть соб- ственности	Внесено ранее	Внесено потом	% взноса		Внесено потом	% взноса
3	Акционер1	25%	500	–200	25%		=C$8*B3–C3	=(C3+D3)/C$8
4	Акционер2	30%	100	260	30%		=C$8*B4–C4	=(C4+D4)/C$8
5	Акционер3	20%		240	20%		=C$8*B5–C5	=(C5+D5)/C$8
6	Акционер4	10%		120	10%		=C$8*B6–C6	=(C6+D6)/C$8
7	Акционер5	15%	600	–420	15%		=C$8*B7–C7	=(C7+D7)/C$8
8	ВСЕГО	100%	1200	0	100%	Рис. 5.6	=СУММ(D3:D7)	=СУММ(E3:E7)

Или
в виде формулы для первого акционера:
D3=C$8*B3–C3.

	A	B	C	D	E	F	G
1	Коэф.	оплаты:	воскр.:	2	суббота:	1,5
2	ТАБЕЛЬ И ЗАРПЛАТА
3	Дата	День недели	Петр	Иван	Олег	Всего часов	Всего с коэфф.
4	10р/ч	8р/ч	6р/ч
5	1.окт	Вт		9ч		9ч	9ч
6	2.окт	Ср	8ч	2ч	8ч	18ч	18ч
7	3.окт	Чт
8	4.окт	Пт	5ч	6ч	8ч	19ч	19ч
9	5.окт	Сб	2ч	10ч		12ч	18ч
10	6.окт	Вс	9ч	5ч	8ч	22ч	44ч
11	7.окт	Пн	8ч	6ч		14ч	14ч
12	8.окт	Вт	9ч	7ч		16ч	16ч
35	Всего часов:	41ч	45ч	24ч	110ч	1 38ч
36	Часов с коэф.:	51ч	55ч	32ч		138ч
37	Зарплата:	510р	440р	192р	1142р
		Рис.	5.7а	дол	жно с	овпасть

В таблице
некоторые значения получились со знаком
минус (т.е. акционер, ранее внесший
деньги, получит часть их обратно), другие
– со знаком плюс (акционер заплатит
деньги). Видим, что сумма всех последующих
взносов (D8=СУММ(D3:D7))
равна нулю, т.е. наблюдается баланс
выплат. Еще раз убедиться в правильности
вычислений можно, определив процент
окончательных взносов (столбец Е)

=(внесено_сразу+внесено_потом)/внесено_всего.

Или
для первого акционера: E3=(C3+D3)/C$8.
Видим, что относительные
размеры окончательных выплат совпали
с размерами относительной собственности
каждого из акционеров.

Пример 5.7.
Ведение табельной ведомости. Создать
таблицу табельной ведомости (документа,
фиксирующего число отработанных часов)
работников подразделения с расчетом
их ежедневной и месячной заработной
платы. Считаем, что здесь принята
почасовая оплата труда, а рабочий график
индивидуальный. Тарифная часовая ставка
оплаты установлена своя для каждого
работника (ячейки С4, D4, E4). Кроме того,
установлена повышенная оплата труда в
субботние (с коэффициентом 1,5) и воскресные
(с коэффициентом 2) дни. В будний день
коэффициент считается равным 1. Пусть,
нужно создать таблицу за октябрь месяц.
Для быстрого ввода дат месяца воспользуемся
механизмом автозаполнения. Внесем в
клетку А5 значение 1.окт,
а затем мышью скопируем его вниз до
конца месяца. Excel расставит нужные
последовательные даты месяца автоматически.
В столбец День
недели введем выражение,

формирующее
название дня недели
B5=
ВЫБОР(ДЕНЬНЕД(A5;2);”Пн”;”Вт”;”Ср”;”Чт”;”Пт”;”Сб”;”Вс”),
где номер дня недели (ДЕНЬНЕД(A5;2))
замещается на его имя Пн,
Вт и т.д.

В
столбце Всего
часов определяется сумма
астрономических рабочих часов сотрудника
(F5=СУММ(C5:E5))
за день, а в столбце Всего
с коэффициентом – число часов
с учетом увеличивающих коэффициентов
за работу в выходные дни
(G5=ЕСЛИ(B5=”Вс”;D$1;ЕСЛИ(B5=”Сб”;F$1;1))*F5).
Таким образом, увеличение оплаты за
работу в выходные дни трансформируется
в увеличение отработанных
часов при их обычной оплате. В
итоговой строке 35 введены очевидные
формулы суммирования отработанных
часов вида С35=СУММ(C5:C34).

В
строке 36 – находятся эквивалентные
рабочие часы каждого из сотрудников в
зависимости от тарифной ставки и работы
в выходные

часы_с_коэфф.=общее_число_часов+

воскресных_часов*разность_между_к-том_воскресенья_и_будним_днем+

субботних_часов*разность_между_к-том_субботы_и_будним_днем.

Так,
Петром
отработано 45 час, а с учетом выходных:
41час+9час(2–1)+2час(1,5–1)=51час.

Или
в виде формулы:

C36=C35+СУММЕСЛИ($B5:$B34;”Вс”;C5:C34)*($D1–1)+СУММЕСЛИ($B5:$B34;”Сб”;C5:C34)*($F1–1).

В
строке 37 вычисляется заработок

зарплата=тарифная_ставка
* часы_с_коэффициентом.

Отсюда
его зарплата (55час*10руб/час=510руб):
C37=C$4*C6.

Все
Часы
с коэфф. для всех работников
просуммированы в клетке G36. Видим, что
эта сумма (138 час.) совпала с вертикальной
суммой, полученной в G35, что показывает
правильность расчета эквивалентных
часов. Вообще, если имеется какая-либо
возможность альтернативного вычисления
тех же самых величин, следует это сделать
чтобы проверить правильность построения
таблицы.

	A	B	C	D	E	F	G
1	Коэф. оплаты:	Воскр.:	2	Суббота:	1,5
2	ТАБЕЛЬ И ЗАРПЛАТА
3	Дата	День недели	Петр		Олег	Всего часов	Всего с коэфф.
4	10р/ч	8	6р/ч
5	1.окт	=ВЫБОР(ДЕНЬНЕД (A5;2);”Пн”;”Вт”;”Ср”;”Чт”;”Пт”;”Сб”;”Вс”)	2ч	10ч		=СУММ (C5:E5)	=ЕСЛИ(B5=”Вс”; D$1;ЕСЛИ(B5= “Сб”;F$1;1))*F5
12	8.окт	=ВЫБОР(ДЕНЬНЕД (A12;2);”Пн”;”Вт”;”Ср”;”Чт”;”Пт”;”Сб”;”Вс”)	9ч	7ч		=СУММ (C12:E12)	=ЕСЛИ(B12=”Вс”; D$1;ЕСЛИ(B12= “Сб”;F$1;1))*F12
35	Всего часов:	=СУММ(C5:C34)		=СУММ(E5:E34)	=СУММ (F5:F34)	=СУММ(G5:G34)
36	Часов с коэфф.:	=C35+СУММЕСЛИ($B5: $B34;”Вс”;C5:C34)*($D1-1) +СУММЕСЛИ($B5:$B34; “Сб”;C5:C34)*($F1-1)		=E35+СУММЕСЛИ($B5: :$B34;”Вс“;E5:E34)*($D1-1) +СУММЕСЛИ($B5:$B34; “Сб”;E5:E34)*($F1-1)		=СУММ(C36:E36)
37	Зарплата:	=C36*C$4		=E36*E$4	=СУММ( C37:E37)	Рис. 5.7б

К
оформлению. Для ячеек С4:Е4 установлен
пользовательский формат вида 0,0″р/ч”,
а для колонок F и G – формат [>0]#”ч”;#.
На рисунке табель показан
по текущий день месяца (например, по 8
октября). Остальные пустые пока строки
скрыты, с тем, чтобы не отвлекать внимание
пользователя.

П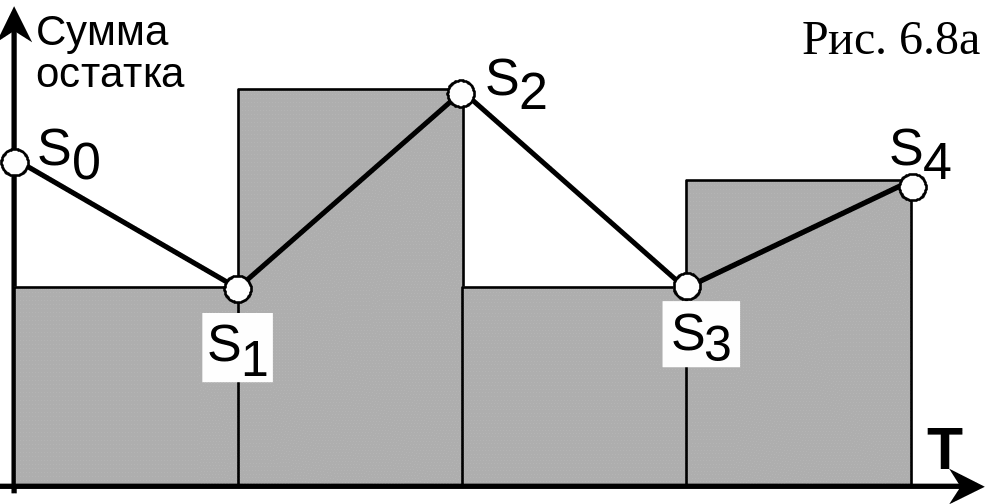
ример 5.8.
Расчеты с вкладчиками банка. Построить
таблицу вычисления годовой премии
вкладчику банка. Здесь возможно несколько
подходов:

1.
Абсолютный размер премии исчисляется
исходя из остатка на счету к концу года.
Это самый простой и самый несправедливый
способ. Если вкладчик 30 декабря снял
крупную (или даже всю) сумму со счета,
он получит маленькую премию (или не
получит ничего) несмотря на то, что банк
пользовался его деньгами весь год
(пострадает клиент). Наоборот, если сумма
была внесена на счет только 30 декабря,
вкладчик получит большую премию за один
день хранения, несмотря на то, что ранее
на счету, возможно, не было ничего
(пострадает банк). Учитывая, что в банке
много клиентов, такие потери и приобретения
банка, вероятнее всего будут взаимно
скомпенсированы, однако этого не скажешь
об отдельном вкладчике, особенно, если
он понесет финансовый ущерб.

2.
Премия исчисляется на основе значений
остатков (S₁,
S₂,
S₃,
S₄)
на счету в каждом из четырех кварталов
года. Здесь мы исходим из
предположения, что в течение всего
квартала на счету находилась именно
эта величина. Это, конечно, не так, но
лучше чем предыдущий подход. Тогда
средний годовой остаток вычисляется
как сумма всех этих остатков, деленная
на число кварталов (S₁+S₂+S₃+S₄)/4.
На рис. 5.8а искомое значение пропорционально
сумме площадей прямоугольников с высотой
S_i.
(закрашены), которую легко вычислить.
Назовем поэтому этот метод методом
прямоугольников. Ясно, что он имеет
значительные погрешности, которые будут
уменьшаться с уменьшением элементарных
периодов расчета, например, до двух или
одного месяцев и меньше.

3.
Более точным будет исчисление среднего
годового остатка как суммы среднеквартальных
остатков (площадь под ломаной линией
на рисунке), деленной на четыре.

средний_вклад_за_год=(ср._остаток_1_кв.+ср._остаток_2кв+ср._остаток
3кв+ср._остаток
4кв)/4

или
[(S₀+S₁)/2+(S₁+S₂)/2+(S₂+S₃)/2+(S₃+S₄)/2]/4=[S₀+S₄+2(S₁+S₂+S₃)]/8.

Назовем
этот метод методом трапеций. В
таблице на рис. 5.8б сделаны вычисления
значения премий методами прямоугольников
и трапеций. Для первого вкладчика это
следующие формулы

G5=СУММ(C5:F5)/4*D$1, H5=(B5+F5+2*(C5+D5+E5))/8*D$1.

	A	B	C	D	E	F	G	H		G	H
1	Проце	нт прем	ии	10%
2	СЧЕТА КЛИЕНТОВ
3	Номер	Начало	Остатки по кварталам	Премия	Премия		Премия	Премия
4	счета	года	I	II	III	IV	(прямоуг.)	(трапеции)		(прямоуг.)	(трапеции)
5	Счет1	0	0	40	120	200	9,0	6,50		=СУММ(C5:F5)/4*D$1	=(B5+F5+2*(C5+D5+E5))/8*D$1
6	Счет2	60	80	40	100	0	5,5	6,25		=СУММ(C6:F6)/4*D$1	=(B6+F6+2*(C6+D6+E6))/8*D$1
7	Счет3	350	300	200	150	100	18,8	21,88		=СУММ(C7:F7)/4*D$1	=(B7+F7+2*(C7+D7+E7))/8*D$1
8	Сумма	410	380	280	370	300	33,3	34,63		=СУММ(G7:G7)	=СУММ(H7:H7)

Рис.
5.8б

Заметим,
что задача нахождения среднего вклада
является задачей вычисления определенного
интеграла в заданных пределах, и здесь
фактически использованы известные
методы ее решения (метод прямоугольников
и метод трапеций).

4. Все
перечисленные методы являются
приближенными, поскольку предполагают
довольно грубые допущения в отношении
сумм на счетах в течение некоторого
периода. Как уже указывалось, более
точным будет подсчет среднего значения
не по кварталам, а по меньшим периодам,
но абсолютно точным был бы учет
фактического времени нахождения средств
клиента на счетах в каждый момент
времени. Этот механизм может быть
реализован только с привлечением средств
программирования (языка VBA), имеющихся
в Excel.

Пример 5.9. Продуктовый
расчет. При планировании производственной
программы, например, в пищевой
промышленности, необходимо иметь полное
представление об ожидаемых абсолютных
потерях и объемном/весовом количестве
продукта на каждом этапе обработки.
Поскольку все пищевое производство
(виноделие, консервирование, хлебобулочная
промышленность) является многоступенчатым,
контроль за этими параметрами здесь
чрезвычайно актуален и осуществляется
с помощью так называемого продуктового
расчета.

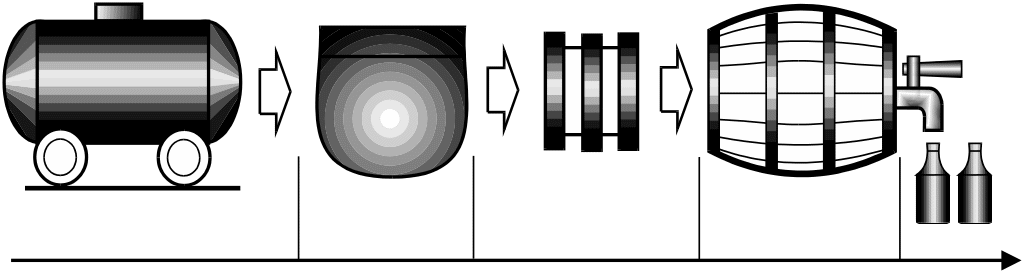
перекачка
отстой фильтрация выдержка
розлив

К₁

К₂
К₃
К₄ К₅

Рис.
5.9а

Пвх

На
рис. 5.9а, например, изображена типовая
технологическая цепочка обработки
виноматериалов. Относительные нормативные
потери на каждом из этапов обработки
известны из опытных данных и заданы
директивно. Обозначим (рис. 5.9б): Пвх –
количество продукта на входе всего
процесса или его отдельного этапа, Пвых
– количество продукта на выходе, К –
коэффициент потерь на этапе обработки,

– объем потерь на этапе обработки
в абсолютном исчислении. Отсюда можем
записать рабочие формулы для каждого
этапаПвых=Пвх–,
где К^Пвх

Задача
может быть поставлена как прямая
(известен объем сырья, нужно найти объем
продукта), так и как обратная (известен
объем продукта, найти объем потребного
для него сырья).

Прямая
задача. Заданы:
исходное количество продукта (сырья)
на входе процесса к началу обработки
Пвх, количество этапов обработки N и
коэффициенты нормативных потерь на
каждом i-ом этапе – Кi от поступившего
на данный вид обработки объема продукта.
Вычислить абсолютные величины потерь
на каждом этапе обработки i
и итоговый выход продукта Пвых.

Обратная
задача. Задано потребное количество
готового продукта Пвых. Вычислить
абсолютные величины потерь на каждом
этапе обработки i
и необходимое количество исходного
продукта Пвх.

Рабочие
формулы для каждого этапа обратной
задачи: Пвых^К/(1–К)
и Пвх=Пвых+

На
основании простых рассуждений можно
записать итоговые формулы расчета
конечного/начального (Пвых/Пвх) продукта
для прямой/обрат­ной задачи для всего
процесса в целом

Пвых=Пвх(1–К1)(1–К2)
… (1–КN),
Пвх=Пвых/((1–К1)
(1–К2) … (1–КN)).

Решение
задачи прямого продуктового расчета
приведено в верхней части рис. 5.9в, а
формулы рабочего листа на рис. 5.9г.
Исходное количество сырья для наглядности
взято равным 100. При трехэтапной обработке
с относительными потерями в 0,05,
0,11 и 0,02 итоговый выход продукта составит
82,859.

Решение
обратной задачи изображено на тех же
рисунках в их нижней половине. В качестве
выхода технологического процесса взято
значение, ранее найденное в прямой
задаче (82,859). Как видим, в результате
расчетов для обратной задачи получено
число 100, т.е. вычисления выполнены верно.

Если
вспомнить задачу 5.2, можно заметить, что
прямой продуктовый расчет очень похож
на задачу определения вклада для сложных
процентов. Только там происходит
наращивание вклада, а здесь уменьшение
продукта. Это обстоятельство можно
учесть, изменив на минус знаки при всех
коэффициентах потерь. Тогда объем
продукта на выходе получим воспользовавшись
функцией

=БЗРАСПИС(C2;{–0,05;–0,11;–0,02})
=82,859 или (введя
выражение как массив) {=БЗРАСПИС(C2;–B4:B6)}
=82,859.

Пример 5.10.
Продуктовый расчет с дополнительным
сырьем.

Продуктовый
расчет, выполненный выше, предполагает,
что перерабатывается только исходный
продукт. На практике, часто в технологическом
процессе предусмотрено внесение (или
изъятие) на разных его этапах дополнительных
компонентов. Объем вносимого элемента
зависит от объема продукта, поступающего
на обработку. Решим такую задачу. В
таблицу продуктового расчета внесем
новый столбец Дополнительное
сырье, где разместим коэффициенты
(проценты), связывающие объем дополнительного
материала с объемом исходного для
данного этапа.

Для
первого этапа в таблице сформируем
выражения:

объем_потерь=коэффициент_потерь*(исходный_объем+дополнительный_объем).

Для
любого следующего этапа

объем_на_выходе=исходный_объем+дополнительное_сырье–объем_потерь.

Или
в форме клеточных функций:
D4=C4*(C2+C2*B4)=C4*C2*(1+B4),
E4=C2+C2*B4–D4=C2*(1+B4)–D4.

	A	B	C	D
1	ПРОДУКТОВЫЙ РАСЧЕТ (прямая задача)
2	Объем сырья:	100
3	Этап	Коэфф. потерь	Объем потерь	Объем продукта на выходе
4	1	0,05	5,000	95,000
5	2	0,11	10,450	84,550
6	3	0,02	1,691	82,859
7
8	ПРОДУКТОВЫЙ РАСЧЕТ (обратная задача)
9	Объем продукта:	82,859
10	Этап	Коэфф. потерь	Объем потерь	Объем продукта на входе
11	3	0,02	1,691	84,550
12	2	0,11	10,450	95,000
13	1	0,05	5,000	100,000

	A	B	C	D
1	ПРОДУКТОВЫЙ РАСЧЕТ (прямая задача)
2	Объем сырья:	100
3	Этап	Коэфф. потерь	Объем потерь	Объем продукта на выходе
4	1	0,05	=B4*C2	=C2–C4
5	2	0,11	=B5*D4	=D4–C5
6	3	0,02	=B6*D5	=D5–C6
7
8	ПРОДУКТОВЫЙ РАСЧЕТ (обратная задача)
9	Объем продукта:	82,859
10	Этап	Коэфф. потерь	Объем потерь	Объем продукта на входе
11	3	0,02	=C9*B11/(1–B11)	=C9+C11
12	2	0,11	=D11*B12/(1–B12)	=D11+C12
13	1	0,05	=D12*B13/(1–B13)	=D12+C13

Рис.
5.9в Рис. 5.9г

В
случае, если речь идет об изъятии
продукта, элементы в столбце В вводятся
со знаком минус. Аналогичным образом
строятся формулы для остальных этапов.

Хотя
приведенный выше расчет рассматривался
именно как продуктовый, очевидно,
подобные же технологические (и не
технологические) процессы существуют
и в других отраслях производства и
коммерческой деятельности.

	A	B	C	D	Е		D	Е
1	ПРОДУКТОВЫЙ РАСЧЕТ (прямая задача)
2	Объем сырья:	100
3	Этап	Доп. сырье	Коэф. потерь	Объем потерь	Объем на выходе		Объем потерь	Объем на выходе
4	1	1%	0,05	5,050	95,950		=C4*C2*(1+B4)	=C2*(1+B4)–D4
5	2	30%	0,11	13,721	111,014		=C5*E4*(1+B5)	=E4*(1+B5)–D5
6	3	20%	0,02	2,664	130,553	Рис. 5.10	=C6*E5*(1+B6)	=E5*(1+B6)–D6

	A	B	C	D	E	F	G	H
1	Работники	Оценки	Всего КТУ	КТУ	КТУ1
2	Петр	0,90	0,70	0,70	0,90	3,20	0,277	0,98
3	Иван	0,60	0,55	0,60	0,40	2,15	0,186	0,66
4	Олег	0,80	0,80	0,55	0,80	2,95	0,255	0,91
5	Вера	0,90	0,90	0,45	1,00	3,25	0,281	1,00
6	Сумма					11,55
				Рис.	5.11

Пример 5.11.
Определение коэффициента трудового
участия (КТУ). На таком производстве,
где невозможно оценить индивидуальное
количество труда, принято по итогам
месяца/недели оценивать его при помощи
КТУ, которое в дальнейшем влияет на
оплату. Чтобы исключить необъективность
оценок, все члены бригады анонимно
заполняет анкету, где выставляет КТУ
(например, в диапазоне от 0 до 1) для
каждого из своих коллег. Необходимо
как-то обработать эти данные и сформировать
обобщенные значения КТУ. На рисунке в
колонках В:Е зафиксированы оценки для
каждого из четырех членов бригады, в F
они просуммированы, в G – вычисляется
собственно КТУ

КТУ_работника=Всего_КТУ_работника/Сумма_КТУ_бригады.

Эти
значения (в таблице колонка G) уже можно
использовать для оценки результатов
труда, однако более удобно, если они
находятся в том же диапазоне, что и
исходные оценки, т.е. в диапазоне от 0 до
1. Назовем его КТУ1 (столбец Н)

КТУ1_работника=КТУ_работника/МАКС(КТУ_всех_работников).

Рабочие
формулы для первого работника приведены
ниже

F2=СУММ(B2:E2),
F6=СУММ(F2:F5), G2=F2/F$6, H2=G2/МАКС(G$2:G$5).

	A	B	C	D	E	F
1		Весовые коэффициенты
2		Упаковка	Цвет	Консистенция	Вкус
3		1	0,7	1,5	2
4	ЭКСПЕРТНЫЕ ОЦЕНКИ
5	Оценки	Упаковка	Цвет	Консистенция	Вкус	Итог
6	Эксперт1	3	5	4	8
7	Эксперт2	4	7	5	7
8	Эксперт3	5	8	5	9
9	Эксперт4	6	7	6	6
10	Всего	4,5	4,9	7,5	15	31,9
			Рис.	5.12

Пример 5.12.
Экспертная оценка качества.
Похожая задача из совершенно иной сферы
деятельности. Построим таблицу для
экспертной оценки некоторого продукта.
Рассматриваемый ниже подход используется
в случае, когда нет четкого формального
критерия анализа его качества (например
качества вина). Здесь прибегают к услугам
группы специалистов (экспертов), которые
и оценивают продукт, исходя из своего
опыта по нескольким параметрам. Для
каждого из параметров они выставляют
оценку по, например, десятибалльной
шкале. При подведении итогов следует
учесть разную значимость этих параметров.
Очевидно, что значимость (весá) таких
параметров, как вкус и цвет для
пищевых продуктов существенно отличны
(первый гораздо важнее). В виду этого
для подсчета итоговой оценки вводится
специальная нормативная таблица весовых
коэффициентов (область В1:Е3) всех
исследуемых параметров, которая также
составляется экспертами для вин вообще.
По каждому из параметров находится
среднее арифметическое их оценок,
причем, максимальная и минимальная
оценки отбрасываются

B10=(СУММ(B6:B9)–МАКС(B6:B9)–МИН(B6:B9))*B3/2, C10=(СУММ(C6:C9)–МАКС(C6:C9)–МИН(C6:C9))*C3/2,

D10=(СУММ(D6:D9)–МАКС(D6:D9)–МИН(D6:D9))*D3/2, E10=(СУММ(E6:E9)–МАКС(E6:E9)–МИН(E6:E9))*E3/2.

Их
сумма и даст интегральную оценку качества
данного продукта, подвергшегося
экспертизе (у нас 31,9 балла) F10=СУММ(B10:E10),
на основании которой далее
можно сравнивать между собой аналогичные
продукты и принять решение об их
дальнейшей коммерческой судьбе.

К
оформлению таблицы.
Здесь мы выделим жирным курсивным
шрифтом для каждого из параметров
оценки, не принимаемые в расчет (т.е.
максимальные и минимальные значения).
Для этого придется прибегнуть к условному
форматированию
клеток с оценками следующего вида
(например для В6):

Условие 1
формула
 =ИЛИ(B6=МАКС(B$6:B$9);B6=МИН(B$6:B$9)) 

Пример 5.13.
Расчет сдельной зарплаты. Построить
таблицу вычисления сдельной (т.е.
пропорциональной количеству
произведенной продукции) зарплаты, а
также налога и суммы на руки.

Зарплата
работника определяется числом обработанных
деталей, умноженным на стоимость
обработки. Если работник допустил брак
и испортил деталь, ее стоимость вычитается
из заработка

зарплата=обработано_деталей*стоимость_работы
– деталей_брака
* стоимость_детали.

Таким
образом, Зарплата
Ивана
будет определяться формулой D6=B6*
C$2–C6*C$3.
Полагаем, что налог исчисляется в
зависимости от зарплаты: если она выше
5000 – налог составляет 20%, если нет –
13%.

Иными
словами сумма_налога=зарплата*ЕСЛИ(зарплата
>5000, то 13%, иначе 20%) или 

E6=D6*ЕСЛИ(D6>=5000;F$1;C$1).
Сумма
на руки –
F6=D6–E6.
Итог по вертикали F9=СУММ(F6:F8).

	A	B	C	D	E	F
1	Налог до:	5000р	13%	Налог от:	5000р	20%
2	Стоимость	работы:	80
3	Стоимость	детали:	200
4	РАСЧЕТ ЗАРПЛАТЫ
5	Работник	Обработано деталей	Деталей брака	Зарплата	Сумма налога	Сумма на руки
6	Петр	75	2	5600	1120,0	4480,0
7	Иван	12		960	124,8	835,2
8	Олег	62	4	4160	540,8	3619,2
9	ВСЕГО	149	6	10720	2144,0	8934,4
			Рис.	5.13а

Может
случиться, что если брака окажется
много, зарплата станет отрицательной
(работник должен компенсировать
нанесенный ущерб). В этом случае, конечно,
никакой налог не удерживается и,
следовательно, в формуле для налога
следует предусмотреть выявление
отрицательности заработка. С учетом
вышесказанного уточним Е6

Е6=D6*ЕСЛИ(D6<=0;0;ЕСЛИ(D6>=5000;F$1;C$1)).

Замечание
к условию задачи.
Следует отметить, что с 2001г. в России с
физических лиц прогрессивный подоходный
налог (когда процент налога увеличивается
с увеличением доходов) заменен на
фиксированный в 13% независимо от доходов
и исчисление налогов сильно упростилась.
Однако, автор оставил этот и другие
такого рода примеры в книге по двум
причинам: с юридических лиц налоги
берутся аналогичным образом (но по
регрессивной шкале); сам механизм
исчисления налогов имеет хождение не
только для налогов и не только в денежном
обращении и поэтому представляет
самостоятельный интерес.

	C	D	E	F
1	13%	Налог от:	5000р	20%
2	80
3	200
5	Деталей брака	Зарплата	Сумма налога	Сумма на руки
6	2	=B6*C$2–C6*C$3	=D6*ЕСЛИ(D6<=0;0;ЕСЛИ(D6>=5000;F$1;C$1))	=D6–E6
7		=B7*C$2–C7*C$3	=D7*ЕСЛИ(D7<=0;0;ЕСЛИ(D7>=5000; F$1;C$1))	=D7–E7
8	4	=B8*C$2–C8*C$3	=D8*ЕСЛИ(D8<=0;0;ЕСЛИ(D8>=5000;F$1;C$1))	=D8–E8
9	=СУММ(C6:C8)	=СУММ(D6:D8)	=СУММ(E6:E8)	=СУММ(F6:F8)	Рис. 5.13б

К
оформлению.
Для удобства последующего анализа
данных сделаем так, чтобы работник,
имеющий максимальный заработок, был
выделен красным цветом, а минимальный
– желтым. Для этого понадобится прибегнуть
к условному форматированию клеток F6,
F7, F8 вида:

Условие 1
значение

равно
=МАКС(F$6:F$8)
– красный фон

Условие 2
значение

равно
=МИН(F$6:F$8)
– желтый фон

	A	B	C	D	E	F
1		Тарифная сетка
2	Разряд:	1	2	3	4	5
3	Тариф:	30	40	50	70	90
4	Премия:	100	120	135	150	160
5		З А Р П Л А Т А
6	Работник	Дней	Разряд	Зарплата	Премия	Начислено
7	Петр	20	2	800	120	920
8	Иван	10	3	500	135	635
9	Олег	15	5	1350	160	1510
10	ВСЕГО	45		2650	415	3065
			Рис.	5.14а

Пример 5.14.
Повременная зарплата. Построить
таблицу вычисления повременной (т.е.
зависящей от длительности рабочего
времени) заработной платы работников
на некотором производстве. Последняя
зависит от числа отработанных дней в
месяце, разряда рабочего и премии. Для
вычисления собственно зарплаты (область
D7:D9) нужно число дней умножить на тариф,
зависящий от разряда

зарплата=дней*тариф_по_разряду.

Для
розыска разрядного тарифа нам понадобится
функция горизонтального поиска ГПР().
Например, для Петра
должна быть использована формула
D7=
ГПР(C7;B$2:F$4;2;0)*B7.
Премия также зависит от разряда
E7=ГПР(C7;B$2
:F$4;3;0). Всего
работнику будет начислена сумма F7=E7+D7.
В данном примере расчет
начисленной суммы только для наглядности
был разложен на отдельные компоненты.
Ничто не мешает нам, при необходимости,
соединить все формулы в одну, уменьшив
размер таблицы F7=ГПР(C7;B$2:F$4;2;0)*B7+
ГПР(C7; B$2:F$4;3;0).

	A	B	C	D	E	F
1	Тарифная сетка
2	Разряд:	1	2	3	4	5
3	Тариф:	30	40	50	70	90
4	Премия:	100	120	135	150	160
5			З А Р П Л А Т А
6	Работник	Дней	Разряд	Зарплата	Премия	Начислено
7	Петр	21	2	=ГПР(C7;B$2:F$4;2;0)*B7	=ГПР(C7;B$2:F$4;3;0)	=E7+D7
8	Иван	25	4	=ГПР(C8;B$2:F$4;2;0)*B8	=ГПР(C8;B$2:F$4;3;0)	=E8+D8
9	Олег	18	5	=ГПР(C9;B$2:F$4;2;0)*B9	=ГПР(C8;B$2:F$4;3;0)	= Рис. 5.14б E9+D9
10	ВСЕГО	=СУММ(B7:B9)		=СУММ(D7:D9)	=СУММ(E7:E9)	=СУММ(F7:F9)

Пример 5.15.
Расчет зарплаты с учетом квалификации
работника (должностного класса) и
коэффициента (КТУ) трудового участия.
Здесь класс и КТУ одинаковым образом
влияют на заработок, но только класс
присваивается “навсегда” (до пересмотра),
а КТУ изменяется в зависимости от
качества исполнения конкретной работы.

Положим,
заказчик оценил всю работу в 10000 руб. и
выдал аванс в размере 4000 руб., который
и был распределен между людьми произвольным
образом (кто сколько попросил). Наша
задача состоит в том, чтобы по завершении
работы распределить остальную часть
заработанного (6000 руб.).

Прежде
всего необходимо определить влияние
класса и КТУ на размеры выплат. Найдем
сумму этих величин. Поскольку коэффициент
доплат за класс работника имеет тот же
смысл, что и КТУ, то эта сумма образуется
сложением пар сомножимых, образованных
из обеих величин. В нашем случае это

итого_КТУ=1*1,4+2*1,2+3*1=3,7
или D9=СУММПРОИЗВ(C6:C8;D6:D8).

	A	B	C	D	E	F	G
1	Всего:	10000	Аванс:	4000	Остаток:	6000
2	Надбавки за класс	класс:	1	2	3
3	коэфф.:	1,4	1,2	1
4	РАСПРЕДЕЛЕНИЕ ЗАРПЛАТЫ
5	Имя	Класс	Коэфф. за класс	КТУ	Получен аванс	Заработано	Выдать остаток
6	Петр	1	1,4	1	1000	3784	2784
7	Иван	2	1,2	1,5	800	4865	4065
8	Олег	3	1	0,5	2200	1351	–849
9	ИТОГО			3,7	4000	10000	6 Рис. 5.15а 000

	C	D	E	F	G
5	Коэфф. за класс	КТУ	Получен аванс	Зара ботано	Выдать остаток
6	=ГПР(B6;C$2:E$3;2;0)	1	100	=B$1/D$9*C6*D6	=F6–E6
7	=ГПР(B7;C$2:E$3;2;0)	1,5	80	=B$1/D$9*C7*D7	=F7–E7
8	=ГПР(B8;C$2:E$3;2;0)	0,5	220	=B$1/D$9*C8*D8	=F8–E8
9		=СУММПРОИЗВ (C6:C8;D6:D8)	=СУММ(E6:E8)	=СУММ(F6:F8)	= Рис. 5.15б СУММ(G6:G8)

Теперь
можно определить причитающуюся рабочему
сумму

заработано=всего*коэфф._за_класс*КТУ/итого_КТУ
для первого рабочего это
F6=$B$1*C6*D6/D$9.

Поскольку
работник уже получил аванс, ему предстоит
выдать (а может быть и взыскать с него,
если аванс не был “отработан”) сумму
выдать_остаток=заработано–получен_аванс
или G6=F6–E6.

Правильность
наших расчетов подтверждает совпадение
значений F9=B1 и G9=F1.

Пример 5.16.
Распределение премии. Положим, отделу
выделена недельная премия-помощь в
размере 800 руб. Ее нужно поделить между
сотрудниками следующим образом –
малооплачиваемым (считаем таковыми
тех, у кого недельный заработок менее
пяти минимальных зарплат) делается
доплата до 5 минимальных зарплат, а
остаток делится между всеми пропорционально
зарплате. Сформируем необходимые
выражения.

Расчет остатка предоплаты

ArtemM Дата: Воскресенье, 20.12.2015, 20:47 | Сообщение № 1 Группа: Пользователи Ранг: Новичок Сообщений: 15 Репутация: 0 ± Замечаний: 0% ± Excel 2010 Здравствуйте! В организации существует авансовая форма расчетов. Можно ли в Excel написать формулу,которая отражала бы сумму остатка предоплаты, которой компания пользуется в данный момент, после выполнения каждого заказа, а также рядом с остатком предоплаты отражался бы порядковый номер аванса? К сообщению приложен файл: 2172918.xlsx (77.5 Kb)   Ответить

krosav4ig Дата: Воскресенье, 20.12.2015, 22:28 | Сообщение № 2 Группа: Друзья Ранг: Старожил Сообщений: 2346 Репутация: 989 ± Замечаний: 0% ± Excel 2007,2010,2013 Здравствуйте. До 25.10.2013 есть какой-то остаток? email:krosav4ig26@gmail.com WMR R207627035142 WMZ Z821145374535 ЯД 410012026478460   Ответить

ArtemM Дата: Воскресенье, 20.12.2015, 22:31 | Сообщение № 3 Группа: Пользователи Ранг: Новичок Сообщений: 15 Репутация: 0 ± Замечаний: 0% ± Excel 2010 Нет. Остатка нету.   Ответить

krosav4ig Дата: Воскресенье, 20.12.2015, 22:39 | Сообщение № 4 Группа: Друзья Ранг: Старожил Сообщений: 2346 Репутация: 989 ± Замечаний: 0% ± Excel 2007,2010,2013 тогда как-то так номер предоплаты (массивная формула) Код =ПРОСМОТР(СУММ($E$16:E16);МУМНОЖ((СТРОКА($C$5:$C$11)>ТРАНСП(СТРОКА($C$5:$C$11)))*Ч(ТРАНСП($C$5:$C$11));СТРОКА($C$5:$C$11)^0);$A$5:$A$11) остаток предоплаты Код =СУММ($C$6:ИНДЕКС($C$6:$C$11;F16))-СУММ($E$16:E16) К сообщению приложен файл: 7896059.xlsx (77.0 Kb) email:krosav4ig26@gmail.com WMR R207627035142 WMZ Z821145374535 ЯД 410012026478460 Сообщение отредактировал krosav4ig – Воскресенье, 20.12.2015, 22:41   Ответить

ArtemM Дата: Воскресенье, 20.12.2015, 22:46 | Сообщение № 5 Группа: Пользователи Ранг: Новичок Сообщений: 15 Репутация: 0 ± Замечаний: 0% ± Excel 2010 Спасибо огромное. Очень помогли.   Ответить

Michael_S Дата: Понедельник, 21.12.2015, 13:13 | Сообщение № 6 Группа: Друзья Ранг: Старожил Сообщений: 2012 Репутация: 373 ± Замечаний: 0% ± Excel2016 ПРОСМОТР(СУММ($E$16:E16);МУМНОЖ((СТРОКА($C$5:$C$11)>ТРАНСП(СТРОКА($C$5:$C$11)))*Ч(ТРАНСП($C$5:$C$11));СТРОКА($C$5:$C$11)^0);$A$5:$A$11) чет какая-то навороченная формула… я в ней не разобрался. можно чуть проще: Код =ПРОСМОТР(СУММ($E$16:E16);СУММЕСЛИ(СМЕЩ($C$5;;;СТРОКА($C$5:$C$11)-4);”<>”);$A$16:A16) К сообщению приложен файл: 0514193.xlsx (77.2 Kb) Сообщение отредактировал Michael_S – Понедельник, 21.12.2015, 13:29   Ответить