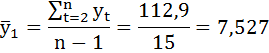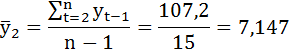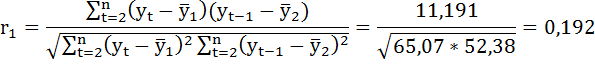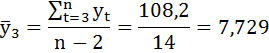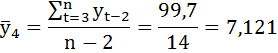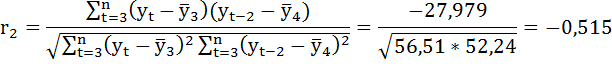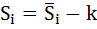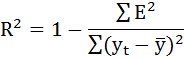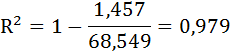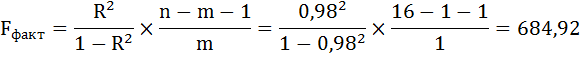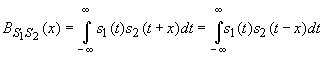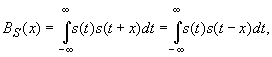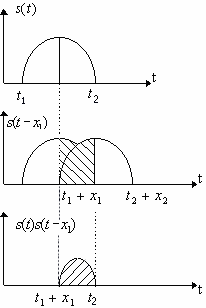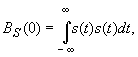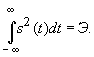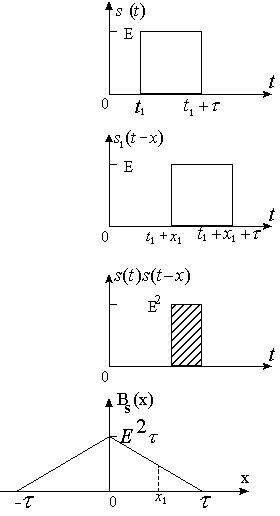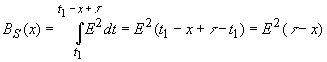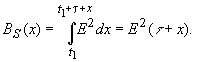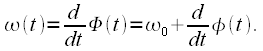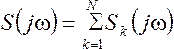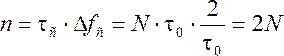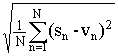Имеются условные данные об объемах потребления электроэнергии yt жителями региона за 16 кварталов.
| t | yt | t | yt |
|---|---|---|---|
| 1 | 5,6 | 9 | 8,2 |
| 2 | 4,7 | 10 | 5,6 |
| 3 | 5,2 | 11 | 6,4 |
| 4 | 9,1 | 12 | 10,8 |
| 5 | 7,0 | 13 | 9,1 |
| 6 | 5,1 | 14 | 6,7 |
| 7 | 6,0 | 15 | 7,5 |
| 8 | 10,2 | 16 | 11,3 |
Требуется:
1. Построить автокорреляционную функцию и сделать вывод о наличии сезонных колебаний.
2. Построить аддитивную модель временного ряда.
3. Сделать прогноз на 2 квартала вперед.
Решение:
1. Рассчитаем коэффициент автокорреляции уровней ряда первого порядка, то есть между соседними уровнями ряда yt и yt-1 (лаг = 1), и измерим тесноту связи между объёмом потребления электроэнергии в текущем и предыдущем году.
Для этого составим таблицу расчётных данных.
Расчёт коэффициента автокорреляции первого порядка для временного ряда объемов потребления электроэнергии жителями региона:
| t | yt | yt-1 | 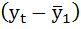 |
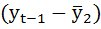 |
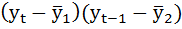 |
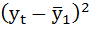 |
 |
|---|---|---|---|---|---|---|---|
| 1 | 5,6 | – | – | – | – | – | – |
| 2 | 4,7 | 5,6 | -2,827 | -1,547 | 4,371911 | 7,990044 | 2,392178 |
| 3 | 5,2 | 4,7 | -2,327 | -2,447 | 5,692578 | 5,413378 | 5,986178 |
| 4 | 9,1 | 5,2 | 1,573 | -1,947 | -3,06276 | 2,475378 | 3,789511 |
| 5 | 7 | 9,1 | -0,527 | 1,953 | -1,02876 | 0,277378 | 3,815511 |
| 6 | 5,1 | 7 | -2,427 | -0,147 | 0,355911 | 5,888711 | 0,021511 |
| 7 | 6 | 5,1 | -1,527 | -2,047 | 3,124578 | 2,330711 | 4,188844 |
| 8 | 10,2 | 6 | 2,673 | -1,147 | -3,06542 | 7,146711 | 1,314844 |
| 9 | 8,2 | 10,2 | 0,673 | 3,053 | 2,055911 | 0,453378 | 9,322844 |
| 10 | 5,6 | 8,2 | -1,927 | 1,053 | -2,02942 | 3,712044 | 1,109511 |
| 11 | 6,4 | 5,6 | -1,127 | -1,547 | 1,742578 | 1,269378 | 2,392178 |
| 12 | 10,8 | 6,4 | 3,273 | -0,747 | -2,44409 | 10,71471 | 0,557511 |
| 13 | 9,1 | 10,8 | 1,573 | 3,653 | 5,747911 | 2,475378 | 13,34684 |
| 14 | 6,7 | 9,1 | -0,827 | 1,953 | -1,61476 | 0,683378 | 3,815511 |
| 15 | 7,5 | 6,7 | -0,027 | -0,447 | 0,011911 | 0,000711 | 0,199511 |
| 16 | 11,3 | 7,5 | 3,773 | 0,353 | 1,333244 | 14,23804 | 0,124844 |
| Итого | 112,9 | 107,2 | – | – | 11,19133 | 65,06933 | 52,37733 |
Рассчитаем выборочные средние:
Определим коэффициент автокорреляции уровней ряда первого порядка:
Полученное значение свидетельствует об очень слабой зависимости текущих уровней ряда от непосредственно им предшествующих уровней.
Рассчитаем коэффициент автокорреляции 2-го порядка.
| t | yt | yt-2 | 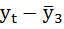 |
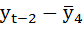 |
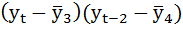 |
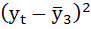 |
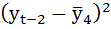 |
|---|---|---|---|---|---|---|---|
| 1 | 5,6 | – | – | – | – | – | – |
| 2 | 4,7 | – | – | – | – | – | – |
| 3 | 5,2 | 5,6 | -2,529 | -1,521 | 3,847041 | 6,393673 | 2,314745 |
| 4 | 9,1 | 4,7 | 1,371 | -2,421 | -3,32082 | 1,880816 | 5,863316 |
| 5 | 7 | 5,2 | -0,729 | -1,921 | 1,399898 | 0,530816 | 3,691888 |
| 6 | 5,1 | 9,1 | -2,629 | 1,979 | -5,20082 | 6,909388 | 3,914745 |
| 7 | 6 | 7 | -1,729 | -0,121 | 0,209898 | 2,987959 | 0,014745 |
| 8 | 10,2 | 5,1 | 2,471 | -2,021 | -4,99582 | 6,107959 | 4,086173 |
| 9 | 8,2 | 6 | 0,471 | -1,121 | -0,52867 | 0,222245 | 1,257602 |
| 10 | 5,6 | 10,2 | -2,129 | 3,079 | -6,55296 | 4,530816 | 9,477602 |
| 11 | 6,4 | 8,2 | -1,329 | 1,079 | -1,43296 | 1,765102 | 1,163316 |
| 12 | 10,8 | 5,6 | 3,071 | -1,521 | -4,67296 | 9,433673 | 2,314745 |
| 13 | 9,1 | 6,4 | 1,371 | -0,721 | -0,98939 | 1,880816 | 0,520459 |
| 14 | 6,7 | 10,8 | -1,029 | 3,679 | -3,78367 | 1,057959 | 13,53189 |
| 15 | 7,5 | 9,1 | -0,229 | 1,979 | -0,45224 | 0,052245 | 3,914745 |
| 16 | 11,3 | 6,7 | 3,571 | -0,421 | -1,5051 | 12,7551 | 0,177602 |
| Итого | 108,2 | 99,7 | – | – | -27,9786 | 56,50857 | 52,24357 |
Выборочные средние:
Коэффициент автокорреляции уровней ряда первого порядка:
Продолжив расчёты аналогичным образом, получим автокорреляционную функцию этого ряда. Её значения приведены в таблице:
| Лаг | Коэффициент автокорреляции уровней |
|---|---|
| 1 | 0,1917 |
| 2 | -0,5149 |
| 3 | 0,1272 |
| 4 | 0,9862 |
| 5 | 0,1448 |
| 6 | -0,6487 |
| 7 | -0,00647 |
| 8 | 0,9632 |
Анализ значений автокорреляционной функции позволяет сделать вывод о наличии в изучаемом временном ряде линейной тенденции и сезонных колебаний периодичностью в 4 квартала.
2. Построим аддитивную модель временного ряда.
Общий вид аддитивной модели следующий:
Y = T + S + E
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент.
Рассчитаем компоненты аддитивной модели временного ряда.
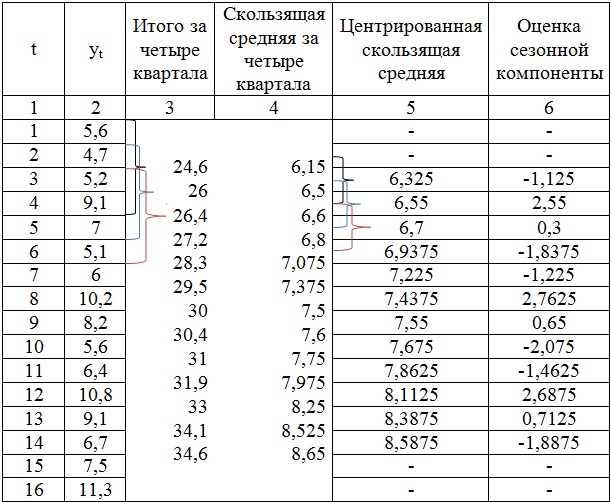
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1) просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объёмы потребления электроэнергии (гр. 3);
2) разделив полученные суммы на 4, найдём скользящие средние (гр. 4). Отметим, что полученные таким образом выравненные значения уже не содержат сезонной компоненты;
3) приведём эти значения в соответствие с фактическими моментами времени, для чего найдём средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр.5).
Расчёт оценок сезонной компоненты в аддитивной модели
Шаг 2. Рассчитаем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6). Используем эти оценки для расчета значений сезонной компоненты S. Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты Si. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Расчёт значений сезонной компоненты:
| Показатели | Год | № квартала, i | |||
|---|---|---|---|---|---|
| I | II | III | IV | ||
| 1 | – | – | -1,125 | 2,55 | |
| 2 | 0,3 | -1,8375 | -1,225 | 2,7625 | |
| 3 | 0,65 | -2,075 | -1,4625 | 2,6875 | |
| 4 | 0,7125 | -1,8875 | – | – | |
| Итого за i-й квартал | 1,6625 | -5,8 | -3,8125 | 8 | |
Средняя оценка сезонной компоненты для i-го квартала, 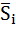 |
0,554167 | -1,93333 | -1,27083 | 2,666667 | |
| Скорректированная сезонная компонента, Si | 0,55 | -1,9375 | -1,275 | 2,6625 |
Для данной модели имеем:
0,554167 + ( -1,93333) + (-1,27083) + 2,666667 = 0,016667
Определим корректирующий коэффициент:
k = 0,016667 / 4 = 0,004167
Рассчитаем скорректированные значения сезонной компоненты как разность между её средней оценкой и корректирующим коэффициентом k:
Проверим условие равенство нулю суммы значений сезонной компоненты:
0,55 + (-1,9375) + (-1,275) + 2,6625 = 0
Таким образом, получены следующие значения сезонной компоненты:
I квартал: S1 = 0,55;
II квартал: S2 = -1,9375;
III квартал: S3 = -1,275;
IV квартал: S4 = 2,6625.
Занесём полученные значения в таблицу для соответствующих кварталов каждого года (гр. 3).
| t | yt | Si | T + E = yt – Si | T | T + S | E = yt – (T + S) | E2 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 5,6 | 0,55 | 5,05 | 5,8588235 | 6,408824 | -0,80882 | 0,654196 |
| 2 | 4,7 | -1,9375 | 6,6375 | 6,0651471 | 4,127647 | 0,572353 | 0,327588 |
| 3 | 5,2 | -1,275 | 6,475 | 6,2714706 | 4,996471 | 0,203529 | 0,041424 |
| 4 | 9,1 | 2,6625 | 6,4375 | 6,4777941 | 9,140294 | -0,04029 | 0,001624 |
| 5 | 7 | 0,55 | 6,45 | 6,6841176 | 7,234118 | -0,23412 | 0,054811 |
| 6 | 5,1 | -1,9375 | 7,0375 | 6,8904412 | 4,952941 | 0,147059 | 0,021626 |
| 7 | 6 | -1,275 | 7,275 | 7,0967647 | 5,821765 | 0,178235 | 0,031768 |
| 8 | 10,2 | 2,6625 | 7,5375 | 7,3030882 | 9,965588 | 0,234412 | 0,054949 |
| 9 | 8,2 | 0,55 | 7,65 | 7,5094118 | 8,059412 | 0,140588 | 0,019765 |
| 10 | 5,6 | -1,9375 | 7,5375 | 7,7157353 | 5,778235 | -0,17824 | 0,031768 |
| 11 | 6,4 | -1,275 | 7,675 | 7,9220588 | 6,647059 | -0,24706 | 0,061038 |
| 12 | 10,8 | 2,6625 | 8,1375 | 8,1283824 | 10,79088 | 0,009118 | 8,31E-05 |
| 13 | 9,1 | 0,55 | 8,55 | 8,3347059 | 8,884706 | 0,215294 | 0,046352 |
| 14 | 6,7 | -1,9375 | 8,6375 | 8,5410294 | 6,603529 | 0,096471 | 0,009307 |
| 15 | 7,5 | -1,275 | 8,775 | 8,7473529 | 7,472353 | 0,027647 | 0,000764 |
| 16 | 11,3 | 2,6625 | 8,6375 | 8,9536765 | 11,61618 | -0,31618 | 0,099968 |
Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины T + E = Y – S (гр. 4 табл.). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Шаг 4. Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда (T + E) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
T = 5,6525 + 0,206 * t
Подставляя в это уравнение значения t = 1,…,16, найдем уровни T для каждого момента времени (гр. 5 табл.).
Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням T значения сезонной компоненты для соответствующих кварталов (гр. 6 табл.).
Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.
Коэффициент детерминации.
| t | yt | Е2 | 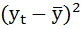 |
|---|---|---|---|
| 1 | 5,6 | 0,654196 | 3,262539 |
| 2 | 4,7 | 0,327588 | 7,323789 |
| 3 | 5,2 | 0,041424 | 4,867539 |
| 4 | 9,1 | 0,001624 | 2,868789 |
| 5 | 7 | 0,054811 | 0,165039 |
| 6 | 5,1 | 0,021626 | 5,318789 |
| 7 | 6 | 0,031768 | 1,977539 |
| 8 | 10,2 | 0,054949 | 7,805039 |
| 9 | 8,2 | 0,019765 | 0,630039 |
| 10 | 5,6 | 0,031768 | 3,262539 |
| 11 | 6,4 | 0,061038 | 1,012539 |
| 12 | 10,8 | 8,31E-05 | 11,51754 |
| 13 | 9,1 | 0,046352 | 2,868789 |
| 14 | 6,7 | 0,009307 | 0,498789 |
| 15 | 7,5 | 0,000764 | 0,008789 |
| 16 | 11,3 | 0,099968 | 15,16129 |
| Итого | 118,5 | 1,457029 | 68,549 |
Рассчитаем коэффициент детерминации.
Следовательно, можно сказать, что аддитивная модель объясняет 97,9% общей вариации уровней временного ряда.
Далее необходимо провести проверку адекватности модели данным наблюдения. Воспользуемся F-критерием Фишера:
где m – количество факторов в уравнении тренда (m=1).
Табличное значение F-критерия Фишера при уровне значимости α = 0,05,
k1 = m = 1, k2 = n – m – 1 = 14,
Fтабл = 4,60
Поскольку F > Fтабл, то уравнение статистически значимо, надёжно.
Шаг 6. Прогнозирование по аддитивной модели.
Прогнозное значение Ft уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда:
T = 5,6525 + 0,206 × t
Прогноз на 1 период:
T17 = 5,6525 + 0,206 × 17 = 9,16
Значение сезонного компонента за соответствующий период равно:
S1 = 0,55
Таким образом,
F17 = T17 + S1 = 9,16 + 0,55 = 9,71
Прогноз на 2 период:
T18 = 5,6525 + 0,206 × 18 = 9,366
Значение сезонной компоненты за соответствующий период равно:
S2 = – 1,9375
Таким образом, прогнозное значение на 2 квартала вперёд составит:
F18 = T18 + S2 = 9,366 – 1,9375 = 7,429
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 мая 2021 года; проверки требуют 3 правки.
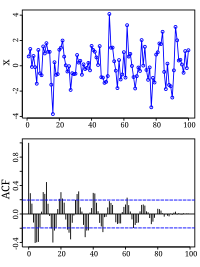
График 100 случайных величин, суммированный с синусоидальным сигналом малой амплитуды. График автокорреляционной функции позволяет увидеть периодичность в ряде данных.
Автокорреляционная функция — зависимость взаимосвязи между функцией (сигналом) и её сдвинутой копией от величины временного сдвига.
Для детерминированных сигналов автокорреляционная функция (АКФ) сигнала 
и показывает связь сигнала (функции 

Для случайных процессов АКФ случайной функции 
,
где 
Если исходная функция строго периодическая, то на графике автокорреляционной функции тоже будет строго периодическая функция. Таким образом, из этого графика можно судить о периодичности исходной функции, а, следовательно, и о её частотных характеристиках. Автокорреляционная функция применяется для анализа сложных колебаний, например, электроэнцефалограммы человека.
Применение в технике[править | править код]
Корреляционные свойства кодовых последовательностей, используемых в широкополосных системах, зависят от типа кодовой последовательности, её длины, частоты следования её символов и от её посимвольной структуры.
Изучение АКФ играет важную роль при выборе кодовых последовательностей с точки зрения наименьшей вероятности установления ложной синхронизации.
Другие применения[править | править код]
Автокорреляционная функция играет важную роль в математическом моделировании и анализе временных рядов, показывая характерные времена для исследуемых процессов (см., например: Турчин П. В. Историческая динамика. М.: УРСС, 2007. ISBN 978-5-382-00104-3). В частности, циклам в поведении динамических систем соответствуют максимумы автокорреляционной функции некоторого характерного параметра.
Скоростное вычисление[править | править код]
Часто приходится вычислять автокорреляционную функцию для временного ряда 


Метод основан на теореме Хинчина — Колмогорова (она же Винера-Хинчина), утверждающей, что автокорреляционная функция сигнала есть фурье-образ его спектральной плотности мощности. Поскольку для дискретных сигналов для вычисления их спектров существует алгоритм быстрого преобразования Фурье, имеющий порядок сложности 
Суть способа состоит в следующем. Можно сделать некое обратное взаимно однозначное преобразование данных, называемое преобразованием Фурье, которое поставит им во взаимно однозначное соответствие набор данных в другом пространстве, называемом пространством частот (частотный спектр сигнала — набор спектральных амплитуд ). Вместо прямого вычисления автокорреляционной функции на наших исходных данных можно произвести соответствующую ей операцию над соответствующими данными в пространстве частот Фурье-спектра, что делается за линейное время O(T) — вычислению автокорреляционной функции в пространстве частот соответствует вычисление мощностей частот возведением в квадрат модулей спектральных амплитуд. После этого мы по полученным спектральным мощностям восстановим соответствующие им в обычном пространстве значения автокорреляционной функции. Вычисление спектра по функции и обратно делается с помощью быстрого преобразования Фурье за 
Подготовка. Вычитаем из ряда среднее арифметическое. Преобразуем в комплексные числа. Дополняем нулями до 

Вычисление. Автокорреляционная функция вычисляется с помощью быстрого преобразования Фурье и прямо пропорциональна первым 
Квадрат комплексного модуля берётся поэлементно: 

См. также[править | править код]
- Теорема Хинчина-Колмогорова
- Корреляционная функция
- Взаимнокорреляционная функция
- Периодическая функция
- Корреляция
- Критерий Дарбина — Уотсона
- Дисперсия случайной величины
- Свёртка (математический анализ)
Примечания[править | править код]
- ↑ Charles Therrien, Murali Tummala. Probability and Random Processes for Electrical and Computer Engineers. — CRC Press, 2012. — P. 287. Дата обращения: 8 сентября 2016. Архивировано 17 сентября 2016 года.
Ссылки[править | править код]
- функция xcorr в MATLAB
Автокорреляционная функция и аддитивная модель временного ряда
Краткая теория
При
наличии во временном ряде тенденции и циклических колебаний значения каждого
последующего уровня ряда зависят от предыдущих.
Корреляционную зависимость между последовательными уровнями временного ряда
называют автокорреляцией уровней ряда. Количественно ее можно измерить с
помощью линейного коэффициента корреляции между уровнями исходного временного ряда
и уровнями этого ряда, сдвинутыми на несколько шагов во времени.
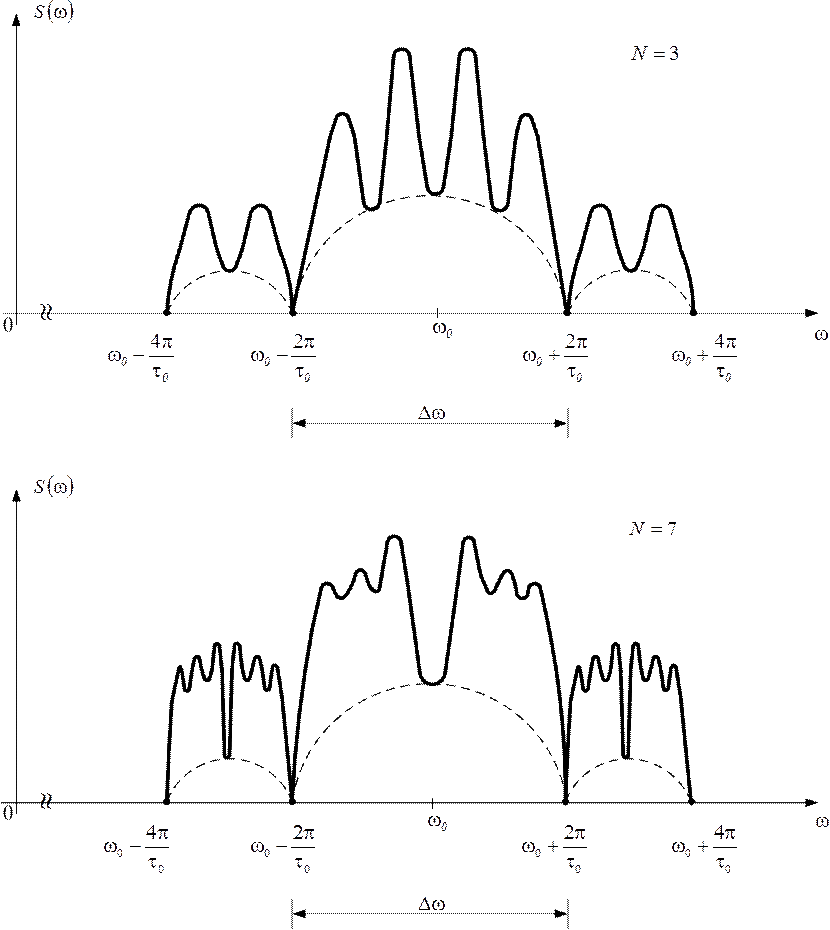
Число
периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом.
С увеличением лага число пар значений, по которым рассчитывается коэффициент
автокорреляции, уменьшается. Некоторые авторы считают целесообразным для
обеспечения статистической достоверности коэффициентов автокорреляции
использовать правило – максимальный лаг должен быть не больше
.
Отметим
два важных свойства коэффициента автокорреляции. Во-первых, он строится по аналогии
с линейным коэффициентом корреляции и таким образом характеризует тесноту
только линейной связи текущего и предыдущего уровней ряда. Поэтому по
коэффициенту автокорреляции можно судить о наличии линейной (или близкой к
линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную
тенденцию (например, параболу второго порядка или экспоненту), коэффициент
автокорреляции уровней исходного ряда может приближаться к нулю.
Во-вторых,
по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или
убывающей тенденции в уровнях ряда. Большинство временных рядов экономических
данных содержит положительную автокорреляцию уровней, однако при этом могут
иметь убывающую тенденцию.
Последовательность
коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют
автокорреляционной функцией временного рада. График зависимости ее значений от
величины лага (порядка коэффициента автокорреляции) называется коррелограммой.
Анализ
автокорреляционной функции и коррелограммы позволяет
определить лаг, при котором автокорреляция наиболее высокая, а
следовательно, и лаг, при котором связь между текущим и предыдущими уровнями
ряда наиболее тесная, т. е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Если
наиболее высоким оказался коэффициент автокорреляции первого порядка,
исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался
коэффициент автокорреляции порядка
, ряд содержит
циклические колебания с периодичностью в
моментов времени.
Если ни один из коэффициентов автокорреляции не является значимым, можно
сделать одно из двух предположений относительно структуры этого ряда: либо ряд
не содержит тенденции и циклических колебаний, либо ряд содержит сильную
нелинейную тенденцию, для выявления которой нужно провести дополнительный
анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию
целесообразно использовать для выявления во временном ряде наличия или
отсутствия трендовой компоненты (
)
и
циклической (сезонной) компоненты (
).
Существует несколько подходов к
анализу структуры временных рядов, содержащих сезонные или циклические
колебания. Простейший подход – расчет значений сезонной компоненты методом
скользящей средней и построение аддитивной или мультипликативной модели
временного ряда. Общий вид аддитивной модели следующий:
Эта модель
предполагает, что каждый уровень временного ряда может быть представлен как
сумма трендовой
,
сезонной
и случайной
компонент. Общий вид
мультипликативный модели выглядит так:
Эта модель
предполагает, что каждый уровень временного ряда может быть представлен как
произведение трендовой
,
сезонной
и случайной
компонент. Выбор одной из двух моделей
осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда
колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в
которой значения сезонной компоненты предполагаются постоянными для различных
циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят
мультипликативную модель временного ряда, которая ставит уровни ряда в
зависимость от значений сезонной компоненты.
Построение аддитивной и
мультипликативной моделей сводится к расчету значений
и
для каждого уровня ряда.
Процесс построения
модели включает в себя следующие шаги.
1. Выравнивание
исходного ряда методом скользящей средней.
2. Расчет значений
сезонной компоненты
.
3. Устранение сезонной
компоненты из исходных уровней ряда и получение выравненных данных
в аддитивной или
в мультипликативной модели.
4. Аналитическое
выравнивание уровней
или
и расчет значений
с использованием полученного уравнения тренда.
5. Расчет полученных по
модели значений
или
.
6. Расчет абсолютных
и/или относительных ошибок.
Если полученные
значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни
ряда и в дальнейшем использовать временной ряд ошибок
для анализа взаимосвязи исходного ряда и
других временных рядов.
Пример решения задачи
Задача
Имеются
условные данные об объемах потребления электроэнергии
жителями региона за 16 кварталов.
Требуется:
1.
Построить автокорреляционную функцию и сделать вывод о наличии сезонных
колебаний.
2.
Построить аддитивную модель временного ряда (для нечетных вариантов) или
мультипликативную модель временного ряда (для четных вариантов).
3.
Сделать прогноз на 2 квартала вперед.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
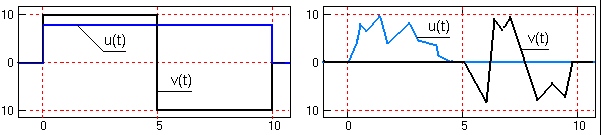
1) Построим поле корреляции:
Поле корреляции
Уже
исходя из графика видно, что значения
образуют пилообразную фигуру. Рассчитаем несколько
последовательных коэффициентов автокорреляции. Для этого составляем первую
вспомогательную таблицу:
Следует
заметить. что среднее
значение получается путем деления не на 16, а на 15, так как у нас теперь на
одно наблюдение меньше.
Коэффициент
автокорреляции первого порядка:
Составляем
вспомогательную таблицу для расчета коэффициента автокорреляции второго
порядка:
Следовательно:
Аналогично
находим коэффициенты автокорреляции более высоких порядков, а все полученные
значения заносим в сводную таблицу:
Коэффициенты автокорреляции
| Лаг |
Коэффициент автокорреляции уровней |
| 1 | 0.180 |
| 2 | -0.542 |
| 3 | 0.129 |
| 4 | 0.980 |
| 5 | 0.987 |
| 6 | -0.686 |
| 7 | 0.019 |
| 8 | 0.958 |
| 9 | 0.117 |
| 10 | -0.707 |
| 11 | -0.086 |
| 12 | 0.937 |
Коррелограмма
Анализ
коррелограммы и графика исходных уровней временного
ряда позволяет сделать выводы о наличии в изучаемом временном ряде сезонных
колебаний периодичностью в четыре квартала.
2) Проведем выравнивание исходных уровней ряда
методом скользящей средней. Для этого:
Просуммируем
уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент
времени и определим условные годовые объемы потребления электроэнергии.
Разделив
полученные суммы на 4, найдем скользящие средние. Полученные таким образом
выровненные значения уже не содержат сезонной компоненты.
Приведем
эти значения в соответствие с фактическими моментами времени, для чего найдем
средние значения из двух последовательных скользящих средних – центрированные
скользящие средние.
Расчет сезонной компоненты
|
|
|
Итого за четыре квартала |
Скользящая средняя за четыре квартала |
Центрированая скользящая средняя |
Оценка сезонной компоненты |
| 1 | 5.5 | — | — | — | — |
| 2 | 4.8 | 24.4 | 6.1 | — | — |
| 3 | 5.1 | 26 | 6.5 | 6.300 | -1.200 |
| 4 | 9 | 26.1 | 6.525 | 6.513 | 2.488 |
| 5 | 7.1 | 27.1 | 6.775 | 6.650 | 0.450 |
| 6 | 4.9 | 28.1 | 7.025 | 6.900 | -2.000 |
| 7 | 6.1 | 29.2 | 7.3 | 7.163 | -1.063 |
| 8 | 10 | 29.8 | 7.45 | 7.375 | 2.625 |
| 9 | 8.2 | 30.2 | 7.55 | 7.500 | 0.700 |
| 10 | 5.5 | 31.2 | 7.8 | 7.675 | -2.175 |
| 11 | 6.5 | 31.9 | 7.975 | 7.888 | -1.388 |
| 12 | 11 | 32.9 | 8.225 | 8.100 | 2.900 |
| 13 | 8.9 | 33.7 | 8.425 | 8.325 | 0.575 |
| 14 | 6.5 | 33.9 | 8.475 | 8.450 | -1.950 |
| 15 | 7.3 | — | — | — | — |
| 16 | 11.2 | — | — | — | — |
Найдем
оценки сезонной компоненты как разность между фактическими уровнями ряда и
центрированными скользящими среднеми. Используем эти оценки для расчета
значений сезонной компоненты
. Для этого найдем средние
за каждый квартал (по всем годам) оценки сезонной компоненты
:
В моделях
с сезонной компонентой обычно предполагается, что сезонные воздействия за
период взаимопогашаются. В аддитивной модели это выражается в том, что сумма
значений сезонной компоненты по всем кварталам должны быть равна нулю.
Для данной
модели имеем:
Корректирующий
коэффициент:
Рассчитываем
скорректированные значения сезонной компоненты
и заносим полученные данные в таблицу.
Проверим
равенство нулю суммы значений сезонной компоненты:
Исключим влияние сезонной компоненты, вычитая ее
значения из каждого уровня исходного временного ряда. Получим величины
. Эти значения
рассчитываются за каждый момент времени и содержат только тенденцию и случайную
компоненту.
Определим
компоненту
данной модели. Для этого проведем
аналитическое выравнивание ряда
с помощью линейного тренда. Результаты
аналитического выравнивания следующие:
Подставляя
в это уравнение значения
, найдем уровни
для каждого момента времени
Найлем
значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к
уровням
значения сезонной компоненты для
соответствующих кварталов.
На одном
графике отложим фактические значения уровней временного ряда и теоретические,
полученные по аддитивной модели.
Фактические и теоретические уровни
Для оценки
качества построенной модели применим сумму квадратов полученных абсолютных
ошибок:
Следовательно,
можно сказать, что аддитивная модель объясняет 99.3% общей вариации уровней
временного ряда.
3)
Прогнозное значение
уровня временного ряда в аддитивной модели
есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты
воспользуемся уравнением тренда:
Получим:
Значения
сезонных компонент за соответствующие кварталы равны:
Таким
образом:
Взаимная и автокорреляционные функции сигнала
Корреляционный
анализ используется при необходимости
оценить временные свойства сигнала без
применения спектрального анализа,
например, для оценки скорости изменения
или длительности сигнала, временной
связи (корреляции) одного сигнала с
другим.
Взаимная
корреляционная функцияопределяет
временную связь двух сигналов во времени.
Если сигналы не зависимы друг от друга,
их корреляционная функция равна нулю.
Чем шире корреляционная функция, тем
большая степень связи двух сигналов
друг с другом.
Взаимная
корреляционная функция определяется
соотношением
Пример
получения взаимной корреляционной
функции показан на рис.1. Значение
корреляционной функции в любой момент
xопределяется площадью пересечения
функцийи
сдвинутой копии.
Рис.
1
Взаимная
корреляционная функция не обязательно
симметрична и её максимум может оказаться
не в точке x=0.
Автокорреляционной
функцией (АКФ) ограниченного во времени
сигнала называется выражение вида
где
x – временной сдвиг исходного
сигнала.
Геометрический
смысл автокорреляционной функции
заключается в определении площади
пересечения функции
и
её копии, сдвинутой на времяx(Рис.2)
Рис.
2
Изменяя
время сдвига xдо тех пор, пока сигнал
и его копия перестанут пересекаться (в
данном случае),
получим АКФ.
Очевидно, что при изменении знака сдвига
при одинаковой его величине функция
автокорреляции одинакова, т.е.,
что говорит о четном её характере. Ясно,
что приx=0автокорреляционная
функция имеет максимум, при этом
а
в свою очередь полная энергия сигнала
равна
Таким
образом, максимум автокорреляционной
функции определяет полную энергию
сигнала. При увеличении сдвига x АКФ
убывает до нуля.
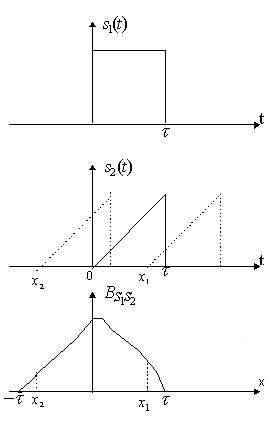
Примеры
-
Прямоугольный
импульс (рис.
3).
|
|
а) б) в) г) |
|
Рис. |
Для
x>0
имеем
и
интеграл для x<0
Максимум
АКФ равен энергии сигнала:
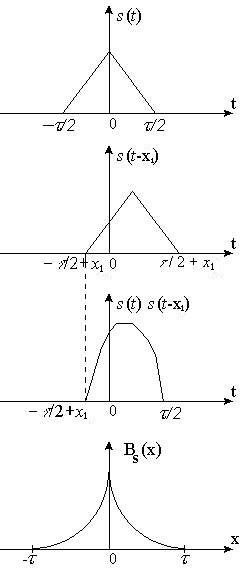
2)
Треугольный импульс. Построение АКФ
показано на рис.
4.
Рис.
4
Произведение
представляет собой нелинейную функцию
от t.
Полная энергия сигнала (максимум АКФ)
равнаДлительность
АКФ равна удвоенной длительности
сигнала.
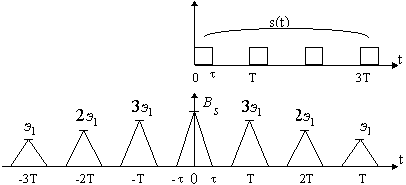
3.
Сигнал представляет собой пачку из
идентичных импульсов, расположенных
на равных расстояниях друг относительно
друга. АКФ также будет иметь вид пачки
импульсов, удаленных друг от друга на
те же расстояния, причем амплитуды
импульсов в пачке будут убывать от
центра к краям (см. рис.
5)
Рис.
5
14.
Общая
теория радиосигналов.
Понятие
узкополосного
и широкополосного
сигнала.
Понятие
частоты и фазы радиосигнала, их
взаимосвязь.
Понятие
базы сигнала.
Общие определения
К
радиосигналам относят высокочастотные
почти гармонические (квазигармонические)
колебания, в которых амплитуда или
мгновенная частота или фаза медленноменяются по некоторому закону. Процесс
изменения одного или нескольких
параметров высокочастотного гармонического
колебания называется модуляцией. В
системе радиосвязи закон модуляции
должен соответствовать закону изменения
передаваемого низкочастотного сообщения.
Частота
исходного высокочастотного гармонического
колебания называется несущей частотой.
Устройство, создающее это колебание,
называется генератором несущей частоты
или задающим генератором. К нему
предъявляются высокие требования к
стабильности амплитуды и частоты.
Несущее
колебание имеет вид
где
-амплитуда,
-частота,0-начальная
фаза.
Различают
амплитудную (АМ),частотную (ЧМ) и фазовую
(ФМ) модуляцию. При амплитудной модуляции
по закону низкочастотного сигнала
меняется мгновенная амплитуда, при
частотной модуляции – частота, при
фазовой модуляции – фаза. Бывают и
смешанные виды модуляции. В отдельный
класс можно выделить импульсные виды
модуляции и манипуляции, при которых
происходит дискретное изменение
параметра высокочастотного колебания.
-
Основные понятия о базе сигнала
В системах
связи используется такое понятие как
база сигнала, которое определяется
теоремой Котельникова. То есть исходя
из нее любой сигнал с финитным спектром
можно разложить на несколько отсчетов,
взятых через интервалы времени
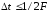
где F
– верхняя граничная частота спектра
сигнала (рис. 1).
Рис.
1. Пояснение
к тереме Котельникова
В данном
случае, если сигнал существует только
в течение времени – Т‚
то количество отсчетов будет равно
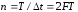
Эта величина определяет
размерность пространства, в котором
представляется сигнал координатами
(отсчетами мгновенных значений через
временные интервалы
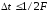
В этой связи в теории связи эту величину
называют базой сигнала:
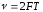
(2.2)
В иных случаях
говорят, что величина
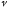
базис сигнала, т.е. количество осей
координат, в котором раскладывается
сигнал.
-
Сравнительный анализ узкополосных и
широкополосных сигналов
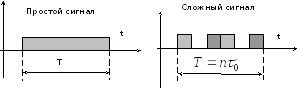
В действующих
системах связи, использующих дискретные
сигналы значение базы для простых
сигналов равно

в виде сложного сигнала, база которого
будет равна –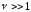
Рис. 2.
Простой и сложный сигналы
База сигнала
указывает на зависимость ширины спектра
от длительности сигнала. В случае
применения простых сигналов ширина его
спектра мала:
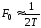
в связи с чем такие сигналы
называют узкополосными. Следует заметить,
что спектр узкополосного сигнала после
модуляции не намного отличается от
спектра первичного сигнала.
Для сложных
сигналов
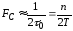
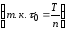
В этом случае спектр сложного
сигнала как до, так и после модуляции
намного превышает спектр первичного
сигнала, поэтому его принято называть
широкополосным.
Для
начала вспомним понятие полной фазы
радиосигнала
|
|
(2) |
а
также понятие мгновенной частоты
радиосигнала, как производной от полной
фазы:
|
|
(3) |
Сигналы,
у которых изменяется полная фаза в
соответствии с модулирующим сигналом
называются сигналами с угловой модуляцией.
Для
начала рассмотрим сигналы с фазовой
модуляцией (phase modulation PM). У сигналов с PM
полная фаза изменяется в соответствии
с модулирующим сигналом:
|
|
(4) |
где
называется
индексом фазовой модуляции или девиацией
фазы, а модулирующий сигнал по модулю
не превосходит единицы
Тогда
комплексная огибающая PM сигнала имеет
вид:
|
|
(5) |
а
сам радиосигнал может быть представлен
следующим образом:
|
|
(6) |
Теперь
рассмотрим сигнал с частотной модуляцией
(frequency modulation FM). В отличии от PM при частотной
модуляции происходит изменение мгновенной
частоты радиосигнала:
|
|
(7) |
где
называется
индексом частотной модуляции или
девиацией частоты, а модулирующий сигнал
по модулю не превосходит единицыТогда
полную фазу радиосигнала можно рассчитать
как интеграл от мгновенной частоты:
|
|
(8) |
Сигнал
с FM имеет вид:
|
|
(9) |
где
–
произвольная постоянная интегрирования
полной фазы (8). Обратите внимание, что
абсолютно не верно подставлять выражение
для мгновенной частоты вместо несущей
частоты в выражение для полосового
сигнала:
|
|
(10) |
так
как
Правильным
является выражение (9)!
16.
Сигналы
с внутриимпульсной модуляцией. Сигналы
с линейной частотной модуляцией.
Фазо-кодо-манипулированные сигналы.
Математические модели, спектральные
характеристики, особенности применения.
Фазо-кодо-манипулированные
импульсы (ФКМ)
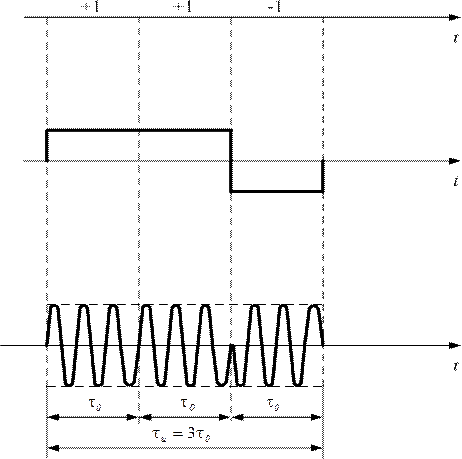
ФКМ
радиоимпульсы характеризуются
скачкообразным изменением фазы внутри
импульса по определенному закону,
например (рис. 1.66):
код
трехэлементного сигнала
закон
изменения фазы
трехэлементный
сигнал
Рис.
1.66
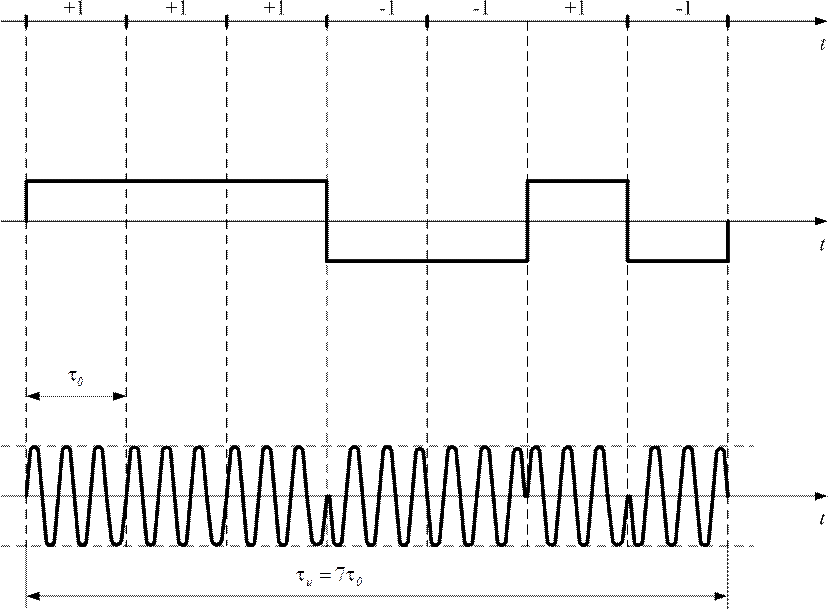
или
семиэлементный сигнал (рис. 1.67)
Таким
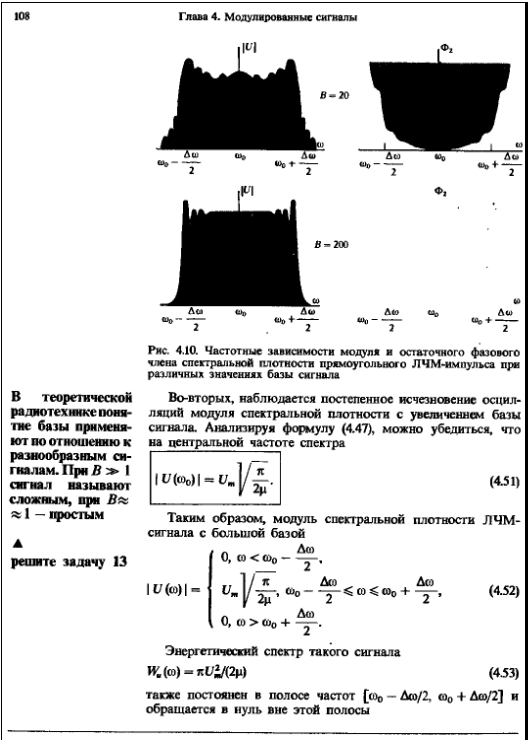
образом, можно сделать выводы:
·
АЧС сигналов с ЛЧМ является сплошным.
·
Огибающая АЧС определяется формой
огибающей сигнала.
·
Максимальное значение АЧС определяется
энергией сигнала, которая в свою очередь,
прямопропорциональна амплитуде и
длительности сигнала.
·
Ширина спектра равна
где
девиация
частоты и не зависит от длительности
сигнала.
·
База сигнала (коэффициент широкополостности)
может
бытьn>>1.Поэтому
ЛЧМ сигналы называют широкополосными.
Рис.
1.67
ФКМ
радиоимпульсы длительностью
представляют
собой совокупность следующих друг за
другом без интерваловэлементарных
радиоимпульсов,длительность каждого
из них одинакова и равна
и частоты элементарных импульсов
одинаковы, а начальные фазы могут
отличаться на(или
какое-либо другое значение). Закон (код)
чередования начальных фаз определяется
назначением сигнала. Для ФКМ радиоимпульсов,
используемых в радиолокации разработаны
соответствующие коды, например:
+1,
+1, -1 – трехэлементные коды
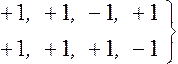
варианта четырехэлементного кода
+1
+1 +1, -1, -1, +1, -2 – семиэлементный код
Спектральную
плотность кодированных импульсов
определяют,используя свойство аддитивности
преобразований Фурье, в виде суммы
спектральных плотностей элементарных
радиоимпульсов.
Графики
АЧС для трехэлементного и семиэлементного
импульсов приведены на рисунке 1.68
Рис.
1.68
Как
видно из приведенных рисунков, ширина
спектра ФКМ радиосигналов определяется
длительностью элементарного радиоимпульса
или

Коэффициент
широкополостности
,где
N-количество
элементарных радиоимпульсов.
ФКМ
сигналы применяются в широкополосных
системах связи, радиолокации, в устройствах
идентификации обьектов.
6.
Понятие нормированной функции. Понятие
ортонормированной системы функций.
Нормирование
метрических параметров.
Норма
функций в пространстве L2[a,
b] определяется выражением:
||s(t)||
=.
Нетрудно
заключить, что чем больше интервал [a,
b] в этой формуле, тем больше (при прочих
равных условиях) будет значение нормы.
При анализе и сравнении сигналов (как
аналоговых, так и многомерных дискретных)
такое понятие не всегда удобно, и вместо
него очень часто используют понятие
нормы, нормированной относительно длины
интервала[a, b]. Для символьного обозначения
нормирования будем применять знак
:
||s(t)||
=,
||sn||
=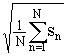
Метрика
сигналов (расстояние между сигналами)
при аналогичном нормировании:
d
(s(t), v(t)) =,
d
(sn,
vn)
=
Эти
выражения применяются для вычисления
среднеквадратического расхождения
сигналов или среднеквадратической
погрешности выполнения какой-либо
операции при сравнении ее результата
с теоретически ожидаемым или априорно
известным.
Нормированное
скалярное произведение сигналов:
б
s(t), v(t)
=s(t)v(t) dt = ||s(t)||
||v(t)||
cos .
б
sn,
vn
=(1/N)sn
vn
= ||sn||
||sn||
cos .
Косинус
угла (коэффициент корреляции) между
сигналами – функциями не изменяет своих
значений при вычислении как по
нормированным, так и по ненормированным
значениям скалярного произведения и
нормы сигналов (значения нормировки в
числителе и знаменателе выражения
(2.1.8) сокращаются). Взаимная перпендикулярность
функций определяется аналогично взаимной
перпендикулярности векторов условием
нулевого значения скалярного произведения.
Норма,
метрика и скалярное произведение
периодических функций обычно нормируются
на длину главного периода Т.
Ортогональные
сигналы.
Два
сигнала называются ортогональными
(orthogonal), если имеют нулевое скалярное
произведение
б
u(t), v(t)
=u(t)v(t)
dt = 0.
Соответственно,
два таких сигнала в своем функциональном
пространстве являются взаимно
перпендикулярными (угол между сигналами
равен
= 90о),
полностью независимыми друг от друга
(некоррелированными, r = cos ,
и имеют нулевую энергию взаимодействия
(Euv
= 0).
На
рисунке 2.3.1 приведены примеры взаимно
ортогональных сигналов. Нулевое скалярное
произведение двух левых сигналов
обеспечивается их формой (равна нулю
сумма положительных и отрицательных
значений произведения сигналов), а двух
правых – взаимным расположением (ненулевые
значения сигналов не имеют общих
координат).
Рис.
2.3.1. Ортогональные сигналы.
Попутно
заметим, что энергия и мощность суммы
ортогональных сигналов обладают
свойством аддитивности, т.к. имеют
нулевое значение скалярного произведения
и, соответственно, энергии взаимодействия.
Ортонормированный
базис пространства.
Множество сигналов – векторов {vk,
k = 1, 2, …, N} в N-мерном декартовом пространстве
при единичной норме и выполнении условий
взаимной ортогональности:
б
vm,
vn
=
(2.3.1)
могут
быть приняты в качестве ортонормированного
базиса данного пространства. Выражение
(2.3.1) обычно записывается в следующей
форме:
б
vm,
vn
=
mn,
(2.3.1′)
где
mn
–
импульс Кронекера, равный правой части
выражения (2.3.1).
С
использованием ортонормированного
базиса любой произвольный сигнал можно
представить в виде линейной комбинации
взвешенных базисных векторов:
s =
c1v1
+ c2v2
+ … + cNvN,
где
весовое значение сk
определяется проекцией вектора s на
соответствующее координатное направление:
ck
=
s, vk
.
При
распространении данных положений на
функциональное пространство L2[a,
b] в качестве координатного базиса
пространства мы должны использовать
совокупность функций {u0(t),
u1(t),
u2(t),
…}, в пределе – бесконечную, которая
должна быть системой
ортогональных функций
{uk(t),
k=0, 1, 2, …}, т.е. все функции на этом отрезке
должны быть взаимно ортогональны:
б
um(t),
un(t)
=um(t)
un(t)
dt = 0, m = 1, 2, … ; n = 1, 2, … ; m
n.
Система
ортогональных функций на интервале [a,
b] будет ортонормированной
(orthonormal
functions), если все функции системы при m=n
имеют единичную норму, т.е. выполняются
условия:
б
um(t),
um(t)
= ||um(t)||2
=(um(t))2
dt = 1, ||um(t)||
= 1,
m
= 1, 2, ….
Эти
условия можно записать в следующей
обобщенной форме:
um(t)·un*(t)
dt = m,n.
Система
ортогональных функций всегда может
быть превращена в ортонормированную
путем нормировки, т.е. деления всех
функций на их норму.
Продолжаем разговор про беспроводные технологии связи. На прошлом занятии речь шла об автокорреляционных и корреляционных функциях. Мы рассмотрели задачу о том, как можно найти период функции, используя автокорреляционный анализ. Напоминаю графики, на которых мы остановились на прошлом занятии.
Сегодня мы продолжим эту тему, но зайдем немного с другой стороны. Зайдем именно со стороны спектрального анализа. Если на прошлом занятии мы говорили с точки зрения временной координаты, с точки зрения времени, то сегодня поговорим с точки зрения спектра.
Дело в том, что когда мы работаем с сигналами, когда мы их излучаем, то сигнал всегда излучается на какой-либо частоте. Это связано с тем, что, во-первых, так его удобнее сгенерировать, удобнее управлять сигналом и переносить его на какой-то другой спектральный
диапазон.
Например, все вы видели что такое волна. Вы видите периодичные изменения, как распространяется волна. Что такое по сути волна? Это
периодические
изменения физической величины,
распространяющиеся в пространстве. Это может быть амплитуда волны, которая побежала. Это может быть какая-то упругая волна. Я сейчас говорю, возникают вариации давления и вы их слышите, причем эти вариации, которые сейчас создаются
в воздухе, они очень похожи на те круги, которые вы видите от брошенного камня. И та, и та – акустическая волна.
Радиосигналы распространяются за счет электромагнитного поля, то есть есть такие электромагнитные
волны, например, светодиод излучает в видимом диапазоне – это пример электромагнитной волны, на очень высокой частот. Радиоволна – это распространяющиеся колебания электромагнитного поля.
Шум в радиодиапазоне, окружающий нас, также имеет электромагнитную природу. Мощными источниками шума в радиодипазоне являются: Солнце, линии электропередач, аэропорты, сигнализация и так далее.
Мы начали со спектрального подхода, основанный на том, что достаточно гладкую
функцию
можно разложить или представить в виде
набора синусоид. Мы сейчас рассматриваем синусоиду как наиболее простую привычную нам функцию, с которой мы привыкли иметь дело. Практически любой сигнал можно представить как некоторый многомерный вектор. Любой вектор можно представить
в виде некоторой сумма базисных векторов. Так и наш сигнал можно в виде линейной комбинации базисных векторов.
Рассмотрим отдельную синусоиду (нижний рисунок, серая линия). Добавим к ней еще что-то, еще одну синусоиду, еще, еще и еще… Мы добавляем порядка 20 синусоид, и при сложении они начинают образовывать сигнал, который вы уже видели (нижний рисунок, синяя
линяя).
Обратите внимание, что у этого сигнала фронты немного завалены. То есть они не идеально вертикальные, как мы их видели на первом занятии, когда изображали прямоугольные импульсы. Добавим еще 20 синусоид. Обратите внимание фронты стали еще круче. Добавим
еще 20 синусоид, фронты стали еще круче. И обратите внимание, что волна, которая вроде бы как видна на плато импульса, она с добавлением порции все новых и новых синусоид становится все меньше и меньше. То есть результат сложения наших волн
все больше и больше напоминает прямоугольный импульс (верхний рисунок).
Обратите внимание на следующую интересную картинку. Почему мы взяли все-таки синусоиды? Потому что это, так называемый,
ортогональный
базис. Например, мы возьмем и найдем тем же способом, которым мы находили автокорреляционную функцию на прошлом занятии для двух синусоид. Вот одна синусоида, а вот другая синусоида. У них немного отличаются периоды. А теперь найдем кросс
корреляционную функцию. Чему она равна? Она равна нулю. То есть синусоиды с различными частотами линейно независимы.
Таким образом, мы можем любой сигнал представить в виде набора синусоид или их линейной комбинации. Это очень интересное свойство синусов как ортогонального базиса. Это не единственный ортогональный базис, который есть в природе, но наиболее естественный.
Если вы в школе изучали резонансные колебания, например, колебательный контур, электрическую цепочку, вы знаете, что есть резонансная частота, которая определяется значениями индуктивности и емкости.
Давайте теперь посмотрим на следующий момент, связанный с тем, как выглядит белый
шум, который рассматривали на прошлом занятии и у которого автокорреляционная функция была четкий пик. Как можно такой белый шум представить в виде набора синусоид?
Для того, чтобы было понятнее, мы представим график, на котором по оси x (оси абсцисс) отложена частота синусоиды, а по оси y – амплитуда синусоиды. И посмотрите внимательно на этот график, обратите внимание, что для белого шума все синусоиды входят с
одной и той же амплитудой. Так называемый спектр белого шума – равномерный. То есть все синусоиды сюда входят какими-то случайными фазами и одной и той же амплитудой. То есть нет выделенных частот в спектре белого шума. А как же выглядит спектр
одной синусоиды? Просто одна палочка. Одна синусоида – одна палочка.
А теперь давайте посмотрим как выглядит наш прямоугольный сигнал, который мы промоделировали как сумму синусоид. Обратите внимание, что некоторые синусоиды имеют большую амплитуду, некоторые меньшую, но на краях амплитуда этих гармонических составляющих уменьшается. Фактически вы сейчас видите спектр прямоугольного сигнала. Так называемая у радиофизиков функция Синка (sinc(x)). И энергия сигнала, которую мы сейчас рассматриваем, равна энергии тех синусоид, тех гармонических сигналов, которые его образуют.
Получается, белый шум заполняет весь спектр равномерно. Наш прямоугольный сигнал имеет выделенную часть в спектре. Что напрашивается? Напрашивается такой интересный вопрос. Мы сказали про сигнал, что у него энергия, но тогда если следовать той
же самой логике, мы можем сказать, что энергия белого шума бесконечна. Но естественно не бесконечна, вы ее видите. Спектр широкий, но каждая амплитуда входит с приближимо маленькой составляющей, а в сумме они дают такую бесконечность.
Если рассматривать сигнал на языке математики, то мы должны говорить, что когда мы работаем со спектрами, мы работаем с функциями из L2 пространства, то есть они должны быть интегрируемы, то есть иметь конечную энергию во всем спектральном
диапазоне. Хорошо, если у нас сигнал имеет какую-то конечную полосу, как набор тех частот, с которыми мы работаем, имеет конечную полосу, и сейчас выбрана полоса примерно 3 кГц.
Прошу обратить внимание на ширину этого импульса в спектральном диапазоне. 3 кГц – это примерно тот диапазон звуковых волн, которого достаточно, чтобы в нормальном виде передать мою речь, то есть вы будете спокойно понимать о чем я говорю без
сильных искажений. Голос будет уже не таким как в реальности, но все-таки близким к реальности. Можно прослушать, как будет меняться моя интонация, мой голос в зависимости от полосы: 15 кГц, 10 кГц, 5 кГц, 3 кГц, 1 кГц. Вы видите, что то,
что я говорю понятно, тембр моего голоса меняется. Он становится глуховатым, меняются индивидуальные моменты в голосе.
Полоса сигнала, чтобы передать звуковой сигнал, нужна примерно 3 кГц. Соответственно, для того чтобы передать несколько сигналов, независимых. Обратите внимание, что если мы добавим сюда еще один сигнал, но сдвинем его в спектре. Вот у нас два
синка. Они не пересекаются, друг другу не мешают. Тогда уже, соответственно, мы занимаем полосу 6 кГц. А как мы сдвинули импульс? Под ними сигналы, но уже во временной области.
Импульс, который соответствует первому спектру, он заполнен одной частотой, а импульс, который соответствует второму спектру, он заполнен другой частотой и вы видите, что частота выше. По сути дела, мы осуществили параллельный перенос спектральной области. Таким образом, чем больше у нас разрешенный диапазон частот, в котором мы можем работать, тем больше таких частотно-независимых каналов мы можем организовать.
Этим мы и пользуемся, когда используем какую-то сотовую связь или радиосвязь, но источников становится все больше и больше. Соответственно, каждый источник хочет свой выделенный диапазон частот. Потому что если мы их будем совмещать, то они будут друг другу мешать. Что можно делать? Можно, конечно, ужать полосу. Но тогда вы, скорее всего, вообще ничего не поймете из того, что будет передаваться. Или же можно уйти во все более высокие частоты. Мы видим, что в сторону нуля можно двигаться ограниченно, а в сторону высоких частот можно двигаться еще далеко. Этим как раз и вызван переход в диапазон 5G. Потому что нужно все больше и больше для наших абонентов выделить свой соответствующий спектральный диапазон.
Ну а что происходит с шумом?
http://docs.cntd.ru/document/1200025699
Здесь приведен рисунок, на котором показано как зависит мощность окружающего нас шума от частоты. Вы видите, что картина не равномерна, и где бы нам хотелось работать? Нам бы хотелось работать в тех местах, где шум имеет меньшую амплитуду. Кстати,
обратите внимание, что шум имеет меньшую амплитуду на все более высоких частотах.
Мы уже сказали, что информация
передается с помощью радиоволн, а волна
распространяется со скоростью. Электромагнитная волна в воздухе распространяется в воздухе примерно
со
скоростью света 3⋅108 м/с.
А что такое частота? Частота – это количество колебаний, совершенных в единицу времени. То есть скорость – это на какое расстояние продвинулась волна в единицу времени. Таким образом, если мы разделим скорость распространения на частоту,
мы получим то расстояние, на которое распространилась волна за одно колебание. Это так называемая длина
волны.
Длина волны – фундаментальный параметр вообще в радиосвязи. Почему она имеет такое важное значение? Потому что если какое-то препятствие сильно меньше длины волны, то волна его проходит, не заметив. Можно сказать препятствие не является препятствием.
Но если какой-то объект препятствия сравним с длиной волны, то он уже оказывает на распространение достаточно серьезное влияние. Таким образом, если у нас низкие частоты, длинные волны, то длина волны большая и для такой волны препятствия
все меньше и меньше. Но как мы видели, диапазон таких длин волн достаточно ограничен. А для высоких частот, для маленьких длин волн есть куда двигаться, но практически все является препятствием. А для диапазона 5G, миллиметровых длин, у вас
препятствием является практически все. Поэтому такие волны фактически распространяться только в зоне прямой видимости.
Для размышления
Подумайте и составьте список всех плюсов и минусов перехода на диапазон 5G.
Материалы
- Баскаков С.И. Радиотехнические цепи и сигналы (3-е издание, 2000) (3 глава, об автокорреляции)