Как найти автокорреляцию остатков

Важной предпосылкой построения
качественной регрессионной модели по
МНК является независимость значений
случайных отклонений ε_iот значений отклонений во всех других
наблюдениях. Отсутствие зависимости
гарантирует отсутствие коррелированности
между любыми отклонениями, т.е.cov(ε_i,
ε_j)
i ≠ jи, в частности, между соседними отклонениями
(cov(ε_i-1,
ε_i)=0).

Автокорреляция (последовательная
корреляция) остатковопределяется
как корреляция между соседними значениями
случайных отклонений во времени
(временные ряды) или в пространстве
(перекрестные данные). Она обычно
встречается во временных рядах и очень
редко – в пространственных данных. В
экономических задачах значительно чаще
встречается положительная автокорреляция
(cov(ε_i-1,
ε_i,)>
0), чем отрицательная автокорреляция

(cov(ε_i-1,
ε_i,)<0).

Чаще всего положительная автокорреляция
вызывается направленным постоянным
воздействием некоторых не учтенных в
регрессии факторов. Например, при
исследовании спроса уна прохладительные
напитки в зависимости от доходахна трендовую зависимость накладываются
изменения спроса в летние и зимние
периоды. Аналогичная картина может
иметь место в макроэкономическом анализе
с учетом циклов деловой активности.

Отрицательная автокорреляция фактически
означает, что за положительным отклонением
следует отрицательное и наоборот. Такая
ситуация может иметь место, если ту же
зависимость между спросом на прохладительные
напитки и доходами рассматривать не
ежемесячно, а раз в сезон (зима-лето).

Применение МНК к данным, имеющим
автокорреляцию в остатках, приводит к
таким последствиям:

1- Оценки параметров, оставаясь линейными
и несмещенными, перестают быть
эффективными. Они перестают быть
наилучшими линейными несмещенными
оценками.

2-Дисперсии оценок являются
смещенными. Часто дисперсии, вычисляемые
по стандартным формулам, являются
Сниженными, что влечет за собой увеличениеt –статистик.
Это может привести к признанию
статистически значимыми факторов,
которые в действительности таковыми
не являются.

3. Оценка дисперсии регрессии является
смещенной оценкой истинного значения
σ², во многих случаях
занижая его.

4. Выводы по t– иF –
статистикам, возможно, будут неверными,
что ухудшает прогнозные качества модели.

Для обнаружения автокорреляции используют
либо графический метод, либо статистические
тесты. Рассмотрим два наиболее популярных
теста.

Метод рядов. По этому методу последовательно
определяются знаки отклонений
от регрессионной зависимости. Например,
имеем при 20 наблюдениях

(—–)(+++++++)(—)(++++)(-).

Ряд определяется как непрерывная
последовательность одинаковых знаков.
Количество знаков в ряду называется
длиной ряда. Если рядов слишком мало по
сравнению с количеством наблюдений, то
вполне вероятна положительная
автокорреляция. Если же рядов слишком
много, то вероятна отрицательная
автокорреляция.

Пусть п– объём выборки,п₁– общее количество положительных
отклонений;п₂–
общее количество отрицательных
отклонений;k– количество рядов.
В приведенном примереn=20,п₁=11,
п₂=5.

При достаточно большом количестве
наблюдений (п₁>10,п₂>10)
и отсутствии автокорреляции СВkимеет асимптотически нормальное
распределение, в котором

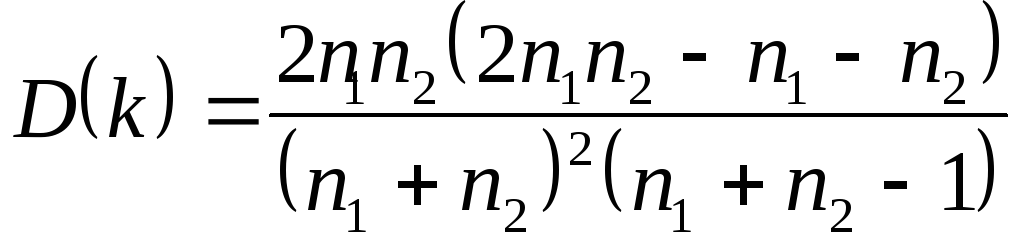
Тогда, если

M(k)-u_a/2·D(k)<k<M(k)+u_a/2·D(k),

по гипотеза об отсутствии автокорреляции
не отклоняется. Если k ≤. M(k)-u_a/2·D(k),
то констатируется положительная
автокорреляция; в случаеk ≥
M(k)+u_a/2·D(k)признается наличие отрицательной
автокорреляции.

Для небольшого числа наблюдений (n₁<20,n₂<20) были разработаны
таблицы критических значений количества
рядов припнаблюдениях. В одной
таблице в зависимости отn₁
иn₂определяется нижняя границаk₁
количества рядов, в другой – верхняя
границаk₂.Еслиk₁<k<k₂то говорят об отсутствии автокорреляции.
Еслиk≤k₁,то говорят о положительной автокорреляции.
Еслиk≥k₂,
тoговорят об
отрицательной автокорреляции. Например,
для приведенных выше данныхk₁=6,k₂=16 при
уровне значимости 0,05. Посколькуk=5<k₁=6,определяем положительную автокорреляцию.

Критерий Дарбина-Уотсона.Это
наиболее известный критерий обнаружения
автокорреляции первого порядка.
СтатистикаZWДарбина-Уотсона
приводится во всех специальных
компьютерных программах как одна из
важнейших характеристик качества
регрессионной модели.

Сначала по построенному эмпирическому
уравнению регрессии определяются
значения отклонений
.
Рассчитывается статистика

(65)

Далее по таблице критических точек
Дарвина-Уотсона определяется два числа
d₁ и d_ии осуществляются выводы по правилу:

0≤DW≤d₁
– положительная автокорреляция;

d₁<DW<d_u
– зона неопределенности;

d_u≤DW≤4-d_u
– автокорреляция
отсутствует;

4-d_u<DW<4-d₁
– зона неопределенности;

4-d₁≤DW≤4
– отрицательная автокорреляция.

Можно сказать, что статистика DW тесно
связана с коэффициентом автокорреляции
первого порядка:

. (66)

Связь выражается формулой:

(67)

Отсюда вытекает смысл статистического
анализа автокорреляции. Поскольку
значения rизменяются
от -1 до +1,DW изменяется
от 0 до 4. Когда автокорреляция отсутствует,
коэффициент автокорреляции равен нулю,
и статистикаDW равна 2.DW=Oсоответствует положительной автокорреляции,
когда выражение в скобках равно нулю(r=1).При отрицательной автокорреляции (r=
-1)DW=4,и
выражение в скобках равно двум.

Ограничения критерия Дарбина-Уотсона:

1. Критерий DWприменяется лишь для
тех моделей, которые содержат свободный
член.

2. Предполагается, что случайные отклонения
определяются по итерационной схеме

(68)

называемой авторегрессионой схемой
первого порядка AR(1).Здесьν_t–
случайный член.

3. Статистические данные должны иметь
одинаковую периодичность (не должно
быть пропусков в наблюдениях).

4. Критерий Дарбина – Уотсона не применим
к авторегрессионым моделям вида:

(69)

которые содержат в числе факторов также
зависимую переменную с временным лагом
(запаздыванием) в один период.

Для авторегрессионых моделей предлагается
h –статистика
Дарбина

(70)

где β– оценка коэффициента
автокорреляции первого порядка (66),D(c)
–выборочная дисперсия коэффициента
при лаговой переменнойy_t-1,
п –число наблюдений.

При большом пи справедливости
нуль – гипотезыН₀:р=0h~N(0,1).Поэтому при заданном уровне значимости
определяется критическая точка из
условия

,

и h –статистика сравнивается
си_α/2.Если|h|>
и_α/2, то
нуль – гипотеза об отсутствии автокорреляции
должна быть отклонена. В противном
случае она не отклоняется.

Обычно значение
рассчитывается по формулеaD(c)равна квадрату стандартной ошибкит_с
оценки коэффициентас.Следует отметить, что вычислениеh
–статистики невозможно приnD(c)>1.

Автокорреляция чаще всего вызывается
неправильной спецификацией модели.
Поэтому следует попытаться скорректировать
саму модель, в частности, ввести какой
– нибудь неучтенный фактор или изменить
форму модели (например, с линейной на
полулогарифмическую или гиперболическую).
Если все эти способы не помогают и
автокорреляция вызвана какими – то
внутренними свойствами ряда {е_t},можно воспользоваться преобразованием,
которое называется авторегрессионой
схемой первого порядкаAR(1).

Рассмотрим AR(1)на
примере парной регрессии:

y=a+bx+e. (71)

Тогда соседним наблюдениям соответствует
формула:

y_t=a+bx_t+e_t, (72)

y_t-1=a+bx_t-1+e_t-1. (73)

Если случайные отклонения определяются
выражением (68), где коэффициент ризвестен, то можем получить

y_t –
py_t-1=a(1-
p)+b(x_t
-px_t-1)+(e_t
–pe_t-1). (74)

Сделаем замены переменных

(75)

получим с учетом (68):

(76)

Поскольку случайные отклонения v_tудовлетворяют предпосылкам МНК, оценкиa^*иbбудут обладать свойства­ми наилучших
линейных несмещенных оценок. По
преобразованным значениям всех переменных
с помощью обычногоMНKвычисляются оценки параметров а* иb,
которые затем можно использовать в
регрессии (71).

Однако способ вычисления преобразованных
переменных (75) приводит к потере первого
наблюдения, если нет информации о
предшествующих наблюдениях. Это уменьшает
на единицу число степеней свободы, что
при больших выборках не очень существенно,
однако при малых выборках приводит к
потере эффективности. Тогда первое
наблюдение восстанавливается с помощью
поправки Прайса – Уинстена:

(77)

Авторегрессионое преобразование может
быть обобщено на произвольное число
объясняющих переменных, т.е. использовано
для уравнения множественной регрессии.

Для преобразования АR(1)важно оценить коэффициент автокорреляциир.Это делается несколькими
способами. Самое простое – оценитьрна основе статистикиDW:

(78)

где rберется в
качестве оценкир. Этот метод
хорошо работает при большом числе
наблюдений.

Существуют и другие методы оценивания
р,например, метод Кокрена
– Оркатта и метод Хилдрета – Лу. Они
являются итерационными, и их рассмотрение
выходит за рамки данного конспекта
лекций.

В случае, когда есть основания считать,
что автокорреляция отклонений очень
велика, можно использовать метод
первых разностей.В частности, при
высокой положительной автокорреляции
полагаютр=1, и уравнение
(74) принимает вид

или

(79)

где

Из уравнения (79) по МНК оценивается
коэффициент b.Параметраздесь не определяется
непосредственно, однако из МНК известно,
что

В случае р=–1, сложив (72)
и (73) с учетом (68), получаем уравнение
регрессии:

или

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Постановка задачи

Критерий Дарбина-Уотсона (Durbin–Watson statistic) – один из самых распространенных критериев для проверки автокорреляции.

Данный критерий входит в стандартный инструментарий python:

• присутствует в таблице выдачи результатов регрессионного анализа модуля линейной регрессии Linear Regression;

• может быть рассчитан с помощью функции statsmodels.stats.stattools.durbin_watson.

К сожалению, стандартные инструменты python не позволяют получить табличные значения статистики критерия Дарбина-Уотсона, нам предлагается воспользоваться методом грубой оценки: считается, что при расчетном значении статистики критерия в интервале [1; 2] автокорреляция отсутствует (см. Durbin–Watson statistic). Однако, для качественного статистического анализа такой подход неприемлем.

Представляет интерес реализовать в полной мере критерий Дарбина-Уотсона средствами python, добавив этот важный критерий в инструментарий специалиста DataScience.

В данном обзоре мы коснемся только собственно критерия Дарбина-Уотсона и его применения для выявления автокорреляции. Особенности построения регрессионных моделей и прогнозирования в условиях автокорреляции (двухшаговый метод наименьших квадратов и пр.) мы рассматривать не будем.

Применение пользовательских функций

Как и в предыдущем обзоре, здесь будут использованы несколько пользовательских функций для решения разнообразных задач. Все эти функции созданы для облегчения работы и уменьшения размера программного кода. Данные функции загружается из пользовательского модуля my_module__stat.py, который доступен в моем репозитории на GitHub.

Вот перечень данных функций:

• graph_plot_sns_np – функция строит линейный график средствами seaborn;

• graph_regression_plot_sns – функция строит график регрессионной модели и график остатков средствами seaborn;

• regression_error_metrics – функция возвращает ошибки аппроксимации регрессионной модели;

• graph_hist_boxplot_probplot_sns – функция позволяет визуализировать исходные данные для одной переменной путем одновременного построения гистограммы, коробчатой диаграммы и вероятностного графика средствами seaborn; имеется возможность выбирать, какие графики строить (h – hist, b – boxplot, p – probplot);

• norm_distr_check – проверка нормальности распределения исходных данных с использованием набора из нескольких статистических тестов.

• Goldfeld_Quandt_test, Breush_Pagan_test, White_test – проверка гетероскедастичности с использование тестов Голдфелда-Квандта, Бриша-Пэгана и Уайта соответственно;

• graph_regression_pair_predict_plot_sns – прогнозирование: построение графика регрессионной модели (с доверительными интервалами) и вывод расчетной таблицы с данными для заданной области значений X.

В процессе данного обзора мы создаем пользовательскую функцию Durbin_Watson_test, которая проверяет гипотезу о наличии автокорреляции (она тоже включена в пользовательский модуль my_module__stat.py).

Основы теории

Информацию о критерии Дарбина-Уотсона можно почерпнуть в [1, с.659], [2, с.117], [3, с.239], [4, с.188], а также:

• Durbin–Watson statistic

• Критерий Дарбина — Уотсона

Итак, предположим, мы рассматриваем регрессионную модель:

или в матричном виде:

Критерий Дарбина-Уотсона применяется в ситуации, когда регрессионные остатки связаны автокорреляционной зависимостью 1-го порядка [2, с.111]:

где – некоторое число (), а случайные величины удовлетворяют требованиям, предъявляемым к регрессионным остаткам классической модели (т.е. равенство нулю среднего значения, постоянство дисперсии и некоррелированность между собой):

Проверяется нулевая гипотеза об отсутствии автокорреляции:

Альтернативной гипотезой может быть:

• существование отрицательной автокорреляции (левосторонняя критическая область):

• существование положительной автокорреляции (правосторонняя критическая область):

• существование автокорреляции вообще (двусторонняя критическая область):

Расчетное значение статистики критерия Дарбина-Уотсона имеет вид:

где – остатки (невязки) регрессионной модели.

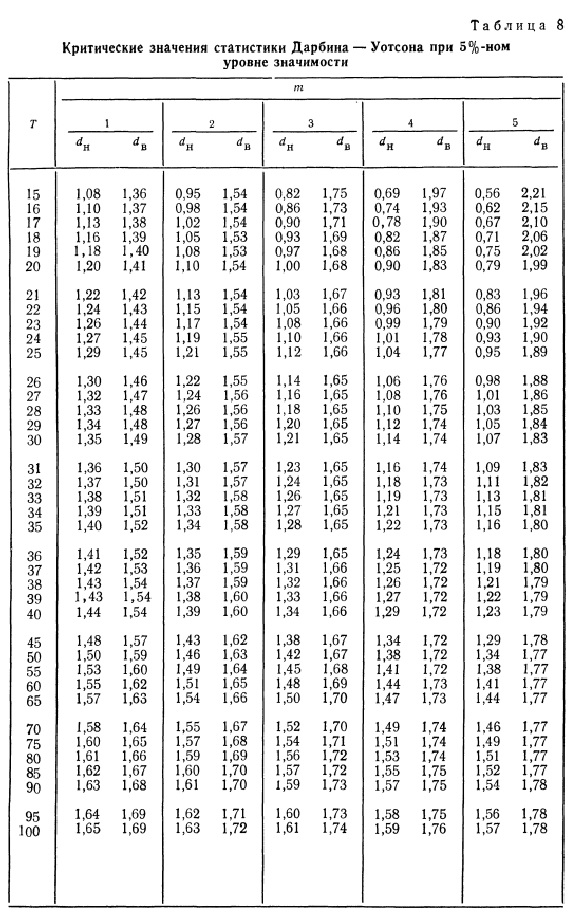
По таблицам (см. [1, с.659], [2, с.402], [3, с.291]) в зависимости от уровня значимости (5%, 2.5%, 1%), числа параметров регрессионной модели (кроме свободного члена ) (от 1 до 5) и объема выборки (от 15 до 100) определяются критические значения статистики Дарбина-Уотсона: нижний и верхний предел.

Правила принятия гипотез по критерию Дарбина-Уотсона выглядят довольно своеобразно – критические значения образуют пять областей различных статистических решений (причем критические границы принятия и непринятия не совпадают):

Есть очень удачная мнемоническая схема, приведенная в [3, с.240]:

Особенности критерия Дарбина-Уотсона:

1. Критические значения критерия табулированы для объема выборки от 15 до 100, аппроксимаций мне обнаружить не удалось. При меньших значениях критерий применять нельзя, при больших – очевидно, приходиться пользоваться грубым оценочным правилом: при расчетном значении статистики критерия в интервале [1; 2] автокорреляция отсутствует (см. https://en.wikipedia.org/wiki/Durbin–Watson_statistic).

2. Критерий позволяет выявить только автокорреляцию 1-го порядка. Отклонение нулевой гипотезы не означает, что автокорреляции нет вообще – возможно наличие автокорреляции более высоких порядков.

3. Критерий построен в предположении, что регрессоры и ошибки не коррелированы, поэтому его нельзя применять, в частности, для моделей авторегрессии [4, с.191].

4. Критерий не подходит для моделей без свободного члена .

5. Критерий имеет зону неопределенности, когда нет оснований ни принимать, ни отвергать нулевую гипотезу.

6. Между статистикой критерия и коэффициентом автокорреляции существует приближенное соотношение:

Существуют и другие критерии для проверки автокорреляции (тест Бройша-Годфри, Льюнга-Бокса и пр.).

Как было указано выше, большой проблемой является отсутствие табличных значений статистики критерия Дарбина-Уостона в стандартном инструментарии python. Для реализации возможностей данного критерия в полном объеме нам потребуется оцифровка весьма объемных таблиц критических значений.

Оцифровка табличных значений статистики критерия Дарбина – Уотсона

Я решил добавить в обзор этот раздел, хотя, строго говоря, можно было обойтись и без него, а сразу воспользоваться оцифрованными таблицами статистики критерия Дарбина-Уотсона.

Однако, если мы хотим выполнять качественный статистический анализ, неизбежно придется работать с большим количеством статистических критериев и далеко не все из них реализованы в python. Критерий Дарбина-Уотсона – это только один из многих. Количество критериев, рассматриваемых в литературе по прикладной статистике в последние годы постоянно увеличивается. Специалисту придется реализовывать многие критерии самостоятельно и одна из проблем, с которой придется столкнуться – это таблицы критических значений. Далеко не все табличные значения имеют аппроксимации, а значит придется каким-то образом оцифровывать эти таблицы. Небольшие таблицы можно сохранить в файлах вручную, а вот такой подход с объемными таблицами (как в нашем случае) – это слишком непроизводительно и нерационально.

В общем, на мой взгляд, представляет интерес разобрать пример оцифровки статистических таблиц на примере нашего критерия Дарбина-Уотсона – это позволит специалистам сэкономить человеко-часы работы и облегчить совершенствование инструментов статистического анализа.

Замечу сразу, что я не являюсь глубоким специалистом в области анализа и обработки изображений и текстов на python – это не совсем мой профиль. Профессионалы в этой области, возможно, раскритикуют то, как решается поставленная задача и предложат более удачное решение. Если будет так – то заранее спасибо. Я же эту задачу старался решить наиболее простым и рациональным способом, доступным для широкого круга специалистов. На всякий случай могу процитировать Давоса Сиворта из “Игры престолов”: “Простите за то, что увидите”.

Алгоритм действий:

Для оцифровки я использовал таблицы, приведенные в [3, с.290-292].

1. Сканируем таблицы, сохраняем в виде jpg-файлов (Durbin_Watson_test_1.jpg, Durbin_Watson_test_2.jpg, Durbin_Watson_test_3.jpg) в папке text_processing, расположенной внутри папки с рабочим .ipynb-файлом:

1. Распознаем текст (я воспользовался онлайн-сервисом https://convertio.co/), полученные текстовые файлы Durbin-Watson-test-1.ocr.txt, Durbin-Watson-test-2.ocr.txt, Durbin-Watson-test-3.ocr.txt также помещаем в папке text_processing.

2. Откроем файлы, запишем содержимое файлов в переменные, каждая из которых соответствует одной странице:

with open('text_processingDurbin-Watson-test-1.ocr.txt') as f1:
    Durbin_Watson_test_1 = f1.readlines()
display(Durbin_Watson_test_1, type(Durbin_Watson_test_1), len(Durbin_Watson_test_1))

С остальными файлами – действуем аналогично:

with open('text_processingDurbin-Watson-test-2.ocr.txt') as f2:
    Durbin_Watson_test_2 = f2.readlines()
display(Durbin_Watson_test_2, type(Durbin_Watson_test_2), len(Durbin_Watson_test_2))

with open('text_processingDurbin-Watson-test-3.ocr.txt') as f3:
    Durbin_Watson_test_3 = f3.readlines()
display(Durbin_Watson_test_3, type(Durbin_Watson_test_3), len(Durbin_Watson_test_3))

Видим, что переменные представляют собой списки, элементами которых является строки.

Для облегчения дальнейшей обработки данных создадим список, элементами которого являются переменные-страницы:

Durbin_Watson_test = [Durbin_Watson_test_1, Durbin_Watson_test_2, Durbin_Watson_test_3]

Далее я не стал публиковать здесь скриншоты с обработкой страниц – из-за экономии места. В ipyng-файле, который доступен в моем репозитории, весь процесс обработки представлен достаточно подробно.

1. Исключаем все строки, которые начинаются не с цифр; при этом воспользуемся алгоритмом перезаписи списка:

# создаем новый список
Durbin_Watson_test_new = list()

# удаляем строки
for page in Durbin_Watson_test:
    page_temp = list()    # временная страница
    for line in page:
        if line[0].isdigit():
            page_temp.append(line)    # перезаписываем список
    Durbin_Watson_test_new.append(page_temp)

1. Исключаем из текста управляющие символы (t, n) – с помощью регулярных выражений (regex) (модуль re):

# задаем шаблон для удаления символов
pattern = r'[t+n+]'    

# выполняем обработку
Durbin_Watson_test_new = [
    [re.sub(pattern, '  ', elem) for elem in page] 
    for page in Durbin_Watson_test_new]

1. Удаляем все символы, кроме цифр, точек, запятых и пробелов:

# задаем шаблон для удаления символов
pattern = r'[^0-9,. ]'    

# выполняем обработку
Durbin_Watson_test_new = [
    [re.sub(pattern, '', elem) for elem in page] 
    for page in Durbin_Watson_test_new]

1. Заменяем запятые на точки:

# задаем шаблон для удаления символов
pattern = r'[,]'

# выполняем обработку
Durbin_Watson_test_new = [
    [re.sub(pattern, '.', elem) for elem in page] 
    for page in Durbin_Watson_test_new]

1. Разделяем строки:

# задаем шаблон
pattern = r'[ ]+'

# выполняем обработку
Durbin_Watson_test_new = [[re.split(pattern, elem) for elem in page] 
                          for page in Durbin_Watson_test_new]

1. Сохраняем данные в DataFrame – для этого создадим список Durbin_Watson_list_df, элементами которого являются отдельные DataFrame, каждый из которых соответствует отдельной странице:

# создаем новый список
Durbin_Watson_list_df = list()
for page in Durbin_Watson_test_new:
    Durbin_Watson_list_df.append(pd.DataFrame(page))

1. Исправляем вручную отдельные аномалии, возникшие при распознавании отсканированных данных – к сожалению, работы вручную совсем избежать не удается.

• Корректируем DataFrame, соответствующий 1-й странице:

# создаем временный DataFrame
temp_df = Durbin_Watson_list_df[0]
# удаляем последние столбцы
temp_df = temp_df.drop(columns=[11, 12])
# корректируем вручную отдельные ошибки
temp_df.loc[[4],] = [19, 1.18, 1.40, 1.08, 1.53, 0.97, 1.68, 0.86, 1.85, 0.75, 2.02]
temp_df.loc[[8],[3]] = 1.17
temp_df.loc[[10],[3]] = 1.21
temp_df.loc[[17],[9]] = 1.11
temp_df.loc[[21],[4]] = 1.59
temp_df.loc[[25],[5]] = 1.34
temp_df.loc[[31],[10]] = 1.77
# записываем изменения
Durbin_Watson_list_df[0] = temp_df

• Корректируем DataFrame, соответствующий 2-й странице:

# создаем временный DataFrame
temp_df = Durbin_Watson_list_df[1]
# удаляем последние столбцы
temp_df = temp_df.drop(columns=[11, 12])
# корректируем вручную отдельные ошибки
temp_df.loc[[2],[8]] = 1.77
temp_df.loc[[10],[9]] = 0.86
temp_df.loc[[10],[10]] = 1.77
temp_df.loc[[14],[9]] = 0.96
temp_df.loc[[17],[10]] = 1.71
temp_df.loc[[34],[10]] = 1.71
# записываем изменения
Durbin_Watson_list_df[1] = temp_df

• Корректируем DataFrame, соответствующий 3-й странице:

# создаем временный DataFrame
temp_df = Durbin_Watson_list_df[2]
# удаляем последние столбцы
temp_df = temp_df.drop(columns=[11, 12])
# корректируем вручную отдельные ошибки
temp_df.loc[[2],[9]] = 0.48
temp_df.loc[[13],] = [28, 1.10, 1.24, 1.04, 1.32, 0.97, 1.41, 0.90, 1.51, 0.83, 1.62]
temp_df.loc[[20],[3]] = 1.14
temp_df.iloc[21:26, 7] = [1.04, 1.06, 1.07, 1.09, 1.10]
temp_df.loc[[26],[9]] = 1.11
temp_df.loc[[35],] = [90, 1.50, 1.54, 1.47, 1.56, 1.45, 1.59, 1.43, 1.61, 1.41, 1.64]
# записываем изменения
Durbin_Watson_list_df[2] = temp_df

Обращаем внимание, что откорректированные вручную значения являются числовыми, а все остальные значения – еще имеют строковый тип.

11. Преобразуем значения из строкового в числовой тип:

for elem_df in Durbin_Watson_list_df:
    for col in elem_df.columns:
        elem_df[col] = pd.to_numeric(elem_df[col], errors='ignore')

1. Корректируем структуру DataFrame:

• меняем индекс – индексом теперь будет объем выборки n

• каждый DataFrame снабжаем мультииндексом по столбцам (подробнее см. [7, с.169])

# меняем индекс
Durbin_Watson_list_df = [
    elem_df.set_index([0])
    for elem_df in Durbin_Watson_list_df]

# добавляем мультииндекс по столбцам
multi_index_list = ['p=0.95', 'p=0.975', 'p=0.99']    # список, содержащий значения для верхней строки мульииндекса
for i, elem_df in enumerate(Durbin_Watson_list_df):
    elem_df.index.name = 'n'
    elem_df.columns = pd.MultiIndex.from_product(
        [[multi_index_list[i]],
         ['m=1', 'm=2', 'm=3', 'm=4', 'm=5'],
         ['dL','dU']])

1. Объединяем отдельные DataFrame в один:

Durbin_Watson_test_df = Durbin_Watson_list_df[0].copy()

for i, elem_df in enumerate(Durbin_Watson_list_df):
    if i > 0:
        Durbin_Watson_test_df = Durbin_Watson_test_df.join(elem_df)

display(Durbin_Watson_test_df)        

Durbin_Watson_test_df.info()

Итак, мы сформировали DataFrame с оцифрованными данными таблиц критических значений статистики Дарбина-Уотсона. Получить доступ к данным теперь очень просто – например, нам требуется вывести табличные значения статистики критерия при объеме выборки , доверительной вероятности и числе параметров регрессионной модели :

n = 40
p = 0.95
m=2

Durbin_Watson_test_df.loc[[n], (f'p={p}', f'm={m}')]

1. Построим график табличных значений.

График получился весьма объемным – 3х5 элементов – однако он необходим: на графике можно увидеть те ошибки (пики и впадины), которые мы могли пропустить при ручной обработке ранее (некорректно отсканированные и распознанные цифры), тогда придется вернуться к этапу 10.

# меняем настройки Mathplotlib
plt.rcParams['axes.titlesize'] = 10      # шрифт заголовка
plt.rcParams['legend.fontsize'] = 9      # шрифт легенды
plt.rcParams['xtick.labelsize'] = 8      # шрифт подписей меток
plt.rcParams['ytick.labelsize'] = 8

fig = plt.figure(figsize=(297/INCH, 420/INCH))

ax_1_1 = plt.subplot(5,3,1)
ax_2_1 = plt.subplot(5,3,2)
ax_3_1 = plt.subplot(5,3,3)
ax_1_2 = plt.subplot(5,3,4)
ax_2_2 = plt.subplot(5,3,5)
ax_3_2 = plt.subplot(5,3,6)
ax_1_3 = plt.subplot(5,3,7)
ax_2_3 = plt.subplot(5,3,8)
ax_3_3 = plt.subplot(5,3,9)
ax_1_4 = plt.subplot(5,3,10)
ax_2_4 = plt.subplot(5,3,11)
ax_3_4 = plt.subplot(5,3,12)
ax_1_5 = plt.subplot(5,3,13)
ax_2_5 = plt.subplot(5,3,14)
ax_3_5 = plt.subplot(5,3,15)

fig.suptitle('Табличные значения статистики критерия Дарбина-Уотсона', fontsize = 16)

(Ymin, Ymax) = (0.3, 2.2)
x = Durbin_Watson_test_df.index

title_fontsize = 10

name_1_1 = ['p=0.95', 'm=1']
ax_1_1.set_title(name_1_1[0] + ' ' + name_1_1[1])
ax_1_1.plot(x, Durbin_Watson_test_df[tuple(name_1_1 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_1_1 + ['dU'])])

name_1_2 = ['p=0.95', 'm=2']
ax_1_2.set_title(name_1_2[0] + ' ' + name_1_2[1])
ax_1_2.plot(x, Durbin_Watson_test_df[tuple(name_1_2 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_1_2 + ['dU'])])

name_1_3 = ['p=0.95', 'm=3']
ax_1_3.set_title(name_1_3[0] + ' ' + name_1_3[1])
ax_1_3.plot(x, Durbin_Watson_test_df[tuple(name_1_3 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_1_3 + ['dU'])])

name_1_4 = ['p=0.95', 'm=4']
ax_1_4.set_title(name_1_4[0] + ' ' + name_1_4[1])
ax_1_4.plot(x, Durbin_Watson_test_df[tuple(name_1_4 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_1_4 + ['dU'])])

name_1_5 = ['p=0.95', 'm=5']
ax_1_5.set_title(name_1_5[0] + ' ' + name_1_5[1])
ax_1_5.plot(x, Durbin_Watson_test_df[tuple(name_1_5 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_1_5 + ['dU'])])

name_2_1 = ['p=0.975', 'm=1']
ax_2_1.set_title(name_2_1[0] + ' ' + name_2_1[1])
ax_2_1.plot(x, Durbin_Watson_test_df[tuple(name_2_1 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_2_1 + ['dU'])])

name_2_2 = ['p=0.975', 'm=2']
ax_2_2.set_title(name_2_2[0] + ' ' + name_2_2[1])
ax_2_2.plot(x, Durbin_Watson_test_df[tuple(name_2_2 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_2_2 + ['dU'])])

name_2_3 = ['p=0.975', 'm=3']
ax_2_3.set_title(name_2_3[0] + ' ' + name_2_3[1])
ax_2_3.plot(x, Durbin_Watson_test_df[tuple(name_2_3 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_2_3 + ['dU'])])

name_2_4 = ['p=0.975', 'm=4']
ax_2_4.set_title(name_2_4[0] + ' ' + name_2_4[1])
ax_2_4.plot(x, Durbin_Watson_test_df[tuple(name_2_4 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_2_4 + ['dU'])])

name_2_5 = ['p=0.975', 'm=5']
ax_2_5.set_title(name_2_5[0] + ' ' + name_2_5[1])
ax_2_5.plot(x, Durbin_Watson_test_df[tuple(name_2_5 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_2_5 + ['dU'])])

name_3_1 = ['p=0.99', 'm=1']
ax_3_1.set_title(name_3_1[0] + ' ' + name_3_1[1])
ax_3_1.plot(x, Durbin_Watson_test_df[tuple(name_3_1 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_3_1 + ['dU'])])

name_3_2 = ['p=0.99', 'm=2']
ax_3_2.set_title(name_3_2[0] + ' ' + name_3_2[1])
ax_3_2.plot(x, Durbin_Watson_test_df[tuple(name_3_2 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_3_2 + ['dU'])])

name_3_3 = ['p=0.99', 'm=3']
ax_3_3.set_title(name_3_3[0] + ' ' + name_3_3[1])
ax_3_3.plot(x, Durbin_Watson_test_df[tuple(name_3_3 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_3_3 + ['dU'])])

name_3_4 = ['p=0.99', 'm=4']
ax_3_4.set_title(name_3_4[0] + ' ' + name_3_4[1])
ax_3_4.plot(x, Durbin_Watson_test_df[tuple(name_3_4 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_3_4 + ['dU'])])

name_3_5 = ['p=0.99', 'm=5']
ax_3_5.set_title(name_3_5[0] + ' ' + name_3_5[1])
ax_3_5.plot(x, Durbin_Watson_test_df[tuple(name_3_5 + ['dL'])],
            x, Durbin_Watson_test_df[tuple(name_3_5 + ['dU'])])

ax_1_1.set_ylim(Ymin, Ymax)
ax_2_1.set_ylim(Ymin, Ymax)
ax_3_1.set_ylim(Ymin, Ymax)
ax_1_2.set_ylim(Ymin, Ymax)
ax_2_2.set_ylim(Ymin, Ymax)
ax_3_2.set_ylim(Ymin, Ymax)
ax_1_3.set_ylim(Ymin, Ymax)
ax_2_3.set_ylim(Ymin, Ymax)
ax_3_3.set_ylim(Ymin, Ymax)
ax_1_4.set_ylim(Ymin, Ymax)
ax_2_4.set_ylim(Ymin, Ymax)
ax_3_4.set_ylim(Ymin, Ymax)
ax_1_5.set_ylim(Ymin, Ymax)
ax_2_5.set_ylim(Ymin, Ymax)
ax_3_5.set_ylim(Ymin, Ymax)

legend = (r'$d_L$', r'$d_U$')
ax_1_1.legend(legend)
ax_2_1.legend(legend)
ax_3_1.legend(legend)
ax_1_2.legend(legend)
ax_2_2.legend(legend)
ax_3_2.legend(legend)
ax_1_3.legend(legend)
ax_2_3.legend(legend)
ax_3_3.legend(legend)
ax_1_4.legend(legend)
ax_2_4.legend(legend)
ax_3_4.legend(legend)
ax_1_5.legend(legend)
ax_2_5.legend(legend)
ax_3_5.legend(legend)

plt.show()

# возвращаем настройки Mathplotlib
plt.rcParams['axes.titlesize'] = f_size + 10      # шрифт заголовка
plt.rcParams['legend.fontsize'] = f_size + 6      # шрифт легенды
plt.rcParams['xtick.labelsize'] = f_size + 4      # шрифт подписей меток
plt.rcParams['ytick.labelsize'] = f_size + 4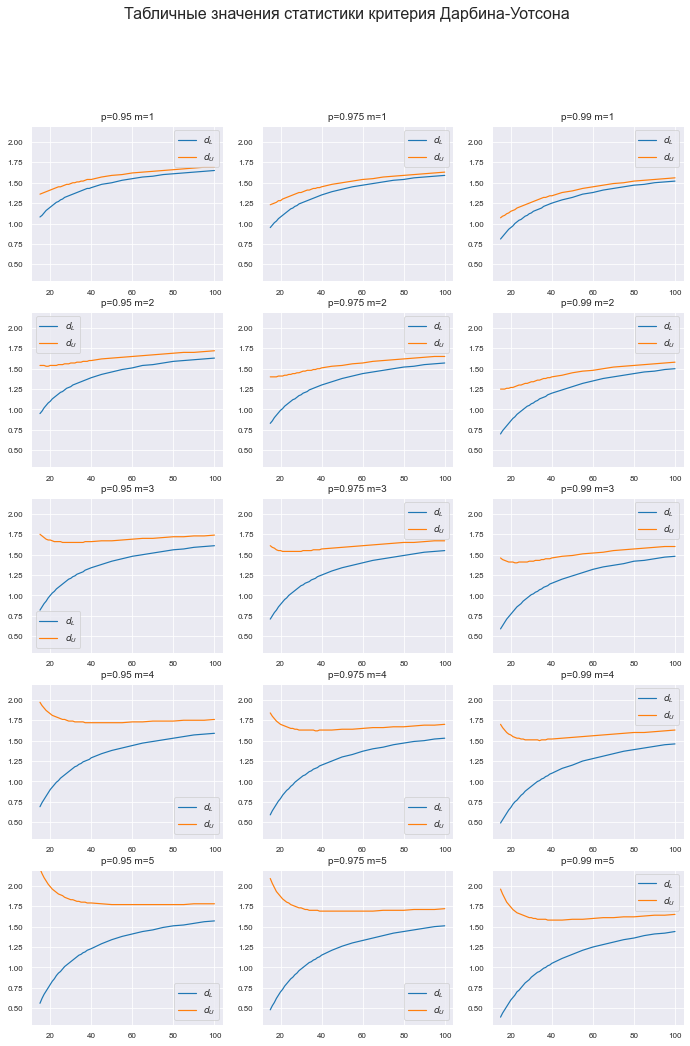

1. Сохраняем полученный DataFrame в csv-файл, помещаем его в папку table, расположенную внутри папки с рабочим .ipynb-файлом (в которой папку table у нас хранятся файлы с данными из статистических таблиц):

Durbin_Watson_test_df.to_csv(
    path_or_buf='tableDurbin_Watson_test_table.csv',
    mode='w+',
    sep=';',
    index_label='n')

Табличные значения статистики критерия Дарбина-Уотсона у нас теперь имеются, можем приступать к созданию пользовательской функции.

Создание пользовательской функции для реализации критерия Дарбина – Уотсона

Рассчитать статистику критерия Дарбина-Уотсона мы можем с помощью функции statsmodels.stats.stattools.durbin_watson.

Создадим пользовательскую функцию Durbin_Watson_test для проверки гипотезы об автокорреляции:

def Durbin_Watson_test(
    data,
    m = None,
    p_level: float=0.95):
    
    a_level = 1 - p_level
    data = np.array(data)
    n = len(data)
    
    # расчетное значение статистики критерия
    DW_calc = sms.stattools.durbin_watson(data)
    
    # табличное значение статистики критерия
    if (n >= 15) and (n <= 100):
        # восстанавливаем структуру DataFrame из csv-файла
        DW_table_df = pd.read_csv(
            filepath_or_buffer='table/Durbin_Watson_test_table.csv',
            sep=';',
            #index_col='n'
            )
                            
        DW_table_df = DW_table_df.rename(columns={'Unnamed: 0': 'n'})
        DW_table_df = DW_table_df.drop([0, 1, 2])
        
        for col in DW_table_df.columns:
            DW_table_df[col] = pd.to_numeric(DW_table_df[col], errors='ignore')
            
        DW_table_df = DW_table_df.set_index('n')

        DW_table_df.columns = pd.MultiIndex.from_product(
            [['p=0.95', 'p=0.975', 'p=0.99'],
            ['m=1', 'm=2', 'm=3', 'm=4', 'm=5'],
            ['dL','dU']])    
        
        # интерполяция табличных значений
        key = [f'p={p_level}', f'm={m}']
        f_lin_L = sci.interpolate.interp1d(DW_table_df.index, DW_table_df[tuple(key + ['dL'])])
        f_lin_U = sci.interpolate.interp1d(DW_table_df.index, DW_table_df[tuple(key + ['dU'])])
        DW_table_L = float(f_lin_L(n))
        DW_table_U = float(f_lin_U(n))
                   
        # проверка гипотезы
        Durbin_Watson_scale = {
            1: DW_table_L,
            2: DW_table_U,
            3: 4 - DW_table_U,
            4: 4 - DW_table_L,
            5: 4}
        
        Durbin_Watson_comparison = {
            1: ['0 ≤ DW_calc < DW_table_L',                   'H1: r > 0'],
            2: ['DW_table_L ≤ DW_calc ≤ DW_table_U',          'uncertainty'],
            3: ['DW_table_U < DW_calc < 4 - DW_table_U',      'H0: r = 0'],
            4: ['4 - DW_table_U ≤ DW_calc ≤ 4 - DW_table_L',  'uncertainty'],
            5: ['4 - DW_table_L < DW_calc ≤ 4',               'H1: r < 0']}
        
        r_scale = list(Durbin_Watson_scale.values())
        for i, elem in enumerate(r_scale):
            if DW_calc <= elem:
                key_scale = list(Durbin_Watson_scale.keys())[i]
                comparison = Durbin_Watson_comparison[key_scale][0]
                conclusion = Durbin_Watson_comparison[key_scale][1]
                break
           
    elif n < 15:        
        comparison = '-'
        conclusion = 'count less than 15'
    else:
        comparison = '-'
        conclusion = 'count more than 100'
    
    
    # формируем результат            
    result = pd.DataFrame({
        'n': (n),
        'm': (m),
        'p_level': (p_level),
        'a_level': (a_level),
        'DW_calc': (DW_calc),
        'ρ': (1 - DW_calc/2),
        'DW_table_L': (DW_table_L if (n >= 15) and (n <= 100) else '-'),
        'DW_table_U': (DW_table_U if (n >= 15) and (n <= 100) else '-'),
        'comparison of calculated and critical values': (comparison),
        'conclusion': (conclusion)
        },
        index=['Durbin-Watson_test'])
    
    
    return result

Протестируем созданную функцию – будем моделировать временные ряды с различными свойствами и выполнять проверку автокорреляции:

y_func = lambda x, b0, b1: b0 + b1*x

N = 30    # число наблюдений
(mu, sigma) = (0, 25)    # параметры моделируемой случайной компоненты (среднее и станд.отклонение)

1. Смоделируем временной ряд с трендом, без автокорреляции остатков:

# моделирование
T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения
(b0, b1) = (100, 5)    # параметры моделируемого временного ряда
Y_model = np.array(y_func(T_model, b0, b1)) + np.random.normal(mu, sigma, N)

# визуализация
axes = sns.jointplot(
    x=T_model, y=Y_model,
    kind='reg')
plt.show()

# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))

# моделирование
T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения
(b0, b1) = (100, -5)    # параметры моделируемого временного ряда
Y_model = np.array(y_func(T_model, b0, b1)) + np.random.normal(mu, sigma, N)

# визуализация
axes = sns.jointplot(
    x=T_model, y=Y_model,
    kind='reg')
plt.show()

# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))

1. Смоделируем временной ряд без тренда:

# моделирование
T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения
(b0, b1) = (100, 0)    # параметры моделируемого временного ряда
Y_model = np.array(y_func(T_model, b0, b1)) + np.random.normal(mu, sigma, N)

# визуализация
axes = sns.jointplot(
    x=T_model, y=Y_model,
    kind='reg')
plt.show()

# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))

# моделирование
T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения
(b0, b1) = (0, 0)    # параметры моделируемого временного ряда
Y_model = np.array(y_func(T_model, b0, b1)) + np.random.normal(mu, sigma, N)

# визуализация
axes = sns.jointplot(
    x=T_model, y=Y_model,
    kind='reg')
plt.show()

# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))

1. Смоделируем временной ряд с трендом, с положительной автокорреляцией:

# моделирование
T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения
(b0, b1) = (100, 5)    # параметры моделируемого временного ряда

E = np.array([np.random.normal(mu, sigma, 1)])
r = 0.9
for i in range(1, N):
    elem = r*E[i-1] + np.random.normal(mu, sigma, 1)
    E = np.append(E, elem)
Y_model = np.array(y_func(T_model, b0, b1)) + E

# визуализация
axes = sns.jointplot(
    x=T_model, y=Y_model,
    kind='reg')
plt.show()

# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))

1. Смоделируем временной ряд с трендом, с отрицательной автокорреляцией:

# моделирование
T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения
(b0, b1) = (100, 5)    # параметры моделируемого временного ряда

E = np.array([np.random.normal(mu, sigma, 1)])
r = -0.9
for i in range(1, N):
    elem = r*E[i-1] + np.random.normal(mu, sigma, 1)
    E = np.append(E, elem)
Y_model = np.array(y_func(T_model, b0, b1)) + E

# визуализация
axes = sns.jointplot(
    x=T_model, y=Y_model,
    kind='reg')
plt.show()

# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))

1. Смоделируем временной ряд без тренда, с положительной автокорреляцией:

# моделирование
T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения
(b0, b1) = (100, 0)    # параметры моделируемого временного ряда

E = np.array([np.random.normal(mu, sigma, 1)])
r = 0.9
for i in range(1, N):
    elem = r*E[i-1] + np.random.normal(mu, sigma, 1)
    E = np.append(E, elem)
Y_model = np.array(y_func(T_model, b0, b1)) + E

# визуализация
axes = sns.jointplot(
    x=T_model, y=Y_model,
    kind='reg')
plt.show()

# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))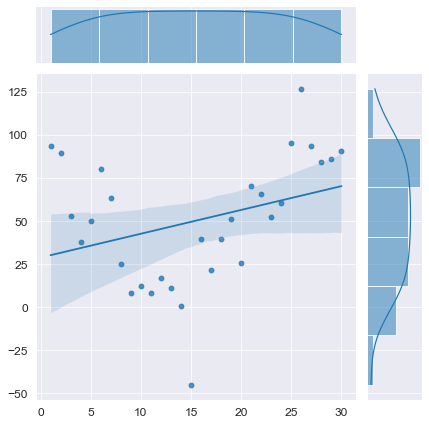

# моделирование
T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения
(b0, b1) = (0, 0)    # параметры моделируемого временного ряда

E = np.array([np.random.normal(mu, sigma, 1)])
r = 0.9
for i in range(1, N):
    elem = r*E[i-1] + np.random.normal(mu, sigma, 1)
    E = np.append(E, elem)
Y_model = np.array(y_func(T_model, b0, b1)) + E

# визуализация
axes = sns.jointplot(
    x=T_model, y=Y_model,
    kind='reg')
plt.show()

# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))

1. Смоделируем временной ряд без тренда, с отрицательной автокорреляцией:

# моделирование
T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения
(b0, b1) = (100, 0)    # параметры моделируемого временного ряда

E = np.array([np.random.normal(mu, sigma, 1)])
r = -0.9
for i in range(1, N):
    elem = r*E[i-1] + np.random.normal(mu, sigma, 1)
    E = np.append(E, elem)
Y_model = np.array(y_func(T_model, b0, b1)) + E

# визуализация
axes = sns.jointplot(
    x=T_model, y=Y_model,
    kind='reg')
plt.show()

# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))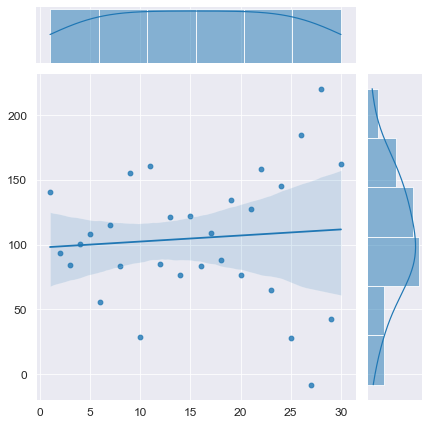

# моделирование
T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения
(b0, b1) = (0, 0)    # параметры моделируемого временного ряда

E = np.array([np.random.normal(mu, sigma, 1)])
r = -0.9
for i in range(1, N):
    elem = r*E[i-1] + np.random.normal(mu, sigma, 1)
    E = np.append(E, elem)
Y_model = np.array(y_func(T_model, b0, b1)) + E

# визуализация
axes = sns.jointplot(
    x=T_model, y=Y_model,
    kind='reg')
plt.show()

# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))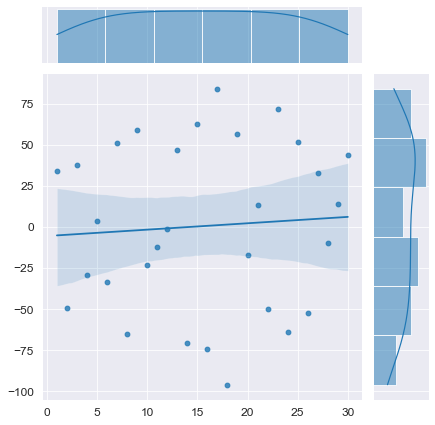

Конечно, данный вычислительный эксперимент не может претендовать на всеобъемлемость, однако определенный любопытный предварительный вывод можно сделать: при наличии любого тренда (даже если этот тренда представляет собой равенство постоянной величине ) критерий Дарбина-Уотсона выдает нам наличие положительной автокорреляции (даже если в модели автокорреляция не заложена нет или она отрицательная). Такой вывод нужно исследовать более глубоко, но это не входит в цель данного обзора. Специалист должен помнить об особенностях критерия Дарбина-Уотсона.

Теперь мы можем перейти к практическим примерам.

Пример 1: проверка автокорреляции модели временного ряда

Формирование исходных данных

В качестве исходных данных рассмотрим динамику показателей индексов пересчета сметной стоимости проектно-изыскательских работ в РФ. Эти показатели ежеквартально публикует Министерство строительства и ЖКХ РФ, а все проектные и изыскательские организации используют эти показатели при составлении смет на свои работы.

В данном случае мы имеем набор показателей в виде временного ряда, для которого будем строить регрессионную модель долговременной тенденции (тренда), и остатки этой регрессионной модели будем исследовать на автокорреляцию.

Исходные данные содержаться в файле Ежеквартальные индексы ПИР.xlsx, который помещен в папку data.

Прочитаем xlsx-файл:

data_df = pd.read_excel('data/Ежеквартальные индексы ПИР.xlsx', sheet_name='БД')  
#display(data_df)
display(data_df.head(), data_df.tail())
data_df.info()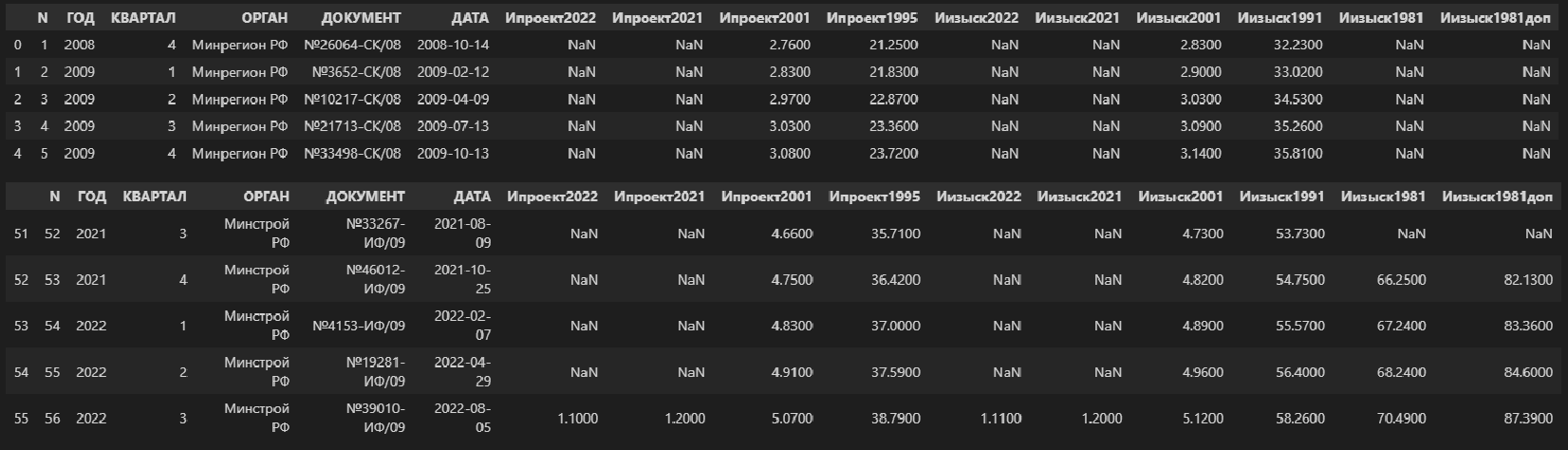

Не будем подробно останавливаться на содержимом файла и его первичной обработке – это выходит за пределы данного обзора. Специалисты, причастные к сфере строительства и проектирования, поймут, а для остальных специалистов эти цифры можно воспринимать по аналогии с индексами инфляции Росстата и Минэкономразвития.

Прочитаем из этого файла интересующие нас данные – индексы изменения сметной стоимости проектных работ к уровню цен на 01.01.2001 г.:

Ind_design_2001 = np.array(data_df['Ипроект2001'])
print(Ind_design_2001, 'n', type(Ind_design_2001), len(Ind_design_2001))

Сохраним также вспомогательные (технические) переменные, необходимые при анализе временных рядов – дату (Date) и номер наблюдения (T):

# Дата показателя
Date = np.array(data_df['ДАТА'])

# Номер наблюдения
T = np.array(data_df['N'])

Для удобства дальнейшей работы сформируем сформируем отдельный DataFrame:

dataset_df = pd.DataFrame({
    'T': T,
    'Date': Date,
    'Ind_design_2001': Ind_design_2001})
display(dataset_df.head(), dataset_df.tail())

Визуализация

Настройка заголовков:

# Общий заголовок проекта
Task_Project = "Анализ динамики индексов изменения сметной стоимости проектно-изыскательских работ в РФ"
# Заголовок, фиксирующий момент времени
AsOfTheDate = "за 2008-2022 гг."
# Заголовок раздела проекта
Task_Theme = ""
# Общий заголовок проекта для графиков
Title_String = f"{Task_Project}n{AsOfTheDate}"
# Наименования переменных
Variable_Name_T_month = "Ежемесячные данные"
Variable_Name_Ind_design_2001 = "Индекс изменения сметной стоимости проектных работ к уровню цен на 01.01.2001 г."

# Границы значений переменных (при построении графиков):
(X_min_graph, X_max_graph) = (0.0, max(T))
(Y_min_graph, Y_max_graph) = (2.0, 6.0)

graph_plot_sns_np(
    Date, Ind_design_2001,
    Ymin_in=Y_min_graph, Ymax_in=Y_max_graph,
    color='orange',
    title_figure=Title_String, title_figure_fontsize=12,
    title_axes=Variable_Name_Ind_design_2001, title_axes_fontsize=15,
    x_label=Variable_Name_T_month, label_fontsize=12)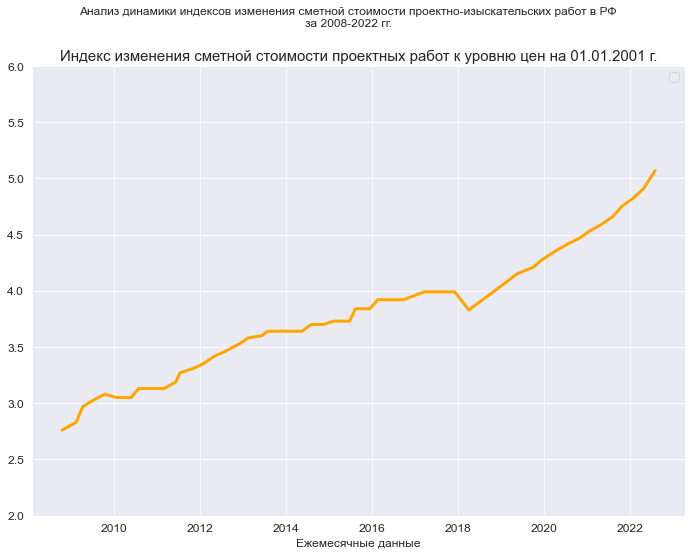

Построение и анализ регрессионной модели

Построим линейную регрессионную модель и проведем ее экспресс-анализ:

model_linear_ols_1 = smf.ols(formula='Ind_design_2001 ~ T', data=dataset_df)
result_linear_ols_1 = model_linear_ols_1.fit()
print(result_linear_ols_1.summary2())

Формализация модели:

# Функция линейной регрессионной модели (SLRM - simple linear regression model)
SLRM_func = lambda x, b0, b1: b0 + b1*x

# параметры модели
b0 = result_linear_ols_1.params['Intercept']
b1 = result_linear_ols_1.params['T']

# уравнение модели
regr_model_linear_ols_1_func = lambda x: SLRM_func(x, b0, b1)

График модели:

R2 = round(result_linear_ols_1.rsquared, DecPlace)
legend_equation = f'линейная регрессия ' + r'$Y$' + f' = {b0:.4f} + {b1:.5f}{chr(183)}' + r'$X$' if b1 > 0 else 
                  f'линейная регрессия ' + r'$Y$' + f' = {b0:.4f} - {abs(b1):.5f}{chr(183)}' + r'$X$'

# Пользовательская функция
graph_regression_plot_sns(
    T, Ind_design_2001,
    regression_model=regr_model_linear_ols_1_func,
    #Xmin=X_min_graph, Xmax=X_max_graph,
    Ymin=Y_min_graph, Ymax=Y_max_graph,
    display_residuals=True,
    title_figure=Variable_Name_Ind_design_2001, title_figure_fontsize=16,
    title_axes = 'Линейная регрессионная модель',
    x_label=Variable_Name_T_month,
    #y_label=Variable_Name_Ind_design_2001,
    label_legend_regr_model = legend_equation + 'n' + r'$R^2$' + f' = {R2}',
    s=60)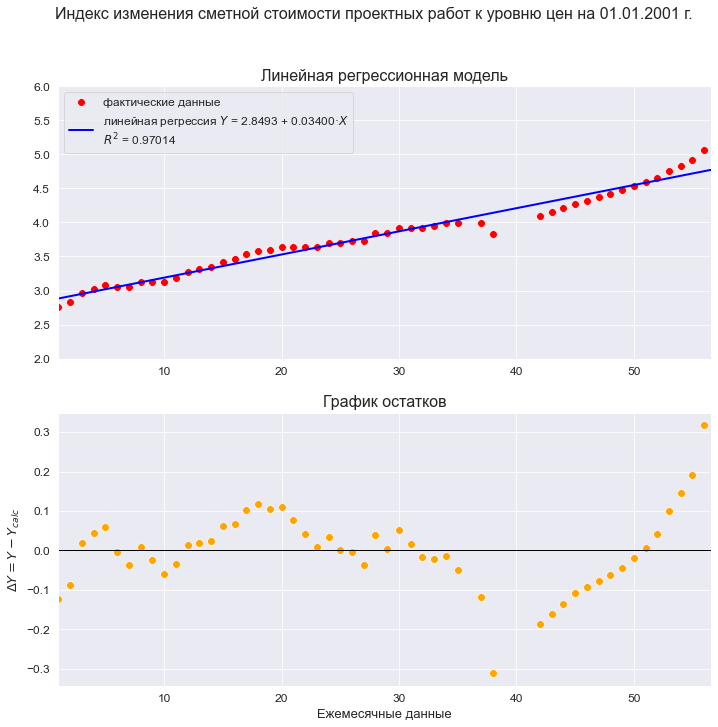

Ошибки аппроксимации модели:

(model_error_metrics, result) = regression_error_metrics(model_linear_ols_1, model_name='linear_ols')
display(result)

Проверка нормальности распределения остатков:

res_Y_1 = np.array(result_linear_ols_1.resid)

# Пользовательская функция
graph_hist_boxplot_probplot_sns(
    data=res_Y_1,
    data_min=-0.25, data_max=0.25,
    graph_inclusion='hbp',
    data_label=r'$ΔY = Y - Y_{calc}$',
    #title_figure=Task_Project,
    title_axes='Остатки линейной регрессионной модели', title_axes_fontsize=16)    

norm_distr_check(res_Y_1)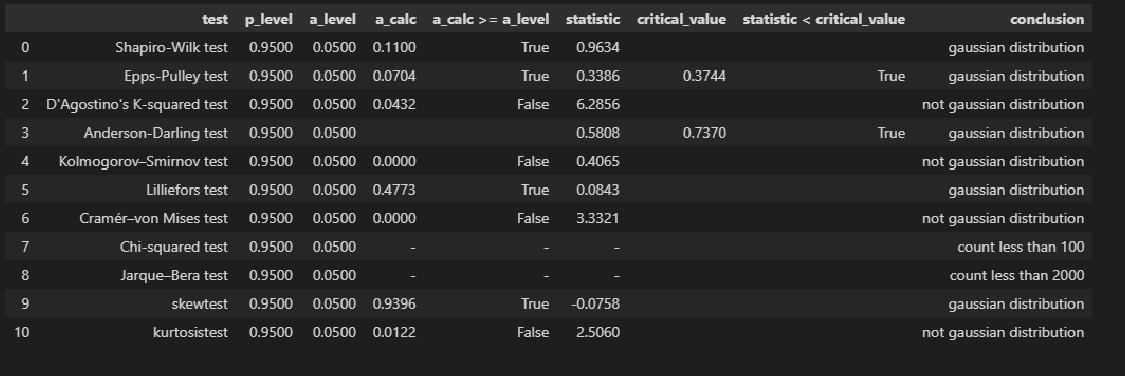

Проверка гетероскедастичности:

Goldfeld_Quandt_test_df = Goldfeld_Quandt_test(result_linear_ols_1, p_level=0.95, model_name='linear_ols')
Breush_Pagan_test_df = Breush_Pagan_test(result_linear_ols_1, p_level=0.95, model_name='linear_ols')
White_test_df = White_test(result_linear_ols_1, p_level=0.95, model_name='linear_ols')

heteroscedasticity_tests_df = pd.concat([Breush_Pagan_test_df, White_test_df, Goldfeld_Quandt_test_df])
display(heteroscedasticity_tests_df)

Проверка автокорреляции:

sms.stattools.durbin_watson(res_Y_1)

Как видим, результат совпадает со значением статистики критерия в таблице выдачи регрессионного анализа.

display(Durbin_Watson_test(res_Y_1, m=1, p_level=0.95))

Выводы по результатам анализа модели:

Итак, мы провели статистический анализ регрессионной модели и установили:

1. Регрессионная модель хорошо аппроксимирует фактические данные.

2. Остатки модели имеют нормальное распределение (хотя результаты тестов противоречивы).

3. Коэффициент детерминации значим; модель объясняет 97% вариации независимой переменной.

4. Коэффициенты регрессии значимы.

5. Обнаружена гетероскедастичность.

6. Тест критерия Дарбина-Уотсона свидетельствует о наличии значимой положительной автокорреляции остатков.

Резюме – несмотря на вроде бы формально хорошие качественные показатели, нам следует признать эту модель некачественной и отвергнуть по следующим негативным причинам:

1. На графике модели хорошо заметна точка излома, которая говорит о смене тенденции (существуют специальные статистические тесты для проверки гипотез о смене тенденции, например, тест Чоу, но мы в данном обзоре рассматривать их не будем).

2. График остатков показывает нам крайне неприглядную картину: на начальном этапе тенденции явно прослеживаются колебания, а после точки излома тенденция вообще кардинально меняется.

3. Противоречивость тестов проверки нормальности распределения остатков.

4. Наличие гетероскедастичности.

5. Наличие автокорреляции. Явление автокорреляции может возникать в случае смены тенденции [5, с.118].

Тот факт, что распределение остатков признается нормальным по результатам таких тестов как Шапиро-Уилка, Эппса-Палли, Андерсона-Дарлинга может иметь разные причины, например, мы можем иметь дело со смесью двух распределений. Этот вопрос требует отдельного тщательного исследования.

Применение построенной модели приведет к ошибке, так как модель хорошо аппроксимирует существующие данные, но из-за смены тенденции неспособна дать качественный прогноз. Проиллюстрировать это можно, построив доверительный интервалы прогноза (формально мы можем это сделать, так как распределение остатков признано нормальным):

graph_regression_pair_predict_plot_sns(
    model_fit=result_linear_ols_1,
    regression_model_in=regr_model_linear_ols_1_func,
    Xmin=X_min_graph, Xmax=X_max_graph+12, Nx=25,
    Ymin_graph=2.0, Ymax_graph=Y_max_graph,
    title_figure=Variable_Name_Ind_design_2001, title_figure_fontsize=16,
    title_axes='Линейная регрессионная модель', title_axes_fontsize=14,
    #x_label=Variable_Name_X,
    #y_label=Variable_Name_Y,
    label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X',
    s=50,
    result_output=False)

Нет, такой прогноз нам не нужен.

Пример 2: проверка автокорреляция регрессионной модели

Формирование исходных данных

Рассмотрим пример множественной линейной регрессионной модели, приведенный в источнике [6, с.192].

В качестве исходных данных рассматриваются ряд макроэкономических показателей США за 1960-1985 гг. (в сопоставимых ценах 1982 г., млрд.долл):

• DPI – годовой совокупный располагаемый личный доход;

• CONS – годовые совокупные потребительские расходы;

• ASSETS – финансовые активы населения на начало календарного года.

Предполагается, что между переменной CONS и регрессорами DPI, ASSETS имеется линейная регрессионная связь.

Исходные данные содержаться в файле Macroeconomic_indicators_USA_1960_1985.csv, который помещен в папку data.

Прочитаем csv-файл:

data_df = pd.read_csv(filepath_or_buffer='data/Macroeconomic_indicators_USA_1960_1985.csv', sep=';')
display(data_df)
#display(data_df.head(), data_df.tail())
data_df.info()

Визуализация

fig, axes = plt.subplots(figsize=(297/INCH, 210/INCH))

title_figure = 'Анализ макроэкономических показателей США за 1960-1985 гг.'
fig.suptitle(title_figure, fontsize = 18)

sns.lineplot(
    x = data_df['YEAR'], y = data_df['DPI'],
    linewidth=3,
    legend=True,
    label='DPI',
    ax=axes)

sns.lineplot(
    x = data_df['YEAR'], y = data_df['CONS'],
    linewidth=3,
    legend=True,
    label='CONS',
    ax=axes)

sns.lineplot(
    x = data_df['YEAR'], y = data_df['ASSETS'],
    linewidth=3,
    legend=True,
    label='ASSETS',
    ax=axes)

axes.set_xlabel('Year')
axes.set_ylabel('US$ billion')

plt.show()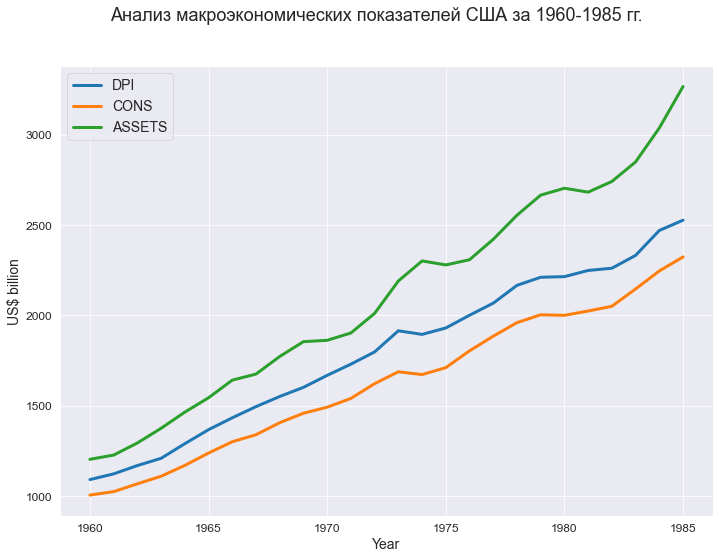

Построение и анализ регрессионной модели

Построим линейную регрессионную модель и проведем ее экспресс-анализ:

y = data_df['CONS']
X = data_df[['DPI', 'ASSETS']]
X = sm.add_constant(X)
model_linear_ols_2 = sm.OLS(y, X)
result_linear_ols_2 = model_linear_ols_2.fit()
print(result_linear_ols_2.summary2())

График модели:

fig = plt.figure(figsize=(297/INCH, 420/INCH/1.5))
ax1 = plt.subplot(2,1,1)
ax2 = plt.subplot(2,1,2)

title_figure = 'Анализ макроэкономических показателей США за 1960-1985 гг.'
fig.suptitle(title_figure, fontsize = 18)

fig = sm.graphics.plot_fit(
    result_linear_ols_2, 'DPI',
    vlines=True,    # это параметр отвечает за отображение доверительных интервалов для Y
    ax=ax1)
ax1.set_ylabel('CONS (US$ billion)', fontsize = 12)
ax1.set_xlabel('DPI (US$ billion)', fontsize = 12)
ax1.set_title('Fitted values vs. DPI', fontsize = 15)

fig = sm.graphics.plot_fit(
    result_linear_ols_2, 'ASSETS',
    vlines=True,    # это параметр отвечает за отображение доверительных интервалов для Y
    ax=ax2)
ax2.set_ylabel('CONS (US$ billion)', fontsize = 12)
ax2.set_xlabel('ASSETS (US$ billion)', fontsize = 12)
ax2.set_title('Fitted values vs. ASSETS', fontsize = 15)

plt.show()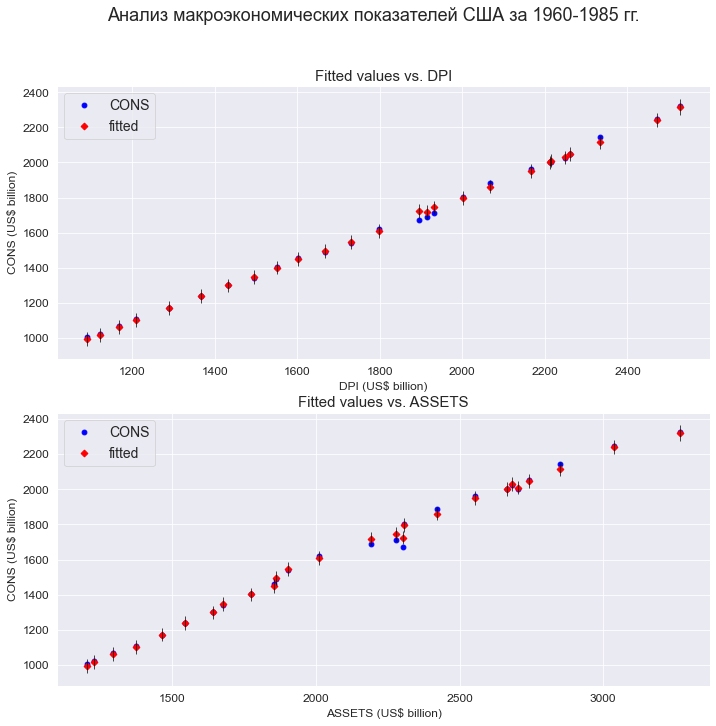

Ошибки аппроксимации модели:

(model_error_metrics, result) = regrpy
ession_error_metrics(model_linear_ols_2, model_name='linear_ols')
display(result)

Проверка нормальности распределения остатков:

res_Y_2 = np.array(result_linear_ols_2.resid)

# Пользовательская функция
graph_hist_boxplot_probplot_sns(
    data=res_Y_2,
    data_min=-60, data_max=60,
    graph_inclusion='hbp',
    data_label=r'$ΔY = Y - Y_{calc}$',
    #title_figure=Task_Project,
    title_axes='Остатки линейной регрессионной модели', title_axes_fontsize=16)    

norm_distr_check(res_Y_2)

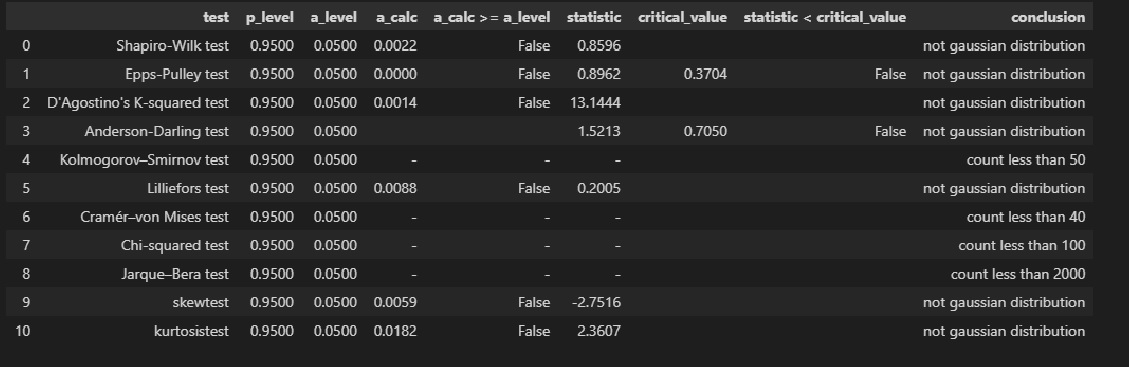
Прроверка гетероскедастичности:

Goldfeld_Quandt_test_df = Goldfeld_Quandt_test(result_linear_ols_2, p_level=0.95, model_name='linear_ols')
Breush_Pagan_test_df = Breush_Pagan_test(result_linear_ols_2, p_level=0.95, model_name='linear_ols')
White_test_df = White_test(result_linear_ols_2, p_level=0.95, model_name='linear_ols')

heteroscedasticity_tests_df = pd.concat([Breush_Pagan_test_df, White_test_df, Goldfeld_Quandt_test_df])
display(heteroscedasticity_tests_df)

Проверка автокорреляции:

display(Durbin_Watson_test(res_Y_2, m=1, p_level=0.95))

Выводы по результатам анализа модели:

Как видим, в целом результаты расчетов совпадают с результатами из первоисточника [6], в части выявления автокорреляции аналогично.

Информация к размышлению.

Анализ показывает, что модель хорошо аппроксимирует фактические данные, но имеет место отклонение от нормального закона распределения остатков, противоречивые выводы о гетероскедастичности и наличие автокорреляции, то есть модель некачественная.

Также мы видим, что динамика макроэкономических показателей свидетельствует о наличии трендов, однако, если в модель добавить еще один фактор – год или номер наблюдения – то, этот фактор окажется незначимым.

В дальнейшем автор при анализе остатков модели [6, с.198] выявляет структурный сдвиг (обусловленный мировым топливно-энергетическим кризисом в 1973 г.) и вводит в модель фиктивные переменные, учитывающие этот структурный сдвиг

Итоги

Итак, подведем итоги:

• мы рассмотрели способы реализации в полной мере критерия Дарбина-Уотсона средствами python, создали пользовательскую функцию, уменьшающую размер кода;

• разобрали пример оцифровки таблицы критических значений статистического критерия для реализации пользовательской функции.

Исходный код находится в моем репозитории на GitHub.

Надеюсь, данный обзор поможет специалистам DataScience в работе.

Литература

1. Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. – М.: ФИЗМАТЛИТ, 2006. – 816 с.

2. Айвазян С.А. Прикладная статистика. Основы эконометрики: В 2 т. – Т.2: Основы эконометрики. – 2-е изд., испр. – М.: ЮНИТИ-ДАНА, 2001. – 432 с.

3. Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа / пер с нем. – М.: Финансы и статистика, 1983. – 302 с.

4. Магнус Я.Р. и др. Эконометрика. Начальный курс – М.: Дело, 2004. – 576 с.

5. Тихомиров Н.П., дорохина Е.Ю. Эконометрика. – М.: Экзамен, 2003. – 512 с.

6. Носко В.П. Эконометрика. Кн.1. Ч.1, 2. – М.: Издательский дом “Дело” РАНХиГС, 2011. – 672 с.

7. Вандер Плас Дж. Python для сложных задач: наука о данных и машинное обучение. – СПб: Питер, 2018. – 576 с.

Все курсы > Оптимизация > Занятие 4 (часть 1)

Прежде чем обратиться к теме множественной линейной регрессии, давайте вспомним, что было сделано до сих пор. Возможно, будет полезно посмотреть эти уроки, чтобы освежить знания.

• В рамках вводного курса мы узнали про моделирование взаимосвязи переменных и минимизацию ошибки при обучении алгоритма, а также научились строить несложные модели линейной регрессии с помощью библиотеки sklearn.
• При изучении объектно-ориентированного программирования мы создали класс простой линейной регрессии. Сегодня эти знания пригодятся при создании классов более сложных моделей.
• Также рекомендую вспомнить умножение векторов и матриц.
• Кроме того, в рамках текущего курса по оптимизации мы познакомились с понятием производной и методом градиентного спуска, а также построили модель простой линейной регрессии (использовав метод наименьших квадратов и градиент).
• Наконец, на прошлом занятии мы вновь поговорили про взаимосвязь переменных.

В рамках сегодняшнего занятия мы с нуля построим несколько алгоритмов множественной линейной регрессии.

Регрессионный анализ

Прежде чем обратиться к практике, обсудим некоторые теоретические вопросы регрессионного анализа.

Генеральная совокупность и выборка

Как мы уже знаем, множество всех имеющихся наблюдений принято считать генеральной совокупностью (population). И эти наблюдения, если в них есть взаимосвязи, можно теоретически аппроксимировать, например, линией регрессии. При этом важно понимать, что это некоторая идеальная модель, которую мы никогда не сможем построить.

Единственное, что мы можем сделать, взять выборку (sample) и на ней построить нашу модель, предполагая, что если выборка достаточно велика, она сможет достоверно описать генсовокупность.

Отклонение прогнозного значения от фактического для «идеальной» линии принято называть ошибкой (error или true error).

$$ varepsilon = y-hat{y} $$

Отклонение прогноза от факта для выборочной модели (которую мы и строим) называют остатками (residuals или residual error).

$$ varepsilon = y-f(x) $$

В этом смысле среднеквадратическую ошибку (mean squared error, MSE) корректнее называть средними квадратичными остатками (mean squared residuals).

На практике ошибку и остатки нередко используют как взаимозаменяемые термины.

Уравнение множественной линейной регрессии

Посмотрим на уравнение множественной линейной регрессии.

$$ y = theta_0 + theta_1x_1 + theta_2x_2 + … + theta_jx_j + varepsilon $$

В отличие от простой линейной регрессии в данном случае у нас несколько признаков x (независимых переменных) и несколько коэффициентов $ theta $ («тета»).

Интерпретация результатов модели

Коэффициент $ theta_0 $ задает некоторый базовый уровень (baseline) при условии, что остальные коэффициенты равны нулю и зачастую не имеет смысла с точки зрения интерпретации модели (нужен лишь для того, что поднять линию на нужный уровень).

Параметры $ theta_1, theta_2, …, theta_n $ показывают изменение зависимой переменной при условии «неподвижности» остальных коэффициентов. Например, каждая дополнительная комната может увеличивать цену дома в 1.3 раза.

Переменная $ varepsilon $ (ошибка) представляет собой отклонение фактических данных от прогнозных. В этой переменной могут быть заложены две составляющие. Во-первых, она может включать вариативность целевой переменной, описанную другими (не включенными в нашу модель) признаками. Во-вторых, «улавливать» случайный шум, случайные колебания.

Категориальные признаки

Модель линейной регрессии может включать категориальные признаки. Продолжая пример с квартирой, предположим, что мы строим модель, в которой цена зависит от того, находится ли квартира в центре города или в спальном районе.

Перед этим переменную необходимо закодировать, создав, например, через Label Encoder признак «центр», который примет значение 1, если квартира в центре, и 0, если она находится в спальном районе.

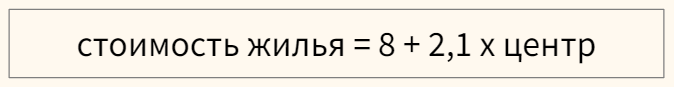
В модели, представленной выше, если квартира находится в центре (переменная «центр» равна единице), ее стоимость составит 10,1 миллиона рублей, если на окраине (переменная «центр» равна нулю) — лишь восемь.

Для категориального признака с множеством классов можно использовать one-hot encoding, если между классами признака отсутствует иерархия,

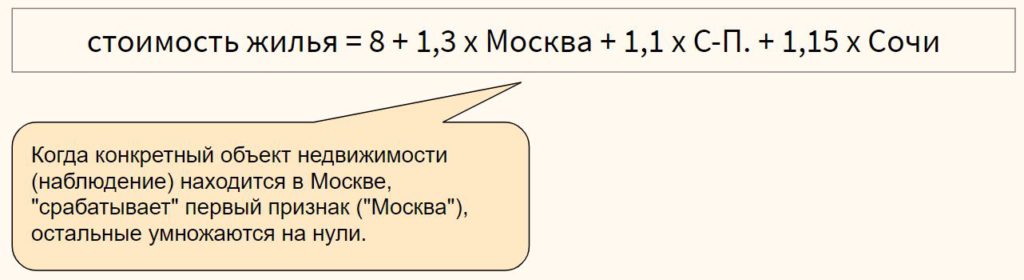
или, например, ordinal encoding в случае наличия иерархии классов в признаке

Выбросы в линейной регрессии

Как и коэффициент корреляции Пирсона, модель линейной регрессии чувствительна к выбросам (outliers), то есть наблюдениям, серьезно выпадающим из общей совокупности. Сравните рисунки ниже.

При наличии выброса (слева), линия регрессии имеет наклон и может использоваться для построения прогноза. Удалив это наблюдение (справа), линия регрессии становится горизонтальной и построение прогноза теряет смысл.

При этом различают два типа выбросов:

• горизонтальные выбросы или влиятельные точки (leverage points) — они сильно отклоняются от среднего по оси x; и
• вертикальные выбросы или просто выбросы (influential points) — отклоняются от среднего по оси y

Ключевое отличие заключается в том, что вертикальные выбросы влияют на наклон модели (изменяют ее коэффициенты), а горизонтальные — нет.

Сравним два графика.

На левом графике черная точка (leverage point) сильно отличается от остальных наблюдений, но наклон прямой линии регрессии с ее появлением не изменился. На правом графике, напротив, появление выброса (influential point) существенно изменяет наклон прямой.

На практике нас конечно больше интересуют influential points, потому что именно они существенно влияют на качество модели.

Если в простой линейной регрессии мы можем оценить leverage и influence наблюдения графически⧉, в многомерной модели это сделать сложнее. Можно использовать график остатков (об этом ниже) или применить один из уже известных нам методов выявления выбросов.

Про выявление leverage и infuential points можно почитать здесь⧉.

Допущения модели регрессии

Применение алгоритма линейной регрессии предполагает несколько допущений (assumptions) или условий, при выполнении которых мы можем говорить о качественно построенной модели.

1. Правильный выбор модели

Вначале важно убедиться, что данные можно аппроксимировать с помощью линейной модели (correct model specification).

Оценить распределение данных можно через график остатков (residuals plot), где по оси x отложен прогноз модели, а на оси y — сами остатки.

В отличие от простой линейной регрессии мы не используем точечную диаграмму X vs. y, потому что хотим оценить зависимость целевой переменной от всех признаков сразу.

Остатки модели относительно ее прогнозных значений должны быть распределены случайным образом без систематической составляющей (residuals do not follow a pattern).

• Если вы попробовали применить линейную модель с коэффициентами первой степени ($x_n^1$) и выявили некоторый паттерн в данных, можно попробовать полиномиальную или какую-либо еще функцию (об этом ниже).
• Кроме того, количественные признаки можно попробовать преобразовать таким образом, чтобы их можно было аппроксимировать прямой линией.
• Если ни то, ни другое не помогло, вероятно данные не стоит моделировать линейной регрессией.

Также замечу, что график остатков показывает выбросы в данных.

2. Нормальность распределения остатков

Среднее значение остатков должно быть равно нулю. Если это не так, и среднее значение меньше нуля (скажем –5), то это значит, что модель регулярно недооценивает (underestimates) фактические значения. В противном случае, если среднее больше нуля, переоценивает (overestimated).

Кроме того, предполагается, что остатки следуют нормальному распределению.

$$ varepsilon sim N(0, sigma) $$

Проверить нормальность остатков можно визуально с помощью гистограммы или рассмотренных ранее критериев нормальности распределения.

Если остатки не распределены нормально, мы не сможем провести статистические тесты на значимость коэффициентов или построить доверительные интервалы. Иначе говоря, мы не сможем сделать статистически значимый вывод о надежности нашей модели.

Причинами могут быть (1) выбросы в данных или (2) неверный выбор модели. Решением может быть, соответственно, исследование выбросов, выбор новой модели и преобразование как признаков, так и целевой переменной.

3. Гомоскедастичность остатков

Гомоскедастичность (homoscedasticity) или одинаковая изменчивость остатков предполагают, что дисперсия остатков не изменяется для различных наблюдений. Противоположное и нежелательное явление называется гетероскедастичностью (heteroscedasticity) или разной изменчивостью.

Гетероскедастичность остатков показывает, что модель ошибается сильнее при более высоких или более низких значениях признаков. Как следствие, если для разных прогнозов у нас разная погрешность, модель нельзя назвать надежной (robust).

Как правило, гетероскедастичность бывает изначально заложена в данные. Ее можно попробовать исправить через преобразование целевой переменной (например, логарифмирование)

4. Отсутствие мультиколлинеарности

Еще одним важным допущением является отсутствие мультиколлинеарности. Мультиколлинеарность (multicollinearity) — это корреляция между зависимыми переменными. Например, если мы предсказываем стоимость жилья по квадратным метрам и количеству комнат, то метры и комнаты логичным образом также будут коррелировать между собой.

Почему плохо, если такая корреляция существует? Базовое предположение линейной регрессии — каждый коэффициент $theta$ оказывает влияние на конечный результат при условии, что остальные коэффициенты постоянны. При мультиколлинеарности на целевую переменную оказывают эффект сразу несколько признаков, и мы не можем с точностью интерпретировать каждый из них.

Также говорят о том, что нужно стремиться к экономной (parsimonious) модели то есть такой модели, которая при наименьшем количестве признаков в наибольшей степени объясняет поведение целевой переменной.

Variance inflation factor

Расчет коэффициента

Variance inflation factor (VIF) или коэффициент увеличения дисперсии позволяет выявить корреляцию между признаками модели.

Принцип расчета VIF заключается в том, чтобы поочередно делать каждый из признаков целевой переменной и строить модель линейной регрессии на основе оставшихся независимых переменных. Например, если у нас есть три признака $x_1, x_2, x_3$, мы поочередно построим три модели линейной регрессии: $x_1 sim x_2 + x_3, x_2 sim x_1 + x_3$ и $x_3 sim x_1 + x_3$.

Обратите внимание на новый для нас формат записи целевой и зависимых переменных модели через символ $sim$.

Затем для каждой модели (то есть для каждого признака $x_1, x_2, x_3$) мы рассчитаем коэффициент детерминации $R^2$. Если он велик, значит данный признак можно объяснить с помощью других независимых переменных и имеется мультиколлинеарность. Если $R^2$ мал, то нельзя и мультиколлинеарность отсутствует.

Теперь рассчитаем VIF на основе $R^2$:

$$ VIF = frac{1}{1-R^2} $$

При таком способе расчета большой (близкий к единице) $R^2$ уменьшит знаменатель и существенно увеличит VIF, при небольшом коэффициенте детерминации коэффициент увеличения дисперсии наоборот уменьшится.

Замечу, что $1-R^2$ принято называть tolerance.

Другие способы выявления мультиколлинеарности

Для выявления корреляции между независимыми переменными можно использовать точечные диаграммы или корреляционные матрицы. При этом важно понимать, что в данном случае мы выявляем зависимость лишь между двумя признаками. Корреляцию множества признаков выявляет только коэффициент увеличения дисперсии.

Интерпретация VIF

VIF находится в диапазон от единицы до плюс бесконечности. Как правило, при интерпретации показателей variance inflation factor придерживаются следующих принципов:

• VIF = 1, между признаками отсутствует корреляция
• 1 < VIF $leq$ 5 — умеренная корреляция
• 5 < VIF $leq$ 10 — высокая корреляция
• Более 10 — очень высокая

После расчета VIF можно по одному удалять признаки с наибольшей корреляцией и смотреть как изменится этот показатель для оставшихся независимых переменных.

5. Отсутствие автокорреляции остатков

На занятии по временным рядам (time series), мы сказали, что автокорреляция (autocorrelation) — это корреляция между значениями одной и той же переменной в разные моменты времени.

Применительно к модели линейной регрессии автокорреляция целевой переменной (для простой линейной регрессии) и автокорреляция остатков, residuals autocorrelation (для модели множественной регрессии) означает, что результат или прогноз зависят не от признаков, а от самой этой целевой переменной. В такой ситуации признаки теряют свою значимость и применение модели регрессии становится нецелесообразным.

Причины автокорреляции остатков

Существует несколько возможных причин:

• Прогнозирование целевой переменной с высокой автокорреляцией (например, если мы моделируем цену акций с помощью других переменных, то можем ожидать высокую автокорреляцию остатков, поскольку цена акций как правило сильно зависит от времени)
• Удаление значимых признаков
• Другие причины

Автокорреляция первого порядка

Дадим формальное определение автокорреляции первого порядка (first order correlation), то есть автокорреляции с лагом 1.

$$ varepsilon_t = pvarepsilon_{t-1} + u_t $$

где $u_t$ — некоррелированная при различных t одинаково распределенная случайная величина (independent and identically distributed (i.i.d.) random variable), а $p$ — коэффициент автокорреляции, который находится в диапазоне $-1 < p < 1$. Чем он ближе к нулю, тем меньше зависимость остатка $varepsilon_t$ от остатка предыдущего периода $varepsilon_{t-1}$.

Такое уравнение также называется схемой Маркова первого порядка (Markov first-order scheme).

Обратите внимание, что для модели автокорреляции первого порядка коэффициент автокорреляции $p$ совпадает с коэффициентом авторегрессии AR(1) $varphi$.

$$ y_t = c + varphi cdot y_{t-1} $$

Разумеется, мы можем построить модель автокорреляции, например, третьего порядка.

$$ varepsilon_t = p_1varepsilon_{t-1} + p_2varepsilon_{t-2} + p_3varepsilon_{t-3} + u_t $$

Выявление автокорреляции остатков

Для выявления автокорреляции остатков можно использовать график последовательности и график остатков с лагом 1, график автокорреляционной функции или критерий Дарбина-Уотсона.

График последовательности и график остатков с лагом 1

На графике последовательности (sequence plot) по оси x откладывается время (или порядковый номер наблюдения), а по оси y — остатки модели. Кроме того, на графике остатков с лагом 1 (lag-1 plot) остатки (ось y) можно сравнить с этими же значениями, взятыми с лагом 1 (ось x).

Рассмотрим вариант положительной автокорреляции (positive autocorrelation) на графиках остатков типа (а) и (б).

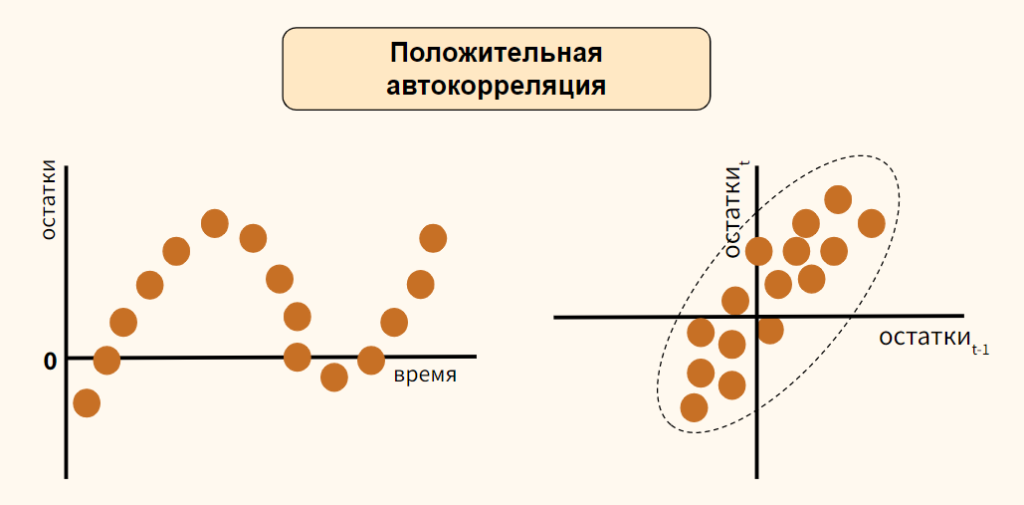
Как вы видите, при положительной автокорреляции в большинстве случаев, если одно наблюдение демонстрирует рост по отношению к предыдущему значению, то и последующее будет демонстрировать рост, и наоборот.

Теперь обратимся к отрицательной автокорреляции (negative autocorrelation).

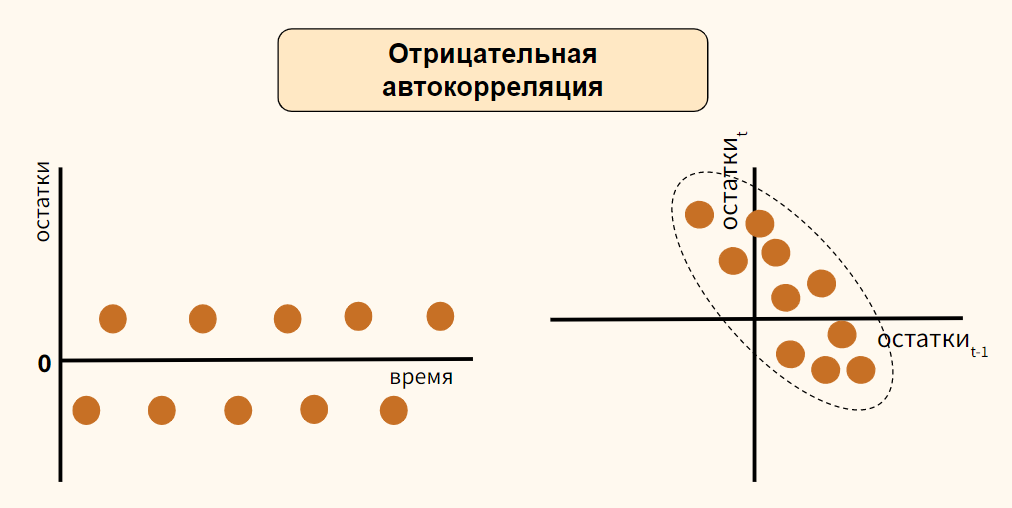
Здесь наоборот, если одно наблюдение демонстрирует рост показателя по отношению к предыдущему значению, то последующее наблюдение будет наоборот снижением. Опять же справедливо и обратное утверждение.

В случае отсутствия автокорреляции мы не должны увидеть на графиках какого-либо паттерна.

График автокорреляционной функции

Еще один способ выявить автокорреляцию — построить график автокорреляционной функции (autocorrelation function, ACF).

Напомню, такой график показывает автокорреляцию данных с этими же данными, взятыми с первым, вторым и последующими лагами.

Критерий Дарбина-Уотсона

Количественным выражением автокорреляции является критерий Дарбина-Уотсона (Durbin-Watson test). Этот критерий выявляет только автокорреляцию первого порядка.

• Нулевая гипотеза утверждает, что такая автокорреляция отсутствует ($p=0$),
• Альтернативная гипотеза соответственно утверждает, что присутствует
  • Положительная ($p approx -1$) или
  • Отрицательная ($p approx 1$) автокорреляция

Значение теста находится в диапазоне от 0 до 4.

• При показателе близком к двум можно говорить об отсутствии автокорреляции
• Приближение к четырем говорит о положительной автокорреляции
• К нулю, об отрицательной

Как избавиться от автокорреляции

Автокорреляцию можно преодолеть, добавив значимый признак в модель, выбрав иной тип модели (например, полиномиальную регрессию) или в целом перейдя к моделированию и прогнозированию временного ряда.

Рассмотрение этих методов находится за рамками сегодняшнего занятия. Перейдем к практике.

Критерий Дарбина-Уотсона

Рассматриваем уравнение регрессии вида:

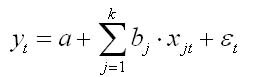
где k — число независимых переменных модели регрессии.

Для каждого момента времени t = 1 : n значение определяется по формуле

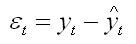
Изучая последовательность остатков как временной ряд в дисциплине эконометрика, можно построить график их зависимости от времени. В соответствии с предпосылками метода наименьших квадратов остатки должны быть случайными (а). Однако при моделировании временных рядов иногда встречается ситуация, когда остатки содержат тенденцию (б и в) или циклические колебания (г). Это говорит о том, что каждое следующее значение остатков зависит от предыдущих. В этом случае имеется автокорреляция остатков.

Причины автокорреляции остатков

Автокорреляция остатков может возникать по несколькими причинами:

Во-первых, иногда автокорреляция связана с исходными данными и вызвана наличием ошибок измерения в значениях Y.

Во-вторых, иногда причину автокорреляции остатков следует искать в формулировке модели. В модель может быть не включен фактор, оказывающий существенное воздействие на результат, но влияние которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными. Зачастую этим фактором является фактор времени t.

Иногда, в качестве существенных факторов могут выступать лаговые значения переменных, включенных в модель. Либо в модели не учтено несколько второстепенных факторов, совместное влияние которых на результат существенно ввиду совпадения тенденций их изменения или циклических колебаний.

Методы определения автокорреляции остатков

Первый метод — это построение графика зависимостей остатков от времени и визуальное определение наличия автокорреляции остатков.

Второй метод — расчет критерия Дарбина — Уотсона

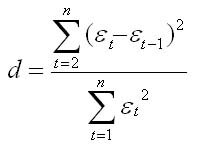
Т.е. Критерий Дарбина — Уотсона определяется как отношение суммы квадратов разностей последовательных значений остатков к сумме квадратов остатков. Практически во всех задачах по эконометрике значение критерия Дарбина — Уотсона указывается наряду с коэффициентом корреляции, значениями критериев Фишера и Стьюдента

Коэффициент автокорреляции первого порядка определяется по формуле

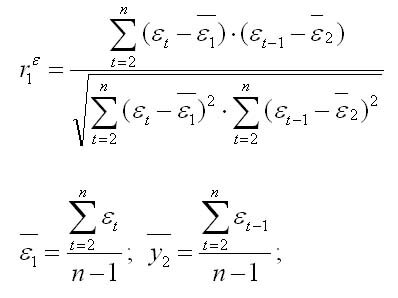
Соотношение между критерием Дарбина — Уотсона и коэффициентом автокорреляции остатков (r1) первого порядка определяется зависимостью

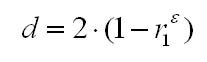
Т.е. если в остатках существует полная положительная автокорреляция r1 = 1, а d = 0, Если в остатках полная отрицательная автокорреляция, то r1 = — 1, d = 4. Если автокорреляция остатков отсутствует, то r1 = 0, d = 2. Следовательно,

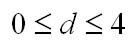
Алгоритм выявления автокорреляции остатков по критерию Дарбина — Уотсона

Выдвигается гипотеза об отсутствии автокорреляции остатков. Альтернативные гипотеэы о наличии положительной или отрицательной автокорреляции в остатках. Затем по таблицам определяются критические значения критерия Дарбина — Уотсона dL и du для заданного числа наблюдений и числа независимых переменных модели при уровня значимости а (обычно 0,95). По этим значениям промежуток [0;4] разбивают на пять отрезков.

Если расчетное значение критерия Дарбина — Уотсона попадает в зону неопределенности, то подтверждается существование автокорреляции остатков и гипотезу отклоняют

Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.

Если Вас интересует решение контрольных по эконометрике щелкните здесь

Понятие и причины автокорреляции остатков. Последствия автокорреляции остатков. Обнаружение автокорреляции остатков

Автокорреляции остатков наблюдается тогда, когда значения предыдущих остатков завышают (положительная) или занижают (отрицательная) значения последующих.

Положительная автокорреляция на графике остатков проявляется в чередовании зон положительных и отрицательных остатков:

Отрицательная автокорреляция на графике выражается в том, что остатки «слишком часто» меняют знак:

Основными причинами автокорреляции являются:

• неправильный выбор формы регрессионной зависимости;

• неучет в модели одного или нескольких важных факторов;

• цикличность значений экономических переменных при построении модели по временным данным.

Автокорреляция может привести к ошибочному выводу о несущественном влиянии исследуемого фактора на результат Y, в то время как на самом деле влияние фактора на Y значимо.

Для обнаружения автокорреляции остатков используется d-статистика Дарбина–Уотсона:

.

Значение d-статистики сравнивается с критическими значениями d₁ и d₂. При этом могут возникнуть следующие ситуации:

• если , то остатки признаются некоррелированными;

• если , то имеется положительная автокорреляция;

• если , то существует отрицательная автокорреляция;

• если или , то это указывает на неопределенность ситуации.

d‑статистика рассчитывается либо по временному ряду остатков, либо по упорядоченному в зависимости от последовательно возрастающих или убывающих расчетных значений Y.

При неопределенности ситуации рассчитывается коэффициент автокорреляции остатков первого порядка

.

Автокорреляция отсутствует, если коэффициент не превышает по модулю критическое значение. В противном случае делают вывод о наличие автокорреляции: положительной при или отрицательной при .

Продолжение примера 3. d‑статистика имеет значение d=3,44. Критические значения составляют d₁=0,66 и d₂=1,86 (=0,05; p=3; n=12). d‑статистика попадает в интервал , что свидетельствует об отрицательной автокорреляции остатков.

Коэффициент автокорреляции остатков первого порядка r₍₁₎=–0,721 превышает по модулю критическое значение r_кр=0,576 (=0,05; n=12), что еще раз свидетельствует об отрицательной автокорреляции остатков.