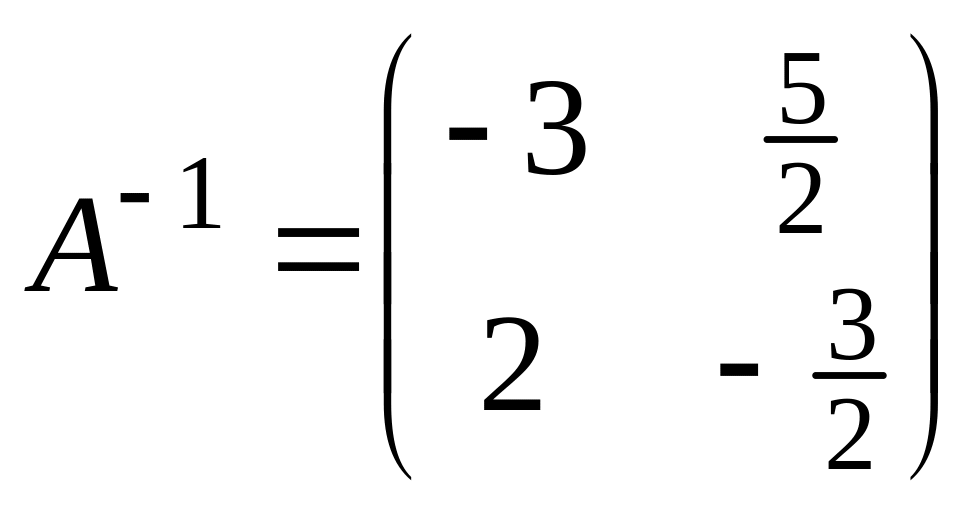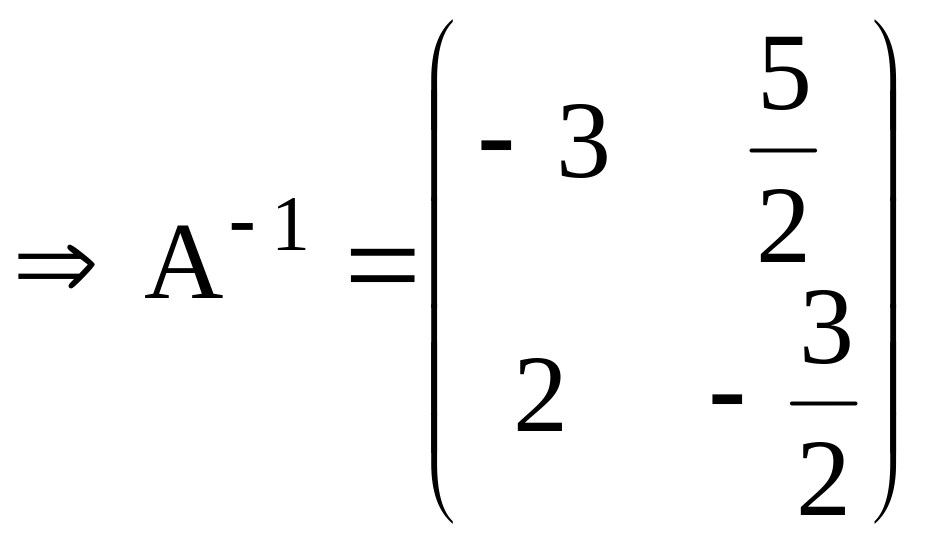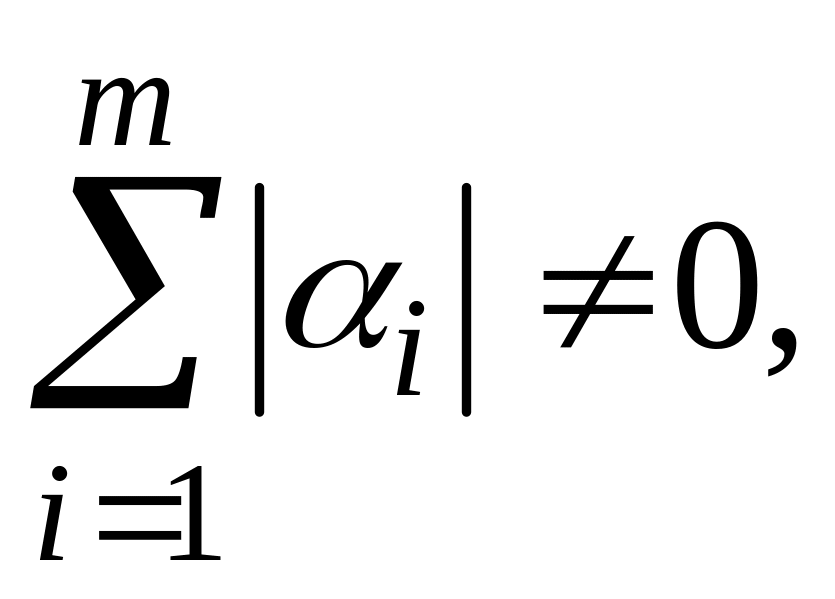Как найти axb c

Решение матричных уравнений: как это делается

Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,

где x — неизвестное.

А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.

Итак, матричным уравнением называется уравнение вида

где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.

Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу слева:

.

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому

.

Так как E — единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :

.

Как решить матричное уравнение во втором случае? Если дано уравнение

то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:

,

,

.

Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X . То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A .

Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения

.

Решение матричных уравнений: примеры

Пример 1. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :

.

Наконец, находим неизвестную матрицу:

Пример 2. Решить матричное уравнение

.

Пример 3. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Находим матрицу, обратную матрице A :

.

Находим неизвестную матрицу:

До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.

Пример 4. Решить матричное уравнение

.

Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:

.

Находим неизвестную матрицу:

Пример 5. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Находим матрицу, обратную матрице A :

.

Находим неизвестную матрицу:

Пример 6. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Находим матрицу, обратную матрице A :

.

Найдём матрицу, обратную матрице B .

Сначала найдём определитель матрицы B :

.

Найдём алгебраические дополнения матрицы B :

Составим матрицу алгебраических дополнений матрицы B :

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :

.

Находим матрицу, обратную матрице B :

.

Рассмотрим матричное уравнение вида

где [math]A[/math] и [math]B[/math] — данные матрицы, имеющие одинаковое количество строк, причем матрица [math]A[/math] квадратная. Требуется найти матрицу [math]X[/math] , удовлетворяющую уравнению (4.5).

Теорема 4.2 о существовании и единственности решения матричного уравнения (4.5). Если определитель матрицы [math]A[/math] отличен от нуля, то матричное уравнение (4.5) имеет единственное решение [math]X=A^<-1>B[/math] .

В самом деле, подставляя [math]X=A^<-1>B[/math] в левую часть равенства (4.5), получаем [math]A(A^<-1>B)=underbrace>_B=B[/math] , т.е. правую часть этого равенства.

Заметим, что решением матричного уравнения [math]AX=E[/math] служит обратная матрица [math]X=A^<-1>[/math] .

Рассмотрим также матричное уравнение вида

где [math]A[/math] и [math]B[/math] — данные матрицы, имеющие одинаковое количество столбцов, причем матрица [math]A[/math] квадратная. Требуется найти матрицу [math]Y[/math] , удовлетворяющую уравнению (4.6).

Теорема 4.3 о существовании и единственности решения матричного уравнения (4.6). Если определитель матрицы [math]A[/math] отличен от нуля, то уравнение (4.6) имеет единственное решение [math]Y=BA^<-1>[/math] .

Заметим, что матрица [math]X[/math] является как бы “левым” частным от “деления” матрицы [math]B[/math] на матрицу [math]A[/math] , поскольку матрица [math]X[/math] в (4.5) умножается на [math]A[/math] слева, а матрица [math]Y[/math] — “правым” частным, так как матрица [math]Y[/math] в (4.6) умножается на [math]A[/math] справа.

Пример 4.5. Даны матрицы

Решить уравнения: а) [math]AX=B[/math] ; б) [math]YB=B[/math] ; в) [math]YA=C[/math] .

Решение. Обратная матрица [math]A^<-1>=egin2&-1 -1/2&1/2 end[/math] была найдена в примере 4.2.

а) Решение уравнения [math]AX=B[/math] находим, умножая обе его части слева на [math]A^<-1>:[/math]

б) Уравнение не имеет решений, так как матрицы [math]A[/math] и [math]B[/math] имеют разное количество столбцов [math](2
e3)[/math] .

в) Решение уравнения [math]YA=C[/math] находим, умножая обе его части справа на [math]A^<-1>:[/math]

Пример 4.6. Решить уравнение: [math]BX+2X=E[/math] , где [math]B=egin-1&21&2end[/math] .

Решение. Преобразуя левую часть уравнения:

Следовательно, [math]X=A^<-1>E=A^<-1>[/math] . Обратная матрица найдена в примере 4.2:

Пример 4.7. Решить уравнение [math]AXB=C[/math] , где

Решение. Обратные матрицы

были найдены в примерах 4.2, 4.3 соответственно. Решение уравнения находим по формуле

Пример 4.8. Решить уравнение [math]AX=B[/math] , где

Решение. Определитель матрицы [math]A[/math] равен нулю, следовательно, обратная матрица не существует. Поэтому нельзя использовать формулу [math]X=A^<-1>B[/math] . Будем искать элементы матрицы [math]X=egina&bc&dend[/math] . Подставляя в уравнение, получаем

Находим произведение, а затем приравниваем соответствующие элементы матриц в левой и правой частях уравнения:

Здесь, учитывая пропорциональность уравнений, в системе оставлены только два уравнения из четырех. Выразим неизвестные [math]a[/math] и [math]b:[/math]

Следовательно, решение матричного уравнения имеет вид

AX = B, где матрица A обратима

Поскольку умножение матриц не всегда коммутативно, умножаем слева обе части уравнения на$ A^<-1>$.

$A^<-1>cdot|Acdot X = B$

$A^<-1>cdot Acdot X = A^<-1>cdot B$

$I_cdot X = A^<-1>cdot B$

Решение уравнения имеет общий вид
$colorcdot B>$

Пример 50
Решить уравнение
$egin 1 & 3 2 & 5 endcdot X egin 3 & 5 2 & 1 end$

Убедимся, что первая матрица обратима.
$left|A
ight|=5-6=-1
eq 0$, следовательно, матрица обратима.

Умножаем слева на обратную ей матрицу.
$egin 1 & 3 2 & 5 end^<-1>cdot egin 1 & 3 2 & 5 endcdot X= egin 1 & 3 2 & 5 end^<-1>cdot egin 3 & 5 2 & 1 end$

$I_<2>cdot X = egin 1 & 3 2 & 5 end^<-1>cdot egin 3 & 5 2 & 1 end$

$egin 1 & 3 2 & 5 end^<-1>= egin -5 & 3 2 & -1 end
ightarrow X= egin -5 & 3 2 & -1 endcdot egin 3 & 5 2 & 1 end= egin -9 & -22 4 & 9 end$

XA = B, где матрица A обратима

Поскольку умножение матриц не всегда коммутативно, умножаем справа обе части уравнения на$ A^<-1>$.

$Xcdot A = B |cdot A^<-1>$

$Xcdot Acdot A^ <-1>= Bcdot A^<-1>$

$X cdot I_ =Bcdot A^<-1>$

Решение уравнения имеет общий вид
$color>$

Пример 51
Решить уравнение
$X egin 1 & 3 2 & 5 end= egin 3 & 5 2 & 1 end$

Убедимся, что первая матрица обратима.
$left|A
ight|=5-6=-1
eq 0$, следовательно, матрица обратима.

Умножаем справа на обратную ей матрицу.
$X egin 1 & 3 2 & 5 endcdot egin 1 & 3 2 & 5 end^<-1>= egin 3 & 5 2 & 1 endcdot egin 1 & 3 2 & 5 end^<-1>$

$Xcdot I_<2>= egin 3 & 5 2 & 1 endcdot egin 1 & 3 2 & 5 end^<-1>$

$egin 1 & 3 2 & 5 end^<-1>= egin -5 & 3 2 & -1 end
ightarrow X= egin 3 & 5 2 & 1 end cdot egin -5 & 3 2 & -1 end= egin -5 & 4 -8 & 5 end$

Определение.
Квадратная матрица A называется
вырожденной
(невырожденной),
если

.

Определение.
Матрица

называется правой
(левой) обратной
матрице

,
если AB=I (CA=I).

Теорема.
Если для матрицы

существуют левая обратная матрица C и
правая обратная матрица B, то C=B.

Доказательство.

C=CI=C(AB)=(CA)B=IB=B,
ч.т.д.

Определение.
Матрица A^-1
называется обратной
по отношению
к квадратной матрице A, если при умножении
матрицы A^-1
на данную матрицу A как справа, так и
слева, получается единичная матрица:
A^-1A=AA^-1=I.

Понятие
о
необходимом
и
достаточном
условиях.

Любую
теорему можно записать в виде:

где A – условие теоремы, а B – её заключение.
Высказывание B называется необходимым
условием
для A, а высказывание A – достаточным
условием
для B.

Если
высказывания A и B таковы, что

и

(каждое следует из другого), то говорят,
что каждое из этих условий является
необходимым
и достаточным условием
другого и пишут

Необходимое
и
достаточное
условие
существования
и
единственности
обратной
матрицы.

Теорема.
Обратная
матрица A^-1
существует и единственна тогда и только
тогда, когда исходная матрица является
невырожденной.

Пример.
Вычислить для матрицы A матрицу A^-1,
пользуясь определением обратной матрицы.

Решение.
detA=18-20=-2

Пусть

Тогда, по определению обратной матрицы,
AA^-1=I.

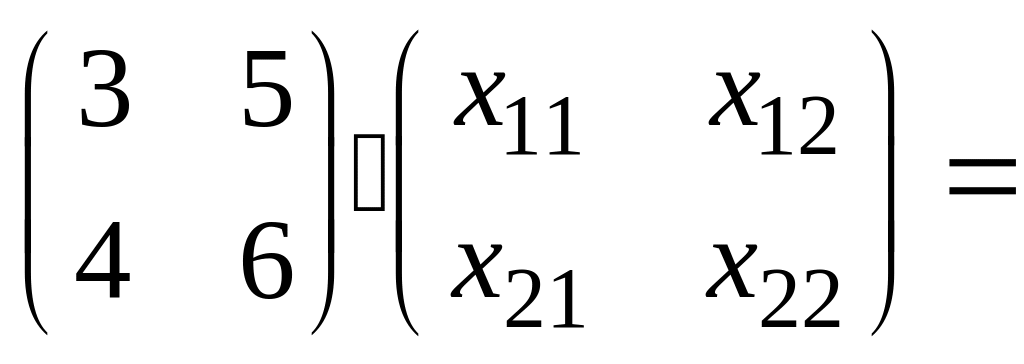
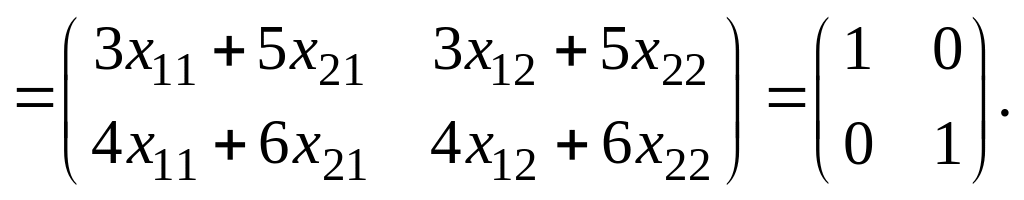
Следовательно,

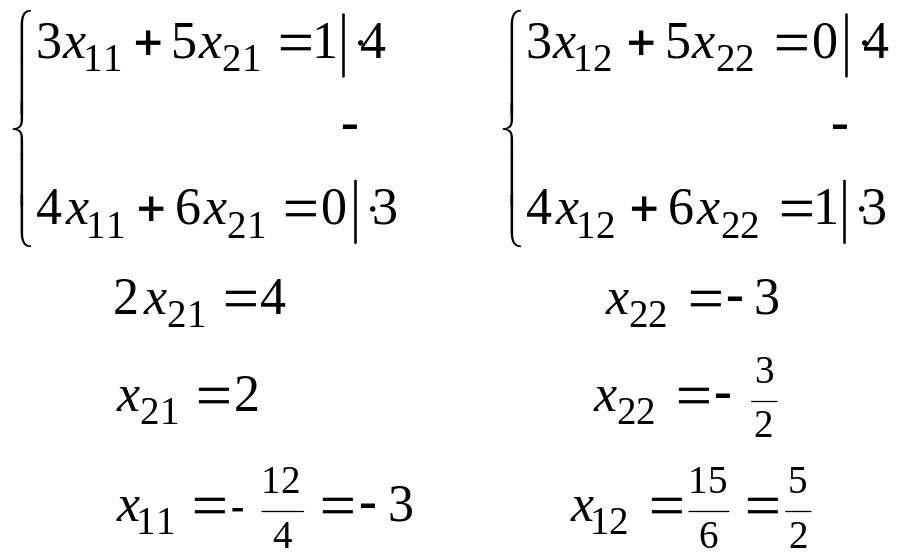
Получили,
что

.
Проверим выполнение условия A^-1A=I:

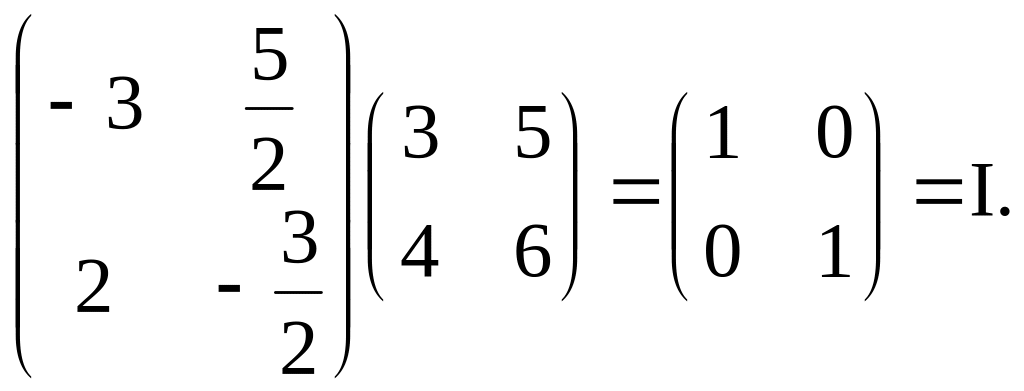
Итак,
A^-1A=AA^-1=I

.

Свойства обратной
матрицы.

Если

,
то:

1. (A^-1)^-1=A;

2. (A^-1)^T=(A^T)^-1;

3. (AB)^-1=B^-1A^-1;

4. 

5. 

6. 

Вычисление обратной матрицы (через алгебраические дополнения).

Пусть

Тогда

,
где матрица С имеет вид:

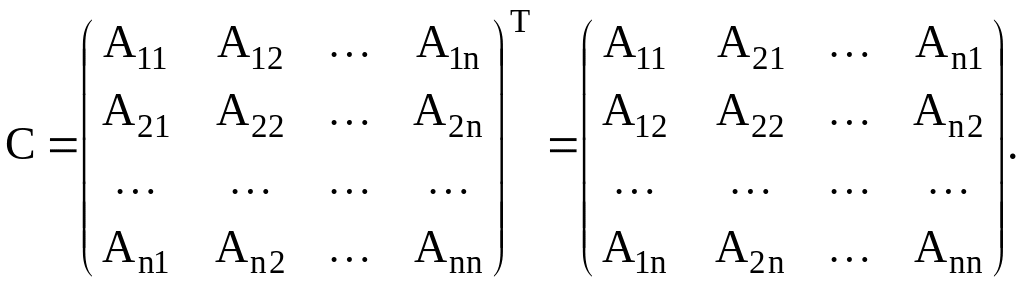
Матрица
С называется союзной
или присоединённой
по отношению к матрице А. Элемент c_ij
матрицы С равен алгебраическому
дополнению элемента a_ji
исходной матрицы А,

Пример.
Найти матрицу, обратную к матрице:

Решение.

.
Значит,

.
Вычислим алгебраические дополнения
всех элементов матрицы:

A₁₁=(-1)¹⁺¹3=3;
A₁₂=(-1)¹⁺²4=-4;

A₂₁=(-1)²⁺¹1=-1;
A₂₂=(-1)²⁺²2=2.

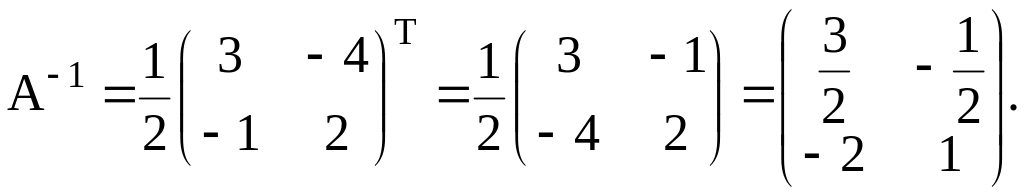
Решение
матричных уравнений.

Матричным
уравнением называется уравнение, в
котором роль неизвестной играет некоторая
матрица X. Простейшими примерами таких
уравнений могут служить уравнения AX=C,
XB=C, AXB=C, где X и C – прямоугольные матрицы
равных размеров, A и B – квадратные
матрицы соответствующих размеров. Если
предположить, что

и

,
то эти уравнения имеют единственные
решения.

AX=C A-1AX=A-1C IX=A-1C X= A-1C

XB=C XBB-1=CB-1 XI=CB-1 X=CB-1

AXB=C A-1AXBB-1=A-1CB-1 IXI=A-1CB-1 XI=A-1CB-1 X=A-1CB-1

3.5. Линейная зависимость строк и столбцов матрицы.

Определение.
Количество элементов вектор-строки
(столбца) называется длиной
(высотой) вектор-строки (столбца).

Определение.
Столбец (строка) q называется линейной
комбинацией
столбцов (строк) p₁,
p₂,
,
p_m
одинаковой высоты (длины), если при
некоторых числах ₁,
₂,
,
_m

Теорема.
Если столбец (строка) a есть линейная
комбинация столбцов (строк) a₁,
a₂,
,
a_s,
то он (она) является также линейной
комбинацией любой системы столбцов
(строк), содержащей a₁,
a₂,
,
a_s.

10
и
11
свойства
определителя
n-го
порядка.

1. Если
   в определителе строка (столбец) является
   линейной комбинацией других строк
   (столбцов), то он равен нулю.

2. Значение
   определителя не изменится, если к любой
   его строке (столбцу) прибавить линейную
   комбинацию других строк (столбцов).

Определение.
Столбцы (строки) матрицы p₁,
p₂,
,
p_m
называются линейно
зависимыми,
если существуют числа ₁,
₂,
,
_m,
не равные одновременно нулю, т.е.

такие,
что линейная комбинация столбцов (строк)
матрицы равна нулевому столбцу (строке):

Если линейная комбинация столбцов
(строк) равна нулевому столбцу (строке)
тогда и только тогда, когда

то столбцы (строки) p₁,
p₂,
,
p_m
называются линейно
независимыми.

Теорема.
Для того, чтобы система из s>1 столбцов
(строк) была линейно зависима, необходимо
и достаточно, чтобы хотя бы один из них
был линейной комбинацией остальных.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Калькулятор матриц – действия с матрицами онлайн

С помощью калькулятора матриц вы сможете выполнять различные преобразования матриц, решать СЛАУ, а также находить некоторые характеристики, как, например, определитель, след и ранг. Подробнее о функционале и использовании калькулятора смотрите после блока с самим калькулятором.

Также может быть интересно:

• Калькулятор таблицы истинности. СДНФ. СКНФ. Полином Жегалкина
• Калькулятор комплексных чисел

Как пользоваться калькулятором матриц

1. Выберите матрицу (или матрицы) с помощью переключателей ()
2. Укажите размер с помощью выпадающих списков под матрицей ( × )
3. Заполните элементы (нулевые элементы можно не заполнять.)
4. Выберите в выпадающем списке требуемую функцию и, если требуется, введите дополнительные параметры.
5. Нажмите кнопку .
6. Если вывод чисел не устраивает, просто поменяйте его — доступны три варианта представления: правильные дроби (2), неправильные дроби () и десятичные дроби (2.4) с указанием числа знаков после запятой.

Ввод данных и функционал

• В качестве элементов используются обыкновенные правильные дроби (1/2, 29/7, -1/125), десятичные дроби (12, -0.01, 3.14), а также числа в экспоненциальной форме (2.5e3, 1e-2).
• Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
• Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
• Вставляйте результат в A или B с помощью кнопок “Вставить в A” и “Вставить в B”.
• Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
• Используйте стрелки (←, ↑, →, ↓) для перемещения по элементам

Что умеет наш калькулятор матриц?

С одной матрицей (только Матрица A или Матрица B)

• Транспонировать;
• Вычислять определитель;
• Находить ранг и след;
• Возводить в степень;
• Умножать на число;
• Вычислять обратную матрицу;
• Приводить к треугольному и ступенчатому вид;
• Находить LU-разложение;
• Выполнять элементарные преобразования;
• Выполнять действия с выражениями, содержащими матрицы.

С двумя матрицами (Матрица A и Матрица B)

• Складывать;
• Вычитать;
• Умножать;
• Решать системы линейных алгебраических уравнений (СЛАУ) вида AX=B;
• Выполнять действия с выражениями, содержащими матрицы.

Вычисление выражений с матрицами

Вы можете вычислять различные арифметические выражения с матрицами, а также с результатами некоторых преобразований этих матриц.

Из чего могут состоять выражения?

• Целые и дробные числа
• Матрицы A, B
• Знаки арифметических действий: + - * /
• Круглые скобки для изменения приоритета операций: ( )
• Транспонирование: ^T
• Возведение в целую степень: ^

Примеры корректных выражений

• Cложение двух матриц: A+B, (A)+(B), ((A) + B)
• Возведение линейной комбинации матриц в степень: (3A - 0.5B)^5
• Произведение транспонированной матрицы на исходную: A^TA
• Обратная матрица в квадрате для B: B^-2

Что такое матрица?

Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами. Матрицы обозначаются заглавными латинскими буквами. При необходимости размер записывается следующим образом: An×m.

Примеры матриц

Элементы матрицы

Элементы A обозначаются aij, где i – номер строки, в которой находится элемент, j – номер столбца.

Некоторые теоретические сведения

Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: aTij = aji

Главная диагональ квадратной матрицы — диагональ, которая проходит через верхний левый и нижний правый углы. Элементы главной диагонали — aii

Единичная матрица E_n×n — квадратная матрица из n столбцов и n строк с единицами на главной диагонали и нулями вне её.

Ранг — это максимальное количество линейно независимых строк (столбцов) этой матрицы. Обозначение: rank(A)

След — это сумма элементов, находящихся на её главной диагонали. Обозначение: tr(A) или track(A)

Умножение матрицы на число — матрица такой же размерности, что и исходная, каждый элемент которой является произведением соответствующего элемента исходной матрицы на заданное число.

Возведение в степень — умножение заданной матрицы саму на себя n-ое количество раз, где n – степень, в которую необходимо возвести исходную матрицу. Обозначение: An

Обратная матрица A⁻¹ — матрица, произведение которой на исходную матрицу A равно единичной матрице: A-1×A = A×A-1 = E

Треугольная матрица — квадратная матрица, у которой выше (верхнетреугольная матрица) или ниже (нижнетреугольная матрица) главной диагонали находятся нули.

LU-разложение — представление матрицы в виде произведения двух матриц L и U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица. A = L·U

Сложение матриц A_n×m и B_n×m — матрица C_n×m, получаемая попарной суммой соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: сij=aij+bij

Разность матриц A_n×m и B_n×m — матрица C_n×m, получаемая попарной разностью соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: сij=aij-bij

Умножение матриц A_n×k и B_k×m — матрица C_n×m, у которой элемент (c_ij) равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B: cij = ai1·b1j + ai2·b2j + ... + aik·bkj