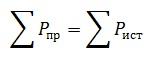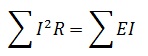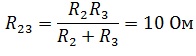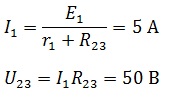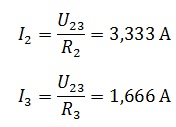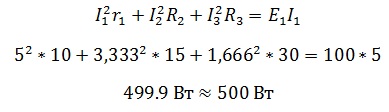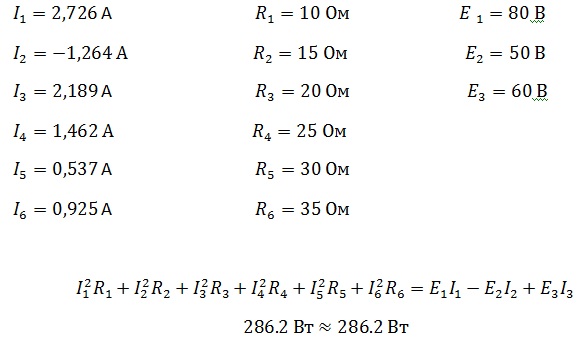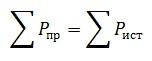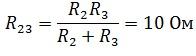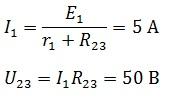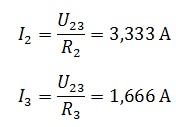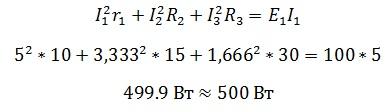Баланс мощностей электрической цепи
Электрическая цепь предполагает передачу определенной мощности от источника к потребителю. При этом, должно сохраняться равновесие, если схема состоит из сопротивлений, индуктивности. Статья раскроет тему, что такое баланс мощностей в простой цепи переменного тока. Будет описан этот показатель для постоянного напряжения, приведены формулы вычисления.
Определение
Вычисление данного параметра в электрической цепи основано на известном законе сохранения энергии. Из него следует, что мгновенные показатели, передаваемые от источника, должны быть равны сумме значений, которую получают потребители.
Баланс для мощностей представляет собой общеизвестный нам закон сохранения энергии. Выражение данного закона в этом случае — сумма всей энергии от источников (генератора или блока питания) равняется сумме, которую получают приемники.
Можно использовать альтернативный вариант. Для него формула при этом имеет вид как на рисунке ниже:
Стоит принять во внимание, что любая электрическая схема имеет сопротивление. Описываемая величина с сопутствующими значениями рассчитывается с учетом разновидности напряжений. Принимая во внимание закон сохранения энергии, стоит учитывать, что по электрической схеме всегда передается энергия.
Назначение
Составление простого баланса мощностей используют для точного определения расхождений между передаваемой и получаемой энергиями. Также, уравнение баланса мощностей применяется для решения многих электротехнических задач.
Переменный ток
Баланс мощностей в простой цепи переменного тока рассчитывается по более сложной формуле. Баланс мощностей в простой цепи синусоидального тока учитывает комплексные, реактивные и активные параметры.
- Комплексная. Состоит из мощностей передаваемых и получаемых. Необходимо будет выполнить расчет, в котором все слагаемые левой части формулы являются положительными (идут со знаками +), при условии, когда совпадает направление заряженных частиц «Ik» с «ЭДС». Должно соблюдаться правило не совпадения «Jk» с направлением напряжения «Uk». Если условия не соответствуют установленным требованиям, все данные левой части формулы становятся отрицательными. Формула приведена ниже.
- Активные. Значения, отдающиеся источником равны принимаемым потребителями. Вычисление активной мощности полностью зависит от представленной комплексной энергии. Активное значение является расходуемым, невосполнимым, так как уходит на работу приборов. Данный метод вычисления и его формула представлены ниже.
- Реактивная мощность источника с потребителем равны. Единственное отличие заключается в том, что этот параметр не растрачиваемый. Данный показатель просто циркулирует по схеме. Формула представлена ниже.
Главное отличие рассматриваемой величины — это наличие ненаправленного движения переменного тока по проводникам. Параметр такой схемы может быть увеличен или уменьшен (например, генератором), что может повлиять на конечный результат.
Постоянный ток
В электрической цепи постоянного тока напряжение и мощность всегда одного значения. Поэтому сделать вычисление намного проще. Можно сделать расчет на основе достаточно простого примера.
- В цепи имеется ЭДС «Е» и резистор «R». При расчете должна быть найдена сила тока.
- I=E/R. Подставляем имеющиеся значения, получаем I=10/10=1 ампер.
- Так мы нашли силу тока. Теперь нам будет нужен параметр мощности приемника «R» и источника.
- Pист=I×E=1×10=10 Ватт. Это значение для источника.
- Теперь для того, чтобы найти Р для приемника делаем расчет как на рисунке ниже.
- Теперь составим общий баланс — 10 ватт=10 ватт. Данный подсчет показал, что для представленной схемы сохраняется равновесие.
При вычислении параметров этой схемы имеет смысл учесть расход приемника. Резистор при нагреве выделяет тепло, а значит выполняется преобразование электричества в тепло. Беря во внимание физический закон сохранения, тепло выделяемое резистором также будет равно 10 Ватт.
Заключение
В статье было приведено описание, способ расчета баланса мощностей для постоянного и переменного тока. Для электротехники данный баланс очень важен, ведь с помощью него можно выполнять различные расчеты.
Видео по теме
Баланс мощностей: сумма мощностей, выделяемых источниками, равна сумме мощностей, потребляемых приемниками.
А теперь давайте рассмотрим по порядку и на конкретных примерах, что такое баланс мощностей и как он составляется для различных цепей постоянного тока (о балансе мощностей цепи переменного тока, мы поговорим позже).
Чтобы было более понятно, сразу рассмотрим пример.
Имеется схема цепи, изображенная на рисунке 1. Дано значение ЭДС E и сопротивление резистора R. Требуется составить баланс мощностей для данной цепи.
Для начала нужно определить ток:
I=E/R=10/10=1 (A)
Следующим шагом определим мощности источника и приемника. Поскольку это цепь постоянного тока (в цепи действует постоянный источник напряжения), то мощность, отдаваемая источником и мощность, потребляемая приемником, (в данной схеме цепи, приемник только один – это резистор R ) будет активной.
Определим активную мощность, отдаваемую источником напряжения E:
Pист=I·E=1·10=10 (Вт)(Единица измерения активной мощности “Ватт”)
Активная мощность обозначается буквой P. Индекс “ист” сокращенно от “источников”.
Определяем активную мощность приемника:
Для определения активной мощности источника, применяется формула произведения тока I через источник на величину E источника. Для определения активной мощности приемника, применяется формула произведения квадрата тока через приемник (в данном случае приемником является резистор R) на сопротивление этого резистора. Если ранее было известно напряжение резистора, то можно применить формулу для нахождения активной мощности приемника:
Pпр=Ur·I (Индекс “пр” сокращенно от “приемников”).
Таким образом, в источниках напряжения (ЭДС) происходит генерация электрической энергии, а в элементе R происходит потребление энергии. Электрическая энергия преобразуется в тепловую, т. е. резистор R потребляет электрическую энергию, отдаваемую источником E.
Отсюда следует правило баланса мощностей:
Сумма мощностей, выделяемых источниками, равна сумме мощностей, потребляемых приемниками.
Для нашей задачи, схема цепи которой изображена на рисунке 1, запишем баланс активных мощностей:
Pист=Pпр
10 (Вт)=10 (Вт). Баланс выполняется.
Для расчета электрических цепей и проверки правильности найденных токов, делаем проверку баланса мощностей. Если полученная мощность приемников отличается от полученной мощности источников, то баланс мощностей нарушается. Это говорит о том, что токи в цепи найдены неверно. Погрешность баланса мощностей может составлять до 3%.
Т. е отличие между Pист и Pпр не должно превышать 3%. Для определения погрешности, пользуются следующей формулой:
В данном случае, погрешность равна нулю и баланс выполняется.
Рассмотрим следующий пример.
Требуется составить баланс мощностей для цепи, изображенной на рисунке 4.
Для начала определим ток в цепи. Резисторы R1 и R2 включены последовательно. Следовательно, общее сопротивление цепи, запишется как:
Rобщ=R1+R2=10+10=20 (Ом)
Тогда ток по закону Ома:
Так как все ЭДС и сопротивления известны, а ток в цепи мы нашли, определим активную мощность источников и приемников.
Активная мощность, потребляемая резисторами, составляет 20 (Вт) Определим активную мощность источников.
Pист=I·E1+I·E3-I·E2=1·10+1·30-1·20=20 (Вт)
Активная мощность, отдаваемая всеми источниками ЭДС, составляет 20 (Вт)
Запишем баланс мощностей для данной цепи:
Баланс мощностей выполняется, погрешность равна нулю.
В левой части равенства получили сумму мощностей, потребляемых приемниками, а в правой части равенства получили сумму мощностей, генерируемых источниками. В данном случае ЭДС E2 работает как приемник, например, аккумулятор в режиме зарядки.
Если действие ЭДС E и тока через Eсовпадают по направлению, то произведение E·I берется со знаком “+”, если не совпадает, то “-“. В нашей цепи I и E2 направлены навстречу друг другу, поэтому произведение I·E2 взяли с минусом.
Баланс мощностей с источниками тока, мы рассмотрим в следующих статьях.
Если понравилась статья, подписывайтесь на канал и не пропускайте новые публикации.
Читайте также:
1. Как электроэнергия передается от электростанций до наших домов;
2. Что такое электрический ток – простыми словами;

Баланс мощностей является следствием закона сохранения энергии — суммарная мощность вырабатываемая (генерируемая) источниками электрической энергии равна сумме мощностей потребляемой в цепи.
Баланс мощностей используют для проверки правильности расчета электрических цепей.
Здесь мы рассмотрим баланс для цепей постоянного тока.
Например. У нас есть электрическая цепь.
Мы нашли все токи.
Для проверки правильности решения составляем баланс мощностей.
Источники E1 и E2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадают (если ЭДС и ток в ветвях направлены в противоположную сторону, то источник ЭДС потребляет энергию и его записывают со знаком минус). Баланс мощностей для заданной цепи запишется так:
С учетом погрешности расчетов баланс мощностей получился.
Баланс мощностей
При решений электротехнических задач, часто нужно проверить правильность найденных значений. Для этого в науке ТОЭ, существует так называемый баланс мощностей.
Баланс мощностей – это выражение закона сохранения энергии, в электрической цепи. Определение баланса мощностей звучит так: сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками. То есть если источник ЭДС в цепи отдает 100 Вт, то приемники в этой цепи потребляют ровно такую же мощность.
Или
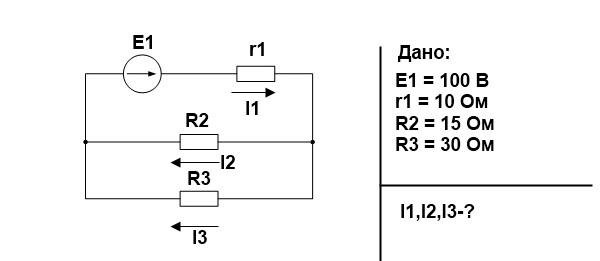
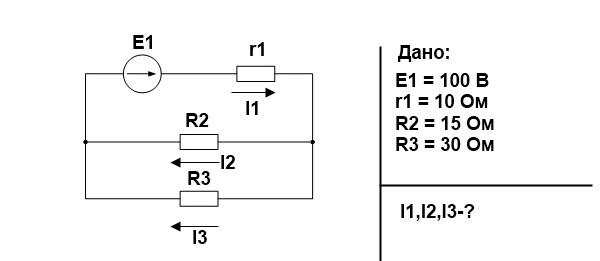
Проверим это соотношение на простом примере.
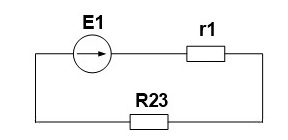
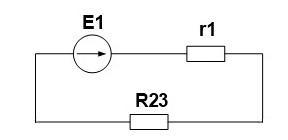
Для начала свернем схему и найдем эквивалентное сопротивление. R2 и R3 соединены параллельно.
Найдем по закону Ома ток источника и напряжение на R23, учитывая, что r1 и R23 соединены последовательно, следовательно, сила тока одинаковая.
Найдем токи I2 и I3
Теперь проверим правильность с помощью баланса мощностей.
Небольшое различие в значениях связано с округлениями в ходе расчета.
С помощью баланса мощностей, можно проверить не только простую цепь, но и сложную. Давайте проверим сложную цепь из статьи метод контурных токов.
Как видите независимо от сложности цепи, баланс сошелся, и должен сойтись в любой цепи!
При
решений электротехнических задач, часто
нужно проверить правильность найденных
значений. Для этого в науке ТОЭ, существует
так называемый баланс
мощностей.
Баланс
мощностей – это
выражение закона сохранения энергии,
в электрической цепи. Определение
баланса мощностей звучит так: сумма
мощностей потребляемых приемниками,
равна сумме мощностей отдаваемых
источниками. То есть если источник
ЭДС в
цепи отдает 100 Вт, то приемники в этой
цепи потребляют ровно такую же мощность.
Или
Проверим
это соотношение на простом примере.
Для
начала свернем схему и найдем эквивалентное
сопротивление.
R2 и R3 соединены параллельно.
Найдем
по закону
Ома ток
источника и напряжение на R23,
учитывая, что r1 и
R23 соединены
последовательно, следовательно, сила
тока одинаковая.
Найдем
токи I2 и
I3
Теперь
проверим правильность с помощью баланса
мощностей.
Небольшое
различие в значениях связано с округлениями
в ходе расчета.
С
помощью баланса мощностей, можно
проверить не только простую цепь, но и
сложную. Давайте проверим сложную цепь
из статьи метод
контурных токов.
Как
видите независимо от сложности цепи,
баланс сошелся, и должен сойтись в любой
цепи!
13. Линия передачи постоянного тока.
Преимущества
линий электропередач постоянного тока
состоят в следующем:
1.
Предел передаваемой мощности по линии
не зависит от ее длины и значительно
больше, чем у линий электропередач
переменного тока;
2.
Снимается понятие предела по статической
устойчивости, характерные для воздушных
линий электропередачи переменного
тока;
3.
Энергосистемы, связанные воздушные
линии электропередачи постоянного тока
могут работать несинхронно или с
различными частотами;
4.
Требуется лишь два провода вместо трех
или даже один, если использовать в
качестве второго землю.
На
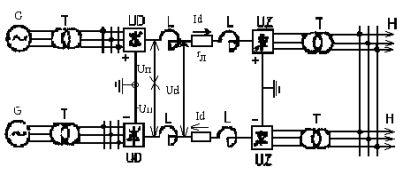
рис. 1. приведена схема
передачи постоянного тока, осуществленная
по биполярной схеме(«два полюса – земля»).
На
этом рисунке UD и UZ, преобразовательные
(выпрямительная и инвекторная) подстанции;
L – реактор или фильтр для уменьшения
влияния высоких гармоник, пульсации
напряжения и аварийных токов; rл
-сопротивление линии; G, Т – генераторы
и трансформаторы.
Выработка
и потребление электроэнергии осуществляется
на переменном токе.
Рис.1.
Схема передачи постоянного тока в
послеаварийном режиме
Основные
элементы линии постоянного тока:
1.
Управляемые высоковольтные выпрямители
из которых собирается схема
преобразовательной подстанции.
2.
Управляемые высоковольтные инверторы,
из них также собирается схема
преобразовательной подстанции.
Схема
инверторной подстанции принципиально
не отличается от схемы выпрямительной
подстанции, так как выпрямители обратимы.
Единственное отличие состоит в том, что
на инверторной подстанции приходится
устанавливать компенсирующие устройства,
конденсаторы, либо синхронные компенсаторы
для выдачи инверторам реактивной
мощности, которая составляет около
50… 60% передаваемой активной мощности.
Средние
точки обоих преобразовательных подстанций
в биполярной передаче заземлены, а
полюсы изолированы.
Напряжение
полюса UП равно напряжению между полюсом
и землей. Например, на передаче энергии
Волгоград – Донбасс напряжение полюса
относительно земли +400 кВ, а второго –
400 кВ. Напряжение Ud между полюсами 800 кВ.
Передача может быть разделена на две
независимые полуцепи. В нормальном
режиме при равных точках в полуцепях
ток через землю близок к нулю. Обе
полуцепи передачи могут работать
автономно и в случае аварии одного
полюса половина мощности может
передаваться по другому полюсу с
возвратом через землю.
При
аварии одного полюса или одной полуцепи
вторая полуцепь может работать по
униполярной схеме.
Рис.
2. Схема передачи постоянного тока в
послеаварийном режиме
В
униполярной передаче заземлен один из
полюсов и имеется один провод, изолированный
от земли. Второй провод либо заземлен
с двух сторон передачи, либо отсутствует.
Такой заземленный второй провод
применяется в тех случаях, когда
недопустимо применение тока в земле
(например, при вводах в крупные города).
Как правило, одна цепь униполярной
передачи может состоять из одного
провода и земли, а биполярная – из двух
проводов. Описан опыт длительного
пропускания постоянного тока через
землю до 1200 А.
Униполярные
схемы применяются для передачи небольших
мощностей до 100… 200МВт на небольшие
расстояния. Большие мощности на большие
расстояния целесообразно передавать
по биполярным схемам.
Преобразовательные
подстанции из-за сложного и дорогостоящего
оборудования очень увеличивают стоимость
передач постоянного тока. В тоже время
сама линия постоянного тока стоит
дешевле, чем линия переменного тока,
из-за меньшего количества проводов,
изоляторов, линейной арматуры и более
легких опор.
Пропускная
способность мощности линии постоянного
тока определяется значением и разностью
напряжений по концам линии, ограничивается
активными сопротивлениями линиями и
концевых устройств, а также мощностью
преобразовательных подстанций.
Однако
пропускная способность мощности линии
постоянного тока значительно больше,
чем у линии переменного тока.
Полная
мощность биполярной передачи линии
Волгоград – Донбасс напряжением Ud = 800
кВ составляет 720 МВт. Введена в эксплуатацию
крупнейшая в мире линия Экибастуз –
Центр с UП = ±750 кВ, напряжением между
полюсами Ud = 1500 кВ и длиной 2500 км. Пропускная
способность мощности может быть доведена
до 6000 МВт.
Основная
область применения линий постоянного
тока – передача больших мощностей на
дальние расстояния. Однако особые
свойства этих линий позволяют с успехом
использовать их и в других случаях.
Например, линии постоянного тока
оказываются эффективными при необходимости
пересечения морских проливов, а также
связи несинхронных систем или систем,
работающих с разной частотой (так
называемые вставки постоянного тока).
Наряду
с линиями постоянного тока высокого и
сверхвысокого напряжения в военном
деле применяются и линии постоянного
тока малого и среднего напряжения.
Широкое
распространение получили следующие
напряжения: малые напряжения – 6, 12, 24,
36,48, 60 вольт, средние напряжения – 110, 220,
400 вольт.
Для
всех напряжений линии постоянного тока
имеют следующие достоинства:
1.
Они не требуют расчета устойчивости.
2.
Напряжение в таких линиях более
равномерно, так как в установившемся
режиме они не генерируют реактивной
мощности.
3.
Конструкции линий постоянного тока
проще, чем переменного: меньше число
гирлянд изоляторов, меньшая затрата
металла.
4.
Направление потока мощности можно
изменять (реверсивные линии).
Недостатки:
1.
Необходимость сооружения сложных
концевых подстанций с большим числом
преобразователей напряжения и
вспомогательной аппаратуры. Известно,
что выпрямители и инверторы сильно
искажают форму кривой напряжения на
стороне переменного тока. Поэтому
приходится ставить мощные сглаживающие
устройства, что значительно снижает
надежность.
2.
Отбор мощности от линии постоянного
тока пока затруднителен.
3.
В линиях постоянного тока требуется,
чтобы перед включением были примерно
одинаковыми полярность и напряжения
по обоим концам.
Таким
образом, возможно сделать вывод, что
из-за больших затрат к0 (рис.3) строительство
линий электропередач постоянного тока
(кривая 2) становится экономически
целесообразным только при больших
расстояниях равных примерно 1000… 1200 км
(точка m).
Рис.
3. Зависимость капитальных затрат к от
длины линии l для переменного тока – 1 и
для постоянного тока – 2