Как найти баланс мощностей в схеме

Баланс мощностей: сумма мощностей, выделяемых источниками, равна сумме мощностей, потребляемых приемниками.

А теперь давайте рассмотрим по порядку и на конкретных примерах, что такое баланс мощностей и как он составляется для различных цепей постоянного тока (о балансе мощностей цепи переменного тока, мы поговорим позже).

Чтобы было более понятно, сразу рассмотрим пример.

Имеется схема цепи, изображенная на рисунке 1. Дано значение ЭДС E и сопротивление резистора R. Требуется составить баланс мощностей для данной цепи.

Для начала нужно определить ток:

I=E/R=10/10=1 (A)

Следующим шагом определим мощности источника и приемника. Поскольку это цепь постоянного тока (в цепи действует постоянный источник напряжения), то мощность, отдаваемая источником и мощность, потребляемая приемником, (в данной схеме цепи, приемник только один – это резистор R ) будет активной.

Определим активную мощность, отдаваемую источником напряжения E:

Pист=I·E=1·10=10 (Вт)(Единица измерения активной мощности “Ватт”)

Активная мощность обозначается буквой P. Индекс “ист” сокращенно от “источников”.

Определяем активную мощность приемника:

Для определения активной мощности источника, применяется формула произведения тока I через источник на величину E источника. Для определения активной мощности приемника, применяется формула произведения квадрата тока через приемник (в данном случае приемником является резистор R) на сопротивление этого резистора. Если ранее было известно напряжение резистора, то можно применить формулу для нахождения активной мощности приемника:

Pпр=Ur·I (Индекс “пр” сокращенно от “приемников”).

Таким образом, в источниках напряжения (ЭДС) происходит генерация электрической энергии, а в элементе R происходит потребление энергии. Электрическая энергия преобразуется в тепловую, т. е. резистор R потребляет электрическую энергию, отдаваемую источником E.

Отсюда следует правило баланса мощностей:

Сумма мощностей, выделяемых источниками, равна сумме мощностей, потребляемых приемниками.

Для нашей задачи, схема цепи которой изображена на рисунке 1, запишем баланс активных мощностей:

Pист=Pпр

10 (Вт)=10 (Вт). Баланс выполняется.

Для расчета электрических цепей и проверки правильности найденных токов, делаем проверку баланса мощностей. Если полученная мощность приемников отличается от полученной мощности источников, то баланс мощностей нарушается. Это говорит о том, что токи в цепи найдены неверно. Погрешность баланса мощностей может составлять до 3%.

Т. е отличие между Pист и Pпр не должно превышать 3%. Для определения погрешности, пользуются следующей формулой:

В данном случае, погрешность равна нулю и баланс выполняется.

Рассмотрим следующий пример.

Требуется составить баланс мощностей для цепи, изображенной на рисунке 4.

Для начала определим ток в цепи. Резисторы R1 и R2 включены последовательно. Следовательно, общее сопротивление цепи, запишется как:

Rобщ=R1+R2=10+10=20 (Ом)

Тогда ток по закону Ома:

Так как все ЭДС и сопротивления известны, а ток в цепи мы нашли, определим активную мощность источников и приемников.

Активная мощность, потребляемая резисторами, составляет 20 (Вт) Определим активную мощность источников.

Pист=I·E1+I·E3-I·E2=1·10+1·30-1·20=20 (Вт)

Активная мощность, отдаваемая всеми источниками ЭДС, составляет 20 (Вт)

Запишем баланс мощностей для данной цепи:

Баланс мощностей выполняется, погрешность равна нулю.

В левой части равенства получили сумму мощностей, потребляемых приемниками, а в правой части равенства получили сумму мощностей, генерируемых источниками. В данном случае ЭДС E2 работает как приемник, например, аккумулятор в режиме зарядки.

Если действие ЭДС E и тока через Eсовпадают по направлению, то произведение E·I берется со знаком “+”, если не совпадает, то “-“. В нашей цепи I и E2 направлены навстречу друг другу, поэтому произведение I·E2 взяли с минусом.

Баланс мощностей с источниками тока, мы рассмотрим в следующих статьях.

Если понравилась статья, подписывайтесь на канал и не пропускайте новые публикации.

Читайте также:

1. Как электроэнергия передается от электростанций до наших домов;

2. Что такое электрический ток – простыми словами;

Баланс мощностей является следствием закона сохранения энергии — суммарная мощность вырабатываемая (генерируемая) источниками электрической энергии равна сумме мощностей потребляемой в цепи.

Баланс мощностей используют для проверки правильности расчета электрических цепей. 

Здесь мы рассмотрим баланс для цепей постоянного тока.

Например. У нас есть электрическая цепь.

Мы нашли все токи.

Для проверки правильности решения  составляем баланс мощностей.

Источники E1 и E2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадают (если  ЭДС и ток в ветвях направлены в противоположную сторону, то источник ЭДС потребляет энергию и его записывают со знаком минус). Баланс мощностей для заданной цепи запишется так:

С учетом погрешности расчетов баланс мощностей получился.

Баланс мощностей

Баланс мощностей

Для любой электрической цепи суммарная мощность , развиваемая источниками электрической энергии (источниками тока и ЭДС), равна суммарной мощности , расходуемой потребителями (резисторами):

Мощность, рассеиваемая резистором, , мощность источника ЭДС , мощность источника тока .

Мощности, рассеиваемые резисторами, всегда положительные, в то время как мощности источников электрической энергии, в зависимости от соотношения направления падений напряжения и тока в них, могут иметь любой знак. Мощность положительна, когда направление тока через источник тока противоположно падению напряжения на нем. Он питает электрическую цепь. В противном случае источник питания является отрицательным, и вы являетесь потребителем электрической энергии. Следует заметить, что направление падения напряжения всегда противоположно направлению ЭДС, поэтому для источника ЭДС условием положительной мощности является совпадение направлений ЭДС и тока.

Пример расчёта разветвлённой цепи постоянного тока

Рассмотрим решение задачи для цепи, представленной на рис. 1.6, описанными выше методами расчёта.

Дано

1) все неизвестные токи, используя законы Кирхгофа; показать, что баланс мощностей имеет место;

1) Применение законов Кирхгофа. Баланс мощностей.

Всего в схеме семь ветвей =7, ветвей с источниками тока = 1, число неизвестных токов равно , количество узлов — , число уравнений по первому закону Кирхгофа , число уравнений по второму закону Кирхгофа —

Возможно вам будут полезны данные страницы:

Выберем положительные направления токов и обозначим их стрелками. Выберем и обозначим стрелками направления обхода трёх независимых контуров: Составим систему уравнений по законам Кирхгофа

для узла а ;

для узла b

для узла с или ;

для контура ,

для контура

для контура

Полученные уравнения после подстановки в них числовых значений будут иметь следующий вид:

Решение данной системы:

Баланс мощностей для рассматриваемой цепи

Получено тождество 252 Вт = 252 Вт.

Примечание: падение напряжения на источнике тока определено по второму закону Кирхгофа для контура, содержащего и , как

Баланс мощностей

В любой электрической цепи должен соблюдаться энергетический баланс -баланс мощностей: алгебраическая сумма мощностей всех источников равна арифметической сумме мощностей всех приемников энергии.

В левой части равенства слагаемое берется со знаком «+» если Е и I совпадают по направлению и со знаком если не совпадают.

Если направления ЭДС и тока I в источнике противоположны, то физически это означает, что данный источник работает в режиме потребителя.

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник

Баланс мощностей в цепи постоянного тока

Баланс мощностей является следствием закона сохранения энергии — суммарная мощность вырабатываемая (генерируемая) источниками электрической энергии равна сумме мощностей потребляемой в цепи.

Источники E1 и E2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадают (если ЭДС и ток в ветвях направлены в противоположную сторону, то источник ЭДС потребляет энергию и его записывают со знаком минус). Баланс мощностей для заданной цепи запишется так:

С учетом погрешности расчетов баланс мощностей получился.

Какова допустимая погрешность?? У меня выходит 0,561

По идее баланс мощности должен равняться нулю, но так как мы округляем некоторые значения при расчете — возникает погрешность, которая может составлять примерно 0,1 — 5% от потребляемой мощности.

Про знаки ЭДС сказано про знаки мощностей приёмников — нет.

Источник

Баланс мощностей

При решений электротехнических задач, часто нужно проверить правильность найденных значений. Для этого в науке ТОЭ, существует так называемый баланс мощностей.

Баланс мощностей – это выражение закона сохранения энергии, в электрической цепи. Определение баланса мощностей звучит так: сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками. То есть если источник ЭДС в цепи отдает 100 Вт, то приемники в этой цепи потребляют ровно такую же мощность.

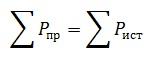
Или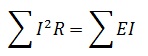

Проверим это соотношение на простом примере.

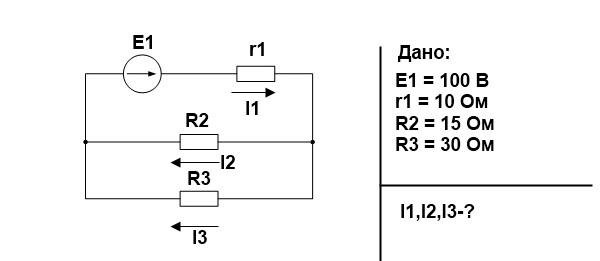
Для начала свернем схему и найдем эквивалентное сопротивление. R2 и R3 соединены параллельно.

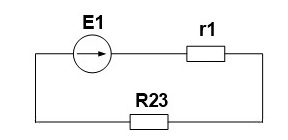
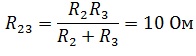
Найдем по закону Ома ток источника и напряжение на R₂₃, учитывая, что r₁ и R₂₃ соединены последовательно, следовательно, сила тока одинаковая.

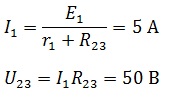
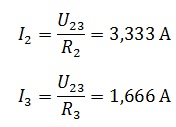
Теперь проверим правильность с помощью баланса мощностей.

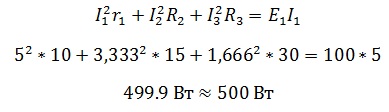
Небольшое различие в значениях связано с округлениями в ходе расчета.

С помощью баланса мощностей, можно проверить не только простую цепь, но и сложную. Давайте проверим сложную цепь из статьи метод контурных токов.

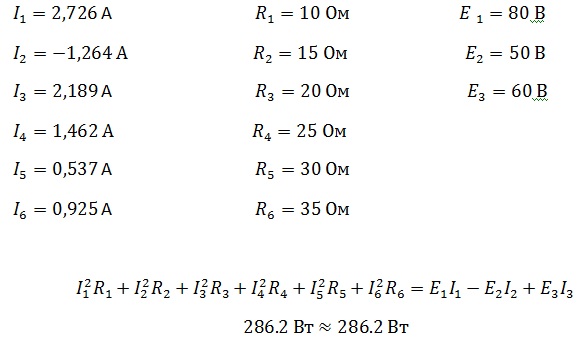
Как видите независимо от сложности цепи, баланс сошелся, и должен сойтись в любой цепи!

Источник

Баланс мощностей электрической цепи

Электрическая цепь предполагает передачу определенной мощности от источника к потребителю. При этом, должно сохраняться равновесие, если схема состоит из сопротивлений, индуктивности. Статья раскроет тему, что такое баланс мощностей в простой цепи переменного тока. Будет описан этот показатель для постоянного напряжения, приведены формулы вычисления.

Определение

Вычисление данного параметра в электрической цепи основано на известном законе сохранения энергии. Из него следует, что мгновенные показатели, передаваемые от источника, должны быть равны сумме значений, которую получают потребители.

Баланс для мощностей представляет собой общеизвестный нам закон сохранения энергии. Выражение данного закона в этом случае — сумма всей энергии от источников (генератора или блока питания) равняется сумме, которую получают приемники.

Можно использовать альтернативный вариант. Для него формула при этом имеет вид как на рисунке ниже:

Стоит принять во внимание, что любая электрическая схема имеет сопротивление. Описываемая величина с сопутствующими значениями рассчитывается с учетом разновидности напряжений. Принимая во внимание закон сохранения энергии, стоит учитывать, что по электрической схеме всегда передается энергия.

Назначение

Составление простого баланса мощностей используют для точного определения расхождений между передаваемой и получаемой энергиями. Также, уравнение баланса мощностей применяется для решения многих электротехнических задач.

Переменный ток

Баланс мощностей в простой цепи переменного тока рассчитывается по более сложной формуле. Баланс мощностей в простой цепи синусоидального тока учитывает комплексные, реактивные и активные параметры.

1. Комплексная. Состоит из мощностей передаваемых и получаемых. Необходимо будет выполнить расчет, в котором все слагаемые левой части формулы являются положительными (идут со знаками +), при условии, когда совпадает направление заряженных частиц «Ik» с «ЭДС». Должно соблюдаться правило не совпадения «Jk» с направлением напряжения «Uk». Если условия не соответствуют установленным требованиям, все данные левой части формулы становятся отрицательными. Формула приведена ниже.
2. Активные. Значения, отдающиеся источником равны принимаемым потребителями. Вычисление активной мощности полностью зависит от представленной комплексной энергии. Активное значение является расходуемым, невосполнимым, так как уходит на работу приборов. Данный метод вычисления и его формула представлены ниже.
3. Реактивная мощность источника с потребителем равны. Единственное отличие заключается в том, что этот параметр не растрачиваемый. Данный показатель просто циркулирует по схеме. Формула представлена ниже.

Главное отличие рассматриваемой величины — это наличие ненаправленного движения переменного тока по проводникам. Параметр такой схемы может быть увеличен или уменьшен (например, генератором), что может повлиять на конечный результат.

Постоянный ток

В электрической цепи постоянного тока напряжение и мощность всегда одного значения. Поэтому сделать вычисление намного проще. Можно сделать расчет на основе достаточно простого примера.

1. В цепи имеется ЭДС «Е» и резистор «R». При расчете должна быть найдена сила тока.
2. I=E/R. Подставляем имеющиеся значения, получаем I=10/10=1 ампер.
3. Так мы нашли силу тока. Теперь нам будет нужен параметр мощности приемника «R» и источника.
4. Pист=I×E=1×10=10 Ватт. Это значение для источника.
5. Теперь для того, чтобы найти Р для приемника делаем расчет как на рисунке ниже.
6. Теперь составим общий баланс — 10 ватт=10 ватт. Данный подсчет показал, что для представленной схемы сохраняется равновесие.

При вычислении параметров этой схемы имеет смысл учесть расход приемника. Резистор при нагреве выделяет тепло, а значит выполняется преобразование электричества в тепло. Беря во внимание физический закон сохранения, тепло выделяемое резистором также будет равно 10 Ватт.

Заключение

В статье было приведено описание, способ расчета баланса мощностей для постоянного и переменного тока. Для электротехники данный баланс очень важен, ведь с помощью него можно выполнять различные расчеты.

Видео по теме

Источник

В соответствии с законом сохранения
энергии в любой электрической цепи
энергия, вырабатываемая всеми источниками
в единицу времени, равна энергии,
потребляемой приемниками электрической
энергии в единицу времени. Т.е. в
электрических цепях энергетический
баланс можно свести к балансу мощностей.

Рассмотрим обобщенную электрическую
цепь постоянного тока произвольной
конфигурации, с произвольным числом
источников электрической энергии и
произвольным числом приемников
электрической энергии. Если все источники
являются источниками ЭДС, то уравнение
баланса мощностей для такой цепи можно
записать в виде:

.

Левая часть уравнения баланса мощностей
представляет собой арифметическую
сумму мощностей, обусловленных выделением
тепла на сопротивлениях Rпри протекании через них токаIв соответствии с законом Джоуля-Ленца.
Эта сумма охватывает все сопротивленияR электрической
цепи, в том числе и внутренние сопротивления
источниковR_i.

Правая часть уравнения баланса мощностей
представляет собой алгебраическую
сумму мощностей источников ЭДС. Выбор
знака очередного члена алгебраической
суммы производится в соответствии с
энергетическими соотношениями,
характерными для режимов генерирования
и потребления электрической энергии
реальным источником ЭДС, которые были
рассмотрены в предыдущем параграфе. А
именно: если знаки EиIодинаковы, то
мощность источникаEI
положительна, и он работает в
режиме генерирования электрической
энергии; если знакиEиIразличны, то мощность
источникаEI
отрицательна, и он работает в
режиме потребления электрической
энергии.

При наличии в схеме источников тока их
мощность также необходимо учесть в
правой части уравнения баланса мощностей.
Предположим, что источник тока включен
между узлами a иb схемы: в узелaвтекает токI_kисточника тока, а из узлаbон вытекает. Тогда на выводных зажимах
источника тока будет напряжениеU_ab.
Если знакиI_kиU_abодинаковы, то мощность источника токаU_abI_k
положительна, и он работает в
режиме генерирования электрической
энергии. Если знакиI_kиU_abразличны, то мощность источника токаU_abI_k
отрицательна, и он работает в
режиме потребления электрической
энергии.

С учетом изложенного уравнение баланса
мощностей для цепи, содержащей как
источники ЭДС, так и источники тока,
можно записать в следующем виде:

.

Уравнения баланса мощностей удобно
использовать для проверки правильности
расчета токов в ветвях электрической
цепи.

Пример 7. Проверить правильность
расчета токов в примере 3 для схемы рис.
31 путем составления баланса мощностей.

Решение

Составляем уравнение баланса мощностей
для схемы рис. 31:

R₁
I₁²
+
R₂
I₂²
+
R₃
I₃²
+
R₄
I₄²
+
R_i4
I₄²
+
R₅
I₅²
+
R₆
I₆²
+
R_i6
I₆²
=
E₄I₄
+
E₆I₆.

Подставляем численные значения:

6∙2,82²
+ 10∙0,96²
+ 2∙1,86²
+ 7∙1,69²
+ 1∙1,69²
+ 8∙0,73²
+ 9∙1,13² +
1∙1,13²
=

=
40∙1,69 + 32∙1,13.

Производя вычисления, получаем:

103,7
= 103,7 Вт.

Баланс мощностей сошелся. Токи рассчитаны
правильно.

17. Режимы работы электрических цепей постоянного тока

В настоящем параграфе рассматривается
вопрос выбора возможного режима работы
электрической цепи постоянного тока с
точки зрения энергопотребления от
генератора.

Схема обобщенной линейной электрической
цепи постоянного тока представлена на
рис. 1. Она состоит из источника с ЭДС Еи внутренним сопротивлениемR_iи приемника с сопротивлениемR.
Источник работает в режиме генератора
и отдает энергию приемнику. ЭДСЕи
внутреннее сопротивлениеR_iисточника являются константами.
СопротивлениеRприемника величина переменная. Изменяя
величину сопротивленияRприемника, можно изменить ток в схеме.
ЗависимостьI(R)
при неизменных значенияхEиR_iвыражает формула закона Ома (3). Связь
между напряжениемUи токомIвыражается
формулой:

,

которой
соответствует внешняя характеристика
источника U(I),
представленная на рис. 55 отрезком прямой
между точками холостого хода 1 и короткого
замыкания 2.

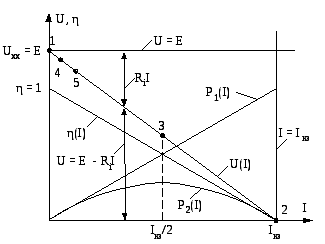
Рис. 55.
Зависимости U(I),
P₁(I),
P₂(I),
η(I)
для обобщенной линейной

электрической
цепи постоянного тока

Режим работы электрической цепи
определяется положением рабочей точки
на внешней характеристике источника.
Каждой точке внешней характеристики и
соответственно каждому режиму работы
электрической цепи соответствуют свое
напряжение Uи токI.
Кроме того, каждый режим работы
электрической цепи характеризуется и
другими параметрами, такими как мощностьP₁ =EI,
вырабатываемая источником, мощностьюP₂=UI,
потребляемая приемником, КПД η =P₂/P₁.
Графики зависимостейP₁(I),P₂(I),
и η(I) приведены на
рис. 55 наряду с внешней характеристикой.
ЗависимостьP₁(I)
представляет собой отрезок прямой
линии, выходящий из начала координат.
ЗависимостьP₂(I) – это кривая,
выходящая из начала координат и приходящая
в точку короткого замыкания 2. График
функцииP₂(I)
имеет явно выраженный экстремум.
Зависимость η(I)
представляет собой отрезок прямой,
который строится в соответствии с
формулой

.

На внешней характеристике можно выделить
четыре характерных режима работы
электрической цепи. Это режим холостого
хода 1, режим короткого замыкания 2, так
называемый согласованный режим работы
3 и номинальный режим работы. Номинальный
режим – это основной расчетный режим
работы электрической цепи. Положение
точки номинального режима работы
электрической цепи на внешней
характеристике зависит от назначения
электрической цепи.

В режиме холостого хода выходные зажимы
источника разомкнуты (рис. 56). Сопротивление
приемника в режиме холостого хода равно
бесконечности (R_xx=
).
Ток холостого хода равен нулю (I_xx= 0). Напряжение холостого хода равно ЭДС
источника (U_xx=E). Источник не отдает
энергию во внешнюю цепь (P₁= 0). Приемник энергию не потребляет (P₂= 0). КПД в режиме холостого хода максимален
(η_xx= 1, см. рис.1.20).
Реальные источники электрической
энергии работают в режиме холостого
хода только непродолжительное время.
Например, перед подключением на их
зажимы нагрузки или после ее снятия.

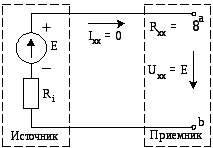
Рис. 56.
Схема цепи постоянного тока, работающей

в
режиме холостого хода

В режиме короткого замыкания выходные
зажимы источника соединены между собой
(рис. 57).

Сопротивление приемника в режиме
короткого замыкания равно нулю (R_кз= 0). Ток короткого замыкания достигает
максимально возможного значения и
ограничивается только внутренним
сопротивлением источника

.

ЭДС источника уравновешивается падением
напряжения на внутреннем сопротивлении
источника, то есть E=R_iI_кз.
Напряжение, подводимое к приемнику,
равно нулю (U_кз= 0). МощностьP₁,
вырабатываемая источником, максимальна.
Энергия, вырабатываемая источником,
выделяется в виде тепла на внутреннем
сопротивлении источника. МощностьP₂,
потребляемая приемником, равна нулю.
КПД режима короткого замыкания равен
нулю (η_кз= 0, см. рис. 55).

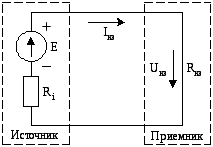
Рис. 57.
Схема цепи постоянного тока, работающей

в
режиме короткого замыкания

Для большинства электрических цепей
(прежде всего, силовых) режим короткого
замыкания неприемлем из-за нулевого
КПД и нулевой мощности P₂,
потребляемой приемником. Поэтому
большинство электрических цепей для
работы в режиме короткого замыкания не
рассчитаны. Для них режим короткого
замыкания является аварийным, т.к. токI_кзи мощностьP_1кз, вырабатываемая
источником, в режиме короткого замыкания
существенно превышают значениеI_ниP_1нноминального
режима работы. Однако для некоторых
слаботочных цепей режим, близкий к
режиму короткого замыкания, может
использовать в качестве номинального
режима. Например, когда возникает
необходимость в подключении приемника
с малым входным сопротивлением к
источнику с большим внутренним
сопротивлением.

Итак, точка рабочего режима электрической
цепи на внешней характеристике может
лежать между точками холостого хода 1
и короткого замыкания 2 (см. рис. 55). Выбор
оптимального режима работы электрической
цепи зависит от назначения электрической
цепи.

Для ряда цепей, например, оптимальным
будет режим, при котором от источника
к приемнику передается максимальная
мощность. Этот режим называется
согласованным режимом работы. Для
установления условия передачи от
источника к приемнику максимальной
мощности необходимо выразить зависимость
мощности P₂,
выделяющейся в приемнике, от величины
сопротивления приемникаR,
взять производнуюdP₂/dRи приравнять ее к нулю.

Ток I(рис. 1) определяется
в соответствии с законом Ома

.

Мощность P₂,
выделяющаяся в приемнике, определяется
законом Джоуля-Ленца

.

Производная мощности

.

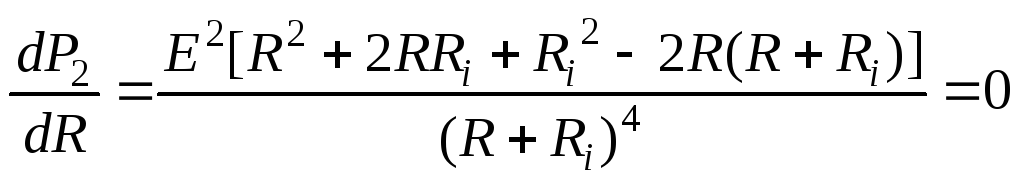Полученное выражение равно нулю, если
равен нулю числитель

,

а это возможно,
если сопротивление приемника Rравно внутреннему сопротивлению
источникаR_i.
Итак, равенствоR =
R_iявляется условием передачи максимальной
мощности от источника к приемнику. На
внешней характеристике режиму передачи
максимальной мощности соответствует
точка 3 (рис. 55).

В приемнике выделяется мощность P₂
= RI², в источнике
ΔP = R_iI².
ЕслиR = R_i,
то эти мощности одинаковы. МощностьP₂,
выделяющаяся в приемнике, является
полезной. Мощность ΔP,
выделяющаяся в источнике, представляет
собой потери мощности. Вся энергия
вырабатывается источником. Поэтому в
согласованном режиме полезная мощность
составляет только половину от мощностиP₁ = P₂
+ ΔP, вырабатываемой
источником. КПД такого режима равен 50
%. Поэтому согласованный режим может
быть номинальным только в цепях, для
которых энергетические показатели не
являются определяющими. Это слаботочные
цепи, например, информационные цепи,
электронные цепи устройств автоматики
и другие.

Для силовых цепей при выборе номинального
режима определяющим фактором являются
энергетические показатели и, прежде
всего, высокий КПД. Судовые силовые
электротехнические устройства
рассчитываются так, чтобы в номинальном
режиме их КПД лежал в пределах 85–95 %. На
рис. 55 этот участок расположен между
точками 4–5 внешней характеристики.

БИБЛИОГРАФИЧЕСКИЙ
СПИСОК

1. Бессонов
   Л.А. Теоретические основы электротехники.
   Электрические цепи: Учебник. – М.:
   Гардарики, 2002. – 638 с.

2. Основы
   теории цепей: Учебник для вузов/Г.В.
   Зевеке, П.А. Ионкин, А.В. Нетушил, С.В.
   Страхов. – М.: «Энергоатомиздат», 1989. –
   528 с.

3. Шебес
   М.Р., Каблукова М.В. Задачник по теории
   линейных электрических цепей. – М.:
   Высшая школа, 1990. – 544 с.

52

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #