О барицентрических координатах на пальцах
Время на прочтение
4 мин
Количество просмотров 17K
Привет.
Наверняка всем доводилось быть свидетелями оценки на глазок степени сходства ребенка с родителями: что-нибудь типа «вылитый папа, но на маму тоже похож!!!»
(взято отсюда)
Как в примере на изображении, можно оценить степень похожести в процентах. Можно задействовать еще родственников, для более точного описания лица малыша в виде взвешенной суммы лиц родни…
И будет это выглядеть и восприниматься вполне естественно для «обычного» человека, не связанного с антропологией, или, например, криминалистикой. Для профессионала в области анализа и распознавания лиц, человеческое лицо представляется, скорее, набором параметров. То есть, точкой (набор координат) в некотором пространстве с базисом (оси, соответствующие параметрам). И если описывать лицо ребенка в сравнении с его родственниками, то скорее всего, точка, соответствующая лицу ребенка окажется в этом пространстве параметров внутри выпуклой оболочки облака точек, соответствующих лицам ближайших родственников (но это не точно).
Собственное, к чему я это все… Эти два подхода к описанию лиц соответствуют двум системам координат:
- барицентрической, описание точки в пространстве (в нашем примере: лица) через взвешенную смесь других точек;
- аффинной, описание точки в пространстве через координаты в некотором базисе.
Так что же такое барицентрические координаты?
Пусть в -мерном пространстве заданы
точка
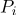


.
В случае одномерного пространства (линия), нам необходимы 2 не совпадающие точки, случае двумерного пространства — невырожденный треугольник, в случае трехмерного — тетраэдр.
Тогда любая точка пространства 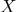

Набор 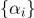
Чем барицентрические координаты лучше/хуже аффинных?
Пожалуй, начнем с относительных недостатков:
- в барицентрическом представлении нам необходимо на одну координату больше, чем в аффинном;
- расстояние между точками, заданными барицентрически, нельзя напрямую вычислять в этих координатах.
Отчасти первый недостаток компенсируется тем, что не смотря на необходимость использования барицентрической координаты при описании точки в
-мерном пространстве, количество степеней не повышается. Барицентрические координаты, определенные в формуле (1), связаны соотношением:
Что касается второго недостатка, если есть необходимость вычисления расстояния между точками, представленными барицентрически, то имеет смысл посчитать скалярные произведения 
Каковы же бонусы от использования барицентрических координат?
- Барицентрические координаты инвариантны к аффинным преобразованиям пространства. Это свойство используется, например, для линейной интерполяции в компьютерной графике. Пусть в вершинах треугольного элемента поверхности определены текстурные координаты
и нормали
(
), тогда каждая точка этого участка поверхности будет обладать барицентрическими координатами
, ее текстурные координаты
и нормаль
могут быть вычислены как:
- По барицентрическим координатам легко определить, принадлежит ли точка
части пространства, ограниченной многогранником с вершинами
: это выполняется только в том случае, если
. Равенство i-й барицентрической координаты 1 означает, что точка
совпадает с
. Если несколько барицентричесих координат равны 0, то это означает, что точка принадлежит подпространству, натянутому на радиус-вектора остальных точек, соответствующие координаты которых больше 0.
Наверное, они очень сложно вычисляются?
Не сложнее, чем любое линейное преобразование системы координат. Потому что по сути вычисление барицентрических координат таковым преобразованием и является.
Перепишем радиус-вектора точек в следующем виде:

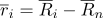
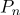
Тогда формулу (1) можно переписать в следующем виде:
Раскроем скобки в сумме:
Согласно свойства (2):
Соответственно:
,
где
Учитывая (2), ограничимся вычислением первых n барицентрических координат. Представим переход в барицентрические координаты как линейное преобразование:
,
где — вектор n барицентрических координат (кроме последней),
— матрица преобразования.
Учитывая свойства барицентрического представления, если в качестве подставить один из векторов
(
), то мы получим вектор с нулевыми компонентами, кроме одной i-й, которая будет равна 1.
Если матрицу умножить на матрицу
, составленную по столбцам из
, то мы должны получить единичную матрицу (матрицу с единицами на главной диагонали и нулями в остальных элементах):
,
где ,
— единичная матрица (
— символ Кронекера: 1, если
, иначе — 0).
Из (10) находим :
Таким образом, имея набор из точек с радиус-векторами 

Используя эту матрицу, мы можем получить первые барицентрических координат точки
с радиус-вектором
:
Вновь воспользовавшись соотношением (2), получим последнюю барицентрическую координату:
Заключение
Может с первого взгляда барицентрика и кажется неуклюжей и сложной. Но на самом деле, это очень удобный и незаменимый во многих задачах инструмент, к которому довольно быстро привыкаешь. Потому, что тут нет никакой магии, это линейная алгебра в чистом виде!
У этого термина существуют и другие значения, см. Координаты.
Барицентри́ческие координа́ты — скалярные параметры, набор которых однозначно задаёт точку аффинного пространства (при условии, что в данном пространстве выбран некоторый точечный базис).
Точечный базис (иногда используется[1] термин «базис барицентрических координат») в 




Определение[править | править код]
Пусть 


барицентричность стоящей в правой части линейной комбинации точек означает, что действительные числа 
Барицентрические координаты (λ1,λ2,λ3) на равностороннем треугольнике и на прямоугольном треугольнике
Числа 


Записанное выше равенство в символике барицентрического исчисления может быть переписано так:
Свойства[править | править код]
- её трилинейные координаты. Трилинейные координаты, как и барицентрические, определены с точностью до пропорциональности.
История[править | править код]
Барицентрические координаты введены Мёбиусом в 1827 г.[2]
Примечания[править | править код]
- ↑ Александров П. С., Пасынков В. А. Введение в теорию размерности. — М.: Наука, 1973. — 576 с. — C. 197.
- ↑ Боголюбов, 1983, с. 95—96.
Литература[править | править код]
- Балк М. Б., Болтянский В. Г. Геометрия масс. — М.: Наука, 1987. — 160 с. — (Библиотечка «Квант». Вып. 61).
- Кострикин А. И., Манин Ю. И. Линейная алгебра и геометрия. — М.: Наука, 1986. — 304 с.
- Боголюбов А. Н. Математики. Механики. Биографический справочник. — Киев: Наукова думка, 1983. — 639 с.
См. также[править | править код]
- Трилинейные координаты
- Аффинные преобразования
- Аффинное пространство
Барицентрические координаты треугольника в пространстве
Фролов В., Фролов А.
Ray-tracing.ru
Введем следующие обозначения: P – origin луча, v – его направление. v0,v1,v2 – вершины треугольника. z – точка пересечения. t – рассточние от точки вылета луча до точки пересечения луча и треугольника. u,v,t1 – барицентрические координаты. Барицентрические координаты представляют собой отношения площадей маленьких треугольников к болшому (рис. 1.).
X u := u/S, v := v/S, t1 := t1/S
Рисунок 1 – Пересечение луча и треугольника
Барицентрический тест (fast minimal storage ray triangle intersection)
Это самый известный тест на пересечение луч-треугольник. Имея 3 точки на плоскости, можно выразить любую другую точку через ее барицентричечкие координаты. Первое уравнение берется просто из определения барицентрических координат, выражая точку пересечения z. С другой стороны, эта же точка z лежит на прямой. Второе уроавнение таким образом, это просто параметрическое уравнение пямой. Приравняв правые части уравенний 1 и 2 получаем третье уравнение, которое по сути является системой 3 уравнений (p,v,v1,v2,v3 – векторы) с 3 неивестными (u,v,t).
Проведя алгебраические преобразования получми ответ в следующем виде:
Юнит тест (Woop’s unit test)
Основная идея данного алгоритма заключается в том, чтобы посчитать матрицу перобразования его в некий единичный треугольник (отсюда название) с вершинами (1,0,0); (0,1,0); (0,0,0); Во время подсчета пересечения луч преобразуется этой матрицей в пространство, где треугольник имеет единичное представление. После преобразования вычислить пересечение намного проще, так как нужно считать пересечение с заранее известным треугольником (1,0,0); (0,1,0); (0,0,0);. Пусть задан треугольник с вершинами A,B,C.
Рисунок 2 – Афинное преобразование треугольника в пространство, где он имеет единичное представление.
Рассмотрим преобразование T∆ -1 :
Если применить данное преобразование к треугольнику (1,0,0); (0,1,0); (0,0,0); то получим исходный треугольник.
Для того чтобы найти нужное нам преобразование необходимо дополнить матрицу T∆ -1 до 4×4 (добавить еще одну строчку (0,0,0,1)) и найти обратную матрицу. Это будет соответствовать обратному T∆ -1 преобразованию. После необходимо лишь умножить луч на полученную матрицу и посчитать пересечение с единичным треугольником.
float3 o = mul3x4(m, ray_origin);
float3 d = mul3x3(m, ray_direction);
float t = -o.z/d.z;
float u = o.x + t*d.x;
float v = o.y + t*d.y;
Функция mul3x4 выполняет умножение подматрицы 3×3 на трехмерный вектор и добавляет к результату последний столбец (3 его компоненты). Функция mul3x3 просто умножает подматрицу 3×3 на трехмерный вектор.
Немного об эффективности
Несмотря на то, что юнит тест делает немного меньше вычислений (в худшем случае), с алгоритмической точки зрения он менее эффекивен. Причина заключается в том, что в юнит-тесте сначала вычисляется координата t а потом уже u и v. Как правило, если в сцене много мелких треугольников, именно по кооринатам u и v можно быстро отбросить те треугольники, которые заведомо не пересекаются.
Основное достоинства юнит-теста заключается в том, что он позволяет экономить регистры графического процессора при реализации алгоритма на GPU. Причина по которой данный тест позволяет экономить регистры заключается в том, что можно умножать матрицу последовательно по строкам и не хранить ее всю на регистрах. Сначала нужно прочитать из памяти третью строчку матрицы, умножить ее (как скалярное произведение двух векторов) на луч и получить координату t. Если она лежит в требуемом интервале, можно прочитать первую и вторую строчки и получить координаты u и v соответственно.
ru.knowledgr.com
Читайте также: Аффинное пространство # Барицентрические координаты.
3-, с барицентрическими подразбиениями 1-граней (гранями) 2-граней (треугольниками) и 3-гранями (телом). В -метрии барицентрическая система координат – это система координат, в которой местоположение точки задается ссылкой на (треугольник для точек в плоскости, тетёдр для точек в трёхдёмном пространстве и т. д.). Барицентрические координаты точки можно интерпретировать как массы, размещённые в вершинах, так что точка является центром масс (или барицентром) этих масс. Эти массы могут быть нулевыми или отрицательными, все они положительны тогда и только тогда, когда точка находится внутри .
Каждая точка имеет барицентрические координаты, и их сумма не равна нулю. Две точки барицентрических координат задают одну и ту же точку тогда и только тогда, когда они пропорциональны; то есть, если одну точку можно получить, умножив элементы другой точки на одно и то же ненулевое число. Следовательно, барицентрические координаты либо считаются определяемыми вплоть до лицензии нонзеровой константой, либо нормализуются для суммирования к единице.
Барицентрические координаты были введены Августом Фьинандом Биусом в 1827 году. Они являются специальными гомогенными координатами. Барицентрические координаты тесно связаны с картезианскими координатами и, в более общем плане, с аффинными координатами (см.).
Барицентрические координаты особенно полезны в треугольнике для исследования свойств, которые не зависят от углов треугольника, таких как Ceva’s em. В компьютерном дизайне они полезны для определения некоторых видов насадок Bé er.
Определение
Пусть это точки в пространстве Евклидиана, плоское или аффинное пространство размерности, которые являются аффинно независимыми; это означает, что нет аффинного подпространства размерности, которое содержит все точки, или, эквивалентно, что точки определяют . Учитывая любую точку есть скаляры, которые не все равны нулю, такие, что
для любой точки. (Как обычно, обозначение представляет вектор трансляции или свободный вектор, который отображает точку в точку.)
Элементы сгустка, которые этом уравнении называются барицентрическими координатами относительно Использование двоеточий в обозначении сгустка означает, что барицентрические координаты являются своего рода гомогенными координатами, то есть точка не изменяется, если все координаты одной и той же нонцеро константой. Более того, барицентрические координаты также не изменяются, если изменяется вспомогательная точка, начало координат.
Барицентрические координаты точки уникальны вплоть до масштабирования. То есть две трубки и являются барицентрическими координатами одной и той же точки тогда и только тогда, когда есть нонцероскалар такой, что для каждого.
В некоторых контекстах полезно сделать уникальные барицентрические координаты точки. Это достигается путем навязывания условия
или эквивалентно путем каждого по сумме всех этих конкретных барицентрических координат называются нормализованными или абсолютными барицентрическими координатами. Иногда их называют также аффинными координатами, хотя этот термин обычно относится к несколько другому понятию.
Иногда это нормированные барицентрические координаты, которые называются барицентрическими координатами. В этом случае указанные выше координаты называются однородными барицентрическими координатами.
При приведенном выше обозначении гомогенные барицентрические координаты всех равны нулю, кроме единицы индекса. При работе над вещественными числами (приведённое выше определение также используется для аффинных пространств над арбит полем) точки, все нормализованные барицентрические координаты которых неотрицательны, образуют выпуклый корпус, которого имеет эти точки в качестве своих вершин.
С вышеприведенной нотацией, тапл такой, что
не определяет ни одну точку, но вектор
не зависит от начала координат. Так как направление этого вектора не изменяется, если все одним и тем же скаляром, то гомогенный клубок определяет направление прямых, то есть точку в бесконечности. Дополнительные сведения см. ниже.
Связь с картезианскими или аффинными координатами
Барицентрические координаты тесно связаны с картезианскими координатами и, в более общем плане, аффинными координатами. Для пространства размерности эти системы координат определяются относительно точки, начала координат которой равны нулю, и точек, координаты которых равны нулю, за исключением точки индекса, равного единице.
Точка имеет координаты
для такой системы координат, если и только если ее нормализованные барицентрические координаты
Основным преимуществом барицентрических систем координат является symm c по отношению к определяющим точкам. Поэтому они часто полезны для изучения свойств, которые являются symm c по отношению к точкам. С другой стороны, расстояния и углы трудно выразить в общих барицентрических координатных системах, и, когда они задействованы, обычно легче использовать картезианскую координационную систему.
Связь с проективными координатами
Гомогенные барицентрические координаты также сильно связаны с некоторыми проективными координатами. Однако эта взаимосвязь является более субтитровой, чем в случае аффинных координат, и, для четкого понимания, требует определения без координат проективной компи аффинного пространства и определения проективного кадра.
Проективная компи ́ кция аффинного пространства размерности – проективное пространство той же размерности, которое содержит аффинное пространство в качестве дополнения гиперплоскости. Проективный компан уникален вплоть до изоморфизма. Гиперплоскость называется гиперплоскостью в бесконечности, а её точки – точками в бесконечности аффинного пространства.
При наличии проективного пространства размерности проективный кадр представляет собой упорядоченное множество точек, не содержащихся в одной и той же гиперплоскости. Проективный кадр определяет систему проективных координат так, что координаты первой точки кадра равны, а в противном случае все координаты второй точки равны нулю, за исключением первой точки.
При отборе проективной компы из аффинной системы координат обычно определяют её относительно проективного кадра пересечений с гиперплоскостью при бесконечности координатных осей, начале аффинного пространства и точке, у которой все его аффинные координаты равны единице. Это предполагает, что точки бесконечности имеют свою последнюю координату, равную нулю, и что проективные координаты точки аффинного пространства получаются путем заполнения ее аффинных координат на единицу в качестве th-й координаты.
Когда есть точки в аффинном пространстве, которые определяют барицентрическую систему координат, это другой проективный кадр проективной компы, который удобно выбрать. Этот кадр состоит из этих точек и их центроид, то есть точка, которая имеет все его барицентрические координаты равны. В этом случае гомогенные барицентрические координаты точки в аффинном пространстве совпадают с проективными координатами этой точки. Точка находится в бесконечности тогда и только тогда, когда сумма ее координат равна нулю. Эта точка находится в направлении вектора, определенного в конце.
Барицентрические координаты на треугольниках
Барицентрические координаты на равностороннем треугольнике и на правом треугольнике. В контексте треугольника барицентрические координаты также известны как зональные координаты или зональные координаты, потому что координаты P по отношению к треугольнику эквивалентны (подписанным) соотношениям областей PBC, PCA и PAB по отношению к области эталонного треугольника.
Барицентрические или ареальные координаты чрезвычайно полезны в инженерных применениях, включающих триангулярные субдомены. Они делают аналитические integrals часто легче, и Gaussian ure таблицы часто представлены в терминах области координации.
Рассмотрим треугольник, определяемый тремя вершинами, и. Каждая точка, расположенная внутри этого треугольника, может быть записана как уникальная выпуклая комбинация трех вершин. Другими словами, для каждой существует уникальная последовательность из трех чисел, такая, что и
Три числа указывают на “барицентрические” или “области” координаты точки относительно треугольника. Они часто обозначаются как вместо. Обратите внимание, что хотя есть три координаты, есть только две степени свободы, так как. Таким образом, каждая точка однозначно определяется любыми двумя из барицентрических координат.
Для того чтобы объяснить, почему эти координаторы подписаны в отношении областей, давайте предположим, что мы работаем в пространстве Евклидиана. Здесь рассмотрим систему координат Картезиана и связанную с ней основу, а именно. Рассмотрим также положительно ориентированный треугольник, лежащий в плоскости. Известно, что для любого основания и любого свободного вектора
где означает смешанное произведение этих трех векторов.
Возьмите, где arbit point в плоскости, и заметьте, что
Подзаголовок в отношении нашего выбора свободных векторов: фактически является классом pollence вектора bound.
Мы получили, что
Учитывая положительную (контрклоивизную) ориентацию треугольника, знаменателем обоих и является именно двойник площади треугольника. Также,
и так числители и являются двойниками подписанных областей треугольников и соответственно.
Далее, мы посвящаем это
что означает, что числа, и являются барицентрическими координатами. Аналогично, третья барицентрическая координация читается как
Эта буквенная запись барицентрических координат происходит от того, что точка может быть интерпретирована как центр масс,, которые расположены в, и.
Переключение назад и вперед между барицентрическими координатами и другими координационными системами значительно облегчает решение некоторых проблем.
Преобразование между барицентрическими и картезианскими координатами
Учитывая точку в плоскости треугольника можно получить барицентрические координаты, а из картезианских координат или наоборот.
Мы можем написать картезианские координаты точки в терминах картезианских компонентов треугольников вершин, где и в терминах барицентрических координат как
То есть, координаты Картезиана любой точки – это среднее значение координат Картезиана вершин треугольника, причем координаты точки являются барицентрическими координатами, суммирующими к единице.
Чтобы найти преобразование, от картезианских координат к барицентрическим координатам, мы сначала подставляем в вышеуказанное, чтобы получить
Это линейное преобразование может быть записано более сукцино.
где – вектор первых двух барицентрических координат, – вектор картезианских координат и – матрица, заданная
Теперь матрикс является неразрывным, так как и являются линейными независимыми (если бы это не было так, то, и был бы коллинеарным и не образовал бы треугольник).
Таким образом, поиск барицентрических координат был сведен к поиску матрицы 2 × 2, что является легкой проблемой.
Откровенно, формулями для барицентрических координат точки в терминах её картезианских координат (x, y) и в терминах картезианских координат вершин треугольника являются:
Другой способ решить конверсию из картезианских в барицентрические координаты – переписать проблему в матричной форме так, чтобы
с и. Затем условие читается и барицентрические координаты могут быть решены как решение линейной системы
Преобразование между барицентрическими и трилинейными координатами
Точка с трилинейными координатами x: y: z имеет барицентрические координаты ax: by: cz где a, b, c – длины сторон треугольника.
Уравнения в барицентрических координатах
Три стороны a, b, c соответственно имеют уравнения
Используя ранее заданное преобразование между барицентрическими и трилинейными координатами, различные другие уравнения, приведенные в Trilear coordinates # Formulas, могут быть повторно преобразованы в терминах барицентрических координат.
Расстояние между точками
Вектор смещения двух нормализованных точек
Расстояние между и или длина вектора смещения равна
где a, b, c – длины треугольника. Из этого следует эквивалентность двух последних выражений, поскольку
Барицентрические координаты точки можно вычислить на основе расстояний di до трех вершин треугольника, решив уравнение
Приложения
Два решения для 8, 5 и 3 & thinsp; L воды с использованием барицентрического графика. Желтая область обозначает комбинации, доступные с s. Сплошные красные и пунктирные синие дорожки показывают испорченные переходы. Когда ex падает на точечный треугольник, измерено 4 & thinsp; L.
Местоположение установки по отношению к треугольнику
Хотя барицентрические координаты чаще всего используются для обработки точек внутри треугольника, они также могут быть использованы для описания точки вне треугольника. Если точка не находится внутри треугольника, то мы все еще можем использовать формул выше для вычисления барицентрических координат.
Если точка лежит во внутренней части треугольника, все барицентрические координаты лежат в открытой Если точка лежит на краю треугольника, но не в ex, одна из областей координат (связанная с противоположной ex) равна нулю, в то время как две другие лежат в открытой inter Если точка лежит на ex, то координата, связанная с этим ex, равна 1, а другие равны нулю. Наконец, если точка лежит вне треугольника, по крайней мере, одна координата отрицательна.
Точка лежит внутри треугольника тогда и только тогда.
лежит на ребре или углу треугольника, если и.
В противном случае лежит вне треугольника.
В частности, если точка лежит на противоположной стороне sideline от ex, противоположной sideline, то барицентрическая координата этой точки, соответствующая этому ex, отрицательна.
Интерполяция на триангулярной неструктурированной сетке
Поверхность (верхняя часть), полученная из линейной интерполяции по заданной триангулярной сетке (нижняя часть) в плоскости x, y. Поверхность аппроксимирует функцию z = f (x, y), учитывая только значения f на вертикали сетки. если известны величины, но значения внутри треугольника, определяемые неизвестны, они могут быть аппроксимированы с помощью линейной интерполяции. барицентрические координаты обеспечивают удобный способ вычисления этой интерполяции. если является точкой внутри треугольника с барицентрическими координатами. то
В общем, учитывая любую неструктурированную сетку или многоугольник меш, этот вид que может быть использован для аппроксимации значения во всех точках, пока значение функции известно во всех вершинах сетки. в этом случае, у нас есть много треугольников, каждый соответствует разной части пространства. Затем значение может быть интерполировано, как описано выше.
Эти методы имеют множество применений, таких как метод конечных элементов (КЭМ).
Интеграция по треугольнику или tet edron
Целое функции над областью треугольника может раздражать, чтобы вычислить в картезианской системы координат. Обычно нужно разделить треугольник на две половины, и большая беспорядочность последует. Вместо этого, часто легче сделать изменение переменных в любые две барицентрические координаты, например.
где – площадь треугольника. Этот результат следует из того, что ректанг в барицентрических координатах соответствует квадрилатеральу в картезианских координатах, а отношение площадей соответствующих форм в соответствующих координатных системах задаётся. Аналогично, для интеграции по tet edron, вместо того, чтобы разбить интеграл на две или три отдельные части, можно было бы перейти на 3D tet edral координаты под изменение переменных
где – объём tet edron.
Примеры специальных пунктов
Три вершины треугольника имеют барицентрические координаты
Центроид имеет барицентрику
Циркумцентр треугольника ХХ имеет барицентрические координаты
где – длины кромок треугольника соответственно.
Ортоцентр имеет барицентрические координаты
Инцентр имеет барицентрические координаты
Барицентрикой эксцентриков являются
Центр из девяти точек имеет барицентрические координаты
Барицентрические координации на tet edra
Барицентрические координаты могут быть легко расширены до трех дим. 3D представляет собой тетоэдр, многогранник, имеющий четыре триангулярные грани и четыре вертикали.
Это снова линейное преобразование, и мы можем расширить вышеописанную процедуру для треугольников, чтобы найти барицентрические координаты точки относительно tet edron:
где теперь является матрицей 3 × 3:
и с соответствующими картезианскими координатами: Опять-таки, задача нахождения барицентрических координат сводится к инверсии матрицы 3 × 3. 3D барицентрические координаты могут использоваться для решения, лежит ли точка внутри tet edral объема, и для интерполяции функции в tet edral mesh, аналогично 2D процедуре. Tet edral meshes часто используются в Barharity анализа, потому что try interponify элемент может использоваться.
Обобщенные барицентрические координаты
Барицентрические координаты, которые определяются относительно конечного множества точек вместо называются обобщёнными барицентрическими координатами. Для них уравнение
по-прежнему требуется удерживать, где находятся заданные точки. Если эти заданные точки не образуют, обобщённые барицентрические координаты точки не уникальны (вплоть до скалярной лицензии). Что касается, то точки с неотрицательными обобщенными координатами образуют выпуклый корпус.
Таким образом, определение формально не изменяется, но в то время как с n вершинами необходимо встроить в векторное пространство размерности, по меньшей мере, n-1, многогранник может быть встроен в векторное пространство меньшей размерности. Самым примером является четырехугольник в плоскости. Следовательно, даже нормализованные обобщенные барицентрические координаты (т.е. координаты, так что сумма коэффикентов равна 1) обычно не являются однозначно определенными anymore, в то время как это имеет место для нормализованных барицентрических координат относительно .
Более абстраметрические, обобщённые барицентрические координаты выражают выпуклый многогранник с n вершинами, не зависящими от размерности, как изображение стандарта -simp, имеющего n вершин – карта находится на: Карта является одной к одной тогда и только тогда, когда многогранник является, в этом случае карта является изоморфизмом; это соответствует точке, не имеющей уникальной обобщенной барицентрической координатой, кроме когда p.
Дуальные к обобщённым барицентрическим координатам являются слабыми переменными, которые измеряют по количеству маржин точки, линейном констра, и даёт встраивание в f-ортант, где f – число граней (dual к вершинам). Эта карта является одной к одной (вариабельности слабости однозначно определены), но не к (не все комбинации могут быть реализованы).
Это использование стандартного -simp и f-orthant в качестве стандартных объектов, которые отображают на многогранник или что многогранник отображает в должны быть с использованием стандартного векторного пространства в качестве стандартного объекта для векторных пространств, и стандартный аффинный гиперплан в качестве стандартного объекта для аффинных пространств, где в каждом случае выбирая линейный базис или аффинный базис обеспечивает изоморфизм, позволяя всем векторным пространствам быть продуманными пространствами и аффинными пространствами, а, а, а, а не каждый из них). Кроме того, n-ортант является стандартным объектом, который соответствует конусам.
Приложения
Обобщенные барицентрические координаты имеют применение в компьютерной графике и, более конкретно, в моделировании. Часто трёхдымная модель может быть аппроксимирована многогранником так, что обобщённые барицентрические координаты относительно этого многогранника имеют значение c. Таким образом, обработка модели может быть оформлена с использованием этих ловких координат. Барицентрические координаты также используются в геофизиках
Барицентрические координаты треугольника в пространстве
Барицентрические координаты. Пусть дан треугольник ABC. Тогда любую точку P в плоскости треугольника можно представить как центр некоторых масс a , b , g , помещенных в его вершины A, B, C. Тройка чисел ( a , b , g ) называется барицентрическими координатами точки P относительно треугольника. Барицентрические координаты точки определены с точностью до ненулевого множителя: все тройки (k a , k b , k g ) при любом задают одну и ту же точку P. Любые три числа с ненулевой суммой являются барицентрическими координатами некоторой точки. Иногда барицентрическими координатами называют ту из пропорциональных троек, у которой сумма чисел равна единице. Соответствие между такими тройками и точками плоскости взаимно-однозначно.
Если точка P лежит внутри треугольника ABC, то ее барицентрические координаты пропорциональны площадям треугольников PAB, PBC и PCA. Для точек вне треугольника это тоже верно, только нужно брать ориентированные площади.
Приведем барицентрические координаты некоторых замечательных точек треугольника.
[spoiler title=”источники:”]
http://ru.knowledgr.com/17369903/%D0%A1%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0%D0%9A%D0%BE%D0%BE%D1%80%D0%B4%D0%B8%D0%BD%D0%B0%D1%82Barycentric
http://school-collection.edu.ru/dlrstore-wrapper/8fda0b73-1c63-4efd-bb2e-99ed6381069d/Baricentricheskie_koordinaty.html
[/spoiler]
Рассмотрим метод барицентрических
координат на плоскости. Пусть в
пространстве
задан
треугольники
произвольная точка.
Координаты точкизапишем
как барицентрическую комбинацию
координат точек:
|
|
( 2 ) |
где
–
барицентрические координаты точкиотносительно
треугольника,
который называется базисным, или
координатным. Его вершины имеют следующие
барицентрические координаты:,
,
.
Точки, лежащие на отрезке,
имеют координаты
,
гдеи
,
.
Применяя
геометрический подход к понятию
барицентрических координат, выразим
их через площади некоторых треугольников.
Сначала рассмотрим случай, когда точка
лежит
внутри треугольника.
Здесь справедлива следующая теорема.
Теорема.Пусть точка(рис.
3) лежит внутри базисного треугольникаи
пусть–
площади треугольников,
,
,
.
Тогда барицентрические координаты
точкиравны
|
|
( 3 ) |
Для вычисления площадей этих треугольников
воспользуемся векторным представлением
их вершин. Выберем точку
за
начало радиус-векторов и обозначим
радиус-векторы точекчерез
.
Тогда
,
или
,
где
знак
обозначает
внешнее произведение векторов.
Внешнее
произведение двух векторов
и
выражается
формулой
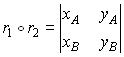
следовательно,
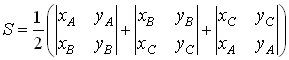
или
|
|
( 4 ) |
Вычисление барицентрических
координат точки можно свести к вычислению
площадей треугольников и в том случае,
если точка лежит вне координатного
треугольника или на его границе. Для
этого необходимо ввести понятие
ориентированного треугольника, когда
кроме задания его вершин также задается
направление их обхода. Если обход
производится “против часовой стрелки”,
то треугольник ориентирован положительно,
если “по часовой стрелке” –
отрицательно. В соответствии с этим
определяется ориентированная площадь
треугольника, которая будет при этом
положительной или отрицательной, а
также нулевой, если базисные точки
коллинеарные. Именно поэтому в правой
части уравнения ( 4 ) необходимо поставить
знак
.
Для корректности
уравнений ( 3 ) необходимо, чтобы площадь
,
т.е. точкидолжны
быть неколлинеарными.
Барицентрические
координаты на плоскости, как и на прямой,
обладают свойством аффинной
инвариантности.
Таким образом, любые
три неколлинеарные точки
определяют
на плоскости барицентрическую систему
координат.
Рис. 13.3. Определение
барицентрических координат через
площади треугольников
Мы используем
барицентрические координаты для
определения линейной интерполяции трех
неколлинеарных точек. Предположим, что
в пространстве
заданы
три точки.
Любая точка, координаты которой вычислены
с помощью уравнения
|
|
(5) |
лежит в плоскости, определяемой этими
точками. Это отображение пространствана
пространствобудет
линейной интерполяцией трех точек. Так
как,
томожно
считать барицентрическими координатами
точкиотносительно
заданных точек.
Также можно считатьбарицентрическими
координатами точки, принадлежащей,
относительно некоторого треугольника.
Следовательно, уравнение ( 5 ) можно
интерпретировать как отображение
треугольникана
треугольник.
Соседние файлы в предмете Компьютерная Графика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
A 3-simplex, with barycentric subdivisions of 1-faces (edges) 2-faces (triangles) and 3-faces (body).
In geometry, a barycentric coordinate system is a coordinate system in which the location of a point is specified by reference to a simplex (a triangle for points in a plane, a tetrahedron for points in three-dimensional space, etc.). The barycentric coordinates of a point can be interpreted as masses placed at the vertices of the simplex, such that the point is the center of mass (or barycenter) of these masses. These masses can be zero or negative; they are all positive if and only if the point is inside the simplex.
Every point has barycentric coordinates, and their sum is not zero. Two tuples of barycentric coordinates specify the same point if and only if they are proportional; that is to say, if one tuple can be obtained by multiplying the elements of the other tuple by the same non-zero number. Therefore, barycentric coordinates are either considered to be defined up to multiplication by a nonzero constant, or normalized for summing to unity.
Barycentric coordinates were introduced by August Möbius in 1827.[1][2][3] They are special homogenous coordinates. Barycentric coordinates are strongly related with Cartesian coordinates and, more generally, to affine coordinates (see Affine space § Relationship between barycentric and affine coordinates).
Barycentric coordinates are particularly useful in triangle geometry for studying properties that do not depend on the angles of the triangle, such as Ceva’s theorem, Routh’s theorem, and Menelaus’s theorem. In computer-aided design, they are useful for defining some kinds of Bézier surfaces.[4][5]
Definition[edit]
Let 



for any point O. (As usual, the notation 
The elements of a (n + 1) tuple 

The barycentric coordinates of a point are unique up to a scaling. That is, two tuples 



In some contexts, it is useful to constrain the barycentric coordinates of a point so that they are unique. This is usually achieved by imposing the condition
or equivalently by dividing every 

Sometimes, it is the normalized barycentric coordinates that are called barycentric coordinates. In this case the above defined coordinates are called homogeneous barycentric coordinates.
With above notation, the homogeneous barycentric coordinates of Ai are all zero, except the one of index i. When working over the real numbers (the above definition is also used for affine spaces over an arbitrary field), the points whose all normalized barycentric coordinates are nonnegative form the convex hull of 
With above notation, a tuple 
does not define any point, but the vector
is independent from the origin O. As the direction of this vector is not changed if all 

Relationship with Cartesian or affine coordinates[edit]
Barycentric coordinates are strongly related to Cartesian coordinates and, more generally, affine coordinates. For a space of dimension n, these coordinate systems are defined relative to a point O, the origin, whose coordinates are zero, and n points 
A point has coordinates
for such a coordinate system if and only if its normalized barycentric coordinates are
relatively to the points 
The main advantage of barycentric coordinate systems is to be symmetric with respect to the n + 1 defining points. They are therefore often useful for studying properties that are symmetric with respect to n + 1 points. On the other hand, distances and angles are difficult to express in general barycentric coordinate systems, and when they are involved, it is generally simpler to use a Cartesian coordinate system.
Relationship with projective coordinates[edit]
Homogeneous barycentric coordinates are also strongly related with some projective coordinates. However this relationship is more subtle than in the case of affine coordinates, and, for being clearly understood, requires a coordinate-free definition of the projective completion of an affine space, and a definition of a projective frame.
The projective completion of an affine space of dimension n is a projective space of the same dimension that contains the affine space as the complement of a hyperplane. The projective completion is unique up to an isomorphism. The hyperplane is called the hyperplane at infinity, and its points are the points at infinity of the affine space.[8]
Given a projective space of dimension n, a projective frame is an ordered set of n + 2 points that are not contained in the same hyperplane. A projective frame defines a projective coordinate system such that the coordinates of the (n + 2)th point of the frame are all equal, and, otherwise, all coordinates of the ith point are zero, except the ith one.[8]
When constructing the projective completion from an affine coordinate system, one defines commonly it with respect to a projective frame consisting of the intersections with the hyperplane at infinity of the coordinate axes, the origin of the affine space, and the point that has all its affine coordinates equal to one. This implies that the points at infinity have their last coordinate equal to zero, and that the projective coordinates of a point of the affine space are obtained by completing its affine coordinates by one as (n + 1)th coordinate.
When one has n + 1 points in an affine space that define a barycentric coordinate system, this is another projective frame of the projective completion that is convenient to choose. This frame consists of these points and their centroid, that is the point that has all its barycentric coordinates equal. In this case, the homogeneous barycentric coordinates of a point in the affine space are the same as the projective coordinates of this point. A point is at infinity if and only if the sum of its coordinates is zero. This point is in the direction of the vector defined at the end of § Definition.
Barycentric coordinates on triangles[edit]
Barycentric coordinates 
In the context of a triangle, barycentric coordinates are also known as area coordinates or areal coordinates, because the coordinates of P with respect to triangle ABC are equivalent to the (signed) ratios of the areas of PBC, PCA and PAB to the area of the reference triangle ABC. Areal and trilinear coordinates are used for similar purposes in geometry.
Barycentric or areal coordinates are extremely useful in engineering applications involving triangular subdomains. These make analytic integrals often easier to evaluate, and Gaussian quadrature tables are often presented in terms of area coordinates.
Consider a triangle 







The three numbers 




To explain why these coordinates are signed ratios of areas, let us assume that we work in the Euclidean space 







where 
Take 


A subtle point regarding our choice of free vectors: 

We have obtained that
Given the positive (counterclockwise) orientation of triangle 



and so the numerators of 



Further, we deduce that
which means that the numbers 



This 







Switching back and forth between the barycentric coordinates and other coordinate systems makes some problems much easier to solve.
Conversion between barycentric and Cartesian coordinates[edit]
Edge approach[edit]
Given a point 




We can write the Cartesian coordinates of the point 





That is, the Cartesian coordinates of any point are a weighted average of the Cartesian coordinates of the triangle’s vertices, with the weights being the point’s barycentric coordinates summing to unity.
To find the reverse transformation, from Cartesian coordinates to barycentric coordinates, we first substitute 
Rearranging, this is
This linear transformation may be written more succinctly as
where 


Now the matrix 





Finding the barycentric coordinates has thus been reduced to finding the 2×2 inverse matrix of 
Explicitly, the formulae for the barycentric coordinates of point 
Vertex approach[edit]
Another way to solve the conversion from Cartesian to barycentric coordinates is to write the relation in the matrix form
with 

To get the unique normalized solution we need to add the condition 
which is
where
is twice the signed area of the triangle. The area interpretation of the barycentric coordinates can be recovered by applying Cramer’s rule to this linear system.
Conversion between barycentric and trilinear coordinates[edit]
A point with trilinear coordinates x : y : z has barycentric coordinates ax : by : cz where a, b, c are the side lengths of the triangle. Conversely, a point with barycentrics 

Equations in barycentric coordinates[edit]
The three sides a, b, c respectively have equations[10]
The equation of a triangle’s Euler line is[10]
Using the previously given conversion between barycentric and trilinear coordinates, the various other equations given in Trilinear coordinates#Formulas can be rewritten in terms of barycentric coordinates.
Distance between points[edit]
The displacement vector of two normalized points 

The distance 



where a, b, c are the sidelengths of the triangle. The equivalence of the last two expressions follows from 

The barycentric coordinates of a point can be calculated based on distances di to the three triangle vertices by solving the equation
Applications[edit]
Two solutions to the 8, 5 and 3 L water pouring puzzle using a barycentric plot. The yellow area denotes combinations achievable with the jugs. The solid red and dashed blue paths show pourable transitions. When a vertex lands on the dotted triangle, 4 L has been measured.
Determining location with respect to a triangle[edit]
Although barycentric coordinates are most commonly used to handle points inside a triangle, they can also be used to describe a point outside the triangle. If the point is not inside the triangle, then we can still use the formulas above to compute the barycentric coordinates. However, since the point is outside the triangle, at least one of the coordinates will violate our original assumption that 
If a point lies in the interior of the triangle, all of the Barycentric coordinates lie in the open interval 


Summarizing,
- Point
lies inside the triangle if and only if
.
lies on the edge or corner of the triangle if
and
.
- Otherwise,
lies outside the triangle.
In particular, if a point lies on the far side of a line the barycentric coordinate of the point in the triangle that is not on the line will have a negative value.
Interpolation on a triangular unstructured grid[edit]
Surface (upper part) obtained from linear interpolation over a given triangular grid (lower part) in the x,y plane. The surface approximates a function z=f(x,y), given only the values of f on the grid’s vertices.
If 






In general, given any unstructured grid or polygon mesh, this kind of technique can be used to approximate the value of 






These methods have many applications, such as the finite element method (FEM).
Integration over a triangle or tetrahedron[edit]
The integral of a function over the domain of the triangle can be annoying to compute in a cartesian coordinate system. One generally has to split the triangle up into two halves, and great messiness follows. Instead, it is often easier to make a change of variables to any two barycentric coordinates, e.g. 
where 

where 
Examples of special points[edit]
In the homogeneous barycentric coordinate system defined with respect to a triangle 

The three vertices 


The centroid has coordinates 
If 














The circumcenter has coordinates[10][11][12][13]
The orthocenter has coordinates[10][11]
The incenter has coordinates 
The excenters have coordinates[14]
The nine-point center has coordinates[10][14]
The Gergonne point has coordinates 
The Nagel point has coordinates 
The symmedian point has coordinates 
Barycentric coordinates on tetrahedra[edit]
Barycentric coordinates may be easily extended to three dimensions. The 3D simplex is a tetrahedron, a polyhedron having four triangular faces and four vertices. Once again, the four barycentric coordinates are defined so that the first vertex 


This is again a linear transformation, and we may extend the above procedure for triangles to find the barycentric coordinates of a point 
where 
and 
Once again, the problem of finding the barycentric coordinates has been reduced to inverting a 3×3 matrix.
3D barycentric coordinates may be used to decide if a point lies inside a tetrahedral volume, and to interpolate a function within a tetrahedral mesh, in an analogous manner to the 2D procedure. Tetrahedral meshes are often used in finite element analysis because the use of barycentric coordinates can greatly simplify 3D interpolation.
Generalized barycentric coordinates[edit]
Barycentric coordinates 


is still required to hold.[15] Usually one uses normalized coordinates, 


is underdetermined. The simplest example is a quadrilateral in the plane. Various kinds of additional restrictions can be used to define unique barycentric coordinates.[16]
Abstraction[edit]
More abstractly, generalized barycentric coordinates express a convex polytope with n vertices, regardless of dimension, as the image of the standard 

Dual to generalized barycentric coordinates are slack variables, which measure by how much margin a point satisfies the linear constraints, and gives an embedding 
This use of the standard 


Applications[edit]
Barycentric coordinates are used for blending three colors over a triangular region evenly in computer graphics.
Generalized barycentric coordinates have applications in computer graphics and more specifically in geometric modelling.[17] Often, a three-dimensional model can be approximated by a polyhedron such that the generalized barycentric coordinates with respect to that polyhedron have a geometric meaning. In this way, the processing of the model can be simplified by using these meaningful coordinates. Barycentric coordinates are also used in geophysics.[18]
See also[edit]
- Ternary plot
- Convex combination
- Water pouring puzzle
- Homogeneous coordinates
References[edit]
- ^ Möbius, August Ferdinand (1827). Der barycentrische Calcul. Leipzig: J.A. Barth.
Reprinted in Baltzer, Richard, ed. (1885). “Der barycentrische Calcul”. August Ferdinand Möbius Gesammelte Werke. Vol. 1. Leipzig: S. Hirzel. pp. 1–388. - ^ Max Koecher, Aloys Krieg: Ebene Geometrie. Springer-Verlag, Berlin 2007, ISBN 978-3-540-49328-0, S. 76.
- ^ Hille, Einar. “Analytic Function Theory, Volume I”, Second edition, fifth printing. Chelsea Publishing Company, New York, 1982, ISBN 0-8284-0269-8, page 33, footnote 1
- ^ Josef Hoschek, Dieter Lasser: Grundlagen der geometrischen Datenverarbeitung. Teubner-Verlag, 1989, ISBN 3-519-02962-6, S. 243.
- ^ Gerald Farin: Curves and Surfaces for Computer Aided Geometric Design. Academic Press, 1990, ISBN 0-12-249051-7, S. 20.
- ^ Reventós Tarrida, Agustí. “Affine Maps, Euclidean Motions and Quadrics”. Springer, 2011, ISBN 978-0-85729-709-9, page 11
- ^ Deaux, Roland. “Introduction to The Geometry of Complex Numbers”. Dover Publications, Inc., Mineola, 2008, ISBN 978-0-486-46629-3, page 61
- ^ a b Berger, Marcel (1987), Geometry I, Berlin: Springer, ISBN 3-540-11658-3
- ^ Danby, J.M.A. “Fundamentals of Celestial Mechanics”, Second edition, revised & enlarged, fifth printing. Willmann-Bell, Inc., Richmond, 2003, ISBN 0-943396-20-4, page 26, problem 11
- ^ a b c d e f g h Scott, J. A. “Some examples of the use of areal coordinates in triangle geometry”, Mathematical Gazette 83, November 1999, 472–477.
- ^ a b c d e Schindler, Max; Chen, Evan (July 13, 2012). “Barycentric Coordinates in Olympiad Geometry” (PDF). Retrieved 14 January 2016.
- ^ Clark Kimberling’s Encyclopedia of Triangles “Encyclopedia of Triangle Centers”. Archived from the original on 2012-04-19. Retrieved 2012-06-02.
- ^ a b Wolfram page on barycentric coordinates
- ^ a b c Dasari Naga, Vijay Krishna, “On the Feuerbach triangle”,
Forum Geometricorum 17 (2017), 289–300: p. 289. http://forumgeom.fau.edu/FG2017volume17/FG201731.pdf - ^ Meyer, Mark; Barr, Alan; Lee, Haeyoung; Desbrun, Mathieu (6 April 2012). “Generalized Barycentric Coordinates on Irregular Polygons” (PDF). Journal of Graphics Tools. 7: 13–22. doi:10.1080/10867651.2002.10487551. S2CID 13370238.
- ^ Floater, Michael S. (2015). “Generalized barycentric coordinates and applications *” (PDF). Acta Numerica. 24: 161–214. doi:10.1017/S0962492914000129. ISSN 0962-4929. S2CID 62811364.
- ^ Floater, Michael S. (2003). “Mean value coordinates”. Computer Aided Geometric Design. 20 (1): 19–27. doi:10.1016/S0167-8396(03)00002-5.
- ^ ONUFRIEV, VG; DENISIK, SA; FERRONSKY, VI, BARICENTRIC MODELS IN ISOTOPE STUDIES OF NATURAL-WATERS. NUCLEAR GEOPHYSICS, 4, 111-117 (1990)
- Scott, J. A. Some examples of the use of areal coordinates in triangle geometry, Mathematical Gazette 83, November 1999, 472–477.
- Schindler, Max; Chen, Evan (July 13, 2012). Barycentric Coordinates in Olympiad Geometry (PDF). Retrieved 14 January 2016.
- Clark Kimberling’s Encyclopedia of Triangles Encyclopedia of Triangle Centers. Archived from the original on 2012-04-19. Retrieved 2012-06-02.
- Bradley, Christopher J. (2007). The Algebra of Geometry: Cartesian, Areal and Projective Co-ordinates. Bath: Highperception. ISBN 978-1-906338-00-8.
- Coxeter, H.S.M. (1969). Introduction to geometry (2nd ed.). John Wiley and Sons. pp. 216–221. ISBN 978-0-471-50458-0. Zbl 0181.48101.
- Barycentric Calculus In Euclidean And Hyperbolic Geometry: A Comparative Introduction, Abraham Ungar, World Scientific, 2010
- Hyperbolic Barycentric Coordinates, Abraham A. Ungar, The Australian Journal of Mathematical Analysis and Applications, Vol.6, No.1, Article 18, pp. 1–35, 2009
- Weisstein, Eric W. “Areal Coordinates”. MathWorld.
- Weisstein, Eric W. “Barycentric Coordinates”. MathWorld.
- Barycentric coordinates computation in homogeneous coordinates, Vaclav Skala, Computers and Graphics, Vol.32, No.1, pp. 120–127, 2008
External links[edit]
- Law of the lever
- The uses of homogeneous barycentric coordinates in plane euclidean geometry
- Barycentric Coordinates – a collection of scientific papers about (generalized) barycentric coordinates
- Barycentric coordinates: A Curious Application (solving the “three glasses” problem) at cut-the-knot
- Accurate point in triangle test
- Barycentric Coordinates in Olympiad Geometry by Evan Chen and Max Schindler
- Barycenter command and TriangleCurve command at Geogebra.


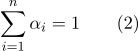
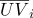 и нормали
и нормали  (
(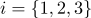 ), тогда каждая точка этого участка поверхности будет обладать барицентрическими координатами
), тогда каждая точка этого участка поверхности будет обладать барицентрическими координатами 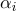 , ее текстурные координаты
, ее текстурные координаты 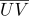 и нормаль
и нормаль 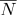 могут быть вычислены как:
могут быть вычислены как:
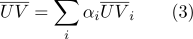
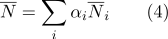
 . Равенство i-й барицентрической координаты 1 означает, что точка
. Равенство i-й барицентрической координаты 1 означает, что точка 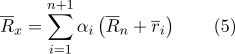

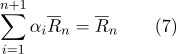




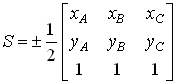 .
.









![{displaystyle mathbf {h} ={frac {1}{(mathbf {e} ,mathbf {f} ,mathbf {g} )}}cdot left[(mathbf {h} ,mathbf {f} ,mathbf {g} )mathbf {e} +(mathbf {e} ,mathbf {h} ,mathbf {g} )mathbf {f} +(mathbf {e} ,mathbf {f} ,mathbf {h} )mathbf {g} right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b1318f42d7c5bac15a253331f26a3a18a519e45)






















![{displaystyle d^{2}=left|PQright|^{2}=-a^{2}yz-b^{2}zx-c^{2}xy={frac {1}{2}}[x^{2}(b^{2}+c^{2}-a^{2})+y^{2}(c^{2}+a^{2}-b^{2})+z^{2}(a^{2}+b^{2}-c^{2})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc8615c8fe62884423e5e671a2b1a4cf5cd145ad)
















![{displaystyle =[a^{2}(b^{2}+c^{2})-(b^{2}-c^{2})^{2}]:[b^{2}(c^{2}+a^{2})-(c^{2}-a^{2})^{2}]:[c^{2}(a^{2}+b^{2})-(a^{2}-b^{2})^{2}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f089d53cef3483e79aa1e2c5214b4c1744867c70)






