Барометрическая формула — зависимость давления или плотности газа от высоты в поле силы тяжести в стационарных условиях.
Для идеального газа, имеющего постоянную температуру 

где 







где 

Барометрическая формула может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле (см. Статистика Максвелла — Больцмана). При этом должны выполняться три условия: стационарность, постоянство температуры газа с высотой и однородность силового поля. Аналогичные условия могут выполняться и для мельчайших твёрдых частичек, взвешенных в жидкости или газе. Основываясь на этом, французский физик Ж. Перрен в 1908 году применил барометрическую формулу к распределению по высоте частичек эмульсии, что позволило ему непосредственно определить значение постоянной Больцмана.
Барометрическая формула показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Величина 






Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.
Реальное распределение давления и плотности воздуха в земной атмосфере не следует барометрической формуле, так как в пределах атмосферы температура меняется с высотой и во времени; ускорение свободного падения меняются с высотой и географической широтой. Кроме того, атмосферное давление увеличивается с концентрацией в атмосфере паров воды.
Барометрическая формула лежит в основе барометрического нивелирования — метода определения разности высот 


(в м)
где 

См. также[править | править код]
- Барометрическая ступень
Литература[править | править код]
- Хргиан А. Х. Физика атмосферы. — Л.: Гидрометеоиздат. — 1969. — 645 с.
При
рассмотрении закона распределения
Максвелла предполагалось, что молекулы
равномерно распределяются по всему
объему сосуда, что справедливо, если
объем сосуда небольшой.
Для
больших объемов равномерность
распределения молекул по объему
нарушается из-за действия силы тяжести,
вследствие чего плотность, а
следовательно, и число молекул в единице
объема будут неодинаковым.
Рассмотрим
молекулы газа, находящегося в поле
тяготения Земли.
Выясним
зависимость давления атмосферы от
высоты над поверхностью Земли.
Допустим, на поверхности Земли (h
= 0) давление атмосферы P0.
На высоте h
оно равно P.
При увеличении высоты на dh
давление уменьшится на dP:
dP
= – ρgdh
(9.49)
[ρ
— плотность воздуха на данной высоте,
ρ
= mn0,
где m
— масса молекулы, n0
— концентрация молекул].
Используя
соотношение P
= n0kТ,
получаем
тогда
![]()
(9.50)
Полагая,
что на некоторой высоте h
Т = соnst,
g
= соnst,
разделяя переменные, интегрируем
выражение (9.50):
![]() ,
,
![]()
Получаем
![]()
(9.51)
—
барометрическая
формула.
Барометрическая
формула показывает зависимость давления
газа от высоты над поверхностью Земли.
Если
учесть, что концентрация молекул воздуха
в атмосфере определяет давление, то
формулу (9.51) можно записать в виде
![]() (9.52)
(9.52)
Из
формулы (9.52) следует, что с понижением
температуры число частиц на высоте,
отличной от нуля, убывает и при Т = 0К
обращается в нуль, т. е. при 0К все молекулы
расположились бы на земной поверхности.
Так
как потенциальная энергия молекул на
различной высоте различна и на высоте
h
определяется по формуле где ЕП
= mgh,
то [см.
![]()
(9.53)
— закон
Больцмана,
показывающий распределение участвующих
в тепловом движении молекул в
потенциальном поле сил, в частности в
поле силы тяжести.
Методика решения задач
В задачах
данного типа используют свойства
распределения Максвелла и Больцмана.
Пример
3.3. Определите
среднюю арифметическую скорость <υ˃
молекул идеального газа, плотность
которого при давлении 35 кПа составляет
0,3 кг/м3.
Дано:
Р=35кПа=35∙103
Па; ρ=0,3
кг/м3.
Найти:
<υ˃.
Решение:
Согласно
основному уравнению молекулярно-кинетической
теории идеальных газов,
![]() ,
,
(1)
где
n
– концентрация молекул; m0–
масса одной молекулы; <υкв˃.-
средняя квадратичная скорость молекул.
Учитывая,
что
![]() ,
,
а![]() ,
,
получаем
![]()
Так
как плотность газа
![]() ,
,
где
m
– масса газа; V
– его объём; N
– число молекул газа, уравнение (1) можно
записать в виде
![]()
или
![]() .
.
Подставляя это выражение в формулу (2),
находим искомую среднюю арифметическую
скорость:
![]()
Ответ:
<υ˃=545
м/с.
Пример
3.5. Найти относительное
число газа, скорость которого отличается
не более чем на δη = 1% значения средней
квадратичной скорости.
Дано:
δη = 1%.
Найти:
![]()
Решение В распределении
Максвелла
![]()
подставим
значение
![]() ;
;
δυ = υквδη.
Относительное
число молекул будет
![]()
Ответ:
![]()
Пример
3.6. При какой температуре
газа число молекул со скоростями в
заданном интервале υ, υ + dυ будет
максимальной? Масса каждой молекулы m.
Решение
Для
нахождения искомой температуры необходимо
исследовать функцию распределения
Максвелла на экстремум
![]() .
.
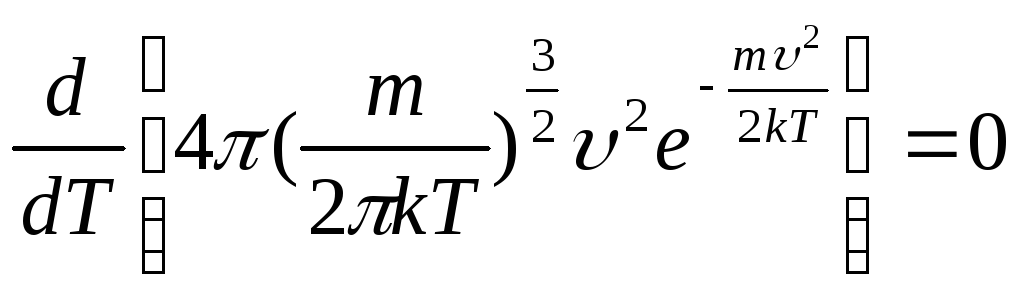
![]() .
.
Пример
3.7. Вычислить наиболее
вероятную, среднюю и среднюю квадратичную
скорости молекул идеального газа, у
которого при нормальном атмосферном
давлении плотность ρ = 1кг/м3.
Решение
Умножив числитель и знаменатель
в подкоренных выражениях (3.4) на число
Авогадро Nа,
получим следующие формулы для скоростей:
![]()
![]()
![]() .
.
Запишем уравнение Менделеева-Клапейрона,
введя в него плотность
ΡRT = MP
Определим отсюда величину
![]() и, подставив её в выражения, определяющие
и, подставив её в выражения, определяющие
скорость молекул, получим:
![]()
![]()
![]()
Пример
3.4. Идеальный газ с
молярной массой M находится в однородном
поле тяжести, ускорение свободного
падения в котором g. Найти давление газа
как функцию высоты h, если при h = 0 давление
Р = Р0,
а температура меняется с высотой как T
= T0(1
– α·h), где α – положительная постоянная.
Решение
При
увеличении высоты на бесконечно малую
величину давление получает приращение
dP = – ρgdh, где ρ – плотность газа. Знак
минус появился, так как с увеличением
высоты давление уменьшилось.
Поскольку рассматривается идеальный
газ, плотность ρ может быть найдена из
уравнения Mенделеева-Клапейрона:
![]()
Подставим значение плотности
ρ и температуры Т, получим разделяя
переменные:
![]()
Интегрируя это выражение, находим
зависимость давления газа от высоты h:
![]()
Так
как при h = 0 Р = Р0
получаем значение постоянной интегрирования
С = Р0.
Окончательно функция Р( h ) имеет вид
![]()
Необходимо отметить, что, так
как давление является величиной
положительной, полученная формула
справедлива для высот
![]() .
.
Пример.
Французский
физик Ж.Перрен, наблюдал под микроскопом
изменение концентрации взвешенных в
воде (ρ=1г/см3)
шариков гуммигута (ρ 1=1,25г/см3)
с изменением высоты, экспериментально
определил постоянную Авогадро. Определите
это значение, если температура взвеси
Т=298К, радиус шариков =0,21 мкм, а при
расстоянии между двумя слоями Δh=30мкм
число шариков гуммигута в одном слое в
два раза больше, чем в другом.
Дано:
ρ=1г/см3=1000кг/м3;
ρ=1,25 г/см3=1250кг/м3;
Т=280 К; r=0,21мкм=0,21∙10-6
м; Δh=30мкм=3∙10-5
м;
![]() .
.
Найти:
NA.
Решение.
Барометрическую
формулу
![]() ,
,
Используя
уравнение состояния P=nkT,
можно преобразовать для высот h1
и h2
к виду
![]() и
и
![]() ,
,
где
n0,
n1
и n2–
соответственно концентрация молекул
на высоте h0,
h1
и h2;
М – молярная масса; g-
ускорение свободного падения; R-
молярная газовая постоянная.
Тогда
 .
.
(1)
Прологарифмировав
выражение (1), получим
![]() (2)
(2)
Масса
частицы
![]() ;
;
m=ρV=ρ![]() πr3.
πr3.
Подставив эти формулы в (2) и учитывая
поправку на закон Архимеда, получим

Откуда
искомое выражение для постоянной
Авогадро

Ответ:
NA=6,02∙1023моль-1.
Пример.
Какова
температура Т азота, если средняя длина
свободного пробега <ℓ˃ молекул азота
при давлении Р=8кПа составляет 1мкм.
Эффективный диаметр молекул азота
d=0,38нм.
.
Дано:
<ℓ˃
=1мкм=1∙10-6
м;
Р=8кПа=8∙103
Па;
d=0,38нм=0,38∙10-9м;
Найти:
Т.
Решение.
Согласно
уравнению состояния идеального газа
P=nkT,
где
n
– концентрация молекул; k
– постоянная Больцмана.
Средняя
длина свободного пробега молекул газа
![]() ,
,
откуда
![]() .
.
Подставив эту формулу в выражение (1),
найдём искомую температуру азота
![]()
Ответ:
Т=372 К.
Пример.
При
температуре Т=280 К и некотором давлении
средняя длина <ℓ1˃
свободного
пробега молекул равна 0,1 мкм. Определите
среднее число <z2˃
столкновений
молекул в 1с, если давление в сосуде
уменьшить до 0,02 первоначального давления.
Температуру считать постоянной, а
эффективный диаметр молекулы кислорода
принять равным 0,36нм .
Дано:
Т=280 К; <ℓ1˃
=0,1мкм=0,1∙10-6
м;
М=32∙10-3
кг/моль;
![]() ;
;
d=0,36нм=0,36∙10-9м;
Найти:
<z2˃.
Решение.
Среднее число <z2˃
столкновений молекулы в 1с при конечном
давлении определяется отношением
средней скорости <υ˃.
молекулы к средней длине её свободного
пробега <ℓ2˃.
при том же давлении:
![]() ,
,
(1)
где
средняя скорость молекул определяется
по формуле
![]() (2)
(2)
где
R
– молярная газовая постоянная; М –
молярная масса вещества.
Из
формул
![]() иP=nkT
иP=nkT
следует, что средняя длина свободного
пробега молекул обратно пропорциональна
давлению:
![]() ,
,
откуда
![]() .
.
Подставив это выражение в формулу (1) и
учитывая (2), получаем искомое среднее
число столкновений молекул в 1с:

Ответ:
<z2˃
= 8,61∙107с-1.
Пример.
Можно
ли считать вакуум 100мкПа высоким, если
он создан в колбе радиусом r=15
см, содержащей азот при 0ºС. Эффективный
диаметр молекулы азота d=0,38нм.
.
Дано:
P=100мкПа=10-4Па;
r
=15см=0,15
м;
T=273
К;
d=0,38нм=0,38∙10-9м.
Найти:
![]()
Решение.
Вакуум
можно считать высоким, если средняя
длина свободного пробега молекул газа
гораздо больше линейных размеров сосуда,
т.е. должно выполняться условие
![]() ˃˃2r
˃˃2r
Средняя
длина свободного пробега молекул газа
![]()
(учли
P=nkT).
Вычисляя,
получаем
![]() =58,8
=58,8
м, т.е 58,8 м ˃˃0,3 м.
Ответ:
да, вакуум высокий.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
The barometric formula is a formula used to model how the pressure (or density) of the air changes with altitude.
Pressure equations[edit]
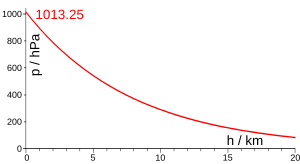
Pressure as a function of the height above the sea level
There are two equations for computing pressure as a function of height. The first equation is applicable to the standard model of the troposphere in which the temperature is assumed to vary with altitude at a lapse rate of 
The second equation is applicable to the standard model of the stratosphere in which the temperature is assumed not to vary with altitude:
where:
Or converted to imperial units:[1]
where:
The value of subscript b ranges from 0 to 6 in accordance with each of seven successive layers of the atmosphere shown in the table below. In these equations, g0, M and R* are each single-valued constants, while P, L, T, and h are multivalued constants in accordance with the table below. The values used for M, g0, and R* are in accordance with the U.S. Standard Atmosphere, 1976, and the value for R* in particular does not agree with standard values for this constant.[2] The reference value for Pb for b = 0 is the defined sea level value, P0 = 101 325 Pa or 29.92126 inHg. Values of Pb of b = 1 through b = 6 are obtained from the application of the appropriate member of the pair equations 1 and 2 for the case when h = hb+1.[2]
| Subscript b | Height above sea level | Static pressure | Standard temperature (K) |
Temperature lapse rate | Exponent g0 M / R L |
|||
|---|---|---|---|---|---|---|---|---|
| (m) | (ft) | (Pa) | (inHg) | (K/m) | (K/ft) | |||
| 0 | 0 | 0 | 101 325.00 | 29.92126 | 288.15 | 0.0065 | 0.0019812 | 5.2558 |
| 1 | 11 000 | 36,089 | 22 632.10 | 6.683245 | 216.65 | 0.0 | 0.0 | — |
| 2 | 20 000 | 65,617 | 5474.89 | 1.616734 | 216.65 | -0.001 | -0.0003048 | -34.1626 |
| 3 | 32 000 | 104,987 | 868.02 | 0.2563258 | 228.65 | -0.0028 | -0.00085344 | -12.2009 |
| 4 | 47 000 | 154,199 | 110.91 | 0.0327506 | 270.65 | 0.0 | 0.0 | — |
| 5 | 51 000 | 167,323 | 66.94 | 0.01976704 | 270.65 | 0.0028 | 0.00085344 | 12.2009 |
| 6 | 71 000 | 232,940 | 3.96 | 0.00116833 | 214.65 | 0.002 | 0.0006096 | 17.0813 |
Density equations[edit]
The expressions for calculating density are nearly identical to calculating pressure. The only difference is the exponent in Equation 1.
There are two equations for computing density as a function of height. The first equation is applicable to the standard model of the troposphere in which the temperature is assumed to vary with altitude at a lapse rate of 
Equation 1:
which is equivalent to the ratio of the relative pressure and temperature changes
Equation 2:
where
or, converted to U.S. gravitational foot-pound-second units (no longer used in U.K.):[1]
The value of subscript b ranges from 0 to 6 in accordance with each of seven successive layers of the atmosphere shown in the table below. The reference value for ρb for b = 0 is the defined sea level value, ρ0 = 1.2250 kg/m3 or 0.0023768908 slug/ft3. Values of ρb of b = 1 through b = 6 are obtained from the application of the appropriate member of the pair equations 1 and 2 for the case when h = hb+1.[2]
In these equations, g0, M and R* are each single-valued constants, while ρ, L, T and h are multi-valued constants in accordance with the table below. The values used for M, g0 and R* are in accordance with the U.S. Standard Atmosphere, 1976, and that the value for R* in particular does not agree with standard values for this constant.[2]
| Subscript b | Height Above Sea Level (h) | Mass Density ( ) )
|
Standard Temperature (T’) (K) |
Temperature Lapse Rate (L) | |||
|---|---|---|---|---|---|---|---|
| (m) | (ft) | (kg/m3) | (slug/ft3) | (K/m) | (K/ft) | ||
| 0 | 0 | 0 | 1.2250 | 2.3768908×10−3 | 288.15 | 0.0065 | 0.0019812 |
| 1 | 11 000 | 36,089.24 | 0.36391 | 7.0611703×10−4 | 216.65 | 0.0 | 0.0 |
| 2 | 20 000 | 65,616.79 | 0.08803 | 1.7081572×10−4 | 216.65 | -0.001 | -0.0003048 |
| 3 | 32 000 | 104,986.87 | 0.01322 | 2.5660735×10−5 | 228.65 | -0.0028 | -0.00085344 |
| 4 | 47 000 | 154,199.48 | 0.00143 | 2.7698702×10−6 | 270.65 | 0.0 | 0.0 |
| 5 | 51 000 | 167,322.83 | 0.00086 | 1.6717895×10−6 | 270.65 | 0.0028 | 0.00085344 |
| 6 | 71 000 | 232,939.63 | 0.000064 | 1.2458989×10−7 | 214.65 | 0.002 | 0.0006096 |
Derivation[edit]
The barometric formula can be derived using the ideal gas law:
Assuming that all pressure is hydrostatic:
and dividing the 

Integrating this expression from the surface to the altitude z we get:
Assuming linear temperature change 
Instead, assuming constant temperature, integrating gives the second barometric formula:
In this formulation, R* is the gas constant, and the term R*T/Mg gives the scale height (approximately equal to 8.4 km for the troposphere).
(For exact results, it should be remembered that atmospheres containing water do not behave as an ideal gas. See real gas or perfect gas or gas for further understanding.)
See also[edit]
- Hypsometric equation
- NRLMSISE-00
- Vertical pressure variation
References[edit]
- ^ a b Mechtly, E. A., 1973: The International System of Units, Physical Constants and Conversion Factors. NASA SP-7012, Second Revision, National Aeronautics and Space Administration, Washington, D.C.
- ^ a b c d U.S. Standard Atmosphere, 1976, U.S. Government Printing Office, Washington, D.C., 1976. (Linked file is 17 Mb)
Содержание:
Атмосферное давление и его измерение:
Нашу планету Земля окружает мощная газовая оболочка, которую называют атмосферой ( от греческих слов атмос – пар и сфера — шар).
Исследования околоземного пространства с помощью искусственных спутников Земли показали, что её атмосфера простирается на тысячу и более километров в высоту. Резкой границы она не имеет. Её верхние пласты очень разрежены и постепенно переходят в безвоздушное межпланетное пространство (вакуум). С уменьшением высоты плотность воздуха возрастает. Почти 80 % всей массы воздушной оболочки Земли сосредоточены в пределах 15 км над Землей. Опытами установлено, что при температуре 0 0С масса 1 м3 воздуха на уровне моря равна 1,29 кг. На воздушные слои действует сила тяжести, поэтому верхние слои давят на средние, а средние — на нижние. Наибольшее давление, обусловленное весом всей атмосферы, испытывает поверхность Земли, а также все находящиеся на ней тела.
Давление, оказываемое атмосферой на все находящиеся в ней тела, а также на земную поверхность, называют атмосферным давлением.
Выясним, насколько велико это давление.
Формула гидростатического давления 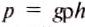
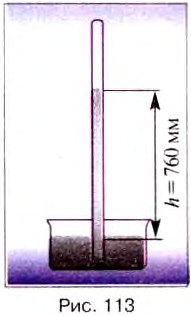
При этом высота столба ртути в трубке составляла приблизительно 760 мм.
Результаты этого опыта Торричелли объяснил так: «До сих пор существовала мысль, будто сила, которая не даёт возможности ртути, вопреки её естественному свойству, падать вниз, содержится внутри верхней части трубки, т. е. – или в пустоте, или в разрежённом веществе. Однако я утверждаю, что эта сила — внешняя и что сила берётся снаружи. На поверхность жидкости, находящейся в сосуде, действуют своей тяжестью 50 миль воздуха. Что же странного, если ртуть… поднимается настолько, чтобы уравновесить тяжесть внешнего воздуха».
Итак, атмосферное давление согласно закону Паскаля равно давлению столба ртути в трубке: ратм = р ртути
Если бы эти давления не были равны, то ртуть не находилась бы в равновесии: при увеличении давления ртути она выливалась бы из трубки в сосуд, а при уменьшении — поднималась бы по трубке вверх.
Итак, давление атмосферы можно измерить высотой соответствующего ртутного столба. Его высоту обычно измеряют в миллиметрах.
Если, например, говорят, что в некотором месте атмосферное давление равно 760 мм рт. ст., то это означает, что воздух в этом месте создаёт такое же давление, что и вертикальный столб ртути высотой 760 мм.
Чтобы определить это давление в паскалях, воспользуемся формулой гидростатичного давления: 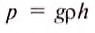 . Подставляя в эту формулу значения
. Подставляя в эту формулу значения
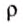 = 13 595,10
= 13 595,10 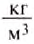 (плотность ртути при 0°С),
(плотность ртути при 0°С),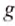 = 9,81
= 9,81 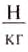 и
и 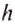 = 760 мм = 0,76 м (высота столба ртути), получим такое значение нормального атмосферного давления: р =101 325 Па.
= 760 мм = 0,76 м (высота столба ртути), получим такое значение нормального атмосферного давления: р =101 325 Па.
Давление атмосферы, которое равно давлению столба ртути высотой 760 мм при температуре О 0С, называют нормальным атмосферним давлением.
Единицами атмосферного давления являются 1 мм рт. ст., один паскаль (1 Па) и один гектопаскаль (1 гПа), между ними существуют такие соотношения:
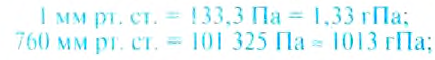
Об опытах Торричелли узнал французский учёный Блез Паскаль. Он повторил их с разными жидкостями (маслом, вином и водой). Столб воды, уравновешивающий давление атмосферы, оказался намного выше столба ртути.
Однако Паскаль считал, что для окончательного доказательства факта существования атмосферного давления нужен ещё один решающий опыт. Для этого он выполнил опыт Торричелли сначала у подножия горы, а потом — на её вершине. Результаты удивили всех присутствующих. Давление воздуха на вершине горы было почти на 100 мм рт. ст. меньше, чем у подножия. Этим было доказано, что ртуть в трубке в самом деле поддерживается атмосферным давлением.
Если измерить атмосферное давление на разных высотах, то получим такие результаты.

Наблюдая ежедневно за высотой ртутного столба в трубке, можно заметить, что она изменяется: то увеличивается, то уменьшается. Существованием атмосферного давления можно объяснить много явлений. На рисунке 114 изображена стеклянная трубка, внутри которой имеется поршень, плотно прилегающий к её стенкам. Конец трубки опущен в воду. Если поднимать поршень, то за ним будет подниматься и вода. Между поршнем и водой вследствие поднятия поршня образуется безвоздушное пространство, в котором нет давления атмосферы. В это пространство под давлением внешнего воздуха и входит за поршнем вода. Данное явление используют в работе шприца, водяного насоса.
Опыт 1. Возьмём цилиндрический сосуд, закрытый пробкой, через которую пропущена трубку с краном Выкачаем из неё воздух, закроем кран, трубку опустим в воду и откроем кран. Поскольку атмосферное давление больше давления в сосуде, то под его действием вода будет бить фонтаном внутри сосуда (рис. 115).
Опыт 2. Нальём в стакан воды и накроем его листом бумаги, немного большим диаметра стакана. Держа стакан за нижнюю часть, прижмём бумагу к краям стакана ладонью и перевернём его кверху дном, убрав затем руку от бумаги (рис. 116).
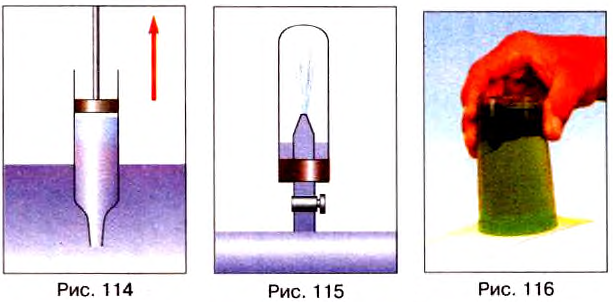
Удивительно, но вода будет удерживаться в стакане и листок останется на месте — почему? Дело в том, что давление атмосферы на бумагу больше, чем давление столба воды в стакане.
Наблюдение. Влияние атмосферного давления весьма заметно проявляется во время ходьбы по вязкой почве (засасывающее действие трясины). При подъёме ноги под ней образуется разрежённое пространство, и вследствие присасывания нога тянет за собой тяжёлую трясину (как поршень — жидкость в насосе).
Благодаря давлению атмосферного воздуха работают присоски для крепления предметов на гладких плоских поверхностях. Если вытеснить воздух под присоской, то она прижмётся силой давления атмосферы, и чтобы её оторвать, нужно приложить довольно большое усилие (рис. 117).
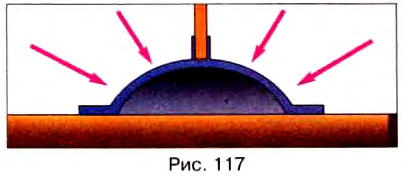
Результаты простых вычислений показывают, что сила давления атмосферы на поверхность обычной тетради равна 3000 Н. Почему же вы так легко можете поднять тетрадь? Дело в том, что силы давления воздуха зверху и снизу тетради уравновешиваются, и при подъёме вам приходится преодолевать лишь вес самой тетради.
Для измерения атмосферного давления используют ртутный барометр, барометр-анероид и барограф.
Если трубку, подобную той, что использовал в своём опыте Торричелли, снабдить шкалой, то получим простейший прибор для измерения атмосферного давления — ртутный барометр (от греческих слов барос – вес, тяжесть; метрео — измеряю) (рис. 118).
Барометр-анероид (от греческих слов: барос, метрео, анероид) изображён на рисунке 119. Основная часть прибора — круглые гофрированные металлические коробочки, соединённые между собой. Внутри коробок создано разряжение (давление в коробках ниже атмосферного). С увеличением атмосферного давления коробки сжимаются и тянут прикреплённую к ним пружину. Перемещение конца пружины через специальные устройства передаётся стрелке, а её указатель движется вдоль шкалы. Против штрихов шкалы нанесены значения атмосферного давления. Например, если стрелка останавливается напротив отметки 750, то это значит, что атмосферное давление равно 750 мм рт. ст. При уменьшении давления стенки коробочек расходятся, растяжение пружины уменьшается, и стрелка движется в сторону уменьшения значений давления.
Барометр-анероид — это один из основных приборов, который используют метеорологи для составления прогнозов погоды на ближайшие дни, так как её изменение зависит от изменения атмосферного давления.
Для автоматической и непрерывной записи изменений атмосферного давления используют барограф (от греческих слов барос; графо — пишу). Кроме металлических гофрированных коробочек в этом приборе есть механизм для движения бумажной ленты, на которой нанесены сетка значений давления и дни недели (рис. 120). По таким лентам можно выяснить, как изменялось атмосферное давление в течение любой недели.

Кстати:
Вывод о существовании атмосферного давления независимо от Э. Торричелли сделал немецкий физик Отто фон Герике (1602-1686). Откачивая воздух из тонкостенного металлического шара, от увидел, что шар сплющился. Анализируя причины сплющивания шара, он понял, что оно произошло под действием давления окружающей среды.
Открыв атмосферное давление. Герике построил перед фасадом своего дома в г. Магдебурге водяной барометр, в котором на поверхности жидкости плавала фигурка человека, указывающая на деления, нанесённые на стекле. • В 1654 г Герике, желая убедить всех в существовании атмосферного давления, выполнил знаменитый опыт с «магде-бургскими полушариями». На демонстрации опыта присутствовали члены Регенсбургского рейхстага и император Фердинанд III. В их присутствии из полости между двумя составленными вместе металлическими полушариями выкачали воздух. При этом силы атмосферного давления так крепко прижали эти полушария одно к другому, что их не смогли разъединить восемь пар лошадей (рис. 121).

В природе существует более 400 растений-барометров. Цветочный барометр можно найти и на огороде. Это маленькая ветвистая трава-мокрец. По её мелким белым цветкам можно предсказывать погоду в течение всего лета: если утром венчики не раскрываются – днем будет дождь.
- Заказать решение задач по физике
Атмосферное давление и опыт Торричелли
Атмосфера Земли — это смесь различных газов, удерживающихся возле планеты благодаря действию силы тяжести на их молекулы, которые одновременно и беспрерывно двигаются, создавая давление. Это давление называют атмосферным.
Доказать существование атмосферного давления можно при помощи простых опытов.
Какие последствия действия атмосферного давления
Если взять трубку с поршнем, опустить ее одним концом в сосуд с водой и поднимать поршень вверх, то вода будет подниматься вслед за поршнем (рис. 102). Это возможно только тогда, когда давление воды в сосуде будет больше, чем под поршнем. За счет весового давления вода не сможет подниматься, так как уровень воды под поршнем выше, чем в сосуде, а поэтому и его давление больше. Вода должна вылиться обратно в сосуд. Следовательно, на жидкость в сосуде действует дополнительное давление, значение которого больше давления жидкости столба воды под поршнем. Это давление создают молекулы атмосферного воздуха. Действуя на свободную поверхность воды, атмосферное давление согласно закону Паскаля передается во всех направлениях одинаково.
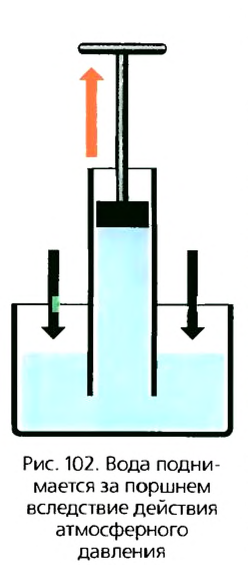
Так как под поршнем воздуха нет, то вода будет заходить в трубку под действием неуравновешенного давления.
Каково значение атмосферного давления
Значение атмосферного давления достаточно большое. Убедиться в этом можно на многих опытах.
Возьмем два полых полушария, имеющие хорошо отшлифованные поверхности сечений. В одной из них есть специальный штуцер с краном, через который можно откачивать воздух.
Подвесим к штативу одно из полушарий, присоединим к нему снизу другое и начнем откачивать насосом через кран воздух из полости. Нижнее полушарие крепко прижмется к верхнему. Это возможно только тогда, когда давление в полости шара будет меньше давления снаружи.
В результате действия воздушного насоса, который откачивает воздух, давление в полости полушарий уменьшится, а наружное давление останется без изменений. Поэтому нижнее полушарие плотно прижмется к верхнему. ЮЗ
О значении силы при некотором уменьшении давления в шаре можно судить по массе груза, который может удерживаться, если его подвесить к нижнему полушарию. Если же открыть кран и в полость шара зайдет воздух, то нижнее полушарие вместе с грузом отпадет.
Как начали исследовать атмосферное давление
Подобный опыт провел и описал в 1654 г. немецкий физик, бургомистр города Магдебург а Отто Герике.
 Отто Герике (1602-1686) – немецкий физик, который экспериментально изучал атмосферное давление. С помощью «магдебургских полушарий» он продемонстрировал действие атмосферного давления. Изучал также электрические явления, объяснил природу трения. Сконструировал первую электрическую машину.
Отто Герике (1602-1686) – немецкий физик, который экспериментально изучал атмосферное давление. С помощью «магдебургских полушарий» он продемонстрировал действие атмосферного давления. Изучал также электрические явления, объяснил природу трения. Сконструировал первую электрическую машину.
Это событие осталось в истории науки благодаря образной гравюре того времени (рис. 103).

В современном производстве используют множество приспособлений, основанных на действии атмосферного давления. Для расчетов результатов их работы нужно знать значение атмосферного давления.
Способ измерения атмосферного давления впервые предложил итальянский ученый Эванджелиста Торричелли.
 Эванджелиста Торричелли (1608-1647) – итальянский ученый. Первым измерил атмосферное давление с помощью сконструированного им ртутного барометра. Доказал, что высота ртутного столба барометра равна примерно
Эванджелиста Торричелли (1608-1647) – итальянский ученый. Первым измерил атмосферное давление с помощью сконструированного им ртутного барометра. Доказал, что высота ртутного столба барометра равна примерно 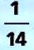 высоты водяного столба.
высоты водяного столба.
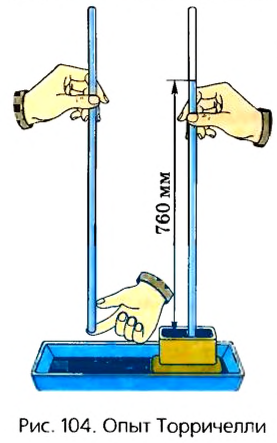
Он установил, что если закрытую с одной стороны трубку заполнить полностью ртутью, перевернуть ее и опустить в сосуд с ртутью, то выльется только часть этой ртути (рис. 104). Высота столба ртути в его опытах была примерно 760 мм. Результаты опыта дали возможность сделать вывод, что давление ртутного столба уравновешивается атмосферным давлением, которое действует на свободную поверхность ртути в сосуде. Атмосферное давление при таких условиях называют нормальным. С того времени в науку была введена единица измерения атмосферного давления – миллиметр ртутного столба (мм рт. ст.).
Как рассчитать атмосферное давление
Выразим значение давления столба ртути высотой 760 мм (нормальное) в системных единицах измерения давления паскалях. Из предыдущих параграфов известно, что давление жидкости рассчитывается по формуле:

Учитывая, что плотность ртути 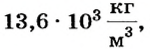 получаем
получаем
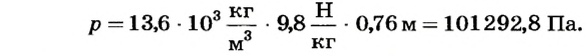
- Манометры в физике
- Барометры в физике
- Жидкостные насосы в физике
- Выталкивающая сила в физике
- Движение жидкостей и газов
- Гидравлические машины в физике
- Весовое давление жидкостей в физике
- Сообщающиеся ссуды в физике
Барометрическая формула — определяет зависимость давления или плотности газа от высоты в поле тяжести
![]()
Давайте теперь узнаем, откуда же получается барометрическая формула. Давление газа на некой высоте, определяется как :
![]()
Теперь возьмем колонну в атмосфере и выделим в ней тонкий слой воздуха высотой dh. Ясно, что такой слой вызывает изменение давления на величину dP :
![]()
Знак минус необходим для того, что с увеличением высоты давление уменьшается

Рассматривая атмосферный воздух как идеальный газ, можно воспользоваться уравнением Менделеева — Клапейрона
![]()
Из этого уравнения выражаем давление
![]()
А теперь можно и плотность газа
![]()
Подставляя найденную плотность газа в дифференциальное уравнение dP, мы получаем :
![]()
Сделав все преобразования. мы получаем зависимость давления P от высоты подъема h. Теперь необходимо проинтегрировать обе части нашего уравнения:
![]()
Проинтегрировав, у нас полечилась вот такое уравнение:
![]()
И теперь последний рывок, это взять логарифм. И у нас получится Барометрическое уравнение.
![]()
В Формуле мы использовали :
![]() — Давление газа (атмосферное)
— Давление газа (атмосферное)
![]() — Давление газа над уровнем моря
— Давление газа над уровнем моря
![]() — Высота над уровнем моря
— Высота над уровнем моря
![]() — Плотность газа
— Плотность газа
![]() — Ускорение свободного падения
— Ускорение свободного падения
![]() — Постоянная Больцмана
— Постоянная Больцмана
![]() — Температура
— Температура
![]() — Масса одной молекулы
— Масса одной молекулы
![]() — Универсальная газовая постоянная
— Универсальная газовая постоянная
![]() — Молярная масса
— Молярная масса
![]() — Количество вещества
— Количество вещества
![]() — Число Авогадро
— Число Авогадро
![p=p_{0}exp left[-Mg{frac {h-h_{0}}{RT}}right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8bec831485878b6b3b92292ab95b24a4c68afb5)
![n=n_{0}exp left[-mg{frac {h-h_{0}}{kT}}right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/f61c9d49615ec2d9f00afaaf0baaf617526e23be)
![{displaystyle P=P_{b}left[{frac {T_{b}-left(h-h_{b}right)L_{b}}{T_{b}}}right]^{tfrac {g_{0}M}{R^{*}L_{b}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9dde90a2d37bb5093e226abf9f7257b8eb0e30e)
![{displaystyle P=P_{b}exp left[{frac {-g_{0}Mleft(h-h_{b}right)}{R^{*}T_{b}}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a1d2266092d8012226a677d32455c75adf2f5d8)
![{displaystyle rho =rho _{b}left[{frac {T_{b}-(h-h_{b})L_{b}}{T_{b}}}right]^{left({frac {g_{0}M}{R^{*}L_{b}}}-1right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5d6a42b1448ee9b7f539d10a2f8593df1b769d5)

![{displaystyle rho =rho _{b}exp left[{frac {-g_{0}Mleft(h-h_{b}right)}{R^{*}T_{b}}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d5367beea036fb4f0423a2949a1d08f835fb7c)




![{displaystyle P=P_{0}cdot left[{frac {T}{T_{0}}}right]^{textstyle {frac {Mg}{R^{*}L}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18247095fe5ee08cbd5d33dee816eb6a288eb9c7)

