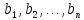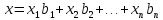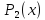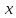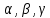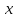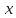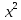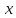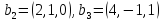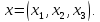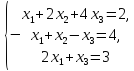Как найти базис линейного пространства многочленов - Сайт, где вы сможете решить свои вопросы

В
линейном
пространстве наибольший
интерес представляют системы
векторов, в
виде линейной
комбинации которых
можно представить любой вектор, причем
единственным образом. Если зафиксировать
такую систему векторов, то любой вектор
можно будет однозначно представить
набором чисел, являющихся коэффициентами
соответствующей
линейной
комбинации, а
всевозможные векторные соотношения
превратить в соотношения числовые.

Этот
подход применялся уже в аналитической
геометрии. В пространстве
векторов на плоскости любые два
неколлинеарных вектора образуют базис,
так как через такую пару векторов любой
вектор плоскости выражается однозначно
в виде линейной комбинации. Аналогично
в(множестве векторов в пространстве)
базис образуют любые три некомпланарных
вектора. Для матриц использовалось
понятие базисных строк и базисных
столбцов. По теореме о базисном миноре
базисные строки (столбцы) линейно
независимы, а любая строка (столбец)
матрицы является линейной комбинацией
базисных строк (столбцов).

Определение
1.3. Базисом
линейного пространства
называют
любую упорядоченную систему векторов,
для которой выполнены два условия:

1) эта
система
векторов линейно независима,

2) каждый
вектор в линейном пространстве может
быть представлен в виде линейной
комбинации векторов этой системы.

Пусть

—
базис в
.
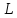
Определение 1.3 говорит о том, что любой
векторможет быть записан следующим образом:

Такую
запись называют разложением
вектора х
по
базису
.

Данное
нами определение базиса согласовывается
с понятием базиса в пространстве
свободных
векторов в
,
или
.
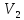
Например, вбазисом была названа любая тройка
некомпланарных векторов. Такая тройка
векторов является линейно независимой,
так как представление одного ее вектора
в виде линейной комбинации двух других
равносильна компланарности трех
векторов. Но, кроме того, из курса
векторной алгебры мы знаем, что любой
вектор в пространстве можно выразить
через произвольные три некомпланараных
вектора в виде
их
линейной
комбинации. Три компланарных вектора
не могут быть базисом в
,
так как любая линейная комбинация таких
векторов даст вектор, им компланарный.

Теорема
1.2 (о единственности разложения). В
линейном пространстве разложение любого
вектора по данному базису единственно.

Выберем
в линейном пространстве

произвольный
базис

и
предположим, что вектор х
имеет
в этом базисе два разложения

Воспользуемся
тем, что аксиомы
линейного пространства позволяют
преобразовывать линейные комбинации
так же, как и обычные алгебраические
выражения. Вычитая записанные равенства
почленно, получим

Так
как базис – это линейно независимая
система векторов, ее линейная комбинация
равна 0,
лишь,
если она тривиальная
(см.
определение 1.2). Значит, все коэффициенты
этой линейной комбинации равны нулю:
.
Таким образом,и
два разложения векторах
в
базисе
совпадают.

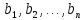
Замечание
1.3. Условие
линейной независимости векторов базиса
означает, что нулевой
вектор имеет
в этом базисе единственное разложение,
а именно тривиальное: все коэффициенты
этого разложения равны нулю. Из
доказательства теоремы 1.2 следует, что
из единственности разложения нулевого
вектора по данной системе векторов
вытекает единственность разложения
любого другого вектора.

Согласно
определению 1.3, базис является упорядоченной
системой векторов. Это значит, что,
изменив порядок векторов в системе, мы
получим другой базис. Порядок векторов
в базисе фиксируют для того, чтобы задать
определенный порядок коэффициентов
разложения произвольного вектора. Это
позволяет заменить линейную комбинацию,
представляющую вектор, упорядоченным
набором ее коэффициентов и тем самым
упростить запись. Порядок векторов в
базисе определяется их нумерацией.

Определение
1.4. Коэффициенты
разложения вектора по базису линейного
пространства, записанные в соответствии
с порядком векторов в базисе, называют
координатами
вектора в этом
базисе.

Пример
1.8. В
линейном пространстве

многочленов
переменного

степени
не выше 2 (см. пример 1.1) элементы

и
линейно
независимы: их линейная комбинация
есть многочлен, который равен нулю
(нулевому многочлену) лишь при.
В то же время пара этих элементов не
образует базиса. Действительно, многочлен
1 нулевой степени, являющийся элементом,
нельзя
представить в виде линейной комбинации
многочленов

и
.Дело
в том, что линейная комбинация

многочленов

и
есть
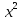
либо многочлен второй степени (при
),
либо многочлен первой степени(,
),
либо нулевой многочлен().
Значит, равенство

двух
многочленов невозможно ни при каких
значениях коэффициентов.

В
то же время три многочлена 1,

и
образуют
базис линейного пространства
.
Докажем это.

Во-первых,
система многочленов 1,

и
линейно
независима. Составим их линейную
комбинацию с произвольными коэффициентами

и
приравняем нулю:
.
Это равенство есть равенство двух
многочленов, и оно возможно только в
случае, когда коэффициенты этих двух
многочленов совпадают. Значит,.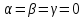

Во-вторых,
через многочлены 1,

и

можно
выразить любой многочлен второй степени,
т.е. любой элемент линейного пространства

можно
представить в виде линейной комбинации
указанных трех элементов.

Итак,
система трех многочленов 1,

и

линейно
независима, а любой элемент линейного
пространства

является
линейной комбинацией указанной системы.
Согласно определению 1.3, система
многочленов 1,

и

есть
базис в
.

Пример
1.10.
В
линейном
арифметическом пространстве
векторы

образуют
базис
,
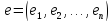
так как они линейно независимы (см.
пример 1.5) и любой векторпредставим
в виде

Такой
базис (1.5) в пространстве
называютстандартным.
Отметим,
что запись элементов арифметического
пространства в виде столбца не противоречит
определению арифметического пространства,
понимаемого как множество упорядоченных
совокупностей чисел. Порядок же элементов
можно указывать как при помощи записи
в строку, так и при помощи записи в
столбец.

Пример
1.11.
Покажем,
что в
система векторов

образует
базис и найдем в этом базисе координаты
вектора

Для
того чтобы доказать, что система векторов
,,

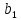
образует базис, надо убедиться в линейной
независимости этих векторов и в том,
что любой вектор
является их линейной комбинацией.

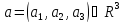
В
стандартном базисе е в
векторыимеют следующие столбцы координат:

Из
стобцов координат векторов
составим матрицу

и
рассмотрим квадратную систему линейных
алгебраических уравнений (СЛАУ)
,Так как,
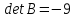
то матрицаневырожденная, ее ранг равен 3 и все ее
столбцы являются базисными. Поэтому,
во-первых, согласно теореме о базисном
миноре, эти столбцы линейно независимы,
значит, СЛАУ
при
любом столбце

правых
частей имеет решение

В
частности, решив СЛАУ
,
которая в координатной форме имеет вид

находим
координаты вектора
в базисе:

Соседние файлы в папке Геометрия

Источник

You can proceed as in the first answer, or you can try guessing and verifying.

An approach I like is to express the subspace as the null space of some operator. The form of the operator is often fairly clear from the question.

For the first, you are looking for a basis for the set of polynomials of degree 3 or less that satisfy the given condition. You know that $dim P^3 = 4$, and the condition expresses one scalar constraint, so intuitively we expect that the dimension of $W$ will be three.

If we define the linear operator $L:P^3 to mathbb{R}$ by $Lp = p(2)-p(-2)$, we see that $W = ker L$ and $dim {cal R}L = 1$ from which we confirm that $dim ker L = 4 -1 = 3$.

The even members (that is, the polynomials $x mapsto 1$, $x mapsto x^2$) of the basis you mentioned clearly lie in this space, so we need just one more element to form a basis. Try some combination $x mapsto x+ax^3$, for this to satisfy the condition we need $2+8a = -2 – 8a$ or $a=-{1 over 4}$. Hence the functions $x mapsto 1$, $x mapsto x^2$ and $x mapsto x – {1 over 4} x^3$ from a basis for $W$.

For the second, let $H:mathbb{P}^3 to mathbb{R}^2$ be defined by $H(p) = (p(-1), p(1))$. We see that $W = ker H$. Since $H(x mapsto (x-1)) = (-2,0)$ and $H(x mapsto (x+1)) = (0,2)$, we see that $dim {cal R}H = 2$, and so
$dim W = 4 – 2 = 2$. If a polynomial has roots $1,-1$, then we know that it must have a factor $x^2-1$, so we try that first to get $H(x mapsto x^2-1) = (0,0)$. Similarly we have $H(x mapsto x(x^2-1)) = (0,0)$, so the functions
$x mapsto x^2-1$, $x mapsto x^3-x$ form a basis.

Источник

Ранг системы векторов равен 3, поэтому размерность линейной оболочки также равна 3. Из последней матрицы также можно определить, что в качестве базиса линейной оболочки можно выбрать векторы , , .

Общий вид векторов линейной оболочки:

Из последней матрицы также следует, что дополнением этого базиса до базиса всего пространства является вектор .

2.12. Доказать, что многочлены вида образуют линейное подпространство в пространстве Р₂. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.

Решение:

Поскольку

то многочлены данного вида образуют линейную оболочку для системы многочленов и поэтому образуют линейное подпространство пространства Р₂.

Данные вектора, очевидно, линейно независимы и поэтому образуют базис своей линейной оболочки.

Количество векторов базиса подпространства равно 2, поэтому размерность подпространства L также равна 2, и сами вектора образуют в ней базис: . Очевидным дополнением этого базиса до базиса всего пространства является линейно независимый с ними вектор

2.13. Доказать, что многочлены вида образуют линейное подпространство в пространстве Р₃. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.

Решение:

Поскольку

то многочлены данного вида образуют линейную оболочку для системы многочленов и поэтому образуют линейное подпространство пространства Р₃.

Находим ранг данной системы: в каноническом базисе многочлены данной системы могут быть записаны как . Находим ранг этой системы векторов:

Ранг системы векторов равен 3, поэтому размерность подпространства L также равна 3, и сами вектора образуют в ней базис: . Из последней матрицы также следует, что очевидным дополнением этого базиса до базиса всего пространства является вектор

2.14. Пусть L – множество многочленов степени не выше 2, удовлетворяющих условию . Доказать, что L – линейное подпространство в пространстве Р₂. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.

Решение:

Множество многочленов степени не выше 2, удовлетворяющих условию , образует подпространство в Р₂, поскольку при умножении таких многочленов на любое число и сложении получается многочлен, для которого выполняется указанное свойство.

При этом если многочлен принадлежит этому подпространству, то

Пространство решений последнего уравнения имеет размсерность 2, поэтому размерность подпространства L также равна 2. Выбирая два базисных решения последнего уравнения, получаем базис подпространства L: . Очевидным дополнением этого базиса до базиса всего пространства является вектор

2.15. Пусть L – множество многочленов степени не выше 2, удовлетворяющих условию . Доказать, что L – линейное подпространство в пространстве Р₂. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.

Решение:

При этом если многочлен принадлежит этому подпространству, то

2.16. В пространстве Р₂ задана система многочленов , , . Найти размерность и базис линейной оболочки этой системы многочленов. Записать общий вид многочленов, принадлежащих линейной оболочке. Дополнить базис линейной оболочки до базиса пространства Р₂.

Решение:

В данную систему входят 3 вектора, что равно размерности пространства Р₂.

В каноническом базисе многочлены данной системы могут быть записаны как . Находим ранг этой системы векторов:

Ранг системы векторов равен 2, следовательно, размерность линейной оболочки данных векторов также равен 2. В качестве базиса линейной оболочки можно взять два первых вектора системы, т.е.

Общий вид многочленов принадлежащих линейной оболочке этих векторов: , Для дополнения базиса линейной оболочки до базиса пространства Р₂, как следует из последней матрицы определения ранга, можно выбрать вектор .

2.17. Образуют ли многогчлены , , , базис в пространстве Р₃?

Решение:

Данная система включает 4 многочлена, что равно размерности пространства Р₃, поэтому для того, чтобы доказать, что данная система образует базис в пространстве Р₃ многочленов степени не выше 3, достаточно доказать ее линейную независимость. В каноническом базисе многочлены данной системы могут быть записаны как . Определитель, составленный из координат этих векторов, равен

Следовательно, данная система векторов линейно независима, т.е. данная система многочленов образует базис в Р₃.

2.18. Доказать, что система многочленов образует базис в пространстве Р₂ многочленов степени не выше 2. Найти матрицу перехода от базиса S к каноническому базису и координаты многочлена в базисе S.

Решение:

Данная система включает 3 многочлена, что равно размерности пространства Р₂, поэтому для того, чтобы доказать, что данная система образует базис в пространстве Р₂ многочленов степени не выше 2, достаточно доказать ее линейную независимость. В каноническом базисе многочлены данной системы могут быть записаны как . Определитель, составленный из координат этих векторов, равен

Следовательно, данная система векторов линейно независима, т.е. данная система многочленов образует базис в Р₂.

Матрица перехода от канонического базиса к базису S имеет вид:

следовательно, матрица перехода от базиса S к каноническому базису имеет вид:

Многочлен в каноническом базисе имеет координаты (-3;4,-7) поэтому в базисе S он имеет координаты

т.е. , где

2.19. Установить, являются ли заданные множества подпространствами пространства Р_n. В случае положительного ответа найти базис и размерность подпространства.

1) Множество многочленов степени не выше n, у которых коэффициенты при нечетных степенях равны нулю.

2) Множество многочленов f(x) степени не выше n, таких, что f(x₀)=0 для некоторого .

3) Множество многочленов f(x) степени не выше n, таких, что f(x₀)=1 для некоторого .

Решение:

1) Множество многочленов степени не выше n, у которых коэффициенты при нечетных степенях равны нулю: при умножении таких многочленов на любое число и сложении получается многочлен, у которого коэффициенты при нечетных степенях равны нулю. Следовательно, множество таких многочленнов образует подпространство пространства Р_n. В качестве базиса такого подпространства можно выбрать систему многочленов (x, x³, …, x^k), где k – наибольшее нечетное число, не превосходящее n.

2) Множество многочленов f(x) степени не выше n, таких, что f(x₀)=0 для некоторого : при умножении таких многочленов на любое число и сложении получается многочлен, для которого также выполняется условие f(x₀)=0. Следовательно, множество таких многочленнов образует подпространство пространства Р_n. В качестве базиса такого подпространства можно выбрать систему многочленов (x–x₀, x(x–x₀), …, xⁿ^-1(x–x₀), т.к. если f(x₀)=0, то многочлен f(x) делится без остатка на x–x₀ и частным является многочлен степени n-1.

3) Множество многочленов f(x) степени не выше n, таких, что f(x₀)=1 для некоторого , не является подпространством пространства Р_n, поскольку, например, при умножении такого многочлена на 2 получается многочлен, для которого f(x₀)=2 и который поэтому не принадлежит данному множеству.

2.21. Доказать, что матрицы вида образуют линейное подпространство в пространстве матриц М₂₂. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.

Решение:

Линейность данного множества матриц следует из линейности операций умножения матриц на число и сложения матриц, например:

При этом каждая матрица данного подпространства может быть представлена в виде:

Отсюда следует, что размерность подпространства L равна 3 и вкачестве его базиса можно взять матрицы .

Для дополнения этого базиса до базиса всего пространства М₂₂ можно выбрать матрицу

Источник

Размерность и базис линейного пространства

Определения размерности и базиса

Линейное пространство называется n-мерным, если в нем существует система из линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число называется размерностью (числом измерений) линейного пространства и обозначается operatorname{dim}V . Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве найдется система, состоящая из линейно независимых векторов, то такое пространство называют бесконечномерным (записывают: operatorname{dim}V=infty ). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.

Базисом n-мерного линейного пространства называется упорядоченная совокупность линейно независимых векторов (базисных векторов).

Теорема 8.1 о разложении вектора по базису. Если $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n$ — базис n-мерного линейного пространства , то любой вектор mathbf{v}in V может быть представлен в виде линейной комбинации базисных векторов:

$mathbf{v}=mathbf{v}_1cdot mathbf{e}_1+mathbf{v}_2cdot mathbf{e}_2+ldots+mathbf{v}_ncdot mathbf{e}_n$

(8.4)

и притом единственным образом, т.е. коэффициенты $mathbf{v}_1, mathbf{v}_2,ldots, mathbf{v}_n$ определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.

Действительно, размерность пространства равна . Система векторов $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n$ линейно независима (это базис). После присоединения к базису любого вектора mathbf{v} , получаем линейно зависимую систему $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n, mathbf{v}$ (так как это система состоит из (n+1) векторов n-мерного пространства). По свойству 7 линейно зависимых и линейно независимых векторов получаем заключение теоремы.

Следствие 1. Если $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n$ — базис пространства , то $V=operatorname{Lin} (mathbf{e}_1,mathbf{e}_2, ldots,mathbf{e}_n)$ , т.е. линейное пространство является линейной оболочкой базисных векторов.

В самом деле, для доказательства равенства $V=operatorname{Lin} (mathbf{e}_1,mathbf{e}_2, ldots, mathbf{e}_n)$ двух множеств достаточно показать, что включения $Vsubset operatorname{Lin}(mathbf{e}_1,mathbf{e}_2, ldots,mathbf{e}_n)$ и $operatorname{Lin}(mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n)subset V$ выполняются одновременно. Действительно, с одной стороны, любая линейная комбинация векторов линейного пространства принадлежит самому линейному пространству, т.е. $operatorname{Lin}(mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n)subset V$ . С другой стороны, любой вектор пространства по теореме 8.1 можно представить в виде линейной комбинации базисных векторов, т.е. $Vsubset operatorname{Lin}(mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n)$ . Отсюда следует равенство рассматриваемых множеств.

Следствие 2. Если $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n$ — линейно независимая система векторов линейного пространства и любой вектор mathbf{v}in V может быть представлен в виде линейной комбинации (8.4): $mathbf{v}=v_1mathbf{e}_1+ v_2mathbf{e}_2+ldots+v_nmathbf{e}_n$ , то пространство имеет размерность , а система $mathbf{e}_1,mathbf{e}_2, ldots,mathbf{e}_n$ является его базисом.

В самом деле, в пространстве имеется система линейно независимых векторов, а любая система $mathbf{u}_1,mathbf{u}_2,ldots,mathbf{u}_n$ из большего количества векторов (k>n) линейно зависима, поскольку каждый вектор из этой системы линейно выражается через векторы $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n$ . Значит, operatorname{dim} V=n и $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n$ — базис .

Теорема 8.2 о дополнении системы векторов до базиса. Всякую линейно независимую систему векторов n-мерного линейного пространства (1leqslant k<n) можно дополнить до базиса пространства.

В самом деле, пусть $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_k$ — линейно независимая система векторов n-мерного пространства V~(1leqslant k<n) . Рассмотрим линейную оболочку этих векторов: $L_k=operatorname{Lin}(mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_k)$ . Любой вектор $mathbf{v}in L_k$ образует с векторами $mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_k$ линейно зависимую систему $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_k,mathbf{v}$ , так как вектор линейно выражается через остальные. Поскольку в n-мерном пространстве существует линейно независимых векторов, то L_kne V и существует вектор $mathbf{e}_{k+1}in V$ , который не принадлежит L_k . Дополняя этим вектором линейно независимую систему $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_k$ , получаем систему векторов $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_k,mathbf{e}_{k+1}$ , которая также линейно независимая. Действительно, если бы она оказалась линейно зависимой, то из пункта 1 замечаний 8.3 следовало, что $mathbf{e}_{k+1}in operatorname{Lin}(mathbf{e}_1, mathbf{e}_2, ldots,mathbf{e}_k)=L_k$ , а это противоречит условию $mathbf{e}_{k+1}notin L_k$ . Итак, система векторов $mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_k, mathbf{e}_{k+1}$ линейно независимая. Значит, первоначальную систему векторов удалось дополнить одним вектором без нарушения линейной независимости. Продолжаем аналогично. Рассмотрим линейную оболочку этих векторов: $L_{k+1}=operatorname{Lin} (mathbf{e}_1, mathbf{e}_2,ldots, mathbf{e}_k, mathbf{e}_{k+1})$ . Если $L_{k+1}=V$ , то $mathbf{e}_1,mathbf{e}_2, ldots,mathbf{e}_k, mathbf{e}_{k+1}$ — базис и теорема доказана. Если $L_{k+1}ne V$ , то дополняем систему $mathbf{e}_1,mathbf{e}_2, ldots,mathbf{e}_k,mathbf{e}_{k+1}$ вектором $mathbf{e}_{k+2}notin L_{k+1}$ и т.д. Процесс дополнения обязательно закончится, так как пространство конечномерное. В результате получим равенство $V=L_n=operatorname{Lin} (mathbf{e}_1,ldots,mathbf{e}_k,ldots,mathbf{e}_n)$ , из которого следует, что $mathbf{e}_1,ldots,mathbf{e}_k,ldots,mathbf{e}_n$ — базис пространства . Теорема доказана.

Замечания 8.4

1. Базис линейного пространства определяется неоднозначно. Например, если $mathbf{e}_1,mathbf{e}_2, ldots, mathbf{e}_n$ — базис пространства , то система векторов $lambda mathbf{e}_1,lambda mathbf{e}_2,ldots,lambda mathbf{e}_n$ при любом lambdane0 также является базисом . Количество базисных векторов в разных базисах одного и того же конечномерного пространства, разумеется, одно и то же, так как это количество равно размерности пространства.

2. В некоторых пространствах, часто встречающихся в приложениях, один из возможных базисов, наиболее удобный с практической точки зрения, называют стандартным.

3. Теорема 8.1 позволяет говорить, что базис — это полная система элементов линейного пространства, в том смысле, что любой вектор пространства линейно выражается через базисные векторы.

4. Если множество mathbb{L} является линейной оболочкой $operatorname{Lin}(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)$ , то векторы $mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k$ называют образующими множества . Следствие 1 теоремы 8.1 в силу равенства $V=operatorname{Lin} (mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n)$ позволяет говорить, что базис — это минимальная система образующих линейного пространства , так как нельзя уменьшить количество образующих (удалить хотя бы один вектор из набора $mathbf{e}_1, mathbf{e}_2,ldots,mathbf{e}_n$ ) без нарушения равенства $V=operatorname{Lin}( mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n)$ .

5. Теорема 8.2 позволяет говорить, что базис — это максимальная линейно независимая система векторов линейного пространства, так как базис — это линейно независимая система векторов, и ее нельзя дополнить каким-либо вектором без потери линейной независимости.

6. Следствие 2 теоремы 8.1 удобно применять для нахождения базиса и размерности линейного пространства. В некоторых учебниках оно берется за определение базиса, а именно: линейно независимая система $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n$ векторов линейного пространства называется базисом, если любой вектор пространства линейно выражается через векторы $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n$ . Количество базисных векторов определяет размерность пространства. Разумеется, что эти определения эквивалентны приведенным выше.

Примеры базисов линейных пространств

Укажем размерность и базис для примеров линейных пространств, рассмотренных выше.

1. Нулевое линейное пространство {mathbf{o}} не содержит линейно независимых векторов. Поэтому размерность этого пространства полагают равной нулю: dim{mathbf{o}}=0 . Это пространство не имеет базиса.

2. Пространства V_1,,V_2,,V_3 имеют размерности 1, 2, 3 соответственно. Действительно, любой ненулевой вектор пространства V_1 , образует линейно независимую систему (см. пункт 1. замечаний 8.2), а любые два ненулевых век тора пространства V_1 коллинеарны, т.е. линейно зависимы (см. пример 8.1). Следовательно, $dim{V_1}=1$ , а базисом пространства V_1 является любой ненулевой вектор. Аналогично доказывается, что $dim{V_2}=2$ и $dim{V_3}=3$ . Базисом пространства V_2 служат любые два неколлинеарных вектора, взятые в определенном порядке (один из них считается первым базисным вектором, другой — вторым). Базисом пространства V_3 являются любые три некомпланарных (не лежащих в одной или параллельных плоскостях) вектора, взятые в определенном порядке. Стандартным базисом в V_1 является единичный вектор vec{i} на прямой. Стандартным базисом в V_2 считается базис vec{i},,vec{j} , со стоящий из двух взаимно перпендикулярных единичных векторов плоскости. Стандартным базисом в пространстве V_3 считается базис vec{i},,vec{j},,vec{k} , составленный из трех единичных попарно перпендикулярных векторов, образующих правую тройку.

3. Пространство $mathbb{R}^n$ содержит не более, чем , линейно независимых векторов. В самом деле, возьмем столбцов из $mathbb{R}^n$ и составим из них матрицу размеров ntimes k . Если k>n , то столбцы линейно зависимы по теореме 3.4 о ранге матрицы. Следовательно, $dim{mathbb{R}^n}leqslant n$ . В пространстве $mathbb{R}^n$ не трудно найти п линейно независимых столбцов. Например, столбцы единичной матрицы

$mathbf{e}_1=begin{pmatrix}1\0\vdots\0end{pmatrix}!,quad mathbf{e}_2= begin{pmatrix}0\1\vdots\0end{pmatrix}!,quad ldots,quad mathbf{e}_n= begin{pmatrix} 0\0\vdots\1 end{pmatrix}!.$

линейно независимы. Следовательно, $dim{mathbb{R}^n}=n$ . Пространство $mathbb{R}^n$ называется n-мерным вещественным арифметическим пространством. Указанный набор векторов считается стандартным базисом пространства $mathbb{R}^n$ . Аналогично доказывается, что $dim{mathbb{C}^n}=n$ , поэтому пространство $mathbb{C}^n$ называют n-мерным комплексным арифметическим пространством.

4. Напомним, что любое решение однородной системы Ax=o можно представить в виде $x=C_1varphi_1+C_2varphi_2+ldots+C_{n-r}varphi_{n-r}$ , где r=operatorname{rg}A , a $varphi_1,varphi_2,ldots,varphi_{n-r}$ — фундаментальная система решений. Следовательно, ${Ax=o}=operatorname{Lin} (varphi_1,varphi_2,ldots,varphi_{n-r})$ , т.е. базисом пространства {Ax=0} решений однородной системы служит ее фундаментальная система решений, а размерность пространства dim{Ax=o}=n-r , где — количество неизвестных, а — ранг матрицы системы.

5. В пространстве $M_{2times3}$ матриц размеров 2times3 можно выбрать 6 матриц:

$begin{gathered}mathbf{e}_1= begin{pmatrix}1&0&0\0&0&0end{pmatrix}!,quad mathbf{e}_2= begin{pmatrix}0&1&0\0&0&0end{pmatrix}!,quad mathbf{e}_3= begin{pmatrix} 0&0&1\0&0&0end{pmatrix}!,hfill\[5pt] mathbf{e}_4= begin{pmatrix} 0&0&0\1&0&0 end{pmatrix}!,quad mathbf{e}_5= begin{pmatrix}0&0&0\0&1&0end{pmatrix}!,quad mathbf{e}_6= begin{pmatrix}0&0&0\0&0&1end{pmatrix}!,hfill end{gathered}$

которые линейно независимы. Действительно, их линейная комбинация

$alpha_1cdot mathbf{e}_1+alpha_2cdot mathbf{e}_2+alpha_3cdot mathbf{e}_3+ alpha_4cdot mathbf{e}_4+alpha_5cdot mathbf{e}_5+alpha_6cdot mathbf{e}_6= begin{pmatrix}alpha_1&alpha_2&alpha_3\ alpha_4&alpha_5&alpha_6end{pmatrix}$

(8.5)

равна нулевой матрице только в тривиальном случае alpha_1=alpha_2= ldots= alpha_6=0 . Прочитав равенство (8.5) справа налево, заключаем, что любая матрица из $M_{2times3}$ линейным образом выражается через выбранные 6 матриц, т.е. $M_{2times}= operatorname{Lin} (mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_6)$ . Следовательно, $dim{M_{2times3}}=2cdot3=6$ , а матрицы $mathbf{e}_1, mathbf{e}_2,ldots,mathbf{e}_6$ являются базисом (стандартным) этого пространства. Аналогично доказывается, что $dim{M_{mtimes n}}=mcdot n$ .

6. Для любого натурального в пространстве P(mathbb{C}) многочленов с комплексными коэффициентами можно найти п линейно независимых элементов. Например, многочлены $mathbf{e}_1=1,$ $mathbf{e}_2=z,$ $mathbf{e}_3=z^2,,ldots,$ $mathbf{e}_n=z^{n-1}$ линейно независимы, так как их линейная комбинация

$a_1cdot mathbf{e}_1+a_2cdot mathbf{e}_2+ldots+a_ncdot mathbf{e}_n= a_1+a_2z+ldots+a_nz^{n-1}$

равна нулевому многочлену (o(z)equiv0) только в тривиальном случае a_1=a_2=ldots=a_n=0 . Поскольку эта система многочленов линейно независима при любом натуральном л, пространство P(mathbb{C}) бесконечномерное. Аналогично делаем вывод о бесконечной размерности пространства P(mathbb{R}) многочленов с действительными коэффициентами. Пространство $P_n(mathbb{R})$ многочленов степени не выше, чем , конечномерное. Действительно, векторы $mathbf{e}_1=1,$ $mathbf{e}_2=x,$ $mathbf{e}_3=x^2,,ldots,$ $mathbf{e}_{n+1}=x^n$ образуют базис (стандартный) это го пространства, так как они линейно независимы и любой многочлен из $P_n(mathbb{R})$ можно представить в виде линейной комбинации этих векторов:

$a_nx^n+ldots+a_1x+a_0=a_0cdot mathbf{e}_1+a_1 mathbf{e}_2+ldots+a_ncdot mathbf{e}_{n+1}$ . Следовательно, $dim{P_n(mathbb{R})}=n+1$ .

7. Пространство C(mathbb{R}) непрерывных функций является бесконечно мерным. Действительно, для любого натурального многочлены $1,x,x^2,ldots, x^{n-1}$ , рассматриваемые как непрерывные функции, образуют линейно независимые системы (см. предыдущий пример).

В пространстве $T_{omega}(mathbb{R})$ тригонометрических двучленов (частоты omegane0 ) с действительными коэффициентами базис образуют одночлены $mathbf{e}_1(t)=sinomega t,~mathbf{e}_2(t)=cosomega t$ . Они линейно независимы, так как тождественное равенство asinomega t+bcosomega tequiv0 возможно только в тривиальном случае (a=b=0) . Любая функция вида f(t)=asinomega t+bcosomega t линейно выражается через базисные: $f(t)=a,mathbf{e}_1(t)+b,mathbf{e}_2(t)$ .

8. Пространство $mathbb{R}^X$ действительных функций, определенных на множестве , в зависимости от области определения может быть конечномерным или бесконечномерным. Если — конечное множество, то пространство $mathbb{R}^X$ конечномерное (например, X={1,2,ldots,n} ). Если — бесконечное множество, то пространство $mathbb{R}^X$ бесконечномерное (например, пространство $mathbb{R}^N$ последовательностей).

9. В пространстве $mathbb{R}^{+}$ любое положительное число $mathbf{e}_1$ , не равное единице, может служить базисом. Возьмем, например, число $mathbf{e}_1=2$ . Любое положительное число можно выразить через $mathbf{e}_1$ , т.е. представить в виде $alpha_1cdot mathbf{e}_1colon~ r=2^{log_2r}=log_2rast2=alpha_1ast mathbf{e}_1$ , где alpha_1=log_2r . Следовательно, размерность этого пространства равна 1, а число $mathbf{e}_1=2$ является базисом.

10. Пусть $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n$ — базис вещественного линейного пространства . Определим на линейные скалярные функции $mathcal{E}_1, mathcal{E}_2,ldots, mathcal{E}_n$ , положив:

$mathcal{E}_i(mathbf{e}_j)=begin{cases}1,&i=j,\ 0,&ine j.end{cases}$

При этом, в силу линейности функции $mathcal{E}_i$ , для произвольного вектора $mathbf{v}=v_1 mathbf{e}_1+v_2 mathbf{e}_2+ldots+v_n mathbf{e}_n$ получаем $mathcal{E}(mathbf{v})=sum_{j=1}^{n}v_j mathcal{E}(mathbf{e}_j)=v_i$ .

Итак, определены элементов (ковекторов) $mathcal{E}_1, mathcal{E}_2, ldots, mathcal{E}_n$ сопряженного пространства $V^{ast}$ . Докажем, что $mathcal{E}_1, mathcal{E}_2,ldots, mathcal{E}_n$ — базис $V^{ast}$ .

Во-первых, покажем, что система $mathcal{E}_1, mathcal{E}_2,ldots, mathcal{E}_n$ линейно независима. В самом деле, возьмем линейную комбинацию этих ковекторов $(alpha_1 mathcal{E}_1+ldots+alpha_nmathcal{E}_n)(mathbf{v})=$ и приравняем ее нулевой функции

$mathbf{o}(mathbf{v})~~ (mathbf{o}(mathbf{v})=0~ forall mathbf{v}in V)colon~ alpha_1mathcal{E}_1(mathbf{v})+ldots+alpha_nmathcal{E}_n(mathbf{v})= mathbf{o}(mathbf{v})=0~~forall mathbf{v}in V.$

Подставляя в это равенство $mathbf{v}=mathbf{e}_i,~ i=1,ldots,n$ , получаем alpha_1=alpha_2cdot= alpha_n=0 . Следовательно, система элементов $mathcal{E}_1,mathcal{E}_2,ldots,mathcal{E}_n$ пространства $V^{ast}$ линейно независима, так как равенство $alpha_1mathcal{E}_1+ldots+ alpha_nmathcal{E}_n =mathbf{o}$ возможно только в тривиальном случае.

Во-вторых, докажем, что любую линейную функцию $fin V^{ast}$ можно представить в виде линейной комбинации ковекторов $mathcal{E}_1, mathcal{E}_2,ldots, mathcal{E}_n$ . Действительно, для любого вектора $mathbf{v}=v_1 mathbf{e}_1+v_2 mathbf{e}_2+ldots+v_n mathbf{e}_n$ в силу линейности функции получаем:

$begin{aligned}f(mathbf{v})&= f(v_1 mathbf{e}_1+ldots+v_n mathbf{e}_n)= v_1 f(mathbf{e}_1)+ldots+v_n f(mathbf{e}_n)= f(mathbf{e}_1)mathcal{E}_1(mathbf{v})+ ldots+ f(mathbf{e}_n)mathcal{E}_n(mathbf{v})=\[2pt] &=(f(mathbf{e}_1)mathcal{E}_1+ldots+ f(mathbf{e}_n)mathcal{E}_n)(mathbf{v})= (beta_1mathcal{E}_1+ ldots+beta_nmathcal{E}_n) (mathbf{v}),end{aligned}$

т.е. функция представлена в виде линейной комбинации $f=beta_1 mathcal{E}_1+ldots+beta_nmathcal{E}_n$ функций $mathcal{E}_1,mathcal{E}_2,ldots, mathcal{E}_n$ (числа $beta_i=f(mathbf{e}_i)$ — коэффициенты линейной комбинации). Следовательно, система ковекторов $mathcal{E}_1, mathcal{E}_2,ldots, mathcal{E}_n$ является базисом сопряженного пространства $V^{ast}$ и $dim{V^{ast}}=dim{V}$ (для конечномерного пространства ).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Размерность и базис линейного пространства

Определения размерности и базиса

Примеры базисов линейных пространств

Вам также может понравиться

Как найти местное солнечное время

Как найти свой вес по физике

Как найти периметр подобных треугольников зная площадь

Добавить комментарий Отменить ответ