Оглавление — Линейная алгебра
Матрица и определитель Грама: определение, свойства, приложения
Определение матрицы Грама
Квадратная симметрическая матрица [math]G(mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n)[/math], составленная из скалярных произведений системы векторов [math]mathbf{e}_1,mathbf{e}_2, ldots, mathbf{e}_n[/math] называется матрицей Грама
[math]G(mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n)= begin{pmatrix} langle mathbf{e}_1,mathbf{e}_1rangle& langle mathbf{e}_1,mathbf{e}_2rangle &cdots&langle mathbf{e}_1, mathbf{e}_nrangle\ langle mathbf{e}_2,mathbf{e}_1rangle& langle mathbf{e}_2, mathbf{e}_2rangle &cdots&langle mathbf{e}_2,mathbf{e}_nrangle\ vdots&vdots&ddots&vdots\ langle mathbf{e}_n,mathbf{e}_1rangle& langle mathbf{e}_n,mathbf{e}_2rangle &cdots&langle mathbf{e}_n,mathbf{e}_nrangle end{pmatrix}!.[/math]
Изменение матрицы Грама при переходе от одного базиса к другому
Пусть [math](mathbf{e})=(mathbf{e}_1,ldots,mathbf{e}_n)[/math] и [math](mathbf{f})= (mathbf{f}_1,ldots,mathbf{f}_n)[/math] — два базиса евклидова пространства [math]mathbb{E}[/math], a [math]S[/math] — матрица перехода от базиса [math](mathbf{e})[/math] к базису [math](mathbf{f})colon, (mathbf{f})=(mathbf{e})S[/math]. Требуется найти связь матриц Грама систем векторов [math](mathbf{e})[/math] и [math](mathbf{f})[/math]
По формуле (8.32) вычислим скалярное произведение векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math] в разных базисах:
[math]langle mathbf{x},mathbf{y}rangle= {mathop{x}limits_{(mathbf{e})}}^Tcdot, G(mathbf{e}_1,ldots,mathbf{e}_n)cdot mathop{mathbf{y}}limits_{(mathbf{e})}= {mathop{x}limits_{(mathbf{f})}}^Tcdot, G(mathbf{f}_1,ldots,mathbf{f}_n)cdot mathop{mathbf{y}}limits_{(mathbf{f})},[/math]
где [math]mathop{x}limits_{(mathbf{e})},, mathop{x}limits_{(mathbf{f})}[/math] и [math]mathop{y}limits_{(mathbf{e})},, mathop{y}limits_{(mathbf{f})}[/math] — координатные столбцы векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math] в соответствующих базисах. Подставляя в последнее равенство связи [math]mathop{x}limits_{(mathbf{e})}= S mathop{x}limits_{(mathbf{f})},[/math] [math]mathop{y}limits_{(mathbf{e})}= S mathop{y}limits_{(mathbf{f})}[/math], получаем тождество
[math]{mathop{x}limits_{(mathbf{f})}}^Tcdot S^Tcdot, G(mathbf{e}_1,ldots,mathbf{e}_n)cdot Scdot mathop{mathbf{y}}limits_{(mathbf{f})}= {mathop{x}limits_{(mathbf{f})}}^Tcdot, G(mathbf{f}_1,ldots,mathbf{f}_n)cdot mathop{mathbf{y}}limits_{(mathbf{f})}.[/math]
Отсюда следует формула изменения матрицы Грама при переходе от одного базиса к другому:
[math]G(mathbf{f}_1,ldots,mathbf{f}_n)= S^Tcdot G(mathbf{e}_1,ldots,mathbf{e}_n)cdot S.[/math]
Записав это равенство для ортонормированных базисов [math](mathbf{e})[/math] и [math](mathbf{f})[/math], получаем [math]E=S^TES[/math], так как матрицы Грама ортонормированных базисов единичные: [math]G(mathbf{e}_1,ldots,mathbf{e}_n)= G(mathbf{f}_1,ldots,mathbf{f}_n)=E[/math]. Поэтому матрица [math]S[/math] перехода от одного ортонормированного базиса к другому является ортогональной: [math]S^{-1}=S^T[/math].
Определитель Грама и его свойства
Определитель матрицы [math]G(mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n)[/math] называется определителем Грама. Рассмотрим свойства этого определителя.
1. Критерий Грама линейной зависимости векторов: система векторов [math]mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_k[/math] линейно зависима тогда и только тогда, когда определитель Грама этой системы равен нулю.
Действительно, если система [math]mathbf{v}_1, mathbf{v}_2, ldots,mathbf{v}_k[/math] линейно зависима, то существуют такие числа [math]x_1,x_2,ldots,x_k[/math], не равные нулю одновременно, что
[math]x_1cdot mathbf{v}_1+x_2cdot mathbf{v}_2+ldots+ x_kcdot mathbf{v}_k= mathbf{o}.[/math]
Умножая это равенство скалярно на [math]mathbf{v}_1[/math], затем на [math]mathbf{v}_2[/math] и т.д. на [math]mathbf{v}_k[/math], получаем однородную систему уравнений [math]G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)x=o[/math], которая имеет нетривиальное решение [math]x=begin{pmatrix}x_1&cdots&x_k end{pmatrix}^T[/math]. Следовательно, ее определитель равен нулю. Необходимость доказана. Достаточность доказывается, проводя рассуждения в обратном порядке.
Следствие. Если какой-либо главный минор матрицы Грама равен нулю, то и определитель Грама равен нулю.
Главный минор матрицы Грама системы [math]mathbf{v}_1, mathbf{v}_2,ldots,mathbf{v}_k[/math] представляет собой определитель Грама подсистемы векторов. Если подсистема линейно зависима, то и вся система линейно зависима.
2. Определитель Грама [math]det{G (mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_k)}[/math] не изменяется в процессе ортогонализации системы векторов [math]mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k[/math]. Другими словами, если в процессе ортогонализации векторов [math]mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k[/math] получены векторы [math]mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_k[/math], то
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2, ldots,mathbf{w}_k)= langle mathbf{w}_1,mathbf{w}_1ranglecdot langle mathbf{w}_2,mathbf{w}_2ranglecdot ldotscdot langle mathbf{w}_k,mathbf{w}_krangle.[/math]
Действительно, в процессе ортогонализации по векторам [math]mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_k[/math] последовательно строятся векторы
[math]mathbf{w}_1=mathbf{v}_1,quad mathbf{w}_2= mathbf{v}_2- alpha_{21} mathbf{w}_1,quad ldots,quad mathbf{w}_k= mathbf{v}_k- sum_{j=1}^{k-1}alpha_{kj} mathbf{w}_j.[/math]
После первого шага определитель Грама не изменяется
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{v}_2, ldots,mathbf{v}_k).[/math]
Выполним с определителем [math]det G(mathbf{w}_1, mathbf{v}_2, ldots,mathbf{v}_k)[/math] следующие преобразования. Прибавим ко второй строке первую, умноженную на число [math](-alpha_{21})[/math], а затем ко второму столбцу прибавим первый, умноженный на [math](-alpha_{21})[/math]. Получим определитель
[math]det G(mathbf{w}_1,mathbf{v}_2-alpha_{21}mathbf{w}_1,ldots,mathbf{v}_k)= det G(mathbf{w}_1,mathbf{w}_2, mathbf{v}_3, ldots,mathbf{v}_k).[/math]
Так как при этих преобразованиях определитель не изменяется, то
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2,mathbf{v}_3, ldots,mathbf{v}_k).[/math]
Значит, после второго шага в процессе ортогонализации определитель не изменяется. Продолжая аналогично, получаем после [math]k[/math] шагов:
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2, ldots,mathbf{w}_k).[/math]
Вычислим правую часть этого равенства. Матрица [math]G(mathbf{w}_1,mathbf{w}_2,ldots, mathbf{w}_k)[/math] Грама ортогональной системы [math]mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_k[/math] векторов является диагональной, так как [math]langle mathbf{w}_i,mathbf{w}_jrangle=0[/math] при [math]ine j[/math]. Поэтому ее определитель равен произведению элементов, стоящих на главной диагонали:
[math]det G(mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_k)= langle mathbf{w}_1, mathbf{w}_1ranglecdot langle mathbf{w}_2,mathbf{w}_2ranglecdot ldots langle mathbf{w}_k, mathbf{w}_krangle.[/math]
3. Определитель Грама любой системы [math]mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k[/math] векторов удовлетворяет двойному неравенству
[math]0leqslant det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k) leqslant langle mathbf{v}_1, mathbf{v}_1ranglecdot langle mathbf{v}_2,mathbf{v}_2ranglecdot ldots langle mathbf{v}_k, mathbf{v}_krangle.[/math]
Докажем неотрицательность определителя Грама. Если система [math]mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_k[/math] линейно зависима, то определитель равен нулю (по свойству 1). Если же система [math]mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k[/math] линейно независима, то, выполнив процесс ортогонализации, получим ненулевые векторы [math]mathbf{w}_1,mathbf{w}_2, ldots, mathbf{w}_k[/math], для которых по свойству 2:
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2, ldots, mathbf{w}_k)= |mathbf{w}_1|^2cdot |mathbf{w}_2|^2cdot ldotscdot |mathbf{w}_k|^2>0.[/math]
Оценим теперь скалярный квадрат [math]langle mathbf{v}_j,mathbf{w}_jrangle[/math]. Выполняя процесс ортого-1нализации, имеем [math]mathbf{v}_j= mathbf{w}_j+ alpha_{j,1}mathbf{w}_1+ ldots+ alpha_{j,j-1}mathbf{w}_{j-1}[/math]. Отсюда
[math]langle mathbf{v}_j,mathbf{w}_jrangle= langle mathbf{w}_j,mathbf{w}_jrangle+ sum_{i=1}^{j-1}alpha_{i,i}^2 langle mathbf{w}_j,mathbf{w}_jrangle geqslant langle mathbf{w}_j, mathbf{w}_jrangle.[/math]
Следовательно, по свойству 2 имеем
[math]langle mathbf{v}_1,mathbf{v}_1ranglecdot langle mathbf{v}_2,mathbf{v}_2 ranglecdot ldotscdot langle mathbf{v}_k,mathbf{v}_kranglegeqslant langle mathbf{w}_1, mathbf{w}_1ranglecdot langle mathbf{w}_2,mathbf{w}_2ranglecdot ldotscdot langle mathbf{w}_k, mathbf{w}_krangle= det G(mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_k).[/math]
Замечания
1. Матрица Грама любой системы векторов является неотрицательно определенной, так как все ее главные миноры также являются определителями Грама соответствующих подсистем векторов и неотрицательны в силу свойства 3.
2. Матрица Грама любой линейно независимой системы векторов является положительно определенной, так как все ее угловые миноры положительны (в силу свойств 1,3), поскольку являются определителями Грама линейно независимых подсистем векторов.
Метрические приложения определителя Грама
Пусть [math]boldsymbol{v}_1,boldsymbol{v}_2, ldots,boldsymbol{v}_k[/math] — линейно независимая система векторов n-мерного евклидова пространства [math](kleqslant n)[/math]. Определим по индукции понятие многомерного объема. Обозначим через [math]boldsymbol{h}_j[/math] — перпендикуляр, опущенный из конца вектора [math]boldsymbol{v}_j[/math] на подпространство [math]operatorname{Lin} (boldsymbol{v}_1, ldots,boldsymbol{v}_{j-1}),[/math] [math]j=2,ldots,k[/math].
Обозначим
[math]V_{ast boldsymbol{v}_1}=|boldsymbol{v}_1|[/math] — одномерный объем — длина вектора [math]boldsymbol{v}_1[/math];
[math]V_{ast boldsymbol{v}_1,boldsymbol{v}_2}= V_{ast boldsymbol{v}_1}cdot |boldsymbol{h}_2|= |boldsymbol{v}_1|cdot|boldsymbol{h}_2|[/math] — двумерный объем — площадь параллелограмма, построенного на векторах [math]boldsymbol{v}_1,,boldsymbol{v}_2[/math];
[math]V_{ast boldsymbol{v}_1,boldsymbol{v}_2, boldsymbol{v}_3}= V_{ast boldsymbol{v}_1, boldsymbol{v}_2}cdot |boldsymbol{h}_3|= |boldsymbol{v}_1|cdot |boldsymbol{h}_2|cdot |boldsymbol{h}_3|[/math] — трехмерный объем — объем параллелепипеда, построенного на векторах [math]boldsymbol{v}_1,,boldsymbol{v}_2,, boldsymbol{v}_3[/math];
[math]V_{ast boldsymbol{v}_1,ldots,boldsymbol{v}_{k}}= V_{ast boldsymbol{v}_1, ldots, boldsymbol{v}_{k-1}}cdot |boldsymbol{h}_k|= |boldsymbol{v}_1|cdot|boldsymbol{h}_2|cdot ldotscdot |boldsymbol{h}_k|[/math] — k-мерный объем — объем параллелепипеда, построенного на векторах [math]boldsymbol{v}_1, boldsymbol{v}_2, ldots,boldsymbol{v}_k[/math].
Проводя ортогонализацию системы векторов [math]boldsymbol{v}_1,boldsymbol{v}_2, ldots, boldsymbol{v}_k[/math], получаем, согласно пункту 4 замечаний 8.14, перпендикуляры [math]boldsymbol{h}_1= boldsymbol{v}_1,boldsymbol{h}_2, ldots,boldsymbol{h}_k[/math]. Тогда по свойству 2 определителя Грама имеем
[math]V_{ast boldsymbol{v}_1,ldots,boldsymbol{v}_k}^2= |boldsymbol{h}_1|^2cdot |boldsymbol{h}_2|^2cdot ldotscdot |boldsymbol{h}_k|^2= det G(boldsymbol{v}_1, boldsymbol{v}_2,ldots, boldsymbol{v}_k),[/math]
(8.37)
т.е. определитель Грама векторов [math]boldsymbol{v}_1, boldsymbol{v}_2, ldots, boldsymbol{v}_k[/math] равен квадрату k-мерного объема параллелепипеда, построенного на этих векторах. В этом заключается геометрический смысл определителя Грама.
Расстоянием от конца вектора [math]boldsymbol{v}[/math] до подпространства [math]L[/math] называется наименьшее значение длин векторов [math](boldsymbol{v}-boldsymbol{l})[/math], где [math]boldsymbol{l}in L[/math], т.е.
[math]d=min_{boldsymbol{l}in L}|boldsymbol{v}-boldsymbol{l}|.[/math]
Аналогично определяется расстояние от конца вектора до многообразия.
Углом между ненулевым вектором [math]boldsymbol{v}[/math] и подпространством [math]L[/math] называется наименьший угол [math]varphi[/math] между вектором [math]boldsymbol{v}[/math] и ненулевыми векторами подпространства, т.е.
[math]varphi= min_{boldsymbol{l}in L}!left(arccosfrac{langle boldsymbol{v}, boldsymbol{l}rangle}{|boldsymbol{v}|cdot|boldsymbol{l}|}right)!.[/math]
Аналогично определяется угол между вектором и многообразием, как угол между вектором и однородной частью многообразия.
Из неравенств пункта 1 замечаний 8.14 следует, что
1) расстояние [math]d[/math] от конца вектора [math]boldsymbol{v}[/math] до подпространства [math]L[/math] равно длине перпендикуляра [math]boldsymbol{h}[/math], опущенного из конца вектора [math]boldsymbol{v}[/math] на подпространство [math]L[/math], т.е. [math]d=|boldsymbol{h}|[/math];
2) угол между ненулевым вектором [math]boldsymbol{v}[/math] и подпространством [math]L[/math] равен углу между вектором [math]boldsymbol{v}[/math] и его ортогональной проекцией на подпространство [math]L[/math].
Для нахождения расстояний и углов можно использовать формулу (8.37).
Пусть задан вектор [math]boldsymbol{v}[/math] и подпространство [math]L=operatorname{Lin} (boldsymbol{e}_1,ldots,boldsymbol{e}_r)[/math], причем векторы [math]boldsymbol{e}_1, ldots, boldsymbol{e}_r[/math] линейно независимы. Тогда [math]V_{ast boldsymbol{e}_1,ldots, boldsymbol{e}_r, boldsymbol{v}}= V_{ast boldsymbol{e}_1,ldots,boldsymbol{e}_r}cdot |boldsymbol{h}|[/math], где [math]boldsymbol{h}[/math] — ортогональная составляющая вектора [math]boldsymbol{v}[/math] относительно подпространства [math]L[/math]. Отсюда, [math]boldsymbol{h}= frac{V_{ast boldsymbol{e}_1,ldots, boldsymbol{e}_r, boldsymbol{v}}}{V_{ast boldsymbol{e}_1,ldots,boldsymbol{e}_r}}[/math]. Используя (8.37) для вычисления объемов, получаем, что длина [math]|boldsymbol{h}|[/math] ортогональной составляющей (расстояние от конца вектора [math]boldsymbol{v}[/math] до подпространства [math]L=operatorname{Lin}( boldsymbol{e}_1,ldots,boldsymbol{e}_r)[/math] находится по формуле
[math]|boldsymbol{h}|= sqrt{frac{det G(boldsymbol{e}_1, ldots, boldsymbol{e}_r, boldsymbol{v})}{det G(boldsymbol{e}_1,ldots,boldsymbol{e}_r)}},,[/math]
(8.38)
а угол [math]varphi[/math] между ненулевым вектором [math]boldsymbol{v}[/math] и подпространством находится по формуле
[math]varphi= arcsinfrac{|boldsymbol{h}|}{|boldsymbol{v}|},.[/math]
(8.39)
Пример 8.22. В пространстве [math]mathbb{R}^4[/math] со стандартным скалярным произведением (8.27) заданы: вектор [math]v=begin{pmatrix}-3&2&0&0end{pmatrix}^T[/math] и подпространство [math]L[/math] — множество [math]{Ax=o}[/math] решений однородной системы:
[math]begin{cases}x_1+x_2+2x_3+x_4=0,\ 2x_1+3x_2+x_4=0,\ 3x_1+4x_2+2x_3+2x_4=0. end{cases}[/math]
Требуется найти расстояние [math]|h|[/math] от конца вектора [math]boldsymbol{v}[/math] до подпространства [math]L[/math] и угол между вектором [math]boldsymbol{v}[/math] и подпространством [math]L[/math].
Решение. Базис подпространства был найден в примере 8.9:
[math]L=operatorname{Lin}(varphi_1,varphi_2),[/math] где [math]varphi_1=begin{pmatrix}-6&4&1&0end{pmatrix}^T,quad varphi_2=begin{pmatrix}-2&1&0&1end{pmatrix}^T.[/math]
Составляем определители Грама [math]Bigl(langle boldsymbol{v}, boldsymbol{v}_1rangle= (-3)^2+ 2^2+0^2+0^2=13Bigr)[/math], остальные скалярные произведения векторов найдены в примере 8.20):
[math]det G(varphi_1,varphi_2,v)= begin{vmatrix}53&16&26\ 16&6&8\ 26&8&13 end{vmatrix}=14,quad det G(varphi_1,varphi_2)= begin{vmatrix}53&16\ 16&6 end{vmatrix}=62.[/math]
Тогда [math]|h|=sqrt{frac{14}{62}}=sqrt{frac{7}{31}}[/math], а [math]varphi= arcsinsqrt{frac{7}{403}}[/math]. В найдены ортогональная проекция [math]l=begin{pmatrix}dfrac{-92}{31}&dfrac{60}{31}&dfrac{14}{31}&dfrac{4}{31}end{pmatrix}^T[/math] и ортогональная составляющая [math]h=begin{pmatrix}dfrac{-1}{31}& dfrac{2}{31}&dfrac{-14}{31}& dfrac{-4}{31} end{pmatrix}^T[/math]. Вычисляя длину вектора [math]h[/math], получаем [math]|h|=sqrt{frac{7}{31}}[/math]. Результаты совпадают.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Грама. Определитель Грамма, его геометрический смысл
Пусть
–
система векторов в евклидовом (унитарном)
пространстве.
Матрицей Грама данной системы
векторов называется матрица вида:

Матрице Грама
поставим в соответствие ее определитель:
.
Свойства определителя Грама:
1.
2.
–
линейно зависимы.
3. Для,
–
квадрат длины вектора.
,
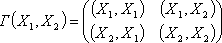
квадрат площади.
,

квадрат объема.
,
–
квадрат объема-мерного
параллелепипеда, со сторонами.
4. Процесс ортогонализации
Грама-Шмидта не меняет определитель
Грама.
Для доказательства этого установим,
что если к одному из векторов прибавить
линейную комбинацию остальных, состоящую
из одного вектора, то определитель не
изменится.
Умножим первый столбец на
и
прибавим к-тому
столбцу:
умножим первую строку на
и
прибавим к-той
строке, получим определитель Грама:
.
Что и требовалось доказать.
Используя это обстоятельство, мы
ортогонализируем систему векторов
методом Грама-Шмидта:
,
где.Следовательно

При этом, для
,
–
квадрат площади,
для
,
–
квадрат объема исходного параллелепипеда.
Чтобы найти высоту
,
опущенную изна
основаниедостаточно
вычислить.
Скалярное произведение в произвольном базисе
Пусть
–
базис евклидова пространства,

рассмотрим скалярное произведение:
=
(*)
Если записать (*) в матричном виде, то
получим:
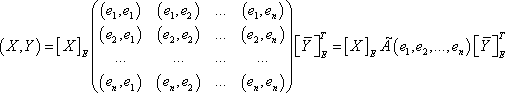
Если базис
–
ортонормированный, то
то
.
Ортогональное дополнение подпространства m из l
Пусть
–
евклидово (унитарное) пространство,
подпространство.
Векторназываетсяортогональным к подпространству
,
если для всех.
Множество всех векторов
ортогональных
к подпространству называется
ортогональным дополнением
и
обозначается.
Очевидно, М┴
является подпространством пространства,
причем для размерности подпространств и
размерность пространства связаны
соотношением
.
Действительно, выберем базис
подпространства
,
дополним его до базиса,
получим.
Ортогонализируем данный базис
методом Грамма-Шмидта, получим:–
базис пространства,
–
базис подпространства,
–
базис подпространства ортогонального дополнения.
Говорят, что пространство
является
прямой ортогональной суммой своих
подпространств и
:
Прямая сумма подпространств
Пространство
являетсяпрямой суммой подпространств
,
если
1. любой вектор
представляется
в виде,
где
2. представление
единственно.
Обозначается
.
Если пространство евклидовои
выполняется дополнительно условие
3.
при
,
то прямая сумма состоит из попарно
ортогональных подпространств
(ортогональная сумма) и обозначается
так
Билет
12+13
Теорема.
Пусть
—
линейный оператор в евклидовом (унитарном)
пространстве. Сопоставим ему билинейную
(полуторалинейную) функцию,
.
Это соответствие является биекцией
между операторами и билинейными
(полуторалинейными) функциями.
Рассмотрим
билинейную (полуторалинейную) функцию
,
заданную формулой.
Тогда матрица для функциив
ортонормированном базисе—
это матрица,
т.е..
Будем говорить, что функцияопределяетсопряженный
оператор
.
Более подробно
Определение.
Сопряженным
оператором
к оператору
называется
такой оператор,
который удовлетворяет равенству.
Определение.
Оператор
называетсясамосопряженным
или симметричным
(эрмитовым),
если
,
т.е..
Операторназываетсякососимметричным
(
косоэрмитовым),
если
,
т.е..
Операторназываетсяортогональным
(унитарным
для
),
если.
Теорема.
Пусть
—
ортонормальный базис в евклидовом
(унитарном) пространстве,
и—
линейный оператор. Операторявляется
самосопряженным (эрмитовым)
тогда и только тогда, когда его матрица
в
базисесимметрична
(эрмитова
).
Теорема.
Пусть
—
ортонормальный базис в евклидовом
(унитарном) пространстве,
и—
линейный оператор. Операторявляется
кососимметричным (косоэрмитовым)
тогда и только тогда, когда его матрица
в
базисекососимметрична
(косоэрмитова
).
Лемма.
Если
—
инвариантное подпространство для
самосопряженного операторав
евклидовом (унитарном) пространстве,
тотоже
инвариантно относительно.
Лемма.
Пусть
—
самосопряженный оператор на-мерном
евклидовом пространстве. Тогда длясуществует
собственный вектор.
Теорема.
Для всякого самосопряженного оператора
в
-мерном
евклидовом (унитарном) пространствесуществует
ортонормальный базис, состоящий из
собственных векторов оператора,
т.е. в таком базисе матрица оператора
диагональна. Матрицаоператора
одна
и та же во всех таких канонических
базисах, с точностью до перестановки
диагональных элементов. Верно и обратно.
Замечание.
В унитарном пространстве
все
собственные числа для самосопряженного
операторавещественны,
.
Если
(
— евклидово или унитарное пространство)
— собственные векторы с разными
собственными значениямидля
самосопряженного оператора,
то,
так как.
Следствие.
Для всякой (эрмитовой) квадратичной
функции
в
-мерном
евклидовом (унитарном) пространствесуществует
ортонормальный базис, в котором(
).
При этом, системане
зависит от выбора базиса, с точностью
до перестановок.
Пусть
—
ортогональный (унитарный) оператор в
евклидовом (унитарном) пространстве.
Тогда,
т.е..
Если—
собственное значения, то,
так как.
Лемма.
Ортогональный (унитарный) оператор
невырожден.
Теорема.Следующие
свойства линейного оператора
в
-мерном
евклидовом (унитарном) пространстве
равносильны.
—
ортогональный (унитарный) оператор.
В
любом ортонормальном базисе матрица
оператора
ортогональна
(унитарна, т.е.).
В
некотором ортонормальном базисе матрица
оператора
ортогональна
(унитарна).
Оператор
переводит
любой ортонормальный базис в ортонормальный
базис.
Оператор
переводит
некоторый ортонормальный базис в
ортонормальный базис.
Лемма.
Если
—
ортогональный (унитарный) оператор в
евклидовом (унитарном) пространстве, и—
инвариантное дляподпространство
в,
то ортогональное дополнениетакже
является инвариантным подпространством
для.
Лемма.
Пусть
—
ортогональный оператор без собственных
векторов в-мерном
евклидовом пространстве. Тогда в
ортонормальном базисе его матрицаимеет
вид
Теорема.
Для всякого ортогонального (унитарного)
оператора
в
-мерном
евклидовом (унитарном) пространстве
существует ортонормальный базис,
в котором матрица оператора имеет вид:
для
евклидова случая и
,
где,
для унитарного пространства.
Определение.
Пусть
—
самосопряженный оператор в-мерном
евклидовом пространстве. Он определяет
билинейную функцию,
заданную формулой.
Операторназываетсяположительно
определенным,
если
—
положительно определенная симметрическая
функция, т.е.для
любого вектора.
Лемма.
Для всякого невырожденного оператора
в
-мерном
евклидовом пространствепроизведение
является
положительно определенным самосопряженным
оператором.
Лемма.
Самосопряженный оператор
в
-мерном
евклидовом пространствеявляется
положительно определенным тогда и
только тогда, когда все собственные
значения дляположительны.
Лемма.
Для всякого невырожденного положительно
определенного самосопряженного оператора
в
-мерном
евклидовом пространствесуществует
такой невырожденный положительно
определенный самосопряженный оператор,
что.
Теорема.[о
полярном разложении] Всякий невырожденный
линейный оператор
в
-мерном
евклидовом пространствеможет
быть разложен в произведение,
где—
ортогональный оператор, а—
самосопряженный положительно определенный
оператор.
Билет
14
Билинейные
функции
Определение.Пусть—
линейное пространство над полем.
Тогда отображениеназываетсябилинейной функцией, если
для
любых векторови
любых чисел,
для
любых векторови
любых чисел.
Определение.Матрицейбилинейной
функциив
базисеназывается
матрица,
где.
Теорема.Пусть—
базис-мерного
линейного пространства.
Тогда для любой квадратной матрицыпорядка
существует,
причем единственная, билинейная функцияна
пространствес
матрицейв
базисе.
При этом значения,
гдеи
,
могут быть найдены по формуле.
Замечание.Билинейные функцииобразуют
линейное пространство. Линейная
комбинация двух функций—
это функция,
заданная формулой.
Если зафиксировать базис в пространстве
,
то мы получаем изоморфизм из пространства
билинейных функций в пространствоквадратных
матриц порядканад
полем.
Лемма.Пустьи
—
матрицы размераи
соответственно.
Тогда.
Теорема.Еслии
—
матрицы билинейной функциив
разных базисахи
пространства
,
то,
гдематрица
перехода от базисак
,
т.е..
Определение.Билинейная функцияназываетсясимметрической, если
для
любых векторов.
Билинейная функция
называетсякососимметрической, если
для
любых векторов.
Теорема.Если
матрицабилинейной
функциив
некотором базисе симметрическая
(кососимметрическая), т.е.(
),
то функцияявляется
симметрической (кососимметрической)
билинейной функцией.
Если
билинейная функцияявляется
симметрической (кососимметрической),
то ее матрицав
любом базисе симметрическая
(кососимметрическая).
Определение.Пусть—
линейное пространство над полем.
Функцияназываетсяполуторалинейной, если
для
любых векторови
любых чисел,
для
любых векторови
любых чисел.
Для полуторалинейной функции имеем
.
Определение.Полуторалинейная
функцияназываетсяэрмитовой, если
.
Теорема.Если
матрицаполуторалинейной
функциив
некотором базисе эрмитова, т.е.,
то функцияявляется
эрмитовой полуторалинейной функцией.
Если
полуторалинейная функцияявляется
эрмитовой, то ее матрицав
любом базисе эрмитова, т.е..
Определение.Рангомбилинейной
функцииназывается
рангее
матрицыв
некотором базисе.
Замечание.При умножении на
невырожденную матрицу ранг не меняется,
поэтому определение ранга функции
корректно. Заметим, чтотогда
и только тогда, когда.
Определение.Ядросимметрической
билинейной функции—
это множестводля
любого.
Теорема.Ядро симметрической
билинейной функциина
-мерном
линейном пространствеявляется
подпространством размерности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
In linear algebra, the Gram matrix (or Gramian matrix, Gramian) of a set of vectors 





An important application is to compute linear independence: a set of vectors are linearly independent if and only if the Gram determinant (the determinant of the Gram matrix) is non-zero.
It is named after Jørgen Pedersen Gram.
Examples[edit]
For finite-dimensional real vectors in 









Given square-integrable functions 
![{displaystyle left[t_{0},t_{f}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dc901ebd356de06d879650339ff78a293159bb1)
![{displaystyle G=left[G_{ij}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c88387ce30e4df6fa123fe0886bb467a0e30e2d)
where 

For any bilinear form 




Applications[edit]
- In Riemannian geometry, given an embedded
-dimensional Riemannian manifold
and a parametrization
for
, the volume form
on
induced by the embedding may be computed using the Gramian of the coordinate tangent vectors:
This generalizes the classical surface integral of a parametrized surface
for
:
- If the vectors are centered random variables, the Gramian is approximately proportional to the covariance matrix, with the scaling determined by the number of elements in the vector.
- In quantum chemistry, the Gram matrix of a set of basis vectors is the overlap matrix.
- In control theory (or more generally systems theory), the controllability Gramian and observability Gramian determine properties of a linear system.
- Gramian matrices arise in covariance structure model fitting (see e.g., Jamshidian and Bentler, 1993, Applied Psychological Measurement, Volume 18, pp. 79–94).
- In the finite element method, the Gram matrix arises from approximating a function from a finite dimensional space; the Gram matrix entries are then the inner products of the basis functions of the finite dimensional subspace.
- In machine learning, kernel functions are often represented as Gram matrices.[2] (Also see kernel PCA)
- Since the Gram matrix over the reals is a symmetric matrix, it is diagonalizable and its eigenvalues are non-negative. The diagonalization of the Gram matrix is the singular value decomposition.
Properties[edit]
Positive-semidefiniteness[edit]
The Gram matrix is symmetric in the case the real product is real-valued; it is Hermitian in the general, complex case by definition of an inner product.
The Gram matrix is positive semidefinite, and every positive semidefinite matrix is the Gramian matrix for some set of vectors. The fact that the Gramian matrix is positive-semidefinite can be seen from the following simple derivation:
The first equality follows from the definition of matrix multiplication, the second and third from the bi-linearity of the inner-product, and the last from the positive definiteness of the inner product.
Note that this also shows that the Gramian matrix is positive definite if and only if the vectors 


Finding a vector realization[edit]
Given any positive semidefinite matrix 
,
where 


Here 




The columns 



where the dot product 

Thus a Hermitian matrix 


Uniqueness of vector realizations[edit]
If 







This is the only way in which two real vector realizations of 






The same holds in the complex case, with unitary transformations in place of orthogonal ones.
That is, if the Gram matrix of vectors 







Other properties[edit]
Gram determinant[edit]
The Gram determinant or Gramian is the determinant of the Gram matrix:
If 

The Gram determinant can also be expressed in terms of the exterior product of vectors by
When the vectors 


then the Gram determinant can be written as the difference of two Gram determinants,
where each 


Constructing an orthonormal basis[edit]
Given a set of linearly independent vectors 

The matrix 









where we used 
See also[edit]
- Controllability Gramian
- Observability Gramian
References[edit]
- ^ a b c Horn & Johnson 2013, p. 441, p.441, Theorem 7.2.10
- ^ Lanckriet, G. R. G.; Cristianini, N.; Bartlett, P.; Ghaoui, L. E.; Jordan, M. I. (2004). “Learning the kernel matrix with semidefinite programming”. Journal of Machine Learning Research. 5: 27–72 [p. 29].
- ^ Horn & Johnson (2013), p. 452, Theorem 7.3.11
- Horn, Roger A.; Johnson, Charles R. (2013). Matrix Analysis (2nd ed.). Cambridge University Press. ISBN 978-0-521-54823-6.
External links[edit]
- “Gram matrix”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Volumes of parallelograms by Frank Jones
33. Матрица Грама в евклидовом пространстве
Пусть Еn – N-Мерное евклидово пространство и пусть Е = (Е1, Е2, . , Еn ) – базис в нём. Так как в Еn для любой упорядоченной пары векторов определено их скалярное произведение, то определены скалярные произведения всех пар базисных векторов. Составим из них матрицу
Матрица Г Называется Матрицей Грама Скалярного произведения для базиса Е.
Используя матрицу Грама, можно получить формулу для вычисления скалярного произведения векторов,
Пусть в базисе Е заданы векторы А = Х1Е1 + Х2Е2 + … + ХnЕn , В = У1Е1+ У2Е2 + … + УnЕn . Тогда (А, в) = (Х1Е1 + Х2Е2 + … + ХnЕn)×( у1Е1+ У2Е2 + … + УnЕn) = = Х Т×Г×У, где Х Т– строка координат вектора А, У – Столбец координат вектора В . Итак, (А, в) = Х Т×Г×У (42).
Свойства матрицы Грама.
10. Матрица Грама симметрична относительно главной диагонали.
Это следует из того, что (Ек, еS ) = (ЕS, ек ).
20. Диагональные элементы матрицы Грама строго положительны.
Это следует из того, что Ек ¹ 0 и, следовательно, (Ек, ек ) > 0.
30. Для матрицы Грама и любого N-Мерного столбца Х Выполняется условие Х Т×Г×Х > 0.
Это следует из 4-ой аксиомы определения скалярного произведения.
Симметрическую матрицу А, Удовлетворяющую условию Х Т×А×Х > 0 для любого
Ненулевого столбца Х, Называют Положительно определённой. Следовательно, матрица
Грама Положительно определённая.
40. Пусть Е = (Е1, Е2, . , Еn ) и Е1 = (Е11, Е21, . , Еn1 ) –два базиса в Еn , Г И Г1 – матрицы Грама данного скалярного произведения в базисах Е И Е1 соответственно. Пусть Т – матрица перехода от базиса Е К базису Е1. Тогда (А, в) = Х Т×Г×У, х = Т×х1, у = Т×у1, х Т= (Т×х1)Т= (Х1)Т× ТТ. Следовательно, (А, в) = ((Х1)Т× ТТ)× Г× (Т×у1) = (Х1)Т× (ТТ× Г× Т )× У1. Но (А, в) = (Х1)Т× Г1× у1. Отсюда
Г1 = ТТ× Г× Т (43)
Формула (42) даёт связь матриц Грама в разных базисах.
50. Определители матриц Грама во всех базисах имеют один и тот же знак.
60. Все главные миноры матрицы Грама строго положительны.
1. Во множестве М2 Квадратных матриц с действительными элементами скалярное произведение задано формулой . Найти матрицу Грама этого произведения в базисе Е1 = , Е2 = , Е3 = , Е4 = .
Решение. Найдём все попарные произведения базисных элементов: (Е1, е1) = 1, (Е1, е2) = (Е2, е1) = 0, (Е1, е3) = (Е3, е1) = 0, (Е1, е4) = (Е4, е1) = 0, (Е2, е2) = 1, (Е2, е3) = (Е3, е2) = 0, (Е2, е4) = (Е4, е2) = 0, (Е3, е3) = 1, (Е3, е4) = (Е4, е3) = 0, (Е4, е4) = 1. Следовательно,
2. В пространстве R[Х] многочленов степени не выше 3-х скалярное произведение задано формулой , где A И B – фиксированные действительные числа, A < B. Составить матрицу Грама в базисе (1, Х, х2, х3).
Решение. Найдём все попарные произведения базисных элементов: (1, 1) = = B – A,
(1, Х) = (Х, 1) = = ), (1, Х2) = (Х2, 1) = = ), (1, Х3) = (Х3, 1) = = ), (Х, х) = = ), (Х, х2) = (Х2, х) = = ), (Х, х3) = (Х3, х) = = ), (Х2, х2) = = ), (Х2, х3) = (Х3, х2) = = ), (Х3, х3) = = ). Матрица Грама будет иметь вид:
3. В базисе (Е1, е2, е3) пространства Е3 Скалярное произведение задано матрицей Грама Г = . Найти скалярное произведение векторов А = (1, –5, 4) и В = (–3, 2, 7).
Решение. Используя формулу (41), получим (А, В) = (1, –5, 4) × × = 7.
Матрица и определитель Грама
Пусть в евклидовом пространстве $ mathbb E_ $ известным образом задано скалярное произведение $ langle X_,Y rangle $. Матрицей Грама системы векторов $ ,dots,X_m > $ называется квадратная матрица, состоящая из всевозможных скалярных произведений этих векторов: $$ G(X_1,dots,X_m)= left( beginlangle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right) = left[ langle X_j,X_k rangle right]_^m . $$ Матрица Грама является симметричной матрицей. Ее определитель называется определителем Грама (или грамианом) системы векторов $ ,dots,X_m > $: $$ (X_1,dots,X_m)=left| beginlangle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right| = det left[ langle X_j,X_k rangle right]_^m . $$
Пример. Если в пространстве $ mathbb R^ $ строк, состоящих из $ n_ $ вещественных чисел, скалярное произведение определяется по правилу 1)
$$ langle X,Y rangle=x_1y_1+x_2y_2+dots+x_ny_n quad npu quad X=(x_1,x_2,dots,x_n), Y=(y_1,y_2,dots,y_n) , $$ то матрица Грама строк $$ X_1=left(x_,x_,dots, x_right),dots,X_m=left(x_,x_,dots, x_right) $$ вычисляется перемножением матриц: $$ G(X_1,dots,X_m)=Xcdot X^ quad npu quad X= left(beginx_ & x_ &dots & x_ \ dots & & & dots \ x_& x_ & dots & x_ end right) $$ и при $ ^_ $ означающем транспонирование. Из теоремы Бине-Коши немедленно следует, что при $ m>n_ $ (числе строк превышающем размерность пространства) определитель Грама равен нулю. Этот результат обобщен НИЖЕ для произвольных евклидовых пространств.
Пример. Если в пространстве полиномов с вещественными коэффициентами скалярное произведение задано формулой
$$ langle p(x),q(x) rangle =int_0^1 p(t) q(t) d,t ,$$ то $$ G(1,x,x^2)= left( beginint_0^1 1 d,t & int_0^1 t d,t & int_0^1 t^2 d,t \ & & \ int_0^1 t d,t & int_0^1 t^2 d,t & int_0^1 t^3 d,t \ & & \ int_0^1 t^2 d,t & int_0^1 t^3 d,t & int_0^1 t^4 d,t end right)= left( begin1 & 1/2 & 1/3 \ 1/2 & 1/3 & 1/4 \ 1/3 & 1/4 & 1/5 end right) . $$ Обобщение получившейся матрицы известно как матрица Гильберта.
Если система векторов $ ,dots,X_n > $ образует базис пространства $ mathbb E_ $ (т.е. пространство $ mathbb E_ $ является $ n_ $-мерным), то задание матрицы Грама $ G(X_,dots,X_n) $ позволяет свести вычисление скалярного произведения произвольных векторов из $ mathbb E_ $ к действиям над их координатами: $$ X=x_1X_1+x_2X_2+dots+x_nX_n, Y=y_1X_1+y_2X_2+dots+y_nX_n Rightarrow $$ $$ langle X,Y rangle=left(x_1,x_2,dots,x_n right) left( beginlangle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_n rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_n rangle \ dots & & & dots \ langle X_n,X_1 rangle & langle X_n,X_2 rangle & dots & langle X_n,X_n rangle end right) left( beginy_1 \ y_2 \ vdots \ y_n end right) . $$
Линейная независимость векторов
Теорема. $ (X_,dots,X_m)=0 $ тогда и только тогда, когда система векторов $ ,dots,X_m > $ линейно зависима.
Доказательство ☞ ЗДЕСЬ.
Если какой-то главный минор матрицы Грама обращается в нуль, то и все главные миноры бóльших порядков обращаются в нуль.
Свойства определителя Грама
Теорема. $ (X_,dots,X_m) ge 0 $ для любой системы векторов $ ,dots,X_m > $.
Доказательство ☞ ЗДЕСЬ
При $ m=2_ $ получаем неравенство Коши-Буняковского: $$ langle X_1,X_1 rangle cdot langle X_2,X_2 rangle ge langle X_1,X_2 rangle^2 . $$
Матрица Грама линейно независимой системы векторов является положительно определенной.
Доказательство ☞ ЗДЕСЬ
Величина определителя Грама не превосходит его главного члена, т.е. произведения элементов его главной диагонали:
$$mathfrak(X_1,dots,X_,X_m)le left|X_1 right|^2 times dots times left|X_ right|^2 left|X_m right|^2 . $$
Для произвольной квадратной вещественной матрицы
$$A=left( begina_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots & & & dots \ a_ & a_ & dots & a_ end right) $$ справедливо неравенство Адамара 2) : $$ left| det A right| le sqrt^n a_^2> sqrt^n a_^2> times dots times sqrt^n a_^2> . $$ Иными словами: модуль определителя матрицы не превосходит произведения длин его строк. Аналогичное утверждение справедливо и относительно столбцов матрицы.
Доказательство. Обозначим $ j_ $-ю строку матрицы $ A_ $ через $ A^ $. Тогда, поскольку $ det A= det A^ $ (см. свойство 1 ☞ ЗДЕСЬ ), имеем: $$left( det A right)^2= det left(Acdot A^ right)= det left[ beginlangle A^,A^ rangle & langle A^,A^ rangle & dots & langle A^,A^ rangle \ langle A^,A^ rangle & langle A^,A^ rangle & dots & langle A^,A^ rangle \ dots & & & dots \ langle A^,A^ rangle & langle A^,A^ rangle & dots & langle A^,A^ rangle end right]= $$ $$ =mathfrakleft(A^,A^,dots,A^ right) $$ при задании скалярного произведения в $ mathbb R^n $ стандартным способом. На основании предыдущего следствия, имеем: $$ le left|A^ right|^2 left|A^ right|^2 times dots times left|A^ right|^2 . $$ Равенство возможно тогда и только тогда, когда либо все строки попарно ортогональны, либо хотя бы одна строка — нулевая. ♦
Пример.
Теорема. Величина определителя Грама не изменится, если к системе векторов применить алгоритм ортогонализации Грама-Шмидта. В обозначениях этого алгоритма имеет место равенство:
Расстояние до линейного многообразия
Теорема. Расстояние $ d_ $ от точки $ X_ in $ до линейного многообразия в $ mathbb E_ $
Доказательство для случая $ Y_0=mathbb O_ $ ☞ ЗДЕСЬ. Случай $ Y_ne mathbb O $ сводится к предыдущему сдвигом пространства на вектор $ (- Y_) $: см. комментарии к теореме $ 3_ $ ☞ ЗДЕСЬ. ♦
Другие применения определителя Грама в задачах вычисления расстояний между поверхностями в $ ^ $ ☞ ЗДЕСЬ.
Объемы параллелепипедов
Площадь параллелограмма равна произведению его основания на высоту. Если параллелограмм построен на векторах $ X_ $ и $ X_2 $ из $ mathbb R^2 $, то за основание можно принять длину вектора $ X_ $, а за высоту — длину перпендикуляра, опущенного из конца вектора $ X_2 $ на ось вектора $ X_ $.
Аналогично, объем параллелепипеда, построенного на векторах $ X_1,X_2,X_3 $ из $ mathbb R^ $, равен произведению площади основания на высоту; площадь основания — это площадь параллелограмма, построенного на векторах $ X_1,X_2 $, а высота — длина перпендикуляра, опущенного из конца вектора $ X_3 $ на плоскость векторов $ X_1,X_2 $.
Объем $ k_ $-мерного параллелепипеда в евклидовом пространстве $ mathbb E_ $ определим по индукции. Если этот параллелепипед построен на векторах $ X_1,X_2,dots,X_,X_k $, то за его объем примем произведение объема $ (k-1) $-мерного параллелепипеда, построенного на векторах $ X_1,X_2,dots,X_ $ на длину перпендикуляра, опущенного из точки $ X_ $ на линейную оболочку векторов $ X_1,X_2,dots,X_ $ (т.е. на длину ортогональной составляющей $ X_k $ относительно $ mathcal L ( X_1,X_2,dots,X_) $): $$mathbf V(X_1,X_2,dots,X_,X_k)=left|X_k^ right| mathbf V(X_1,X_2,dots,X_) . $$
Теорема. Квадрат объема параллелепипеда, построенного на векторах $ X_1,X_2,dots,X_k $, совпадает с величиной определителя Грама от той же системы векторов: $$[V(X_1,X_2,dots,X_k)]^2= mathfrak G (X_1,X_2,dots,X_k) .$$
Доказательство следует из представления длины ортогональной составляющей $ X_k^> $ через определители Грама (см. теорему $ 2_ $ и следствие к ней ☞ ЗДЕСЬ ).
Модуль определителя вещественной матрицы
$$ A= left( begina_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots & & & dots \ a_ & a_ & dots & a_ end right) $$ равен объему параллелепипеда в пространстве $ mathbb R^_ $, построенного на вершинах с координатами $$ (0,0,dots, 0), (a_,a_, dots , a_),(a_,a_, dots , a_), dots, (a_,a_, dots, a_) $$ (т.е. «построенного на строках матрицы») и равен объему параллелепипеда построенного на вершинах с координатами $$ (0,0,dots, 0), (a_,a_, dots , a_),(a_,a_, dots , a_), dots, (a_,a_, dots, a_) $$ (т.е. «построенного на столбцах матрицы»).
Доказательство фактически совпадает с доказательством неравенства Адамара: $$ left(det A right)^2 = left det left(A cdot A^right)=mathfrak G (A^,A^,dots,A^) &= left[mathbf V(A^,A^,dots,A^)right]^2 \ & \ det left(A^ cdot A right) = mathfrak G (A_,A_,dots,A_) & = left[mathbf V(A_,A_,dots,A_)right]^2 end right. $$ ♦
Матрица Грамма. Ортогональные матрицы и преобразования
Пусть в пространстве Е/г задан базис еРе2, еп. Пусть х и у — векторы в Е„:
Найдем скалярное произведение (х, у):
Обозначим через Г матрицу
Эта матрица называется матрицей Грамма.
Таким образом, скалярное произведение двух векторов х и у можно записать в следующем виде:
Элементы матрицы Грамма обозначают через gij. Эта матрица носит также название метрического тензора.
Если матрица Грамма равна единичной матрице, то базис является ортонормированным.
Рассмотрим, как изменяются элементы матрицы Грамма при переходе от одного базиса к другому.
Пусть ех, е2. еп— некоторый базис в Е„, которому соответствует матрица Грамма Г, а е, е2. еп — некоторый другой базис с матрицей Грамма Г’. Пусть S — матрица преобразования из базиса е в базис е’. Тогда имеем
Для матрицы Грамма получаем:
Следствие 1: Пусть / = 1. п— произвольные векторы, а Г — их матрица Грамма. Если эти векторы линейно независимы, то их можно принять за базис. Тогда существует преобразование S такое, что Г — S ES. Таким образом, если набор векторов линейно независим, то их матрица Грамма невырожденная. Обратно, если матрица Грамма невырожденная, то векторы линейно независимы.
Следствие 2. Если еп / = 1 . п— ортонормированный базис ОНБ в Е„, а е, i = 1. п — другой ОНБ в Е„, то и Г = Е и Г’ = Е. Тогда очевидно, что существует матрица S такая, что Е = S T S.
Определение 5.8. Матрица S, удовлетворяющая условию S S = Е, называется унитарной (ортогональной). Любая унитарная матрица невырожденная и S — S .
Определение 5.9. Преобразование А евклидова пространства называется унитарным, если оно сохраняет скалярное преобразование всех векторов.
Теорема 5.6. В ортонормированием базисе матрица унитарного преобразования унитарная.
Самосопряженные преобразования
Определение 5.10. Пусть в евклидовом пространстве задано линейное преобразование А. Преобразование А’ называется сопряженным к А, если для любых векторов х и у справедливо соотношение (Ах,у) = (хДУ).
Теорема 5.7. Для каждого линейного преобразования существует, и притом только одно, сопряженное с ним преобразование. Сопряженное преобразование также является линейным.
Определение 5.11. Если сопряженное преобразование совпадает с данным, то оно называется самосопряженным (В комплексном пространстве такое преобразование называется эрмитовым).
Теорема 5.8. Все корни характеристического уравнения эрмитова преобразования вещественны.
Теорема 5.9. Собственные векторы, соответствующие различным собственным значениям эрмитова преобразования, ортогональны.
Теорема 5.10. Каждое эрмитово преобразование определяет орто- нормированный базис из собственных векторов (быть может, неоднозначно).
Содержание
§
Вспомогательная страница к разделу ЕВКЛИДОВО ПРОСТРАНСТВО
Матрица и определитель Грама
Пусть в евклидовом пространстве $ mathbb E_{} $ известным образом задано скалярное произведение $ langle X_{},Y rangle $. Матрицей Грама системы векторов $ {X_{1},dots,X_m } $ называется квадратная матрица, состоящая из всевозможных скалярных произведений этих векторов:
$$
G(X_1,dots,X_m)=
left(
begin{array}{cccc}
langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \
langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \
dots & & & dots \
langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle
end{array}
right)
= left[ langle X_j,X_k rangle right]_{j,k=1}^m .
$$
Матрица Грама является симметричной матрицей.
Ее определитель называется определителем Грама (или грамианом) системы векторов $ {X_{1},dots,X_m } $:
$$
{mathfrak G}(X_1,dots,X_m)=left|
begin{array}{cccc}
langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \
langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \
dots & & & dots \
langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle
end{array}
right| = det left[ langle X_j,X_k rangle right]_{j,k=1}^m .
$$
П
Пример. Если в пространстве $ mathbb R^{ n } $ строк, состоящих из $ n_{} $ вещественных чисел, скалярное произведение определяется по правилу1)
$$ langle X,Y rangle=x_1y_1+x_2y_2+dots+x_ny_n quad npu quad X=(x_1,x_2,dots,x_n), Y=(y_1,y_2,dots,y_n) , $$
то матрица Грама строк
$$ X_1=left(x_{11},x_{12},dots, x_{1n}right),dots,X_m=left(x_{m1},x_{m2},dots, x_{mn}right) $$
вычисляется перемножением матриц:
$$ G(X_1,dots,X_m)=Xcdot X^{top} quad npu quad X=
left(begin{array}{cccc}
x_{11} & x_{12} &dots & x_{1n} \
dots & & & dots \
x_{m1}& x_{m2} & dots & x_{mn}
end{array} right)
$$
и при $ ^{top}_{} $ означающем транспонирование. Из теоремы Бине-Коши немедленно следует, что при $ m>n_{} $ (числе строк превышающем размерность пространства) определитель Грама равен нулю. Этот результат обобщен НИЖЕ для произвольных евклидовых пространств.
П
Пример. Если в пространстве полиномов с вещественными коэффициентами скалярное произведение задано формулой
$$ langle p(x),q(x) rangle =int_0^1 p(t) q(t) d,t ,$$
то
$$ G(1,x,x^2)= left(
begin{array}{ccc}
int_0^1 1 d,t & int_0^1 t d,t & int_0^1 t^2 d,t \
& & \
int_0^1 t d,t & int_0^1 t^2 d,t & int_0^1 t^3 d,t \
& & \
int_0^1 t^2 d,t & int_0^1 t^3 d,t & int_0^1 t^4 d,t
end{array} right)=
left( begin{array}{ccc} 1 & 1/2 & 1/3 \ 1/2 & 1/3 & 1/4 \ 1/3 & 1/4 & 1/5
end{array} right) .
$$
Обобщение получившейся матрицы известно как матрица Гильберта.
Если система векторов $ {X_{1},dots,X_n } $ образует базис пространства $ mathbb E_{} $ (т.е. пространство $ mathbb E_{} $ является $ n_{} $-мерным), то задание матрицы Грама $ G(X_{1},dots,X_n) $ позволяет свести вычисление скалярного произведения произвольных векторов из $ mathbb E_{} $ к действиям над их координатами:
$$ X=x_1X_1+x_2X_2+dots+x_nX_n, Y=y_1X_1+y_2X_2+dots+y_nX_n Rightarrow $$
$$
langle X,Y rangle=left(x_1,x_2,dots,x_n right)
left(
begin{array}{cccc}
langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_n rangle \
langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_n rangle \
dots & & & dots \
langle X_n,X_1 rangle & langle X_n,X_2 rangle & dots & langle X_n,X_n rangle
end{array}
right)
left(
begin{array}{c}
y_1 \
y_2 \
vdots \
y_n
end{array}
right) .
$$
Линейная независимость векторов
Т
Теорема. $ {mathfrak G}(X_{1},dots,X_m)=0 $ тогда и только тогда, когда система векторов $ {X_{1},dots,X_m } $ линейно зависима.
Доказательство
☞
ЗДЕСЬ.
=>
Если какой-то главный минор матрицы Грама обращается в нуль, то и все главные миноры бóльших порядков обращаются в нуль.
Свойства определителя Грама
Т
Теорема. $ {mathfrak G}(X_{1},dots,X_m) ge 0 $ для любой системы векторов $ {X_{1},dots,X_m } $.
Доказательство
☞
ЗДЕСЬ
=>
При $ m=2_{} $ получаем неравенство Коши-Буняковского:
$$ langle X_1,X_1 rangle cdot langle X_2,X_2 rangle ge langle X_1,X_2 rangle^2 . $$
=>
Матрица Грама линейно независимой системы векторов является положительно определенной.
Т
Теорема. Пусть $ X_m^{^{bot}} $ означает ортогональную составляющую вектора $ X_m $ относительно $ {mathcal L}(X_1,dots,X_{m-1}) $. Тогда
$$
mathfrak{G}(X_1,dots,X_{m-1},X_m)=mathfrak{G}(X_1,dots,X_{m-1})left|X_m^{^{bot}}
right|^2 .
$$
Доказательство
☞
ЗДЕСЬ
=>
Величина определителя Грама не превосходит его главного члена, т.е. произведения элементов его главной диагонали:
$$mathfrak{G}(X_1,dots,X_{m-1},X_m)le left|X_1 right|^2 times dots
times left|X_{m-1} right|^2 left|X_m right|^2 . $$
=>
Для произвольной квадратной вещественной матрицы
$$A=left( begin{array}{cccc}
a_{11} & a_{12} & dots & a_{1n} \
a_{21} & a_{22} & dots & a_{2n} \
dots & & & dots \
a_{n1} & a_{n2} & dots & a_{nn}
end{array}
right)
$$
справедливо неравенство Адамара2):
$$
left| det A right| le sqrt{ sum_{j=1}^n a_{1j}^2}
sqrt{ sum_{j=1}^n a_{2j}^2} times dots times
sqrt{ sum_{j=1}^n a_{nj}^2} .
$$
Иными словами: модуль определителя матрицы не превосходит произведения длин
его строк. Аналогичное утверждение справедливо и относительно столбцов матрицы.
Доказательство. Обозначим $ j_{} $-ю строку матрицы $ A_{} $ через $ A^{[j]} $. Тогда, поскольку $ det A= det A^{top} $ (см. свойство
1
☞
ЗДЕСЬ ), имеем:
$$left( det A right)^2= det left(Acdot A^{top} right)= det
left[
begin{array}{cccc}
langle A^{[1]},A^{[1]} rangle & langle A^{[1]},A^{[2]} rangle & dots &
langle A^{[1]},A^{[n]} rangle \
langle A^{[2]},A^{[1]} rangle & langle A^{[2]},A^{[2]} rangle & dots &
langle A^{[2]},A^{[n]} rangle \
dots & & & dots \
langle A^{[n]},A^{[1]} rangle & langle A^{[n]},A^{[2]} rangle & dots &
langle A^{[n]},A^{[n]} rangle
end{array}
right]=
$$
$$
=mathfrak{G}left(A^{[1]},A^{[2]},dots,A^{[n]} right)
$$
при задании скалярного произведения в $ mathbb R^n $ стандартным способом. На основании предыдущего следствия, имеем:
$$
le left|A^{[1]} right|^2 left|A^{[2]} right|^2 times dots times left|A^{[n]} right|^2 .
$$
Равенство возможно тогда и только тогда, когда либо все строки попарно ортогональны, либо хотя бы одна строка — нулевая.
♦
П
Пример.
$$
left|detleft(
begin{array}{rrr}
-47 & 40 & -81 \
91 & 68 & -10 \
31 & -51 & 77
end{array}
right) right| le
$$
$$
le
left{ begin{array}{cl}
sqrt{(47^2+40^2+81^2)(91^2+68^2+10^2)(31^2+51^2+77^2)} &le 1131360 \
& \
sqrt{(47^2+91^2+31^2)(40^2+68^2+51^2)(81^2+10^2+77^2)} & le 1127957
end{array}
right.
$$
при точной величине определителя $ 31867 $.
Т
Теорема. Величина определителя Грама не изменится, если к системе векторов применить алгоритм ортогонализации Грама-Шмидта. В обозначениях этого алгоритма имеет место равенство:
$$ {mathfrak G}(X_{1},dots,X_m) = {mathfrak G}left({mathfrak E}_1,dots, {mathfrak E}_m right)=|{mathfrak E}_1|^2times dots times
|{mathfrak E}_m|^2 . $$
Расстояние до линейного многообразия
Т
Теорема. Расстояние $ d_{} $ от точки $ X_{0} in {mathbb E} $ до линейного многообразия в $ mathbb E_{} $
$$
Y_0+mathcal L(Y_1,dots,Y_k)=
{ Y_0+lambda_1 Y_1+dots+lambda_k Y_k mid
{lambda_1,dots,lambda_k} subset {mathbb R} }
$$
и при фиксированных линейно независимых
$ {Y_{0},Y_1,dots,Y_k }subset {mathbb E} $,
вычисляется по формуле
$$
d=sqrt{frac{{mathfrak G}(Y_1,dots,Y_k, X_0-Y_0)}{{mathfrak G}(Y_1,dots,Y_k)}} .
$$
Доказательство для случая $ Y_0=mathbb O_{} $
☞
ЗДЕСЬ. Случай $ Y_{0}ne mathbb O $ сводится к предыдущему сдвигом пространства на вектор $ (- Y_{0}) $: см. комментарии к теореме $ 5_{} $
☞
ЗДЕСЬ.
♦
§
Другие применения определителя Грама в задачах вычисления расстояний между поверхностями в $ {mathbb R}^{n} $
☞
ЗДЕСЬ.
Объемы параллелепипедов
Площадь параллелограмма равна произведению его основания на высоту. Если параллелограмм построен на векторах $ X_{1} $ и $ X_2 $ из $ mathbb R^2 $, то за основание можно принять длину вектора $ X_{1} $, а за высоту — длину перпендикуляра, опущенного из конца вектора $ X_2 $ на ось вектора $ X_{1} $.
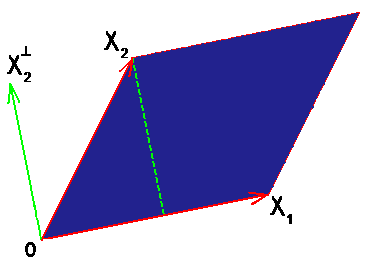
Аналогично, объем параллелепипеда, построенного на векторах $ X_1,X_2,X_3 $ из $ mathbb R^{3} $, равен произведению площади основания на высоту; площадь основания — это площадь параллелограмма, построенного на векторах $ X_1,X_2 $, а высота — длина перпендикуляра, опущенного из конца вектора $ X_3 $ на плоскость векторов $ X_1,X_2 $.
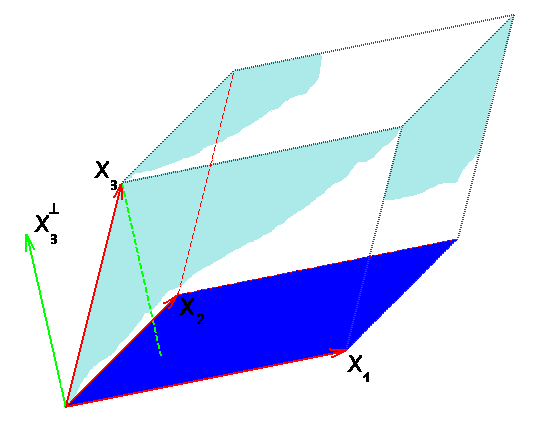
Объем $ k_{} $-мерного параллелепипеда в евклидовом пространстве $ mathbb E_{} $ определим по индукции. Если этот параллелепипед построен на векторах $ X_1,X_2,dots,X_{k-1},X_k $, то за его объем примем произведение объема $ (k-1) $-мерного параллелепипеда, построенного на векторах $ X_1,X_2,dots,X_{k-1} $ на длину перпендикуляра, опущенного из точки $ X_{k} $ на линейную оболочку векторов $ X_1,X_2,dots,X_{k-1} $ (т.е. на длину ортогональной составляющей $ X_k $ относительно $ mathcal L ( X_1,X_2,dots,X_{k-1}) $):
$$mathbf V(X_1,X_2,dots,X_{k-1},X_k)=left|X_k^{bot} right| mathbf V(X_1,X_2,dots,X_{k-1}) . $$
Т
Теорема. Квадрат объема параллелепипеда, построенного на векторах $ X_1,X_2,dots,X_k $, совпадает с величиной определителя Грама от той же системы векторов:
$$[V(X_1,X_2,dots,X_k)]^2= mathfrak G (X_1,X_2,dots,X_k) .$$
Доказательство следует из представления длины ортогональной составляющей $ X_k^{^{bot}} $ через определители Грама (см. теорему $ 2_{} $ и следствие к ней
☞
ЗДЕСЬ ).
=>
Модуль определителя вещественной матрицы
$$ A=
left( begin{array}{cccc}
a_{11} & a_{12} & dots & a_{1n} \
a_{21} & a_{22} & dots & a_{2n} \
dots & & & dots \
a_{n1} & a_{n2} & dots & a_{nn}
end{array}
right)
$$
равен объему параллелепипеда в пространстве $ mathbb R^{n}_{} $, построенного на вершинах с координатами
$$ (0,0,dots, 0), (a_{11},a_{12}, dots , a_{1n}),(a_{21},a_{22}, dots , a_{2n}), dots, (a_{n1},a_{n2}, dots, a_{nn}) $$
(т.е. «построенного на строках матрицы») и равен объему параллелепипеда
построенного на вершинах с координатами
$$ (0,0,dots, 0), (a_{11},a_{21}, dots , a_{n1}),(a_{12},a_{22}, dots , a_{n2}), dots, (a_{1n},a_{2n}, dots, a_{nn}) $$
(т.е. «построенного на столбцах матрицы»).
Доказательство фактически совпадает с доказательством неравенства Адамара:
$$ left(det A right)^2 = left{ begin{array}{cc}
det left(A cdot A^{top}right)=mathfrak G (A^{[1]},A^{[2]},dots,A^{[n]}) &=
left[mathbf V(A^{[1]},A^{[2]},dots,A^{[n]})right]^2 \
& \
det left(A^{top} cdot A right) =
mathfrak G (A_{[1]},A_{[2]},dots,A_{[n]}) & = left[mathbf V(A_{[1]},A_{[2]},dots,A_{[n]})right]^2
end{array} right. $$
♦










![{displaystyle omega ={sqrt {det G}} dx_{1}cdots dx_{k},quad G=left[leftlangle {frac {partial phi }{partial x_{i}}},{frac {partial phi }{partial x_{j}}}rightrangle right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d3b96a447d419a15368a06c085dab203f9a0426)





















