Содержание:
Векторы на плоскости и в пространстве:
Обобщим некоторые сведения о векторах, известные в основном из школьного курса геометрии.
Вектором называется направленный отрезок 
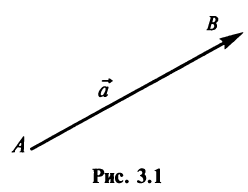
Векторы могут обозначаться как двумя прописными буквами, так и одной строчной с чертой или стрелкой, либо выделяться жирным шрифтом, например:
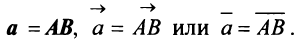
Длиной (или модулем) 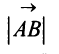 вектора
вектора 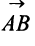 называется число, равное длине отрезка
называется число, равное длине отрезка 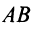 , изображающего вектор.
, изображающего вектор.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коминеарными.
Если начало и конец вектора совпадают, например 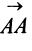 , то такой вектор называют нулевым и обозначают
, то такой вектор называют нулевым и обозначают 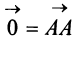 . Длина нулевого вектора равна нулю:
. Длина нулевого вектора равна нулю: 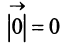 . Так как направление нулевого вектора произвольно, то считают, что он коллинеарен любому вектору.
. Так как направление нулевого вектора произвольно, то считают, что он коллинеарен любому вектору.
Произведением вектора 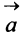 на число
на число 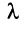 называется вектор
называется вектор 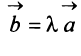 , имеющий длину
, имеющий длину 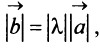 направление которого совпадает с направлением вектора
направление которого совпадает с направлением вектора 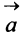 , если
, если 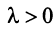 , и противоположно ему, если
, и противоположно ему, если 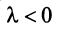 (рис. 3.2).
(рис. 3.2).
Противоположным вектором 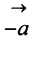 называется произведение вектора
называется произведение вектора 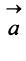 на число
на число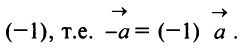
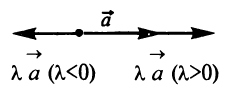
Рис. 32
Суммой двух векторов  и
и  называется вектор
называется вектор 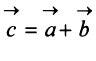 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец с концом вектора
, а конец с концом вектора  при условии, что начало вектора
при условии, что начало вектора  совпадает с концом вектора
совпадает с концом вектора  (рис. 3.3) (правило треугольника).
(рис. 3.3) (правило треугольника). 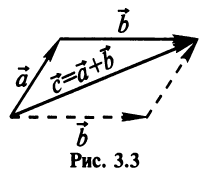
Очевидно, что вектор  в этом случае представляет диагональ параллелограмма, построенного на векторах
в этом случае представляет диагональ параллелограмма, построенного на векторах  и
и  (рис. 3.3) (правило параллелограмма).
(рис. 3.3) (правило параллелограмма).
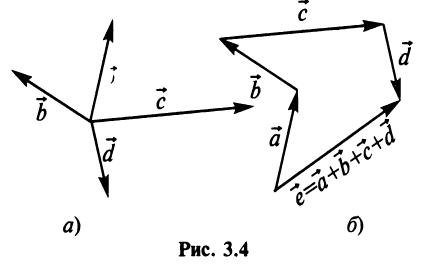
Аналогично определяется сумма нескольких векторов. Так, например, сумма четырех векторов 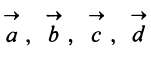 (рис. 3.4а) есть вектор
(рис. 3.4а) есть вектор 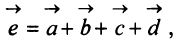 начало которого совпадает с началом вектора
начало которого совпадает с началом вектора  , а конец — с концом вектора
, а конец — с концом вектора 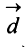 (правило многоугольника) (рис. 3.4 б).
(правило многоугольника) (рис. 3.4 б).
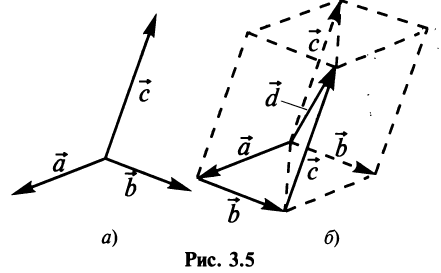
Нетрудно убедиться. что вектор 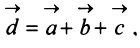 определяемый таким образом, представляет диагональ параллелепипеда, построенного на векторах
определяемый таким образом, представляет диагональ параллелепипеда, построенного на векторах  ,
, и
и 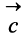 , не лежащих в одной плоскости или в параллельных плоскостях (правило параллелепипеда) (рис. 3.5).
, не лежащих в одной плоскости или в параллельных плоскостях (правило параллелепипеда) (рис. 3.5).
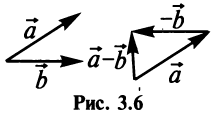
Разностью двух векторов  и
и  называется сумма вектора
называется сумма вектора  и вектора
и вектора  , противоположного
, противоположного  (рис. 3.6).
(рис. 3.6).
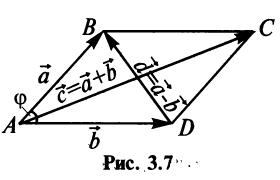
Легко убедиться в том, что в параллелограмме, построенном на векторах 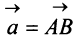 и
и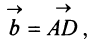 одна диагональ — вектор —представляет сумму векторов
одна диагональ — вектор —представляет сумму векторов  и
и  , а другая диагональ — вектор
, а другая диагональ — вектор 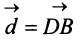 — их разность (рис. 3.7).
— их разность (рис. 3.7).
Перенесем вектор  параллельно самому себе так, чтобы его начало совпало с началом координат. Координатами вектора
параллельно самому себе так, чтобы его начало совпало с началом координат. Координатами вектора  называются координаты его конечной точки. Так, вектор
называются координаты его конечной точки. Так, вектор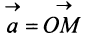 на плоскости
на плоскости 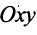 являются два числа
являются два числа 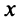 и
и 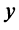 (
( 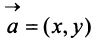 — рис. 3.8.), а в пространстве
— рис. 3.8.), а в пространстве 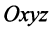 — три числа
— три числа 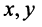 и
и 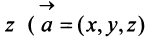 — рис. 3.9).
— рис. 3.9).
В соответствии с определениями, приведенными выше, нетрудно показать, что суммой и разностью векторов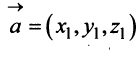 и
и 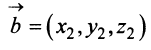 являются соответственно векторы
являются соответственно векторы
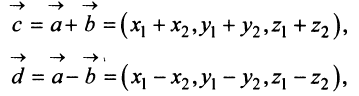 ,
,
а произведение вектора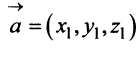 на число
на число 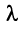 есть вектор
есть вектор 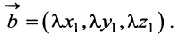 На рис. 3.8 и 3.9 видно, что длина вектора равна корню квадратному из суммы квадратов его координат:
На рис. 3.8 и 3.9 видно, что длина вектора равна корню квадратному из суммы квадратов его координат:
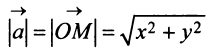 или
или
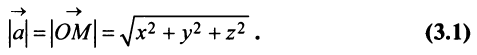
Определение. Скалярным произведением 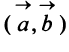 двух векторов
двух векторов  и
и  называется число, равное произведению длин этих векторов на косинус угла
называется число, равное произведению длин этих векторов на косинус угла 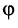 между ними:
между ними:
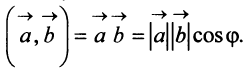
Выразим скалярное произведение через координаты векторов  и
и  .
.
Из треугольника 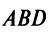 (рис. 3.7), сторонами которого являются векторы
(рис. 3.7), сторонами которого являются векторы 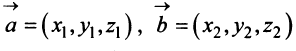 и
и 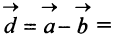
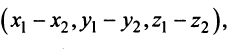 по теореме косинусов следует, что
по теореме косинусов следует, что
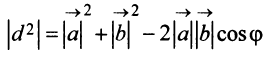 , откуда
, откуда 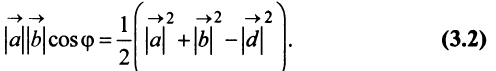
Учитывая формулу длины вектора (3.1) найдем
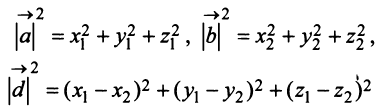 и после преобразования выражения (3.2) получим
и после преобразования выражения (3.2) получим
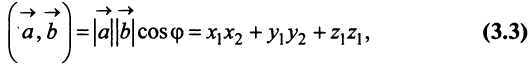
т.е. скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
Заметим, что при 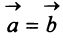 угол
угол 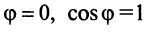 и
и
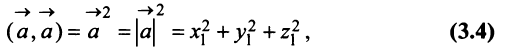
т.е. скалярный квадрат вектора равен квадрату его длины.
В частности, расстояние 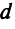 между двумя точками плоскости
между двумя точками плоскости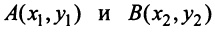 можно рассматривать как длину вектора
можно рассматривать как длину вектора 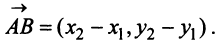
Поэтому 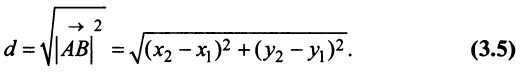
Угол между векторами и
и  определяется по формуле
определяется по формуле
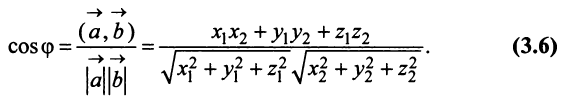
Пример:
Даны векторы 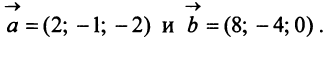
Найти: а)векторы 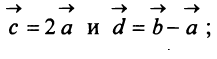 б)длины векторов
б)длины векторов  и
и 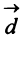 ; в) скалярный квадрат вектора
; в) скалярный квадрат вектора 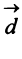 ; г) скалярное произведение векторов
; г) скалярное произведение векторов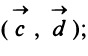 д)угол между векторами
д)угол между векторами 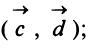
Решение:
а) По определению 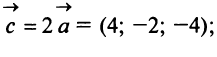
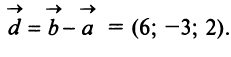
б) По формуле (3.1) найдем длины векторов 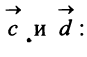
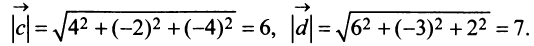
в) По формуле (3.4) скалярный квадрат равен квадрату модуля вектора, т.е.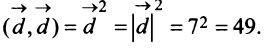
г) По формуле (3.3) скалярное произведение
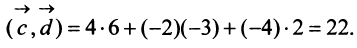
д) По формуле (3.6) угол между векторами 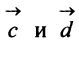 определяется равенством:
определяется равенством:
 >мерный вектор и векторное пространство
>мерный вектор и векторное пространство
Множества всех плоских или пространственных векторов, рассмотренных выше, в которых определены операции сложения векторов и умножения вектора на число, являются простейшими примерами векторных пространств. Ниже обобщается понятие вектора и дается определение векторного пространства.
Определение. -мерным вектором называется упорядоченная совокупность
-мерным вектором называется упорядоченная совокупность 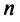 действительных чисел, записываемых в виде
действительных чисел, записываемых в виде 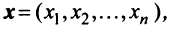 где
где 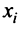 —
— 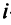 -я компонента вектора
-я компонента вектора 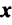 .
.
Понятие  -мерного вектора широко используется в экономике, например некоторый набор товаров можно охарактеризовать вектором
-мерного вектора широко используется в экономике, например некоторый набор товаров можно охарактеризовать вектором 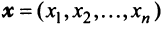 , а соответствующие цены — вектором
, а соответствующие цены — вектором 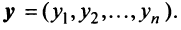
Два  -мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е.
-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е. 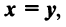 если
если 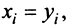
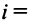
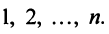
Суммой двух векторов одинаковой размерности п называется вектор 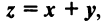 компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е.
компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е. 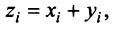
Произведением вектора  на действительное число
на действительное число 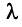 называется вектор
называется вектор 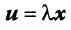 , компоненты
, компоненты 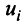 которого равны произведению
которого равны произведению 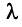 на соответствующие компоненты вектора
на соответствующие компоненты вектора  , т.е.
, т.е. 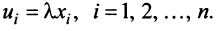
Линейные операции над любыми векторами удовлетворяют следующим свойствам:
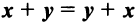 — коммутативное (переместительное) свойство суммы:
— коммутативное (переместительное) свойство суммы: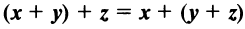 — ассоциативное (сочетательное) свойство суммы;
— ассоциативное (сочетательное) свойство суммы;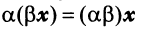 — ассоциативное относительно числового множителя свойство;
— ассоциативное относительно числового множителя свойство;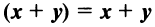 — дистрибутивное (распределительное) относительно суммы векторов свойство;
— дистрибутивное (распределительное) относительно суммы векторов свойство;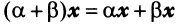 —дистрибутивное относительно суммы числовых множителей свойство;
—дистрибутивное относительно суммы числовых множителей свойство;- Существует нулевой вектор
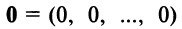 такой, что
такой, что 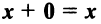 для любого вектора
для любого вектора  (особая роль нулевого вектора);
(особая роль нулевого вектора); - Для любого вектора
 существует противоположный вектор
существует противоположный вектор 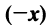 такой, что
такой, что 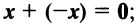
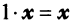 для любого вектора
для любого вектора  (особая роль числового множителя 1).
(особая роль числового множителя 1).
Определение. Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше восьми свойствам (рассматриваемым как аксиомы), называется векторным пространством.
Следует отметить, что под 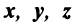 можно рассматривать не только векторы, но и элементы (объекты) любой природы. В этом случае соответствующее множество элементов называется линейным пространством.
можно рассматривать не только векторы, но и элементы (объекты) любой природы. В этом случае соответствующее множество элементов называется линейным пространством.
Линейным пространством является, например, множество всех алгебраических многочленов степени, не превышающей натурального числа 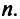 Легко убедиться, что если х и у — многочлены степени не выше п, то они будут обладать свойствами 1—8. Заметим для сравнения, что, например, множество всех многочленов степени, точно равной натуральному числу
Легко убедиться, что если х и у — многочлены степени не выше п, то они будут обладать свойствами 1—8. Заметим для сравнения, что, например, множество всех многочленов степени, точно равной натуральному числу  , не является линейным пространством, так как в нем не определена операция сложения элементов, ибо сумма двух многочленов может оказаться многочленом степени ниже
, не является линейным пространством, так как в нем не определена операция сложения элементов, ибо сумма двух многочленов может оказаться многочленом степени ниже  . А множество многочленов степени не выше
. А множество многочленов степени не выше  , но с положительными коэффициентами также не является линейным пространством, поскольку в этом множестве не определена операция умножения элемента на число: такие многочлены нельзя умножать на отрицательные числа.
, но с положительными коэффициентами также не является линейным пространством, поскольку в этом множестве не определена операция умножения элемента на число: такие многочлены нельзя умножать на отрицательные числа.
Из определения векторного (линейного) пространства, в частности из аксиом 1-8, вытекает существование единственного нулевого вектора, равного произведению произвольного вектора  на действительное число 0 и существование для каждого вектора
на действительное число 0 и существование для каждого вектора 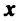 единственного противоположного вектора (—
единственного противоположного вектора (—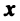 ), равного произведению этого вектора на действительное число (- 1).
), равного произведению этого вектора на действительное число (- 1).
Размерность и базис векторного пространства
Понятия линейной комбинации, линейной зависимости и независимости векторов вводятся аналогично тому, как это было сделано в § 1.6 для строк матрицы.
Определение. Вектор 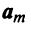 называется линейной комбинацией векторов
называется линейной комбинацией векторов  векторного пространства
векторного пространства 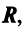 если он равен сумме произведений этих векторов на произвольные действительные числа:
если он равен сумме произведений этих векторов на произвольные действительные числа:
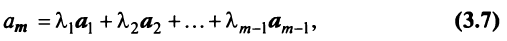
где 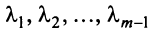 — какие угодно действительные числа.
— какие угодно действительные числа.
Определение. Векторы  векторного пространства
векторного пространства 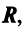 называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 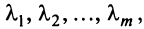 не равные одновременно нулю, что
не равные одновременно нулю, что
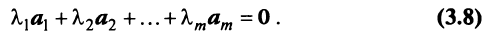
В противном случае векторы  называются линейно независимыми.
называются линейно независимыми.
Из приведенных выше определений следует, что векторы  линейно независимы, если равенство (3.8) справедливо лишь при
линейно независимы, если равенство (3.8) справедливо лишь при 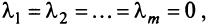 и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел
и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел 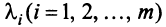 отлично от нуля.
отлично от нуля.
Можно показать (аналогично § 1.6), что если векторы  линейно зависимы, то по крайней мере один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов выражается линейно через остальные, то все эти векторы в совокупности линейно зависимы.
линейно зависимы, то по крайней мере один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов выражается линейно через остальные, то все эти векторы в совокупности линейно зависимы.
Примером линейно независимых векторов являются два не-коллинеарных, т.е. не параллельных одной прямой, вектора 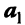 и
и 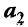 на плоскости. Действительно, условие (3.8)
на плоскости. Действительно, условие (3.8) 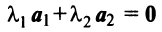 будет выполняться лишь в случае, когда
будет выполняться лишь в случае, когда 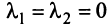 , ибо если, например,
, ибо если, например, 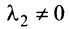 , то
, то 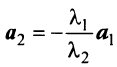 , и векторы
, и векторы 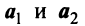 коллинеарны. Однако любые три вектора плоскости линейно зависимы.
коллинеарны. Однако любые три вектора плоскости линейно зависимы.
Отметим некоторые свойства векторов линейного пространства:
- Если среди векторов
 имеется нулевой вектор, то эти векторы линейно зависимы. В самом деле, если, например,
имеется нулевой вектор, то эти векторы линейно зависимы. В самом деле, если, например, 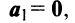 то равенство (3.8) справедливо при
то равенство (3.8) справедливо при 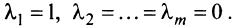
- Если часть векторов
 являются линейно зависимыми, то и все эти векторы — линейно зависимые. Действительно, если, например, векторы
являются линейно зависимыми, то и все эти векторы — линейно зависимые. Действительно, если, например, векторы 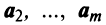 линейно зависимы, то справедливо равенство
линейно зависимы, то справедливо равенство 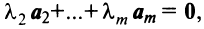 в котором не все числа равны нулю. Но тогда с теми же числами
в котором не все числа равны нулю. Но тогда с теми же числами 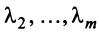 и
и 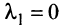 будет справедливо равенство (3.8).
будет справедливо равенство (3.8).
Пример:
Выяснить, являются ли векторы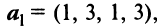
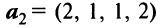 и
и 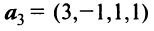 линейно зависимыми.
линейно зависимыми.
Решение:
Составим векторное равенство 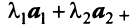
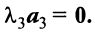 Записывая
Записывая 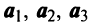 в виде вектор-столбцов, получим
в виде вектор-столбцов, получим 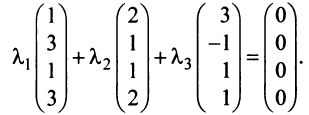
Задача свелась таким образом к решению системы:
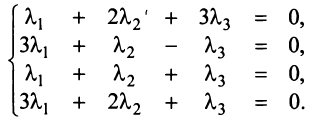
Решая систему методом Гаусса (см. § 2.3), приведем ее к виду:
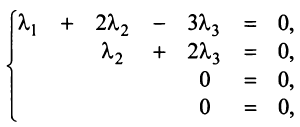
откуда найдем, бесконечное множество ее решений 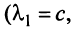
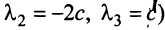 , где с — произвольное действительное число.
, где с — произвольное действительное число.
Итак, для ‘данных векторов условие (3.8) выполняется не только при 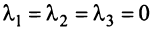 (а, например, при
(а, например, при 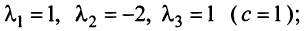 при
при 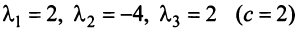 и т.д.), следовательно, эти векторы — линейно зависимые. ►
и т.д.), следовательно, эти векторы — линейно зависимые. ►
Определение. Линейное пространство  называется
называется 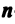 -мерным, если в нем существует я линейно независимых векторов, а любые из
-мерным, если в нем существует я линейно независимых векторов, а любые из 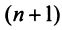 векторов уже являются зависимыми. Другими словами, размерность пространства — это максимальное число содержащихся в нем линейно независимых векторов. Число
векторов уже являются зависимыми. Другими словами, размерность пространства — это максимальное число содержащихся в нем линейно независимых векторов. Число  называется размерностью пространства
называется размерностью пространства  и обозначается
и обозначается 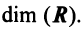
Определение. Совокупность  линейно независимых векторов
линейно независимых векторов  -мерного пространства
-мерного пространства  называется базисом. Справедлива следующая теорема.
называется базисом. Справедлива следующая теорема.
Теорема. Каждый вектор  линейного пространства
линейного пространства  можно представить
можно представить 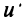 притом единственным способом в виде линейной комбинации векторов базиса.
притом единственным способом в виде линейной комбинации векторов базиса.
 Пусть векторы
Пусть векторы 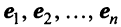 образуют произвольный базис
образуют произвольный базис  -мерного пространства
-мерного пространства  . Так как любые из (
. Так как любые из ( +1) векторов
+1) векторов  -мерного пространства R зависимы, то будут зависимы, в частности, векторы
-мерного пространства R зависимы, то будут зависимы, в частности, векторы 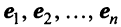 и рассматриваемый вектор
и рассматриваемый вектор  . Тогда существуют такие не равные одновременно нулю числа
. Тогда существуют такие не равные одновременно нулю числа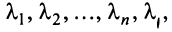 что
что
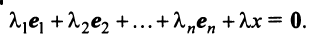
При этом 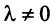 , ибо в противном случае, если
, ибо в противном случае, если 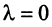 и хотя бы одно из чисел
и хотя бы одно из чисел 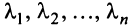 было бы отлично от нуля, то векторы
было бы отлично от нуля, то векторы 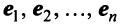 были бы линейно зависимы. Следовательно,
были бы линейно зависимы. Следовательно,
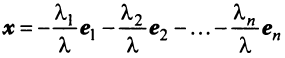 или
или
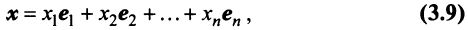
где 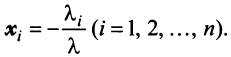
Это выражение 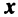 через
через  единственное, так как если допустить какое-либо другое выражение, например,
единственное, так как если допустить какое-либо другое выражение, например,
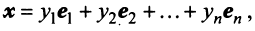 то, вычитая из него почленно (3.9), получим
то, вычитая из него почленно (3.9), получим
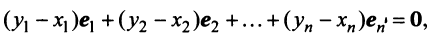 откуда из условия линейной независимости векторов
откуда из условия линейной независимости векторов следует, что ‘
следует, что ‘
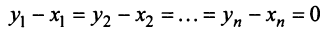 или
или
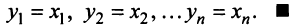
Равенство (3.9) называется разложением вектора  по базису
по базису  , а числа
, а числа 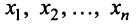 — координатами вектора
— координатами вектора  относительно этого базиса. В силу единственности разложения (3.9) каждый вектор однозначно может быть определен координатами в некотором базисе.
относительно этого базиса. В силу единственности разложения (3.9) каждый вектор однозначно может быть определен координатами в некотором базисе.
Очевидно, что нулевой вектор имеет все нулевые координаты, а вектор, противоположный данному, — противоположные по знаку координаты.
Важное значение имеет следующая теорема.
Теорема. Если  — система линейно независимых векторов пространства
— система линейно независимых векторов пространства  и любой вектор
и любой вектор 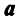 линейно выражается через
линейно выражается через  , то пространство
, то пространство  является n-мерным, а векторы
является n-мерным, а векторы  — его базисом.
— его базисом.
 Возьмем произвольные
Возьмем произвольные 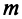 векторов пространства
векторов пространства  , где
, где 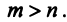 По условию каждый из них можно линейно выразить через
По условию каждый из них можно линейно выразить через  :
:
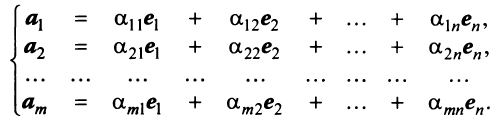 Рассмотрим матрицу
Рассмотрим матрицу 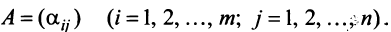
Ранг этой матрицы не превосходит 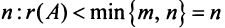 , следовательно, среди ее строк не более
, следовательно, среди ее строк не более 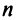 линейно независимых. Так как
линейно независимых. Так как 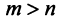 , то
, то 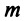 строк этой матрицы, а значит, и
строк этой матрицы, а значит, и 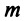 векторов
векторов 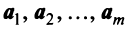 линейно зависимы. Таким образом, пространство
линейно зависимы. Таким образом, пространство 
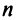 -мерно и
-мерно и  — его базис. ■
— его базис. ■
Пример:
В базисе 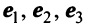 заданы векторы
заданы векторы 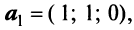
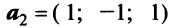 и
и 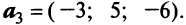 Показать, что векторы
Показать, что векторы 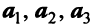 образуют базис.
образуют базис.
Решение:
Векторы 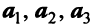 образуют базис, если они линейно независимы. Составим векторное равенство:
образуют базис, если они линейно независимы. Составим векторное равенство: 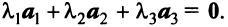 Решая его аналогично примеру 3.2, можно убедиться в единственном нулевом его решении:
Решая его аналогично примеру 3.2, можно убедиться в единственном нулевом его решении: 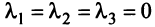 , т.е. векторы
, т.е. векторы 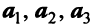 образуют систему линейно независимых векторов и, следовательно, составляют базис. ►
образуют систему линейно независимых векторов и, следовательно, составляют базис. ►
Переход к новому базису
Пусть в пространстве  имеются два базиса: старый
имеются два базиса: старый  и новый
и новый 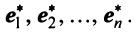 Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:
Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса: 
Полученная система означает, что переход от старого базиса  кновому
кновому 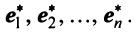 задается матрицей перехода
задается матрицей перехода 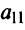 и тд.
и тд. 
причем коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.
Матрица 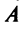 — неособенная, так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса
— неособенная, так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса 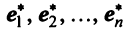 к старому базису
к старому базису 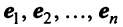 осуществляется с помощью обратной матрицы
осуществляется с помощью обратной матрицы 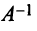 .
.
Найдем зависимость между координатами вектора в разных базисах. Пусть рассматриваемый вектор 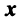 имеет координаты
имеет координаты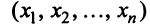 относительно старого базиса и координаты
относительно старого базиса и координаты 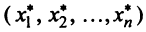 относительно нового базиса, т.е.
относительно нового базиса, т.е.
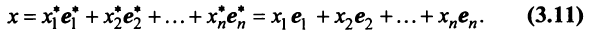
Подставив значения 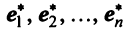 из системы (3.10) в левую часть равенства (3.11), получим после преобразований:
из системы (3.10) в левую часть равенства (3.11), получим после преобразований:
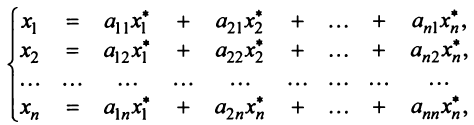
т.е. в матричной форме
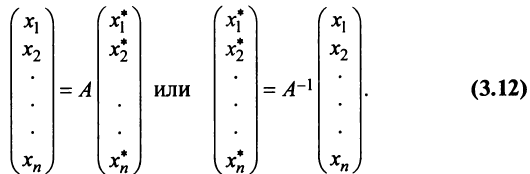
Пример:
По условию примера 3.3 вектор 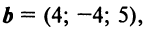 заданный в базисе
заданный в базисе 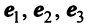 , выразить в базисе
, выразить в базисе 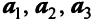 .
.
Решение:
Выразим связь между базисами: 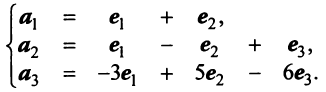
Матрица перехода от базиса 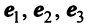 к базису
к базису 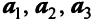 имеет вид
имеет вид 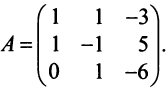 Вычисляем
Вычисляем 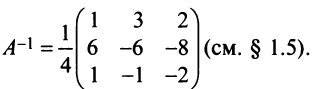 Теперь по (3.12)
Теперь по (3.12) 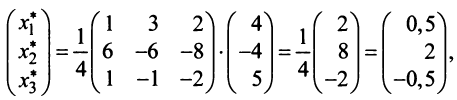
т.е. новые координаты вектора  в базисе
в базисе  есть 0,5; 2 и -0,5 и вектор
есть 0,5; 2 и -0,5 и вектор 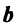 может быть представлен в виде:
может быть представлен в виде: 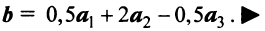
Евклидово пространство
Выше мы определили линейное (векторное) пространство, в котором можно складывать векторы и умножать их на числа, ввели понятие размерности и базиса, а теперь в данном пространстве введем метрику, т.е. способ измерять длины и углы. Это можно, например, сделать, если ввести понятие скалярного произведения.
Определение. Скалярным произведением двух векторов  и
и  называется число
называется число
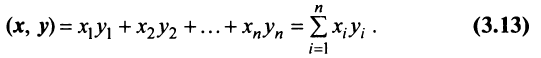
Скалярное произведение имеет экономический смысл. Если 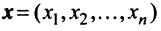 есть вектор объемов различных товаров, а
есть вектор объемов различных товаров, а 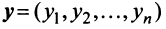 вектор их цен, то скалярное произведение
вектор их цен, то скалярное произведение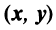 выражает суммарную стоимость этих товаров.
выражает суммарную стоимость этих товаров.
Скалярное произведение имеет следующие свойства:
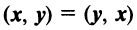 — коммутативное свойство;
— коммутативное свойство;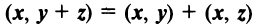 — дистрибутивное свойство;
— дистрибутивное свойство;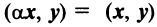 — для любого действительного числа;
— для любого действительного числа;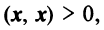 если
если 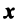 — ненулевой вектор;
— ненулевой вектор; 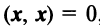 , если
, если 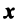 — нулевой вектор.
— нулевой вектор.
Определение. Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам (рассматриваемым как аксиомы), называется евклидовым пространством.
Длиной (нормой) вектора 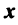 в евклидовом пространстве называется корень квадратный из его скалярного квадрата:
в евклидовом пространстве называется корень квадратный из его скалярного квадрата:
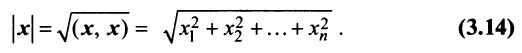
Имеют место следующие свойства длины вектора:
1. 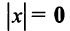 тогда и только тогда, когда
тогда и только тогда, когда 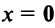 ;
;
2. 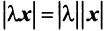 , где
, где 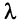 — действительное число;
— действительное число;
3. 
(неравенство Коши—Буняковского);
4. 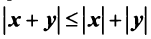 (неравенство треугольника).
(неравенство треугольника).
Угол 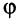 между двумя векторами
между двумя векторами  и
и 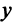 определяется равенством
определяется равенством
 где
где 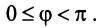
Такое определение вполне корректно, так как согласно неравенству Коши—Буняковского (3.15) 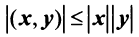 , т.е.
, т.е. 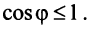
Два вектора называются ортогональными, если их скалярное произведение равно нулю. Очевидно, что нулевой вектор ортогонален любому другому вектору. Из определения следует, что если два ненулевых вектора ортогональны, то угол между ними равен 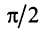 (ибо
(ибо 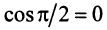 ).
).
Векторы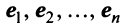
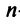 -мерного евклидова пространства образуют ортогональный базис, если эти векторы попарно ортогональны, и ортонормированный базис, если эти векторы попарно ортогональны и норма каждого из них равна единице, т.е. если
-мерного евклидова пространства образуют ортогональный базис, если эти векторы попарно ортогональны, и ортонормированный базис, если эти векторы попарно ортогональны и норма каждого из них равна единице, т.е. если 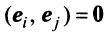 при
при 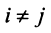 и |
и |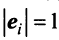 при
при 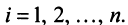
Для установления корректности приведенного определения необходимо убедиться в том, что входящие в него векторы 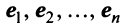 образуют один из базисов рассматриваемого
образуют один из базисов рассматриваемого 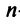 -мерного пространства
-мерного пространства  (т.е.
(т.е. 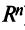 ). Для этого достаточно показать, что векторы
). Для этого достаточно показать, что векторы 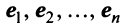 линейно независимы, т.е. равенство
линейно независимы, т.е. равенство
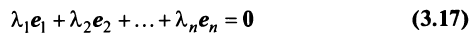
справедливо лишь при 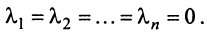
Действительно, умножая скалярно равенство (3.17) на любой вектор 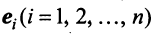 , получим
, получим
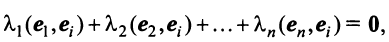
откуда, учитывая, что 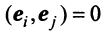 при
при 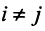 и
и 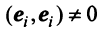 при всех
при всех 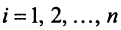 , вытекает, что
, вытекает, что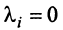 при всех
при всех 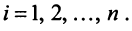
Сформулируем теперь (без доказательства) основную теорему.
Теорема. Во всяком 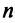 -мерном евклидовом пространстве существует ортонормированный базис.
-мерном евклидовом пространстве существует ортонормированный базис.
Примером ортонормированного базиса является система 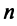 единичных векторов
единичных векторов 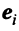 у которых
у которых 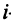 -я компонента равна единице, а остальные компоненты равны нулю:
-я компонента равна единице, а остальные компоненты равны нулю: 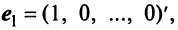
Линейные операторы
Одно из фундаментальных понятий матричной алгебры — понятие линейного оператора.
Рассмотрим два линейных пространства:  размерности
размерности 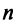 и
и  размерности
размерности 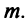
Определение. Если задан закон (правило), по которому каждому вектору  пространства
пространства  ставится в соответствие единственный вектор у пространства
ставится в соответствие единственный вектор у пространства  , то говорят, что задан оператор (преобразование, отображение)
, то говорят, что задан оператор (преобразование, отображение) 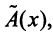 действующий из
действующий из  в
в  , и записывают
, и записывают 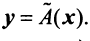
Оператор (преобразование) называется линейным, если для любых векторов  и
и 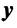 пространства
пространства  и любого числа
и любого числа 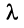 выполнился соотношения:
выполнился соотношения:
- 1.
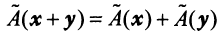 — свойство аддитивности оператора;
— свойство аддитивности оператора; - 2.
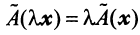 — свойство однородности оператора.
— свойство однородности оператора.
Вектор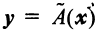 называется образом вектора
называется образом вектора  , а сам вектор
, а сам вектор  — прообразом вектора
— прообразом вектора 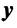 .
.
Если пространства  и
и  совпадают, то оператор
совпадают, то оператор  отображает пространство
отображает пространство  в себя. Именно такие операторы мы будем рассматривать в дальнейшем.
в себя. Именно такие операторы мы будем рассматривать в дальнейшем.
Выберем в пространстве  базис eh
базис eh  и, учитывая (3.9), запишем разложение произвольного вектора
и, учитывая (3.9), запишем разложение произвольного вектора 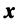 по данному базису:
по данному базису:
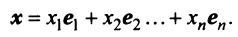
В силу линейности оператора  получаем
получаем
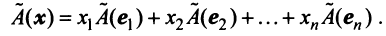
Поскольку 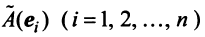 — также вектор из
— также вектор из  , то его можно разложить по базис
, то его можно разложить по базис . Пусть
. Пусть
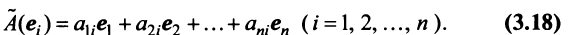
Тогда
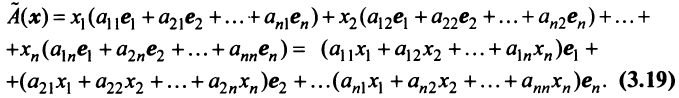
С другой стороны, вектор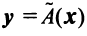 , имеющий в том же базисе
, имеющий в том же базисе  координаты
координаты 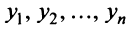 , можно записать так:
, можно записать так:
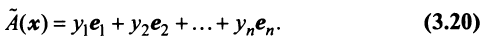
Ввиду единственности разложения вектора по базису равны правые части равенства (3.19) и (3.20), откуда
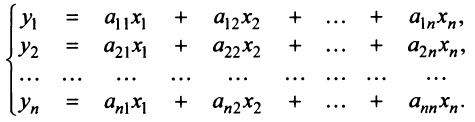
Матрица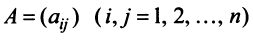 называется матрицей оператора
называется матрицей оператора  в базисе
в базисе  , а ранг
, а ранг 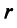 матрицы
матрицы 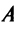 — рангом оператора
— рангом оператора  .
.
Таким образом, каждому линейному оператору соответствует матрица в данном базисе. Справедливо и обратное: всякой матрице 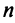 -го порядка соответствует линейный оператор
-го порядка соответствует линейный оператор 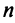 -мерного пространства.
-мерного пространства.
Связь между вектором 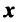 и его образом
и его образом 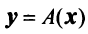 можно выразить в матричной форме уравнением
можно выразить в матричной форме уравнением

где 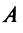 — матрица линейного оператора,
— матрица линейного оператора, 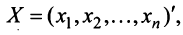
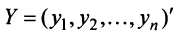 – матрицы-столбцы из координат векторов
– матрицы-столбцы из координат векторов  и
и 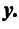
Пример:
Пусть в пространстве 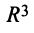 линейный оператор
линейный оператор  в базисе
в базисе 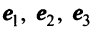 задан матрицей
задан матрицей 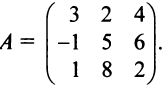 Найти образ
Найти образ 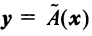 вектора
вектора 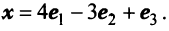
Решение:
По формуле (3.21) имеем 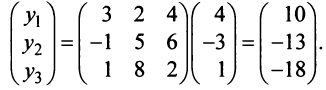
Следовательно, 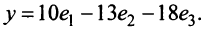 ►
►
Определим действия над линейными операторами.
Суммой двух линейных операторов 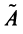 и
и 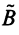 называется оператор
называется оператор 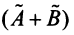 , определяемый равенством:
, определяемый равенством: 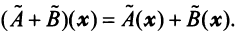
Произведением линейного оператора  на число
на число 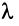 называется оператор
называется оператор 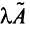 , определяемый равенством
, определяемый равенством 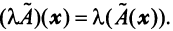
Произведением линейных операторов 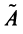 и
и 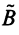 называется оператор
называется оператор 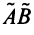 , определяемый равенством:
, определяемый равенством: 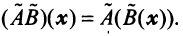
Можно убедиться в том, что операторы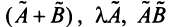 , полученные в результате этих действий, удовлетворяют отмеченным выше свойствам аддитивности и однородности, т.е. являются линейными.
, полученные в результате этих действий, удовлетворяют отмеченным выше свойствам аддитивности и однородности, т.е. являются линейными.
Определим нулевой оператор 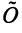 , переводящий все векторы пространства
, переводящий все векторы пространства 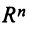 в нулевые векторы
в нулевые векторы 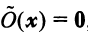 , и тождественный оператор
, и тождественный оператор 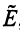 , действующий по правилу:
, действующий по правилу: 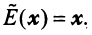
Зависимость между матрицами одного и того же оператора в разных базисах выражается теоремой.
Теорема. Матрицы  и
и 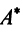 линейного оператора
линейного оператора  в базисах
в базисах 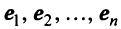 и
и 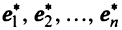 связаны соотношением
связаны соотношением

где  — матрица перехода от старого базиса к новому.
— матрица перехода от старого базиса к новому.
 При воздействии линейного оператора
При воздействии линейного оператора  вектор
вектор  пространства
пространства  переводится в вектор
переводится в вектор  этого пространства, т.е. справедливо равенство (3.21) (в старом базисе) и равенство
этого пространства, т.е. справедливо равенство (3.21) (в старом базисе) и равенство

(в новом базисе). Так как 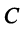 — матрица перехода от старого базиса к новому, то в соответствии с (3.12)
— матрица перехода от старого базиса к новому, то в соответствии с (3.12)

Умножим равенство (3.24) слева на матрицу  , получим
, получим 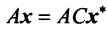 или с учетом (3.21)
или с учетом (3.21) 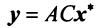 . Заменив левую часть полученного выражения в соответствии с (3.25), имеем:
. Заменив левую часть полученного выражения в соответствии с (3.25), имеем: 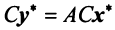 или
или 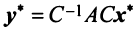 . Сравнивая найденное выражение с (3.23), мы получим доказываемую формулу (3.22).
. Сравнивая найденное выражение с (3.23), мы получим доказываемую формулу (3.22). 
Пример:
В базисе 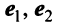 оператор (преобразование)
оператор (преобразование)  имеет матрицу
имеет матрицу 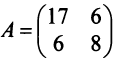 . Найти матрицу оператора
. Найти матрицу оператора  в базисе
в базисе 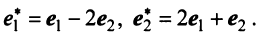
Решение:
Матрица перехода здесь 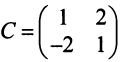 , а обратная к ней матрица
, а обратная к ней матрица 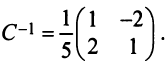 Следовательно, по (3.22)
Следовательно, по (3.22)
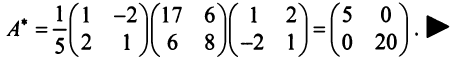
Собственные векторы и собственные значения линейного оператора
Определение. Вектор  называется собственным вектором линейного оператора
называется собственным вектором линейного оператора  , если найдется такое число
, если найдется такое число 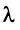 , что
, что

Число 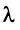 называется собственным значением оператора
называется собственным значением оператора  (матрицы
(матрицы  ), соответствующим вектору
), соответствующим вектору 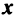 .
.
Из определения следует, что собственный вектор под действием линейного оператора  переходит в вектор, коллинеарный самому себе, т.е. просто умножается на некоторое число. В то же время несобственные векторы преобразуются более сложным образом. В связи с этим понятие собственного вектора является очень полезным и удобным при изучении многих вопросов матричной алгебры и ее приложений.
переходит в вектор, коллинеарный самому себе, т.е. просто умножается на некоторое число. В то же время несобственные векторы преобразуются более сложным образом. В связи с этим понятие собственного вектора является очень полезным и удобным при изучении многих вопросов матричной алгебры и ее приложений.
Равенство (3.26) можно записать в матричной форме:

где вектор 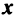 представлен в виде вектора-столбца, или в развернутом виде
представлен в виде вектора-столбца, или в развернутом виде
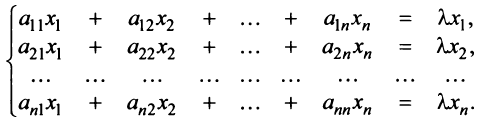
Перепишем систему так, чтобы в правых частях были нули:
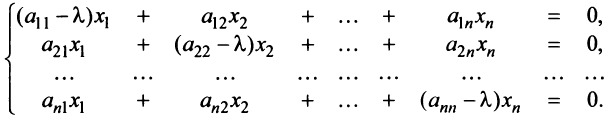
или в матричном виде
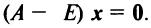
Полученная однородная система всегда имеет нулевое решение 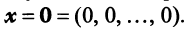 Для существования ненулевого решения (см. § 2.5) необходимо и достаточно, чтобы определитель системы
Для существования ненулевого решения (см. § 2.5) необходимо и достаточно, чтобы определитель системы
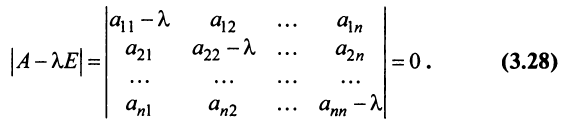
Определитель 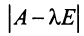 является многочленом
является многочленом 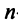 -й степени относительно
-й степени относительно 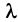 . Этот многочлен называется характеристическим многочленом оператора
. Этот многочлен называется характеристическим многочленом оператора  или матрицы
или матрицы  , а уравнение (3.28) — характеристическим уравнением оператора
, а уравнение (3.28) — характеристическим уравнением оператора  или матрицы
или матрицы  .
.
Характеристический многочлен линейного оператора не зависит от выбора базиса. В самом деле, преобразуем характеристический многочлен 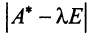 полученный в новом базисе
полученный в новом базисе 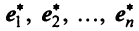 , если известна матрица
, если известна матрица 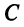 перехода от старого базиса
перехода от старого базиса 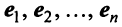 к новому. С учетом (3.22) получим
к новому. С учетом (3.22) получим
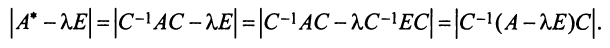
Учитывая, что определитель произведения квадратных матриц одинакового порядка равен произведению определителей этих матриц (см. §1.4), получим
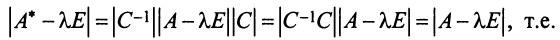
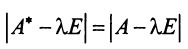 независимо от выбора базиса.
независимо от выбора базиса.
Пример:
Найти собственные значения и собственные векторы линейного оператора  , заданного матрицей
, заданного матрицей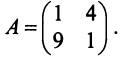
Решение:
Составляем характеристическое уравнение 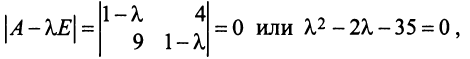
откуда собственные значения линейного оператора 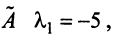
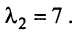
Находим собственный вектор 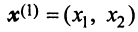 , соответствующий собственному значению
, соответствующий собственному значению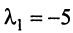 . Для этого решаем матричное уравнение
. Для этого решаем матричное уравнение
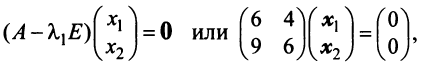 откуда находим
откуда находим 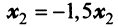 . Положив
. Положив 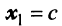 , получим, что векторы
, получим, что векторы 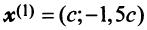 при любом
при любом 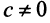 являются собственными векторами линейного оператора
являются собственными векторами линейного оператора  с собственным значением
с собственным значением 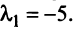
Аналогично можно убедиться в том, что векторы 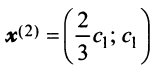 при любом
при любом 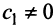 являются собственными векторами линейного оператора
являются собственными векторами линейного оператора  с собственным значением
с собственным значением 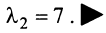
Наиболее простой вид принимает матрица 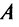 линейного оператора
линейного оператора  , имеющего
, имеющего 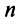 линейно независимых собственных векторов
линейно независимых собственных векторов 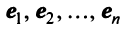 с собственными значениями, соответственно равными
с собственными значениями, соответственно равными 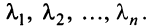 Векторы
Векторы 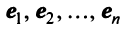 примем за базисные. Тогда
примем за базисные. Тогда 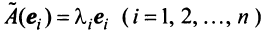 или с учетом (3.18)
или с учетом (3.18)
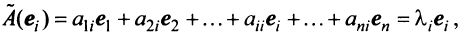
откуда 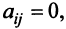 если
если 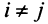 , и
, и 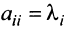 ,если
,если 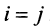 . Таким образом, матрица оператора
. Таким образом, матрица оператора  в базисе, состоящем из его собственных векторов, является диагональной и имеет вид:
в базисе, состоящем из его собственных векторов, является диагональной и имеет вид:
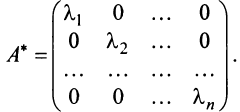 Верно и обратное: если матрица
Верно и обратное: если матрица 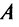 линейного оператора
линейного оператора  в некотором базисе является диагональной, то все векторы этого базиса — собственные векторы оператора
в некотором базисе является диагональной, то все векторы этого базиса — собственные векторы оператора  .
.
Можно доказать, что если линейный оператор имеет 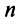 попарно различных собственных значений, то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.
попарно различных собственных значений, то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.
- Заказать решение задач по высшей математике
Пример:
Привести матрицу 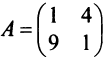 линейного оператора
линейного оператора  к диагональному виду.
к диагональному виду.
Решение:
В примере 3.7 были найдены собственные значения матрицы 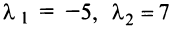 и соответствующие им собственные векторы
и соответствующие им собственные векторы 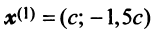 и
и 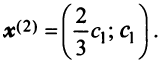 Так как координаты векторов
Так как координаты векторов 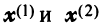 не пропорциональны, то векторы
не пропорциональны, то векторы 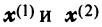 линейно независимы. Поэтому в базисе, состоящем из любых пар собственных векторов
линейно независимы. Поэтому в базисе, состоящем из любых пар собственных векторов 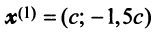 и
и 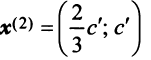 (т.е. при любых
(т.е. при любых 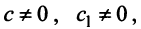 например при
например при 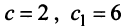 из векторов
из векторов 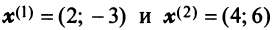 и т.д.), матрица
и т.д.), матрица 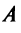 будет иметь диагональный вид:
будет иметь диагональный вид:  Это легко проверить, взяв, например, в качестве нового базиса линейно независимые собственные векторы
Это легко проверить, взяв, например, в качестве нового базиса линейно независимые собственные векторы 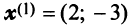 и
и 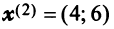 . Действительно, матрица
. Действительно, матрица 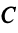 перехода от старого базиса к новому в этом случае будет иметь вид
перехода от старого базиса к новому в этом случае будет иметь вид 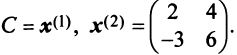 Тогда в соответствии с (3.22) матрица
Тогда в соответствии с (3.22) матрица 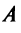 в новом базисе
в новом базисе 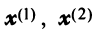 примет вид:
примет вид:
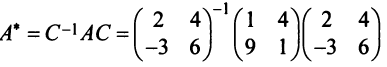
или после вычислений (которые мы опускаем) 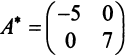
т.е. получим ту же диагональную матрицу, элементы которой по главной диагонали равны собственным значениям матрицы 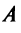 . ►
. ►
Квадратичные формы
При решении различных прикладных задач часто приходится исследовать квадратичные формы.
Определение. Квадратичной формой 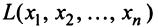 от
от 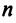 переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
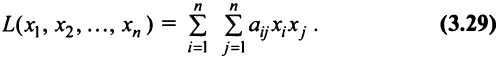
Предполагаем, что коэффициенты квадратичной формы 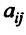 — действительные числа, причем
— действительные числа, причем 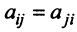 . Матрица
. Матрица 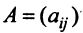
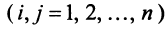 , составленная из этих коэффициентов, называется матрицей квадратичной формы. В матричной записи квадратичная форма имеет вид:
, составленная из этих коэффициентов, называется матрицей квадратичной формы. В матричной записи квадратичная форма имеет вид:

где 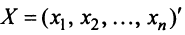 — матрица-столбец переменных. В самом деле :
— матрица-столбец переменных. В самом деле : 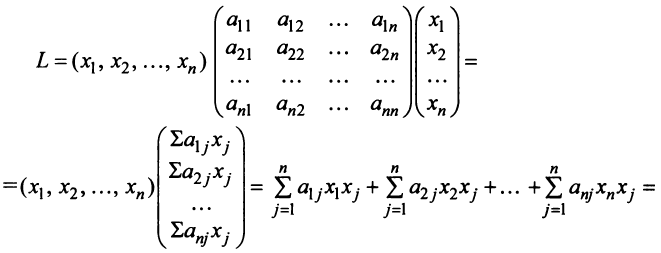
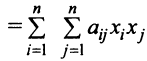 и эквивалентность формул (3.29) и (3.30) установлена.
и эквивалентность формул (3.29) и (3.30) установлена.
Пример:
Дана квадратичная форма 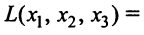
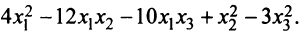 Записать ее в матричном виде.
Записать ее в матричном виде.
Решение:
Найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, т.е. 4, 1, -3, а другие элементы — половинам соответствующих коэффициентов квадратичной формы. Поэтому
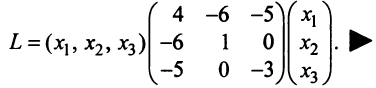
Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.
Пусть матрицы-столбцы переменных 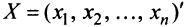 и
и 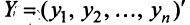 связаны линейным соотношением
связаны линейным соотношением 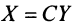 , где,
, где, 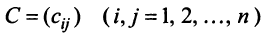 есть некоторая невырожденная матрица
есть некоторая невырожденная матрица 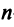 -го порядка. Тогда квадратичная форма
-го порядка. Тогда квадратичная форма
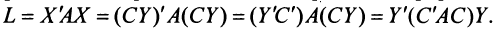
, Итак, при невырожденном линейном преобразовании 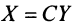 матрица квадратичной формы принимает вид:
матрица квадратичной формы принимает вид:

Пример:
Дана квадратичная форма 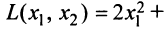
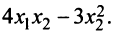 Найти квадратичную форму
Найти квадратичную форму 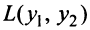 , полученную из данной линейным преобразованием
, полученную из данной линейным преобразованием 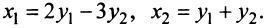
Решение:
Матрица данной квадратичной формы 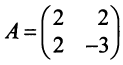 , а матрица линейного преобразования
, а матрица линейного преобразования 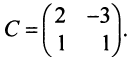
Следовательно, по (3.31) матрица искомой квадратичной формы 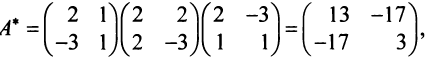 а квадратичная форма имеет вид
а квадратичная форма имеет вид 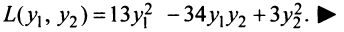
Следует отметить, что при некоторых удачно выбранных линейных преобразованиях вид квадратичной формы можно существенно упростить.
Квадратичная форма 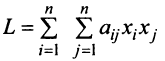 , называется канонической (или имеет канонический вид), если все ее коэффициенты
, называется канонической (или имеет канонический вид), если все ее коэффициенты 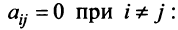
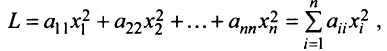
а ее матрица является диагональной. Справедлива следующая теорема.
Теорема. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.
Пример:
Привести к каноническому виду квадратичную форму
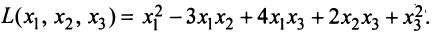
Решение:
Вначале вьделим полный квадрат при переменной 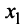 , коэффициент при квадрате которой отличен от нуля:
, коэффициент при квадрате которой отличен от нуля:
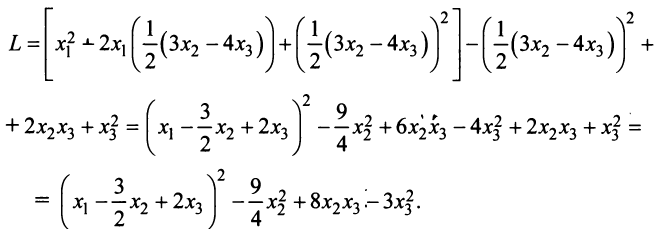
Теперь выделяем полный квадрат при переменной 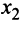 , коэффициент при которой отличен от нуля:
, коэффициент при которой отличен от нуля:
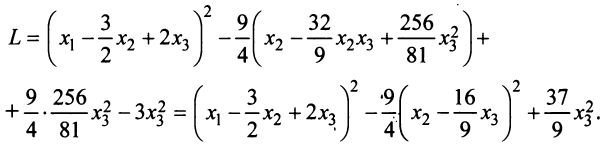 Итак, невырожденное линейное преобразование
Итак, невырожденное линейное преобразование
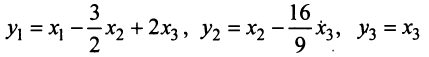
приводит данную квадратичную форму к каноническому виду
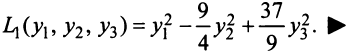
Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств сформулируем в виде теоремы.
Теорема (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду.
Например, квадратичную форму 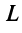 в примере 3.10 можно было привести к виду
в примере 3.10 можно было привести к виду
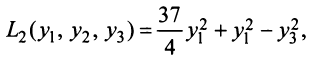
применив невырожденное линейное преобразование
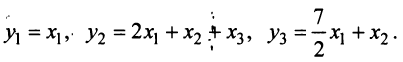
Как видим, число положительных и отрицательных коэффициентов (соответственно два и один) сохранилось.
Следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.
Квадратичная форма 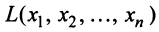 называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля,
называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля,
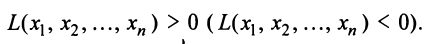
Так, например, квадратичная форма 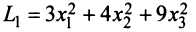 является положительно определенной, а форма
является положительно определенной, а форма 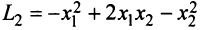 — отрицательно определенной.
— отрицательно определенной.
Теорема. Для того чтобы квадратичная форма 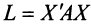 была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения
была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения 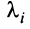 матрицы
матрицы 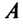 были положительны (отрицательны).
были положительны (отрицательны).
В ряде случаев для установления знакоопределенности квадратичной формы удобнее бывает применить критерий Сильвестра.
Теорема. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е. 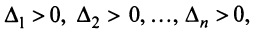 где
где
 Следует отметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака «минус» для минора первого порядка. ‘
Следует отметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака «минус» для минора первого порядка. ‘
Пример:
Доказать, что квадратичная форма 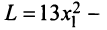
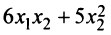 является положительно определенной.
является положительно определенной.
Решение:
Первый способ. Матрица  квадратичной формы имеет вид
квадратичной формы имеет вид 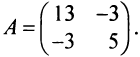 Для матрицы
Для матрицы характеристическое
характеристическое
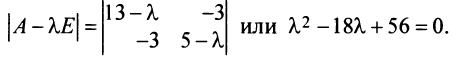
Решая уравнение, найдем 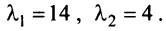 Так как корни характеристического уравнения матрицы
Так как корни характеристического уравнения матрицы  положительны, то на основании приведенной теоремы квадратичная форма
положительны, то на основании приведенной теоремы квадратичная форма 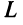 — положительно определенная.
— положительно определенная.
Второй способ. Так как главные миноры матрицы 
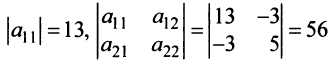 положительны, то по критерию Сильвестра данная квадратичная форма
положительны, то по критерию Сильвестра данная квадратичная форма 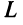 положительно определенная. ►
положительно определенная. ►
Линейная модель обмена
В качестве примера математической модели экономического процесса, приводящейся к понятию собственного вектора и собственного значения матрицы, рассмотрим линейную модель обмена (модель международной торговли).
Пусть имеется 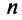 стран
стран 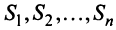 , национальный доход каждой из которых равен соответственно
, национальный доход каждой из которых равен соответственно 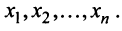 Обозначим коэффициентами
Обозначим коэффициентами 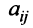 долю национального дохода, которую страна
долю национального дохода, которую страна 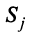 тратит на покупку товаров у страны
тратит на покупку товаров у страны 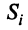 . Будем считать, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.
. Будем считать, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.
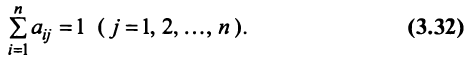
Рассмотрим матрицу 
которая получила название структурной матрицы торговли. В соответствии с (3.32) сумма элементов любого столбца матрицы 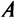 равна 1.
равна 1.
Для любой страны 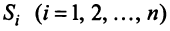 выручка от внутренней и внешней торговли составит:
выручка от внутренней и внешней торговли составит: 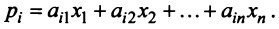
Для сбалансированной торговли необходима бездефицитность торговли каждой страны 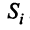 , т.е. выручка от торговли каждой страны должна быть не меньше ее национального дохода:
, т.е. выручка от торговли каждой страны должна быть не меньше ее национального дохода:
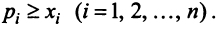
Если считать, что 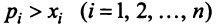 , то получаем систему неравенств
, то получаем систему неравенств
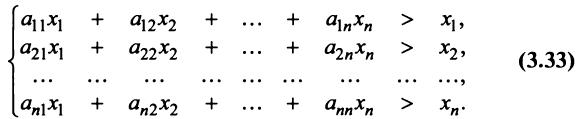
Сложив все неравенства системы (3.33), получим после группировки 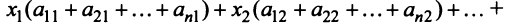
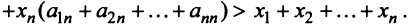
Учитывая (3.32), выражения в скобках равны единице, и мы приходим к противоречивому неравенству
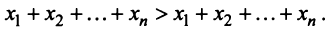
Таким образом, неравенство 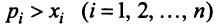 невозможно, и условие
невозможно, и условие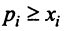 , принимает вид
, принимает вид 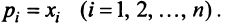 (С экономической точки зрения это понятно, так как все страны не могут одновременно получать прибыль.)
(С экономической точки зрения это понятно, так как все страны не могут одновременно получать прибыль.)
Вводя вектор 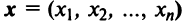 национальных доходов стран, получим матричное уравнение
национальных доходов стран, получим матричное уравнение

В котором вектор х записан в виде вектор-столбца, т.е. задача свелась к отысканию собственного вектора матрицы 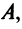 отвечающего собственному значению
отвечающего собственному значению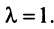
Пример:
Структурная матрица торговли трех стран 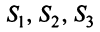 имеет вид:
имеет вид:
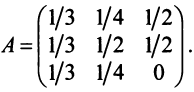
Найти соотношение национальных доходов стран для сбалансированной торговли.
Решение:
Находим собственный вектор 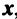 , отвечающий собственному значению
, отвечающий собственному значению 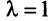 , решив уравнение
, решив уравнение 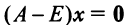 или систему
или систему
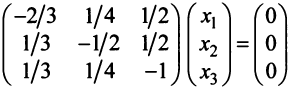
методом Гаусса. Найдем 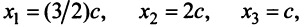 т.е.
т.е. 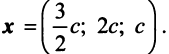 Полученный результат означает, что сбалансированность торговли трех стран достигается при векторе национальных доходов
Полученный результат означает, что сбалансированность торговли трех стран достигается при векторе национальных доходов
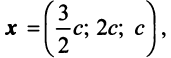 т.е. при соотношении национальных доходов стран
т.е. при соотношении национальных доходов стран 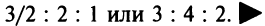
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
- Координаты на прямой
- Системы дифференциальных уравнений
- Числовые ряды
- Знакопеременные ряды
- Степенные ряды
Алгоритм нахождения базиса системы векторов
Для того чтобы найти базис системы векторов Av А2. А , необходимо:
1) составить соответствующую системе векторов однородную систему уравнений
2) привести эту систему к равносильной разрешенной системе вида
- 3) записать базис системы векторов Б = (АрА2, . А ), включив в него векторы, соответствующие разрешенным неизвестным;
- 4) записать разложения векторов по базису; коэффициентами разложения вектора А. по этому базису являются координаты соответствующего вектора
в разрешенной системе уравнений, т.е.
Система векторов, состоящая из п векторов, ранг которой равен г, может иметь несколько базисов. Число возможных базисов системы векторов определяется как число меньшее или равное числу сочетаний из п по г.
Пример 3.3. Найти ранг и базис системы векторов
разложения векторов по базису, перейти к новому базису и найти число возможных базисов системы.
Решение. Составим систему уравнений A t ay + А2х2 + . + А„хп = 0, которая в координатной записи имеет вид
Приведение данной системы уравнений с помощью преобразований Жордана к равносильной разрешенной приведено в ниже следующей таблице.
Разрешенная система имеет вид
В базис системы векторов включаем 1-й и 2-й векторы Б: = (AVA2), которые соответствуют разрешенным неизвестным х1 и х2. Ранг системы векторов равен числу векторов, вошедших в базис, т.е. г = 2.
Запишем разложения векторов по базису. Коэффициентами разложения вектора А3 являются координаты вектора А’3 = (3, -2), т.е. коэффициенты при х3 в разрешенной системе уравнений (в последних трех строках таблицы), они образуют столбец, расположенный под х3 А3 = ЗЛ1 – 2Аг Аналогично, коэффициентами разложения вектора А4 являются координаты вектора А’4 = (4, 1) А4 = 4Ау + 1 Ат
Для нахождения нового базиса необходимо выбрать новый разрешающий элемент. Пусть этим элементом будет элемент я94 = 1.
Как найти базис данной системы векторов
Определение базиса.Система векторов образует базис, если:
1) она линейно-независима,
2) любой вектор пространства через нее линейно выражается.
Пример 1.Базис пространства : .
2. В системе векторов базисом являются векторы: , т.к. линейно выражается через векторы .
Замечание.Чтобы найти базис данной системы векторов необходимо:
1) записать координаты векторов в матрицу,
2) с помощью элементарных преобразований привести матрицу к треугольному виду,
3) ненулевые строки матрицы будут являться базисом системы,
4) количество векторов в базисе равно рангу матрицы.
Теорема Кронекера-Капелли
Теорема Кронеккера–Капелли дает исчерпывающий ответ на вопрос о совместности произвольной системы линейных уравнений с неизвестными
Теорема Кронеккера–Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы, .
Алгоритм отыскания всех решений совместной системы линейных уравнений вытекает из теоремы Кронеккера–Капелли и следующих теорем.
Теорема. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Теорема. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
Алгоритм решения произвольной системы линейных уравнений:
1. Найдем ранги основной и расширенной матриц системы. Если они не равны ( ), то система несовместна (не имеет решений). Если ранги равны ( , то система совместна.
2. Для совместной системы найдем какой-нибудь минор, порядок которого определяет ранг матрицы (такой минор называют базисным). Составим новую систему из уравнений, в которых коэффициенты при неизвестных, входят в базисный минор (эти неизвестные называют главными неизвестными), остальные уравнения отбросим. Главные неизвестные с коэффициентами оставим слева, а остальные неизвестных (их называют свободными неизвестными) перенесем в правую часть уравнений.
3. Найдем выражения главных неизвестных через свободные. Получаем общее решение системы.
4. Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образомнаходим частные решения исходной системы уравнений.
Линейное программирование. Основные понятия
Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.
Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.
Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующихсистему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называетсядопустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи.
Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального).
В общей постановке задача линейного программирования выглядит следующим образом:
Имеются какие-то переменные х = (х1 , х2 , … хn ) и функция этих переменных f(x) = f (х1 , х2 , … хn ), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:
В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что
а) функция f(x) является линейной функцией переменных х1 , х2 , … хn
б) область G определяется системой линейных равенств или неравенств.
Математическая модель любой задачи линейного программирования включает в себя:
Векторное пространство: размерность и базис, разложение вектора по базису
В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:
e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )
Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 )
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A = 3 2 3 – 2 1 – 1 1 2 – 2 A = 3 – 2 1 2 1 2 3 – 1 – 2 = 3 · 1 · ( – 2 ) + ( – 2 ) · 2 · 3 + 1 · 2 · ( – 1 ) – 1 · 1 · 3 – ( – 2 ) · 2 · ( – 2 ) – 3 · 2 · ( – 1 ) = = – 25 ≠ 0 ⇒ R a n k ( A ) = 3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 ) d = ( 0 , 1 , 2 )
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , – 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , – 1 , – 2 ) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
1 2 3 3 0 1 0 2 0 1 – 1 1 0 1 – 2 1
1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 – 2 – 1
1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a ( 1 ) = ( 1 , 2 , – 1 , – 2 ) a ( 2 ) = ( 0 , 2 , 1 , – 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n -мерного векторного пространства – e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :
x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n – некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:
1 – x 1 ) · e ( 1 ) + ( x
2 – x 2 ) · e ( 2 ) + . . . ( x
Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x
2 – x 2 ) , . . . , ( x
n – x n ) будут равны нулю. Из чего справедливым будет: x 1 = x
n . И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .
Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .
Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x
Вектор x → будет представлен следующим образом:
2 · e ( 2 ) + . . . + x
Запишем это выражение в координатной форме:
( x 1 , x 2 , . . . , x n ) = x
1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x
2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x
n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x
2 e 1 ( 2 ) + . . . + x
2 e 2 ( 2 ) + + . . . + x
n e 2 ( n ) , . . . , x
2 e n ( 2 ) + . . . + x
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
n e 2 n ⋮ x n = x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x
n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e ( 1 ) = ( 1 , – 1 , 1 ) e ( 2 ) = ( 3 , 2 , – 5 ) e ( 3 ) = ( 2 , 1 , – 3 ) x = ( 6 , 2 , – 7 )
Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .
Используем метод Гаусса:
A = 1 – 1 1 3 2 – 5 2 1 – 3
1 – 1 1 0 5 – 8 0 3 – 5
1 – 1 1 0 5 – 8 0 0 – 1 5
R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.
Пусть в базисе вектор x → имеет координаты x
3 . Связь этих координат определяется уравнением:
3 e 1 ( 3 ) x 2 = x
3 e 2 ( 3 ) x 3 = x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
∆ = 1 3 2 – 1 2 1 1 – 5 – 3 = – 1 ∆ x
1 = 6 3 2 2 2 1 – 7 – 5 – 3 = – 1 , x
1 ∆ = – 1 – 1 = 1 ∆ x
2 = 1 6 2 – 1 2 1 1 – 7 – 3 = – 1 , x
2 ∆ = – 1 – 1 = 1 ∆ x
3 = 1 3 6 – 1 2 2 1 – 5 – 7 = – 1 , x
Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x
Ответ: x = ( 1 , 1 , 1 )
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
Указанные системы являются также базисами заданного пространства.
n ( 1 ) – координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:
1 ( 1 ) e 1 ( 1 ) + c
2 ( 1 ) e 1 ( 2 ) + . . . + c
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
1 ( 1 ) e 2 ( 1 ) + c
2 ( 1 ) e 2 ( 2 ) + . . . + c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
1 ( 1 ) e n ( 1 ) + c
2 ( 1 ) e n ( 2 ) + . . . + c
В виде матрицы систему можно отобразить так:
( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )
к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .
n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )
к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .
[spoiler title=”источники:”]
http://megaobuchalka.ru/10/21983.html
http://zaochnik.com/spravochnik/matematika/vektory/vektornoe-prostranstvo/
[/spoiler]
В статье о n-мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n-мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n-векторов. Размерность его соответственно равна n. Возьмем систему из n-единичных векторов:
e(1)=(1, 0,…,0)e(2)=(0, 1,…,0)e(n)=(0, 0,…,1)
Используем эти векторы в качестве составляющих матрицы A: она будет являться единичной с размерностью n на n. Ранг этой матрицы равен n. Следовательно, векторная система e(1), e(2),…, e(n) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n, то размерность пространства n-мерных векторов равна n, а единичные векторы e(1), e(2),…, e(n) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n-мерных векторов, в которой число векторов меньше n, не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e(2), e(1),…, e(n). Она также будет являться базисом n-мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n. Система e(2), e(1),…, e(n) линейно независима и является базисом n-мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n-мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n-мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a=(3, -2, 1)b=(2, 1, 2)c=(3, -1, -2)
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A=323-21-112-2A=3-212123-1-2=3·1·(-2)+(-2)·2·3+1·2·(-1)-1·1·3-(-2)·2·(-2)-3·2·(-1)==-25≠0⇒Rank(A)=3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a=(3, -2, 1)b=(2, 1, 2)c=(3, -1, -2)d=(0, 1, 2)
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a=(3, -2, 1), b=(2, 1, 2), c=(3, -1, -2) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a=(1, 2, 3, 3)b=(2, 5, 6, 8)c=(1, 3, 2, 4)d=(2, 5, 4, 7)
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A=1233256813242547
По методу Гаусса определим ранг матрицы:
A=1233256813242547~1233010201-1101-21~~1233010200-1-100-2-1~1233010200-1-10001⇒⇒Rank(A)=4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a(1)=(1, 2, -1, -2)a(2)=(0, 2, 1, -3)a(3)=(1, 0, 0, 5)
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Примем, что произвольные векторы e(1), e(2),…, e(n) являются базисом векторного n-мерного пространства. Добавим к ним некий n-мерный вектор x→: полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n-мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n-мерного векторного пространства – e(1), e(2),…, e(n). Сделаем систему линейно зависимой, добавив к ней n-мерный вектор x→. Этот вектор может быть линейно выражен через исходные векторы e:
x=x1·e(1)+x2·e(2)+…+xn·e(n) , где x1, x2,…, xn – некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
x=x~1e(1)+x2~e(2)+…+x~ne(n), где x~1, x~2,…, x~n – некие числа.
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x=x1·e(1)+x2·e(2)+…+xn·e(n) . Получим:
0=(x~1-x1)·e(1)+(x~2-x2)·e(2)+…(x~n-xn)·e(2)
Система базисных векторов e(1), e(2),…, e(n) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты (x~1-x1), (x~2-x2),…, (x~n-xn) будут равны нулю. Из чего справедливым будет: x1=x~1, x2=x~2,…, xn=x~n. И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x1, x2,…, xn называются координатами вектора x→ в базисе e(1), e(2),…, e(n).
Доказанная теория делает понятным выражение «задан n-мерный вектор x=(x1, x2,…, xn)»: рассматривается вектор x→ n-мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n-мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n-мерного векторного пространства задана система из n линейно независимых векторов
e(1)=(e1(1), e2(1),…, en(1))e(2)=(e1(2), e2(2),…, en(2))⋮e(n)=(e1(n), e2(n),…, en(n))
а также задан вектор x=(x1, x2,…, xn).
Векторы e1(1), e2(2),…, en(n) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x→ в базисе e1(1), e2(2),…, en(n), обозначаемые как x~1, x~2,…, x~n.
Вектор x→ будет представлен следующим образом:
x=x~1·e(1)+x~2·e(2)+…+x~n·e(n)
Запишем это выражение в координатной форме:
(x1, x2,…, xn)=x~1·(e(1)1, e(1)2,…, e(1)n)+x~2·(e(2)1, e(2)2,…, e(2)n)+…++x~n·(e(n)1, e(n)2,…, e(n)n)==(x~1e1(1)+x~2e1(2)+…+x~ne1(n), x~1e2(1)+x~2e2(2)++…+x~ne2(n), …, x~1en(1)+x~2en(2)+…+x~nen(n))
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x~1, x~2,…, x~n:
x1=x~1e11+x~2e12+…+x~ne1nx2=x~1e21+x~2e22+…+x~ne2n⋮xn=x~1en1+x~2en2+…+x~nenn
Матрица этой системы будет иметь следующий вид:
e1(1)e1(2)⋯e1(n)e2(1)e2(2)⋯e2(n)⋮⋮⋮⋮en(1)en(2)⋯en(n)
Пусть это будет матрица A, и ее столбцы – векторы линейно независимой системы векторов e1(1), e2(2),…, en(n). Ранг матрицы – n, и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x~1, x~2,…, x~n вектора x→ в базисе e1(1), e2(2),…, en(n).
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e(1)=(1,-1,1)e(2)=(3, 2, -5)e(3)=(2, 1, -3)x=(6, 2, -7)
Необходимо подтвердить факт, что система векторов e(1), e(2), e(3) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e(1), e(2), e(3) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A, строки которой – заданные векторы e(1), e(2), e(3).
Используем метод Гаусса:
A=1-1132-521-3~1-1105-803-5~1-1105-800-15
Rank (A) = 3. Таким образом, система векторов e(1), e(2), e(3) линейно независима и является базисом.
Пусть в базисе вектор x→ имеет координаты x~1, x~2, x~3. Связь этих координат определяется уравнением:
x1=x~1e1(1)+x~2e1(2)+x~3e1(3)x2=x~1e2(1)+x~2e2(2)+x~3e2(3)x3=x~1e3(1)+x~2e3(2)+x~3e3(3)
Применим значения согласно условиям задачи:
x~1+3x~2+2x~3=6-x~1+2x~2+x~3=2x~1-5x~2-3×3=-7
Решим систему уравнений методом Крамера:
∆=132-1211-5-3=-1∆x~1=632221-7-5-3=-1, x~1=∆x~1∆=-1-1=1∆x~2=162-1211-7-3=-1, x~2=∆x~2∆=-1-1=1∆x~3=136-1221-5-7=-1, x~3=∆x~3∆=-1-1=1
Так, вектор x→ в базисе e(1), e(2), e(3) имеет координаты x~1=1, x~2=1, x~3=1.
Ответ: x=(1,1,1)
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c(1)=(c1(1), c2(1),…, cn(1))c(2)=(c1(2), c2(2),…, cn(2))⋮c(n)=(c1(n), e2(n),…, cn(n))
И
e(1)=(e1(1), e2(1),…, en(1))e(2)=(e1(2), e2(2),…, en(2))⋮e(n)=(e1(n), e2(n),…, en(n))
Указанные системы являются также базисами заданного пространства.
Пусть c~1(1), c~2(1),…, c~n(1) – координаты вектора c(1) в базисе e(1), e(2),…, e(3), тогда связь координат будет задаваться системой линейных уравнений:
с1(1)=c~1(1)e1(1)+c~2(1)e1(2)+…+c~n(1)e1(n)с2(1)=c~1(1)e2(1)+c~2(1)e2(2)+…+c~n(1)e2(n)⋮ сn(1)=c~1(1)en(1)+c~2(1)en(2)+…+c~n(1)en(n)
В виде матрицы систему можно отобразить так:
(c1(1), c2(1),…, cn(1))=(c~1(1), c~2(1),…, c~n(1))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)
Сделаем по аналогии такую же запись для вектора c(2):
(c1(2), c2(2),…, cn(2))=(c~1(2), c~2(2),…, c~n(2))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)
И, далее действуя по тому же принципу, получаем:
(c1(n), c2(n),…, cn(n))=(c~1(n), c~2(n),…, c~n(n))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)
Матричные равенства объединим в одно выражение:
c1(1)c2(1)⋯cn(1)c1(2)c2(2)⋯cn(2)⋮⋮⋮⋮c1(n)c2(n)⋯cn(n)=c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)·e1(1)e2(1)⋯en(1)e1(2)e2(2)⋯en(2)⋮⋮⋮⋮e1(n)e2(n)⋯en(n)
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e(1), e(2),…, e(3) через базис c(1), c(2),…, c(n):
e1(1)e2(1)⋯en(1)e1(2)e2(2)⋯en(2)⋮⋮⋮⋮e1(n)e2(n)⋯en(n)=e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)·c1(1)c2(1)⋯cn(1)c1(2)c2(2)⋯cn(2)⋮⋮⋮⋮c1(n)c2(n)⋯cn(n)
Дадим следующие определения:
Матрица c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n) является матрицей перехода от базиса e(1), e(2),…, e(3)
к базису c(1), c(2),…, c(n).
Матрица e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n) является матрицей перехода от базиса c(1), c(2),…, c(n)
к базису e(1), e(2),…, e(3).
Из этих равенств очевидно, что
c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)·e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)=10⋯001⋯0⋮⋮⋮⋮00⋯1e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)·c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)=10⋯001⋯0⋮⋮⋮⋮00⋯1
т.е. матрицы перехода взаимообратны.
Рассмотрим теорию на конкретном примере.
Исходные данные: необходимо найти матрицу перехода от базиса
c(1)=(1, 2, 1)c(2)=(2, 3, 3)c(3)=(3, 7, 1)
к базису
e(1)=(3, 1, 4)e(2)=(5, 2, 1)e(3)=(1, 1, -6)
Также нужно указать связь координат произвольного вектора x→ в заданных базисах.
Решение
1. Пусть T – матрица перехода, тогда верным будет равенство:
314521111=T·121233371
Умножим обе части равенства на
121233371-1
и получим:
T=31452111-6·121233371-1
2. Определим матрицу перехода:
T=31452111-6·121233371-1==31452111-6·-18537-2-15-1-1=-2794-712012-4198
3. Определим связь координат вектора x→:
допустим, что в базисе c(1), c(2),…, c(n) вектор x→ имеет координаты x1,x2,x3, тогда:
x=(x1,x2,x3)·121233371,
а в базисе e(1), e(2),…, e(3) имеет координаты x~1,x~2,x~3, тогда:
x=(x~1,x~2,x~3)·31452111-6
Т.к. равны левые части этих равенств, мы можем приравнять и правые:
(x1,x2,x3)·121233371=(x~1,x~2,x~3)·31452111-6
Умножим обе части справа на
121233371-1
и получим:
(x1,x2,x3)=(x~1,x~2,x~3)·31452111-6·121233371-1⇔⇔(x1,x2,x3)=(x~1,x~2,x~3)·T⇔⇔(x1,x2,x3)=(x~1,x~2,x~3)·-2794-712012-4198
С другой стороны
(x~1,x~2,x~3)=(x1,x2,x3)·-2794-712012-4198
Последние равенства показывают связь координат вектора x→ в обоих базисах.
Ответ: матрица перехода
-2794-712012-4198
Координаты вектора x→ в заданных базисах связаны соотношением:
(x1,x2,x3)=(x~1,x~2,x~3)·-2794-712012-4198
или
(x~1,x~2,x~3)=(x1,x2,x3)·-2794-712012-4198-1
Фундаментальным
вопросом теории линейных пространств
является вопрос о том, можно ли, а если
можно, то как, произвольный вектор
пространства представить в виде линейной
комбинации фиксированного набора
векторов из этого пространства. Далее
мы получим ответ на этот вопрос.
Система
линейно независимых векторов
![]() векторного пространства
векторного пространства![]() называетсябазисом
называетсябазисом
этого пространства, если любой вектор
из
![]() может быть представлен в виде линейной
может быть представлен в виде линейной
комбинации векторов этой системы, т.е.
для каждого вектора![]() существуют вещественные числа
существуют вещественные числа![]() такие, что имеет место равенство
такие, что имеет место равенство
![]() .
.
Это
равенство называется разложением
вектора
![]()
по базису
![]() ,
,
а числа![]() называютсякоординатами
называютсякоординатами
вектора
![]() относительно базиса
относительно базиса
(или в базисе)
![]() .
.
Утверждение
Базисом
линейного пространства решений
однородной системы является ее
фундаментальная система решений.
ТЕОРЕМА
(о единственности разложения по базису).
Каждый вектор
![]() пространства
пространства![]() может быть разложен по базису
может быть разложен по базису
![]() единственным
единственным
образом, т.е. координаты каждого вектора
![]() в базисе
в базисе
![]()
определяются однозначно.
Главное
значение базиса заключается в том, что
операции сложения векторов и умножения
их на числа при задании базиса превращаются
в соответствующие операции над числами
– координатами этих векторов. А именно,
справедлива следующая
ТЕОРЕМА.
При сложении
двух любых векторов линейного пространства
![]() их координаты (относительно любого
их координаты (относительно любого
базиса пространства) складываются; при
умножении
произвольного вектора на любое число
![]() все координаты этого вектора умножаются
все координаты этого вектора умножаются
на![]() .
.
Типовой
пример
Исследуем
вопрос о базисе пространства
![]() ,
,
введенного ранее при рассмотрении
Типовой примеров векторных пространств.
Покажем, что![]() элементов
элементов![]() указанного пространства образуют базис.
указанного пространства образуют базис.
►Во-первых,
эти векторы линейно независимы. Проверка
линейной независимости набора
![]() состоит в определении значений
состоит в определении значений![]() ,
,
при которых возможно равенство
![]() .
.
Но в
силу только что доказанной теоремы
![]() ,
,
а
последний вектор является нулевым лишь
при условии
![]() .
.
Во-вторых, всякий вектор![]() заведомо представим в виде линейной
заведомо представим в виде линейной
комбинации векторов![]() :
:![]() и, значит, набор
и, значит, набор![]() образует базис. ◄
образует базис. ◄
Векторное
пространство
![]() называется
называется
![]() -мерным,
-мерным,
если в нем существуют![]() линейно независимых векторов, а любые
линейно независимых векторов, а любые![]() векторов уже являются линейно зависимыми.
векторов уже являются линейно зависимыми.
При этом число![]() называетсяразмерностьюпространства
называетсяразмерностьюпространства![]() .
.
Размерность
векторного пространства, состоящего
из одного нулевого вектора, принимается
равной нулю.
Размерность
пространства
![]() обычно обозначают символом
обычно обозначают символом![]() .
.
Векторное
пространство
![]() называетсябесконечномерным, если
называетсябесконечномерным, если
в нем существует любое число линейно
независимых векторов. В этом случае
пишут![]() .
.
Выясним
связь между понятиями базиса и размерности
пространства.
ТЕОРЕМА.Если
![]() – векторное пространство размерности
– векторное пространство размерности![]() ,
,
то любые![]() линейно независимых векторов этого
линейно независимых векторов этого
пространства образуют его базис.
ТЕОРЕМА.Если векторное пространство
![]() имеет базис, состоящий из
имеет базис, состоящий из![]() векторов, то
векторов, то![]() .
.
Утверждение
![]() Rn=n.
Rn=n.
Типовые примеры
-
Образуют
ли базис в пространстве R3
векторы
 ?
?
►По
определению базис составляют линейно
независимые векторы. Линейная зависимость
(или независимость) определяется исходя
из анализа равенства нулю линейной
комбинации этих векторов:
![]() .
.
Последнее
векторное уравнение после записи его
по компонентам представляет собой
систему трёх однородных уравнений
относительно
![]() .
.
Согласно схеме исследования линейной
зависимости векторов вычислим
определитель матрицы, составленной из
координат векторов

Определитель
системы равен нулю, следовательно, она
имеет нетривиальное решение и это
означает, что исходная группа векторов
линейно зависима и не образует базис в
R3. ◄
2.Найти
размерность и один из базисов линейного
пространства решений однородной системы:
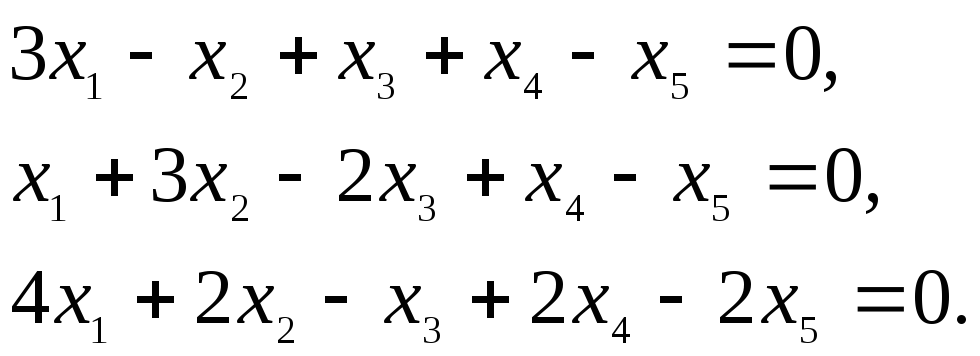
►Представленная
система состоит из трёх уравнений и
содержит 5 неизвестных. Выпишем матрицу
системы и упростим её с помощью
элементарных преобразований, сначала
поменяв местами строки 1 и 2, а затем
вычитая новую первую строку, умноженную
на 3 и 4, соответственно из второй и
третьей строк :

Видно,
что ранг матрицы
![]() равен 2. Следовательно, две неизвестные
равен 2. Следовательно, две неизвестные
являются главными, а три – свободными.
Значит ФСР системы содержит 5-2=3 линейно
независимых решения. Выберем в качестве
главных![]() .
.
Это можно сделать, т.к. минор 2-го порядка,
составленный из коэффициентов при этих
неизвестных, отличен от нуля. Система,
соответствующая преобразованной
матрице, имеет вид
![]()
Отсюда,
выражая главные неизвестные через
свободные, получим общее решение
![]()
Или иначе:
 .
.
Фундаментальная
совокупность решений является базисом
линейного пространства решений исходной
системы и в данном случае имеет вид

Размерность
искомого пространства равна 3.◄
Матрицей
переходаот базиса![]() к базису
к базису![]() называется матрица вида
называется матрица вида

где
для каждого
![]() в
в
![]() -ом
-ом
столбце стоят координаты![]() вектора
вектора![]() в базисе
в базисе![]() .
.
Утверждение
Координаты
![]() вектора
вектора![]() в базисе
в базисе![]() и координаты
и координаты![]() этого же вектора в базисе
этого же вектора в базисе![]() связаны равенством
связаны равенством
где
![]() – матрица перехода от базиса
– матрица перехода от базиса![]() к базису
к базису![]() .
.
Утверждение.
Матрица перехода
![]() от базиса
от базиса![]() к базису
к базису![]() и матрица обратного перехода
и матрица обратного перехода![]() от базиса
от базиса![]() к базису
к базису![]() связаны равенством
связаны равенством![]() =
=![]() .
.
Типовые
примеры
1.Найти координаты вектора![]() в базисе
в базисе![]() ,
,
если известно
![]()
►В
соответствии с определением матрица
перехода от базиса
![]() к базису
к базису![]() есть
есть
![]() .
.
Обозначим
координаты вектора
![]() в базисе
в базисе![]() через
через![]() ,
,
а в базисе![]() через
через![]() .
.
Искомые координаты![]() связаны с известными координатами
связаны с известными координатами![]() следующим соотношением:
следующим соотношением:
 .
.
Видно,
что для получения координат
![]() необходимо вычислить матрицу, обратную
необходимо вычислить матрицу, обратную![]() .
.
Используя стандартную процедуру, имеем
![]() .
.
Вычислим теперь координаты
![]() :
:
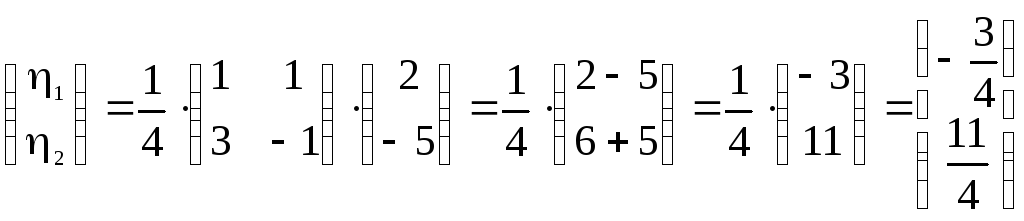 .
.
◄
-
Найти матрицу
перехода от базиса
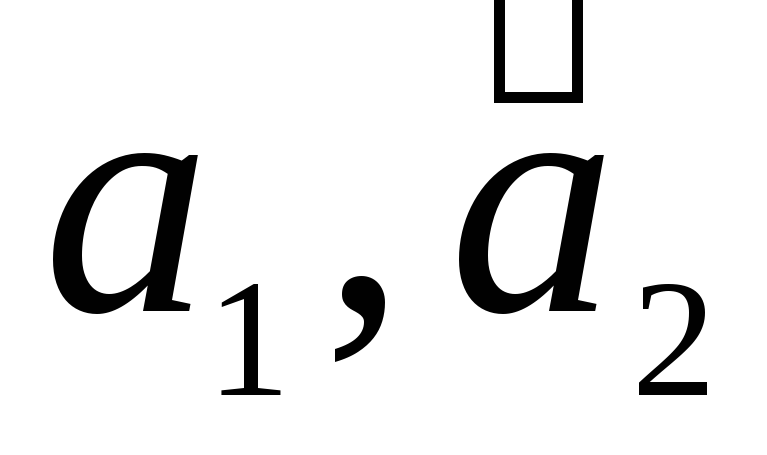 к базису
к базису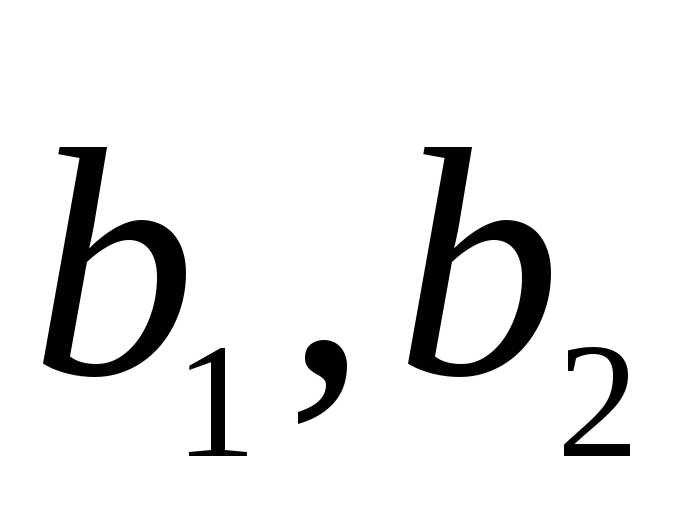 по данным разложениям этих векторов
по данным разложениям этих векторов
в базисе :
:
![]() .
.
►Чтобы
построить матрицу
![]() перехода
перехода
от базиса![]() к базису
к базису![]() ,
,
необходимо найти разложение векторов![]() по базису
по базису![]() .
.
Сделаем это, представив![]() в виде разложения по
в виде разложения по![]() с неизвестными координатами, которые
с неизвестными координатами, которые
требуется определить:
![]() ,
,
или с
учётом вида этих векторов в базисе
![]()
![]() .
.
Откуда для координат
![]() имеем
имеем
Теперь,
зная разложение
![]() по
по![]() ,
,
выпишем матрицу![]() :
:
![]() .◄
.◄
5. Линейные оболочки
и подпространства
Подпространством ![]() линейного пространства
линейного пространства![]() называется множество векторов из
называется множество векторов из![]() такое, что для любых двух векторов
такое, что для любых двух векторов![]() и
и![]() из
из![]() и любых двух вещественных чисел
и любых двух вещественных чисел![]() и
и![]() линейная комбинация
линейная комбинация![]() также принадлежит
также принадлежит![]() .
.
Утверждение. Подпространство само
является линейным пространством.
Линейной оболочкойсистемы векторов![]() называется множество всех линейных
называется множество всех линейных
комбинаций векторов![]() .
.
Обозначается![]() .
.
Утверждение. Линейная оболочка системы
векторов является подпространством.
Пересечениемдвух подпространств![]() и
и
![]() называется множество всех векторов,
называется множество всех векторов,
принадлежащих одновременно и![]() ,
,
и
![]() .
.
Обозначается
![]() .
.
Суммой двух подпространств![]() и
и
![]() называется множество всех векторов
называется множество всех векторов![]() ,
,
представимых в виде![]() ,
,
где![]()
![]() ,
,
![]()
![]() .
.
Обозначается
![]() .
.
Утверждение. Сумма и пересечение
подпространств
![]() и
и
![]()
являются линейными пространствами, и
их размерности связаны равенством
![]()
![]() +
+![]()
![]() =
=![]()
![]() +
+![]()
![]() .
.
Сумма
двух подпространств называется прямой
суммой, если
пересечение этих подпространств состоит
только из нулевого вектора.
Типовой пример
Найти размерность и какой-нибудь базис
суммы и пересечения подпространств,
порождённых векторами
![]() .
.
►Вычислим вначале размерность
подпространств. С этой целью установим,
являются ли линейно независимыми
векторы, порождающие данные подпространства.
Для подпространства
![]() ,
,
порождённого векторами![]() ,
,
равенство нулю линейной комбинации![]() ,
,
эквивалентное системе уравнений![]() ,
,
достигается лишь при условии![]() .
.
Следовательно, векторы![]() линейно независимы и размерность
линейно независимы и размерность
подпространства![]() равна 2:
равна 2:![]() .
.
Для подпространства![]() ,
,
порождённого векторами![]() ,
,
проводя аналогичный анализ, получим![]() .
.
Вычислим теперь размерность пересечения
подпространств
![]() и
и![]() .
.
По определению векторы, составляющие
пересечение, принадлежат одновременно
обоим подпространствам. Произвольный
вектор![]() подпространства
подпространства![]() является линейной комбинацией базисных
является линейной комбинацией базисных
векторов![]() :
:![]() .
.
Аналогично для подпространства![]() имеем
имеем![]() ,
,
тогда условие принадлежности пересечению
есть![]() или
или![]() .
.
Это условие представляет собой систему
уравнений относительно коэффициентов
![]() .
.
Составим матрицу системы и упростим её
с помощью элементарных преобразований:

Как видно ранг системы равен 3. Значит
ФСР состоит из одного линейно независимого
вектора. Найдём его, решив систему
уравнений, соответствующих последней
матрице, получим
![]() ,
,
откуда
![]() .
.
Полагая свободное неизвестное
![]() ,
,
для остальных имеем
![]() .
.
Итак, пересечение подпространств![]() имеет
имеет
один базисный вектор
![]() .
.
Размерность пересечения
![]() .
.
Следовательно, в соответствии с равенством
![]()
![]()
размерность суммы подпространств
![]() .
.
В качестве базиса суммы подпространств
можно взять, например, векторы![]() ,
,
дополненные вектором![]() .
.
В линейной независимости векторов![]() убедиться нетрудно.◄
убедиться нетрудно.◄
Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.
Что означает фраза «ранг матрицы равен $r$»? Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют.
Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.
Во всех изложенных ниже примерах матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde$.
Решить СЛАУ $ left < begin& 3x_1-6x_2+9x_3+13x_4=9\ & -x_1+2x_2+x_3+x_4=-11;\ & x_1-2x_2+2x_3+3x_4=5. end right.$. Если система является неопределённой, указать базисное решение.
Итак, мы имеем СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:
$$ left( begin 3 & -6 & 9 & 13 & 9 \ -1 & 2 & 1 & 1 & -11 \ 1 & -2 & 2 & 3 & 5 end right) rightarrow left|begin & text<поменяем местами первую и третью>\ & text<строки, чтобы первым элементом>\ & text <первой строки стала единица.>endright| rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 5\ -1 & 2 & 1 & 1 & -11 \ 3 & -6 & 9 & 13 & 9 end right) begin phantom <0>\ II+I\ III-3cdot Iend rightarrow left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 3 & 4 & -6 endright) begin phantom <0>\ phantom<0>\ III-IIend rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 0 & 0 & 0 endright) $$
Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.

И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde = 2$.
Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).
Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на «ступеньках». Что это за «ступеньки» показано на рисунке:

На «ступеньках» стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.
В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.
Почему можно принять переменные $x_1$ и $x_3$ в качестве базисных? Для ответа на этот вопрос давайте вспомним, что ранг матрицы системы равен числу $r=2$. Это говорит о том, что все миноры данной матрицы, порядок которых выше 2, либо равны нулю, либо не существуют. Ненулевые миноры есть только среди миноров второго порядка. Выберем какой-либо ненулевой минор второго порядка. Мы можем выбирать его как в исходной матрице системы $A$, т.е. в матрице $left( begin 3 & -6 & 9 & 13 \ -1 & 2 & 1 & 1 \ 1 & -2 & 2 & 3 end right)$, так и в преобразованной матрице системы, т.е. в $left( begin 1 & -2 & 2 & 3 \ 0 & 0 & 3 & 4 \ 0 & 0 & 0 & 0 endright)$. Так как в преобразованной матрице системы побольше нулей, то будем работать именно с нею.
Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:
$$ M_<2>^<(1)>=left| begin 1 & -2 \ 0 & 0 endright|=1cdot 0-(-2)cdot 0=0. $$
Вывод: выбранный нами минор второго порядка не является базисным, ибо он равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №2 (он соответствует переменной $x_2$), то пара переменных $x_1$ и $x_2$ не могут быть базисными переменными.
Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №3 и №4:
$$ M_<2>^<(2)>=left| begin 2 & 3\ 3 & 4 endright|=2cdot 4-3cdot 3=-1. $$
Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №3 (он соответствует переменной $x_3$) и столбца №4 (он соответствует переменной $x_4$), то пару переменных $x_3$ и $x_4$ можно принять в качестве базисных.
Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:
Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №3 (он соответствует переменной $x_3$), то пару переменных $x_1$ и $x_3$ можно принять в качестве базисных.
Как видите, выбор базисных переменных не является однозначным. На самом деле количество вариантов выбора не превышает количество размещений из $n$ элементов по $r$, т.е. не больше чем $C_^$.
В рассматриваемом примере в качестве баисных были приняты переменные $x_1$ и $x_3$ – сугубо из соображений удобства дальнейшего решения. В чём это удобство состоит, будет видно чуток позже.
Базисные переменные выбраны: это $x_1$ и $x_3$. Остальные $n-r=2$ переменных (т.е. $x_2$ и $x_4$) являются свободными. Нам нужно выразить базисные переменные через свободные.
Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 0 & 0 & 0 endright)$ от нулевой строки:
$$ left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 endright) $$
Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:

Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть
Давайте обратимся к расширенной матрице системы, которая после преобразований имеет вид $left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 endright)$. Перейдём от матрицы к уравнениям. Первая строка соответствует уравнению $x_1-2x_2+2x_3+3x_4=5$, а вторая строка соответствует уравнению $3x_3+4x_4=-6$. Теперь перенесём свободные переменные $x_2$ и $x_4$ в правые части уравнений. Естественно, что когда мы переносим выражение $4x_4$ в правую часть уравнения, то знак его изменится на противоположный, и в правой части появится $-4x_4$.
Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.
А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:
$$ left( begin 1 & 2 & 5 & 2 & -3\ 0 & 3 & -6 & 0 & -4 endright) begin phantom <0>\ II:3 end rightarrow left( begin 1 & 2 & 5 & 2 & -3\ 0 & 1 & -2 & 0 & -4/3 endright) begin I-2cdot II \ phantom <0>end rightarrow \ rightarrow left(begin 1 & 0 & 9 & 2 & -1/3\ 0 & 1 & -2 & 0 & -4/3 endright). $$
Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Если вспомнить, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, то получим:
Нами получено общее решение заданной СЛАУ. Чтобы найти базисное решение, нужно все свободные переменные приравнять к нулю. Т.е. полагая $x_2=0$ и $x_4=0$, будем иметь:
Решение $x_1=9$, $x_2=0$, $x_3=-2$, $x_4=0$ и является базисным решением данной СЛАУ. В принципе, задавая свободным переменным иные значения, можно получить иные частные решения данной системы. Таких частных решений бесконечное количество. Например, принимая $x_2=-4$ и $x_4=1$, получим такое частное решение: $left <begin& x_1=frac<2><3>;\ & x_2=-4;\ & x_3=-frac<10><3>;\ & x_4=1. endright.$. Базисное решение, которые мы нашли ранее – лишь одно из бесконечного множества частных решений заданной СЛАУ.
Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=9+2x_2-frac<1><3>x_4$ и $x_3=-2-frac<4><3>x_4$ в левую часть первого уравнения, получим:
$$ 3x_1-6x_2+9x_3+13x_4=3cdot left(9+2x_2-frac<1><3>x_4right)-6x_2+9cdot left(-2-frac<4><3>x_4right)+13x_4=9. $$
Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.
Если система является неопределённой, указать базисное решение.
Похожий пример уже был решен в теме «метод Крамера» (пример №4). Переменные $x_4$ и $x_5$ были перенесены в правые части, а дальше применялись стандартные операции метода Крамера. Однако такой метод решения не гарантирует достижения результата. Например, мы переносим некие переменные в правую часть, а оставшийся определитель оказывается равным нулю, – что тогда? Решать перебором? 🙂 Поэтому гораздо удобнее применять преобразования метода Гаусса, как и в предыдущем примере.
$$ left( begin 1 & -2 & 4 & 0 & 2 & 0\ 4 & -11 & 21 & -2 & 3 & -1\ -3 & 5 & -13 & -4 & 1 & -2 end right) begin phantom <0>\ II-4cdot I\ III+3cdot Iend rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -3 & 5 & -2 & -5 & -1\ 0 & -1 & -1 & -4 & 7 & -2 end right) rightarrow \ rightarrow left|begin & text<поменяем местами вторую и третью>\ & text<строки, чтобы диагональным элементом>\ & text <второй строки стало число (-1).>endright|rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -1 & -1 & -4 & 7 & -2\ 0 & -3 & 5 & -2 & -5 & -1 end right) begin phantom <0>\ phantom<0>\ III-3cdot Iend rightarrow \ rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -1 & -1 & -4 & 7 & -2\ 0 & 0 & 8 & 10 & -26 & 5 end right). $$
Матрица системы и расширенная матрица системы приведены к трапециевидной форме. Ранги этих матриц равны между собой и равны числу 3, т.е. $rang A=rangwidetilde = 3$. Так как ранги равны между собой и меньше, чем количество переменных, то согласно следствию из теоремы Кронекера-Капелли данная система имеет бесконечное количество решений.
Количество неизвестных $n=5$, ранги обеих матриц $r=3$, поэтому нужно выбрать три базисных переменных и $n-r=2$ свободных переменных. Применяя тот же метод «ступенек», что и в предыдущем примере, выберем в качестве базисных переменных $x_1$, $x_2$, $x_3$, а в качестве свободных переменных – $x_4$ и $x_5$.
Столбцы №4 и №5, которые соответствуют свободным переменным, перенесём за черту. После этого разделим третью строку на 8 и продолжим решение методом Гаусса:
$$ left( begin 1 & -2 & 4 & 0 & 0 & -2\ 0 & -1 & -1 & -2 & 4 & -7\ 0 & 0 & 8 & 5 & -10 & 26 end right) begin phantom <0>\ phantom<0>\ III:8end rightarrow left( begin 1 & -2 & 4 & 0 & 0 & -2\ 0 & -1 & -1 & -2 & 4 & -7\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin I-4cdot III \ II+III\ phantom<0>end rightarrow \ left( begin 1 & -2 & 0 & -5/2 & 5 & -15\ 0 & -1 & 0 & -11/8 & 11/4 & -15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin phantom <0>\ IIcdot (-1)\ phantom<0>end rightarrow left( begin 1 & -2 & 0 & -5/2 & 5 & -15\ 0 & 1 & 0 & 11/8 & -11/4 & 15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin I+2cdot II \ phantom<0>\ phantom<0>end rightarrow\ rightarrowleft( begin 1 & 0 & 0 & 1/4 & -1/2 & -15/2\ 0 & 1 & 0 & 11/8 & -11/4 & 15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) $$
Продолжение этой темы рассмотрим во второй части, где разберём ещё два примера с нахождением общего решения.
Метод Жордана-Гаусса онлайн
Данный онлайн калькулятор находит общее решение системы линейных уравнений методом Жордана-Гаусса. Дается подробное решение. Для вычисления выбирайте количество уравнений и количество переменных. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.» Теоретическую часть нахождения решения системы линейных уравнений методом Жордана-Гаусса смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Метод Жордана-Гаусса
Метод Жордана-Гаусса − это метод для решения систем линейных уравнений а также метод нахождения обратной матрицы. Данный метод является модификацией метода Гаусса.
Первый этап метода Жордана-Гаусса аналогична методу Гаусса (прямой ход Гаусса), который подробно можно посмотреть на странице «Метод Гаусса онлайн». Второй этап (обратный ход) метода Жордана-Гаусса заключается в обнулении всех элементов матрицы коэффициентов системы линейных уравнений, выше ведущих элементов. Отметим, что мы здесь рассматриваем произвольную систему линейных уравнений, где число переменных может быть не равным числу ограничений.
Рассмотрим следующую систему линейных уравнений:
 |
(1) |
Запишем систему (1) в матричном виде:
A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.
Построим расшренную матрицу системы:
 |
(4) |
После прямого хода Гаусса (подробнее о прямом ходе Гаусса посмотрите на странице «Метод Гаусса онлайн») получим следующую расширенную матрицу:
 |
(5) |
Если  .
.  равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).
равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).
Пусть  . Тогда в обратном порядке, начиная с ведущего элемента
. Тогда в обратном порядке, начиная с ведущего элемента  применяем обратный ход Гаусса. Суть обратного хода заключается в обнулении всех элементов расширенной матрицы, стоящих выше ведущих элементов.
применяем обратный ход Гаусса. Суть обратного хода заключается в обнулении всех элементов расширенной матрицы, стоящих выше ведущих элементов.
Итак, обнуляем все элементы, стоящие в столбце p, выше элемента  . Так как
. Так как  ≠0, то сложим строки 1,2. p−1 со строкой p, умноженной на
≠0, то сложим строки 1,2. p−1 со строкой p, умноженной на  соответственно.
соответственно.
Расширенная матрица примет следующий вид:

Аналогичным методом обнуляем элементы столбцов p−1, p−2, . 2 выше ведущих элементов  .
.
Расширенная матрица примет следующий вид:

Делим каждую строку на соответствующий ведущий элемент (если ведущий элемент существует):

Тогда решение можно записать так:

где  − произвольные вещественные числа.
− произвольные вещественные числа.
Отметим, что при m=n и rangA=n система линейных уравнений (2) имеет единственное решение.
Рассмотрим численные примеры.
Примеры решения системы линейных уравнений методом Жордана-Гаусса
Пример 1. Найти решение системы линейных уравнений методом Жордана-Гаусса:

Матричный вид записи: Ax=b, где
 .
.
Для решения системы, построим расширенную матрицу:
 .
.
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строки 2,3 со строкой 1, умноженной на 1/2,-3/2 соответственно:
 .
.
Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 1/5:
 .
.
Второй этап. Обратный ход Гаусса
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строки 1, 2 со строкой 3, умноженной на -3/2, -5/4 соответственно:
 .
.
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на -2/5:
 .
.
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
 .
.
 .
.
Векторный вариант решения:
 .
.
Пример 2. Найти решение системы линейных уравнений методом Жордана-Гаусса:

Матричный вид записи: Ax=b, где

Для решения системы, построим расширенную матрицу:

Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строки 2,3 со строкой 1, умноженной на 4/3, 5/3 соответственно:

Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на -2:

Второй этап. Обратный ход Гаусса
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на -3/10:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Выразим переменные x1, x2 относительно остальных переменных.

x3− произвольное действительное число.
Векторный вариант решения:
Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:

Тогда векторное решение можно представить так:
 ,
,
x3− произвольное действительное число.
Как найти базис данной системы векторов
Определение базиса.Система векторов образует базис, если:
1) она линейно-независима,
2) любой вектор пространства через нее линейно выражается.
Пример 1.Базис пространства  :
:  .
.
2. В системе векторов  базисом являются векторы:
базисом являются векторы:  , т.к.
, т.к.  линейно выражается через векторы
линейно выражается через векторы  .
.
Замечание.Чтобы найти базис данной системы векторов необходимо:
1) записать координаты векторов в матрицу,
2) с помощью элементарных преобразований привести матрицу к треугольному виду,
3) ненулевые строки матрицы будут являться базисом системы,
4) количество векторов в базисе равно рангу матрицы.
Теорема Кронекера-Капелли
Теорема Кронеккера–Капелли дает исчерпывающий ответ на вопрос о совместности произвольной системы  линейных уравнений с
линейных уравнений с  неизвестными
неизвестными

Теорема Кронеккера–Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы,  .
.
Алгоритм отыскания всех решений совместной системы линейных уравнений вытекает из теоремы Кронеккера–Капелли и следующих теорем.
Теорема. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Теорема. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
Алгоритм решения произвольной системы линейных уравнений:
1. Найдем ранги основной и расширенной матриц системы. Если они не равны  (
(  ), то система несовместна (не имеет решений). Если ранги равны
), то система несовместна (не имеет решений). Если ранги равны  (
(  , то система совместна.
, то система совместна.
2. Для совместной системы найдем какой-нибудь минор, порядок  которого определяет ранг матрицы (такой минор называют базисным). Составим новую систему из
которого определяет ранг матрицы (такой минор называют базисным). Составим новую систему из  уравнений, в которых коэффициенты при неизвестных, входят в базисный минор (эти неизвестные называют главными неизвестными), остальные уравнения отбросим. Главные неизвестные с коэффициентами оставим слева, а остальные
уравнений, в которых коэффициенты при неизвестных, входят в базисный минор (эти неизвестные называют главными неизвестными), остальные уравнения отбросим. Главные неизвестные с коэффициентами оставим слева, а остальные  неизвестных (их называют свободными неизвестными) перенесем в правую часть уравнений.
неизвестных (их называют свободными неизвестными) перенесем в правую часть уравнений.
3. Найдем выражения главных неизвестных через свободные. Получаем общее решение системы.
4. Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образомнаходим частные решения исходной системы уравнений.
Линейное программирование. Основные понятия
Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.
Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.
Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующихсистему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называетсядопустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи.
Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального).
В общей постановке задача линейного программирования выглядит следующим образом:
Имеются какие-то переменные х = (х1 , х2 , … хn ) и функция этих переменных f(x) = f (х1 , х2 , … хn ), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:

В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что
а) функция f(x) является линейной функцией переменных х1 , х2 , … хn
б) область G определяется системой линейных равенств или неравенств.
Математическая модель любой задачи линейного программирования включает в себя:
источники:
http://matworld.ru/calculator/gauss-jordan-method-online.php
http://megaobuchalka.ru/10/21983.html
