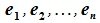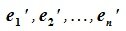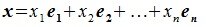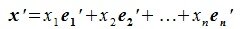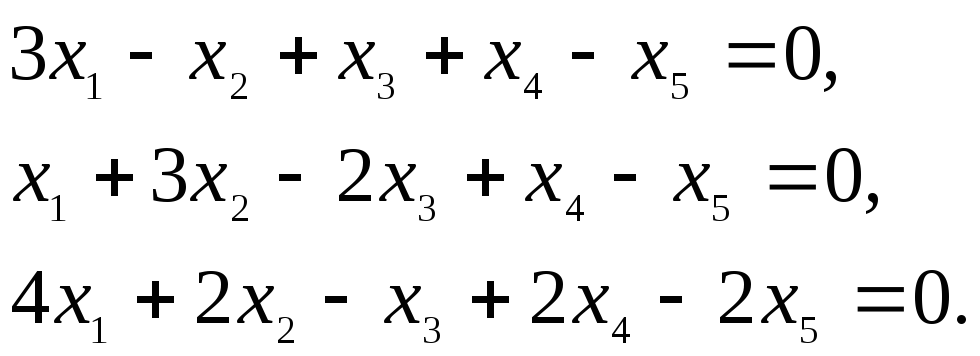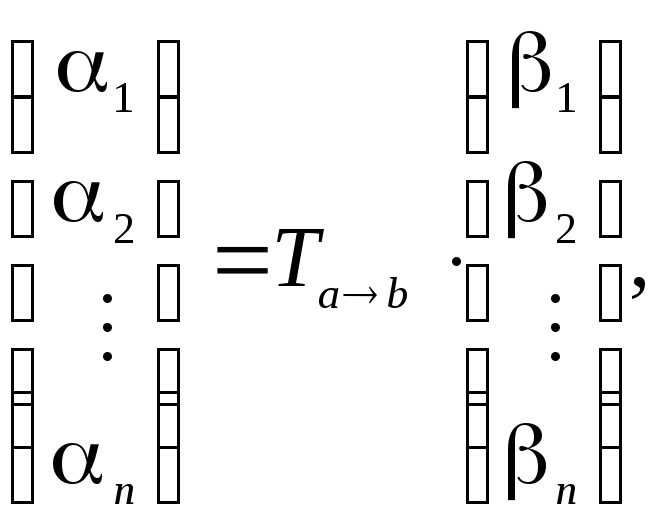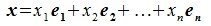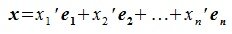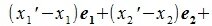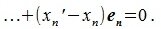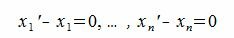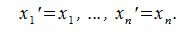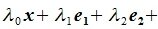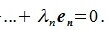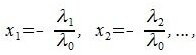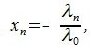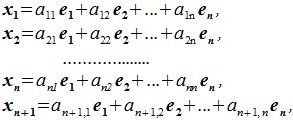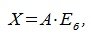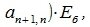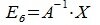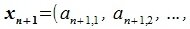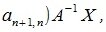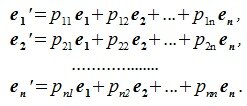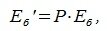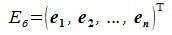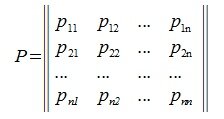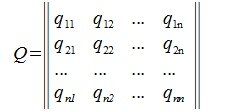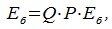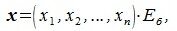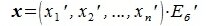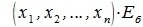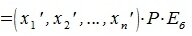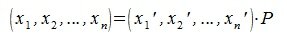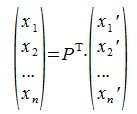Как найти базис множества матриц

Фундаментальным
вопросом теории линейных пространств
является вопрос о том, можно ли, а если
можно, то как, произвольный вектор
пространства представить в виде линейной
комбинации фиксированного набора
векторов из этого пространства. Далее
мы получим ответ на этот вопрос.

Система
линейно независимых векторов
векторного пространстваназываетсябазисом
этого пространства, если любой вектор
из
может быть представлен в виде линейной
комбинации векторов этой системы, т.е.
для каждого векторасуществуют вещественные числатакие, что имеет место равенство

.

Это
равенство называется разложением
вектора

по базису
,
а числаназываютсякоординатами
вектора
относительно базиса
(или в базисе)
.

Утверждение

Базисом
линейного пространства решений
одно­родной системы является ее
фундаментальная система реше­ний.

ТЕОРЕМА
(о единственности разложения по базису).
Каждый вектор
пространстваможет быть разложен по базису
единственным
образом, т.е. координаты каждого вектора
в базисе

определяются однозначно.

Главное
значение базиса заключается в том, что
операции сложения векторов и умножения
их на числа при задании базиса превращаются
в соответствующие операции над числами
– координатами этих векторов. А именно,
справедлива следующая

ТЕОРЕМА.
При сложении
двух любых векторов линейного пространства
их координаты (относительно любого
базиса пространства) складываются; при
умножении
произвольного вектора на любое число
все координаты этого вектора умножаются
на.

Типовой
пример

Исследуем
вопрос о базисе пространства
,
введенного ранее при рассмотрении
Типовой примеров векторных пространств.
Покажем, чтоэлементовуказанного пространства образуют базис.

►Во-первых,
эти векторы линейно независимы. Проверка
линейной независимости набора
состоит в определении значений,
при которых возможно равенство

.

Но в
силу только что доказанной теоремы

,

а
последний вектор является нулевым лишь
при условии
.
Во-вторых, всякий векторзаведомо представим в виде линейной
комбинации векторов:и, значит, наборобразует базис. ◄

Векторное
пространство
называется
-мерным,
если в нем существуютлинейно независимых векторов, а любыевекторов уже являются линейно зависимыми.
При этом числоназываетсяразмерностьюпространства.

Размерность
векторного пространства, состоящего
из одного нулевого вектора, принимается
равной нулю.

Размерность
пространства
обычно обозначают символом.

Векторное
пространство
называетсябесконечномерным, если
в нем существует любое число линейно
независимых векторов. В этом случае
пишут.

Выясним
связь между понятиями базиса и размерности
пространства.

ТЕОРЕМА.Если
– векторное пространство размерности,
то любыелинейно независимых векторов этого
пространства образуют его базис.

ТЕОРЕМА.Если векторное пространство
имеет базис, состоящий извекторов, то.

Утверждение

Rⁿ=n.

Типовые примеры

1. Образуют
   ли базис в пространстве R³
   векторы
   ?

►По
определению базис составляют линейно
независимые векторы. Линейная зависимость
(или независимость) определяется исходя
из анализа равенства нулю линейной
комбинации этих векторов:

.

Последнее
векторное уравнение после записи его
по компонентам представляет собой
систему трёх однородных уравнений
относительно
.
Согласно схеме исследования линейной
зависимости векторов вычислим
определитель матрицы, составленной из
координат векторов

Определитель
системы равен нулю, следовательно, она
имеет нетривиальное решение и это
означает, что исходная группа векторов
линейно зависима и не образует базис в
R³. ◄

2.Найти
размерность и один из базисов линейного
пространства решений однородной системы:

►Представленная
система состоит из трёх уравнений и
содержит 5 неизвестных. Выпишем матрицу
системы и упростим её с помощью
элементарных преобразований, сначала
поменяв местами строки 1 и 2, а затем
вычитая новую первую строку, умноженную
на 3 и 4, соответственно из второй и
третьей строк :

Видно,
что ранг матрицы
равен 2. Следовательно, две неизвестные
являются главными, а три – свободными.
Значит ФСР системы содержит 5-2=3 линейно
независимых решения. Выберем в качестве
главных.
Это можно сделать, т.к. минор 2-го порядка,
составленный из коэффициентов при этих
неизвестных, отличен от нуля. Система,
соответствующая преобразованной
матрице, имеет вид

Отсюда,
выражая главные неизвестные через
свободные, получим общее решение

Или иначе:

.

Фундаментальная
совокупность решений является базисом
линейного пространства решений исходной
системы и в данном случае имеет вид

Размерность
искомого пространства равна 3.◄

Матрицей
переходаот базисак базисуназывается матрица вида

где
для каждого
в
-ом
столбце стоят координатывекторав базисе.

Утверждение

Координаты
векторав базисеи координатыэтого же вектора в базисесвязаны равенством

где
– матрица перехода от базисак базису.

Утверждение.
Матрица перехода
от базисак бази­суи матрица обратного переходаот базисак базисусвязаны равенством=.

Типовые
примеры

1.Найти координаты векторав базисе,
если известно

►В
соответствии с определением матрица
перехода от базиса
к базисуесть

.

Обозначим
координаты вектора
в базисечерез,
а в базисечерез.
Искомые координатысвязаны с известными координатамиследующим соотношением:

.

Видно,
что для получения координат
необходимо вычислить матрицу, обратную.
Используя стандартную процедуру, имеем

.

Вычислим теперь координаты
:

.
◄

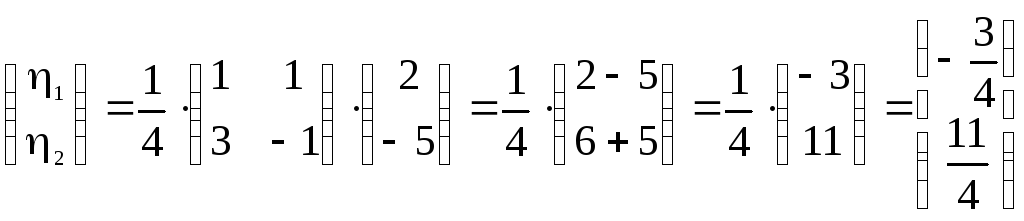
1. Найти матрицу
   перехода от базиса
   к базисупо данным разложениям этих векторов
   в базисе:

.

►Чтобы
построить матрицу
перехода
от базисак базису,
необходимо найти разложение векторовпо базису.
Сделаем это, представивв виде разложения пос неизвестными координатами, которые
требуется определить:

,

или с
учётом вида этих векторов в базисе

.

Откуда для координат
имеем

Теперь,
зная разложение
по,
выпишем матрицу:

.◄

5. Линейные оболочки
и подпространства

Подпространством линейного пространстваназывается множество векторов изтакое, что для любых двух векторовиизи любых двух вещественных чиселилинейная комбинациятакже принадлежит.

Утверждение. Подпространство само
является линейным про­странством.

Линейной оболочкойсистемы векторовназывается множество всех линейных
комбинаций векторов.
Обозначается.

Утверждение. Линейная оболочка системы
векторов является подпространством.

Пересечениемдвух подпространстви
на­зывается множество всех векторов,
принадлежащих одновре­менно и,
и
.
Обозначается
.

Суммой двух подпространстви
называется множество всех векторов,
представимых в виде,
где,
.
Обозначается
.

Утверждение. Сумма и пересечение
подпространств
и

являются линейными пространствами, и
их размерности связаны равенством

+=+.

Сумма
двух подпространств называется прямой
суммой, если
пересечение этих подпространств состо­ит
только из нулевого вектора.

Типовой пример

Найти размерность и какой-нибудь базис
суммы и пересечения подпространств,
порождённых векторами
.

►Вычислим вначале размерность
подпространств. С этой целью установим,
являются ли линейно независимыми
векторы, порождающие данные подпространства.
Для подпространства
,
порождённого векторами,
равенство нулю линейной комбинации,
эквивалентное системе уравнений,
достигается лишь при условии.
Следовательно, векторылинейно независимы и размерность
подпространстваравна 2:.
Для подпространства,
порождённого векторами,
проводя аналогичный анализ, получим.

Вычислим теперь размерность пересечения
подпространств
и.
По определению векторы, составляющие
пересечение, принадлежат одновременно
обоим подпространствам. Произвольный
векторподпространстваявляется линейной комбинацией базисных
векторов:.
Аналогично для подпространстваимеем,
тогда условие принадлежности пересечению
естьили.

Это условие представляет собой систему
уравнений относительно коэффициентов
.
Составим матрицу системы и упростим её
с помощью элементарных преобразований:

Как видно ранг системы равен 3. Значит
ФСР состоит из одного линейно независимого
вектора. Найдём его, решив систему
уравнений, соответствующих последней
матрице, получим
,

откуда
.

Полагая свободное неизвестное
,
для остальных имеем

.
Итак, пересечение подпространствимеет
один базисный вектор

.

Размерность пересечения
.
Следовательно, в соответствии с равенством

размерность суммы подпространств
.
В качестве базиса суммы подпространств
можно взять, например, векторы,
дополненные вектором.
В линейной независимости векторовубедиться нетрудно.◄

Алгоритм нахождения базиса системы векторов

Для того чтобы найти базис системы векторов A_v А₂. А , необходимо:

1) составить соответствующую системе векторов однородную систему уравнений

2) привести эту систему к равносильной разрешенной системе вида

• 3) записать базис системы векторов Б = (А_рА₂, . А ), включив в него векторы, соответствующие разрешенным неизвестным;
• 4) записать разложения векторов по базису; коэффициентами разложения вектора А. по этому базису являются координаты соответствующего вектора

в разрешенной системе уравнений, т.е.

Система векторов, состоящая из п векторов, ранг которой равен г, может иметь несколько базисов. Число возможных базисов системы векторов определяется как число меньшее или равное числу сочетаний из п по г.

Пример 3.3. Найти ранг и базис системы векторов

разложения векторов по базису, перейти к новому базису и найти число возможных базисов системы.

Решение. Составим систему уравнений A _t ay + А₂х₂ + . + А„х_п = 0, которая в координатной записи имеет вид

Приведение данной системы уравнений с помощью преобразований Жордана к равносильной разрешенной приведено в ниже следующей таблице.

Разрешенная система имеет вид

В базис системы векторов включаем 1-й и 2-й векторы Б_: = (A_VA₂), которые соответствуют разрешенным неизвестным х₁ и х₂. Ранг системы векторов равен числу векторов, вошедших в базис, т.е. г = 2.

Запишем разложения векторов по базису. Коэффициентами разложения вектора А₃ являются координаты вектора А’₃ = (3, -2), т.е. коэффициенты при х₃ в разрешенной системе уравнений (в последних трех строках таблицы), они образуют столбец, расположенный под х₃ А₃ = ЗЛ₁ – 2А_г Аналогично, коэффициентами разложения вектора А₄ являются координаты вектора А’₄ = (4, 1) А₄ = 4А_у + 1 А_т

Для нахождения нового базиса необходимо выбрать новый разрешающий элемент. Пусть этим элементом будет элемент я₉₄ = 1.

Как найти базис данной системы векторов

Определение базиса.Система векторов образует базис, если:

1) она линейно-независима,

2) любой вектор пространства через нее линейно выражается.

Пример 1.Базис пространства : .

2. В системе векторов базисом являются векторы: , т.к. линейно выражается через векторы .

Замечание.Чтобы найти базис данной системы векторов необходимо:

1) записать координаты векторов в матрицу,

2) с помощью элементарных преобразований привести матрицу к треугольному виду,

3) ненулевые строки матрицы будут являться базисом системы,

4) количество векторов в базисе равно рангу матрицы.

Теорема Кронекера-Капелли

Теорема Кронеккера–Капелли дает исчерпывающий ответ на вопрос о совместности произвольной системы линейных уравнений с неизвестными

Теорема Кронеккера–Капелли. Система линейных алгебраических урав­нений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы, .

Алгоритм отыскания всех решений совместной системы линейных уравнений вытекает из теоремы Кронеккера–Капелли и следующих теорем.

Теорема. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.

Теорема. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.

Алгоритм решения произвольной системы линейных уравнений:

1. Найдем ранги основной и расширенной матриц системы. Если они не равны ( ), то система несовместна (не имеет решений). Если ранги равны ( , то система совместна.

2. Для совместной системы найдем какой-нибудь минор, порядок которого определяет ранг матрицы (такой минор называют базисным). Составим новую систему из уравнений, в которых коэффициенты при неизвестных, входят в базисный минор (эти неизвестные называют главными неизвестными), остальные уравнения отбросим. Главные неизвестные с коэффициентами оставим слева, а остальные неизвестных (их называют свободными неизвестными) перенесем в правую часть уравнений.

3. Найдем выражения главных неизвестных через свободные. Получаем общее решение системы.

4. Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образомнаходим частные решения исходной системы уравнений.

Линейное программирование. Основные понятия

Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.

Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.

Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующихсистему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называетсядопустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи.

Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального).

В общей постановке задача линейного программирования выглядит следующим образом:

Имеются какие-то переменные х = (х₁ , х₂ , … х_n ) и функция этих переменных f(x) = f (х₁ , х₂ , … х_n ), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:

В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что
а) функция f(x) является линейной функцией переменных х₁ , х₂ , … х_n
б) область G определяется системой линейных равенств или неравенств.

Математическая модель любой задачи линейного программирования включает в себя:

Векторное пространство: размерность и базис, разложение вектора по базису

В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:

e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )

Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.

Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

Рассмотрим применение данной теории на конкретных примерах.

Исходные данные: векторы

a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 )

Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.

Решение

Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.

A = 3 2 3 – 2 1 – 1 1 2 – 2 A = 3 – 2 1 2 1 2 3 – 1 – 2 = 3 · 1 · ( – 2 ) + ( – 2 ) · 2 · 3 + 1 · 2 · ( – 1 ) – 1 · 1 · 3 – ( – 2 ) · 2 · ( – 2 ) – 3 · 2 · ( – 1 ) = = – 25 ≠ 0 ⇒ R a n k ( A ) = 3

Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.

Ответ: указанные векторы являются базисом векторного пространства.

Исходные данные: векторы

a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 ) d = ( 0 , 1 , 2 )

Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.

Решение

Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , – 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , – 1 , – 2 ) является базисом.

Ответ: указанная система векторов не является базисом.

Исходные данные: векторы

a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )

Могут ли они являться базисом четырехмерного пространства?

Решение

Cоставим матрицу, используя в качестве строк координаты заданных векторов

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

По методу Гаусса определим ранг матрицы:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

1 2 3 3 0 1 0 2 0 1 – 1 1 0 1 – 2 1

1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 – 2 – 1

1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4

Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.

Ответ: заданные векторы являются базисом четырехмерного пространства.

Исходные данные: векторы

a ( 1 ) = ( 1 , 2 , – 1 , – 2 ) a ( 2 ) = ( 0 , 2 , 1 , – 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )

Составляют ли они базис пространства размерностью 4?

Решение

Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.

Ответ: нет, не составляют.

Разложение вектора по базису

Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Докажем эту теорему:

зададим базис n -мерного векторного пространства – e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :

x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n – некоторые числа.

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:

1 – x 1 ) · e ( 1 ) + ( x

2 – x 2 ) · e ( 2 ) + . . . ( x

Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x

2 – x 2 ) , . . . , ( x

n – x n ) будут равны нулю. Из чего справедливым будет: x 1 = x

n . И это доказывает единственный вариант разложения вектора по базису.

При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .

Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .

Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x

Вектор x → будет представлен следующим образом:

2 · e ( 2 ) + . . . + x

Запишем это выражение в координатной форме:

( x 1 , x 2 , . . . , x n ) = x

1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x

2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x

n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x

2 e 1 ( 2 ) + . . . + x

2 e 2 ( 2 ) + + . . . + x

n e 2 ( n ) , . . . , x

2 e n ( 2 ) + . . . + x

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x

n e 2 n ⋮ x n = x

Матрица этой системы будет иметь следующий вид:

e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )

Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x

n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .

Применим рассмотренную теорию на конкретном примере.

Исходные данные: в базисе трехмерного пространства заданы векторы

e ( 1 ) = ( 1 , – 1 , 1 ) e ( 2 ) = ( 3 , 2 , – 5 ) e ( 3 ) = ( 2 , 1 , – 3 ) x = ( 6 , 2 , – 7 )

Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.

Решение

Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .

Используем метод Гаусса:

A = 1 – 1 1 3 2 – 5 2 1 – 3

1 – 1 1 0 5 – 8 0 3 – 5

1 – 1 1 0 5 – 8 0 0 – 1 5

R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.

Пусть в базисе вектор x → имеет координаты x

3 . Связь этих координат определяется уравнением:

3 e 1 ( 3 ) x 2 = x

3 e 2 ( 3 ) x 3 = x

Применим значения согласно условиям задачи:

Решим систему уравнений методом Крамера:

∆ = 1 3 2 – 1 2 1 1 – 5 – 3 = – 1 ∆ x

1 = 6 3 2 2 2 1 – 7 – 5 – 3 = – 1 , x

1 ∆ = – 1 – 1 = 1 ∆ x

2 = 1 6 2 – 1 2 1 1 – 7 – 3 = – 1 , x

2 ∆ = – 1 – 1 = 1 ∆ x

3 = 1 3 6 – 1 2 2 1 – 5 – 7 = – 1 , x

Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x

Ответ: x = ( 1 , 1 , 1 )

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

Указанные системы являются также базисами заданного пространства.

n ( 1 ) – координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:

1 ( 1 ) e 1 ( 1 ) + c

2 ( 1 ) e 1 ( 2 ) + . . . + c

n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c

1 ( 1 ) e 2 ( 1 ) + c

2 ( 1 ) e 2 ( 2 ) + . . . + c

n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c

1 ( 1 ) e n ( 1 ) + c

2 ( 1 ) e n ( 2 ) + . . . + c

В виде матрицы систему можно отобразить так:

( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c

n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Сделаем по аналогии такую же запись для вектора c ( 2 ) :

( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c

n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

И, далее действуя по тому же принципу, получаем:

( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c

n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Матричные равенства объединим в одно выражение:

c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c

n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :

e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e

n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )

Дадим следующие определения:

n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )

к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .

n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )

к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .

[spoiler title=”источники:”]

http://megaobuchalka.ru/10/21983.html

http://zaochnik.com/spravochnik/matematika/vektory/vektornoe-prostranstvo/

[/spoiler]

В статье о n-мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n-мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n-векторов. Размерность его соответственно равна n. Возьмем систему из n-единичных векторов:

e(1)=(1, 0,…,0)e(2)=(0, 1,…,0)e(n)=(0, 0,…,1)

Используем эти векторы в качестве составляющих матрицы A: она будет являться единичной с размерностью n на n. Ранг этой матрицы равен n. Следовательно, векторная система e(1), e(2),…, e(n) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n, то размерность пространства n-мерных векторов равна n, а единичные векторы e(1), e(2),…, e(n) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n-мерных векторов, в которой число векторов меньше n, не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e(2), e(1),…, e(n). Она также будет являться базисом n-мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n. Система e(2), e(1),…, e(n) линейно независима и является базисом n-мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n-мерного векторного пространства.

Рассмотрим применение данной теории на конкретных примерах.

Разложение вектора по базису

Примем, что произвольные векторы e(1), e(2),…, e(n) являются базисом векторного n-мерного пространства. Добавим к ним некий n-мерный вектор x→: полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n-мерного векторного пространства единственным образом раскладывается по базису.

Доказанная теория делает понятным выражение «задан n-мерный вектор x=(x1, x2,…, xn)»: рассматривается вектор x→ n-мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n-мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n-мерного векторного пространства задана система из n линейно независимых векторов

e(1)=(e1(1), e2(1),…, en(1))e(2)=(e1(2), e2(2),…, en(2))⋮e(n)=(e1(n), e2(n),…, en(n))

а также задан вектор x=(x1, x2,…, xn).

Векторы e1(1), e2(2),…, en(n) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x→ в базисе e1(1), e2(2),…, en(n), обозначаемые как x~1, x~2,…, x~n.

Вектор x→ будет представлен следующим образом:

x=x~1·e(1)+x~2·e(2)+…+x~n·e(n)

Запишем это выражение в координатной форме:

(x1, x2,…, xn)=x~1·(e(1)1, e(1)2,…, e(1)n)+x~2·(e(2)1, e(2)2,…, e(2)n)+…++x~n·(e(n)1, e(n)2,…, e(n)n)==(x~1e1(1)+x~2e1(2)+…+x~ne1(n), x~1e2(1)+x~2e2(2)++…+x~ne2(n), …, x~1en(1)+x~2en(2)+…+x~nen(n))

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x~1, x~2,…, x~n:

x1=x~1e11+x~2e12+…+x~ne1nx2=x~1e21+x~2e22+…+x~ne2n⋮xn=x~1en1+x~2en2+…+x~nenn

Матрица этой системы будет иметь следующий вид:

e1(1)e1(2)⋯e1(n)e2(1)e2(2)⋯e2(n)⋮⋮⋮⋮en(1)en(2)⋯en(n)

Пусть это будет матрица A, и ее столбцы – векторы линейно независимой системы векторов e1(1), e2(2),…, en(n). Ранг матрицы – n, и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x~1, x~2,…, x~n вектора x→ в базисе e1(1), e2(2),…, en(n).

Применим рассмотренную теорию на конкретном примере.

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c(1)=(c1(1), c2(1),…, cn(1))c(2)=(c1(2), c2(2),…, cn(2))⋮c(n)=(c1(n), e2(n),…, cn(n))

И

e(1)=(e1(1), e2(1),…, en(1))e(2)=(e1(2), e2(2),…, en(2))⋮e(n)=(e1(n), e2(n),…, en(n))

Указанные системы являются также базисами заданного пространства.

Пусть c~1(1), c~2(1),…, c~n(1) – координаты вектора c(1) в базисе e(1), e(2),…, e(3), тогда связь координат будет задаваться системой линейных уравнений:

с1(1)=c~1(1)e1(1)+c~2(1)e1(2)+…+c~n(1)e1(n)с2(1)=c~1(1)e2(1)+c~2(1)e2(2)+…+c~n(1)e2(n)⋮                                                           сn(1)=c~1(1)en(1)+c~2(1)en(2)+…+c~n(1)en(n)

В виде матрицы систему можно отобразить так:

(c1(1), c2(1),…, cn(1))=(c~1(1), c~2(1),…, c~n(1))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)

Сделаем по аналогии такую же запись для вектора c(2):

(c1(2), c2(2),…, cn(2))=(c~1(2), c~2(2),…, c~n(2))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)

И, далее действуя по тому же принципу, получаем:

(c1(n), c2(n),…, cn(n))=(c~1(n), c~2(n),…, c~n(n))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)

Матричные равенства объединим в одно выражение:

c1(1)c2(1)⋯cn(1)c1(2)c2(2)⋯cn(2)⋮⋮⋮⋮c1(n)c2(n)⋯cn(n)=c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)·e1(1)e2(1)⋯en(1)e1(2)e2(2)⋯en(2)⋮⋮⋮⋮e1(n)e2(n)⋯en(n)

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e(1), e(2),…, e(3) через базис c(1), c(2),…, c(n):

e1(1)e2(1)⋯en(1)e1(2)e2(2)⋯en(2)⋮⋮⋮⋮e1(n)e2(n)⋯en(n)=e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)·c1(1)c2(1)⋯cn(1)c1(2)c2(2)⋯cn(2)⋮⋮⋮⋮c1(n)c2(n)⋯cn(n)

Дадим следующие определения:

Из этих равенств очевидно, что

c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)·e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)=10⋯001⋯0⋮⋮⋮⋮00⋯1e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)·c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)=10⋯001⋯0⋮⋮⋮⋮00⋯1 

т.е. матрицы перехода взаимообратны.

Рассмотрим теорию на конкретном примере.

(все матрицы образуют динейно независимую систему).

2.21. Доказать, что матрицы вида образуют линейное подпространство в пространстве матриц М₂₃. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.

Решение:

Линейность данного множества матриц следует из линейности операций умножения матриц на число и сложения матриц, например:

При этом каждая матрица данного подпространства может быть представлена в виде:

Отсюда следует, что размерность подпространства L равна 2 и вкачестве его базиса можно взять матрицы .

Для дополнения этого базиса до базиса всего пространства М₂₃ можно выбрать матрицы

(все матрицы образуют динейно независимую систему).

2.22. Найти общий вид матрицы, антиперестановочной (AX=-XA) с данной матрицей . Доказать, что множество матриц Х образует линейное подпространство в пространстве М₂₂ матриц 2-го порядка. Найти его базис и размерность.

Решение:

Проверяем линейность данного множества L матриц:

Все условия выполнены – L является линейным пространством.

Если матрица антиперестановочная с данной матрицей , то:

т.е. матрица Х может быть представлена в виде:

Отсюда следует, что размерность подпространства L равна 2 и вкачестве его базиса можно взять матрицы .

2.23. Образуют ли матрицы базис в пространстве матриц М₂₂?

Решение:

Запишем данные матрицы в каноническом базисе, получим векторы

найдем ранг этой системы векторов:

Ранг системы векторов равен 3, следовательно, данные матрицы не образуют базис в пространстве матриц М₂₂

2.24. Найти размерность и какой-нибудь базис линейной оболочки системы матриц

Решение:

Запишем данные матрицы в каноническом базисе, получим векторы

найдем ранг этой системы векторов:

Ранг системы векторов равен 3, следовательно:

1) размерность данной системы матриц равна 3,

2) в качестве базиса их линейной оболочки можно взять первые три матрицы, т.е. (Е₁, Е₂, Е₃).

2.25. Установить, являются ли заданные множества подпространствами пространства M_nn. В случае положительного ответа найти базис и размерность подпространства.

1) множество всех симметрических квадратных матриц порядка n (A^T = A).

2) множество всех кососимметрических квадратных матриц порядка n (A^T = -A).

3) множество всех квадратных вырожденных матриц порядка n (detA = 0).

Решение:

1) При умножении любой симметрической квадратной матрицы порядка n (A^T = A) на любое число получается также симметрическая квадратная матрица порядка n , сумма двух симметрических квадратных матриц порядка n также является симметрической квадратной матрицей порядка n. Следовательно, множество всех симметрических квадратных матриц порядка n является подпространством пространства M_nn.

2) При умножении любой кососимметрической квадратной матрицы порядка n (A^T=-A) на любое число получается также симметрическая квадратная матрица порядка n , сумма двух кососимметрических квадратных матриц порядка n также является кососимметрической квадратной матрицей порядка n. Следовательно, множество всех кососимметрических квадратных матриц порядка n является подпространством пространства M_nn.

3) Определитель суммы двух матриц, определители которых равны нулю, может быть отличен от нуля, например:

Следовательно, множество всех квадратных матриц порядка n, определитель которых равен нулю, не является подпространством пространства M_nn.

2.26. Доказать, что множество функций образует линейное пространство. Найти его размерность и базис.

Решение:

Проверяем линейность заданного множества функций:

Все условия выполнены – L является линейным пространством.

В системе функций только любые две функции линейно независимы, поскольку они связаны соотношением , и любой вектор пространства L может быть представлен в виде линейной комбинации, например, первых двух функций системы, следовательно, эти две функции образуют базис пространства L, размерность которого поэтому равна 2.

2.27. Доказать, что множество функций образует линейное пространство. Найти его размерность и базис.

Решение:

Проверяем линейность заданного множества функций:

Все условия выполнены – L является линейным пространством.

Функции линейно независимы: если , то, записывая это равенство для t=-1, t=0 и t=1, получим:

и любой вектор пространства L может быть представлен в виде линейной комбинации этих функций (по определению L), следовательно, эти функции образуют базис пространства L, размерность которого поэтому равна 3.

2.28. Исследовать на линейную независимость систему функций {sint, cost, sin2t}

Решение:

Предположим, что входящие в данную систему функции линейно зависимы, т.е. найдутся такие , не все равные нулю, для которых выполняется равенство . Тогда, записывая это равенство для получим:

Получили противоречие, из чего следует, что данная система функций является линейно независимой.

2.29. Исследовать на линейную независимость систему функций {1, lnt, ln2t}

Решение:

Для доказательства того, что данная система функций является линейно зависимой, достаточно указать такие , не все равные нулю, для которых выполняется равенство .

Рассмотрим , для которых для имеем:

Следовательно, данная система функций является линейно зависимой.

2.30. Исследовать на линейную независимость систему функций {1, cost, cos2t}

.

Решение:

Предположим, что входящие в данную систему функции линейно зависимы, т.е. найдутся такие , не все равные нулю, для которых выполняется равенство . Тогда, записывая это равенство для получим:

Получили противоречие, из чего следует, что данная система функций является линейно независимой.

30

Линейное (векторное) пространство

1. Понятие линейного пространства

Определение 1.1. Множество R элементов x, y, z, … любой природы называется линейным (или векторным) пространством, если выполнены следующие три требования:

1. Существует правило, посредством которого любым двум элементам x и y множества R ставится в соответствие третий элемент z этого множества, называемый суммой элементов x и y и обозначаемый z=x+y.
2. Существует правило, посредством которого любому элементу x множества R и любому вещественному числу α ставится в соответствие элемент w этого множества, называемый произведением элемента x на число α и обозначаемый w=αx или w=xα.
3. Представленные два правила подчинены следующим восьми аксиомам:
   1. x+y=y+x (переместительное свойство суммы);
   2. (x+y)+z=x+(y+z) (сочетательное свойство суммы);
   3. существует нулевой элемент 0 такой, что x+0=x для любого элемента x.
   4. для любого элемента x существует противоположный элемент элемент x’ такой, что x+x’=0;
   5. 1·x=x для любого x;
   6. λ(μx)=(λμ)x (сочетательное свойство относительно числового множителя);
   7. (λ+μ)x=λx+μx (распределительное свойство относительно числовых множителей);
   8. λ(x+y)=λx+λy (распределительное свойство относительно суммы элементов).

Элементы линейного (векторного) пространства называются векторами.

2. Базис линейного пространства

Определение 2.1. Совокупность линейно независимых элементов пространства R называется базисом этого пространства, если для каждого элемента x пространства R существуют вещественные чиcла такие, что выполнено равенство

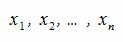
(2.1)

Равенство (2.1) называется разложением элемента x по базису а числа называются координатами элемента x (относительно базиса ).

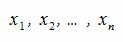
Докажем, что любой элемент x линейного пространства R может быть разложен по базису единственным образом.

Пусть существует и другое разложение x:

(2.2)

Вычитая (2.1) из (2.2) имеем:

(2.3)

Так как базисные элементы линейно независимы из соотношения (2.3) следует, что

или

Следовательно каждый элемент линейного пространства R может быть разложен по базису единственным образом.

Теорема 2.2. При сложении произвольных двух элементов линейного пространства R их координаты (относительно любого базиса пространства R) складываются, а при умножении любого элемента x на любое число α все координаты x умножаются на α.

Доказательство следует из аксиом 1-8 определения 1.1.

3. Размерность линейного пространства

Рассмотрим произвольное вещественное пространство R.

Определение 3.1. Линейное пространство R называется n-мерным, если в нем существует n линейно независимых элементов, а любые (n+1) элементов уже являются линейно зависимыми. При этом число n называется размерностью пространства R.

Размерность пространства обозначают символом dim.

Определение 3.2. Линейное пространство R называется бесконечномерным, если в нем существует любое число линейно независимых элементов.

Теорема 3.3. Пусть R является линейным пространствам размерности n (dim R=n). Тогда любые n линейно независимых элементов этого пространства образуют его базис.

Доказательство. Так как R является n -мерным пространством, то из определения 2.1 следует, что в нем существует совокупность из n линейно независимых элементов . Пусть x – любой элемент из R. Тогда согласно определению 3.1 линейно зависимы, т.е. существуют числа (не все равные нулю) такие, что справедливо равенство

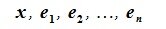
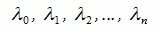
(3.1)

Заметим, что λ₀≠0 т.к. в противном случае из равенства (3.1) следовала, что элементы линейно зависимы. Поделив равенство (3.1) на λ₀ и положив

(3.2)

получим

(3.3)

Из равенства (3.3) следует, что любой вектор из пространства R может быть разложен по элементам и, следовательно, они образуют базис пространства R. ■

Теорема 3.4. Пусть линейное пространство R имеет базис, состоящий из n элементов. Тогда размерность R равна n (dim R=n).

Доказательство. Пусть множество n элементов является базисом пространства R. Достаточно доказать, что любые n+1 элементы этого пространства линейно зависимы. Разложив эти элементы по базису, получим:

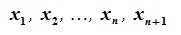
(3.4)

где a₁₁, a₁₂,…, a_n+1,n вещественные числа.

Пусть элементы 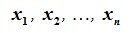линейно независимы. Перепишем (3.4) в матричном виде:

(3.5)

(3.6)

где, n×n-матрицы(элементы здесь являются вектор-строками),

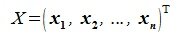
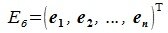
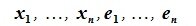
(3.7)

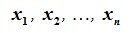
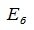
Так как линейно независимы, матрица A имеет обратную матрицу A^-1. Решив матричное уравнение (3.5) относительно получим :

(3.8)

Подставляя (3.8) в (3.6), получим:

(3.9)

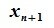
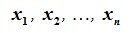
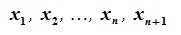
Как видно из уравнения (3.9) можно представить линейной комбинацией векторов . Следовательно векторы линейно зависимы. ■

4. Замена базиса и преобразование координат

Пусть в пространстве R наряду с исходным базисом имеется другой базис . Векторы этого базиса можно выразить через линейную комбинацию векторов исходного базиса следующим образом:

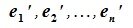
(4.1)

или

(4.2)

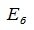
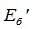
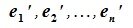
где и матрицы составленные из векторов строк и соответственно (), а матрица P имеет вид:

(4.3)

Матрица P называется матрицей замены базиса на .

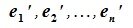
В свою очередь, векторы исходного базиса выражаются через векторы нового следующим соотношением:

(4.4)

где

(4.5)

Подставляя (4.2) в (4.4) имеем:

(4.6)

Из (4.6) следует, что QP=E, где E-единичная матрица, а матрицы Q и P взаимно обратные матрицы.

Рассмотрим как изменяются координаты векторов при замене базиса.

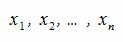
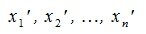
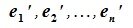
Пусть вектор x имеет координаты в базисе и координаты в базисе , тогда

(4.7)

или

(4.8)

Из (4.8) и из (4.2) имеем:

(4.9)

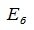
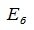
Так как квадратная матрица полного ранга, она имеет обратную матрицу. Умножив левые и правые части уравнения (4.9) на обратную к матрицу получим:

или

(4.10)

Матрица P^T называется матрицей преобразования координат. Она транспонирована с матрицей замены базиса. Обратная матрица (P^T)^-1 дает выражения новых координат через старые.

Матрица, обратная к транспонированной для некоторой матрицы, называется контраградиентной с ней.

5. Изоморфизм линейных пространств

Определение 5.1. Два произвольных вещественных линейных пространства R и R’ называются изоморфными, если между элементами этих пространств можно установить взаимно однозначное соответствие так, что если x, y∈R отвечают x’, y’∊R’ соответственно, то элементу x+y∈R отвечает элемент x’+y’∈R’, а для любого вещественного α, элементу αx∈R отвечает элемент αx’∈R’.

Теорема 5.2. Если пространства R и R’ изоморфны, то они имеют одинаковую размерность.

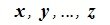
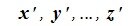
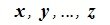
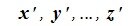
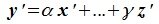
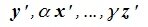
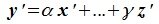
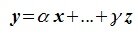
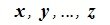
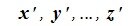
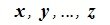
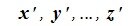
Доказательство. Пусть линейные пространства R и R’ изоморфны, и пусть элементам пространства R отвечают элементы пространства R’ соответственно. Допустим элементы линейно независимы. Покажем, что элементы также линейно независимы. Исходя из обратного предположения допустим, что элементы линейно зависимы. тогда один из них можно представить линейной комбинацией остальных элементов:. Но элементам отвечают элементы y в пространстве R, а сумме отвечает сумма . Но последнее означает линейную зависимость элементов . Следовательно линейно независимы. Из линейной зависимости элементов следует линейная зависимость элементов . Следовательно максимальное количество линейно независимых векторов для пространств R и R’ одно и то же, т.е. эти пространства имеют одинаковую размерность. ■

Теорема 5.3. Любые два n-мерных вещественных линейных пространства R и R’ изоморфны.

Доказательство. Выберем базисы и для пространств R и R’ соответственно. Тогда каждый элемент пространства R можно представить линейной комбинацией базисных элементов: . Этому элементу в пространстве R’ поставим в соответствие элемент теми же координатами:. В свою очередь элементу x’ пространства R’ соответствует элемент x пространства R . Отметим, что если элементам x и y пространства R отвечают элементы x’ и y’ пространства R’ соответственно , то исходя из теоремы 2.2 элементу x+y пространства R отвечает элемент x’+y’ пространства R’, а элементу αx отвечает элемент αx’. ■