Сообщения без ответов | Активные темы
Найдитее базис направляющего подпространства и вектор сдвига
Модераторы: Prokop, mad_math
| Автор | Сообщение | ||
|---|---|---|---|
|
helpmepleaseeee |
Заголовок сообщения: Найдитее базис направляющего подпространства и вектор сдвига
|
||
|
для многообразия решений системы уравнений:
|
||
| Вернуться к началу |
|
||
|
_Sasha_ |
Заголовок сообщения: Re: Найдитее базис направляющего подпространства и вектор сдвига
|
|
Базисом направляющего подпространства многообразия решений системы уравнений является фундаметальная система решений (ФСР) соотвеетствующей однородной системы уравнений. Вектором сдвига является любое частное решение данной неоднородной системы линейных уранений.
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Базис подпространства и вектор сдвига
в форуме Линейная и Абстрактная алгебра |
belka4204 |
1 |
424 |
17 июн 2015, 12:06 |
|
Базис и вектор сдвига
в форуме Линейная и Абстрактная алгебра |
Arisha1990 |
3 |
1334 |
09 июн 2014, 08:07 |
|
Базис подпространства и базис объемлещего пространства
в форуме Линейная и Абстрактная алгебра |
mathematic_x |
2 |
230 |
30 дек 2020, 16:18 |
|
Базис подпространства
в форуме Линейная и Абстрактная алгебра |
The Royal |
1 |
399 |
23 мар 2014, 12:52 |
|
Найти ортогональный базис для подпространства
в форуме Линейная и Абстрактная алгебра |
CruelShadow |
13 |
916 |
11 мар 2018, 17:55 |
|
Базис, подпространства, описывающее уравнение
в форуме Линейная и Абстрактная алгебра |
Skyfire |
0 |
380 |
24 июн 2013, 17:27 |
|
Ортогональный базис подпространства, натянутого на векторы
в форуме Линейная и Абстрактная алгебра |
kicultanya |
0 |
768 |
10 окт 2017, 18:22 |
|
Найдите базис линейного подпространства R3,заданного уравнен
в форуме Линейная и Абстрактная алгебра |
eliotvaliev |
1 |
429 |
07 апр 2019, 14:25 |
|
Построить базис, включающий вектор
в форуме Линейная и Абстрактная алгебра |
_Baron_Samedi_ |
1 |
174 |
29 дек 2019, 16:17 |
|
Вектор медианы, вектор высоты, вектор биссектрисы
в форуме Аналитическая геометрия и Векторная алгебра |
Higin |
5 |
1525 |
11 окт 2015, 13:40 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 9 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
Определение. Два множества F
и G векторов евклидова
пространства E
называются ортогональными, если каждый
вектор из F ортогонален
каждому вектору из G.
Определение. Пусть F
– подпространство E.
Совокупность всех векторов подпространства
E, ортогональных
подпространству F,
называется ортогональным дополнением
![]()
подпространства F.
Всякое ортогональное дополнение
является, в свою очередь, линейным
подпространством.
Всякое произвольное евклидово пространство
E разлагается в прямую
сумму своего произвольного подпространства
F и его ортогонального
дополнения
![]()
Примеры
1. Требуется найти базис ортогонального
дополнения
![]()
подпространства L,
натянутого на векторы

,
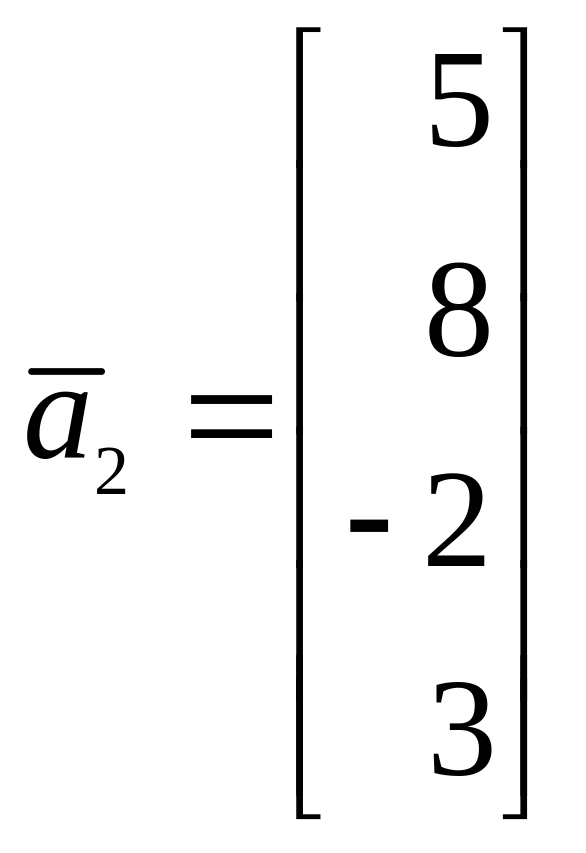
,

Будем считать, что базис, относительно
которого заданы векторы, ортонормированный.
По определению, если
![]()
,
то
![]()
.
Далее, каждый вектор
из
должен быть ортогонален к
.
Для этого достаточно, чтобы
![]()
![]()
.
Расписывая скалярные произведения,
получим три уравнения относительно
координат
![]()
вектора
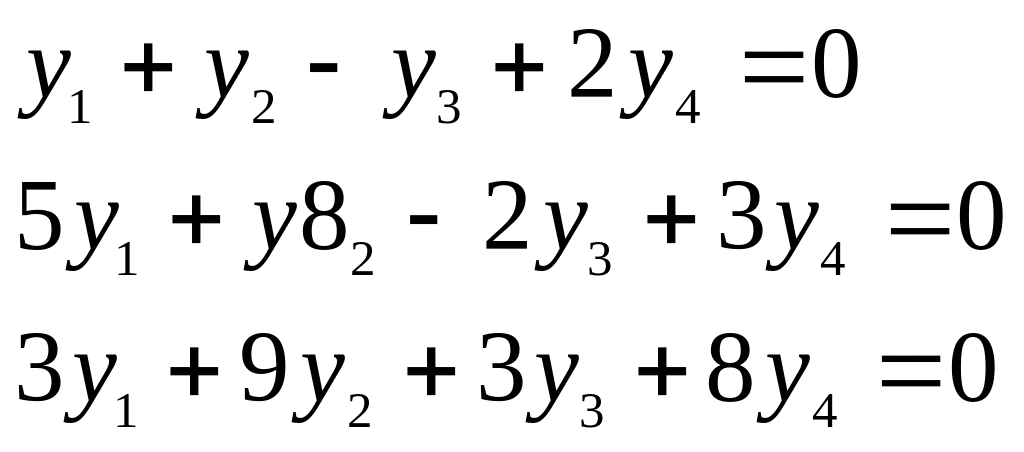
Совокупность решений этой системы и
образует ортогональное дополнение. За
базис в
можно принять любую фундаментальную
систему решений. Например, вектор
![]()
.
2. Линейное подпространство
![]()
задано уравнениями
![]()
Требуется найти уравнения, которые
задают ортогональное дополнение
.
Пусть
![]()
,
![]()
.
Тогда
.
Этому условию удовлетворяют два линейно
независимых вектора
![]()
и
![]()
,
которые образуют коэффициенты системы
уравнений, задающей F.
Далее,
![]()
.
Ранг системы равен 2. Значит
![]()
и, так как
![]()
,
то
![]()
.
Поэтому найденные векторы можно принять
за базис в
,
и
есть линейная оболочка данных векторов.
Далее задача решается так же как в
примере из § 3. Дословно повторяя решение,
получим следующую систему уравнений
![]()
которая и задает
.
5.3. Проектирование вектора на подпространства
Пусть
![]()
.
Тогда всякий вектор
![]()
можно представить в виде
![]()
,
где
![]()
и
![]()
.
Вектор
![]()
называется ортогональной проекцией
вектора x на
подпространство L, а
вектор
![]()
называется ортогональной составляющей
вектора
.
Пусть
![]()
и
![]()
— расстояние между векторами
![]()
,
тогда
![]()
Таким образом, ортогональная проекция
есть ближайший к
вектору подпространства L.
Часто используются следующие обозначения
![]()
,
![]()
.
Укажем в заключение как вычисляются
координаты вектора
![]()
.
Пусть
![]()
— базис в L. Так как
![]()
,
то
![]()
.
Поэтому
![]()
Отсюда имеем, что в случае ортонормированного
базиса
![]()
Примеры
1. Найти ортогональную проекцию
и ортогональную составляющую
![]()
вектора
на линейное подпространство L,
натянутое на векторы
![]()
.
Все векторы заданы координатами
относительно ортонормированного базиса.
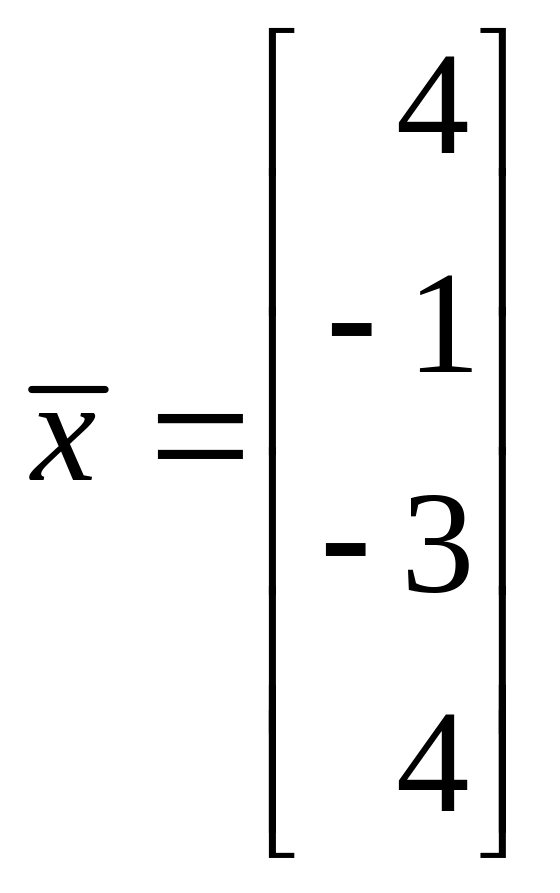
,
,
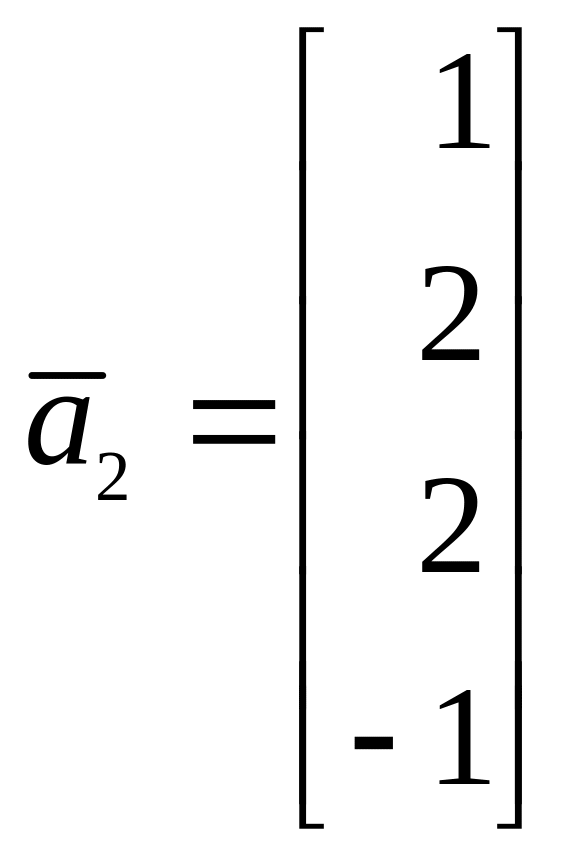
,

Нетрудно убедиться, что
![]()
и что за базис можно принять векторы
и
.
Нам будет удобно перейти к ортонормированному
базису в L. Применяя
процедуру ортогонализации к векторам
и
,
получим ортонормированный базис в L:
![]()
,
![]()
Заметьте, что векторы
и
![]()
линейно выражаются через
и
и, значит, также принадлежат L.
Имеем теперь

2. Требуется найти расстояние от точки,
заданной вектором
![]()
до плоскости (линейного многообразия),
заданной системой уравнений
![]()
Расстояние между точкой
и множеством L
определится следующим образом
![]()
Для вычисления расстояния удобно перейти
к параметрическому уравнению плоскости.
Имеем
и поэтому всякий вектор
![]()
представляется в виде
![]()
где
![]()
— фиксированный радиус-вектор точки
плоскости;
и
— базис направляющего линейного
подпространства, которое задается
соответствующей однородной системой.
Решая уравнение, получим, например,
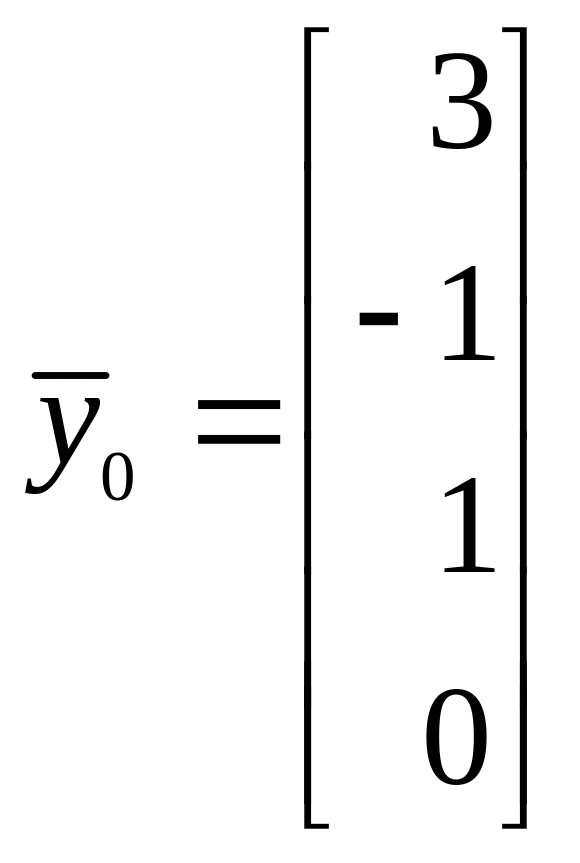
,

,

Затем
![]()
Векторы
и
принадлежат направляющему подпространству
M плоскости L.
Вектор
![]()
.
Так как
![]()
,
а
![]()
,
то
![]()
Правая часть этого неравенства и есть
искомое расстояние. Осталось вычислить
вектор
![]()
и найти его норму. Проделав для этого
аналогичные вычисления и вычислив длину
вектора, получим, что
![]()
.
3. Пусть
![]()
— ортонормированная система векторов
евклидова пространства En.
Нужно доказать, что для любого вектора
имеет место неравенство Бесселя
![]()
с равенством тогда и только тогда, когда
![]()
,
т.е. векторы
образуют ортонормированный базис в En.
Так как
![]()
— ортонормированная система, то ее
всегда можно векторами
![]()
достроить до ортонормированного базиса
в En.
Разложим вектор
по этому базису. Имеем
![]()
Далее,
![]()
или
![]()
С равенством тогда и только тогда, когда
.
Исключение составляют случаи, когда
![]()
![]()
или когда
принадлежит линейной оболочке векторов
![]()
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подпространство линейного пространства
Определение и размерность подпространства
Определение 6.1. Подпространством L n-мерного пространства R называется множество векторов, образующих линейное пространство по отношению к действиям, которые определены в R.
Другими словами, L называется подпространством пространства R, если из x, y∈L следует, что x+y∈L и если x∈L, то λ x∈L, где λ— любое вещественное число.
Простейшим примером подпространства является нулевое подпространство, т.е. подмножество пространства R, состоящее из единственного нулевого элемента. Подпространством может служить и все пространство R. Эти подпространства называются тривиальными или несобственными.
Подпространство n-мерного пространства конечномерно и его размерность не превосходит n: dim L≤ dim R.
Сумма и пересечение подпространств
Пусть L и M — два подпространства пространства R.
Cуммой L+M называется множество векторов x+y, где x∈L и y∈M. Очевидно, что любая линейная комбинация векторов из L+M принадлежит L+M, следовательно L+M является подпространством пространства R (может совпадать с пространством R).
Пересечением L∩M подпространств L и M называется множество векторов, принадлежащих одновременно подпространствам L и M (может состоять только из нулевого вектора).
Теорема 6.1. Сумма размерностей произвольных подпространств L и M конечномерного линейного пространства R равна размерности суммы этих подпространств и размерности пересечения этих подпространств:
dim L+dim M=dim(L+M)+dim(L∩M).
Доказательство. Обозначим F=L+M и G=L∩M. Пусть G g-мерное подпространство. Выберем в нем базис 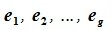 . Так как G⊂L и G⊂M, следовательно базис G можно дополнить до базиса L и до базиса M. Пусть
. Так как G⊂L и G⊂M, следовательно базис G можно дополнить до базиса L и до базиса M. Пусть 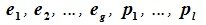 базис подпространства L и пусть
базис подпространства L и пусть 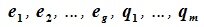 базис подпространства M. Покажем, что векторы
базис подпространства M. Покажем, что векторы
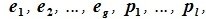
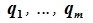
составляют базис F=L+M. Для того, чтобы векторы (6.1) составляли базис пространства F они должны быть линейно независимы и любой вектор пространства F можно представить линейной комбинацией векторов (6.1).
Докажем линейную независимость векторов (6.1). Пусть нулевой вектор пространства F представляется линейной комбинацией векторов (6.1) с некоторыми коэффициентами:
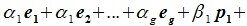
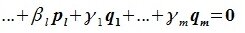
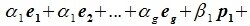

Левая часть (6.3) является вектором подпространства L, а правая часть является вектором подпространства M. Следовательно вектор
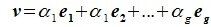
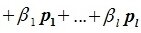
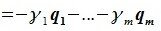
принадлежит подпространству G=L∩M. С другой стороны вектор v можно представить линейной комбинацией базисных векторов подпространства G:
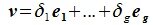
Из уравнений (6.4) и (6.5) имеем:
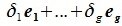
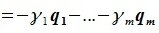
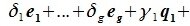
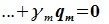
Но векторы 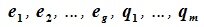 являются базисом подпространства M, следовательно они линейно независимы и
являются базисом подпространства M, следовательно они линейно независимы и 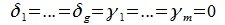 . Тогда (6.2) примет вид:
. Тогда (6.2) примет вид:
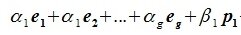
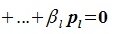
В силу линейной независимости базиса подпространства L имеем:
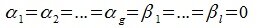
Так как все коэффициенты в уравнении (6.2) оказались нулевыми, то векторы
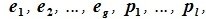
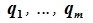
линейно независимы. Но любой вектор z из F (по определению суммы подпространств) можно представить суммой x+y, где x∈L, y∈M. В свою очередь x представляется линейной комбинацией векторов 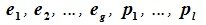 а y — линейной комбинацией векторов
а y — линейной комбинацией векторов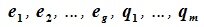 . Следовательно векторы (6.10) порождают подпространство F. Получили, что векторы (6.10) образуют базис F=L+M.
. Следовательно векторы (6.10) порождают подпространство F. Получили, что векторы (6.10) образуют базис F=L+M.
Изучая базисы подпространств L и M и базис подпространства F=L+M (6.10), имеем: dim L=g+l, dim M=g+m, dim (L+M)=g+l+m. Следовательно:
dim L+dim M−dim(L∩M)=dim(L+M). ■
Прямая сумма подпространств
Определение 6.2. Пространство F представляет собой прямую сумму подпространств L и M, если каждый вектор x пространства F может быть единственным способом представлен в виде суммы x=y+z, где y∈ L и z∈M.
Прямая сумма обозначается L⊕M. Говорят, что если F=L⊕M, то F разлагается в прямую сумму своих подпространств L и M.
Теорема 6.2. Для того, чтобы n-мерное пространство R представляло собой прямую сумму подпространств L и M, достаточно, чтобы пересечение L и M содержало только нулевой элемент и чтобы размерность R была равна сумме размерностей подпространств L и M.
Доказательство. Выберем некоторый базис 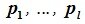 в подпространстве L и некоторый базис
в подпространстве L и некоторый базис 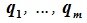 в подпространстве M. Докажем, что
в подпространстве M. Докажем, что
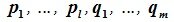
является базисом пространства R. По условию теоремы размерность пространства R n равна сумме подпространств L и M (n=l+m). Достаточно доказать линейную независимость элементов (6.11). Пусть нулевой вектор пространства R представляется линейной комбинацией векторов (6.11) с некоторыми коэффициентами:
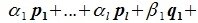
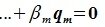
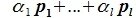
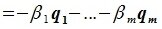
Так как левая часть (6.13) является вектором подпространства L, а правая часть — вектором подпространства M и L∩M= 0, то

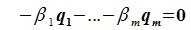
Но векторы  и
и  являются базисами подпространств L и M соответственно. Следовательно они линейно независимы. Тогда
являются базисами подпространств L и M соответственно. Следовательно они линейно независимы. Тогда
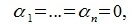
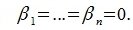
Установили, что (6.12) справедливо лишь при условии (6.15), а это доказывает линейную независимость векторов (6.11). Следовательно они образуют базис в R.
Пусть x∈R. Разложим его по базису (6.11):
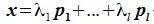
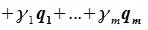
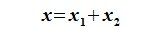
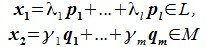
Из (6.17) и (6.18) следует, что любой вектор из R можно представить суммой векторов x1∈L и x2∈M. Остается доказать что это представление является единственным. Пусть кроме представления (6.17) есть и следующее представление:
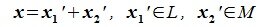
Вычитая (6.19) из (6.17), получим
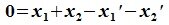
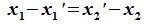
Так как 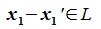 ,
, 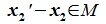 и L∩M= 0, то
и L∩M= 0, то 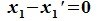 и
и 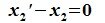 . Следовательно
. Следовательно 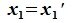 и
и 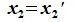 . ■
. ■
Способы описания подпространств линейного пространства
Рассмотрим два важных способа описания линейных подпространств, которые условно будем называть внутренним и внешним. В первом (внутреннем) способе используется понятие линейной оболочки векторов, когда все элементы подпространства выражаются через некоторые его элементы (образующие). При втором (внешнем) способе применяются однородные системы уравнений. В этом случае подпространство описывается как пересечение некоторых содержащих его множеств. Для каждого способа описания подпространств укажем методики на хождения размерностей, базисов, алгебраических дополнений, пересечений и сумм подпространств.
Любое n-мерное вещественное линейное пространство изоморфно n-мерному арифметическому пространству . Чтобы установить изоморфизм , достаточно выбрать в пространстве базис и каждому вектору поставить в соответствие его координатный столбец. Поэтому в данном разделе будем рассматривать описание подпространств n-мерного арифметического пространства .
Первый (внутренний) способ. Пусть в пространстве заданы столбцы . Напомним, что для систем столбцов были определены понятия базы (максимальной линейно независимой подсистемы столбцов) и ранга (максимального числа линейно не зависимых столбцов системы), а также методы их нахождения.
Рассматривая линейную оболочку столбцов как линейное подпространство , заключаем, что база системы столбцов является базисом этого подпространства, а ранг системы столбцов равен размерности подпространства .
Поэтому для нахождения размерности и базиса подпространства нужно выполнить следующие действия:
1) составить из данных столбцов матрицу размеров ;
2) привести ее к ступенчатому виду (1.4), используя элементарные преобразования строк;
3) определить размерность и базис подпространства
– количество ненулевых строк в матрице равняется размерности подпространства, т.е. ,
– столбцы матрицы , содержащие единичные элементы (в начале каждой «ступеньки»), определяют номера линейно независимых столбцов матрицы , т.е. искомый базис.
Таким образом, если подпространство задано своими образующими , то его размерность равна рангу системы столбцов , т.е. , а базисом служит максимальная линейно независимая подсистема образующих.
Второй (внешний) способ. Пусть подпространство задано как множество решений однородной системы уравнений с неизвестными. Множество решений системы уравнений можно рассматривать как пересечение подпространств , где — множество решений i-го уравнения системы . Напомним, что любое решение однородной системы представляется в виде линейной комбинации элементов фундаментальной системы решений. Поэтому раз мерность пространства , а базисом служит фундаментальная система решений однородной системы . Способы нахождения фундаментальной системы решений рассмотрены ранее.
Переход от одного способа описания подпространств к другому
Переход от внутреннего описания к внешнему. Пусть подпространство задано линейной оболочкой столбцов . Требуется составить такую однородную систему уравнений, множество решений которой совпадает с , т.е. . Для этого нужно выполнить следующие действия.
1. Из данных столбцов составить матрицу размеров , а затем блочную матрицу , приписав к матрице единичную матрицу n-го порядка.
2. Элементарными преобразованиями над строками блочной матрицы и первыми ее столбцами привести матрицу к виду , где — простейший вид матрицы .
3. Из последних строк матрицы составить матрицу .
4. Записать искомую систему уравнений .
Поясним содержание алгоритма. Заданное подпространство состоит из линейных комбинаций данных векторов, т.е. все его элементы имеют вид . Решаемую задачу можно сформулировать так: для каких векторов найдутся такие числа , чтобы выполнялось равенство . Другими словами, при каких неоднородная система ( уравнений с неизвестными ) имеет решения? Используя необходимое и достаточное условие (5.24) совместности системы, получаем равенство . Заметим, что решение поставленной задачи неоднозначно, так как существует много однородных систем, имеющих од но и то же множество решений.
Пример 8.8. Подпространство задано линейной оболочкой столбцов . Составить систему уравнений, определяющую подпространство .
Решение. 1. Составляем матрицу и блочную матрицу:
2. Приводим левый блок к простейшему виду. Вычитаем первую строку из остальных, а затем к четвертой строке прибавляем вторую, умноженную на (-2):
Преобразовываем столбцы левого блока: ко второму столбцу прибавим пер вый, умноженный на (-1), к третьему столбцу прибавим первый, умноженный на (-3), а затем второй, умноженный на (-1). Эти преобразования не изменяют правый блок полученной матрицы. Находим простейший вид Л матрицы и матрицу
3. Из последних строк матрицы составляем матрицу искомой системы.
4. Записываем систему уравнений Заданные в условии примера столбцы являются решениями полученной системы, в чем можно убедиться при их подстановке в систему уравнений вместо .
Переход от внешнего описания к внутреннему. Пусть подпространство задано как множество решений однородной системы т уравнений с л неизвестными: . Требуется найти размерность и базис этого подпространства, т.е. представить его в виде линейной оболочки . Для этого нужно выполнить следующие действия.
1. Найти фундаментальную систему решений однородной системы . Искомая размерность .
2. Представить заданное пространство как линейную оболочку .
Первый пункт алгоритма удобно выполнять следующим образом:
– составить блочную матрицу , приписав к матрице единичную матрицу n-го порядка;
– элементарными преобразованиями над столбцами блочной матрицы и строками верхнего блока привести матрицу к виду , где — простейший вид матрицы ;
– из последних столбцов матрицы составить фундаментальную матрицу .
Столбцы фундаментальной матрицы составляют искомую фундаментальную систему решений.
Заметим, что решение поставленной задачи неоднозначно, так как существует много базисов одного и того же линейного подпространства.
Пример 8.9. Найти размерность и базис подпространства , заданного системой уравнений
Решение. 1. Фундаментальная матрица для этой системы была найдена в примере 5.6
Ее столбцы образуют фундаментальную систему решений. Размерность подпространства равна , .
2. Столбцы являются искомым базисом, так как они линейно независимы и .
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Благодарю Ю.А.Смолькина за обнаружение 07.08.19 ошибки на настоящей странице и информирование о ней.
Линейное пространство
Определения
Пусть дано множество $ mathbb V_<>=left < X,Y,Z,U,dots right>$ элементов произвольной природы. Пусть для элементов этого множества определены две операции: сложения $ X+Y_<> $ и умножения на любое вещественное число $ alpha_<> $: $ alpha cdot X_<> $, и множество $ mathbb V_<> $ замкнуто относительно этих операций: $ X+Y in mathbb V , alpha cdot X in mathbb V_<> $. Пусть эти операции подчиняются аксиомам:
1. $ X+Y=Y+X_<> $ для $ < X,, Y>subset mathbb V_<> $;
2. $ (X+Y)+Z_<>=X+(Y+Z) $ для $ < X,, Y,, Z >subset mathbb V_<> $;
3. в $ mathbb V_<> $ cуществует нулевой вектор $ mathbb O_<> $ со свойством $ X+ mathbb O =X_<> $ для $ forall Xin mathbb V_<> $;
4. для каждого $ Xin mathbb V_<> $ существует обратный вектор $ X^<prime>in mathbb V_<> $ со свойством $ X+X^<prime>=mathbb O_<> $;
5. $ 1cdot X=X_<> $ для $ forall Xin mathbb V_<> $;
6. $ lambda left(mu X right)_<>= left(lambda mu right)X $ для $ forall Xin mathbb V_<> $, $ <lambda ,, mu >subset mathbb R_<> $ ;
7. $ (lambda + mu)X=lambda X + mu X_<> $ для $ forall Xin mathbb V_<> $, $ <lambda ,, mu >subset mathbb R_<> $ ;
8. $ lambda (X + Y) =lambda X_<> + lambda Y $ для $ < X,, Y>subset mathbb V_<> , lambda in mathbb R $.
Тогда такое множество $ mathbb V_<> $ называется линейным (векторным) пространством, его элементы называются векторами, и — чтобы подчеркнуть их отличие от чисел из $ mathbb R_<> $ — последние называются скалярами 1) . Пространство, состоящее из одного только нулевого вектора, называется тривиальным .
Элементарно доказывается единственность нулевого вектора, и единственность вектора, обратного вектору $ Xin mathbb V_<> $: $ X^<prime>=-1cdot X_<> $, его привычно обозначают $ — X_<> $.
Подмножество $ mathbb V_ <1>$ линейного пространства $ mathbb V_<> $, само являющееся линейным пространством (т.е. $ mathbb V_ <1>$ замкнуто относительно сложения векторов и умножения на произвольный скаляр), называется линейным подпространством пространства $ mathbb V_<> $. Тривиальными подпространствами линейного пространства $ mathbb V_<> $ называются само $ mathbb V_<> $ и пространство, состоящее из одного нулевого вектора $ mathbb O_<> $.
Примеры линейных пространств
Пример 1. Пространство $ mathbb R^ <3>$ упорядоченных троек вещественных чисел $ (a_1,a_2,a_<3>) $ с операциями, определяемыми равенствами:
$$ (a_1,a_2,a_3)+(b_1,b_2,b_3)= (a_1+b_1,a_2+b_2,a_3+b_3), alpha (a_1,a_2,a_3) = ( alpha a_1, alpha a_2, alpha a_3 ) . $$ Геометрическая интерпретация очевидна: вектор в пространстве, «привязанный» к началу координат, может быть задан координатами своего конца $ (a_1,a_2,a_<3>) $. На рисунке показано и типичное подпространство пространства $ mathbb R^ <3>$: плоскость, проходящая через начало координат.  Точнее говоря, элементами $ mathbb V_1 $ являются векторы, имеющие начало в начале координат и концы — в точках плоскости. Замкнутость такого множества относительно сложения векторов и их растяжения 2) очевидна.
Точнее говоря, элементами $ mathbb V_1 $ являются векторы, имеющие начало в начале координат и концы — в точках плоскости. Замкнутость такого множества относительно сложения векторов и их растяжения 2) очевидна.
Пример 2. Основываясь на том же примере, можно дать и иную интерпретацию векторного пространства $ mathbb V_1 $ (заложенную, кстати, уже в самом происхождении слова «вектор» 3) ) — оно определяет набор «сдвигов» точек пространства $ mathbb R^ <3>$. Эти сдвиги — или параллельные переносы любой пространственной фигуры — выбираются параллельными плоскости $ mathbb V_1 $.
Пример 3. Естественным обобщением $ mathbb R^ <3>$ служит пространство $ mathbb R_<>^ $: векторное пространство строк $ (a_1,dots,a_) $ или столбцов $ (a_1,dots,a_n)^ <^top>$. Один из способов задания подпространства в $ mathbb R_<>^ $ — задание набора ограничений. Множество решений системы линейных однородных уравнений:
$$ left<begin a_<11>x_1 +a_<12>x_2+ldots+a_<1n>x_n &=&0,\ a_<21>x_1 +a_<22>x_2+ldots+a_<2n>x_n &=&0,\ ldots& & ldots \ a_x_1 +a_x_2+ldots+a_x_n &=&0 endright. iff AX=mathbb O $$ образует линейное подпространство пространства $ mathbb R_<>^ $. В самом деле, если $$x_1=alpha_1,dots, x_n=alpha_n $$ — решение системы, то и $$x_1=t alpha_1,dots, x_n= t alpha_n $$ — тоже решение при любом $ t in mathbb R $. Если $$x_1=beta_1,dots, x_n=beta_n $$ — еще одно решение системы, то и $$x_1=alpha_1+beta_1,dots,x_n=alpha_n+beta_n $$ — тоже будет ее решением.
Почему множество решений системы неоднородных уравнений не образует линейного подпространства?
Пример 4. Обобщая далее, можем рассмотреть пространство «бесконечных» строк или последовательностей $ (a_1,dots,a_n, dots ) $, обычно являющееся объектом математического анализа — при рассмотрении последовательностей и рядов. Подпространство этого пространства образуют, например, линейные рекуррентные последовательности $ _ $ удовлетворяющие — при произвольных числах $ > subset mathbb R $ — линейному однородному разностному уравнению $ n_<> $-го порядка, $$ x_=a_1 x_+ dots+ a_n x_K npu K in <0,1,2,dots > ; $$ здесь числа $ < a_1,dots,a_, a_n ne 0 > subset mathbb R $ считаются фиксированными.
Можно рассматривать строки (последовательности) «бесконечные в обе стороны» $ < dots,a_<-2>,a_<-1>,a_0,a_1,a_2,dots > $ — они используются в ТЕОРИИ СИГНАЛОВ.
Пример 5. Множество $ mtimes n_<> $-матриц с вещественными элементами с операциями сложения матриц и умножения на вещественные числа образует линейное пространство. Будем обозначать это пространство $ mathbb R^ $.
В пространстве квадратных матриц фиксированного порядка каждое из следующих подмножеств составляет линейное подпространство: симметричных, кососимметричных, верхнетреугольных, нижнетреугольных и диагональных матриц.
Пример 6. Множество полиномов одной переменной $ x_<> $ степени в точности равной $ n_<> $ с коэффициентами из $ mathbb A_<> $ (где $ mathbb A_<> $ — любое из множеств $ mathbb Z, mathbb Q, mathbb R_<> $ или $ mathbb C_<> $) с обычными операциями сложения полиномов и умножения на число из $ mathbb A_<> $ не образует линейного пространства. Почему? — Потому что оно не является замкнутым относительно сложения: сумма полиномов $ f(x)=x^n -x+1 $ и $ g(x)=-x^n+x^-2 $ не будет полиномом $ n_<> $-й степени. Но вот множество полиномов степени не выше $ n_<> $ $$ mathbb P_n= left < p(x) in mathbb A [x] big| deg p(x) le n right>$$ линейное пространство образует; только к этому множеству надо придать еще и тождественно нулевой полином 4) . Очевидными подпространствами $ mathbb P_ $ являются $ mathbb P_<0>, mathbb P_1,dots,mathbb P_ $. Кроме того, подпространствами будут множество четных и множество нечетных полиномов степени не выше $ n_<> $. Множество всевозможных полиномов $$ mathbb P= bigcup_^ <infty>mathbb P_n $$ (без ограничения на степени) тоже образует линейное пространство.
Пример 7. Обобщением предыдущего случая будет пространство полиномов нескольких переменных $ x_1,dots, x_ <ell>$ степени не выше $ n_<> $ с коэффициентами из $ mathbb A_<> $. Например, множество линейных полиномов $$ left< a_1x_1+dots+a_<ell>x_<ell>+b big| (a_1,dots,a_<ell>,b) in mathbb A^ <ell+1>right> $$ образует линейное пространство. Множество однородных полиномов (форм) степени $ n_<> $ (с присоединением к этому множеству тождественно нулевого полинома) — также линейное пространство.
Изоморфизм
Пусть имеются два линейных пространства разной природы: $ mathbb V_<> $ с операцией $ +_<> $ и $ mathbb W_<> $ с операцией $ boxplus_<> $. Может оказаться так, что эти пространства «очень похожи», и свойства одного получаются простым «переводом» свойств другого.
Говорят, что пространства $ mathbb V_<> $ и $ mathbb W_<> $ изоморфны если между множествами их элементов можно установить такое взаимно-однозначное соответствие, что если $ X_<> leftrightarrow X^ <prime>$ и $ Y_<> leftrightarrow Y^ <prime>$ то $ X+Y leftrightarrow X_<>^ <prime>boxplus Y^ <prime>$ и $ lambda X_<> leftrightarrow lambda X^ <prime>$.
При изоморфизме пространств $ mathbb V_<> $ и $ mathbb W_<> $ нулевому вектору одного пространства будет соответствовать нулевой вектор другого пространства.
Пример. Пространство $ mathbb R^_<> $ изоморфно пространству $ mathbb P_^<> $. В самом деле, изоморфизм устанавливается соответствием $$ [a_1,dots,a_n] leftrightarrow a_1+a_2x+dots + a_nx^ .$$
Пример. Пространство $ mathbb R^ $ вещественных матриц порядка $ m_<>times n $ изоморфно пространству $ mathbb R_<>^ $. Изоморфизм устанавливается с помощью операции векторизации матрицы (матрица «вытягивается» в один столбец).
Пример. Пространство квадратичных форм от $ n_<> $ переменных изоморфно пространству симметричных матриц $ n_<> $-го порядка. Изоморфизм устанавливается соответствием, которое мы проиллюстрируем для случая $ n=3_<> $:
$$ a_<11>x_1^2+a_<12>x_1x_2+a_<13>x_1x_3+a_<22>x_2^2+a_<23>x_2x_3+a_<33>x_3^2 leftrightarrow left( begin a_ <11>& frac<1><2>a_ <12>& frac<1><2>a_ <13>\ frac<1><2>a_ <12>& a_ <22>& frac<1><2>a_ <23>\ frac<1><2>a_ <13>& frac<1><2>a_ <23>& a_ <33>end right) . $$
Линейная зависимость, базис, координаты
Линейной комбинацией системы векторов $ \> $ называется произвольный вектор $$ alpha_1 X_1+dots+ alpha_m X_m $$ при каких-то фиксированных значениях скаляров $ alpha_<1>, dots, alpha_ $.
Множество всевозможных линейных комбинаций системы векторов $ \> $ $$ left< alpha_1 X_1+dots+ alpha_m X_m bigg| <alpha_1,dots,alpha_m>subset mathbb R right> $$ называется линейной оболочкой векторов $ X_1,dots,X_ $ и обозначается $ <mathcal L>(X_1,dots,X_) $.
Теорема 1. Линейная оболочка векторов $ X_1,dots,X_ $ образует линейное подпространство пространства $ mathbb V_<> $.
Пример. В пространстве $ mathbb P_ $ полиномов степеней $ le n_<> ge 3 $ линейной оболочкой полиномов $ x,x^2,x^3 $ будет множество полиномов вида $ a_0x^3+a_1x^2+a_2x $, т.е. множество полиномов степеней $ le 3 $, имеющих корень $ lambda_<>=0 $. ♦
Система векторов $ < X_<1>,dots,X_m > $ называется линейно зависимой (л.з.) если существуют числа $ alpha_<1>,dots,alpha_m $, такие что хотя бы одно из них отлично от нуля и $$ alpha_1X_1+dots+alpha_mX_m=mathbb O $$ Если же это равенство возможно только при $ alpha_<1>=0,dots,alpha_m=0 $, то система векторов называется линейно независимой (л.н.з.).
Пример. Для полиномов нескольких переменных свойство линейной зависимости является частным проявлением более общего свойства функциональной зависимости. Так, однородные полиномы (формы)
$$ f_1=(x_1+x_2+x_3)^2,quad f_2=x_1x_2+x_1x_3+x_2x_3,quad f_3=x_1^2+x_2^2+x_3^2 $$ являются линейно зависимыми, поскольку $$ f_1-2,f_2-f_3 equiv 0 . $$ Полиномы $$ tilde f_1=x_1+x_2+x_3,quad f_2=x_1x_2+x_1x_3+x_2x_3,quad f_3=x_1^2+x_2^2+x_3^2 $$ не являются линейно зависимыми, но являются функционально зависимыми, поскольку $$ tilde f_1^2-2,f_2-f_3 equiv 0 . $$ ♦
Теорема 2. а) Если система содержит хотя бы один нулевой вектор, то она л.з.
б) Если система л.н.з., то и любая ее подсистема л.н.з.
в) При $ m>1 $ система $ ,dots,X_m> $ л.з. тогда и только тогда, когда по меньшей мере один ее вектор линейно выражается через остальные, т.е. существуют $ jin <1,dots,n >$ и константы $ gamma_<1>,dots,gamma_, gamma_,dots,gamma_ $ такие, что $$ X_j=gamma_1X_1+dots+gamma_X_+ gamma_X_+dots + gamma_X_ .$$
Теорема 3. Если каждый из векторов системы $ < X_1,dots,X_> $ линейно выражается через векторы другой системы $ < B_<1>,dots,B_k > $ с меньшим числом векторов: $ k ☞ ЗДЕСЬ.
Две системы векторов называются эквивалентными если каждый вектор одной системы линейно выражается через векторы другой и обратно.
Теорема 4. Системы векторов
$$ < X_1,dots,X_> quad mbox < и >quad < Y_<1>,dots,Y_k > $$ будут эквивалентными тогда и только тогда когда совпадают линейные оболочки этих систем: $$<mathcal L>(X_1,dots,X_m)=<mathcal L>(Y_1,dots,Y_k) . $$
Теорема 5. Если каждая из двух эквивалентных систем
$$ < X_1,dots,X_> quad mbox < и >quad < Y_<1>,dots,Y_k > $$ является л.н.з., то эти системы состоят из одинакового числа векторов: $ m=k_<> $ .
Линейно независимая система векторов $ \>subset mathbb V $ называется базисом этого пространства если каждый $ Xin mathbb V $ можно представить в виде линейной комбинации указанных векторов: $$ X=sum_ alpha_j X_j . $$
При этом не подразумевается конечность системы, т.е. суммирование может распространяться на бесконечное число слагаемых. Так, например, пространство бесконечных строк (или последовательностей) $ left[a_<1>,a_2,dots, right] $ имеет бесконечный базис, состоящий из векторов $$ [underbrace<0,dots,0,1>_j,0,dots , ] quad npu j in mathbb N . $$
В случае, когда базис пространства $ mathbb V_<> $ конечен, пространство $ mathbb V_<> $ называется конечномерным, а число векторов базиса тогда называется размерностью пространства $ mathbb V_<> $ и обозначается 5) : $ dim mathbb V_<> $. Также полагают, что размерность тривиального пространства, состоящего из одного только нулевого вектора, равна нулю: $ dim <mathbb O_<>>= 0 $.
Пример. Линейное пространство $ mtimes n_<> $ матриц имеет размерность $ mn_<> $. Так, для случая $ m_<>=3 ,n=2 $ в качестве базиса можно выбрать следующий набор матриц
$$ left( begin 1 & 0 \ 0 & 0 \ 0 & 0 end right) , left( begin 0 & 1 \ 0 & 0 \ 0 & 0 end right) , left( begin 0 & 0 \ 1 & 0 \ 0 & 0 end right) , left( begin 0 & 0 \ 0 & 1 \ 0 & 0 end right) , left( begin 0 & 0 \ 0 & 0 \ 1 & 0 end right) , left( begin 0 & 0 \ 0 & 0 \ 0 & 1 end right) . $$ ♦
Найти размерности подпространства симметричных и подпространства кососимметричных матриц порядка $ n_<> $.
Пример [1]. Замечательный пример трехмерного линейного пространства дает нам совокупность всех цветов. Под суммой двух цветов будем понимать цвет, образованный их смешением

под умножением цвета на положительное число $ k_<> $ — увеличение в $ k_<> $ раз яркости цвета
Анимация ☞ ЗДЕСЬ (1500 K, gif)
под умножением на $ (-1) $ — взятие дополнительного цвета. При этом оказывается, что совокупность всех цветов выражается линейно через три цвета: красный, зеленый и синий, т.е. образует трехмерное линейное пространство. (Точнее, некоторое тело в трехмерном пространстве, поскольку яркости цветов ограничены верхним порогом раздражения.) Исследование этого трехмерного тела всех цветов является важным орудием цветоведения. ♦
Если $ dim mathbb V=d_<> $ и вектора $ X_1,dots,X_ $ являются базисными для $ mathbb V_<> $, то разложение вектора $ X in mathbb V_<> $ в сумму: $$ X=alpha_1 X_1+dots+ alpha_d X_d .$$ называется разложением вектора $ X_<> $ по базису $ X_1,dots,X_ $; при этом числа $ alpha_1,dots, alpha_ $ называются координатами вектора $ X_<> $ в данном базисе.
Теорема 6. Если $ dim mathbb V=d>0 $, то любая система из $ d_<> $ линейно независимых векторов пространства образует базис этого пространства.
Доказательство. Пусть $ $ — л.н.з. система. Рассмотрим произвольный $ Xin mathbb V_<> $. Если система $ $ л.н.з., то $ dim mathbb V ge d+1 $, что противоречит условию теоремы. Следовательно, система линейно зависима: $ alpha_0X+alpha_1Y_1+dots+alpha_dY_d=mathbb O $ при каком-то из чисел $ <alpha_j>_^ $ не равном нулю. Если $ alpha_0=0 $, то $ alpha_1Y_1+dots+alpha_dY_d=mathbb O $ при каком-то ненулевом коэффициенте. Это означает, что система $ $ линейно зависима, что противоречит предположению. Следовательно $ alpha_0ne 0 $, но тогда вектор $ X_<> $ может быть представлен в виде линейной комбинации векторов $ Y_1,dots,Y_d $: $$X=- <alpha_1>/ <alpha_0>Y_1-dots —<alpha_d>/<alpha_0>Y_d .$$ По определению, система $ $ является базисом $ mathbb V $. ♦
Теорема 7. Любой вектор $ X in mathbb V_<> $ может быть разложен по фиксированному базису пространства единственным образом.
Очевидно, $ dim mathbb R^ = n $: строки из $ n_<> $ элементов $$[1,0,0,dots,0], [0,1,0,dots,0], [0,0,1,dots,0], dots , [0,0,0,dots,1] $$ образуют базис этого пространства.
Имеются два способа задания линейных подпространств в $ mathbb R^_<> $. Пусть $$ mathbb V_1 = <mathcal L>(A_1,dots,A_k) quad npu subset mathbb R^n .$$ В разделе ☞ РАНГ установлено, что $$ dim mathbb V_1 = operatorname < A_1,dots,A_k >= operatorname (A) ,$$ где $ A_<> $ — матрица, составленная из строк (столбцов) $ A_<1>,dots,A_k $.
Пример. Найти базис подпространства
Решение. Ищем $$ operatorname left( begin 1 & 2 & 1 & 1 \ -1&0&-1&0 \ -1& 2 &-1 &1 \ 0& 1& 0 & 1 end right) $$ по методу окаймляющих миноров. Существует минор третьего порядка $$ left| begin 1 & 2 & 1 \ -1&0&0 \ 0& 1 & 1 end right| $$ отличный от нуля, а определитель самой матрицы равен нулю. Замечаем, что найденный отличный от нуля минор расположен в первой, второй и четвертой строках матрицы. Именно эти строки и образуют базис.
Ответ. Базис составляют, например, первая, вторая и четвертая строки.
Другим способом задания линейного подпространства в $ mathbb R^ $ может служить задание набора ограничений, которым должны удовлетворять векторы подпространства. Таким набором ограничений может являться, например, система уравнений $$ left<begin a_<11>x_1 +a_<12>x_2+ldots+a_<1n>x_n &=&0,\ a_<21>x_1 +a_<22>x_2+ldots+a_<2n>x_n &=&0,\ ldots& & ldots \ a_x_1 +a_x_2+ldots+a_x_n &=&0 endright. qquad iff qquad AX=mathbb O . $$ Какова размерность подпространства решений этой системы? На этот вопрос мы ответим сразу же, если вспомним определение фундаментальной системы решений (ФСР). Именно, ФСР — как набор линейно независимых решений, через которые линейно выражается любое решение системы однородных уравнений — является базисом подпространства этих решений.
Теорема 8. Множество решений системы однородных уравнений $ AX=mathbb O_<> $ образует линейное подпространство пространства $ mathbb R^ $. Размерность этого подпространства равна $ n-operatorname (A) $, а фундаментальная система решений образует его базис.
Пример. В пространстве $ mathbb P_ $ полиномов степеней $ le n_<> $ каноническим базисом можно взять систему мономов $ <1,x,x^2,dots, x^n >$, т.е. $ dim mathbb P_ =n+1 $. Координатами полинома
$$ f(x)=a_0+a_1x+a_2x^2+dots+a_nx^n $$ будут его коэффициенты. Можно выбрать и другой базис, например, $ <1, x-c,(x-c)^2,dots,(x-c)^n >$ при произвольном числе $ c_<> $. Координатами полинома в этом базисе будут теперь коэффициенты формулы Тейлора: $$ f(x) equiv f(c)+ frac(c)> <1!>(x-c) + frac(c)> <2!>(x-c)^2+ dots + frac(c)> (x-c)^ . $$
Найти координаты полинома
Теорема 9. Любое векторное пространство $ mathbb V_<> $ размерности $ d_<> $ изоморфно $ mathbb R^ $.
Доказательство. Изоморфизм можно установить следующим соответствием. Если $ $ — какой-то базис $ mathbb V_<> $, то вектору $ X in mathbb V $ поставим в соответствие набор его координат в этом базисе: $$ X=x_1X_1+dots+x_d X_d Rightarrow X mapsto [x_1,dots,x_d]in mathbb R^d . $$ На основании теоремы $ 6 $, такое соответствие будет взаимно-однозначным, а проверка двух свойств изоморфизма тривиальна. ♦
Критерии линейной зависимости
Теорема . Строки
$$ <(a_<11>,dots,a_<1n>),dots, (a_,dots,a_)> subset mathbb C^n $$ линейно зависимы тогда и только тогда, когда $$ left|begin a_<11>&dots & a_ <1n>\ dots & & dots \ a_& dots & a_ end right|=0 , . $$
Теорема . Строки
$$ <(a_<11>,dots,a_<1n>),dots, (a_,dots,a_)> subset mathbb C^n $$ линейно зависимы тогда и только тогда, когда $$ operatorname A
$$ <(a_<11>,dots,a_<1n>),dots, (a_,dots,a_)> subset mathbb R^n $$ линейно зависимы тогда и только тогда, когда $$ det (A^ <top>A) = 0 , . $$ (Определитель в левой части можно интерпретировать как определитель Грама системы строк.)
Теорема . Аналитические на интервале $ ]a,b[ $ функции $ u_1(x),dots,u_n(x) $ линейно зависимы на $ ]a,b[ $ тогда и только тогда, когда их вронскиан
Относительный базис
В настоящем пункте $ mathbb V_1 $ обозначает линейное подпространство пространства $ mathbb V_<> $, отличное от тривиального; обозначаем $ d_1=dim mathbb V_1 $.
Теорема. Произвольный базис подпространства $ mathbb V_1 $ можно дополнить до базиса пространства $ mathbb V_<> $.
Доказательство. Пусть $ > $ — какой-то базис $ mathbb V_1 $. В пространстве $ mathbb V_<> $ найдется вектор $ X_ $ такой, что система $ , X_> $ будет л.н.з. (В противном случае, $ dim mathbb V=d_1 $, что противоречит условию настоящего пункта.) Если $ d_1+1=d = dim mathbb V $, то, на основании теоремы 5 предыдущего пункта, требуемый базис построен. Если же $ d_1+1 ♦

Говорят, что система векторов $ $ линейно независима относительно подпространства $ mathbb V_1 $ пространства $ mathbb V_<> $ если $$<.>_<> mbox < из условия >quad alpha_1X_1+dots+alpha_k X_k in mathbb V_1 quad mbox < следует >quad alpha_1=dots=alpha_k=0 .$$
Теорема. Обозначим $ \> $ — произвольный базис $ mathbb V_1 $. Система $ ,dots,X_k> $ л.н.з. относительно $ mathbb V_1 $ тогда и только тогда, когда система $ ,X_1,dots,X_k> $ линейно независима.
Пример. Найти все значения параметра $ <coloralpha > $, при которых система
Решение. Базисом подпространства $ mathbb V_1 $ является произвольная ФСР заданной системы однородных уравнений, например $ >, Y_2=[6,-5,0,1]^<^<top>>> $. Теорема утверждает, что система $ < X_1, X_2>$ л.н.з. относительно $ mathbb V_1 $ тогда и только тогда, когда система $ < X_1, X_2,Y_1,Y_2>$ л.н.з. (в обычном понимании). Последнее равносильно тому, что матрица, составленная из этих векторов, должна иметь ранг равный $ 4_<> $. $$operatorname left( begin 1 & 1 &-1 & 6 \ 2 & <coloralpha > & 2 & -5 \ <coloralpha > & 2 & 1 & 0 \ 1 & 1 & 0 & 1 end right)=4 iff left| begin 1 & 1 &-1 & 6 \ 2 & <coloralpha > & 2 & -5 \ <coloralpha > & 2 & 1 & 0 \ 1 & 1 & 0 & 1 end right|= <coloralpha >^2-10, <coloralpha > +16 ne 0 . $$
Ответ. $ <coloralpha >not in < 2,, 8>$.
Говорят, что система векторов $ $ образует базис пространства $ mathbb V_<> $ относительно (или над) $ mathbb V_1 $ если она л.н.з. относительно $ mathbb V_1 $ и любой вектор $ Xin mathbb V_<> $ можно представить в виде $$ X=c_1X_1+dots+c_kX_k+Y, quad mbox < где >quad Yin mathbb V_1 . $$
Теорема. Обозначим $ < Y_1,dots,Y_> $ — произвольный базис подпространства $ mathbb V_1 $. Система $ $ образует базис $ mathbb V_<> $ относительно $ mathbb V_1 $ тогда и только тогда, когда система $ < X_1,dots,X_k,Y_1,dots,Y_> $ образует базис $ mathbb V_<> $.
Доказательство. Действительно, любой вектор $ Xin mathbb V_<> $ выражается через векторы $ X_1,dots,X_k,Y_1,dots,Y_ $. По предыдущей теореме для линейной независимости этих векторов необходимо и достаточно относительной линейной независимости $ X_1,dots,X_k $. ♦
Базис $ mathbb V_<> $ строится дополнением базиса $ mathbb V_1 $ векторами $ X_1,dots,X_k $ линейно независимыми относительно $ mathbb V_1 $. Поэтому $$<.>_<> mbox <число векторов относительного базиса > = dim mathbb V — dim mathbb V_1 .$$
Это число называется коразмерностью 6) подпространства $ mathbb V_1 $ в пространстве $ mathbb V $.
Сумма и пересечение линейных подпространств
Пусть $ mathbb V_1 $ и $ mathbb V_2 $ — подпространства линейного пространства $ mathbb V_<> $. Множество $$ mathbb V_1+ mathbb V_2 = left$$ называется суммой, а множество $$ mathbb V_1 cap mathbb V_2 = left$$ — пересечением подпространств $ mathbb V_1 $ и $ mathbb V_2 $. Аналогично определяется сумма и пересечение произвольного количества подпространств.
Понятие пересечения линейных подпространств совпадает с понятием пересечения их как множеств.

Теорема. $ mathbb V_1+ mathbb V_2 $ и $ mathbb V_1 cap mathbb V_2 $ являются подпространствами линейного пространства $ mathbb V_<> $.
Докажите, что $ mathbb V_1+ mathbb V_2 $ — это подпространство минимальной размерности, содержащее как $ mathbb V_1 $, так и $ mathbb V_2 $.
Теорема. Имеет место формула:
$$ dim , mathbb V_1 + dim , mathbb V_2=dim , (mathbb V_1 cap mathbb V_2) + dim , (mathbb V_1 + mathbb V_2) . $$
Доказательство ☞ ЗДЕСЬ.
Можно ли обобщить этот результат на случай трех (и более подпространств)? Cправедлив ли, к примеру, аналог формулы включений-исключений в следующем виде:
$$dim , mathbb V_1 + dim , mathbb V_2 + dim , mathbb V_3 — $$ $$ -left <dim , (mathbb V_1 cap mathbb V_2) + dim , (mathbb V_1 cap mathbb V_3) + dim , (mathbb V_2 cap mathbb V_3) right>+ $$ $$+ dim , (mathbb V_1 cap mathbb V_2 cap mathbb V_3) =dim , (mathbb V_1 + mathbb V_2 + mathbb V_3) ?$$
Теорема. Имеет место формула:
Пример. Найти базис суммы и размерность пересечения
$$mathbb V_1=<mathcal L>left( left[ begin 0 \1 \ 1 \ 1 end right] , left[ begin 1 \1 \ 1 \ 2 end right] , left[ begin -2 \0 \ 1 \ 1 end right] right) quad mbox < и >quad mathbb V_2=<mathcal L>left( left[ begin -1 \3 \ 2 \ -1 end right] , left[ begin 1 \1 \ 0 \ -1 end right] right) $$
Решение. Действуя согласно предыдущей теореме, составляем матрицу из всех векторов $$ left( begin 0 & 1 & -2 & -1 & 1 \ 1 & 1 & 0 & 3 & 1 \ 1 & 1 & 1 & 2 & 0 \ 1 & 2 & 1 & -1 & -1 end right) $$ и ищем ее ранг методом окаймляющих миноров. Имеем: $ operatorname = 3 $ при ненулевом миноре матрицы расположенном в первых трех ее столбцах.
Ответ. Базис $ mathbb V_1 + mathbb V_2 $ составляют векторы $ X_1,X_2,X_3 $; $ dim , (mathbb V_1 cap mathbb V_2) = 3+2 — 3 =2 $.
Алгоритм нахождения базиса $ <mathcal L>(X_1,dots,X_m) cap <mathcal L>(Y_1,dots,Y_<ell>) $ проиллюстрируем на примере.
Пример. Найти базис $ mathbb V_1 cap mathbb V_2 $ при
$$ begin mathbb V_1= <mathcal L>left( left[ begin 1 \ -1 \ 1 \ -1 \ 1 end right],, left[ begin 1 \ 2 \ 1 \ 2 \ 1 end right],, left[ begin 0 \ 1 \ 0 \ 1 \ 0 end right] right) \ <>_<> qquad qquad quad X_1 quad quad X_2 quad quad X_3 end , begin mathbb V_2= <mathcal L>left( left[ begin 1 \ 0 \ 0 \ 0 \ 1 end right],, left[ begin 1 \ 1 \ 0 \ 1 \ 1 end right],, left[ begin 0 \ 1 \ 1 \ 1 \ 0 end right] right) \ <>_<> quad qquad qquad Y_1 qquad Y_2 quad quad Y_3 end . $$
Решение. 1. Сначала найдем базисы каждого из подпространств: $$dim mathbb V_1=2, mathbb V_1=mathcal L(X_1, X_2) ; dim mathbb V_2=3, mathbb V_2=mathcal L(Y_1, Y_2, Y_3) . $$
2. Произвольный вектор $ Zin mathbb R^5 $, принадлежащий $ mathbb V_1 cap mathbb V_2 $, должен раскладываться по базису каждого из подпространств: $$Z=alpha_1 X_1 + alpha_2 X_2= beta_1 Y_1 + beta_2 Y_2 + beta_3 Y_3 .$$ Для определения неизвестных значений координат составляем систему уравнений $$ begin qquad X_1 X_2 \ qquad <colordownarrow> <colordownarrow> \ left( begin 1 & 1 & -1 & &-1 & & 0 \ -1 & 2 & 0 & & -1 & & -1 \ 1 & 1 & 0 & & 0 & & -1 \ -1 & 2 & 0 & & -1 & & -1 \ 1 & 1 & -1 & & -1 & & 0 end right) \ qquad qquad qquad <coloruparrow> qquad <coloruparrow> qquad quad <coloruparrow> \ quad qquad qquad -Y_1 quad — Y_2 quad -Y_3 end left( begin alpha_1 \ alpha_2 \ beta_1 \ beta_2 \ beta_3 end right)= mathbb O_ <5times 1>$$ и решаем ее по методу Гаусса с нахождением фундаментальной системы решений: $$ left( begin 1 & 1 & -1 & -1 & 0 \ 0 & 3 & -1 & -2 & -1 \ 0 & 0 & 1 & 1 & -1 \ 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 end right) left( begin alpha_1 \ alpha_2 \ beta_1 \ beta_2 \ beta_3 end right)= mathbb O quad Rightarrow qquad mbox < ФСР >qquad begin alpha_1 & alpha_2 & beta_1 & beta_2 & beta_3 \ hline -1/3 & 1/3 & -1 & 1 & 0 \ 1/3 & 2/3 & 1 & 0 & 1 end $$
3. Получившиеся значения координат позволяют выразить базис пересечения — либо через базис подпространства $ mathbb V_1 $ (если использовать полученные значения для $ alpha_1,alpha_2 $), либо через базис подпространства $ mathbb V_2 $ (если использовать $ beta_1,beta_2, beta_3 $). Например, $$ Z_1=-1/3 X_1 + 1/3 X_2 = [0,1,0,1,0]^<^<top>>, $$ $$ Z_2=1/3 X_1 + 2/3 X_2 = [1,1,1,1,1]^<^<top>> . $$
Найти базисы суммы и пересечения подпространств
Решение ☞ ЗДЕСЬ.
Прямая сумма линейных подпространств
Пусть $ mathbb V_1 $ и $ mathbb V_2 $ — подпространства линейного пространства $ mathbb V_<> $. Говорят, что $ mathbb V_<> $ раскладывается в прямую сумму подпространств $ mathbb V_1 $ и $ mathbb V_2 $ если любой вектор $ Xin mathbb V_<> $ может быть представлен в виде $ X=X_1+X_2 $, где $ X_1in mathbb V_1,X_2in mathbb V_2 $ и такое представление единственно. Этот факт записывают: $ mathbb V= mathbb V_1 oplus mathbb V_2 $. Вектор $ X_ <1>$ называется проекцией вектора $ X_<> $ на подпространство $ mathbb V_1 $ параллельно подпространству $ mathbb V_ <2>$.

Пример. Линейное пространство квадратных матриц порядка $ n_<> $ раскладывается в прямую сумму подпространств: подпространства симметричных матриц и подпространства кососимметричных матриц. В самом деле, для матрицы $ A_ $ справедливо разложение
$$A=frac<1> <2>left(A+A^ <^top>right) + frac<1> <2>left(A-A^ <^top>right) $$ и в правой части первая скобка дает симметричную матрицу, а вторая — кососимметричную. Покажите, что не существует иного разложения матрицы $ A_<> $ в сумму симметричной и кососимметричной.
Теорема. Пусть $ mathbb V=mathbb V_1 + mathbb V_2 $. Эта сумма будет прямой тогда и только тогда, когда подпространства $ mathbb V_1 $ и $ mathbb V_2 $ имеют тривиальное пересечение:
$$mathbb V_1 cap mathbb V_2= <mathbb O > .$$
Доказательство. Необходимость. Пусть сумма $ mathbb V_1 + mathbb V_2 $ — прямая, но существует вектор $ Xne mathbb O $, принадлежащий $ mathbb V_1 cap mathbb V_2 $. Но тогда и вектор $ (-X) $ принадлежит $ mathbb V_1 cap mathbb V_2 $. Для нулевого вектора $ mathbb O $ получаем два представления в виде суммы проекций на подпространства: $$ mathbb O = mathbb O + mathbb O = X+ (-X) , . $$ Это противоречит понятию прямой суммы.
Достаточность. Если $ mathbb V_1 cap mathbb V_2= <mathbb O >$, но существует вектор $ X in mathbb V_1 + mathbb V_2 $, имеющий два различных разложения в сумму проекций $$ X=X_1+X_2 =Y_1+ Y_2 quad npu quad subset mathbb V_1, subset mathbb V_2, $$ то $$ (X_1-Y_1)+(X_2-Y_2) =mathbb O quad Rightarrow quad X_1-Y_1=Y_2-X_2 , , $$ т.е. вектор $ X_1-Y_1 $ принадлежит $ mathbb V_1 cap mathbb V_2 $. Но, по предположению, $ mathbb V_1 cap mathbb V_2= <mathbb O >$, следовательно, $ X_1-Y_1=mathbb O $, но тогда и $ Y_2-X_2=mathbb O $. ♦
Сумма $ mathbb V=mathbb V_1 + mathbb V_2 $ будет прямой тогда и только тогда, когда базис $ mathbb V_<> $ может быть получен объединением базисов $ mathbb V_ $.
Пример [2]. Доказать, что сумма подпространств
$$mathbb V_1=<mathcal L>left( left[ begin 2 \3 \ 11 \ 5 end right] , left[ begin 1 \1 \ 5 \ 2 end right] , left[ begin 0 \1 \ 1 \ 1 end right] right) quad mbox < и >quad mathbb V_2=<mathcal L>left( left[ begin 2 \1 \ 3 \ 2 end right] , left[ begin 1 \1 \ 3 \ 4 end right] , left[ begin 5 \2 \ 6 \ 2 end right] right) $$ будет прямой и найти проекции вектора $ Z=[2,0,0,3]^ <top>$ на эти подпространства.
Решение. Базисы $ mathbb V_1 $ и $ mathbb V_2 $ составляют соответственно системы $ $ и $ < Y_1,Y_2 >$, т.е. $ dim , mathbb V_1=dim , mathbb V_2 =2 $. На основании следствия достаточно установить, что объединенная система $ $ л.н.з. Для этого достаточно проверить, что определитель матрицы $$ A=left( begin 1 & 0 & 2 & 1 \ 1 & 1 & 1 & 1 \ 5 & 1 & 3 & 3 \ 2 & 1 & 2 & 4 end right) $$ отличен от нуля. Поскольку это условие выполнено, то сумма $ mathbb V_1 + mathbb V_2 $ — прямая и базис этой суммы состоит из взятых векторов. Для нахождения разложения вектора $ X_<> $ по этому базису решаем систему уравнений $$A left[ begin alpha_2 \ alpha_3 \ beta_1 \ beta_2 end right] = Z $$ и получаем единственное решение: $ alpha_2=-1,, alpha_3=-1,, beta_1 =1, , beta_2=1 $. Разложение $ Z=Z_1+Z_2 $ составляют векторы $ Z_1=alpha_2 X_2+alpha_3 X_3 $ и $ Z_2=beta_1 Y_1+beta_2 Y_2 $.
Линейные многообразия
Пусть $ mathbb V_1 $ — линейное подпространство пространства $ mathbb V_<> $, а $ X_ <0>$ — произвольный фиксированный вектор из $ mathbb V_<> $. Множество $$ mathbb M = X_0+ mathbb V_1 = left $$ называется линейным многообразием (порожденным подпространством $ mathbb V_1 $). Размерностью этого многообразия называется размерность порождающего его подпространства: $ dim mathbb M = dim mathbb V_1 $. В случае $ 1 ☞ ОБЩЕЕ РЕШЕНИЕ: если система совместна, то ее общее решение можно представить как сумму какого-то одного ее решения и общего решения соответствующей однородной системы $ AX= mathbb O $. Таким образом, многообразие решений неоднородной системы $ AX= <mathcal B>$ допускает «параметрическое представление»: $$mathbb M=X_0+ <mathcal L>(X_1,dots,X_>)= $$ $$=left> X_> mid (t_1,dots, t_>) in mathbb R^> right> ; $$ здесь $ X_ <0>$ означает частное решение системы (т.е. $ AX_0= <mathcal B>$),
$ >> $ — ФСР для системы $ AX= mathbb O $,
а $ mathfrak r= operatorname A= operatorname [Amid mathcal B] $.
Получаем, следовательно, $ (n-<mathfrak r>) $-мерную плоскость в $ mathbb R^n $, a в случае $ (n-<mathfrak r>)=1 $ — прямую $$mathbb M=X_0+tX_1 quad npu t in mathbb R ; $$ в последнем случае вектор $ X_ <1>$ называют направляющим вектором этой прямой.
Некоторые задачи на линейные многообразия ☞ ЗДЕСЬ.
источники:
http://mathhelpplanet.com/static.php?p=sposoby-opisaniya-podprostranstv
http://vmath.ru/vf5/linear_space




