Как найти базис однородной системы линейных уравнений

Как найти базис однородной системы линейных уравнений

Решебник.Ру / Кузнецов Л.А. Линейная алгебра. Задача 3

Системы линейных однородных уравнений

Постановка задачи. Найти какой-нибудь базис и определить размерность линейного пространства решений системы

1. Записываем матрицу системы:

и с помощью элементарных преобразований преобразуем матрицу к треугольному виду, т.е. к такому виду, когда все элементы, находящиеся ниже главной диагонали равны нулю. Ранг матрицы системы равен числу линейно независимых строк, т.е., в нашем случае, числу строк, в которых остались ненулевые элементы:

.

Размерность пространства решений равна . Если , то однородная система имеет единственное нулевое решение, если , то система имеет бесчисленное множество решений.

2. Выбираем базисных и свободных переменных. Свободные переменные обозначаем . Затем базисные переменные выражаем через свободные, получив таким образом общее решение однородной системы линейных уравнений.

3. Записываем базис пространства решений системы полагая последовательно одну из свободных переменных равной единице, а остальные нулю. Размерность линейного пространства решений системы равна количеству векторов базиса.

Примечание. К элементарным преобразованиям матрицы относят:

1. умножение (деление) строки на множитель, отличный от нуля;

2. прибавление к какой-либо строке другой строки, умноженной на любое число;

3. перестановка строк местами;

4. преобразования 1–3 для столбцов (в случае решения систем линейных уравнений элементарные преобразования столбцов не используются).

Задача 3. Найти какой-нибудь базис и определить размерность линейного пространства решений системы.

Выписываем матрицу системы и с помощью элементарных преобразований приводим ее к треугольному виду:

Полагаем , тогда

.

Размерность линейного пространства решений равна 3.

:: Рекомендуемая литература. Ремендуем покупать учебную литературу в интернет-магазине Озон

Способы описания подпространств линейного пространства

Рассмотрим два важных способа описания линейных подпространств, которые условно будем называть внутренним и внешним. В первом (внутреннем) способе используется понятие линейной оболочки векторов, когда все элементы подпространства выражаются через некоторые его элементы (образующие). При втором (внешнем) способе применяются однородные системы уравнений. В этом случае подпространство описывается как пересечение некоторых содержащих его множеств. Для каждого способа описания подпространств укажем методики на хождения размерностей, базисов, алгебраических дополнений, пересечений и сумм подпространств.

Любое n-мерное вещественное линейное пространство изоморфно n-мерному арифметическому пространству . Чтобы установить изоморфизм , достаточно выбрать в пространстве базис и каждому вектору поставить в соответствие его координатный столбец. Поэтому в данном разделе будем рассматривать описание подпространств n-мерного арифметического пространства .

Первый (внутренний) способ. Пусть в пространстве заданы столбцы . Напомним, что для систем столбцов были определены понятия базы (максимальной линейно независимой подсистемы столбцов) и ранга (максимального числа линейно не зависимых столбцов системы), а также методы их нахождения.

Рассматривая линейную оболочку столбцов как линейное подпространство , заключаем, что база системы столбцов является базисом этого подпространства, а ранг системы столбцов равен размерности подпространства .

Поэтому для нахождения размерности и базиса подпространства нужно выполнить следующие действия:

1) составить из данных столбцов матрицу размеров ;

2) привести ее к ступенчатому виду (1.4), используя элементарные преобразования строк;

3) определить размерность и базис подпространства

– количество ненулевых строк в матрице равняется размерности подпространства, т.е. ,

– столбцы матрицы , содержащие единичные элементы (в начале каждой “ступеньки”), определяют номера линейно независимых столбцов матрицы , т.е. искомый базис.

Таким образом, если подпространство задано своими образующими , то его размерность равна рангу системы столбцов , т.е. , а базисом служит максимальная линейно независимая подсистема образующих.

Второй (внешний) способ. Пусть подпространство задано как множество решений однородной системы уравнений с неизвестными. Множество решений системы уравнений можно рассматривать как пересечение подпространств , где — множество решений i-го уравнения системы . Напомним, что любое решение однородной системы представляется в виде линейной комбинации элементов фундаментальной системы решений. Поэтому раз мерность пространства , а базисом служит фундаментальная система решений однородной системы . Способы нахождения фундаментальной системы решений рассмотрены ранее.

Переход от одного способа описания подпространств к другому

Переход от внутреннего описания к внешнему. Пусть подпространство задано линейной оболочкой столбцов . Требуется составить такую однородную систему уравнений, множество решений которой совпадает с , т.е. . Для этого нужно выполнить следующие действия.

1. Из данных столбцов составить матрицу размеров , а затем блочную матрицу , приписав к матрице единичную матрицу n-го порядка.

2. Элементарными преобразованиями над строками блочной матрицы и первыми ее столбцами привести матрицу к виду , где — простейший вид матрицы .

3. Из последних строк матрицы составить матрицу .

4. Записать искомую систему уравнений .

Поясним содержание алгоритма. Заданное подпространство состоит из линейных комбинаций данных векторов, т.е. все его элементы имеют вид . Решаемую задачу можно сформулировать так: для каких векторов найдутся такие числа , чтобы выполнялось равенство . Другими словами, при каких неоднородная система ( уравнений с неизвестными ) имеет решения? Используя необходимое и достаточное условие (5.24) совместности системы, получаем равенство . Заметим, что решение поставленной задачи неоднозначно, так как существует много однородных систем, имеющих од но и то же множество решений.

Пример 8.8. Подпространство задано линейной оболочкой столбцов . Составить систему уравнений, определяющую подпространство .

Решение. 1. Составляем матрицу и блочную матрицу:

2. Приводим левый блок к простейшему виду. Вычитаем первую строку из остальных, а затем к четвертой строке прибавляем вторую, умноженную на (-2):

Преобразовываем столбцы левого блока: ко второму столбцу прибавим пер вый, умноженный на (-1), к третьему столбцу прибавим первый, умноженный на (-3), а затем второй, умноженный на (-1). Эти преобразования не изменяют правый блок полученной матрицы. Находим простейший вид Л матрицы и матрицу

3. Из последних строк матрицы составляем матрицу искомой системы.

4. Записываем систему уравнений Заданные в условии примера столбцы являются решениями полученной системы, в чем можно убедиться при их подстановке в систему уравнений вместо .

Переход от внешнего описания к внутреннему. Пусть подпространство задано как множество решений однородной системы т уравнений с л неизвестными: . Требуется найти размерность и базис этого подпространства, т.е. представить его в виде линейной оболочки . Для этого нужно выполнить следующие действия.

1. Найти фундаментальную систему решений однородной системы . Искомая размерность .

2. Представить заданное пространство как линейную оболочку .

Первый пункт алгоритма удобно выполнять следующим образом:

– составить блочную матрицу , приписав к матрице единичную матрицу n-го порядка;

– элементарными преобразованиями над столбцами блочной матрицы и строками верхнего блока привести матрицу к виду , где — простейший вид матрицы ;

– из последних столбцов матрицы составить фундаментальную матрицу .

Столбцы фундаментальной матрицы составляют искомую фундаментальную систему решений.

Заметим, что решение поставленной задачи неоднозначно, так как существует много базисов одного и того же линейного подпространства.

Пример 8.9. Найти размерность и базис подпространства , заданного системой уравнений

Решение. 1. Фундаментальная матрица для этой системы была найдена в примере 5.6

Ее столбцы образуют фундаментальную систему решений. Размерность подпространства равна , .

2. Столбцы являются искомым базисом, так как они линейно независимы и .

Системы линейных однородных уравнений

Назначение сервиса . Онлайн-калькулятор предназначен для нахождения нетривиального и фундаментального решения СЛАУ. Полученное решение сохраняется в файле Word (см. пример решения).

  • Шаг №1
  • Шаг №2
  • Видеоинструкция
  • Оформление Word

Свойства систем линейных однородных уравнений

Теорема. Система в случае m=n имеет нетривиальное решение тогда и только тогда, когда определитель этой системы равен нулю.

Теорема. Любая линейная комбинация решений системы также является решением этой системы.
Определение. Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений.

Теорема. Если ранг r матрицы системы меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из ( n-r ) решений.

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=sposoby-opisaniya-podprostranstv

http://math.semestr.ru/gauss/equations.php

[/spoiler]

Источник

Содержание:

  • Однородные СЛАУ
  • Фундаментальная система решений

Однородные СЛАУ

Определение

Однородной СЛАУ называется система, все правые части которой равны нулю одновременно.

Однородная СЛАУ, записанная в
матричном виде, $A X=Theta$ всегда совместна,
так как $X=Theta$ всегда является ее решением.

Заметим, что если $x_{1}, x_{2}$ – это два решения однородной
СЛАУ, то их линейная комбинация также будет решением однородной СЛАУ:

$$Y=lambda_{1} x_{1}+lambda_{2} x_{2}$$
$$A Y=Aleft(lambda_{1} x_{1}+lambda_{2} x_{2}right)=lambda_{1} A x_{1}+lambda_{2} A x_{2}=lambda_{1} Theta+lambda_{2} Theta=Theta$$

Теорема

Если однородная квадратная СЛАУ имеет ненулевое решение, то
определитель матрицы системы равен нулю.

Пример

Задание. Выяснить, имеет ли однородная СЛАУ
$left{begin{array}{l}
3 x-2 y=-1 \
x+3 y=7
end{array}right.$ ненулевые решения.

Решение. Вычислим определитель матрицы системы:

$$Delta=left|begin{array}{rr}
3 & -2 \
1 & 3
end{array}right|=9-(-2)=9+2=11 neq 0$$

Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$

Ответ. Система имеет только нулевое решение.

Фундаментальная система решений

Рассмотрим множество всех столбцов, которые являются решениями исходной системы.

Определение

Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.

Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы.
Любое решение исходной системы есть линейная комбинация решений ФСР.

Теорема

Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и
общего решения соответствующей однородной СЛАУ.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти общее решение и ФСР однородной системы
$left{begin{array}{l}
x_{1}+x_{2}-3 x_{4}-x_{5}=0 \
x_{1}-x_{2}+2 x_{3}-x_{4}=0 \
4 x_{1}-2 x_{2}+6 x_{3}+3 x_{4}-4 x_{5}=0 \
2 x_{1}+4 x_{2}-2 x_{3}+4 x_{4}-7 x_{5}=0
end{array}right.$

Решение. Приведем систему к ступенчатому виду с помощью
метода Гаусса. Для этого записываем
матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец
свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут
получаться нули):

$$A=left(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
1 & -2 & 2 & -1 & 0 \
4 & -2 & 6 & 3 & -4 \
2 & 4 & -2 & 4 & -7
end{array}right)$$

с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем
первую, от третьей – четыре первых, от четвертой – две первых:

$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & -6 & 6 & 15 & 0 \
0 & 2 & -2 & 10 & -5
end{array}right)$$

Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три
вторых, к четвертой прибавляем вторую:

$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 9 & -3 \
0 & 0 & 0 & 12 & -4
end{array}right)$$

От четвертой строки отнимем $frac{4}{3}$ третьей и третью
строку умножим на $frac{1}{3}$ :

$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 3 & -1 \
0 & 0 & 0 & 0 & 0
end{array}right)$$

Нулевые строки можно далее не рассматривать, тогда получаем, что

$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 3 & -1
end{array}right)$$

Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а
ко второй строке прибавляем третью:

$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -6 & 0 \
0 & -2 & 2 & 5 & 0 \
0 & 0 & 0 & 3 & -1
end{array}right)$$

то есть получаем систему, соответствующую данной матрице:

$$left{begin{array}{l}
x_{1}+x_{2}-6 x_{4}=0 \
-2 x_{2}+2 x_{3}+5 x_{4}=0 \
3 x_{4}-x_{5}=0
end{array}right.$$

Или, выразив одни переменные через другие, будем иметь:

$$left{begin{array}{l}
x_{1}=-x_{2}+6 x_{4} \
x_{2}=x_{2} \
x_{3}=x_{2}-frac{5}{2} x_{4} \
x_{4}=x_{4} \
x_{5}=3 x_{4}
end{array}right.$$

Здесь $x_{2}, x_{4}$ – независимые (или свободные)
переменные (это те переменные, через которые мы выражаем остальные переменные), $x_{1}, x_{3}, x_{5}$ – зависимые (связанные) переменные
(то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от
пяти переменных) и ранга матрицы $r$ (в этом
случае получили, что $r=3$ – количество
ненулевых строк после приведения матрицы к ступенчатому виду):
$n-r=5-3=2$

Так как ранг матрицы $r=3$ , а количество неизвестных
системы $n=5$ , то тогда количество решений в ФСР
$n-r=5-3=2$ (для проверки, это число должно равняться количеству свободных переменных).

Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть
для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки).
В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным
придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными
находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:

$$left{begin{array}{l}
x_{1}=-x_{2}+6 x_{4} \
x_{3}=x_{2}-frac{5}{2} x_{4} \
x_{5}=3 x_{4}
end{array}right.$$

Тогда придавая в первом случае, например, независимым переменным значения
$x_{2}=1$ , $x_{4}=0$ получаем, что $left{begin{array}{l}
x_{1}=-1+6 cdot 0=-1 \
x_{3}=1-frac{5}{2} cdot 0=1 \
x_{5}=3 cdot 0=0
end{array}right.$ . Полученные значения записываем в первую
строку таблицы. Аналогично, беря $x_{2}=0$ , $x_{4}=2$, будем иметь, что
{x_{1}=12, x_{3}=-5, x_{5}=6} , что и определяет второе решение ФСР.
В итоге получаем следующую таблицу:

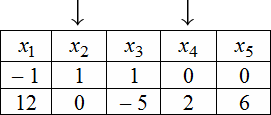
Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:

$$X_{1}=left(begin{array}{r}
-1 \
1 \
1 \
0 \
0
end{array}right), X_{2}=left(begin{array}{r}
12 \
0 \
-5 \
2 \
6
end{array}right)$$

Общее решение является линейной комбинацией частных решений:

$$X=C_{1} X_{1}+C_{2} X_{2}=C_{1}left(begin{array}{r}
-1 \
1 \
1 \
0 \
0
end{array}right)+C_{2}left(begin{array}{r}
12 \
0 \
-5 \
2 \
6
end{array}right)$$

где коэффициенты $C_{1}, C_{2}$ не равны нулю одновременно. Или запишем общее решение в таком виде:

$left{begin{array}{l}
x_{1}=-C_{1}+12 C_{2} \
x_{2}=C_{1} \
x_{3}=C_{1}-5 C_{2} \
x_{4}=2 C_{2} \
x_{5}=6 C_{2}
end{array}right.$
   $C_{1}, C_{2} neq 0$

Придавая константам $C_{1}, C_{2}$ определенные значения
и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.

Читать дальше: примеры решения СЛАУ.

Источник

Рассмотрим
систему линейных однородных уравнений
с

неизвестными ранга

.

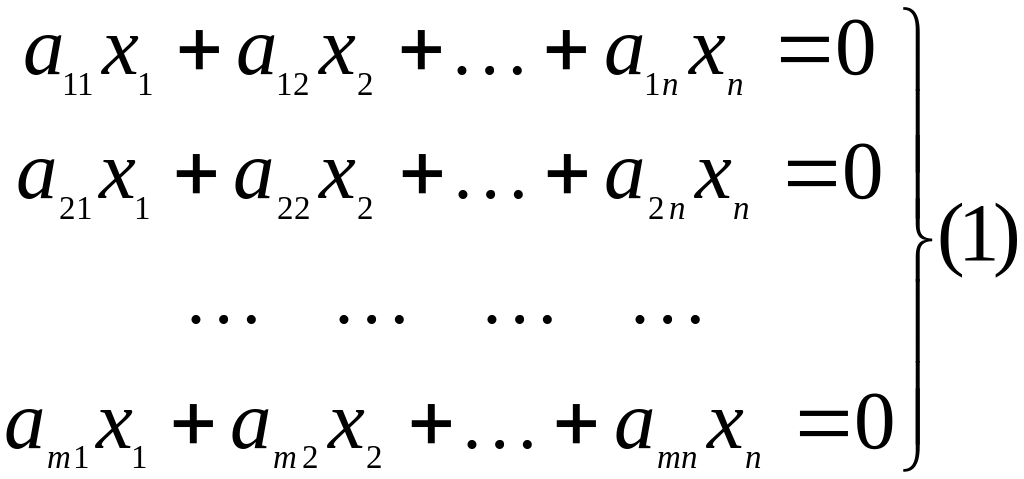
Теорема.
Множество
решений системы (1) является подпространством


-мерного
арифметического пространства Rn.

Для доказательства
теоремы достаточно проверить два
свойства:

1. Если

и

два
решения системы (1), то их сумма

также решение этой
системы. Для этого подставим этот набор
чисел в i-тое
уравнение системы (1), где i=l,m,
получим:

Значит,

является
решением системы уравнений (1).

2.
Докажем, что произведение любого решения
системы (1) на любое число

также
является решением той же системы
уравнений.

Подставим
набор чисел


в
левую часть i-того
ур-ния системы (1):

Значит,

является
решением системы уравнений (1). Таким
образом, мы доказали, что множество
решений системы (1) – подпространство
Rn.

Опр.
Базис
подпространства решений системы линейных
однородных уравнений называется
фундаментальной (базисной) системой
решений (ФСР).

Как
следует из определения базиса,
фундаментальная система решений обладает
двумя свойствами: решения, составляющие
ФСР, линейно независимы, любое решение
системы есть линейная комбинация
фундаментальной системы решений. Теорема
(о ФСР). Если
ранг системы линейных однородных
уравнений с

неизвестными равен

,
то ФСР состоит из

решений.

Опр.
Множество
векторов линейного пространства,
переходящих в нулевой вектор под
действием линейного оператора

,
называется ядром оператора

и обозначается как ker

.

Теорема.
Ядро
оператора

является подпространством линейного
пространства, в котором задан линейный
оператор

.

Доказательство.
Пусть


,
тогда

и


.
Сложим эти равенства, получим

,
так как

линейный оператор, то в силу линейности

,
получим

,
откуда следует, что

.
Аналогично, из

следует,
что

.
В силу линейности


,
отсюда

.
Значит,
ker

– подпространство. Ч.т.д.

Рассмотрим
в линейном пространстве

базис

и оператор

,
который
задается в данном базисе матрицей

А=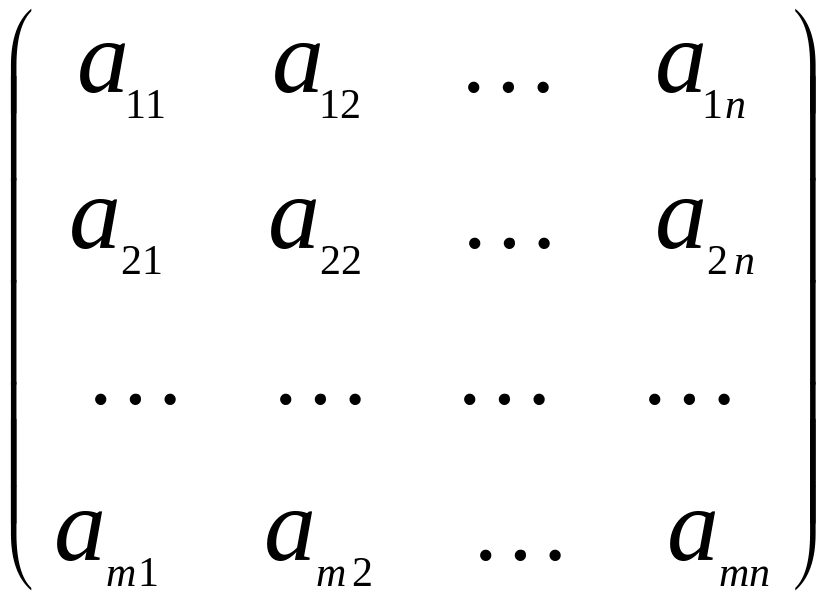

Тогда
ядро оператора

задается уравнением

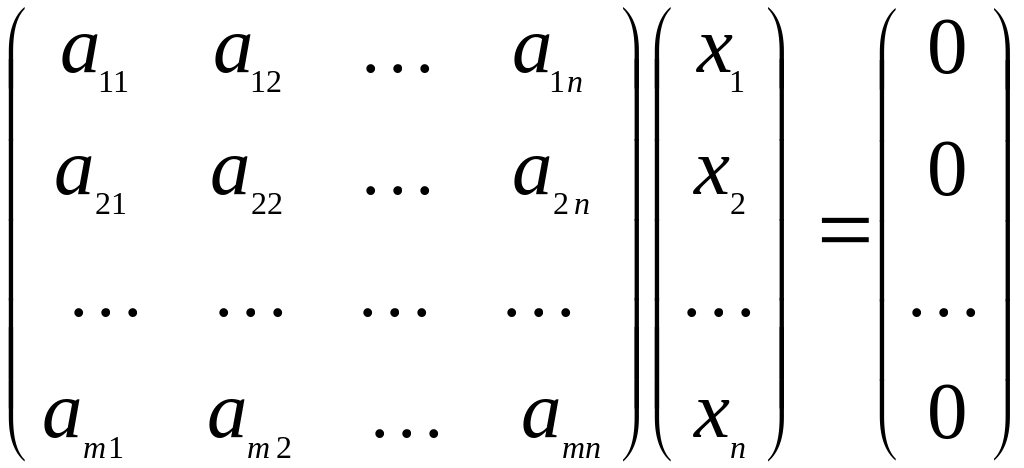
или
системой уравнений:

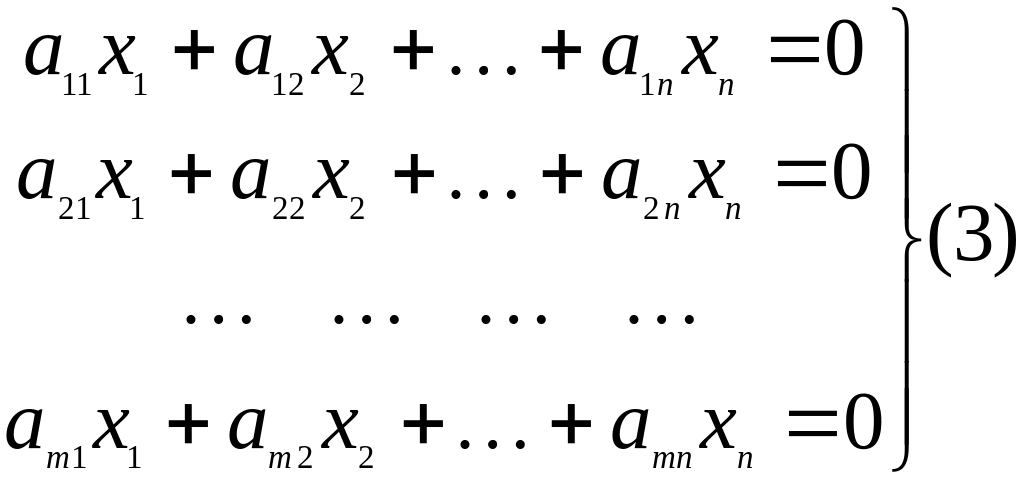
Фундаментальные
решения системы (3) задают базисы ядра
оператора

, заданого матрицей А.

5(1). Полож. Опред. Квадратичные формы.

Квадратичной
формой


от

неизвестных

называется сумма вида

где

.

Опр.2. Квадратичная
форма называется положительно
определенной, если она принимает только
положительные значения для любых
ненулевых векторов.

Лемма.
Знак
определителя матрицы квадратичной
формы не зависит от выбора базиса.

Теорема.
Квадратичная
форма является положительно определенной
тогда и только тогда, когда ее нормальный
вид

,
то есть если и ранг, и положительный
индекс инерции равны числу неизвестных.

Зам.
Решить вопрос о том, является ли данная
квадратичная форма положительно
определенной, возможно и без приведения
формы к нормальному виду. Это позволяет
сделать критерий
Сильвестра.
Чтобы понять формулировку этого критерия,
нам потребуется

Опр.
Пусть

— матрица квадратичной формы. Обозначим
через

минор матрицы А,
элементы которого расположены в ее
первых k
строках и первых k
столбцах.
Другими словами,

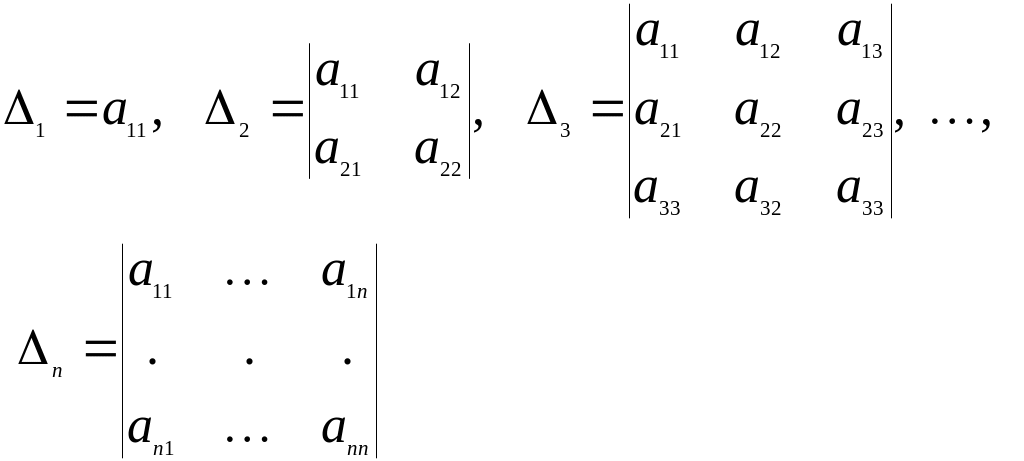
Будем называть
эти миноры главными
минорами квадратичной формы.

Теорема (критерий
Сильвестра).
Квадратичная форма является положительно
определенной тогда и только тогда, когда
все ее главные
миноры строго положительны.

Проведем методом
математической индукции по числу
переменных. База индукции:


.
Очевидно, что
эта
квадратичная форма будет положительно
определенной
тогда и только тогда, когда

.

Шаг
индукции: Предположим,
что квадратичная форма от

переменных является положительно
определенной,
тогда и только тогда, когда все ее главные
миноры

строго
положительные.

Докажем, что это
утверждение справедливо и для квадратичной
формы от

переменных.

Пусть
теперь дана квадратичная форма от

переменных

.

В квадратичной
форме

соберем все члены, не содержащие
переменного

,
тогда, очевидно, мы получим квадратичную
форму f
от

-переменных.
Тогда

можно записать в виде


(1)

Покажем,
что если

является
положительно определенной, то

также
положительно определена. Докажем это
методом от противного. Предположим, что

– положительно определена,

не является положительно определенной.
Значит, существуют такие значения
переменных,

,
среди которых не все равны нулю, при
которых.


.
Полагая
дополнительно

,
подставим

в (1). Получим

,
что невозможно,
так как

положительно определена.
Значит, если

положительно
определена, значит,

также
является положительно определенной.
Кроме того, очевидно, что главные миноры

квадратичной формы

являются одновременно главными минорами
квадратичной формы

.

Необходимость.
Пусть

является
положительно определенной. Докажем,
что все
главные миноры

строго положительны.

Так как


положительно
определена, значит по доказанному раннее

также положительна. Тогда по допущению
все главные миноры

положительны. Осталось доказать, что

Всякую положительную
квадратичную форму с помощью невырожденного
линейного преобразования можно привести
к нормальному виду

с матрицей

,
определитель которой равен 1 > 0

По
лемме, знак определителя матрицы
квадратичной формы не меняется. Значит,

.

Достаточность.
Пусть
строго положительны все главные миноры


квадратичной
формы

.
Докажем,
что

является положительно определенной.

Так как


положительны,
то


по индуктивному
предположению
является
положительно определенной. Следовательно,
существует невырожденное линейное
преобразование переменных

,
которое
приводит форму

к виду

.

Это линейное
преобразование можно дополнить до
невырожденного линейного преобразования
всех неизвестных

,
полагая хп
=уп.

Тогда
форма

приводится указанным преобразованием
к виду


(3)

Дополним
члены, содержащие

до
полных квадратов:


или

где

Рассмотрим следующее
невырожденное линейное преобразование

которое приводит
форму

к виду

с матрицей

,
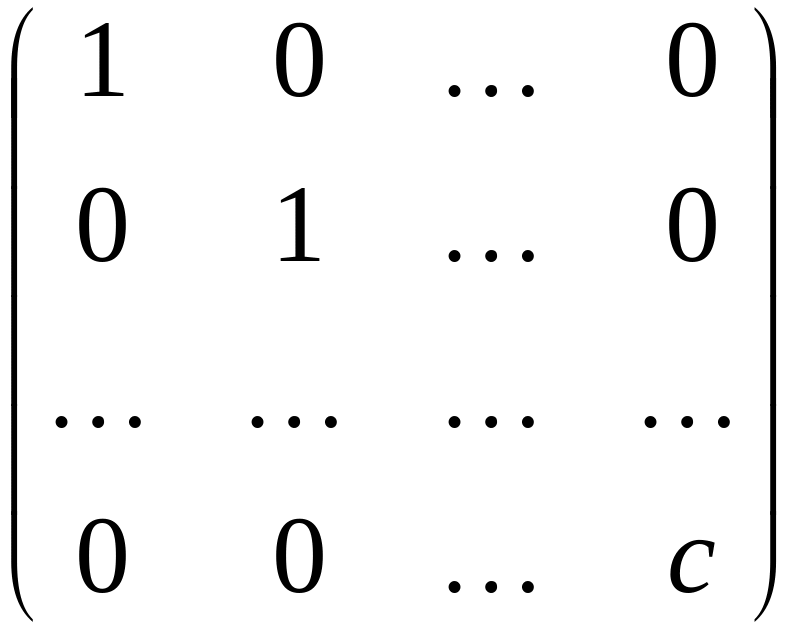
детерминант
этой матрицы равен с.

По
лемме, знак определителя матрицы
квадратичной формы не меняется, так как

(по условию), то

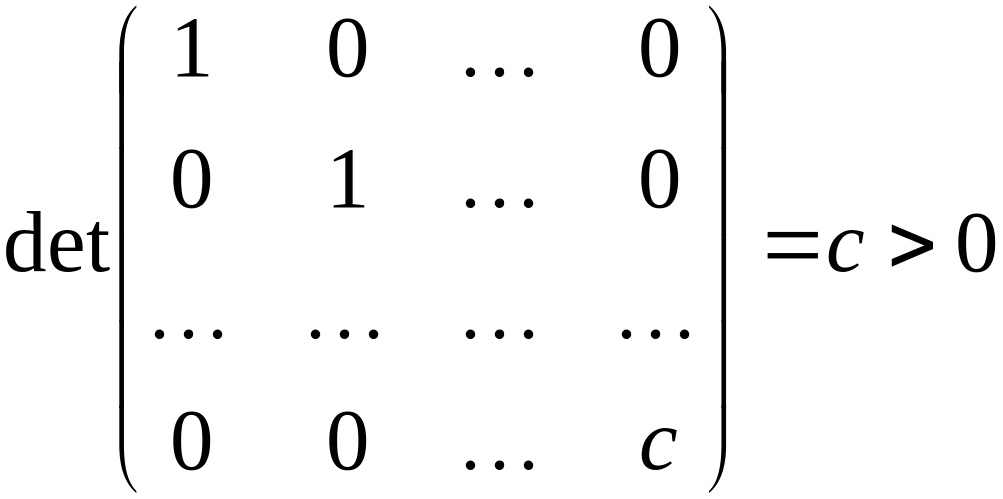
Значит,

является
положительно определенной.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Размерность пространства решений однородной системы линейных уравнений

Как мы отметили ранее, совокупность решений Xодн однородной системы линейных уравнений с матрицей A=(a_{ij}) in mM_{m,n}(K) является линейным пространством, подпространством в Kn.

Теорема 9.17.1. Если r=r(A)<n, то 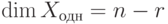dim X_{textup{одн}}=n-r (т. е. размерность пространства решений равна числу свободных неизвестных). (Если r(A)=n, то система линейных уравнений имеет лишь нулевое решение.)

Доказательство. Для удобства записи переупорядочим неизвестные, если это необходимо, так, чтобы

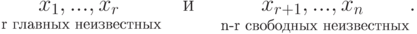
underset{text{ r главных неизвестных}}{x_1,...,x_r} quad text{и}quad underset{text{ n-r свободных неизвестных}}{x_{r+1},...,x_n}.

Пусть 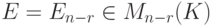E=E_{n-r}in M_{n-r}(K) – единичная матрица размера (n-r)times (n-r). Возьмем ее строки в качестве наборов значений для свободных неизвестных и дополним их (единственно возможным способом) до решений нашей системы линейных уравнений

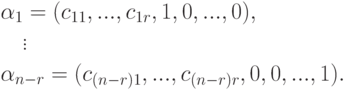
begin{align*} & alpha_1 = (c_{11}, ..., c_{1r}, 1,0,...,0),\ & quad vdots\ & alpha_{n-r} = (c_{(n-r)1},...,c_{(n-r)r},0,0,...,1). end{align*}

Эта система n-r строк-решений линейно независима (поскольку строки единичной матрицы, конечно, линейно независимы). Если

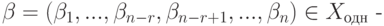
beta=(beta_1,...,beta_{n-r},beta_{n-r+1},...,beta_n)in X_{textup{одн}}text{ -}

произвольное решение, то

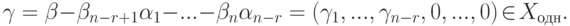
gamma=beta-beta_{n-r+1}alpha_1-...-beta_nalpha_{n-r}= (gamma_1,...,gamma_{n-r},0,...,0)!in! X_{textup{одн}}.

Однако, конечно,

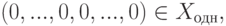
(0,...,0,0,...,0)in X_{textup{одн}},

при этом 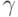gamma и нулевое решение имеют одинаковый набор значений для свободных неизвестных. Так как значения главных неизвестных однозначно определяются по свободным, то 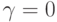gamma=0, следовательно,

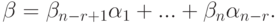
beta=beta_{n-r+1}alpha_1+...+beta_nalpha_{n-r}.

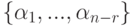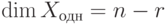Итак, мы построили базис {alpha_1,...,alpha_{n-r}} линейного пространства решений Xодн , поэтому dim X_{textup{одн}}=n-r.

Замечание 9.17.2. Если вместо строк единичной матрицы En-r для свободных неизвестных брать строки всевозможных матриц 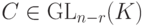CinGL_{n-r}(K) (т. е. 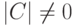Cin M_{n}(K), |C|neq 0 ), то этот алгоритм позволяет построить все базисы в Xодн .

Замечание 9.17.2. Любой базис линейного пространства решений Xодн однородной системы линейных уравнений называется в ряде алгебраических текстов ” фундаментальной системой решений однородной системы линейных уравнений “.

Задание любого подпространства в _K V = K^n как пространства решений однородной системы линейных уравнений

Пусть K – поле, 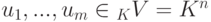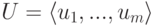u_1,...,u_min {}_K V=K^n, U=langle u_1,...,u_mrangle – подпространство в Kn, являющееся линейной оболочкой строк u1,…,um, т. е. множеством всех линейных комбинаций строк u1,…,um. Мы найдем такую матрицу 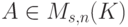Ain M_{s,n}(K), что множество решений однородной системы линейных уравнений

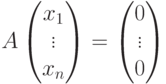
A begin{pmatrix} x_1\ vdots\ x_n end{pmatrix} = begin{pmatrix} 0\ vdots\ 0 end{pmatrix}

совпадает с U.

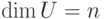Если U – нулевое подпространство, то в качестве A мы можем взять любую матрицу ntimes n с ненулевым определителем (например, A=E ). Если U=Kn (это эквивалентно тому, что dim U=n ), то в качестве A мы можем взять нулевую матрицу из Ms,n, s geq 1. Если же 1 leq dim U = r(u_1,...,u_m)<n, то пусть ui=(ui1,ui2,…,uin), 1 leq i leq m, u_{ij}in K.

Рассмотрим матрицу 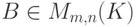Bin M_{m,n}(K), B=(bij), bij=uij, 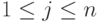1 leq i leq m, 1 leq j leq n, и однородную систему линейных уравнений

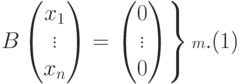begin{equation}label{stelo} B begin{pmatrix} x_1\ vdots\ x_n end{pmatrix} = left. begin{pmatrix} 0\ vdots\ 0 end{pmatrix} right}{scriptstyle m}. end{equation} (
9.2)

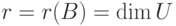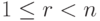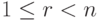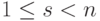Ясно, что r=r(B)=dim U, поэтому 1 leq r < n. Размерность s пространства решений X_одн этой системы равна n-r, и так как 1 leq r<n, то 1 leq s<n.

Пусть строки 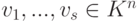v_1,...,v_sin K^n образуют фундаментальную систему решений системы (9.2), vi=(vi1,…,vin), 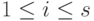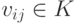1 leq i leq s, v_{ij}in K. Пусть 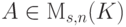Ain mM_{s,n}(K), A=(aij), aij=vij, 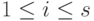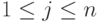1 leq i leq s, 1 leq j leq n. Покажем, что A – искомая матрица.

Действительно, по построению матрицы A любая строка из U (как линейная комбинация строк u1,…,um ) является решением однородной системы уравнений

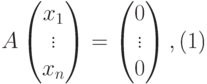begin{equation}label{dusteloj} A begin{pmatrix} x_1\ vdots\ x_n end{pmatrix} = begin{pmatrix} 0\ vdots\ 0 end{pmatrix}, end{equation} (
9.3)

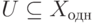т. е. Usubseteq X_{textup{одн}}. С другой стороны,

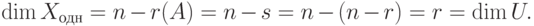
dim X_{textup{одн}} = n-r(A) = n-s = n-(n-r) = r = dim U.

Следовательно, U=Xодн.

В заключение отметим, что матрица A определена неоднозначно. Например, другая матрица A’ может быть получена с помощью другой фундаментальной системы решений системы (9.2).

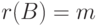Полученное задание линейных подпространств оказывается полезным при решении ряда практических задач. Например, пусть u_1,...,u_min R^n – линейно независимые строки, m<n. Требуется найти такие строки um+1,…,un, что {u1,…,un} – базис линейного пространства Rn. Как и выше, пусть v1,…,vs – какая-нибудь фундаментальная система решений системы (9.2) (в нашем случае r(B)=m, s=n-m ). Положим um+1=v1,…,un=vn-m. Покажем, что {u1,…,un} – базис в Rn. Достаточно показать, что строки u1,…,un линейно независимы над R. 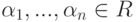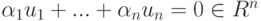Пусть alpha_1,...,alpha_nin R и alpha_1 u_1+...+alpha_n u_n=0in R^n. Тогда для строки

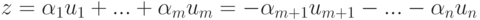
z=alpha_1 u_1+...+alpha_m u_m=-alpha_{m+1}u_{m+1}-...-alpha_n u_n

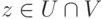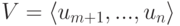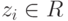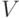имеем zin Ucap V, где V=langle u_{m+1},...,u_nrangle. Если z=(z1,…,zn), z_iin R, 1 leq i leq n, то по построению подпространств U и V (см. (9.2), (9.3)) имеем

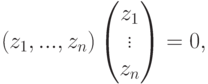
(z_1,...,z_n) begin{pmatrix} z_1\ vdots\ z_n end{pmatrix}=0,

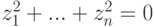z_1^2+...+z_n^2=0, следовательно, z1=…=zn=0, и 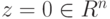z=0in R^n. Значит,

alpha_1 u_1+...+alpha_m u_m=0 (in R^n) = alpha_{m+1}u_{m+1}+...+alpha_nu_n.

Но u1,…,um – линейно независимые строки, поэтому 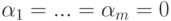alpha_1=...=alpha_m=0. Строки um+1,…,un также линейно независимы, следовательно, 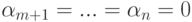alpha_{m+1}=...=alpha_n=0. Итак, 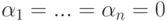alpha_1=...=alpha_n=0 и строки u1,…,un линейно независимы.

Таким образом, мы рассмотрели два способа задания линейных подпространств в K V=Kn :

  1. как множество решений Xодн однородной системы линейных уравнений;
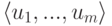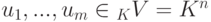  2. как линейную оболочку langle u_1,...,u_mrangle строк u_1,...,u_min {}_K V=K^n.

При этом мы научились переходить от первого задания ко второму (фундаментальная система решений) и от второго задания к первому. Первый способ задания удобен для задания пересечения 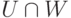Ucap W подпространств (надо к первой однородной системе уравнений приписать вторую). Второй способ задания удобен для задания суммы подпространств:

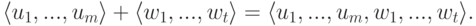
langle u_1,...,u_mrangle+ langle w_1,...,w_trangle= langle u_1,...,u_m,w_1,...,w_trangle.

В следующем примере мы увидим комбинацию этих приемов.

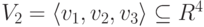Пример 9.18.1. Пусть V_1=langle u_1,u_2,u_3ranglesubseteq R^4 (линейная оболочка строк u1=(1,1,0,0), u2=(0,1,1,0), u3=(0,0,1,1) ), V_2=langle v_1,v_2,v_3ranglesubseteq R^4 (линейная оболочка строк v1=(1,0,1,0), v_2=(0,2,1,1), v3=(1,2,1,2) ). Необходимо найти базисы линейных пространств V1+V2 и V_1cap V_2, при этом строки u1, u2, u3, v1, v2, v3 выразить через базис пространства V1+V2.

Решение Запишем строки u1, u2, u3, v1, v2, v3 по столбцам и приведем полученную матрицу к ступенчатому виду с помощью элементарных преобразований строк:

begin{mult} begin{gathered} u_1 u_2 u_3,, ! v_1 v_2 v_3 kern53mm \ left( begin{array}{cccccc} 1 & 0 & 0 & 1 & 0 & 1\ 1 & 1 & 0 & 0 & 2 & 2\ 0 & 1 & 1 & 1 & 1 & 1\ 0 & 0 & 1 & 0 & 1 & 2 end{array}right)to left( begin{array}{cccccc} 1 & 0 & 0 & phm 1 & 0 & 1\ 0 & 1 & 0 & -1 & 2 & 1\ 0 & 1 & 1 & phm 1 & 1 & 1\ 0 & 0 & 1 & phm 0 & 1 & 2 end{array}right)to{} end{gathered} \[3mm] begin{gathered} kern55mm u'_1, u'_2, u'_3 v'_1; v'_2; v'_3 \ {}to left( begin{array}{cccccc} 1 & 0 & 0 & phm 1 & phm 0 & 1\ 0 & 1 & 0 & -1 & phm 2 & 1\ 0 & 0 & 1 & phm 2 & -1 & 0\ 0 & 0 & 1 & phm 0 & phm 1 & 2 end{array}right)to left( begin{array}{cccccc} multicolumn{1}{|c}{1} & 0 & 0 & phm 1 & phm 0 & phm 1\ cline{1-1} 0 & multicolumn{1}{|c}{1} & 0 & -1 & phm 2 & phm 1\ cline{2-2} 0 & 0 & multicolumn{1}{|c}{1} & phm 2 & -1 & phm 0\ cline{3-3} 0 & 0 & 0 & multicolumn{1}{|c}{phm 1} & -1 & -1\ cline{4-6} end{array}right). end{gathered} end{mult}

Поскольку 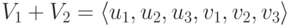V_1+V_2=langle u_1,u_2,u_3,v_1,v_2,v_3rangle и элементарные преобразования строк матрицы не меняют линейных соотношений между столбцами, то {u1,u2,u3,v1} – базис в V_1+V_2 (и так как dim (V_1+V_2)=4, то V1+V2= R^4 ). Из ступенчатого вида мы вычисляем v’2 и v’3 через u’1, u’2, u’3, v’1 :

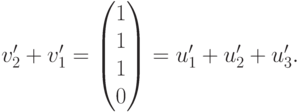
v'_2+v'_1= begin{pmatrix} 1\ 1\ 1\ 0 end{pmatrix}= u'_1+u'_2+u'_3.

Поэтому v’_2=u’_1+u’_2+u’_3-v’_1 и, следовательно, v2=u1+u2+u3-v1. Для v’3 мы видим, что v’3+v’1=(2,0,2,0)*=2u’1+2u’3, поэтому v3=2u1+2u3-v1. Проведенные вычисления равносильны завершению приведения матрицы к главному ступенчатому виду:

left( begin{array}{cccccc} multicolumn{1}{|c}{1} & 0 & 0 & 0 & phm 1 & phm 2\ cline{1-1} 0 & multicolumn{1}{|c}{1} & 0 & 0 & phm 1 & phm 0\ cline{2-2} 0 & 0 & multicolumn{1}{|c}{1} & 0 & phm 1 & phm 2\ cline{3-3} 0 & 0 & 0 & multicolumn{1}{|c}{phm 1} & -1 & -1\ cline{4-6} end{array}right).

Рассмотрим теперь V_1cap V_2. Для этого найдем однородные системы линейных уравнений, чьи множества решений совпадают с V1 и V2 соответственно.

Для V1:

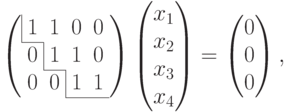
left( begin{array}{cccc} multicolumn{1}{|c}{1} & 1 & 0 & 0\ cline{1-1} 0 & multicolumn{1}{|c}{1} & 1 & 0\ cline{2-2} 0 & 0 & multicolumn{1}{|c}{1} & 1\ cline{3-4} end{array} right) begin{pmatrix} x_1\ x_2\ x_3\ x_4 end{pmatrix} = begin{pmatrix} 0\ 0\ 0 end{pmatrix},

система уже имеет ступенчатый вид, x1, x2, x3 – главные неизвестные, x4 – свободная. Фундаментальная система решений состоит из одной строки (-1,1,-1,1). Итак, подпространство V1 совпадает с пространством решений однородной системы линейных уравнений

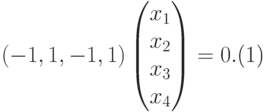begin{equation}label{denovestelo} (-1,1,-1,1) begin{pmatrix} x_1\ x_2\ x_3\ x_4 end{pmatrix} = 0. end{equation} (
9.4)

Для V2 :

begin{align*} & begin{pmatrix} 1 & 0 & 1 & 0\ 0 & 2 & 1 & 1\ 1 & 2 & 1 & 2 end{pmatrix} begin{pmatrix} x_1\ x_2\ x_3\ x_4 end{pmatrix} = begin{pmatrix} 0\ 0\ 0 end{pmatrix} to begin{pmatrix} 1 & 0 & 1 & 0\ 0 & 2 & 1 & 1\ 0 & 2 & 0 & 2 end{pmatrix} begin{pmatrix} x_1\ x_2\ x_3\ x_4 end{pmatrix} = begin{pmatrix} 0\ 0\ 0 end{pmatrix} to{} \[1mm] & quad {}to begin{pmatrix} 1 & 0 & 1 & 0\ 0 & 2 & 1 & 1\ 0 & 1 & 0 & 1 end{pmatrix} begin{pmatrix} x_1\ x_2\ x_3\ x_4 end{pmatrix} !=! begin{pmatrix} 0\ 0\ 0 end{pmatrix} to! %{} %\[3mm] %& quad {}to begin{pmatrix} 1 & 0 & 1 & 0\ 0 & 1 & 0 & 1\ 0 & 2 & 1 & 1 end{pmatrix} begin{pmatrix} x_1\ x_2\ x_3\ x_4 end{pmatrix} !=! begin{pmatrix} 0\ 0\ 0 end{pmatrix} to{} \[1mm] & quad {}to left( begin{array}{cccc} multicolumn{1}{|c}{1} & 0 & 1 & phm 0\ cline{1-1} 0 & multicolumn{1}{|c}{1} & 0 & phm 1\ cline{2-2} 0 & 0 & multicolumn{1}{|c}{1} & -1\ cline{3-4} end{array}right) begin{pmatrix} x_1\ x_2\ x_3\ x_4 end{pmatrix} = begin{pmatrix} 0\ 0\ 0 end{pmatrix}, end{align*}

и мы приходим к ступенчатому виду, при этом x1, x2, x3 – главные неизвестные, а x4 – свободная. Фундаментальная система решений состоит из одной строки (-1,-1,1,1). Значит, однородная система линейных уравнений

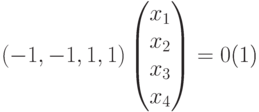begin{equation}label{denovedusteloj} (-1,-1,1,1) begin{pmatrix} x_1\ x_2\ x_3\ x_4 end{pmatrix} = 0 end{equation} (
9.5)

задает подпространство V2.

Ясно, что система

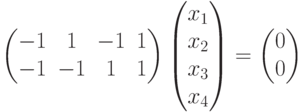
begin{pmatrix} -1 & phm 1 & -1 & 1 \ -1 & -1 & phm 1 & 1 end{pmatrix} begin{pmatrix} x_1 \ x_2 \ x_3 \ x_4 end{pmatrix}= begin{pmatrix} 0 \ 0 end{pmatrix}

задает подпространство V_1cap V_2.

Решим эту систему:

begin{align*} & begin{pmatrix} -1 & phm 1 & -1 & 1\ -1 & -1 & phm 1 & 1 end{pmatrix} begin{pmatrix} x_1\ x_2\ x_3\ x_4 end{pmatrix} = begin{pmatrix} 0\ 0 end{pmatrix} to{} \[1mm] & quad {}to begin{pmatrix} phm 1 & -1 & 1 & -1\ -1 & -1 & 1 & phm 1 end{pmatrix} begin{pmatrix} x_1\ x_2\ x_3\ x_4 end{pmatrix} = begin{pmatrix} 0\ 0 end{pmatrix} to{} \[1mm] & quad {}to left( begin{array}{cccc} multicolumn{1}{|c}{1} & -1 & 1 & -1\ cline{1-1} 0 & multicolumn{1}{|c}{-2} & 2 & phm 0\ cline{2-4} end{array}right) begin{pmatrix} x_1\ x_2\ x_3\ x_4 end{pmatrix} = begin{pmatrix} 0\ 0 end{pmatrix}, end{align*}

x1, x2 – главные неизвестные, x3, x4 – свободные неизвестные. Фундаментальная система решений состоит из двух строк

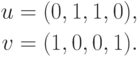
begin{align*} u &= (0,1,1,0),\ v &= (1,0,0,1). end{align*}

Следовательно, {u,v} – базис линейного подпространства V_1cap V_2.

Источник

Добавить комментарий