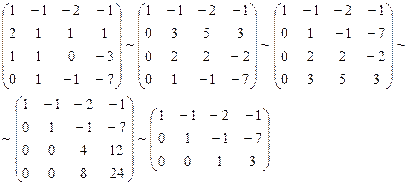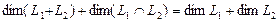Как найти базис подпространства порожденного векторами

Определение
1.
В любой системе векторов
из К,
содержащей ненулевые вектора, всегда
можно выбрать подсистему
,
где r 
m, состоящую
из максимального числа линейно независимых
векторов так, что присоединение любого
вектора из этой системы к указанной
подсистеме делает ее линейно зависимой;
действительно, так
как
в системе имеется не нулевой вектор, а
он всегда линейно независим, то r

1. Такая подсистема линейно независимых
векторов называется базой
исходной системы, а число r
векторов в базе – рангом
этой системы векторов.

Замечание.
База системы определяется неоднозначно,
но число векторов в базе (ранг) всегда
одинаково. Например, из трех векторов
,
один из которых линейно зависим, можно
построить три базы из двух векторов:
.

Свойства базы.

1. Все
   вектора системы можно представить в
   виде линейной комбинации векторов
   базы. (см. предыдущий п.4.3, теорема 2).

2.
Любой вектор подпространства, порожденного
системой векторов, можно представить
в виде линейной комбинации только
векторов, образующих ее базу и это
разложение единственно.

Доказательство.
Пусть G
– подпространство, порожденное векторами

и пусть

r < m
( для r = m
утверждение очевидно) база системы
.
Тогда оставшиеся вектора системы

можно представить в виде линейной
комбинации векторов базы

(4.8)

.
. . . . . . . . . . . . . . . . . . . . . . . . . .

Теперь
рассмотрим любой вектор
:

.

Подставив
в это равенство вектора

из (4.8), получим

или
.

Определение
2.
Для векторного подпространства,
порожденного системой векторов
,
база этой системы векторов называется
базисом,
а ранг системы векторов называется
размерностью
этого
подпространства.

В
качестве наглядного примера рассмотрим
подпространство, порожденное системой
свободных векторов.

4.5. Базис и размерность подпространства, порожденного системой

свободных
векторов

Рассмотрим
подпространство, элементом которого
является линейная комбинация из трех
свободных векторов
.
Предположим, что эта система векторов
линейно зависима. Случай линейно
независимых векторов будет рассмотрен
позже. Мы уже установили, что если
линейная комбинация из трех свободных
векторов линейно зависима, то это
означает, что эти вектора компланарны,
т.е. существует плоскость, которой они
параллельны. Очевидно, компланарным
будет и любой вектор
,
являющийся линейной комбинацией этих
векторов. Поэтому подпространство,
порожденное системой таких трех линейно
зависимых векторов, представляет собой
совокупность всех векторов, компланарных
данным. Изображается такая система
векторов направленными отрезками,
лежащими в одной плоскости, либо в
параллельных ей плоскостях. Далее, так
как система из трех векторов

линейно зависима, то один из этих векторов
является линейной комбинацией двух
других векторов. Пусть этим вектором
будет
,
где
.
Рассмотрим ситуацию, когда оставшиеся
вектора линейно независимы, т.е. это
означает, что они не коллинеарны. Тогда
эти два упорядоченных вектора составят
базис подпространства компланарных
векторов и размерность этого подпространства
равна двум. Следовательно,
базис двумерного подпространства
компланарных свободных векторов
представляет собой два любых упорядоченных
неколлинеарных вектора.
Обычно в качестве базисных векторов
двумерного пространства выбирают
векторы, которые изображаются направленными
отрезками, параллельными координатным
осям Ох
и Оу
на плоскости и равные по модулю масштабному
отрезку координатных осей. Первый
вектор, направленный параллельно оси
Ох,
обозначают
:
его координаты (1,0), а второй вектор,
направленный параллельно оси Оу
обозначают
:
его координаты (0,1). Выбор такого базиса
обусловлен тем, что если представлять
любой вектор

с координатами (х,у)
двумерного подпространства через базис
,,
то в этом случае коэффициентами линейной
комбинации базисных векторов будут
являться координаты х
и у
вектора
,
т.е.
,
и как мы уже видели, это разложение
единственно.

Теперь
рассмотрим случай, когда вектора

и
,
(один из которых не равен
)
коллинеарны, т.е. линейно зависимы (или
).
Естественно и любой вектор, являющийся
линейной комбинацией этих векторов,
будет им коллинеарным. Поэтому
подпространство, порожденное системой
векторов, из которых только один
линейно независим, (им является вектор
не равный
)
представляет собой множество коллинеарных
векторов. Базис такого подпространства
состоит из одного ненулевого вектора
и размерность такого подпространства
равна единице. Одномерное подпространство
изображается множеством направленных
отрезков, расположенных на одной прямой
или на параллельных ей прямых.

Теперь
обобщим понятие базиса для совокупности
векторов, составляющих все векторное
пространство К.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Линейные оболочки и подпространства

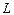
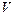
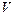
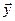
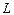
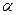
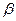
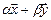
Определение. Подпространством линейного пространства называется множество векторов из такое, что для любых двух векторови из и любых двух вещественных чисел и линейная комбинация также принадлежит .

Утверждение. Подпространство само является линейным про­странством.

Определение. Линейной оболочкой системы векторов называется множество всех линейных комбинаций векторов . Обозначается .

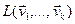
Утверждение. Линейная оболочка системы векторов является подпространством.

Определение. Пересечением двух подпространств и на­зывается множество всех векторов, принадлежащих одновре­менно и ,и . Обозначается .

Определение. Суммой двух подпространств и называется множество всех векторов , представимых в виде , где , . Обозначается .

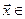
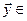
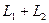
Утверждение. Сумма и пересечение подпространств и являются линейными пространствами, и их размерности связаны равенством

+ = + .

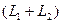
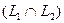
Определение. Сумма двух подпространств называется прямой суммой, если пересечение этих подпространств состо­ит только из нулевого вектора.

Примеры

1. Найти размерность и какой-нибудь базис суммы и пересечения подпространств, порождённых векторами .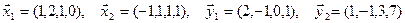

Решение. Вычислим вначале размерность подпространств. С этой целью установим, являются ли линейно независимыми векторы, порождающие данные подпространства. Для подпространства , порождённого векторами , равенство нулю линейной комбинации , эквивалентное системе уравнений , достигается лишь при условии . Следовательно, векторы линейно

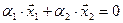
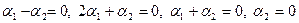
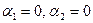
независимы и размерность подпространства равна 2: . Для подпространства , порождённого векторами , проводя аналогичный анализ, получим .

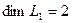
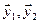
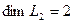
Вычислим теперь размерность пересечения подпространств и . По определению векторы, составляющие пересечение, принадлежат одновременно обоим подпространствам. Произвольный вектор подпространства является линейной комбинацией базисных векторов : . Аналогично для подпространства имеем , тогда условие принадлежности пересечению есть или .

Это условие представляет собой систему уравнений относительно коэффициентов . Составим матрицу системы и упростим её с помощью элементарных преобразований:

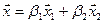
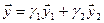
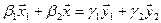
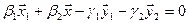
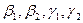
Как видно ранг системы равен 3. Значит ФСР состоит из одного линейно независимого вектора. Найдём его, решив систему уравнений, соответствующих последней матрице, получим ,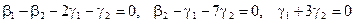

откуда .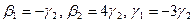

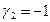
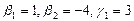
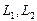
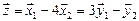
Полагая свободное неизвестное , для остальных имеем

. Итак, пересечение подпространств имеет один базисный вектор

.

Размерность пересечения 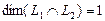. Следовательно, в соответствии с равенством

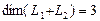
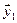
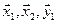
размерность суммы подпространств . В качестве базиса суммы подпространств можно взять, например, векторы , дополненные вектором . В линейной независимости векторов убедиться нетрудно.

Задачи

3.39. Найти размерность и какой-нибудь базис подпространства, порожденного векторами , , , , .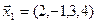

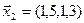
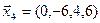
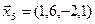
3.40. Найти размерность и какой-либо базис линейной оболочки векторов , , , , .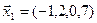

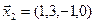
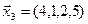
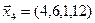
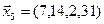
3.41. Является ли подпространством в указанном пространстве множество

а) векторов, выходящих из начала координат и заканчиваю­щихся на фиксированной прямой, в пространстве R 2 ;

б) бесконечно малых числовых последовательностей в про­странстве сходящихся последовательностей;

в) сходящихся к числу последовательностей в простран­стве сходящихся последовательностей;

г) диагональных матриц в пространстве квадратных матриц того же порядка;

д) невырожденных матриц в пространстве симметричных мат­риц того же порядка;

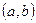
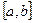
е) дифференцируемых на интервале функций в простран­стве функций, непрерывных на отрезке .

3.42. Почему не является подпространством в указанном про­странстве множество

а) векторов, каждый из которых лежит на одной из коорди­натных плоскостей, в пространстве R 3 ;

б) векторов из пространства R n , координаты которых удовлетворяют уравнению ;

в) расходящихся числовых последовательностей в простран­стве ограниченных последовательностей;

г) вырожденных матриц в пространстве квадратных матриц того же порядка;

д) монотонно возрастающих и ограниченных на множестве 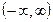функций в пространстве функций, ограниченных на том же множестве.

3.43. Найти размерность и какой-либо базис подпространства ре­шений однородной системы:

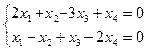
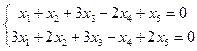
а) ; б) ;

в) .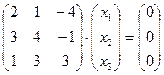

3.44. Доказать, что данное множество является подпространством в R n , найти его размерность и какой-либо базис:

а) все n-мерные векторы, координаты которых удовлетворя­ют уравнению ;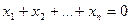

б) все n-мерные векторы, у которых первая координата равна нулю;

в) все n-мерные векторы, у которых первая и последняя координаты равны между собой;

г) все n-мерные векторы, у которых координаты с четными номерами равны нулю;

д) все n-мерные векторы, у которых координаты с нечетны­ми номерами равны между собой.

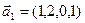
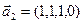
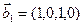
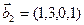
3.45. Найти размерность суммы и пересечения подпространств, порожденных векторами , и , . Является ли эта сумма прямой суммой?

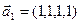
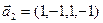
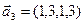
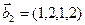
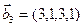
3.46. Найти размерность суммы и пересечения линейных оболочек векторов , , и , , . Является ли их cумма прямой?

3.47. Найти базис суммы и пересечения двух подпространств, порожденных соответственно векторами и , если

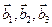
а) , , , , , ;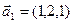

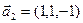
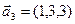
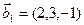
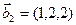
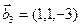
б) , , , , , .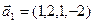

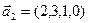
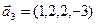
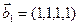
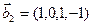
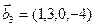
3.48. Найти базис суммы и пересечения линейных оболочек и , если

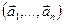
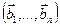
а) , , , ;

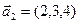
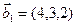
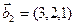
б) , , , , , .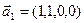

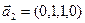
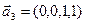
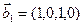
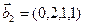
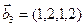
Является ли прямой сумма этих подпространств?

Векторное пространство: размерность и базис, разложение вектора по базису

В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:

e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )

Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.

Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

Рассмотрим применение данной теории на конкретных примерах.

Исходные данные: векторы

a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 )

Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.

Решение

Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.

A = 3 2 3 – 2 1 – 1 1 2 – 2 A = 3 – 2 1 2 1 2 3 – 1 – 2 = 3 · 1 · ( – 2 ) + ( – 2 ) · 2 · 3 + 1 · 2 · ( – 1 ) – 1 · 1 · 3 – ( – 2 ) · 2 · ( – 2 ) – 3 · 2 · ( – 1 ) = = – 25 ≠ 0 ⇒ R a n k ( A ) = 3

Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.

Ответ: указанные векторы являются базисом векторного пространства.

Исходные данные: векторы

a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 ) d = ( 0 , 1 , 2 )

Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.

Решение

Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , – 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , – 1 , – 2 ) является базисом.

Ответ: указанная система векторов не является базисом.

Исходные данные: векторы

a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )

Могут ли они являться базисом четырехмерного пространства?

Решение

Cоставим матрицу, используя в качестве строк координаты заданных векторов

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

По методу Гаусса определим ранг матрицы:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

1 2 3 3 0 1 0 2 0 1 – 1 1 0 1 – 2 1

1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 – 2 – 1

1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4

Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.

Ответ: заданные векторы являются базисом четырехмерного пространства.

Исходные данные: векторы

a ( 1 ) = ( 1 , 2 , – 1 , – 2 ) a ( 2 ) = ( 0 , 2 , 1 , – 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )

Составляют ли они базис пространства размерностью 4?

Решение

Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.

Ответ: нет, не составляют.

Разложение вектора по базису

Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Докажем эту теорему:

зададим базис n -мерного векторного пространства – e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :

x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n – некоторые числа.

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:

1 – x 1 ) · e ( 1 ) + ( x

2 – x 2 ) · e ( 2 ) + . . . ( x

Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x

2 – x 2 ) , . . . , ( x

n – x n ) будут равны нулю. Из чего справедливым будет: x 1 = x

n . И это доказывает единственный вариант разложения вектора по базису.

При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .

Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .

Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x

Вектор x → будет представлен следующим образом:

2 · e ( 2 ) + . . . + x

Запишем это выражение в координатной форме:

( x 1 , x 2 , . . . , x n ) = x

1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x

2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x

n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x

2 e 1 ( 2 ) + . . . + x

2 e 2 ( 2 ) + + . . . + x

n e 2 ( n ) , . . . , x

2 e n ( 2 ) + . . . + x

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x

n e 2 n ⋮ x n = x

Матрица этой системы будет иметь следующий вид:

e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )

Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x

n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .

Применим рассмотренную теорию на конкретном примере.

Исходные данные: в базисе трехмерного пространства заданы векторы

e ( 1 ) = ( 1 , – 1 , 1 ) e ( 2 ) = ( 3 , 2 , – 5 ) e ( 3 ) = ( 2 , 1 , – 3 ) x = ( 6 , 2 , – 7 )

Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.

Решение

Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .

Используем метод Гаусса:

A = 1 – 1 1 3 2 – 5 2 1 – 3

1 – 1 1 0 5 – 8 0 3 – 5

1 – 1 1 0 5 – 8 0 0 – 1 5

R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.

Пусть в базисе вектор x → имеет координаты x

3 . Связь этих координат определяется уравнением:

3 e 1 ( 3 ) x 2 = x

3 e 2 ( 3 ) x 3 = x

Применим значения согласно условиям задачи:

Решим систему уравнений методом Крамера:

∆ = 1 3 2 – 1 2 1 1 – 5 – 3 = – 1 ∆ x

1 = 6 3 2 2 2 1 – 7 – 5 – 3 = – 1 , x

1 ∆ = – 1 – 1 = 1 ∆ x

2 = 1 6 2 – 1 2 1 1 – 7 – 3 = – 1 , x

2 ∆ = – 1 – 1 = 1 ∆ x

3 = 1 3 6 – 1 2 2 1 – 5 – 7 = – 1 , x

Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x

Ответ: x = ( 1 , 1 , 1 )

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

Указанные системы являются также базисами заданного пространства.

n ( 1 ) – координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:

1 ( 1 ) e 1 ( 1 ) + c

2 ( 1 ) e 1 ( 2 ) + . . . + c

n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c

1 ( 1 ) e 2 ( 1 ) + c

2 ( 1 ) e 2 ( 2 ) + . . . + c

n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c

1 ( 1 ) e n ( 1 ) + c

2 ( 1 ) e n ( 2 ) + . . . + c

В виде матрицы систему можно отобразить так:

( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c

n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Сделаем по аналогии такую же запись для вектора c ( 2 ) :

( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c

n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

И, далее действуя по тому же принципу, получаем:

( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c

n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Матричные равенства объединим в одно выражение:

c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c

n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :

e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e

n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )

Дадим следующие определения:

n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )

к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .

n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )

к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/vektory/vektornoe-prostranstvo/

[/spoiler]

1. Линейная алгебра

Лекция 6
Подпространства. Базис и
размерность

2. План лекции

Определение линейного подпространства nмерного координатного пространства
Линейная оболочка набора векторов
Линейное пространство решений однородной
системы линейных уравнений
Базис и размерность
Ортонормированные базисы
2

3. Векторные подпространства. Определение

Подпространством линейного пространства Rnнад полем Rназывают
такое подмножество U R n , которое обладает свойствами:
а ) x, y U x y U ;
б) x U x U .R
Другими словами, подмножество U замкнуто относительно действий
«сложения» и «умножения» на скаляр, определённых в Rn.
Тривиальными подпространствами линейного пространства Rn
называются само Rn и пространство, состоящее из одного нулевого
вектора O.
3

4. Пример

1
2
U X … , 1 , 2 ,.., n R : 1 n
…
n

5. Векторные подпространства. Способ задания

Подпространством, порождённым векторами
e1 , e 2, …e k R n ,
называют подмножество U R n всех линейных комбинаций
этих векторов (линейная оболочка набора векторов), т.е.
U e1 , e2 ,…, ek x 1e1 2e2 … k ek , i R
5

6. Пример

1 1 1 0
U 1 , 1 , 3 , 2 R 3
2 1 3 1

7. Векторные подпространства. Способ задания

Другой способ задания линейного подпространства в Rn может
служить задание набора ограничений, которым удовлетворяют
векторы подпространства. Например, в виде A X = O.
Теорема. Множество решений однородной системы уравнений
A X = O образует линейное подпространство пространства Rn .
7

8. Пример

x1 2 x2 3 x3 4 x4 0
4
V X R
x1 x2 x3 x4 0

9. Базис векторного пространства. Определение

Базис векторного пространства.
Q V Определение
Пусть (e , e ,…, e ) – произвольное множество векторов
1 2
s
линейного пространства Rn. Упорядоченная система векторов
называется базисом в Q, если :
а)
ek Q, k 1,2,…, s ;
б) система
(e1 , e2 ,…, es )
линейно независима;
в) для любого x Q найдутся такие числа
что
x1 , x2 ,…, xs ,
x x1e1 x2 e2 … xs es
9

10. Размерность векторного пространства

Все базисы
M e1 , e2 , … , en V
пространства V
имеют одинаковое число векторов, которое называется
размерностью векторного пространства V и обозначается
n dim( V )
Полагают, что размерность тривиального пространства
(состоящего из одного только нулевого вектора), равна нулю:
dim(O)= 0.
Размерность подпространства, заданного СЛУ, равна n –
rg(A).
10

11. Пример базиса координатного пространства

1
0
0
0
1
0
M e1 .. , e2 .. ,…., en ..
0
0
0
0
0
1
1
1
0
2
0
1
.. 1 .. 2 .. … n
..
0
0
0
0
n
,
0
0
..
0
1
11

12. Теоремы о базисах

1. В любом ненулевом подпространстве
координатного пространства существует
базис.
2. Если размерность подпространства
координатного пространства равна k, то
любая линейно независимая система из k
векторов образует базис этого
подпространства.

13. Нахождение базиса подпространства

Для нахождения базиса в подпространстве, порожденном некоторой
совокупностью векторов, достаточно выбрать из системы образующих
векторов линейно независимую систему.
Например,
1 1 1 0
U 1 , 1 , 3 , 2 R 3
2 1 3 1
1 1
U 1 , 1 , dim( U ) 2
2 1
25.06.2018
Векторные пространства
13

14. Алгоритм построения базиса в

n
1.
2.
3.
U R
Столбцы, порождающие подпространство, записать в матрицу.
Элементарными преобразованиями над столбцами привести эту
матрицу к «ступенчатому» виду.
Ненулевые столбцы данной «ступенчатой» матрицы и будут
составлять базис исходного подпространства, а ранг матрицы будет
равен размерности этого подпространства.
U
1 1
1
2 2
2
.. , .. , … , ..
.. ..
..
n n
n
1 1
2 2
.. ..
.. ..
n n
.. ..
.. ..
.. ..
.. ..
.. ..
1 0
1
c2 1
2
.. ..
..
cr d r
..
.. ..
n
cn d n
0 0
.. 0 0 0
.. … .. ..
.. 1 0 0
.. .. .. ..
.. f n 0 0
.. 0
14

15. Нахождение базиса подпространства. Пример

1 1 1 0
U 1 , 1 , 3 , 2 R 3
2 1 3 1
1 1 1 0 1 0 0 0 1 0 0
3
2 ~ 1 2 2 2 ~ 1 2 0
1 1
2 1 3 1 2 1 1 1 2 1 0
1 1
1 0
U 1 , 1 1 , 2
2 1
2 1
0
0
0
1 1
M U 1 , 1
2 1
15

16. Нахождение базиса подпространства. Пример

x1 2 x2 3×3 4 x4 0
4
V X R
x
x
x
x
0
1
2
3
4
6 5
x1 6 5
1 2 3 4 1 2 3 4
5 4
x2 5 4
~
X
x3
0
1
1 1 1 1 0 1 4 5
x
1 0
4
6 5
5 4
M V ,
0 1
1 0
16

17. Координаты вектора в базисе

Пусть даны M e , e ,…, e V – базис векторного пространства V
1
2
n
и вектор X из V.
Координатами вектора Х в этом базисе называют коэффициенты в
разложении:
X 1e1 2e2 … nen V
17

18. Нахождение координат вектора в базисе.

Найти координаты вектора X в заданном базисе
R4
1
1
0 ,
1
2 1 0
4
1 1 1
4
4
,
,
,
X
R
4
3 0 1
1
1 0 1
1
2
1
0 4
1
1
1
1 4
1 2 3 4
0
3
0
1
4
1
1
0
1 1
4
1 2 2 3
4
2
3
4
1
3 2
4 4
1 2
4 1
4
1
2
1
0
4
1
1
1
1
X 1 2 ( 1) 2
4
0
3
0
1
1
1
1
0
1
18

19. Ортогональный базис

Определение.
Базис
e , e ,…, en
n-мерного пространства называется
ортогональным, если
1
2
(ei , e j ) 0, i j , i, j 1,2, … , n
Другими словами,
ортогональным базисом называется базис, состоящий
из попарно ортогональных векторов.
19

20. Ортонормированный базис

Определение.
Базис
e , e ,…, en
n-мерного пространства называется
ортонормированным, если
1
2
0, i j
(ei , e j ) ij
, i, j 1,2, … , n
1, i j
Другими словами,
ортонормированным базисом называется базис,
состоящий из попарно ортогональных векторов,
каждый из которых имеет длину, равную единице.
20

21. Построение ортогонального базиса

Построение ортогонального
Задача.
базиса
Проверить ортогональность системы векторов
1
2
e1 ,
1
3
e2
2
1
R4
3
1
4
и дополнить ее до ортогонального базиса в R .
1. Вычислим скалярное произведение (e1,e2):
e1, e2 1 2 2 1 1 3 3 1 0
e1 e2 .
2. Задача сводится к построению векторов e3 и e4 таких, что e3 e4 и
оба ортогональны
e1, e2 .
21

22. Построение ортогонального базиса (продолжение)

Для определения
e
3
x1
x
2
x
3
x
4
частное решение системы
достаточно найти какое-либо
e3 , e1 0
e3 , e2 0
x1 2 x2 x3 3 x4 0
.
2 x1 x2 3 x3 x4 0
1 2 1
2 1 3
3 1 2 1 3 1 2 1 3
~
~
1 0 5 5 5 0 1 1 1
Выберем частное решение
e
3
4
2
.
1
3
e
3
с1 с2
с1 с2
.
с1
с
2
22

23. Построение ортогонального базиса (продолжение)

x1
x
Для определения e4 2 достаточно найти какое-либо
x
решение системы
3
x
4
x1 2 x2 x3 3 x4 0
e4 , e1 0
2 x1 x2 3 x3 x4 0 ,
e4 , e2 0
4 x 2 x x 3 x 0
e , e 0
1
2
3
4
4 3
3 1 2 1
3 1 2 1
3
1 2 1 3 1 2 1
1 3 1 ~ 0 5 5 5 ~ 0 1 1 1 ~ 0 1 1 1
2
4 2 1 3 0 6 3 15 0 2 1 5 0 0 1 3
2с1
4с1
e
Общее решение , выберем
4
3с
1
с
1
2
4
.
3
1
23