Как найти базис пространства кососимметрических матриц - Сайт, где вы сможете решить свои вопросы

Сообщения без ответов | Активные темы | Избранное

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте

его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Не ищите на этом форуме халяву

, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения

и указать конкретные затруднения.

Обязательно просмотрите тему

Правила данного раздела, иначе Ваша тема может быть удалена

или перемещена в Карантин, а Вы так и не узнаете, почему.

	базис в пространстве кососимметрических матриц 16.05.2012, 18:13
29/04/12 7 Омск	даны 2 системы, из 3 матриц каждая, размера 3 на 3 доказать что каждая система является базисом и написать матрицу перехода от одного базиса к другому. Я понимаю что нужно каждую матрицу представить через вектор и доказать что полученная система линейно независима, не могу только понять каким будет стандартный базис для пространства кососиметрических матриц. То есть как будут расположены единичные клетки?

ewert

Re: базис в пространстве кососимметрических матриц

16.05.2012, 18:24

Заслуженный участник

11/05/08
32162

каким будет стандартный базис для пространства кососиметрических матриц.

Никаким, т.е. каким угодно. А для доказательства базисности конкретного набора матриц достаточно заметить, что любая кососимметрическая матрица взаимно-однозначно задаётся своими элементами ниже диагонали (ну или выше, конечно).

svv

Re: базис в пространстве кососимметрических матриц

16.05.2012, 19:35

Заслуженный участник

23/07/08
10061
Crna Gora

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Источник

Образуют ли данные матрицы базис пространства кососимметрических матриц порядка 3?

(Обозначения как в wolframalpha)

{{0,1,1},{-1,0,1},{-1,-1,0}}

{{0,1,-1},{-1,0,-1},{1,1,0}}

{{0,1,1},{-1,0,-1},{-1,1,0}}

задан
28 Окт ’17 20:37

curl
673●1●13

60% принятых

Источник

(все матрицы образуют динейно независимую систему).

2.21. Доказать, что матрицы вида образуют линейное подпространство в пространстве матриц М₂₃. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.

Решение:

Линейность данного множества матриц следует из линейности операций умножения матриц на число и сложения матриц, например:

При этом каждая матрица данного подпространства может быть представлена в виде:

Отсюда следует, что размерность подпространства L равна 2 и вкачестве его базиса можно взять матрицы .

Для дополнения этого базиса до базиса всего пространства М₂₃ можно выбрать матрицы

(все матрицы образуют динейно независимую систему).

2.22. Найти общий вид матрицы, антиперестановочной (AX=-XA) с данной матрицей . Доказать, что множество матриц Х образует линейное подпространство в пространстве М₂₂ матриц 2-го порядка. Найти его базис и размерность.

Решение:

Проверяем линейность данного множества L матриц:

Все условия выполнены – L является линейным пространством.

Если матрица антиперестановочная с данной матрицей , то:

т.е. матрица Х может быть представлена в виде:

Отсюда следует, что размерность подпространства L равна 2 и вкачестве его базиса можно взять матрицы .

2.23. Образуют ли матрицы базис в пространстве матриц М₂₂?

Решение:

Запишем данные матрицы в каноническом базисе, получим векторы

найдем ранг этой системы векторов:

Ранг системы векторов равен 3, следовательно, данные матрицы не образуют базис в пространстве матриц М₂₂

2.24. Найти размерность и какой-нибудь базис линейной оболочки системы матриц

Решение:

Запишем данные матрицы в каноническом базисе, получим векторы

найдем ранг этой системы векторов:

Ранг системы векторов равен 3, следовательно:

1) размерность данной системы матриц равна 3,

2) в качестве базиса их линейной оболочки можно взять первые три матрицы, т.е. (Е₁, Е₂, Е₃).

2.25. Установить, являются ли заданные множества подпространствами пространства M_nn. В случае положительного ответа найти базис и размерность подпространства.

1) множество всех симметрических квадратных матриц порядка n (A^T = A).

2) множество всех кососимметрических квадратных матриц порядка n (A^T = -A).

3) множество всех квадратных вырожденных матриц порядка n (detA = 0).

Решение:

1) При умножении любой симметрической квадратной матрицы порядка n (A^T = A) на любое число получается также симметрическая квадратная матрица порядка n , сумма двух симметрических квадратных матриц порядка n также является симметрической квадратной матрицей порядка n. Следовательно, множество всех симметрических квадратных матриц порядка n является подпространством пространства M_nn.

2) При умножении любой кососимметрической квадратной матрицы порядка n (A^T=-A) на любое число получается также симметрическая квадратная матрица порядка n , сумма двух кососимметрических квадратных матриц порядка n также является кососимметрической квадратной матрицей порядка n. Следовательно, множество всех кососимметрических квадратных матриц порядка n является подпространством пространства M_nn.

3) Определитель суммы двух матриц, определители которых равны нулю, может быть отличен от нуля, например:

Следовательно, множество всех квадратных матриц порядка n, определитель которых равен нулю, не является подпространством пространства M_nn.

2.26. Доказать, что множество функций образует линейное пространство. Найти его размерность и базис.

Решение:

Проверяем линейность заданного множества функций:

Все условия выполнены – L является линейным пространством.

В системе функций только любые две функции линейно независимы, поскольку они связаны соотношением , и любой вектор пространства L может быть представлен в виде линейной комбинации, например, первых двух функций системы, следовательно, эти две функции образуют базис пространства L, размерность которого поэтому равна 2.

2.27. Доказать, что множество функций образует линейное пространство. Найти его размерность и базис.

Решение:

Проверяем линейность заданного множества функций:

Все условия выполнены – L является линейным пространством.

Функции линейно независимы: если , то, записывая это равенство для t=-1, t=0 и t=1, получим:

и любой вектор пространства L может быть представлен в виде линейной комбинации этих функций (по определению L), следовательно, эти функции образуют базис пространства L, размерность которого поэтому равна 3.

2.28. Исследовать на линейную независимость систему функций {sint, cost, sin2t}

Решение:

Предположим, что входящие в данную систему функции линейно зависимы, т.е. найдутся такие , не все равные нулю, для которых выполняется равенство . Тогда, записывая это равенство для получим:

Получили противоречие, из чего следует, что данная система функций является линейно независимой.

2.29. Исследовать на линейную независимость систему функций {1, lnt, ln2t}

Решение:

Для доказательства того, что данная система функций является линейно зависимой, достаточно указать такие , не все равные нулю, для которых выполняется равенство .

Рассмотрим , для которых для имеем:

Следовательно, данная система функций является линейно зависимой.

2.30. Исследовать на линейную независимость систему функций {1, cost, cos2t}

Решение:

Получили противоречие, из чего следует, что данная система функций является линейно независимой.

Источник

Содержание

Кососимметричная матрица

Вещественная матрица $ A_{} $ называется кососимметричной¹⁾ если она удовлетворяет соотношению
$$A=-A^{top} ;$$
здесь $ {}^{top} $ означает транспонирование.

Из определения следует, что кососимметричная матрица может быть только квадратной, а ее элементы должны удовлетворять соотношению:
$$ a_{jk}=-a_{kj} quad npu quad {j,k } subset {1,dots, n} . $$
Из этого условия вытекает, что все элементы главной диагонали кососимметричной матрицы должны быть
равны нулю и сама матрица имеет вид
$$
left(
begin{array}{ccccc}
0 & a_{12} & a_{13} & dots & a_{1n} \
-a_{12} & 0 & a_{23} & dots & a_{2n} \
-a_{13} & – a_{23} & 0 & dots & a_{3n} \
vdots & & & ddots & vdots \
-a_{1n} & -a_{2n} & – a_{3n} & dots & 0
end{array}
right) .
$$
Произвольная кососимметричная матрица порядка $ n_{} $ однозначно задается своими
$$ 1+2+ dots + (n-1) =frac{n(n-1)}{2} , $$
элементами, стоящими над главной диагональю (или под ней).

Пример. Векторное произведение вектора $ X=(x_{1},x_2,x_3) $ на вектор $ Y=(y_{1},y_2,y_3) $ может быть задано с помощью кососимметричной матрицы:

$$
Xtimes Y = (x_{1},x_2,x_3) left(begin{array}{rrr}
0 & -y_3 & y_2 \
y_3 & 0 & -y_1 \
-y_2 & y_1 & 0
end{array}
right)
.
$$

Определитель, ранг

Теорема 1. Для алгебраических дополнений $ A_{jk}^{} $ элементов кососимметричной матрицы выполняются равенства

$$ A_{jk}=(-1)^{n-1} A_{kj} . $$
Иными словами, матрица $ operatorname{adj}(A) $ взаимная кососимметричной матрице $ A_{} $ будет симметричной при нечетном $ n_{} $ и кососимметричной при $ n_{} $ четном.

Теорема 2. Определитель кососимметричной матрицы нечетного порядка равен нулю. Определитель кососимметричной матрицы четного порядка $ n_{} $ есть квадрат однородного полинома степени $ n/2_{} $ относительно его элементов.

Доказательство. На основании определения кососимметричной матрицы, имеем:
$$
A=-A^{top} Rightarrow det A = det (-A^{top})=(-1)^n det A
$$
(здесь мы воспользовались свойствами

1

и

4

определителя).

При $ n_{} $ нечетном из последнего равенства следует, что $ det A = 0 $.

Пусть теперь $ n_{} $ — четно. Будем рассматривать кососимметричную матрицу $ B_{} $ четного порядка как полученную из кососимметричной матрицы $ A_{} $ нечетного порядка $ n-1_{} $ окаймлением:
$$
B=left(
begin{array}{cc}
A & begin{array}{l}
a_{1n} \ a_{2n} \ vdots \ a_{n-1,n}
end{array} \
– a_{1n}, – a_{2n},dots, – a_{n-1,n} & 0
end{array}
right)
$$
Тогда, на основании формулы для окаймленного определителя, теоремы 1, доказанного выше условия $ det A = 0 $, а также
тождества Сильвестра вытекает равенство:
$$
det B = – ( – a_{1n}, – a_{2n},dots, – a_{n-1,n}) tilde A
left(
begin{array}{l}
a_{1n} \ a_{2n} \ vdots \ a_{n-1,n}
end{array}
right)= left( sum_{k=1}^n sqrt{A_{kk}} a_{kn} right)^2 ;
$$
в нем знак какого-то одного из корней, например, $ sqrt{A_{11}} $ можно считать произвольным, а
$$ operatorname{sign} ( sqrt{A_{kk}} ) = operatorname{sign} left( frac{A_{k1}}{sqrt{A_{11}} } right)quad npu quad k>1 .
$$
Таким образом, мы получили, что $ sqrt{ det B} $ является однородным полиномом первой степени относительно элементов последнего столбца определителя кососимметричной матрицы $ B_{} $ четного порядка $ n_{} $. Однако же алгебраические дополнения $ A_{kk} $ представляют из себя также определители кососимметричных матриц порядка $ n-2 $ — тоже четного. К ним можно применить те же рассуждения и показать, что каждое выражение $ sqrt{ A_{kk} } $ является однородным полиномом первой степени относительно последнего столбца этого минора. Индукция по $ n_{} $ завершит строгое доказательство.

♦

Пример.

$$ left| begin{array}{cc}
0 & a_{12} \
-a_{12} & 0
end{array}
right|=a_{12}^2 ;
left| begin{array}{cccc}
0 & a_{12} & a_{13} & a_{14} \
-a_{12} & 0 & a_{23} & a_{24} \
-a_{13} & -a_{23} & 0 & a_{34} \
-a_{14} & -a_{24} & -a_{34} & 0
end{array}
right|
=left{begin{array}{l}
(a_{12}a_{34}-a_{13}a_{24}+a_{14}a_{23})^2= \
(a_{12}a_{34}+a_{13}a_{42}+a_{14}a_{23})^2
end{array}
right} ;
$$
$$
left| begin{array}{cccc}
0 & a_{12} & dots & a_{16} \
-a_{12} & 0 & dots & a_{26} \
vdots & & ddots & vdots \
-a_{16} & -a_{26} & dots & 0
end{array}
right|=
left(begin{array}{ll}
&a_{12}a_{34}a_{56}+a_{12}a_{35}a_{64}+a_{12}a_{36}a_{45}+ \
&+a_{13}a_{45}a_{62}+a_{13}a_{46}a_{25}+a_{13}a_{42}a_{56}+ \
&+a_{14}a_{56}a_{23}+a_{14}a_{52}a_{36}+a_{14}a_{53}a_{62}+ \
&+a_{15}a_{62}a_{34}+a_{15}a_{63}a_{42}+a_{15}a_{64}a_{23}+ \
&+a_{16}a_{23}a_{45}+a_{16}a_{24}a_{53}+a_{16}a_{25}a_{34}
end{array} right)^2 , .
$$

Полином из теоремы известен как пфаффиан.

Обратная к кососимметричной матрице может существовать только в случае четности ее порядка, и, в случае ее существования, будет кососимметричной.

Теорема 3 [2]. Ранг кососимметричной матрицы $ A_{} $ равен наивысшему порядку отличных от нуля ведущих миноров этой матрицы, т.е. миноров вида

$$
Aleft(
begin{array}{lll}
alpha_1 & dots & alpha_k \
alpha_1 & dots & alpha_k
end{array}
right) =
left|
begin{array}{lll}
a_{alpha_1 alpha_1} & dots & a_{alpha_1 alpha_k} \
dots & & dots \
a_{alpha_k alpha_1} & dots & a_{alpha_k alpha_k}
end{array}
right|,
$$
стоящих на пересечении строк и столбцов матрицы с одинаковыми номерами²⁾.

Ранг кососимметричной матрицы — четное число.

Собственные числа

Теорема 4. Характеристический полином $ det (A_{}-lambda E) $ вещественной кососимметричной матрицы $ A_{} $ не имеет вещественных корней, кроме, возможно, $ lambda_{}=0 $.

Доказательство. Сначала проведем вычислительные эксперименты:
$$
left| begin{array}{ccc}
-lambda & a_{12} & a_{13} \
-a_{12} & -lambda & a_{23} \
-a_{13} & -a_{23} & -lambda
end{array}
right|=-lambda(lambda^2+a_{12}^2+a_{13}^2+a_{23}^2) ;quad
$$
$$
left| begin{array}{cccc}
-lambda & a_{12} & a_{13} & a_{14} \
-a_{12} & -lambda & a_{23} & a_{24} \
-a_{13} & -a_{23} & -lambda & a_{34} \
-a_{14} & -a_{24} & -a_{34} & -lambda
end{array}
right|=
lambda^4+(a_{12}^2+a_{13}^2+a_{14}^2 +a_{23}^2+a_{24}^2+a_{34}^2)lambda^2+
(a_{12}a_{34}-a_{13}a_{24}+a_{14}a_{23})^2 ;
$$
для кососимметричной матрицы $ A_{} $ порядка $ 5_{} $:
$$
det (A-lambda E)=-lambda bigg(lambda^4 + lambda^2 sum_{1le j < kle 5} a_{jk}^2+
$$
$$
+underbrace{left| begin{array}{cccc}
0 & a_{12} & a_{13} & a_{14} \
-a_{12} & 0 & a_{23} & a_{24} \
-a_{13} & -a_{23} & 0 & a_{34} \
-a_{14} & -a_{24} & -a_{34} & 0
end{array}
right|}_{(a_{12}a_{34}-a_{13}a_{24}+a_{14}a_{23})^2}+
underbrace{left| begin{array}{cccc}
0 & a_{23} & a_{24} & a_{25} \
-a_{23} & 0 & a_{34} & a_{35} \
-a_{24} & -a_{34} & 0 & a_{45} \
-a_{25} & -a_{35} & -a_{45} & 0
end{array}
right|}_{(a_{23}a_{45}-a_{24}a_{35}+a_{25}a_{34})^2}+
underbrace{left| begin{array}{cccc}
0 & a_{13} & a_{14} & a_{15} \
-a_{13} & 0 & a_{34} & a_{35} \
-a_{14} & -a_{34} & 0 & a_{45} \
-a_{15} & -a_{35} & -a_{45} & 0
end{array}
right|}_{(a_{13}a_{45}-a_{14}a_{35}+a_{15}a_{34})^2}+
$$
$$
+underbrace{left| begin{array}{cccc}
0 & a_{12} & a_{14} & a_{15} \
-a_{12} & 0 & a_{24} & a_{25} \
-a_{14} & -a_{24} & 0 & a_{45} \
-a_{15} & -a_{25} & -a_{45} & 0
end{array}
right|}_{(a_{12}a_{45}-a_{14}a_{25}+a_{15}a_{24})^2}+
underbrace{left| begin{array}{cccc}
0 & a_{12} & a_{13} & a_{15} \
-a_{12} & 0 & a_{23} & a_{25} \
-a_{13} & -a_{23} & 0 & a_{35} \
-a_{15} & -a_{25} & -a_{35} & 0
end{array}
right|}_{(a_{12}a_{35}-a_{13}a_{25}+a_{15}a_{23})^2}
bigg) .
$$
Видим, что характеристические полиномы являются четными или нечетными функциями от $ lambda_{} $ в
зависимости от четности порядка матрицы $ n_{} $. Кроме того, их коэффициенты всегда одного знака. Такие полиномы не могут иметь вещественных корней, отличных от $ lambda_{} = 0 $.

Для доказательства общего случая следует воспользоваться формулой представления характеристического полинома через миноры матрицы $ A_{} $. Коэффициент при $ lambda^{n-k} $ будет равен
$$
(-1)^{n-k}
sum_{1le j_1< j_2 < dots < j_kle n} left|begin{array}{llll}
a_{j_1j_1}& a_{j_1j_2} & dots & a_{j_1j_k}\
a_{j_2j_1}& a_{j_2j_2} & dots & a_{j_2j_k}\
vdots & & & vdots \
a_{j_kj_1}& a_{j_kj_2} & dots & a_{j_kj_k}
end{array}right|
$$
и каждый минор под знаком суммы будет кососимметричным. На основании теоремы 2 он будет равен нулю при $ k_{} $ нечетном, и он будет положительным при $ k_{} $ четном.

♦

Теорема 5. Все ненулевые собственные числа кососимметричной матрицы — чисто мнимые, т.е. спектр матрицы, помимо, возможно, нулевых собственных чисел, состоит из пар

$$ pm beta_1 mathbf i, pm beta_2 mathbf i,dots quad npu quad {beta_1,beta_2 dots } subset mathbb R setminus {0} , .
$$

Пример [3]. Характеристический полином матрицы

$$
left(
begin{array}{rrrcrr}
0 & a & 0 & dots & 0 & 0 \
-a & 0 & a & dots & 0 & 0 \
0 & -a & 0 & dots & 0 & 0 \
vdots & & & ddots & & vdots \
0 & 0 & 0 & dots & 0 & a \
0 & 0 & 0 & dots & -a & 0
end{array}
right)_{ntimes n}
$$
равен
$$(-1)^n left(lambda^n+C_{n-1}^1a^2lambda^{n-2}+C_{n-2}^2a^4lambda^{n-4}+C_{n-3}^3a^6lambda^{n-6}+dots right) . $$
При $ a=1 $ и $ lambda=-1 $ из этой формулы и альтернативного способа вычисления трехдиагонального определителя следует формула, связывающая биномиальные коэффициенты с числами Фибоначчи:
$$ sum_{j=0}^{lfloor n/2 rfloor} C_{n-j}^j = C_n^0+C_{n-1}^1+C_{n-2}^2+dots
= F_n .
$$
Здесь $ lfloor rfloor $ — целая часть числа.

Связь с ортогональной матрицей

Теорема 6. Экспоненциал кососимметричной матрицы является ортогональной матрицей.

Доказательство. Для кососимметричной матрицы $ A $:
$$left(exp(A) right)^{top}= left(E+A+frac{A^2}{2}+ frac{A^3}{3!}+dots right)^{top}= $$
$$=E-A+frac{A^2}{2}- frac{A^3}{3!}+dots = exp(-A)= (exp ( A))^{-1} , . $$

♦

Линейное пространство матриц

Линейное пространство матриц порядка $ n $ раскладывается в прямую сумму подпространств симметричных и кососимметричных матриц, или, что то же, произвольная матрица $ A_{ntimes n} $ представляется в виде суммы симметричной и кососимметричной матриц, причем такое представление однозначно:
$$ A= frac{1}{2}(A+A^{top}) +frac{1}{2}(A-A^{top}) , . $$

Если в пространстве квадратных матриц задать скалярное произведение формулой
$$
langle A,B rangle = operatorname{Sp} left(Acdot B^{top} right) = sum_{j,k=1}^n a_{jk}b_{jk} ,
$$
то подпространство кососимметричных матриц является ортогональным дополнением подпространства симметричных матриц. В евклидовой норме расстояние от матрицы $ A $ до ближайшей к ней симметричной матрицы равно
$$ | (A-A^{top})/2 | , . $$

Задачи

Источники

[1]. Нетто Е. Начала теорiи опредѣлителей. Mathesis. Одесса. 1912, cc.86-90

[2]. Проскуряков И.В. Сборник задач по линейной алгебре. М.Наука. 1974.

[3]. Чезаро Э. Элементарный учебник алгебраического анализа и исчисления
бесконечно малых. Часть I. М.-Л., ОНТИ, 1936, сс.47-50

Источник

Элементы называются Линейно независимыми, если из равенства следует, что В противном случае элементы Линейно зависимы.

Если в линейном пространстве 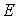найдено 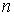линейно независимых элементов, а любые уже линейно зависимы, то число 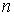называется Размерностью пространства 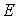и обозначается , т. е. .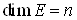

Совокупность элементов из 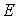называется Базисом линейного пространства 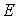, если любой элемент единственным образом представим в виде Числа называются Координатами элемента в базисе

Пример 5. Пусть – линейное пространство, элементами которого являются квадратные матрицы 2-го порядка.

Тогда матрицы образуют базис в . Так, если то т. е. в базисе координатами элемента являются

Пример 6. Рассмотрим линейное -мерное пространство, элементами которого являются упорядоченные наборы вещественных чисел

Которые мы будем называть Векторами, а числа – их Координатами в некотором заданном базисе. Если рассмотренное линейное пространство вещественно, то оно называется Арифметическим векторным пространством и обозначается . Очевидно, векторы …, Образуют базис в .

Для каждого можно составить матрицу-столбец размера

Которую будем называть Вектор-столбец. Такие векторы-столбцы образуют линейное пространство, которое также называется арифметическим векторным пространством. Ортонормированный базис в нём образуют векторы-столбцы

Объектом дальнейших наших исследований будут арифметические векторные пространства .

Задания для решения. 19.1.Проверить, что векторы образуют базис трехмерного пространства; найти координаты вектора в этом базисе:

19.1.Проверить, что векторы образуют базис трехмерного пространства; найти координаты вектора в этом базисе:

19.2.Доказать, что матрицы образуют базис пространства квадратных матриц второго порядка с действительными элементами, и найти координаты матрицы в этом базисе.

19.3. Исследовать на линейную зависимость систему векторов , , .

19.4. Доказать, что векторы образуют базис векторного пространства . Разложить вектор по этому базису, если .

Домашнее задание

19.5. Доказать, что система векторов линейно зависима , , , .

19.6.Доказать, что векторы образуют базис в (если известно, что размерность равна четырем) и разложить вектор по этому базису.

Ответы

19.1. а) , б) (0, -5, 4). 19.2. а) (-2, -1, -2, 6), б) (-5, 4, 3, 11). 19.3. система линейно зависима. 19.4. . 19.6.

Линейные Пространства (Задачи для подготовки к экзамену — Решение), страница 3

Файл «Линейные Пространства» внутри архива находится в папке «Прорешанные задачи для подготовки к экзамену». Документ из архива «Задачи для подготовки к экзамену — Решение», который расположен в категории » «. Всё это находится в предмете «линейная алгебра и аналитическая геометрия» из раздела «», которые можно найти в файловом архиве РТУ МИРЭА. Не смотря на прямую связь этого архива с РТУ МИРЭА, его также можно найти и в других разделах. Архив можно найти в разделе «к экзамену/зачёту», в предмете «алгебра и геометрия» в общих файлах.

Онлайн просмотр документа «Линейные Пространства»

Текст 3 страницы из документа «Линейные Пространства»

(все матрицы образуют динейно независимую систему).

При этом каждая матрица данного подпространства может быть представлена в виде:

Отсюда следует, что размерность подпространства L равна 2 и вкачестве его базиса можно взять матрицы .

Для дополнения этого базиса до базиса всего пространства М₂₃ можно выбрать матрицы

(все матрицы образуют динейно независимую систему).

Проверяем линейность данного множества L матриц:

Все условия выполнены – L является линейным пространством.

Если матрица антиперестановочная с данной матрицей , то:

т.е. матрица Х может быть представлена в виде:

Отсюда следует, что размерность подпространства L равна 2 и вкачестве его базиса можно взять матрицы .

2.23. Образуют ли матрицы базис в пространстве матриц М₂₂?

Запишем данные матрицы в каноническом базисе, получим векторы

найдем ранг этой системы векторов:

Ранг системы векторов равен 3, следовательно, данные матрицы не образуют базис в пространстве матриц М₂₂

2.24. Найти размерность и какой-нибудь базис линейной оболочки системы матриц

Запишем данные матрицы в каноническом базисе, получим векторы

найдем ранг этой системы векторов:

Ранг системы векторов равен 3, следовательно:

1) размерность данной системы матриц равна 3,

2) в качестве базиса их линейной оболочки можно взять первые три матрицы, т.е. (Е₁, Е₂, Е₃).

1) множество всех симметрических квадратных матриц порядка n (A T = A).

2) множество всех кососимметрических квадратных матриц порядка n (A T = -A).

3) множество всех квадратных вырожденных матриц порядка n (detA = 0).

1) При умножении любой симметрической квадратной матрицы порядка n (A T = A) на любое число получается также симметрическая квадратная матрица порядка n , сумма двух симметрических квадратных матриц порядка n также является симметрической квадратной матрицей порядка n. Следовательно, множество всех симметрических квадратных матриц порядка n является подпространством пространства M_nn.

2) При умножении любой кососимметрической квадратной матрицы порядка n (A T =-A) на любое число получается также симметрическая квадратная матрица порядка n , сумма двух кососимметрических квадратных матриц порядка n также является кососимметрической квадратной матрицей порядка n. Следовательно, множество всех кососимметрических квадратных матриц порядка n является подпространством пространства M_nn.