Как найти базис системы многочленов

В
линейном
пространстве наибольший
интерес представляют системы
векторов, в
виде линейной
комбинации которых
можно представить любой вектор, причем
единственным образом. Если зафиксировать
такую систему векторов, то любой вектор
можно будет однозначно представить
набором чисел, являющихся коэффициентами
соответствующей
линейной
комбинации, а
всевозможные векторные соотношения
превратить в соотношения числовые.

Этот
подход применялся уже в аналитической
геометрии. В пространстве
векторов на плоскости любые два
неколлинеарных вектора образуют базис,
так как через такую пару векторов любой
вектор плоскости выражается однозначно
в виде линейной комбинации. Аналогично
в(множестве векторов в пространстве)
базис образуют любые три некомпланарных
вектора. Для матриц использовалось
понятие базисных строк и базисных
столбцов. По теореме о базисном миноре
базисные строки (столбцы) линейно
независимы, а любая строка (столбец)
матрицы является линейной комбинацией
базисных строк (столбцов).

Определение
1.3. Базисом
линейного пространства
называют
любую упорядоченную систему векторов,
для которой выполнены два условия:

1) эта
система
векторов линейно независима,

2) каждый
вектор в линейном пространстве может
быть представлен в виде линейной
комбинации векторов этой системы.

Пусть

—
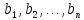
базис в
.
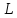Определение 1.3 говорит о том, что любой
векторможет быть записан следующим образом:

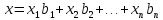
Такую
запись называют разложением
вектора х
по
базису
.

Данное
нами определение базиса согласовывается
с понятием базиса в пространстве
свободных
векторов в
,
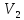или
.
Например, вбазисом была названа любая тройка
некомпланарных векторов. Такая тройка
векторов является линейно независимой,
так как представление одного ее вектора
в виде линейной комбинации двух других
равносильна компланарности трех
векторов. Но, кроме того, из курса
векторной алгебры мы знаем, что любой
вектор в пространстве можно выразить
через произвольные три некомпланараных
вектора в виде
их
линейной
комбинации. Три компланарных вектора
не могут быть базисом в
,
так как любая линейная комбинация таких
векторов даст вектор, им компланарный.

Теорема
1.2 (о единственности разложения). В
линейном пространстве разложение любого
вектора по данному базису единственно.

Выберем
в линейном пространстве

произвольный
базис

и
предположим, что вектор х
имеет
в этом базисе два разложения

Воспользуемся
тем, что аксиомы
линейного пространства позволяют
преобразовывать линейные комбинации
так же, как и обычные алгебраические
выражения. Вычитая записанные равенства
почленно, получим

Так
как базис – это линейно независимая
система векторов, ее линейная комбинация
равна 0,
лишь,
если она тривиальная
(см.
определение 1.2). Значит, все коэффициенты
этой линейной комбинации равны нулю:
.
Таким образом,и
два разложения векторах
в
базисе
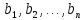совпадают.

Замечание
1.3. Условие
линейной независимости векторов базиса
означает, что нулевой
вектор имеет
в этом базисе единственное разложение,
а именно тривиальное: все коэффициенты
этого разложения равны нулю. Из
доказательства теоремы 1.2 следует, что
из единственности разложения нулевого
вектора по данной системе векторов
вытекает единственность разложения
любого другого вектора.

Согласно
определению 1.3, базис является упорядоченной
системой векторов. Это значит, что,
изменив порядок векторов в системе, мы
получим другой базис. Порядок векторов
в базисе фиксируют для того, чтобы задать
определенный порядок коэффициентов
разложения произвольного вектора. Это
позволяет заменить линейную комбинацию,
представляющую вектор, упорядоченным
набором ее коэффициентов и тем самым
упростить запись. Порядок векторов в
базисе определяется их нумерацией.

Определение
1.4. Коэффициенты
разложения вектора по базису линейного
пространства, записанные в соответствии
с порядком векторов в базисе, называют
координатами
вектора в этом
базисе.

Пример
1.8. В
линейном пространстве

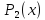
многочленов
переменного

степени
не выше 2 (см. пример 1.1) элементы

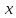
и
линейно
независимы: их линейная комбинация
есть многочлен, который равен нулю
(нулевому многочлену) лишь при.
В то же время пара этих элементов не
образует базиса. Действительно, многочлен
1 нулевой степени, являющийся элементом,
нельзя
представить в виде линейной комбинации
многочленов

и
.Дело
в том, что линейная комбинация

многочленов

и
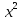есть
либо многочлен второй степени (при
),
либо многочлен первой степени(,
),
либо нулевой многочлен().
Значит, равенство

двух
многочленов невозможно ни при каких
значениях коэффициентов.

В
то же время три многочлена 1,

и
образуют
базис линейного пространства
.
Докажем это.

Во-первых,
система многочленов 1,

и
линейно
независима. Составим их линейную
комбинацию с произвольными коэффициентами

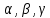
и
приравняем нулю:
.
Это равенство есть равенство двух
многочленов, и оно возможно только в
случае, когда коэффициенты этих двух
многочленов совпадают. Значит,.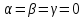

Во-вторых,
через многочлены 1,

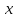
и

можно
выразить любой многочлен второй степени,
т.е. любой элемент линейного пространства

можно
представить в виде линейной комбинации
указанных трех элементов.

Итак,
система трех многочленов 1,

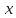
и

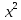
линейно
независима, а любой элемент линейного
пространства


является
линейной комбинацией указанной системы.
Согласно определению 1.3, система
многочленов 1,

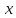
и

есть
базис в
.

Пример
1.10.
В
линейном
арифметическом пространстве
векторы

образуют
базис
,
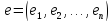так как они линейно независимы (см.
пример 1.5) и любой вектор
представим
в виде

Такой
базис (1.5) в пространстве
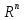называютстандартным.
Отметим,
что запись элементов арифметического
пространства в виде столбца не противоречит
определению арифметического пространства,
понимаемого как множество упорядоченных
совокупностей чисел. Порядок же элементов
можно указывать как при помощи записи
в строку, так и при помощи записи в
столбец.

Пример
1.11.
Покажем,
что в
система векторов

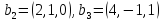
образует
базис и найдем в этом базисе координаты
вектора

Для
того чтобы доказать, что система векторов
,,

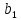образует базис, надо убедиться в линейной
независимости этих векторов и в том,
что любой вектор
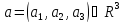является их линейной комбинацией.

В
стандартном базисе е в
векторыимеют следующие столбцы координат:

Из
стобцов координат векторов
составим матрицу

и
рассмотрим квадратную систему линейных
алгебраических уравнений (СЛАУ)
,Так как,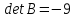
то матрицаневырожденная, ее ранг равен 3 и все ее
столбцы являются базисными. Поэтому,
во-первых, согласно теореме о базисном
миноре, эти столбцы линейно независимы,
значит, СЛАУ
при
любом столбце

правых
частей имеет решение

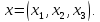
В
частности, решив СЛАУ
,
которая в координатной форме имеет вид

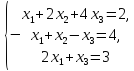
находим
координаты вектора
в базисе:

.

Соседние файлы в папке Геометрия

• #
• #
• #

В линейном пространстве наибольший интерес представляют системы векторов, в виде линейной комбинации которых можно представить любой вектор, причем единственным образом. Если зафиксировать такую систему векторов, то любой вектор можно будет однозначно представить набором чисел, являющихся коэффициентами соответствующей линейной комбинации, а всевозможные векторные соотношения превратить в соотношения числовые.

Этот подход применялся уже в аналитической геометрии [III]. В пространстве V₂ векторов на плоскости любые два не- коллинеарных вектора образуют базис, так как через такую пару векторов любой вектор плоскости выражается однозначно в виде линейной комбинации [III]. Аналогично в V₃ (множестве векторов в пространстве) базис образуют любые три некомпланарных вектора. Для матриц использовалось понятие базисных строк и базисных столбцов. По теореме о базисном миноре базисные строки (столбцы) линейно независимы, а любая строка (столбец) матрицы является линейной комбинацией базисных строк (столбцов) [III].

Определение 1.3. Базисом линейного пространства L называют любую упорядоченную систему векторов, для которой выполнены два условия:

1) эта система векторов линейно независима;

2) каждый вектор в линейном пространстве может быть представлен в виде линейной комбинации векторов этой системы.

Пусть b₁, …, b_n – базис в L. Определение 1.3 говорит о том, что любой вектор х ∈ L может быть записан следующим образом:

х = x₁b₁ + … + x_nb_n.

Такую запись называют разложением вектора х по базису b₁, …, b_n.

Данное нами определение базиса согласовывается с понятием базиса в пространстве свободных векторов в V₁, V₂ или V₃ [III]. Например, в V₃ базисом была названа любая тройка некомпланарных векторов. Такая тройка векторов является линейно независимой, так как представление одного ее вектора в виде линейной комбинации двух других равносильна компланарности трех векторов. Но, кроме того, из курса векторной алгебры [III] мы знаем, что любой вектор в пространстве можно выразить через произвольные три некомпланараных вектора в виде их линейной комбинации. Три компланарных вектора не могут быть базисом в V₃, так как любая линейная комбинация таких векторов даст вектор, им компланарный.

Теорема 1.2 (о единственности разложения). В линейном пространстве разложение любого вектора по данному базису единственно.

Выберем в линейном пространстве L произвольный базис b₁, …, b_n и предположим, что вектор х имеет в этом базисе два разложения

x = x₁b₁ + … + x_nb_n,

x = x’₁b₁ + … + x’_nb_n.

Воспользуемся тем, что аксиомы линейного пространства позволяют преобразовывать линейные комбинации так же, как и обычные алгебраические выражения. Вычитая записанные равенства почленно, получим

(x₁ – x’₁)b₁ +… + (х_n – х’_n)b_n = 0.

Так как базис – это линейно независимая система векторов, ее линейная комбинация равна 0, лишь если она тривиальная (см. определение 1.2). Значит, все коэффициенты этой линейной комбинации равны нулю: х₁ – х’₁ = 0,…, х_n – х’_n = 0. Таким образом, х₁ = x’₁, …, х_n = х’_n и два разложения вектора х в базисе b₁, …, b_n совпадают. ►

Замечание 1.3. Условие линейной независимости векторов базиса означает, что нулевой вектор имеет в этом базисе единственное разложение, а именно тривиальное: все коэффициенты этого разложения равны нулю. Из доказательства теоремы 1.2 следует, что из единственности разложения нулевого вектора по данной системе векторов вытекает единственность разложения любого другого вектора. #

Согласно определению 1.3, базис является упорядоченной системой векторов. Это значит, что, изменив порядок векторов в системе, мы получим другой базис. Порядок векторов в базисе фиксируют для того, чтобы задать определенный порядок коэффициентов разложения произвольного вектора. Это позволяет заменить линейную комбинацию, представляющую вектор, упорядоченным набором ее коэффициентов и тем самым упростить запись. Порядок векторов в базисе определяется их нумерацией.

Определение 1.4. Коэффициенты разложения вектора по оазису линейного пространства, записанные в соответствии с порядком векторов в базисе, называют координатами вектора в этом базисе.

Пример 1.8. В линейном пространстве К₂[х] многочленов переменного х степени не выше 2 (см. пример 1.1) элементы х и х² линейно независимы: их линейная комбинация ах + рх2 есть многочлен, который равен нулю (нулевому многочлену) лишь при α = β = 0. В то же время пара этих элементов не образует базиса. Действительно, многочлен 1 нулевой степени, являющийся элементом К₂[х], нельзя представить в виде линейной комбинации многочленов х и х² Дело в том, что линейная комбинация αх + βх² многочленов х и х² есть либо многочлен второй степени (при β ≠ 0), либо многочлен первой степени (α ≠ 0, β = 0), либо нулевой многочлен (а = β = 0). Значит, равенство 1 = αх + βх² двух многочленов невозможно ни при каких значениях коэффициентов.

В то же время три многочлена 1, х, х² образуют базис линейного пространства К₂[х]. Докажем это.

Во-первых, система многочленов 1, х, х² линейно независима. Составим их линейную комбинацию с произвольными коэффициентами α, β, γ и приравняем нулю: α • 1 + βх + γх² = 0. Это равенство есть равенство двух многочленов, и оно возможно только в случае, когда коэффициенты этих двух многочленов совпадают. Значит, α = β = γ = 0.

Во-вторых, через многочлены 1, x, х² можно выразить любой многочлен второй степени, т.е. любой элемент линейного пространства К₂[x] можно представить в виде линейной комбинации указанных трех элементов. Возьмем произвольный многочлен

р(х) = α + βx² + γx².

Его запись можно рассматривать как линейную комбинацию многочленов 1,x, х²:

р(х) = α • 1 + βx² + γх²,

причем коэффициенты многочлена в то же время являются коэффициентами линейной комбинации.

Итак, система трех многочленов 1, х, х² линейно независима, а любой элемент линейного пространства К₂[х] является линейной комбинацией указанной системы. Согласно определению 1.3, система многочленов 1, x, х² есть базис в K₂[x]

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ

(это всё же относится к линейным пространствам, поэтому опубликую в раздел “Векторы”)

Для заданной системы векторов:
a) найти ранг и какую-н. базу
b) многочлены, не входящие в базу выразить через векторы базы
c) найти размерность и базис лин. оболочки данной системы векторов
(f_1=3+2t^2+5t^3)
(f_2=3t+5t^2+5t^3)
(f_3=1-3t+3t^2+4t^3)
(f_4=2+6t+4t^2+6t^3)

a)
(begin{pmatrix}
3& 0& 2& 5\
0& 3& 5& 5\
1& 3& 3& 4\
2& 6& 4& 6
end{pmatrix} rightarrow … rightarrowbegin{pmatrix}
1& 0& 0& -2\
0& 1& 0& frac{5}{3}\
0& 0& 1& 1 \ 0& 0& 0& 0
end{pmatrix}rightarrow
begin{pmatrix}
1& 0& 0& -2\
0& 1& 0& frac{5}{3}\
0& 0& 1& 1
end{pmatrix})
3 и 4 строчка л.з.
(f_1, f_2, f_3) – база
или можно (f_1, f_2, f_4) – тоже база, тогда придется (f_3) выражать в задании b)

b) (f_4 = -2f_1+frac{5}{3}f_2+f_3)
Должно быть так, но как проверить? Что-то у меня не сходится.

c) (dim V = dim L(f_1, f_2, f_3) = 3)
базис ((0,1,0)(0,0,1),(1,0,0))

Прошу проверить

You can proceed as in the first answer, or you can try guessing and verifying.

An approach I like is to express the subspace as the null space of some operator. The form of the operator is often fairly clear from the question.

For the first, you are looking for a basis for the set of polynomials of degree 3 or less that satisfy the given condition. You know that $dim P^3 = 4$, and the condition expresses one scalar constraint, so intuitively we expect that the dimension of $W$ will be three.

If we define the linear operator $L:P^3 to mathbb{R}$ by $Lp = p(2)-p(-2)$, we see that $W = ker L$ and $dim {cal R}L = 1$ from which we confirm that $dim ker L = 4 -1 = 3$.

The even members (that is, the polynomials $x mapsto 1$, $x mapsto x^2$) of the basis you mentioned clearly lie in this space, so we need just one more element to form a basis. Try some combination $x mapsto x+ax^3$, for this to satisfy the condition we need $2+8a = -2 – 8a$ or $a=-{1 over 4}$. Hence the functions $x mapsto 1$, $x mapsto x^2$ and $x mapsto x – {1 over 4} x^3$ from a basis for $W$.

For the second, let $H:mathbb{P}^3 to mathbb{R}^2$ be defined by $H(p) = (p(-1), p(1))$. We see that $W = ker H$. Since $H(x mapsto (x-1)) = (-2,0)$ and $H(x mapsto (x+1)) = (0,2)$, we see that $dim {cal R}H = 2$, and so
$dim W = 4 – 2 = 2$. If a polynomial has roots $1,-1$, then we know that it must have a factor $x^2-1$, so we try that first to get $H(x mapsto x^2-1) = (0,0)$. Similarly we have $H(x mapsto x(x^2-1)) = (0,0)$, so the functions
$x mapsto x^2-1$, $x mapsto x^3-x$ form a basis.

Пусть $%M$% – множество многочленов $%p in mathbb{P}_4$% с вещественными коэффициентами, удовлетворяющими уcловию $%p(t) in M, p(t)vdots (t^2+t+1)$%.
Доказать, что $%M$% – линейное подпространство в $%mathbb{P}_4$%, найти его базис и размерность. Дополнить базси $%M$% до базиса всего пространства $%mathbb{P}_4$%.

Доказательство я сделал, но вот потом у меня возникли сомнения по поводу базиса подпространства, я представил $%(t^2+t+1)$% как систему линейно независимых векторов $%(a, b, c)$%, где $%a=t^2, b=t, c=1$%, тут уже понятно, что размерность будет равна $%3$%, но вот какой выбрать базис? Получается ли так, что я могу выбрать любые три ненулевых вектора, и это будет базисом подпространства?
И потом у меня какие-то очень слабые соображения по поводу дополнения базиса (очень много сомнений), можете, пожалуйста, назвать примерный алгоритм дополнения в этом случае?